Урок Литература и математика
| Вид материала | Урок |
- Урок. Математика 6 класс. «Длина окружности», 95.5kb.
- Использование художественной литературы на уроках физики, 112.22kb.
- Темы вашего учебного проекта, 97.44kb.
- Математика Древнего Востока 18 ноября в Ахтмеской гимназии был проведён открытый интегрированный, 26.41kb.
- 1 Урок. Рисование, 71.24kb.
- Задачи математических олимпиад, задачные комплексы для школьников и студентов, типовые, 60.51kb.
- Урок ( литература математика) по сказочной повести л. Кэрролла «алиса в стране чудес»., 32.33kb.
- Конспект урока с использованием информационно-коммуникационных технологий (икт). Предмет, 156.53kb.
- «Математика. Прикладная математика», 366.03kb.
- Урока Тема, содержание урока, 532.36kb.
Интегрированный урок
Литература и математика
«А. С. Пушкин и математика»
8 класс
Нельзя быть математиком, не будучи
в то же время и поэтом в душе
Софья Ковалевская
Вдохновение нужно в геометрии,
как и в поэзии
А. С. Пушкин
Методы, используемые на уроке:
- метод группового обучения;
- использование опережающих заданий
- дифференцированное обучение (домашнее задание);
- задания творческого характера
- использование ИКТ на уроке;
- метод взаимо- и самоконтроля;
- самостоятельная работа
Цели:
1Образовательные:
на примере жизни и творчества А. С. Пушкина убедиться в том, что «гениальный человек гениален во всем»
обобщить и расширить сведения о жизни и творчестве А. С. Пушкина
научить применять математические методы анализа поэтического произведения
повторить лингвистический анализ поэтического текста
2. Воспитательные:
- воспитание любви к русской речи, поэзии и математике,
- воспитание сознательной дисциплины,
- формирование навыков контроля и самоконтроля,
- активизация познавательной деятельности в коллективе и формирование навыков сотрудничества в решении поисковых задач.
3. Развивающие:
- развитие логически излагать свои мысли, используя литературный язык;
- развитие умения аргументировать, доказывать:
- развитие умения слушать
- развитие умения применять полученные знания в нестандартных ситуациях;
- развитие умения выделять главное, сравнивать, обобщать;
- развитие абстрактного и наглядно-образного мышления.
Оборудование: презентация «А. С. Пушкин и математика».
Структура урока:
1. Организационный момент.(5мин)
2. Этап проверки заданий. (15 мин)
3. Этап творческих заданий (15 мин)
4. Рефлексия урока.(7 мин)
5. Домашнее задание.(3мин)
Ход урока.
1. Организационный момент.
Взаимное приветствие учителя и учащихся.
Сообщение темы урока, плана работы на уроке
2 Этап проверки домашнего задания. Работа в группах
Учитель Мир Пушкина огромен и прекрасен. Это многочисленные россыпи стихотворений и поэм, замечательные повести и сказки, трагедии и драмы. Пушкин писал во многих жанрах. Оды и послания, сонеты и элегии, поэмы и сказки, роман и повесть в стихах, маленькие трагедии, письма, дневники, исторические исследования, автобиографические записки - всё это писатель нам оставил в наследство, из которого выросла и развивалась великая русская литература. Ведь волновало Пушкина всё: и античность, и искусство, и история родины. Александр Сергеевич был больше, чем поэт. Это был историк, философ, политик, человек, являющий собой эпоху начала девятнадцатого века.
Учитель: В обществе можно выделить два основных направления общей культуры - технократическое и гуманитарное.
Расцвет гения Пушкина совпал по времени с самыми значительными событиями в физике и технике. В частности, в 1820 году А. Ампером детально изучено магнитное действие тока; в 1826 году - Лобачевский создал неевклидову геометрию; в 1831 году - М. Фарадей открыл явление электромагнитной индукции; в 1834 году - Б. Якоби сконструировал электродвигатель постоянного тока; с 1835 года улицы Петербурга стали освещаться газовыми фонарями; в 1837 году пущена в эксплуатацию железная дорога между Петербургом и Царским селом.
Учитель: Хорошо известно, что Александру Сергеевичу математика не давалась с детства, и поэтому он её не любил. По словам сестры Пушкина Павлищевой О.С., «арифметика казалась для него недоступною и он часто над первыми четырьмя правилами, особенно над делением, заливался горькими слезами».
Лицейский друг Пушкина Пущин И.И. вспоминал впоследствии, что «…все профессора смотрели с благоговением на растущий талант Пушкина. В математическом классе вызвал его раз Карцов к доске и задал алгебраическую задачу. Пушкин долго переминался с ноги на ногу, и всё писал молча какие-то формулы. Карцов спросил его, наконец: «Что ж вышло? Чему равняется икс?» Пушкин, улыбаясь, ответил: нулю! «Хорошо! У вас, Пушкин, в моём классе всё кончается нулём. Садитесь на своё место и пишите стихи».
Учитель: Предлагаем решить задачу
1.Как называется самое раннее дошедшее до нас поэтическое произведение Пушкина-лицеиста. В каком году оно было написано?
Подсказка:
Год можно узнать, если найти значение выражения (a-2)× 100+(2× b-1), где а – количество поэм(20), написанных А.С. Пушкиным, b – количество его сказок(7).
В названии стихотворения есть женское имя, номер первой буквы имени в русском алфавите равен количеству строк, уменьшенному на 6, в стихотворении «К Чаадаеву» “Любви, надежды, тихой славы …”.
Ответ: стихотворение «К Наталье», год – 1813.
2. В каком году написано стихотворение «Няне» А.С. Пушкина?
Подсказка: Каждая группа найдет цифру из этой даты.
| 1 | Р 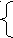 ешить систему ешить системуу=0, у=х-1. |
| 8 | Выполните действие 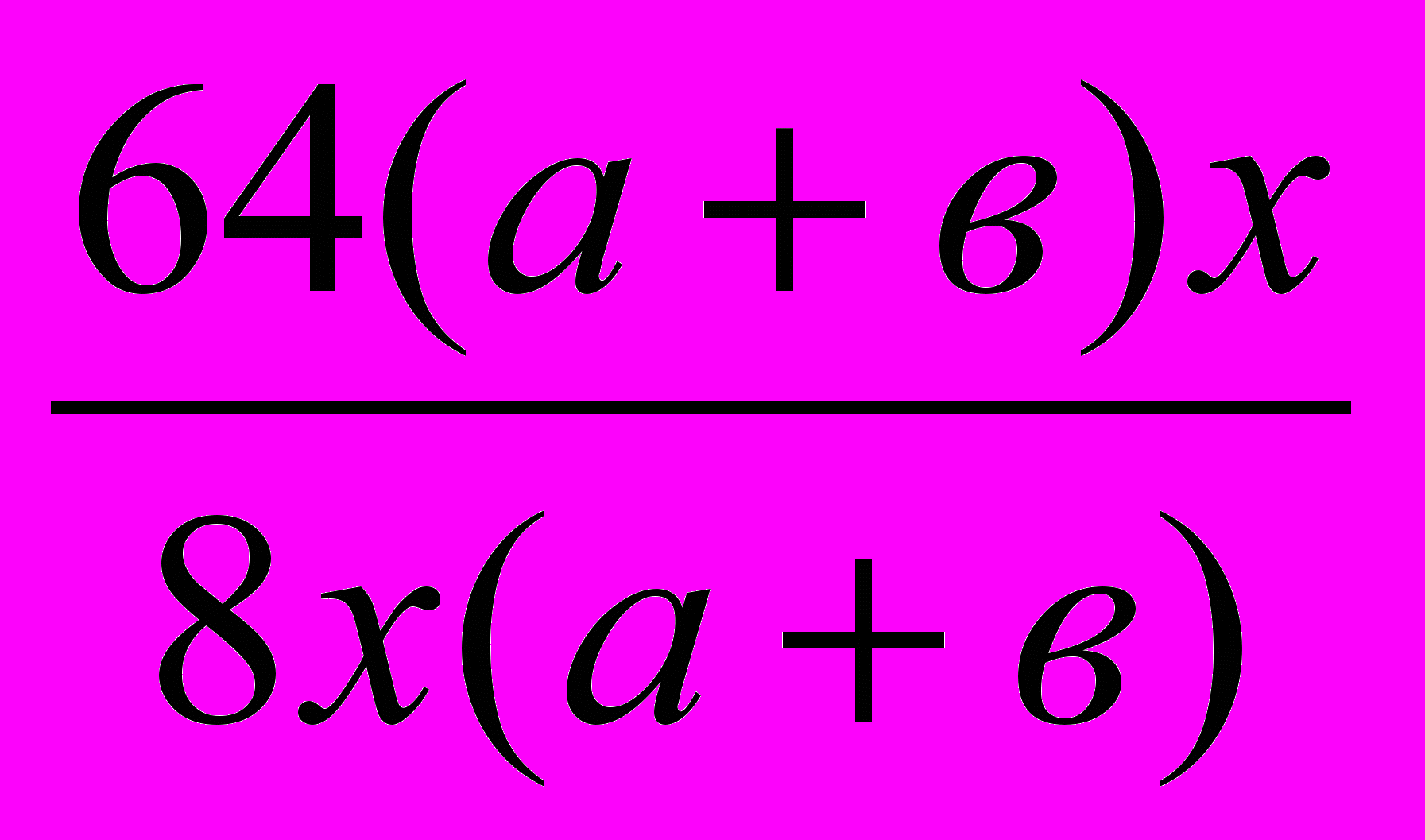 . . |
| 2 | Найдите значение выражения а+3в, при а=11, в=-3. |
| 6 | Решите уравнение 2х+3=15. |
Ответ: 1826 год.
Учитель: Кажется, что Пушкин неприязненно относился к математике.
На самом деле это не верно, но попробуем доказать это. Каждая группа подготовила свое доказательство.
Работа по группам:
Первая группа
В 1936 году А. С. Пушкин издавал журнал «Современник», там он напечатал статью князя П. Б. Козловского по теории вероятностей «О надежде». П.Б. Козловский написал математические статьи для «Современника» по заказу Пушкина.
Он приобщается к обсуждению научных проблем, поднимавшихся на страницах литературных журналов. Поэт общался с выдающимся учёным того времени, членом-корреспондентом Петербургской Академии по изящным наукам, создателем первого в мире телеграфа – П.Л. Шиллингом, с которым Пушкин познакомился в 1818 году. Именно у Шиллинга черпал Александр Сергеевич самую свежую информацию о технических новшествах, и именно это общение привело поэта к новому пониманию роли науки в жизни общества в целом.
Вторая группа
В то время среди писателей существовала мода на математику: А.С. Грибоедов в 1826 году просил прислать ему учебник по дифференциальному исчислению, а Гоголь в 1827 году не только выписал «Ручную математическую энциклопедию» Перевощикова, но даже изучал её.
В 1821 год в стихотворении «Чаадаеву» Пушкин писал:
В уединении мой своенравный гений
Познал и тихий труд, и жажду размышлений.
Владею днём моим; с порядком дружен ум;
Учусь удерживать вниманье долгих дум;
Ищу вознаградить в объятиях свободы
Мятежной младостью утраченные годы
И в просвещении стать с веком наравне…
А.С. Пушкин стремился «стать с веком наравне» даже по отношению к математике.
Третья группа
Хранящаяся в музее-квартире А.С. Пушкина его библиотека, содержащая более четырёх тысяч томов, включает в себя немало книг по естественнонаучной тематике: философские труды Платона, Канта, работы Паскаля, сочинения Лейбница по математическому анализу, труды Гершеля по астрономии, исследования по физике и механике. Также в библиотеке поэта имелись два сочинения по теории вероятностей, одно из которых представляет собой знаменитый труд великого французского математика и механика Лапласа (1749 – 1827) «Опыт философии теории вероятностей», вышедшей в Париже в 1825 году.
Четвертая группа
А. С. Пушкин пытался предсказать отдаленное будущее России:
Когда благому просвещенью
Отдвинем более границ,
Со временем (по расчисленью
Философических таблиц,
Лет через пятьсот) дороги, верно,
У нас изменятся безмерно:
Шоссе Россию здесь и тут,
Соединив, пересекут.
Мосты чугунные чрез воды
Шагнут широкою дугой,
Раздвинем горы под водой,
Пророем дерзостные своды,
И заведёт крещёный мир
На каждой станции трактир.
«Философическими таблицами» Пушкин назвал книгу французского математика, инженера-караблестроителя и статиста Шарля Дюпена, изданную в 1827 году.
Пятая группа
Одним из современников Пушкина был создатель новой геометрии, величайший русский математик Н.И. Лобачевский (1792 – 1856). Когда Пушкин высказал в 1827 году мысль о том, что «вдохновение в поэзии нужно, как и в геометрии», Лобачевский уже сделал доклад о своей воображаемой геометрии. Это событие произошло 24 февраля 1826 года.
Пушкин имел достаточно чёткие знания о том, как соотносятся движения Земли и Солнца и что представляют собой «своды неба».
Шестая группа
Интерес великого поэта к научным достижениям привёл его к пониманию необходимости познания природных явлений и их физических закономерностей. Он признавал, что всесторонние знания и опыт двигают науку вперед, о чём и написал в 1829 году:
О, сколько нам открытий чудных
Готовит просвещенья дух
И опыт, сын ошибок трудных,
И гений, парадоксов друг…
Учитель Но, конечно, самым главным в жизни Пушкина является его поэтическое творчество Что такое поэзия? Это красивые слова и рифмующиеся строки, это умение красиво говорить. Именно в стихах легче высказать свои мысли, чувства так, чтобы они тронули самые сокровенные струны души. Именно в стихах любое признание ещё прекраснее и милее. Некоторые полагают, что содержание стихов то же, что и прозы, что поэзия отличается от неё лишь «красивой формой». Это глубокое заблуждение.
Проделаем простой опыт – попробуем выразить прозой, изменив лишь порядок слов, содержание знаменитого стихотворения: «Я вас любил, может быть, в моей душе любовь ещё не совсем угасла, но пусть она больше вас не тревожит. Я не хочу ничем вас печалить». Слова те же, что и у Пушкина, но содержание их очень обеднено. Исчезло деление на стихотворные строчки, ритмическое движение, рифма – и потускнели нежность, любовь, доброта, деликатность, уважение, возвышенное благородство чувств; вместо выражения переживаний остался сухой их перечень. И только Пушкин смог поставить их в таком порядке, что мы и не представляем себе, как это может быть по-другому.
Учитель:Уже многие годы произведения А.С. Пушкина анализируются с самых разных точек зрения: литературной, художественной, исторической, лингвистической и так далее.
(Лингвистический анализ текста)
Учитель: Но существует «математический анализ» произведений поэта.
Многое в структуре произведений поэзии роднит этот вид искусства с музыкой. Чёткий ритм, закономерное чередование ударных и безударных слогов. Каждый стих обладает своей музыкальной формой – своей ритмикой и мелодией. В строении стихотворений проявятся некоторые черты музыкальных композиций, закономерности музыкальной гармонии, а следовательно, и золотая пропорция, и числа Фибоначчи.
. С поэзии А.С.Пушкина мы и начнем поиски золотой пропорции и, так называемых, чисел Фибоначчи – мерила гармонии и красоты.
ЗОЛОТОЕ СЕЧЕНИЕ (пропорция) - пропорция, которой древние маги приписывали особые свойства. Если произвести деление объекта на две неравные части так, что меньшая будет относиться к большей, как большая ко всему объекту, возникнет так называемое золотое сечение. Упрощенно такое соотношение можно представить как 2/3 или 3/5. Замечено, что объекты, содержащие в себе "золотое сечение", воспринимаются людьми как наиболее гармоничные. "Золотое сечение" обнаружено в египетских пирамидах, многих произведениях искусства - скульптурах, картинах, и даже кинофильмах. Большинство художников использовали пропорции "золотого сечения" интуитивно.
В повести «Пиковая дама» (издания 1978 г.) 853 строки. В каждой из шести глав золотая пропорция приходится на кульминационный момент этой главы. Например: третья глава повести описывает усилия Германна попасть в дом старой графини, выведать у нее тайну трех карт. С помощью Лизы он проникает в дом графини, прячется в темном кабинете и ждет ее возвращения. «Он был спокоен; сердце его билось ровно, как у человека, решившегося на что-нибудь опасное, но необходимое. Часы пробили первый и второй час утра, - и он услышал далекий стук кареты. Невольное волнение овладело им. Карета подъехала и остановилась».
Последняя фраза начинает новый отсчет времени для Германна (и для графини). Эта фраза приходится на 131 строку, а всего в ней 212 строк. Разделив 212 на 131, получим золотую пропорцию (212 : 131= 1,618). Это поразительное, фантастически точное, интуитивное владение поэтом законами гармонической композиции.
Совпадение кульминационных моментов в произведениях прозы у А.С. Пушкина с золотой пропорцией удивительно близкое, в пределах одной-трех строк. Чувство гармонии у него было развито необыкновенно, что объективно подтверждает гениальность великого поэта и писателя.
Числа Фибоначчи – элементы числовой последовательности 1; 1; 2; 3; 5; 8; 13; 21; 34; 55;…(ряда Фибоначчи), в которой каждый последующий член равен сумме двух предыдущих, таким образом, последовательность u1, u2, …чисел Фибоначчи задаётся начальными соотношениями u1=u2=1 и рекуррентным соотношением un+1=un-1+un. (Математический энциклопедический словарь).
Поэт явно предпочитает стихотворения, размер которых близок к числам ряда Фибоначчи. Попробуем сгруппировать стихотворения по их размерам, расположенным около чисел Фибоначчи.
Наиболее выдающиеся произведения поэта, шедевры его творчества явно тяготеют к размерам 8, 13, 21 и 34 строки. К ним относятся стихи «В крови горит огонь желаний…», «Я вас любил, любовь еще, быть может…», и, наконец, одно из последних: «Пора, мой друг, пора! Покоя сердце просит…», - все они состоят из восьми строк. В таких замечательных произведениях поэта, как «Сонет», «Поэту», «Мадонна», «Няне» - 13 – 14 строк. По 20 строк в таких известных стихотворениях, как «Храни меня, мой талисман», «Во глубине сибирских руд», «Поэт», « «Я здесь, Инезилья…» и в предсмертном «Я памятник себе воздвиг нерукотворный…».
Числа Фибоначчи не только доминируют в размерах А.С. Пушкина, они определяют во многих случаях и внутреннюю композицию стихотворений: число стихов и число строк в них.
Вывод: Преобладание в анализе стихотворений А.С. Пушкина чисел ряда Фибоначчи никак нельзя признать случайностью, игрой слепой вероятности. Наличие этих чисел выражает одну из фундаментальных закономерностей творческого метода поэта, его эстетические требования, чувство гармонии.
В своих стихах Пушкин уделяет внимание и асимметрии – это непарное число строк, несимметричном расположении кульминационных моментов, Асимметрия придаёт стихам живость, повышает эмоциональное воздействие. А одним из выражений асимметрии является золотая пропорция, подчинение числам Фибоначчи. Сочетание этих двух основ гармонии и порождает удивительное разнообразие художественных форм в поэзии А.С. Пушкина.
Заключение:Гениальный человек гениален во всем. И на самом деле, не столь уж важно, в какой степени знал А.С. Пушкин точные науки. Каждый человек находит в нем и его творчестве что-то свое, близкое и понятное только ему. Даже люди, которые считают себя далекими от поэзии, от романтических переживаний, занятые только сухими расчетами в своем мире формул и чисел, и они найдут множество «открытий чудных» в мире пушкинских произведений. Но самое главное, что и в наше время А.С. Пушкин учит нас искренности чувств, жизнелюбию; ставит перед нами вечные вопросы: какое место в списке ценностей занимают милосердие, доброта, дружба, любовь.
