Организация и методика статистического исследования
| Вид материала | Закон |
СодержаниеViii. непараметрические критерии Критерий итераций (флуктуаций). При альтернативном распределении |
- И. И. Мечникова Кафедра общественного здоровья и здравоохранения утверждаю зав кафедрой,, 128.92kb.
- Семинарских/ практических занятий Тема Статистическое наблюдение Методология организации, 113.64kb.
- Задачи статистики и ее организация в РФ и в зарубежных странах Этапы статистического, 26.55kb.
- Методика использования дисперсионного анализа в оргпроектировании. 23. Методика и организация, 29.83kb.
- Курс. Предмет статистики. Изучение количественной стороны общественных явлений и процессов, 14.22kb.
- План статистического исследования, его содержание, 81.37kb.
- Темы лекционных занятий: Предмет, метод и задачи статистического исследования Современная, 25.16kb.
- Методология статистического исследования влияния уровня и качества жизни населения, 657.92kb.
- Методика исследования с применением качественной методологии 15 Методика количественного, 5301.04kb.
- Инструкция : Бланк исследования: все без бланков исследования Отчет испытуемого, 39.61kb.
VIII. НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ
Непараметрические критерии используются преимущественно в тех случаях, когда изучаемое явление отличается от нормального распределения. С одной стороны, они позволяют оценить характер, тенденцию явления (увеличение, уменьшение, без перемен), хотя, с другой, большинство из них обладает достаточно высокой статистической мощностью (чувствительностью). Особенно эффективно применение непараметрических критериев при малых выборках (« < 30), при изучении качественных признаков. Преимуществом большинства непараметрических критериев является сравнительная простота расчетов.
Основные направления применения непараметрических критериев:
1. Для характеристики одной совокупности:
- критерий итераций (флуктуаций);
- медиана,квартели.
2. Для оценки связи между явлениями:
- коэффициент ранговой корреляции (Спирмена);
- коэффициент корреляции рангов (Кэндела);
- показатель соответствия у} (хи-квадрат).
3. Для оценки различий двух сравниваемых совокупи остей. При этом следует выделять несколько вариантов:
1. Для сравнения количественных признаков:
2.
| Две выборки | Несколько выборок | ||
| А | Б | В | Г |
| независимые | зависимые | независимые | зависимые |
| Критерий Лорда (U) Критерий Вилконсона-Манна-Уитни (U) Критерий Мостселлера | Ранговый критерий Вилконсона (Т) Критерий знаков (Z) | Сравнение выборок по Немени | Критерий Фридмана Критерий Вил-консона-Вилконс |
| Критерий Розенбаума (Q) | Максимум кри | | |
| Критерий Уайта (К) Серийный критерий Вальда-Вольровича (S) | терий для разности пар | | |
| Критерий Колмогорова-Смирнова | | | |
2. Для сравнения качественных признаков:
| ————- Дв< выбо ———А-— | рки | Нескольк Ж: | о выборок |
| независимые Критерий Стьюдента с поправками Йетса Критерий согласия <2) Точный метод Фишера (X2) Критерий Ван-дер-Вардена. (X) | Е зависимые Критерии Макни-Мара | независимые Критерий ()с2) по Р.Руниони | 3 зависимые Критерий Кокрена (Q) |
Характеристика одной совокупности
Критерий итераций (флуктуаций). Применяется когда п>10.
Схема вычисления критерия итераций.
Допустим, необходимо проверить у одного больного содержание альбуминов в плазме крови, для чего было сделано последовательно 10 исследований:
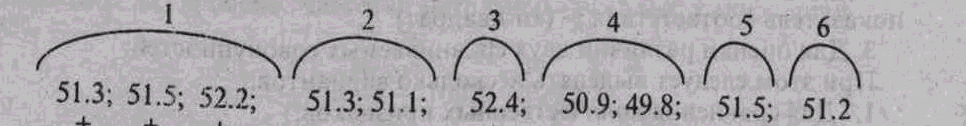
'• - - + - - +
Приведенные данные указывают на колеблемость содержания альбуминов. Необходимо определить характер этих колебаний - существенны или несущественны. Для этого: 1. принимается нулевая гипотеза - колебания содержания альбуминов в плазме крови у больного носят случайный характер.
2. Данные изменения альбумина вновь выписываются по степени возрастания для того, чтобы определить срединное значение результатов исследования (Me).
Определяем место Me -- n\- = 10+1 = 5.6
49.8; 50.9; 51.1; 51.2; 51.3; 51.3; 51.5; 51.5; 52.2; 52.4. Место Me оказалось между величинами 51.3 и 51.3. Чтобы определить размер Me надо получить полусумму измерений, между которыми находится ее место. Me = =(5].3+5].3)/2 = 51.3.
3. В ряду фактически приведенных исследований разность между значением Me и каждым измерением обозначается знаком «+» или «-» Если встречаются величины, равные Me, и допустим первой уже
г •'\
поставлен «+», то второй ставится «-», третьей «+» и т.д. или наоборот.
4. Подсчитываются серии одинаковых знаков. В нашем пример( их 6 (R = 6). Полученный результат сравниваем с табличным. Есл величина R в пределах табличного значения (от-до) - нулевая гипотеза принимается. Если R меньше или больше табличной - нулевая гипотеза отвергается (приложение № 4). Табличное значение R находится на пересечении строки / - число вариант больших по величине чем Me (в нашем примере их 5) и графы Пу - число вариант меньшие чем Me (их тоже 5). Табличное значение R на пересечении чисел 5 рав но 3/9. Рассчитанное значение R = 6 находится в пределах табличного значения R. Следовательно, нулевая гипотеза принимается. Колеба ния измерений альбуминов в плазме крови носят случайный характер и их различия несущественны.
Медиана применяется в случаях, когда неизвестен тип распределе ния либо оно отличается от нормального (а также в случаях, когдг нельзя вычислить среднюю арифметическую). При нечетном числе наблюдений медианой будет являться варианта, расположенная точнс в середине ряда; при четном - ее величина определяется как полусумма двух вариант, расположенных в середине ряда. Порядковый номе]:
медианы в ряду определяется по формуле "±1 (п - общее число на-
2 блюдений).
После определения местоположения медианы каждая из двух половин ряда также может быть разделена пополам путем нахождение квартилей Q (нижней Q„ и верхней (?„). Порядковый номер квартиле? определяется по формулам:
. п+\ 3(п+\) ---' «а——4
При получении дробного числа его округляют до целого.
| № п/п | варианта | №п/п | варианта | № п/п | варианта |
| 1 | 171 | 11 | 210 | 21 | 250 |
| 2 | 174 | 12 | 212 | 22 | 252 |
| 3 | 180 | 13 | 216 | 23 | 270 |
| 4 | 180 | 14 | 216 | 24 | 276 |
| 5 | 180 | 15 | 220 | 25 | 288 |
| 6 | 183 | 16 | 224 | 26 | 294 |
| 7 | 189 | 17 | 225 | 27 | 294 |
| 8 | 194 | 18 | 225 | 28 | 300 |
| 9 | 204 | 19 | 230 | 29' | 330 |
| 10 | 206 | 20 | 240 | 30 | 355 |
Вычисляем порядковые номера и значения медианы и квартилей-
п., =/м-i-зo±l ,сс „. 5+.6 220+224
2 - 2 =15-5 мe= 2 ——2——=222Л"
я+1 30+1
"а = = " = 7-75 « 8 б"» У» «4мг%
(я+1)3 (30+1)3
"а = —4— = --Т— = 23.25 » 23 fi, e 23 » 270мг%
больх003""6 xoлecтePинa в KPOBИ половины обследованных больных находилось в пределах 194-240 мг%, при медиане 222 мг% и амплитуде ряда 171-355 мг%. нс мг/о и
формул"""1'0""0'1 раду медиана и Р™™ определяются по ."'.где
V
Л1 - начальная граница интервала, содержащего медиану (квартиль);
nMv{Q} - порядковый номер медианы (квартили);
(квартиль) накопленная частота) W"
Р- частота интервала, содержащего медиану (квартиль).
Непараметрические методы изучения связи
Коэффициент корреляции рангов Спирмена - р. Рассмотрим методи-
г0 Ф"™ на "РР6 -зи меу коТичест-вом эритроцитов и процентом гемоглобина в крови у 8 человек (табл.
Вычисление коэффициента корреляции рангов Спирмена между количеством эоци8 и процентом гемоглобина в крови
| Обследованные 1 А. К. Б. | Кол-во эритроцитов, х 2 1.98 2.50 2.94 | Гемоглобин, в %, у 3 40 47 60 | Ранги вариант | Разности рангов, | Квадраты разностей рангов, (р 7 0 0 | |
| Гх 4 2 3 | гу 5 2 | d 6 о 0 | ||||
| 3. С. И. Ж. Н. | 3.25 3.64 3.70 3.86 4.29 n=8 | 62 74 65 78 74 | 4 5 6 7 8 | 3 4 6.5 5 8 6.5 | 0 о -1.5 +1 -1 +1.5 | 0 0 2.25 1 2.25 |
| | | | | | | £d2-6.5 |
54
1. Располагаем данные обследованных в порядке возрастания вариант первого признака (в нашем примере - количества эритроцитов) - графы 1,2 и 3 (таблица 18).
2. Заменяем значения вариант в каждом ряду их рангами (графы 4 и 5). Если встречаются одинаковые варианты, то каждой из них присваивается средний ранг. В нашем примере варианта 74% гемоглобина встречается 2 раза, она занимает порядковые места 6 и 7, следовательно, средний ранг равен:
3. Находим разности между смежными рангами сравниваемых рядов (графа 6). Сумма этих разностей должна равняться нулю.
4. Возводим разности в квадрат и суммируем их (графа 7).
5. Вычисляем коэффициент корреляции рангов Спирмена по формуле:
б2>2 - ScP - сумма квадратов разностей рангов;
п - число сравниваемых пар. В нашем примере:
---S————23
Таким образом, между числом эритроцитов и содержанием гемоглобина в крови существует сильная прямая корреляционная связь. Величина коэффициента корреляции рангов Спирмена оценивается также, как величина параметрического коэффициента корреляции.
Оценка надежности коэффициента корреляции рангов Спирмена при числе наблюдений 10 и более производится с помощью критерия / по формуле:
\п-г t=p
Вероятность, соответствующую полученному /, определяем по таблице Стьюдента при числе степеней свободы (п - 2). В тех случаях, когда число наблюдений меньше десяти, оценка значимости производится по таблице 5. Если вычисленный коэффициент корреляции р больше табличного pos, то он значим с вероятностью 95%, если р > poi, то он значим с вероятностью 99%. В нашем примере при п = 8 р > poi (0.92 > 0.833); следовательно, полученный нами коэффициент корреляции значим с высокой вероятностью (р < 0.01).
Показатель соответствия (2) - занимает промежуточное положение: с одной стороны он характеризует наличие связи между явления-
55
ми, с другой - значимость различий между ними. Показатель соответствия 2 вычисляется с помощью абсолютных величин и указывает на существенную или несущественную разницу между эмпирическими числами, полученными в процессе исследования, и теоретическими ожидаемыми", полученными на основе предположения об отсутствии связи между исследуемыми явлениями, то есть на основе принятия нулевой гипотезы. Хи-квадрат Ос2) подтверждает наличие связи, но не устанавливает степень связи. Чем больше величина ?с2, тем больше . полученный результат отличается от теоретического. Оценка у2 производится по специальной таблице (см. приложение № 6). Число степеней свободы равно произведению числа граф (без итоговой) минус единица на число строк (без итоговой) минус единица:
n'=(S-\)-(r-l). Если значение /2 равно или больше табличного, то
нулевая гипотеза отвергается, чем доказана связь, влияние изучаемого явления (фактора). При влиянии большого числа факторов на результативный признак, вычисляется по формуле:
. (Р-РУ~ ;T-Z р -где
Р - фактически.; величины, Pi - «ожидаемые» величины.
Методику вычисления разберем на следующем примере. Пример расчета критерия у1:
Изучение влияния сроков операции от момента поступления больных в стационарно поводу ocTDoro япп»ипигм-г.. ..« ,,„„.... „„..„.,.„-„. ...„...." __ г
| Исходы после ' операции | Сроки оп до 24 | ерации от 24-48 | момента п (час) 48-72 | оступлени» более 72 | я больных | |
| Умерло (чел.) | фактически «ожидаемые» | 12 | 12 | 8 | 14 | всего 46 |
| Выздоровело (чел.) | фактически ~ «ожидаемые» | 22 1203 1193 | 15 832 829 | 5 273 276 | 4 209 219 | 46 2517 2517 |
| Всего ——— В том числе % учерших (летальность) Выздоровело в % | 1215 0.9 99.1 | 844 1.4 | 281 2.8 97.2 | 223 6.3 | 2563 1.8 | |
| | | 70.0 | | 93.7 | 98.2 | |
Из данных таблицы 19 видно, чем позднее сделана операция, тем выше будет послеоперационная летальность. Достоверность такой связи следует доказать критерием х2. Для этого: 1) принимаем нулевую гипотезу (теоретически отвергаем влияние сроков операции от момента госпитализации больных на частоту летальных исходов) и вычисляем «ожидаемые» (Р,) числа умерших и выздоровевших среди оперированных и выписываем их во второй ряд каждой строки таб-
56
лицы. Вычисление «ожидаемых» чисел (при гипотезе отсутствия влияния сроков операции на летальность среди всех групп больных показатель летальности был бы равным и составлял «среднюю» величину 1.8%, а % выздоровлений соответственно - 98.2). Умерло:
до 24 час 24-48 час 24-72 час позднее 72 час
на 100-1.8 на 100-1.8 на 100-1.8 на 100-1.8
на 1215-х на 844-х на 281-х на 223 - х
х = 22 х = 15 х = 5 х = 4
Выздоровело:
на 100-98.2 на 100-98.2 на 100-98.2 на 100-98.2
1215-х на 844-х на 281-х на 223-х
х=1193 х=829 х276 х = 219
2) Вычисление:
, -.(Р-Р,)2 (12-22)2 (12-15)2 (8-5)2 (14-4)'
у = 7 ——————— = ——————— + ——————— + —————— + ————— +
х ZJ />, 22 15 5 4
(1203-1193)2 (832-829)2 (273-276)2 (209 - 219)2 + 1193 + 829 + 276 + 219 = 4.5 + 0.6 +1.8 + 25.0 + 0.08 + 0.01 + 0.03 + 0.46 = 32.48 Табличное значение 2, при числе степеней свободы
т/ = (4 -1) • (2 -1) = 3, равно 7.8-10.3 . Вычисленный f1 больше табличного.
Р - Р
'(15 'Ol
Следовательно, нулевая гипотеза отвергается, что позволяет сделать вывод о влиянии на уровни послеоперационной летальности при остром аппендиците сроков операции от момента госпитализации больных.
При альтернативном распределении у} вычисляется при помощи четырехпольной таблицы, при этом общее число наблюдений должно быть не менее 20, а в каждой клетке таблицы не менее 5. Клетки таблицы условно обозначаются буквами.
Пример расчета '/! при альтернативном распределении:
Изучение побочных явлений при лечении антибиотиками с применением и без поименения витаминов
| Действие антибиотиков | Побочные явления | Процент побочных явлении | ||
| есть | нет | всего | ||
| С применением витаминов | а 9 | b 57 | a+b 66 | 13.0 |
| Без применения витаминов | с 16 | d 29 | c+d 45 | 35.5 |
| Итого | 25 а + с | 86 b+d | 111 a + b + с + d | 22.5 |
57
Из данных таблицы видно, что процент побочных явлений в группе, где применялись витамины, меньше, чем в группе, где они не применялись. Условно отвергая влияние витаминов на снижение побочных явлений от действия антибиотиков, у2 вычисляется по (ьорму-ле: т ' -
2 ____(ad-cb-n____ (9-29-16-57)2
(a+c)-(b+d)-(a+b)-(c+d) 25-86-66.45 ~ 7'3 Рассчитанный y2 больше табличного, который при числе степеней
свободы г!'= (2-1)(2-1) = 1, равен
"OS ~ -Ч)!
нулевую гипотезу и считать доказанным влияние витаминов на снижение побочных явлений при применении антибиотиков.
Когда общее число наблюдений более 20, а в клетках может быть число менее 5, 2 вычисляется по формуле с поправкой Иейтса:
2 _ [ad -cb- 0.5(a 4- b + с + dN / ~ (a+c)-(b+cf)-(a+b)-(c+d)
Оценкарезультата производится по той же таблице (приложение 6). Если y2 = то52 - нулевая гипотеза отвергается, если у2 < уто52 - нулевая гипотеза принимается.
