Организация и методика статистического исследования
| Вид материала | Закон |
- И. И. Мечникова Кафедра общественного здоровья и здравоохранения утверждаю зав кафедрой,, 128.92kb.
- Семинарских/ практических занятий Тема Статистическое наблюдение Методология организации, 113.64kb.
- Задачи статистики и ее организация в РФ и в зарубежных странах Этапы статистического, 26.55kb.
- Методика использования дисперсионного анализа в оргпроектировании. 23. Методика и организация, 29.83kb.
- Курс. Предмет статистики. Изучение количественной стороны общественных явлений и процессов, 14.22kb.
- План статистического исследования, его содержание, 81.37kb.
- Темы лекционных занятий: Предмет, метод и задачи статистического исследования Современная, 25.16kb.
- Методология статистического исследования влияния уровня и качества жизни населения, 657.92kb.
- Методика исследования с применением качественной методологии 15 Методика количественного, 5301.04kb.
- Инструкция : Бланк исследования: все без бланков исследования Отчет испытуемого, 39.61kb.
23
3) Показатели роста (убыли):
1991 58,5-100 1992 53,9-100
53.9-х 51,1-х
х=92,1 х=94,8
1993 51,1-100 1994 49,3-100 49,3 - х . 47,8 - х
х = 96,5 х = 96.9
4) Темп прироста (убыли):
1991 58,5-100 1992 53,9-100
-4.6 - х -2,8 - х
х = -7,9 х = -5,2
1993 51,1-100 1994 49,3-100
-1,8-х -1,5-х
х = -3,5 х = -3 0
Рассчитанные показатели динамического ряда свидетельствуют об убыли числа больничных коек в Санкт-Петербурге, однако темп их убыли снижается.
Выравнивание динамического ряда
Иногда динамика изученного явления представлена не в виде непрерывно меняющегося в одном направлении явления, а скачкообразными изменениями.
В таких случаях используют различные методы выравнивания динамического ряда:
- укрупнение интервалов;
- расчет скользящей средней;
- метод наименьших квадратов.
Укрупнение интервала можно производить за определенные промежутки времени (за квартал, за один, два, три года и т.д.).
Произведено укрупнение интервала за два года и рассчитана средняя длительность пребывания больного на койке для каждого интервала.
1987-1988 - (19,9+19,0)/2=19,5 1989-1990 (19,2+19,3)/2= 19,3 1991-1992 (18,5 + 17,0)/2= 17,8
Показатели преобразованного динамического ряда рассчитываются по общепринятой методике.
Пример выравнивания динамического ряда с помощью укрупнения интервалов (табл.5)
Таблица 5
Динамика средней длительности пребывания больного на терапевтической койке до- и при переходе больниц Санкт-Петербурга на новые условия хозяйствования
| Годы | Средняя длительность пребывания больного на терапевтической койке (в днях) | Укрупненный интервал (годы) | Средняя длительность пребывания больного на терапевтической койке (в днях) |
| 1987 1988 | 19,9 19,0 | 1987-1988 | 19,5 |
| 1989 1990 | 19,2 19,3 | 1989-1990 | 19,3 |
| 1991 1992 | 18,5 17,0 | 1991-1992 | 17,8 |
Влияние случайных колебаний на уровни динамического ряда можно устранить и с помощью скользящей средней. При ее расчете лучше использовать интервалы, включающие три хронологических периода.
Пример выравнивания динамического ряда методом скользящей средней (табл. 6).
Т а бл и ц а 6
Динамика средней длительности пребывания больного на терапевтической койке до- и при переходе стационаров Санкт-Петербурга на новый условия хозяйствования
| Годы | Средняя длительность пребывания больного на терапевтической койке (в днях) | Скользящая средняя | Скользящая средняя по Урбаху |
| 1987 1988 1989 1990 1991 1992 | 19,9-yi 19,0-у2 19,2-уз 19,3-у4 18,5-уз 17,0-уо | 19,4 19,2 19,0 18,3 | 19,7 19,4 19,2 19,0 18,3 17,2 |
Для выравнивания динамического ряда произведено вычисление скользящей средней с использованием интервала в три года.
1988г. (19,9 + 19,0 + 19,2)/3= 19,4
1989г. (19,0 + 19,2 + 19,3)/3= 19,2
1990г. (19,2 + 19,3 + 18,5)/3=19,0
1991г. (19,3 + 18,5 + 17,0)/3= 18,3
Однако этот метод исключает из анализа средние величины первого и последнего уровня.
Поэтому для более точного определения тенденции изучаемого явления можно рассчитать скользящие средние крайних уровней по формуле Урбаха:
1987 г. (7у1+4у2-2уз)/9 = (7х 19,9 + 4х 19,0 2 х 19,2)/9 = 19,7 1992 г. (7уб+4у5-2у4;)/9 = (7х 17,0 + 4х 18,5- 2х 19,3)/9 = 17,2
25
Метод наименьших квадратов позволяет наиболее точно выравнивать тенденции изучаемого явления.
Он позволяет рассчитать точки прохождения такой прямой линии, от которой имеющаяся эмпирическая находится на расстоянии наименьших квадратов от других возможных линий.
Динамический ряд в случае применения данного метода должен иметь не менее 5 хронологических дат, количество их должно быть нечетным, а интервалы между ними - одинаковыми.
? Пример выравнивания динамического ряда методом наименьших квадратов приведен в таблице 7.
Таблица 7
Динамика младенческой смертности в Санкт-Петербурге (на 1000 родившихся живыми) за 1988-1992 гг.
| Хроноло | Младенче | Порядковый | х х у | X2 | Выравненные |
| гические даты | ская смертность, | номер хронологической | | | уровни младенческой |
| (годы) | У | даты от цен | | | смертности |
| | | тральной, х | | | |
| 1988 | 19,1 | -2 | -38,2 | 4 | 19,0 |
| 1989 | 17,4 | -1 | -17,4 | 1 | 18,3 |
| 1990 | 18,2 | 0 | 0 . | 0 | 17,5-0,0 |
| 1991 | 17,1 | 1 | 17,1 | 1 | 16,8 |
| 1992 | 15,5 | 2 | 31,0 | 4 | 16,0 |
| | S:, = 87.3 | | £,=-7.5 | Е-10 | |
Даты искомой прямой линии округляются по следующей формуле:
у, = д„ + я/ • х, где
а„ - это хронологическая средняя (значение центральной хронологической даты), которая вычисляется по формуле:
;., Ь-, где
1 . S - сумма хронологических дат (периодов);
•ЛЕ у - сумма всех значений изучаемого явления.
И|Яв/ - это коэффициент поправки искомого расстояния, который определяется по Дюрмуле:
S,,
0,=--
"г
.v - порядковый номер (расстояние) хронологических дат от центральной, приня-гой за 0.
Сумма произведений х-у определяется с учетом алгебраических
таков.
• Г5_ 10
-0.75
Зная величины ао и ai подставляем их в уравнение:
у, = а„ + а1-х и, придавая последовательные значения чисел ряда х, получим выравненный динамический ряд младенческой смертности.
1988 yi = 17,5 + (-0,75) х (-2) = 19
1989 уз = 17,5 + (-0,75) х (-1) = 18,3
1991 У4 = 17,5 + (-0,75) х (1) = 16,8
1992 у5 = 17,5 + (-0,75) х (2) = 16,0 Динамика младенческой смертности и выравненной младенческой смертности в Санкт-Петербурге за 1988-1992 гг.
Младенческая смерт-
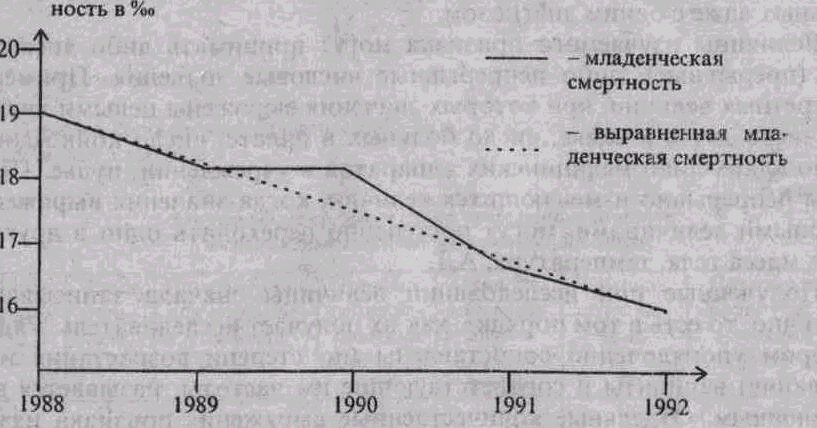
27
V. СРЕДНИЕ ВЕЛИЧИНЫ
В медицине в здравоохранении очень часто используются выражаемые числами признаки, которые могут принимать различные, числовые значения у разных единиц совокупности, нередко повторяющиеся у нескольких единиц. В каждой данной совокупности и в данных конкретных условиях этот признак характеризуется определенной величиной (уровнем), которая отличается от величины этого признака в другой совокупности, при наличии других условии. Пульс, АД, температура тела, длительность временной нетрудоспособности, длительность пребывания в стационаре отличаются (варьируют) у
больных даже с одним диагнозом.
Величины изучаемого признака могут принимать либо дискретные (прерывные), либо непрерывные числовые значения. Примеры дискретных величин, при которых значения выражены целыми числами: число детей в семье, число больных в палате, число койко-днеи, число каких-либо медицинских аппаратов в учреждении, пульс. Примеры непрерывно изменяющихся величин, когда значения выражены дробными величинами, могут постепенно переходить одно в другое:
рост, масса тела, температура, АД.
Полученные при исследовании величины сначала записывают хаотично то есть в том порядке, как их получает исследователь. Ряд, в котором упорядоченно сопоставлены (по степени возрастания или убывания) варианты и соответствующие им частоты, называется вариационным. Отдельные количественные выражения признака называются вариантами (V), а числа, показывающие, как часто эти варианты повторяются, - частотами (Р).
Для обобщенной числовой характеристики изучаемого признака у совокупности обследуемых рассчитываются средние величины, достоинство которых-заключается в том, что одна величина характеризует большую совокупность однородных явлении. - Различают несколько видов средних величин: средняя арифметическая, средняя геометрическая, средняя гармоническая, средняя прогрессивная, средняя хронологическая. Кроме указанных средних, иногда в качестве обобщающих величин вариационного ряда используют особые средние относительного характера - моду и медиану.
Мода (Мо) - наиболее часто повторяющаяся варианта. Медиана (Me) - значение варианты, делящей вариационный ряд пополам; по обе стороны от нее находится равное число вариант.
Наиболее часто используется средняя арифметическая. Средняя арифметическая, которая рассчитана в вариационном ряду, где каждая варианта встречается только один раз (или все варианты встреча-
28
ются с одинаковой частотой) называется средней арифметической простой. Она определяется по формуле:
.. v
М = —— • где И
М ~ средняя арифметическая;
V - значение вариационного признака;
п - общее число наблюдений.
Если в исследуемом ряду одна или несколько вариант повторяются, то вычисляют среднюю арифметическую взвешенную. При этом учитывается вес каждой варианты и чем большую частоту имеет данная варианта, тем больше будет ее влияние на среднюю арифметическую. Расчет такой средней производится по формуле:
м 'р
М = ————— , где
П п - сумма частот
Пример составления вариационного ряда и расчета основных его характеристик представлен в таблице 8.
Таблица 8
Определение среднего срока пребывания больных в специализированном отделении больницы
| Число | Число | Начетный ряд | Произве | Отклоне | Квадрат | Произведение |
| дней, | боль | для определе | дения ва | ния вари | отклоне | квадратов от |
| | ных, | ния места | риант на | ант от | ний, | клонений на |
| | | | их частоты | средней, | | частоты, |
| V | Р | Me | v.p | d=V-M | d2 | d2? |
| 16 | 1 | 1 | 16 | -4 | 16 | 16 |
| 17 | 7 | 8 | 119 | -3 | 9 | 63 |
| 18 | 8 | 16 | 144 | -2 | 4 | . 32 |
| 19 | 16 | 32 | 304 | -1 | 1 | 16 |
| 20 | 29 | 61 | 580 | 0 | 0 | 0 |
| 21 | 20 | 81 | 420 | 1 | 1 | 20 |
| 22 | 7 | 88 | 154 | 2 | 4 | 28 |
| 23 | 5 | 93 | 115 | 3 | 9 | 45 |
| 24 | 2 | 95 | 48 | 4 | 16 | 32 |
п=95 £=1900 £=252
1900 hd-P /252
М=——=10.0лн ————= ±j-q-= ±1.63 дн.
При большом количестве наблюдений число встречающихся размеров вариант может быть очень большим; тогда рекомендуется размеры вариант объединять в группы, причем каждая группа должна иметь равное число значений вариант (иметь равный интервал). Расчет средней арифметической в таком сгруппированном или интервальном ряду требует предварительного определения середины интервала. Середина интервала в непрерывных вариационных рядах опре-
29
деляется как полусумма первых значений соседних групп. Середина интервала в дискретных вариационных рядах определяется как полусумма крайних значений группы (табл. 9).
Т а бли ц а 9 Определение среднего роста 14-летних девочек
| Рост девочек Центральная вариан-V Vi | Р | ViP |
| 133.0-136.9 133.0+137.0 | 3 | 135-3=405 |
| -135 137.0-140.9 137.0+141.0 ,, | 15 | ......2085 |
| 2 - =139 1410-144.9 =143 | 17 | 7431 |
| 1450-1489 = 147 | 41 | ...... £-~vJ 1 ......6027 |
| 1490-1529 =151 | 52 | 7й'7 ...... IQJL |
| 153.0-1569 =155 | 42 | ......6510 |
| 1570-160.9 =159 | 18 | ......2862 |
| 1610-164.9 .... =163 | 5 | 01 С ......61 J |
| 1650-168.9 165.0+169.0 , | 4 | ......668 |
| 2 =167 | | |
•S.V.P 29655
———-liT-150-50"
Средняя арифметическая имеет ряд свойств, которые используются в некоторых случаях для упрощения расчета средней.
1. Алгебраическая сумма отклонений всех вариант от средней равна нулю. На этом свойстве основан расчет средней по способу моментов.
2. Если к каждой варианте вариационного ряда прибавить или отнять одно и то же число, то на столько же увеличится или уменьшится средняя арифметическая величина.
3. Если каждую варианту разделить или умножить на одно и то же число, то во столько же раз уменьшится или увеличится средняя арифметическая.
Эти свойства используют в тех случаях, когда варианты представлены очень малыми или, наоборот большими числами.
В здравоохранении в отдельных случаях может потребоваться расчет средней прогрессивной. Средняя прогрессивная рассчитывается из лучших вариант, вариант, положительно характеризующих явление. Они могут иметь значение больше полученной средней арифметической (процент совпадения диагнозов, число больных, состоящих под диспансерным наблюдением, охват профилактическими осмотрами и т.д.) и меньше (уровень летальности, младенческой смертности,
заболеваемости с временной нетрудоспособностью, частота послеоперационных осложнений и т.д.).
Вычисление средней прогрессивной длительности пребывания больных в терапевтических отделениях стационаров.
| | *. | |
| Средняя длительность (в днях), V 12 13 14 15 | Число стационаров,Р | V.P |
| 2 3 5 | 12 26 42 75 | |
| 16 17 18 19 | 4 3 2 1 | 64 51 36 19 |
| | п= 1 | 325 |
м = .525/21 = 15.47 дней, но в 11 стационарах уровень, средней длительности пребывания больных в стационаре ниже, то есть более благоприятный, чем в среднем по всем больницам. Рассчитанная в этих 11 стационарах новая средняя и будет средней прогрессивкой: Мпр -'= 155/11 = 14.09 дней. Такая средняя, определенная среди оптимальных условий, будет служить ориентиром для других (10) стационаров.
Средняя среди показателей. При одинаковых числах наблюдений ее можно рассчитать, как среднюю простую: то есть достаточно суммировать размеры показателей и затем поделить на их число. Но при разных числах наблюдений среднюю величину среди показателей следует определять всегда как среднюю взвешенную. Например, в трех отделениях стационаров летальность составила:
- хирургическое отделение - 1%;
- терапевтическое отделение - 3%;
- неврологическое отделение - 5%.
Если суммировать показатели и разделить сумму на число отделений, то средний уровень летальности составит У/о. Однако в хирургическом отделении пролечилось 800 больных (умерло 8 человек), в терапевтическом 600 больных (умерло 18 больных), а в неврологическом пролечено 200 (умерло 10 больных). Таким образом, средняя летальность по больнице составляет 2,25 (36 х 100 : 1600). Разница оказалась заметной, чтобы определить средний показатель, надо узнать абсолютное число умерших в каждом отделении, получить сумму умерших, разделить ее на общую численность пролеченных больных и выразить полученную величину в соответствующих единицах (%, %о и т.д.).
Средняя величина абстрактна, она может быть рассчитана в принципе из любой совокупности, например, можно получать среднюю арифметическую в группе больных с повышенным и понижен-
31
ным АД. Но такая средняя будет огульной, она не будет правильно характеризовать совокупность, из которой рассчитана. Средние необходимо рассчитывать из однородных совокупностей.
Средняя арифметическая величина находится в большой зависимости от колеблемости вариационного ряда. чем меньше колеблемость ряда, то есть чем меньше амплитуда колебания ряда (разность между самой большой и самой малой вариантой, что называется степенью рассеяния ряда), тем более точно его будет характеризовать средняя арифметическая.
Если большинство вариант концентрируются около своей средней арифметической величины, то такой вариационный ряд - довольно компактный, однородный, можно говорить о малом варьировании. Если же варианты значительно удалены от своей средней арифметической - налицо большое варьирование, а возможно, и неоднородная совокупность,
Степень варьирования вариационного ряда определяется с помощью вычисления среднего квадратического отклонения (ст). Для вычисления сигмы необходимо (табл. 8) определить отклонения (d) каждой варианты от средней, возвести их в квадрат (d2), перемножить квадрат отклонения на частоту каждой варианты (d2?), получить сумму этих произведений (Sd2?), а затем вычислить сигму по формуле:
1 . \P
Г" л——
g..U. V п
Is При малом числе наблюдений (п < 30) расчет производят по следующей формуле: '
и ' 1р " О- = ±л———-
t- V п-\ Описанный способ расчета среднего квадратического отклонения требует значительной вычислительной работы. Можно использовать приближенный способ вычисления среднего квадратического отклонения по амплитуде (размаху) вариационного ряда. Вычисление ст по амплитуде производится по формуле:
V -V
0-=± тах , "'".где
А
• А - коэффициент для определения сг, соответствующий числу наблюдений (приложение 1).
fe" Л 1 (,
J: В нашем примере о- = ±—:— = ±1.61 W. Ц .:'*?' ' 4.94
1 Для оценки варьирования признака наряду со средним квадрати-ческим отклонением может быть использован коэффициент вариации (С). Особенно необходимо использовать коэффициент "вариации при
сравнении колеблемости двух или более средних величин, выраженных в разных единицах измерения:
c=f•m М
В нашем примере С=-———=8.15%. Значение коэффициента
вариации менее 10% сридетельствует о малой колеблемости, от 10 до 20% - о средней, от 20% и более - о сильной колеблемости вариант вокруг средней.
