Организация и методика статистического исследования
| Вид материала | Закон |
- И. И. Мечникова Кафедра общественного здоровья и здравоохранения утверждаю зав кафедрой,, 128.92kb.
- Семинарских/ практических занятий Тема Статистическое наблюдение Методология организации, 113.64kb.
- Задачи статистики и ее организация в РФ и в зарубежных странах Этапы статистического, 26.55kb.
- Методика использования дисперсионного анализа в оргпроектировании. 23. Методика и организация, 29.83kb.
- Курс. Предмет статистики. Изучение количественной стороны общественных явлений и процессов, 14.22kb.
- План статистического исследования, его содержание, 81.37kb.
- Темы лекционных занятий: Предмет, метод и задачи статистического исследования Современная, 25.16kb.
- Методология статистического исследования влияния уровня и качества жизни населения, 657.92kb.
- Методика исследования с применением качественной методологии 15 Методика количественного, 5301.04kb.
- Инструкция : Бланк исследования: все без бланков исследования Отчет испытуемого, 39.61kb.
Значение среднего квадратического отклонения - ст.
1. ст характеризует однородность вариационного ряда. Если ст мала, значит ряд однородный, и рассчитанная М достаточно верно характеризует данный вариационный ряд. Если ст велика, то ряд неоднородный, наблюдается большая колеблемость вариационного ряда, и полученная М характеризует не весь ряд, а только какую-то его часть.
2. В медицине, здравоохранении интервал М ± 1ст обычно принимают за пределы нормы.
3. С помощью ст оценивается «выскакивающий» результат по
формуле: •<"•" ~ м . Если отношение разности между выделяющейся
<7
(«выскакивающей») вариантой и средней арифметической, рассчитанной без нее, к среднему квадратическому отклонению, рассчитанному также без выделяющейся варианты, будет равно 3 и более, то такую варианту лучше не включать в исследование.
4. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм, которое графически изображается кривой Гаусса* (см. рис. 1).
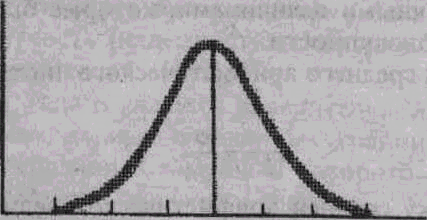
-36 -26 -16 'x +16 +26 +36
М ± 1ст = 68,3% М ± 2ст = 95,5% М ± Зет = 99,7%
Рис. 1. Теоретическая кривая нормального распределения.
В природе возможны и другие виды распределения, отличающиеся от нормального: альтернативное, асимметричное (правостороннее, левостороннее), бимодальное.
33
Если к средней арифметической величине прибавить и отнять от нее одну сигму (М ± 1ст), то при нормальном распределении в этих пределах будет находиться не менее 68,3% всех вариант (наблюдений), что считается нормой для изучаемого явления. Если к М ± 2ст, то в этих пределах будет находиться 95,5% всех наблюдений, а если к М ± За, то в этих пределах будет находиться 99,7% всех наблюдений. Таким образом, среднее квадратическое отклонение является стандартным отклонением, позволяющим предвидеть вероятность появления такого значения изучаемого признака, которое находится в пределах заданных границ.
Выборочный) метод. Оценка достоверности средних арифметических и относительных величин
При изучении сплошной (генеральной) совокупности для ее числовой характеристики достаточно рассчитать М и ст.
На практике, как правило, мы имеем дело не с генеральной, а с выборочной совокупностью.
Для выборочного метода очень важен способ отбора части от целого, так как отобранная часть, как уже упоминалось ранее, должна быть репрезентативной.
При выборке возможны ошибки смещения, то есть такие события, появление которых не может быть точно предсказуемым. Вместе с тем они являются закономерными, объективными, как и необходимые. При определении степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки. Такие ошибки носят название случайных ошибок репрезентативности (т) и являются фактической разностью между средними или относительными величинами, полученными при выборочном исследовании, и аналогичными величинами, которые были бы получены при изучении всей совокупности.
Средняя ошибка среднего арифметического числа определяется по формуле:
СГ
т= ±~г= Vn
Среднюю ошибку средней арифметической величины можно вычислить как и сигму, по амплитуде вариационного ряда:
V -V .
+_S22———а-.где
В - коэффициент для определения ошибки, соответствующий числу наблюдений (приложение 1).
В приведенном примере средняя ошибка составила ±0.16 дней.
о- 1.63 1.63
Тпж-
А при расчете по амплитуде вариационного ряда:
24-16 " г- - /• —_— +о\-/р,неи, что достаточно близко к средней ошибке,
46.9 рассчитанной по обычной формуле.
При оценке полученного результата по размеру средней ошибки, пользуются доверительным коэффициентом (t), который дает возможность определить вероятность правильного ответа, то есть он указывает на то, что полученная величина ошибки выборки будет не больше действительной ошибки, допущенной вследствие сплошного наблюдения. Так, если принять t = 2.6, то вероятность правильного ответа составит 99.0%, а это означает, что из 100 выборочных наблюдений только один раз выборочная средняя может оказаться вне пределов генеральной средней. При t = 1 вероятность правильного ответа составит лишь 68.3%, а 31.7% средних могут оказаться вне вычисленных пределов. Следовательно, увеличением доверительной вероятности увеличивается ширина доверительного интервала, что в свою очередь повышает достоверность суждения, спорность полученного результата (табл. 10).
Таблица 10 Оценка полученного результата по средней ошибке
| Доверительный коэффициент (критерий точности) | Опорность результата (достоверность) Pi | Риск ошибки р |
| ti = М ± 1т t2 = М ± 2т t2,6 = М ± 2,6т t3 = М ± Зт 1з,з = М ± 3,3т | 68,3% (Pi - 0,683) 95,5% (Pi - 0,955) 99,0% (Pi - 0,990) 99,7% (Pi - 0,997) 99,9% (Pi - 0,999) | 0,317 0,05 0.010 0,003 0,001 |
В медико-статистических исследованиях обычно используют доверительную вероятность (надежность), равную 95,5-99,0%, а- в наиболее ответственных случаях - 99,7%.
Таким образом, если ст является доверительной вероятностью появления необходимых данных в заданных границах, то m является доверительным интервалом, с помощью которого определяются границы возможного размера изучаемого явления.
Зная размер ошибки, можно, как отмечалось выше, правильно определить требуемое число наблюдений для выборочного исследования при помощи преобразования формулы предельной оши(жи выборки
/(дельта) = t-m -=• —г=- » в которую входит величина п - число наблю-
\ V/2
дений.
Решая приведенное равенство относительно п, получим формулу для определения числа наблюдений:
t2- п=--
Для примера воспользуемся данными изучения средней длительности пребывания больных в специализированном отделении. Здесь М = 20 дн., о- = ±1,63 дн., т = ±0,16 дн. Сколько же нужно дополнительно исследовать больных, заведомо оперируя ошибкой выборки больше полученной (А = ±0,5 дн.), при доверительной вероятности t = З?
[Определяем требуемое число наблюдений:
З.бЗ2 9-2.66 n="~0~~~025~=95•1 Вывод: для того, чтобы оперировать в использованном нами примере с указанной точностью (99,7%), следует подвергнуть изучению 95-96 больных. Нами исследовано 95 больных, что соответствует искомой величине.
<;' Достоверность разности средних величин
На практике нередко приходится иметь дело не с одной, а с двумя средними: надо сравнить среднюю длительность пребывания больных в 2-х стационарах или за отчетный год и предыдущий, результаты, полученные при исследовании 2-х групп больных, лечившихся разными методами, исследуемую группу и контрольную и т.д. Целью сравнения двух средних является оценка существенности их различий, ус-гановление их достоверности.
Достоверность разности между двумя средними величинами определяется по формуле:
М, - М, , , t= ' --.где
ггг+т
М, н М - две средних арифметических величины, полученные в двух самостоятельных независимых группах наблюдении;
т, и w, - их средние ошибки (выражение -Jm,2 + т называют средней ошибкой
)азности двух средних),
/ - доверительный коэффициент для разности средних.
При / >2 разность средних арифметических может быть признана существенной и неслучайной, то есть достоверной. Это значит, что и в •енеральной совокупности средние величины отличаются, и что при ювторении подобных наблюдений будут получены аналогичные раз-1ичия. При / = 2 надежность такого вывода будет не меньше 95%. С увеличением / степень надежности также увеличивается, а риск ошиб-'<;
ки уменьшается. При t < 2 достоверность разности средних величин считается недоказанной. Например, в больнице «А» средняя длительность пребывания больного на койке равна 16,2 дн., m = ±1,5 дн.; в больнице «В» - 14,8 и 1,0 соответственно. 16.2-14.8 1.4
"таг-иг0-8
Различие средних арифметических недостоверно, статистически незначительно. Но нельзя в таких случаях говорить о том, что «нет разницы»!. Различие есть, но оно может быть случайным, недостоверным.
В сопряженных совокупностях (зависимых рядах) оценка достоверности разности средних проводится про формуле:
рад»
/ = —————
pa'Jit
Алгоритм расчета.
1. Составляем два вариационных ряда (например, по уровню артериального давления у больных до и после введения гипотензивного препарата).
| V, | V: | •paw | dV,-M, | "I |
| 190 180 170 170 165 | 170 150 165 160 150 | 20 30 15 10 15 | 2 12 -3 -8 -3 | 4 144 9 64 9 |
Z;"'
2. Составляется вариационный ряд из разности вариант (Уразн = Vi
-V2).
3. Для нового ряда рассчитываются все его характеристики: Мразн,
Оразн, ГПразн.
1>,5 20+30+15+10+15 М = ——— = —————-————— = 18(лш)
П J
f~4~л I—————
тгТ5'7 "'-у1
1 О
4. Определяем / - -!°. 59-" " 2.6
5. Так как п < 30, полученное значение t сравниваем с табличным (приложение № 2).
Полученное нами t > 1табл о.99, следовательно полученная средняя разность в уровнях АД (18 мм рт. ст.) существенна и неслучайна, то есть достоверна.
Достоверность показателей и разности показателей
Достоверность показателя определяется с помощью его средней
ошибки по формуле: / = ± \- •> г•ae Р ~ РзэР показателя, выраженный в
V п
долях единицы, в процентах, в промилле; q - равно 7 -р или 100 - р или 1000 -р (величина, дополняющая показатель до основания); п - число наблюдений.
Например; обследовано 1800 больных, из них выявлено 90 больных гипертонической болезнью I ст. Процент выявленных больных по
данным проведенного осмотра равен: ————=5 случаев на 100 ос-1800
мотренных. „, = + )5'95 п 5 • Следовательно, с вероятностью 95.5%
~Vl800
показатель выявляемости больных с ГБ-1 в аналогичных условиях будет колебаться в пределах Р ±2т = 5 ±2 • 0.5 = 5 ± 1.0, то есть от 4 до 6 случаев на 100 обследованных.
Достоверность различий между сравниваемыми показателями вычисляется по формуле, аналогичной для средних величин:
t--
/W)2 + т}
Оценивается критерий различия показателей также, как и средних величин.
Для примера сопоставим уровни общей летальности в двух больницах'
| | Больница №1 | Больница №2 |
| Число лечившихся | 4350 | 6760 |
| Из них умерло | 196 | 236 |
| Летальность | 4.5% (Pi) | 3.5% (Р2) |
q = 100% или когда показатель равен 100% (Р = ]00%) или близок к 100%, а q = 0, следует узнать, а каким бы мог быть показатель изучаемого явления при других условиях отбора (другое число наблюдений, другой состав больных по полу, возрасту и т.д.)? Для этого пользуются специальной формулой, по которой можно вычислить «ожидаемый»
д+1 уровень показателя: р, = ——. 100%, где
' п+2
а - результативный показатель (Р).
Допустим, что в больнице лечилось экспериментальным методом 60 больных (п), среди которых летальных исходов не было (Р = 0%). Вычисляем «ожидаемый» показатель летальности:
/',=. юо«/. =1.6%.
Ошибка такого показателя определяется по формуле:
[~pq~ /1.6-98.4 /158.2 , w- - 43 = 43- = 4~W = L58%-При t = 2 возможны колебания ожидаемого показателя в пределах от 0% до 4.76% (1.6 ± 3.16).
Малая выборка
В клинических и экспериментальных работах довольно часто приходится пользоваться малой выборкой, когда число наблюдений меньше 30. При малой выборке средние величины и показатели вычисляются по тем же формулам, что и при большой. При вычислении среднего квад-ратического отклонения и средней ошибки показателя число наблюдений уменьшается на единицу:
„.,Ж; „,=J
V п-\ \п-\
Достоверность результатов (t) оценивается по таблице Стьюдента. Обращаться с таблицей Стьюдента следует по графе 1-й, в которой указано число степеней свободы (п'), равное п - I, то есть числу проведенных наблюдений уменьшенному на единицу. Данные 2, 3 и 4-й граф исчислены для вероятности правильного заключения, равной: 95% - графа 2, при риске ошибки 5% (Роз); 99% - графа 3, при риске ошибки 1% (Poi) и 99.9% - графа 4, при риске ошибки 0.01% (Pool).
VI. МЕТОДЫ ИЗМЕРЕНИЯ СВЯЗИ МЕЖДУ ЯВЛЕНИЯМИ
Корреляционный анализ.
Одной из важных задач исследовательской работы является выявление и измерение связи между признаками, характеризующими изучаемые явления или процессы. Различают функциональную и корреляционную связи.
При наличии функциональной связи изменение величины одного признака неизбежно вызывает совершенно определенные изменения величины другого признака. Примером такой связи может служить зависимость площади круга от его радиуса. Функциональная связь между явлениями присуща неживой природе. В биологических науках чаще приходится иметь дело с иной связью между явлениями, когда одной и той же величине одного признака соответствует ряд варьирующих значений другого признака, что обусловлено чрезвычайным многообразием взаимодействия различных явлений живой природы. Такого рода связь носит название корреляционной (correlation - соответствие, соотносительность). В то время как функциональная связь имеет место в каждом отдельном наблюдении, корреляционная связь проявляется только при многочисленном сопоставлении признаков.
Рассмотрим, например, связь между возрастом детей-дошкольников и их ростом. Из приведенных данных видно, что с возрастом рост детей увеличивается, и поэтому можно предположить наличие связи между указанными признаками.
Табл и ца
| Возраст | 3 года | 4 года | 5 лет | 6 лет | 7 лет |
| Рост в см | 100,3 | 102,9 | 108,1 | 113,7 | 118,3 |
| 92,6 | 100,1 | 106,8 | 113,8 | 119,2 | |
| 93,8 | 101,6 | 107,8 | 113,3 | 119,4 | |
| 93,7 | 98,4 | 104,6 | 111,8 | 116,1 | |
| "94,2 | 99,4 | 107,4 | 112,1 | |
Вместе с тем, следует отметить, что одному и тому же возрасту соответствует различный рост детей. Это происходит потому, что рост детей определяется не только возрастом, на него влияют многие другие факторы, в том числе условия жизни, питание, занятия физкультурой и др. Таким образом, можно прийти к выводу, что связь между возрастом и ростом детей является корреляционной.
Исследователю следует помнить, что обнаружение корреляции между сопоставляемыми явлениями не говорит еще о существовании причинной связи между ними. Для установления последней необходим всесторонний логический и специальный анализ существа изучаемых процессов. Статистический же метод позволяет обосновать получен-
40
ные в результате научного исследования выводы о наличии тех или иных связей между явлениями, выделить самые главные из них.
Сила связи между явлениями, ее теснота и направленность определяются величиной коэффициента корреляции, который колеблется в пределах от 0 до ±1. При г == О связь отсутствует, при г = ±1 - связь полная, функциональная.
, 1л
rs\'~~г.
По направленности связь между явлениями может быть прямой (положительной), когда с увеличением (уменьшением) значений одного признака увеличиваются (уменьшаются) значения другого (то есть когда признаки меняются в одном направлении), и обратной (отрицательной), когда с увеличением значений одного признака значения другого уменьшаются и наоборот (то есть изменения признаков - разнонаправленны).
Т абли ца 12 Схема оценки тесноты корреляционной связи по коэффициенту корреляции
| Теснота связи | Величина коэффициента корреляции при наличии | |
| прямой связи (+) | обратной связи (-) | |
| Связь отсутствует | 0 | 0 |
| Связь слабая | от 0 до +0,3 | от 0 до -0,3 |
| Связь умеренная | от+0,3 до+0,7 | от-0,3 до-0,7 |
| Связь сильная | от +0,7 до + 1,0 | от--0,7 до-1,0 |
| Связь полная (функциональная | +1,0 | -1,0 |
Приведем пример вычисления коэффициента корреляции по приведенной формуле (таблица 13).
Ход вычислений здесь чрезвычайно прост. Суммируя ряды х и у, получаем zjc = 119 и 1.у = 105.2. Деля суммы на число членов ряда (п), получаем средние арифметические этих рядов: М, = 779; 72 = 9.9 и My = 705 ; 72 = 8.8. Ряды d„ и dy, то есть отклонение чисел рядов х и у представляют собой разность между соответствующими значениями х и у и средними арифметическими этих рядов. Так, для рядов х, d равно для января: х - М = 5 - 9.9 = -4.9; для февраля: х-М=2-9.9=-7.9 и т.д. Возводя поочередно числа рядов d и dy в квадрат, получаем ряды d2 и dy2, а перемножая попарно числа рядов d. и dy между собой, получаем ряд • dy. Подставляем значения сумм этих рядов в формулу:
, ., >
"""л-к
41
Таблица 13
Корреляция между среднемесячной температурой воздуха и числом умерших детей до 1 года от кишечных заболеваний
| Месяц | х | У | | | | | | |
| года | средняя температура воздуха (в °С) | среднедневные числа умерших от острых кишечных инфекций | d | X | dy | dx2 | dy2 | dxdy |
| январь | 5 | 5,0 | -4 | 9 | -3,8 | 24,01 | 14,44 | 18,62 |
| февраль | 2 | 5,5 | -7 | 9 | -3,3 | 62,41 | 10,89 | 26,07 |
| март | 4 | 6,2 | -5 | 9 | -2,6 | 34,81 | 6,76 | 15,34 |
| апрель | 8 | 5,4 | -1 | 9 | -3,4 | 3,61 | 11,56 | 6,46 |
| май | 15 | 6,5 | 5, | | -2,3 | 26,01 | 5,29 | -11,73 |
| июнь | 17 | 9,6 | 7, | | 0,8 | 50,41 | 0,64 | 5,68 |
| июль | 18 | 11.2 | 8, | | 2,4 | 65,61 | 5,76 | 19,44 |
| август | 17 | 15,3 | 7, | | 6,5 | 50,41 | 42,25 | 46,15 |
| сентябрь | 15 | 14,9 | 5, | | 6,1 | 26,01 | 37,21 | 31,11 |
| октябрь | 9 | 13,0 | -0, | 9 | 4,2 | 0,81 | 17,64 | -3,78 |
| ноябрь | 6 | 7,0 | -3, | 9 | -1,8 | 15,21 | 3,24 | 7,02 |
| декабрь | 3 | 6,2 | -6, | 9 | -2,6 | 47,61 | 6,76 | 17,94 |
| п= 12 | Sx=119 -.о | £y= 105.2 105.2 Л/„=-"8.8 | | | | = 406.92 | Zdy 162.44 | Sddy = 178.32 |
•• , получим: у 178-32 =0.686 «0.7 ; w V406.92.162.44
и То есть между среднемесячной температурой воздуха и числом умерших от острых кишечных инфекций существует прямая корреляционная связь.
Это чрезвычайно простое для понимания вычисление требует довольно кропотливой, хотя и несложной математической работы. Вычислительная работа особенно затрудняется тогда, когда члены кор-релирумых рядов имеют большие числовые значения, особенно если варианты коррелируемых рядов приведены в виде сгруппированных интервалов и, следовательно, приходится вычислять не простую, а взвешенную среднюю.
Средняя ошибка коэффициента корреляции. Поскольку коэффициент корреляции в клинических исследованиях рассчитывается обычно для ограниченного числа наблюдений, нередко возникает вопрос о надежности полученного коэффициента. С этой целью определяют среднюю ошибку коэффициента корреляции. При достаточно большом числе наблюдений (больше 100) средняя ошибка коэффициента корреляции (mr) вычисляется по формуле:
1- т, = —J— . где
П
n - число парных наблюдений.
В том случае, если число наблюдений меньше 100, но больше 3( точнее определять среднюю ошибку коэффициента корреляции, поль зуясь формулой:
i-. "TirT
С достаточной для медицинских исследований надежностью о на личии той или иной степени связи можно утверждать только тогда когда величина коэффициента корреляции превышает или равняется
величине трех своих ошибок (г > Зт,.). Обычно это отношение ко
эффициента корреляции (гху) к его средней ошибке (mr) обозначай буквой / и называют критерием достоверности:
т,
Если > 3, то коэффициент корреляции достоверен. Допустим, что число наблюдений 142, а коэффициент корреляции
068 Тпгпя- ~г 1 - (0.68)2 .- „ г 0.68 ,. тп рпч. и.об. 1 огда. yyi = —/=— = ——/====— = 0.045 » а / = — — —— —15° естъ
г -Л VT42 ' w, 0.045 коэффициент корреляции вполне достоверен.
В случае малой выборки (число наблюдений меньше 30) для оценки достоверности коэффициента корреляции, то есть для определения соответствия коэффициента корреляции, вычисленного по выборочным данным, действительным размерам связи в генеральной совокупности, средняя ошибка коэффициента корреляции (mr), определяется
ю формуле: = v " , где значения критерия / = J— оцениваются r V/i-2 г т,
ю таблице t Стьюдента при числе степеней свободы v = п - 2. Если »еличина tr больше табличного значения to5, то коэффициент призна-'тся надежным с доверительной вероятностью больше 95%. Например, имеется коэффициент, равный +0.72 при числе наблюдений 28.
-2=-19 -
Полученное tr = 35.9 значительно больше табличного toi=2.779, ледовательно, полученному коэффициенту корреляции можно довеять с высокой степенью вероятности (> 99%).,
Для того, чтобы установить, на сколько может измениться одно явление при изменении другого на единицу, вычисляется коэффициент регрессии (R):
. А.-.?-
При вычислении Ry мы узнаем, на сколько изменится явление у при изменении на 1 единицу измерения х.
При вычислении R мы узнаем, на сколько изменится явление х при изменении на 1 единицу измерения у.
Например, при изменении роста (х) и массы тела {у) у семилетних мальчиков были получены следующие данные:
гху = 0.69
<Тх = 5.8 см ' cry = 2.6 кг
Вычислим коэффициенты регрессии:
R„.=0.69•5-s=\.5кг R = 0.69= 0.3 \см. 2.6 э.о
Вывод: при увеличении роста мальчиков в среднем на 1 см масса тела увеличивается в среднем на 1.5 кг; при увеличении массы тела в среднем на 1 кг рост увеличивается в среднем на 0.31 см.
Ошибки коэффициентов регрессии вычисляются по формулам:
=a-. | '"rv1' ; _ flr' | ч' , а достоверность коэффициента R\y а, V п . й" о-, V п
регрессии - по формуле: / = —. т
При п > 30 результат считается достоверным, когда t>.3, при п < 30 критерий / оценивается по таблице Стьюдента.
Для оценки степени связи качественных признаков рассчитывается коэффициент сопряженности (при числе групп не менее 5):
г"
С) "
=J, ,7
\\+ф~ Методика расчета приведена в таблице 14. Алгоритм расчета.
1. Вносим в таблицу данные о количестве случаев различных по гистологической структуре и типу опухолей (Vi-Vu), которые называются частотами.
2. Возводим частоты в квадрат (V2).
3. Полученные числа делим на общее число больных с разными типами опухолей (п): уз/п.
Таблица 14
| Гистологическая структура опухоли | Типы роста опухоли | частости ЕГ2 ——:ЪУ | |||||
| | ЭКЗО- фит- НЫЙ | язвенно-инфиль-тратив-ный | диффуз-но-инфи-льтра-тивный | переходный | всего, £V | ||
| п | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| аденокар-цинома | V, V,2 Vin | 11 121 6,05 | 6 36 1,09 | 2 4 0.29 | 2 4 0,67 | 21 8,10 | 8,10/2,1 =0,39 |
| Cr simplex | V2 V22 V22/»! | 3 9 0,45 | 10 100 3,03 | 1 0,07 | 1 1 0,17 | 15 3,72 | 3,72/15=0,25 |
| солидный рак | Уз Уз2 Узп | 3 9 0,45 | 5 25 0,76 | 3 9 0,64 | 1 1 0,17 | 12 2,02 | 2,02/ 12=0,17 |
| слизистый рак | V4 V42 V42/n | 0,05 | 7 49 1,40 | 3 9 0,64 | — | 11 2,17 | 2,17/ 11 =0,20 |
| фиброзный рак | V5 V52 V52/n | - | 1 1 0,03 | 5 25 1,78 | - | 6 1,81 | 1,81/6=0,30 |
| смешанный рак | V6 V„2 Ve'/n | 2 4 0/20 | 4 16 0,48 | ~ | 2 4 0,67 | 8 1,35 | 1,35/8=0,17 |
| n=£(Vi-V6) | | 20 | 33 | 14 | 6 | 73 | £:= 1,48 Коэффициент сопричастия |
4. Находим суммы частот и суммы полученных в р. 3 частных, вносим их в колонку 7.
'LV1
5. Находим частости (колонка 8) следующим образом: ——:S)/
п (для каждой структуры опухолей).
6. Суммируя частости, получаем коэффициент сопричастия.
7. Рассчитываема: у~=- коэф.сопричастия - 1 =1.48-1=0.48
8. Рассчитываем коэффициент сопряженности:
ДИг324-0-57
9. Оценка коэффициента сопряженности производится аналогично коэффициенту корреляции.
В данном случае связь между гистологической структурой опухоли и типом роста носит прямой характер и умеренно выражена.
45
VII. ДИСПЕРСИОННЫЙ АНАЛИЗ
Дисперсионный анализ позволяет дать обобщенную характеристику трем и более средним величинам или показателям и позволяет:
- измерить силу влияния;
оценить разность частных средних или показателей;
определить достоверность разности частных средних или показателей.
Дисперсионный анализ показывает степень рассеивания, вариации (дисперсии) измеряемых признаков вокруг среднего типичного уровня, поэтому он дает возможность изучить действие на конечный результат исследования нескольких факторов вместе, роль каждого из них и сравнить действие отдельных факторов между собой.
Изучение действия факторов производится путем сравнения средних значений наблюдаемого признака, полученных в результате воздействия каждого из этих факторов при разном их сочетании.
Различают следующие виды дисперсионного анализа: однофак-торныи, двухфакторный и многофакторный.
Методика проведения дисперсионного анализа.
Факторами принято называть любые воздействия или состояния определяющие ту или иную величину наблюдаемого (результативного) признака. Отдельные значения результативного признака именуются датами.
Вариация изучаемого признака зависит как от организованных (запрограммированных), так и от случайных (неизвестных) факторов. Поэтому общая вариация (дисперсия) слагается из вариации, вызванной организованными факторами - факториальной вариации и вариацией, вызванной остаточными, неизвестными, случайными факторами - случайной вариации.
Таким образом, общая дисперсия (Соб) равна сумме дисперсий факториальной (Сф) и случайной (Сел).
v-об = Сф ' Сел
В своюочередь, общая дисперсия признака равна сумме квадратов
отклонений каждой даты результативного признака (V) от общей средней (Моб):
Соб = £(V - Моб)2
Факториальыая дисперсия (межгрупповая) измеряется суммой квадратов отклонений групповой средней (Мгр) от общей средней
(Моб):
Сф = ЦМгр - Моб)2
Дисперсия остаточная (случайная) - внутригрупповая - определяется суммой квадратов отклонений каждого значения результативного признака (V) в группе от средней этой группы (Мгр):
Ссл=2:(У-Мгр)2
Доля (сила) участия отдельных факторов в формировании результативного признака определяется отношением групповых дисперсий к общей. Вычислением отношения факториальной дисперсии к общей определяется сила влияния организованного фактора, а отношением случайной дисперсии к общей определяется сила влияния неорганизо-
С С
ванных факторов: _J-.ioo%> n2 = -sn- • 100% • При определении с с1
'-,16 'Об
достоверности влияния факторов применяется критерий Фишера, который вычисляется по следующей формуле: р = —ф-, где ст2 (так пазы-
ваемая девиата) обозначает дисперсию (вариацию), приходящуюся на один элемент свободного варьирования или на одну степень свободы. Вычисление девиат производится по следующим формулам:
- с ; . ___.с!————; , ..———__.._ " п - \ ''' кол - во групп -1 " п - кол - во групп
Оценивается критерий F по специальной таблице (приложение №3). Табличное значение F находится на пересечении граф: вертикальной, где значится число степеней свободы для меньшей дисперсии. Если величина F равна или больше табличной - влияние фактора доказано. Рассмотрим следующий пример (табл. 15).
В приведенном примере шок - организованный фактор, уровни поглощения кислорода - результативный признак. Чтобы судить о влиянии видов шока на окислительный процесс, необходимо определить средние уровни поглощения кислорода в каждой группе и всей совокупности. Мы видим (см. графу 3 табл. 15), что вычисленные средние арифметические в разных группах колеблются и отличаются от общей средней. Следует доказать силу влияния вида шока на уровни поглощения кислорода и достоверность его воздействия. Для этого определяются размеры дисперсий (см. графы 4, 5 и 6 табл. 15);, затем сила влияния организованного фактора г|2 и критерий F, после предварительного вычисления ст2:
rf = — .100% = — -100% = 87.7%
—————--4967.5 ' кол - во групп -1 3-1
Изучение окислении (степени поглощения кислорода) изолированной ткани при разных видах шока
| Вид шока (основной фактор) | Степень поглощения кислорода (результативный признак), V | Средние Уровни окисления ЕГ м =—- w | | Дисперсия | |
| Общая, С,=ЦУ-М,)1 | Факториальная, CUM,-M--N | Случайная (остаточная C,,=£(-A,)2 | |||
| ' | 2 | 3 | 4 | 5 | 6 |
| анафилактический | 228 206 217 | М,-р=217 | (228-239)2= =121 =1089 -489 | (239-217)2.3= =222.3=1452 | (228-217)2= =121 121 0 |
| гетеро-трансфу-зионный | 240 223 213 201 238 | М,р=223 | (240-239)2= =1 =256 =676 =1444 | (239-223)2.5= =162.5=1280 | (240-223)2= =289 =0 =100 =484 =225 |
| травматический | 291 295' 278 N-1:! | Мгр=288 | (291-239)2= =2704 =3136 -1521 | (239-288)23= =492.3=7203 | (291-288)2= =9 =49 -100 |
| | | Мо=239 | Со=11433 | Сф-9935 | Сел-1498 |
_ С, 1498 , °tA ~ „, —————————-~-=1о/.2
N - кол - во групп 11-3
4967.5 F=-JI=2Ь•5
Табличное значение F находится в данном случае на пересечении вертикальной 2-й графы (так как число степеней свободы для большей дисперсии равно: кол-во групп - 1 = =3-1 = 2 и горизонтальной 8-й строки (так как число степеней свободы для меньшей дисперсии равно: N - кол-во групп =11-3=8). Итак, рассчитанный критерий т]2 говорит о большой силе влияния вида шока на степень поглощения кислорода, а величина F, превышающая табличное значение
4.46-865,
\F "рТр" позволяет считать полученные результаты досто-г '»}
верными. Результаты дисперсионного анализа можно выразить в виде таблицы (табл. 16).
Таблица 16
Дисперсионный анализ изучения влияния шока на окислительный процесс изолированной ткани
| Виды факторов | Дисперсия, С | Сила влия-ния в %, ц2 | Число степеней свобо-ды | Девиата, (J2 | Fp 'о; | Табличное значение F | |
| Pos | Poi | ||||||
| Шок (основной фактор) Остаточные факторы (случайные) | 9935 1498 | 87.7 12.3 | 2 8 | 4967.5 187.2 | 26.5 | 4.46 | 8.65 |
| Всего | 11433 | 100.0 | 10 | | | | |
При сравнении трех и более показателей дисперсионный анализ проводится по следующей схеме (табл. 17).
Таблица 17
Изучение частоты летальных исходов при различных видах экстренной хирургической патологии
| | Число оперированных, N | Из них умерло, m | Частота летальных ИСХОДОВ Р N | Квадрат колебаний результативного признака, т~ А=- |
| 1 | 2 | 3 | 4 | 5 |
| 1. Аппендицит | 120 | 1 | 1/120=0.01 | 12/120=0.01 |
| 2. 0. Кишечная непроходимость | 60 | 3 | 3/60=0.05 | y/6Q=OA5 |
| 3. Ущемленная грыжа | 80 | 2 | 2/80=0.03 | 2•!/80=0.05 |
| 4. Прободная язва | 30 | 5 | 5/300=0.02 | 52/300=0.08 |
| 5. 0. Холецистит | 50 | 3 | 3/50=0.06 | У/50=0.\» |
| 6. 0. Панкреатит | 30 | 6 | 6/30=0.20 | W30=l.20 |
| 7.ВСЕГО | ZN = 370 | £m = 20 | 20/370 = =0.05 | £h= 1.67 |
Определяются частота летальных исходов (Р) и квадрат колебаний (h) результативного признака при каждом заболевании (см. графы 4 и 5 табл.17).
Расчеты показали, что частота летальных исходов колеблется от 0.01 при аппендиците до 0.20 при остром панкреатите. Следует установить достоверность и силу влияния вида патологии на частоту летальных исходов, то есть определить критерии F и ст2. Для этого вычисляются дисперсии по приведенным ниже формулам, где величина Н определяется отношением квадрата суммы результативного признака (в нашем примере - число летальных исходов) к общему числу наблюдений.
-¥-
С„=т-Н= 20-1.08 =18.92 Сф =h-H= 1.67 -1.08 =0.59 --l 8.92 -0.59 =18.33 или £„,-£/,=20 -1.67 =18.33 Затем вычисляются <т , <т и критерий F.
-——сф——г
кол - во групп -1 6-1
° „——са——— = = 0.05
Л'-кол-во групп 370-6
"-Л-°——-г
0-05
Полученный критерий F больше табличного (р<0.05) (приложение № 3), что подтверждает влияние характера патологии на частоту летальных исходов. Однако, доля влияния учтенного фактора
(патологии) на уровень частоты летальных исходов равна лишь 7.08/0
171 S10-3
Полученные данные свидетельствуют о том, что на частоту летальных исходов влияют и другие факторы (возраст больных, сроки доставки от начала заболевания, степень тяжести при поступлении, сопутствующие заболевания, качество лечения и ухода и т.д.)
