Geum.ru

Методические указания к курсовой работе по дисциплине «Теория автоматического управления»

Вид материалаМетодические указания

Содержание


Кизм - передаточный коэффициент измерительного устройства; К
1 Задание и рекомендуемый порядок выполнения курсовой работы
1.2 Требования к оформлению
1.3 Задание на курсовую работу
D-разбиения в плоскостях К
Для варианта с последовательным корректирующим устройством.
2.1 Устойчивость САУ
2.2 Показатели качества работы САУ
Статический стационарный режим
Медленно меняющиеся входные воздействия
Частотные показатели
б) вид и характерные частоты амплитудно-частотной характеристики замкнутой системы Ф()
2.3 Синтез САУ при регулярных воздействиях
2.4 Построение желаемой амплитудной характеристики САУ
2.6 Синтез последовательных корректирующих устройств
Приложение А (обязательное) Титульный лист к курсовым проектам и работам
Исследование линейной САУ
1 Тема курсовой работы “Исследование линейной САУ”
Календарный план-график
Подобный материал:
  1   2   3   4


Федеральное агентство по образованию

Филиал государственного образовательного учреждения

высшего профессионального образования

УФИМСКого ГОСУДАРСТВЕННого АВИАЦИОННого ТЕХНИЧЕСКого УНИВЕРСИТЕТа

в г. Ишимбае


Методические указания

к курсовой работе

по дисциплине «Теория автоматического управления»








Ишимбай 2009

УДК 681.51.01(07)

ББК 32.965(я7)


Методические указания к курсовой работе по дисциплине “Теория автоматического управления” /Филиал Уфимск. гос. авиац. техн. ун-та в Ишимбае; - Ишимбай, 2009. - 34 с.


Методические указания включают в себя варианты заданий и сведения по содержанию, объему и порядку выполнения курсовой работы по дисциплине “Теория автоматического управления”.

Методические указания предназначены для студентов филиала УГАТУ в г. Ишимбае направления подготовки дипломированного специалиста 657900 (220300) – “Автоматизированные технологии и производства” специальности 210200 (220301) – “Автоматизация технологических процессов и производств” (заочной формы обучения, 8 семестр, филиал УГАТУ в г. Ишимбае), а также могут быть полезны для студентов других специальностей.


Содержание
Введение ……………………………………………………………………
4

1
Задание и рекомендуемый порядок выполнения курсовой работы ………
6




1.1
Основное содержание курсовой работы ………………………….…..
6




1.2
Требования к оформлению …………………………………………….
7




1.3
Задание на курсовую работу………………..………………………….
7

2
Теоретическая часть……………………………………………..…………..
14




2.1
Устойчивость САУ …………………………………………………….
14




2.2
Показатели качества работы САУ …………………………………….
16




2.3

Синтез САУ при регулярных воздействиях ………………………….
23




2.4

Построение желаемой амплитудной характеристики САУ …………
25




2.5

Синтез последовательных корректирующих устройств ……………
28




Рекомендуемая литература …………………………………………………...
30




Приложение А. Титульный лист к курсовым проектам и работам ………...
31




Приложение Б. Задание на курсовую работу ………………………….…….
32




Приложение В. Календарный план-график выполнения

курсовой работы …………………………………………………………..…...

33




Приложение Г. Пример оформления аннотации ………………………..…..
34




Приложение Д. Расположение текста на листах пояснительной

записки …………………………………………………………………….…..

34



Введение

Учебная программа курса "Теория автоматического управления" предусматривает выполнение студентами курсовой работы в 8 семестре. Цель курсовой работы - закрепление теоретических разделов курса и приобретение навыков самостоятельного применения основных положений теории при решении конкретных задач проектирования и расчета систем автоматического управления. Правильное и четкое выполнение курсовой работы и ее защита являются хорошим подготовительным этапом перед дипломным проектированием.

Исследование систем автоматического управления может заключаться в решении одной из двух задач – задачи анализа и задачи синтеза. В первом случае дается система, включая значение параметров, и требуется определить ее свойства. Во втором случае, наоборот, задаются свойства, которыми должна обладать система, т.е. требования к ней, и необходимо создать систему, удовлетворяющую этим требованиям. Очевидно, что задача синтеза много сложнее анализа уже из-за ее неоднозначности.

Математическое описание системы начинается с разбиения ее на звенья и описание этих звеньев. Последнее может осуществляться либо аналитически в виде уравнений, связывающих входные и выходные величины звена, либо графически в виде характеристик, описывающих эту же связь. По уравнениям или характеристикам отдельных звеньев составляются уравнения или характеристики системы в целом, на основании которых и исследуется система.

Динамические свойства линейных звеньев и систем автоматического управления могут быть описаны как дифференциальными уравнениями так и графическими характеристиками. В теории автоматического управления применяются два типа таких характеристик – переходные и частотные. Эти характеристики могут быть определены экспериментальным путем или построены по уравнениям звеньев. Переходные и частотные характеристики однозначно связаны с уравнением звена и наряду с ним являются исчерпывающим описанием динамических свойств звена.

Курсовая работа является расчетно-исследовательской и предполагает проведение в полном объеме анализа динамики системы автоматического управления и синтеза параметров корректирующих устройств.

Объектом исследования является следящая система, структурная схема которой представлена на рис.1.




Рисунок 1 – Структурная схема следящей системы


Здесь Кизм - передаточный коэффициент измерительного устройства; Кфчв, Тф - коэффициент передачи и постоянная времени фазочувствительного выпрямителя; Ку - коэффициент усиления электронного усилителя; Кэму, Тэ - коэффициент передачи и постоянная времени электромашинного усилителя; Кд, Тд - коэффициент усиления и постоянная времени электрического двигателя; Кред - коэффициент передачи редуктора.

Исходные данные для расчета приведены в табл.1.

Курсовая работа выполняется на материале теоретических разделов дисциплины ”ТАУ” изученных в 7 и 8 семестрах, в которых рассматривались непрерывные стационарные линейные системы.

1 Задание и рекомендуемый порядок выполнения курсовой работы

1.1 Основное содержание курсовой работы

Пояснительная записка (ПЗ) курсовой работы должна включать:

- титульный лист;

- задание на курсовую работу;

- содержание (оглавление);

- основную часть курсовой работы;

- заключение;

- список литературы;

- приложения (при необходимости).

Первым листом документа является титульный лист - приложение А, вторым - задание на дипломное (курсовое) проектирование - приложение Б, третьим - календарный план работы над дипломным проектом - приложение В. Эти листы выполняются на бланках установленного образца. Четвертым листом документа является аннотация. В аннотации содержится краткое содержание работы, назначение, цель курсовой работы, основные результаты (обычно не более 10 - 15 строк). Этот лист начинается с полного названия проекта с указанием его вида - курсовая работа и общего числа листов документа. Эту запись выполняют в верхней части листа, затем с интервалом 30 - 35 мм вписывают слово “Аннотация” с прописной буквы, за которым следует текст. Текст заканчивают перечислением количества иллюстраций, таблиц, литературных источников приложение - Г.

Пятым листом курсовой работы является первый (заглавный) лист текста пояснительной записки. Заглавный лист текста выполняют с основной надписью для текстовых документов по ГОСТ 2.104-90, форма 2. На нем помещают первый лист содержания пояснительной записки, которое начинают заголовком “Содержание” с первой прописной буквой. В содержание включают все разделы и подразделы пояснительной записки, начиная с введения и заканчивая заключением, а также список литературы и приложения. Последующие листы содержания имеют основную надпись для текстовых документов по ГОСТ 2.104-90, форма 2а.

После листа с содержанием следует основной текст пояснительной записки, который выполняют на специально расчерченных листах для текстовых документов формата А4 (размер 210297 мм) или листах с рамкой (форма 2а, ГОСТ 2.104-90) с упрощенным изображением основной надписи, в которой проставляют номер листа. Расположение текста на листах пояснительной записки показано в приложении Д.


1.2 Требования к оформлению

Пояснительная записка (ПЗ) должна быть оформлена в формате редактора Win Word 6.0 (или выше), шрифт Times New Roman C (14). ПЗ оформляется на бумаге, формата А4 в соответствии с требованиями ГОСТ 2.105–95 ЕСКД. Общие требования к текстовым документам и ГОСТ 2.104-90 ЕСКД. Основные надписи. Текст печатается через 1,5 интервала, размет – 14pt, красная строка – 1,25 см. Формулы набираются латинским шрифтом. Номера формул ставятся по порядку в круглых скобках. Ссылки на таблицы, рисунки, литературу и т.д. обязательно должны быть в тексте. Ссылки на литературу ставятся в квадратных скобках. Выравнивание текста по ширине. Рисунки выполняются размером не менее 70х120 мм, надписи внутри рисунка шрифт Times New Roman не менее 11 pt.

1.3 Задание на курсовую работу

Для заданного варианта курсовой работы необходимо выполнить следующие пункты задания.

Для варианта с параллельным корректирующим устройством.

1. Построить асимптотическую ЛАХ и ЛФХ разомкнутой нескорректированной САУ (без учета корректирующего устройства), приняв коэффициент усиления электронного усилителя Ку=100. Определить частоту среза с и фазовый сдвиг на этой частоте.

Таблица 1 – Исходные данные


№

вари-анта
Кизм,

В/град
Кэму,

В/мА
Тф,

с
Тэ,

с
Кд,

рад/с·В
Тд,

с
Кред,

град/рад
Кфчв
задающее воздействие g(t)=
допустимые значения ошибок
































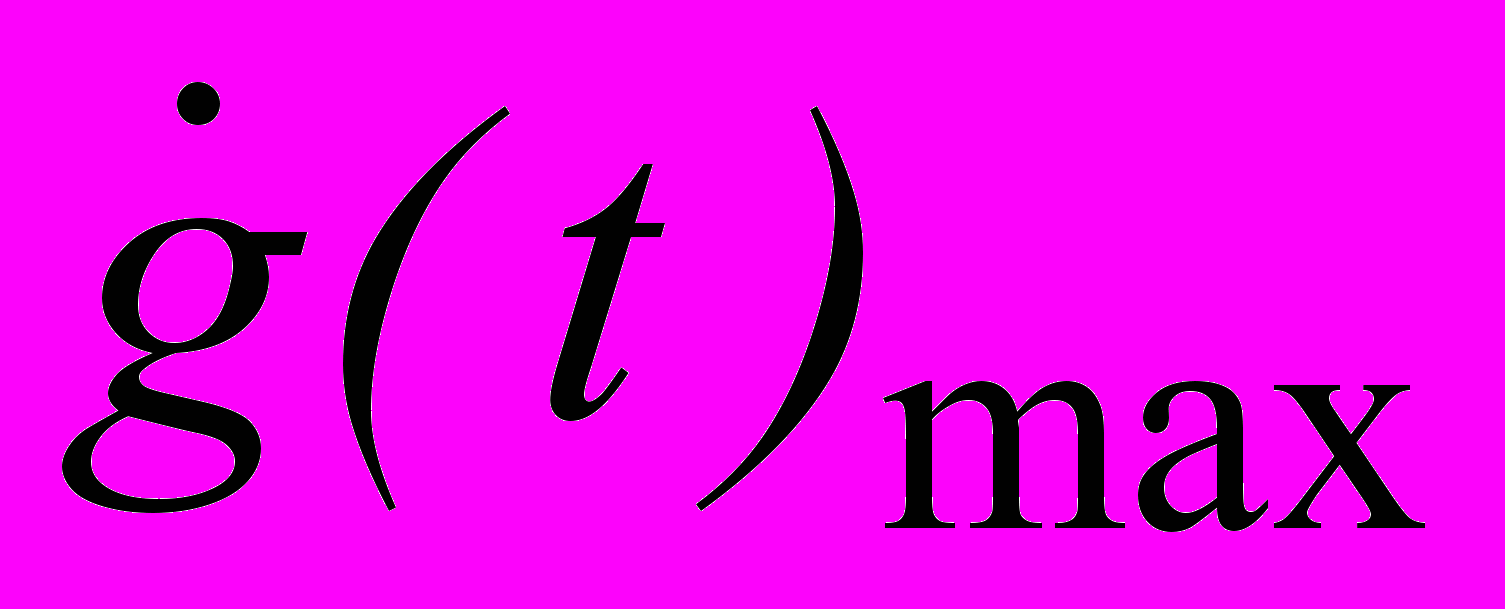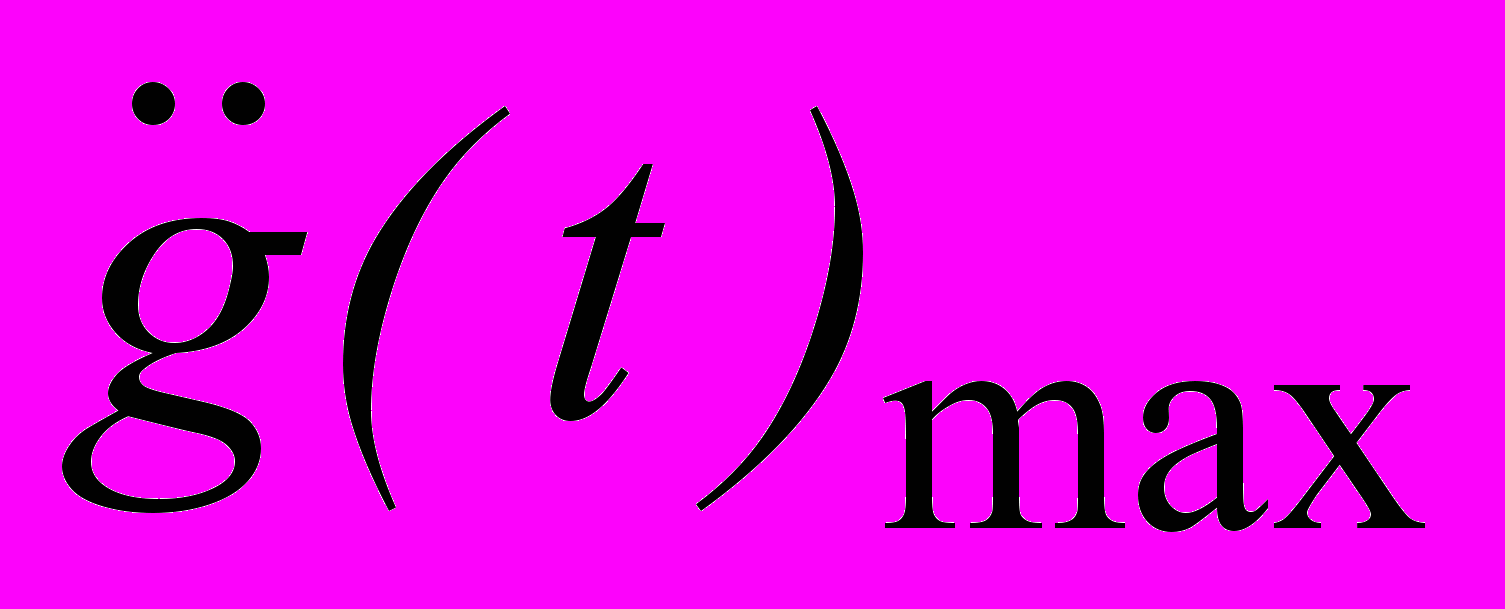v, град
w, град

1
2
3
4
5
6
7
8
9
10
11
12
13

1
30
4
0,008
0,025
1
0,1
0,002
1
15
2
0,12
0,06

2
20
3
0,006
0,03
2
0,2
0,001
0,8
20
3
0,21
0,07

3
18
2,5
0,004
0,01
3
0,1
0,001
0,75
25
4
0,4
0,2

4
30
3,8
0,005
0,028
4
0,2
0,002
0,9
12
1,5
0,1
0,04

5
25
3,2
0,007
0,03
5
0,15
0,001
1
20
2
0,1
0,05

6
15
2,0
0,004
0,02
1
0,13
0,002
0,6
30
5
0,14
0,07

7
28
3,4
0,008
0,029
1,5
0,17
0,003
1
18
2,5
0,16
0,04

8
26
3,6
0,004
0,014
2
0,15
0,005
0,5
16
2,5
0,18
0,06

9
18
2,2
0,008
0,019
2.25
0,2
0,001
0,8
28
4,5
0,25
-

10
22
2,8
0,007
0,03
2,18
0,25
0,004
0,7
20
3
0,18
-

11
24
3,3
0,005
0,015
2,14
0,3
0,005
1
22
3,5
0,14
-

12
14
3,4
0,006
0,018
2,16
0,25
0,001
0,9
26
4,5
0,16
-

13
28
3,8
0,005
0,02
2,14
0,1
0,002
0,8
17
1,6
0,14
-

14
15
2,0
0,004
0,015
2,15
0,3
0,003
1
17
2,8
0,1
-

15
20
4,2
0,007
0,025
2,22
0,15
0,004
0,6
18
4
0,22
-




Продолжение таблицы 1


1
2
3
4
5
6
7
8
9
10
11
12
13

16
22
3,2
0,007
0,02
1,5
0,13
0,005
0,7
30
3,8
0,22
-

17
30
2,8
0,006
0,025
2
0,11
0,001
0,8
32
4,6
0,1
-

18
28
1,6
0,005
0,015
2,5
0,12
0,002
1
28
2,8
0,14
-

19
22
1,4
0,004
0,025
3
0,15
0,003
0,75
18
3,2
0,18
-

20
18
2,2
0,005
0,03
3,5
0,1
0,004
0,5
15
4,5
0,25
-

21
14
3,4
0,006
0,015
4
0,2
0,005
0,5
30
2,5
0,2
-

22
16
4,0
0,007
0,025
1,5
0,15
0,001
0,8
26
2
0,16
-

23
26
2,8
0,008
0,003
2
0,12
0,002
0,9
22
4
0,18
-

24
32
1,6
0,007
0,01
2,5
0,13
0,003
1
18
3
0,22
-

25
24
1,8
0,006
0,02
3
0,2
0,004
1
14
5
0,2
-

26
15
2,6
0,005
0,03
3,5
0,1
0,005
0,7
28
2
0,14
-






Таблица 2 – Корректирующие устройства

№
Передаточная функция
№
Передаточная функция

1


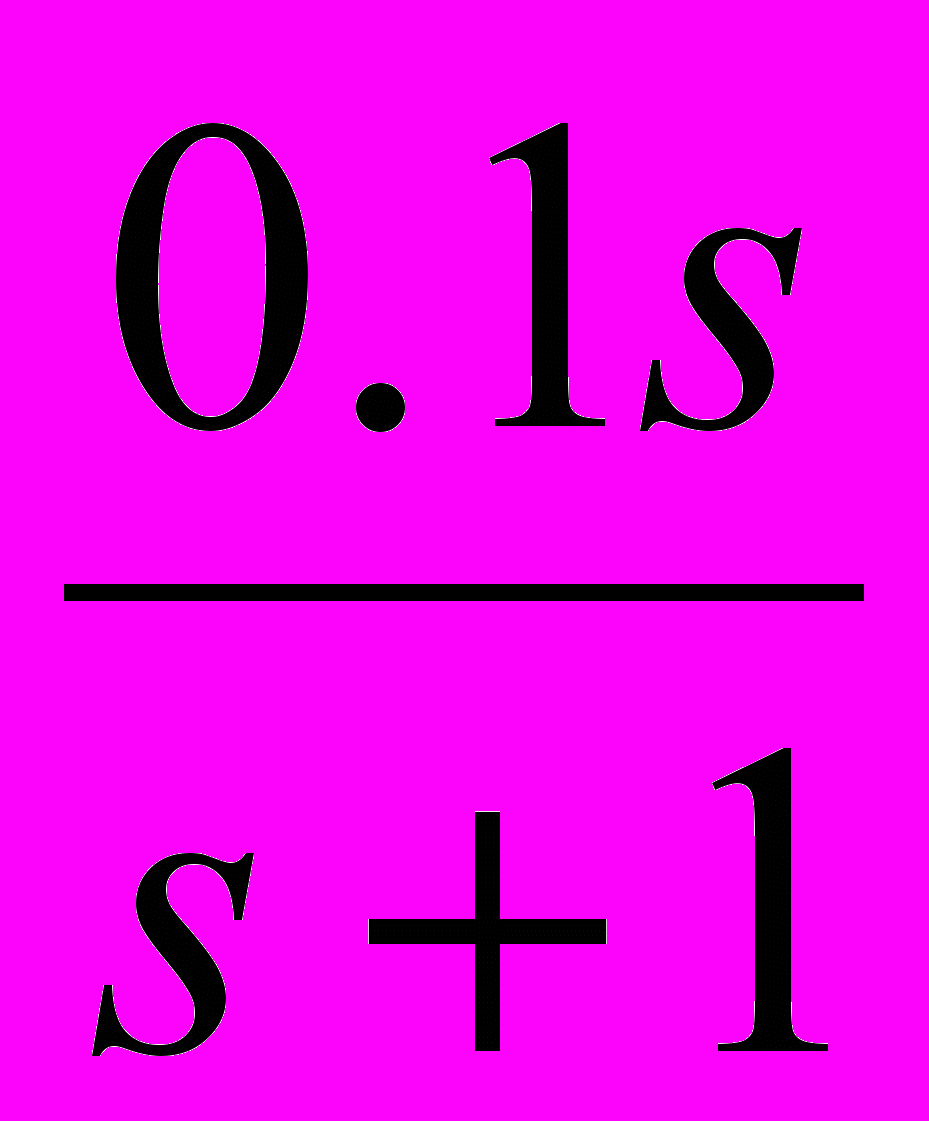
14


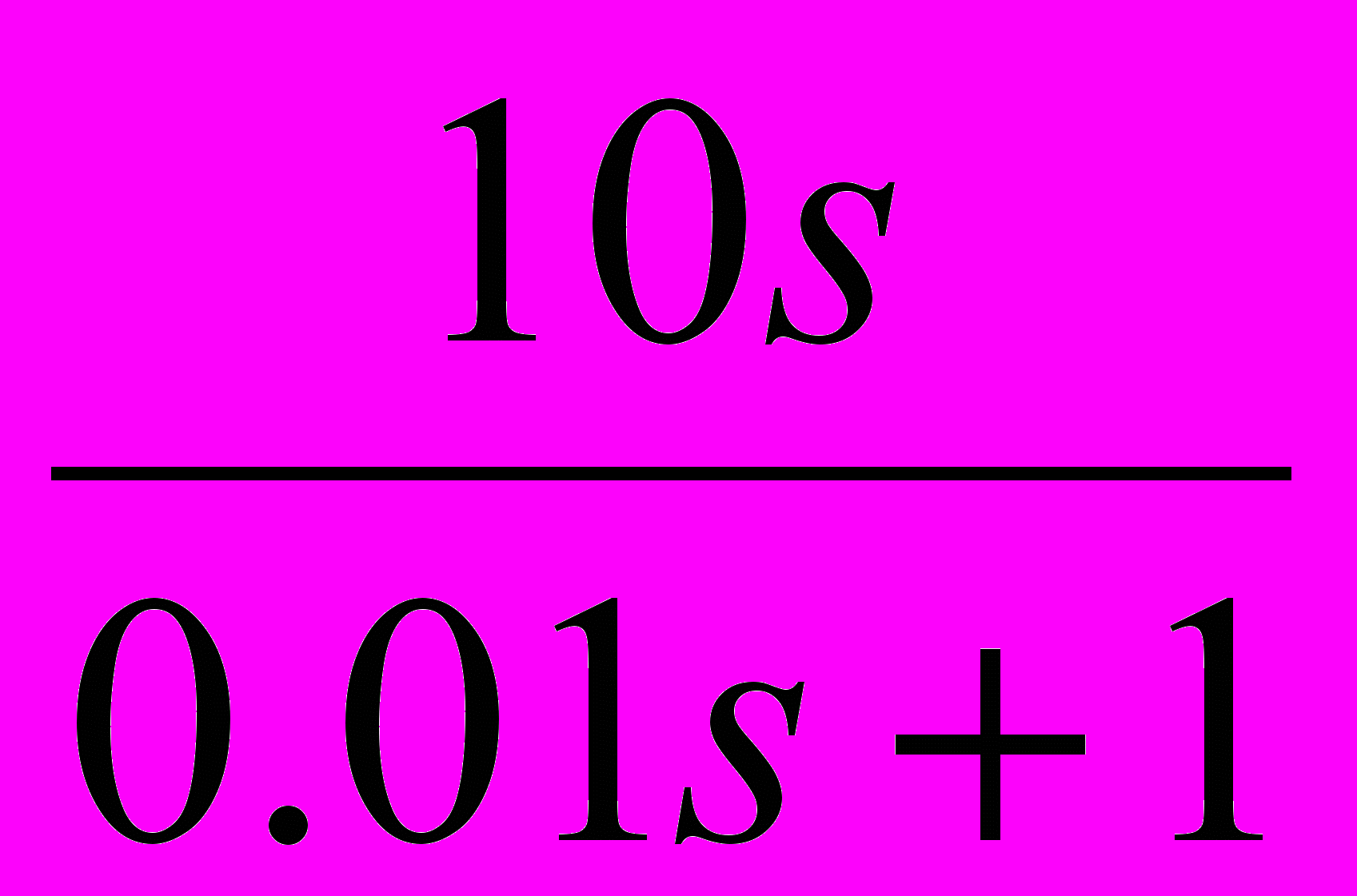
2


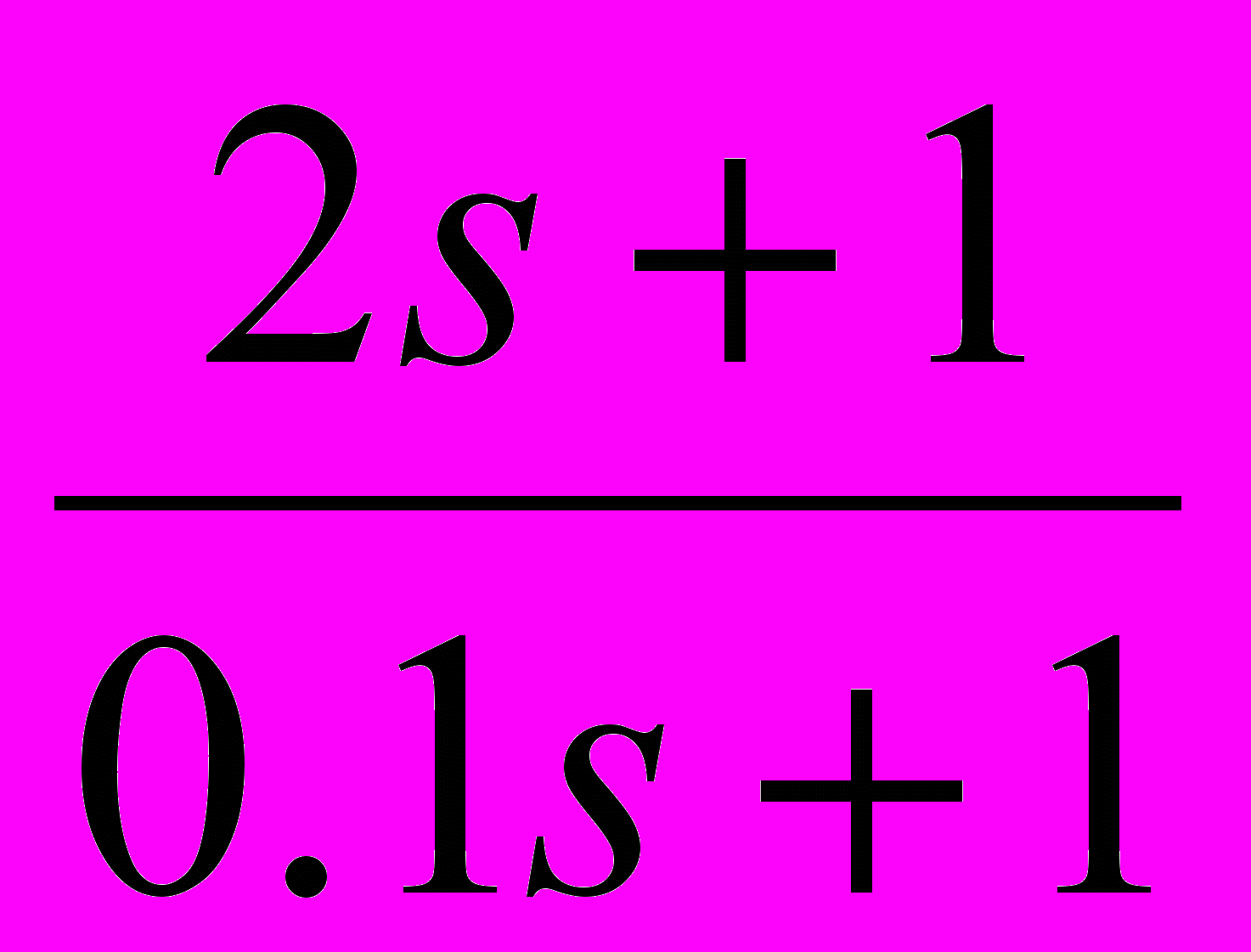
15


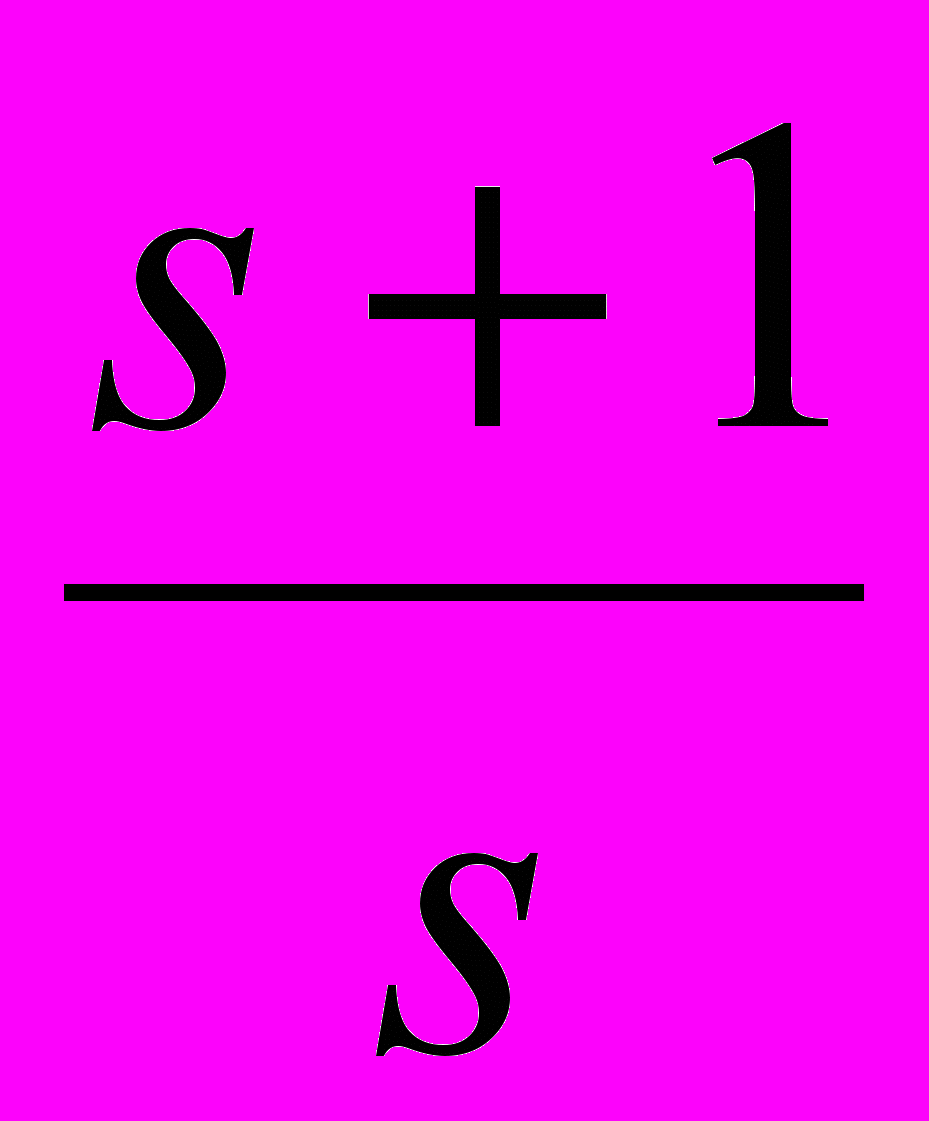
3


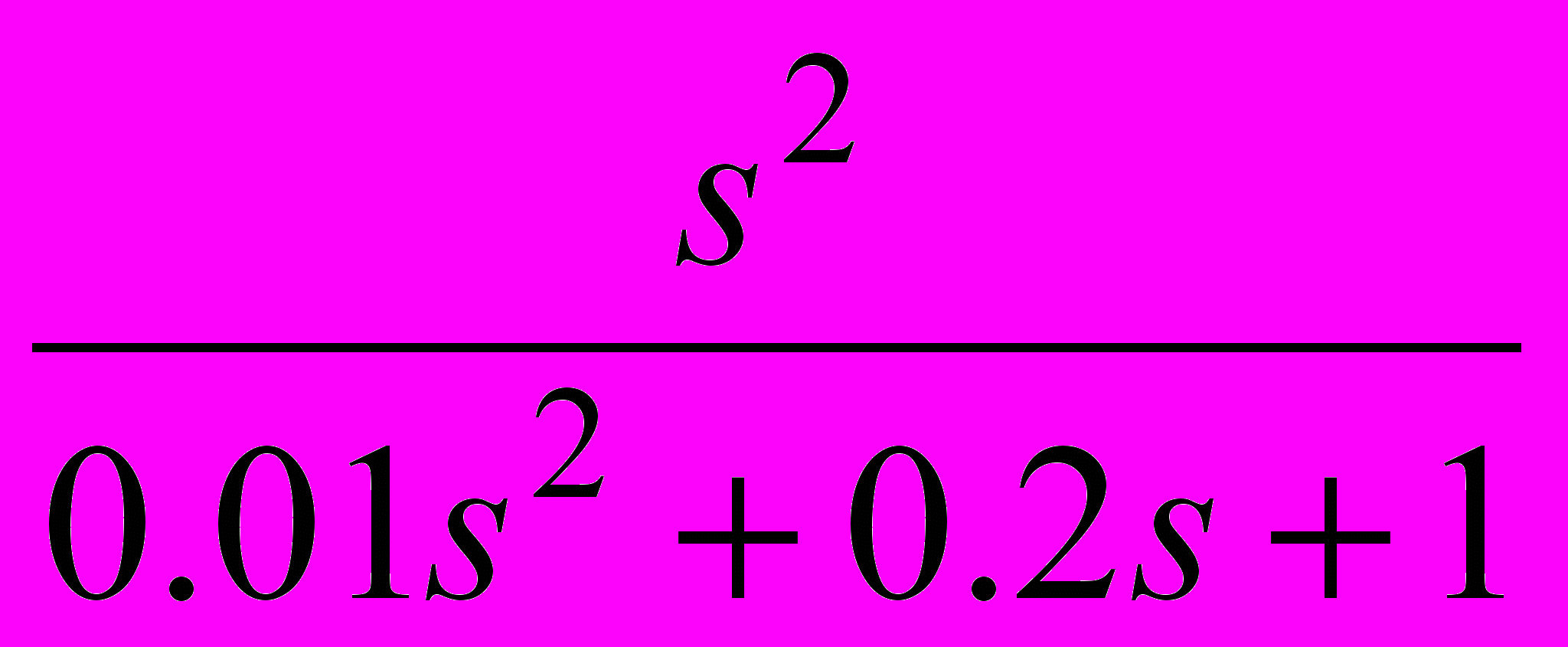
16


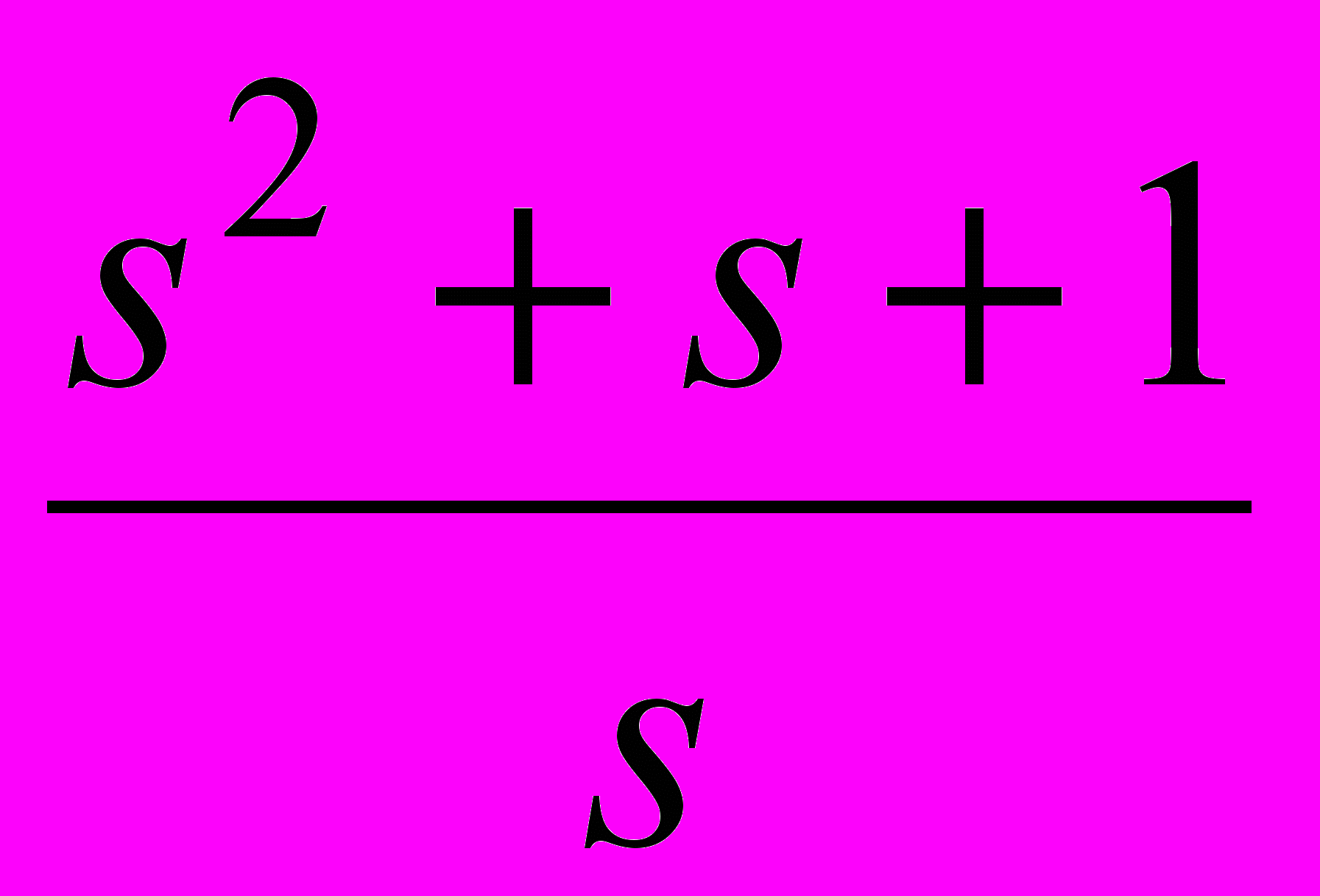
4


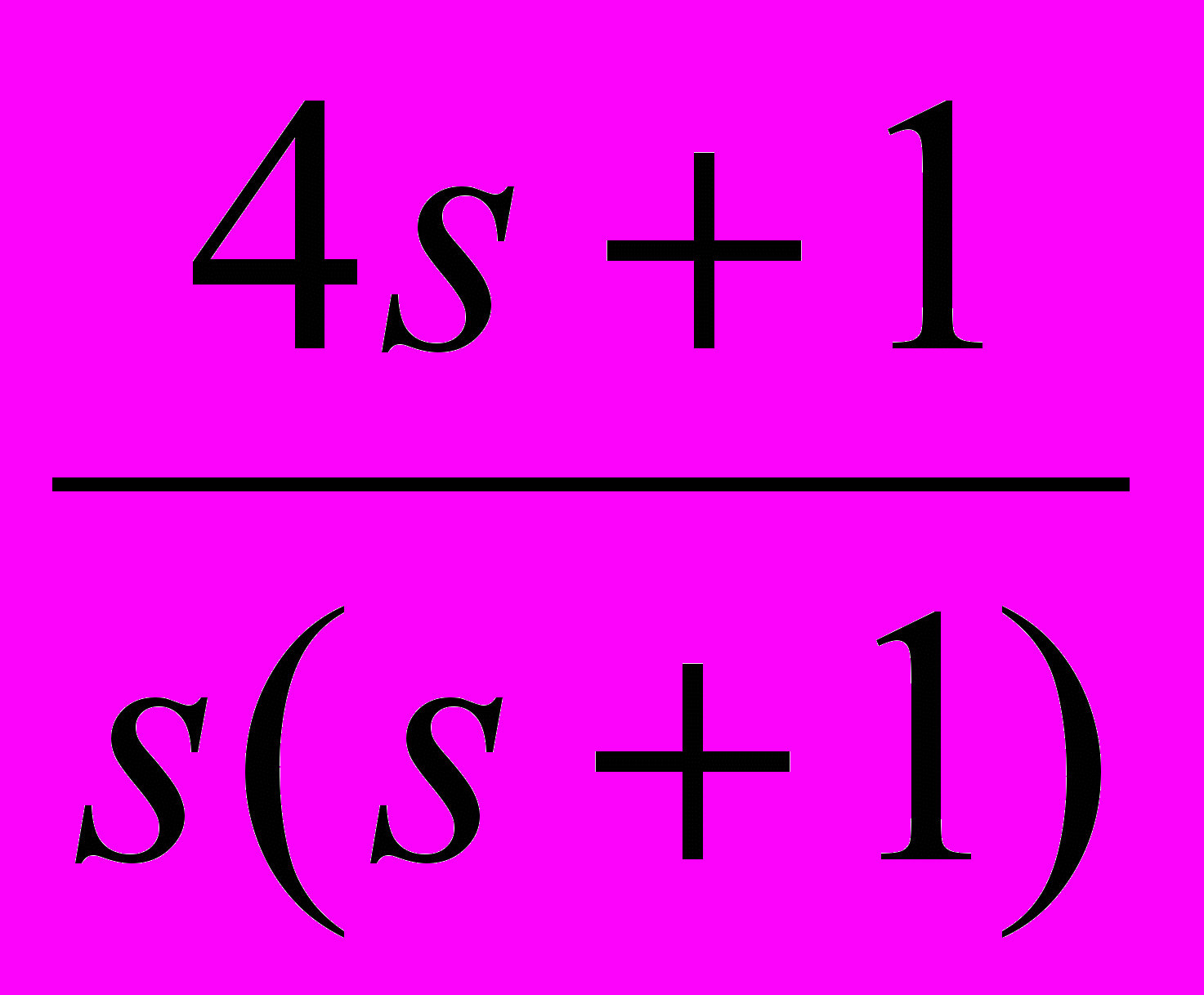
17


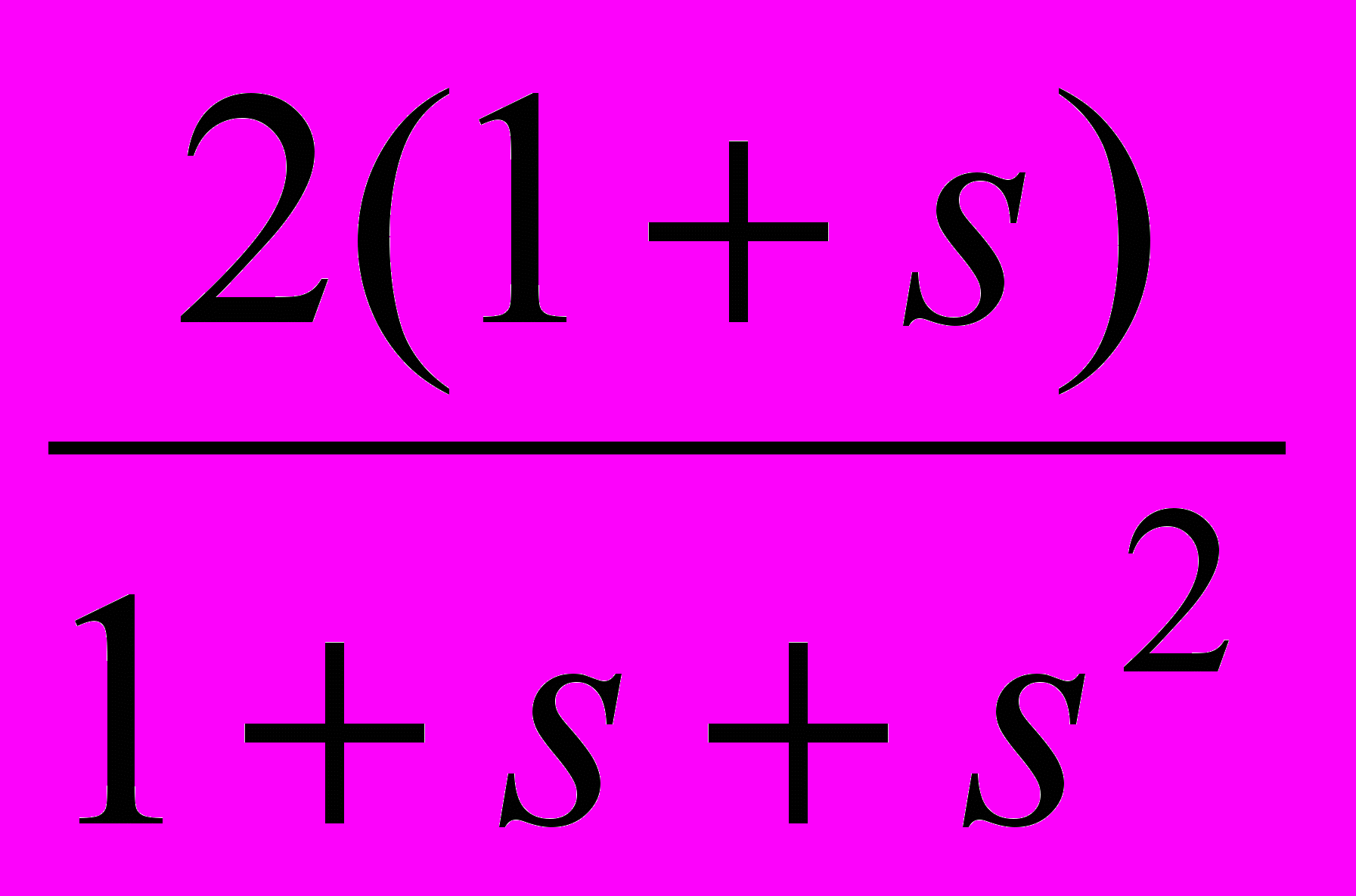
5


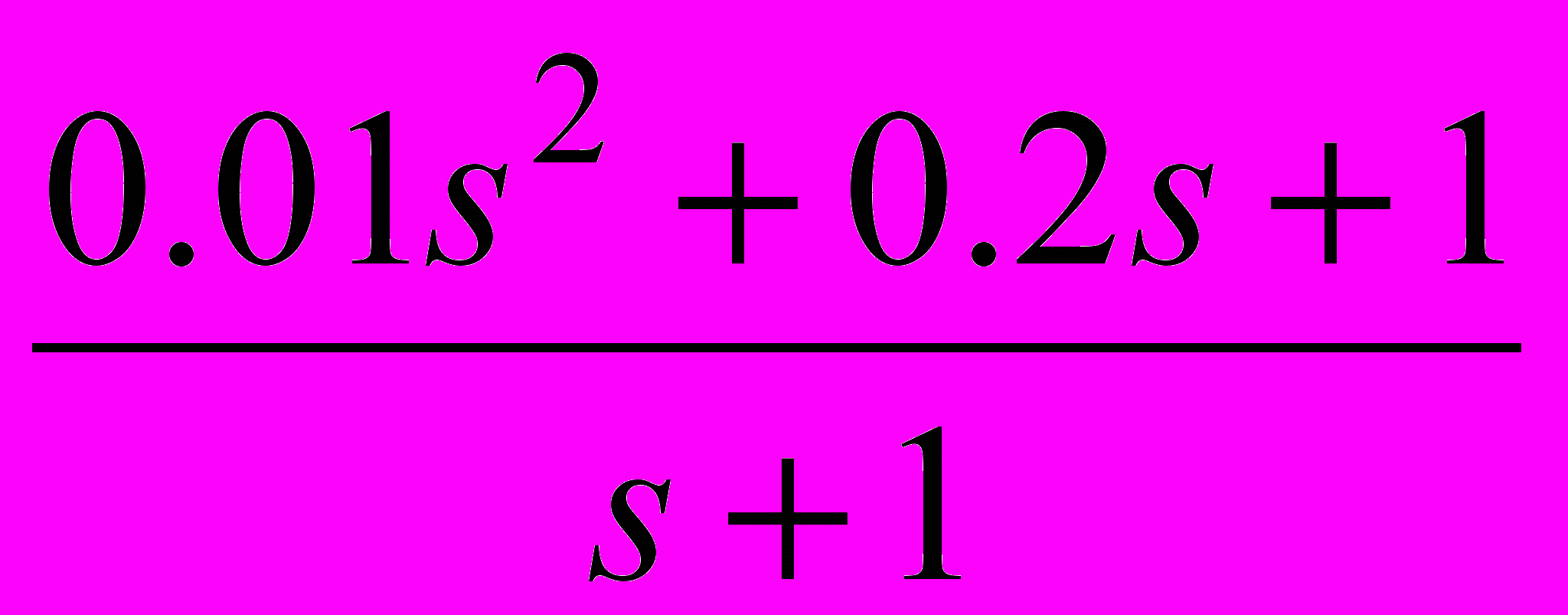
18


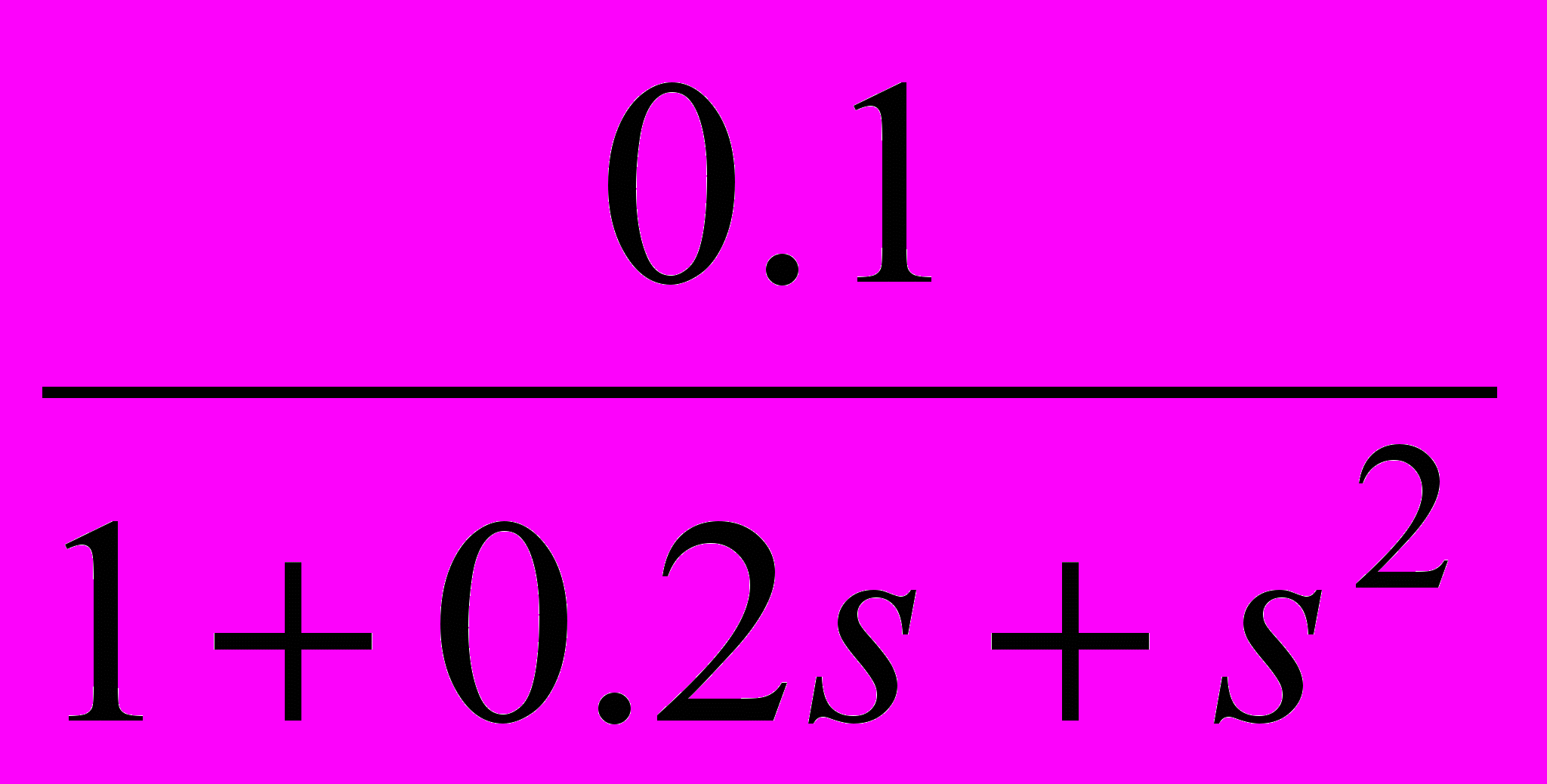
6


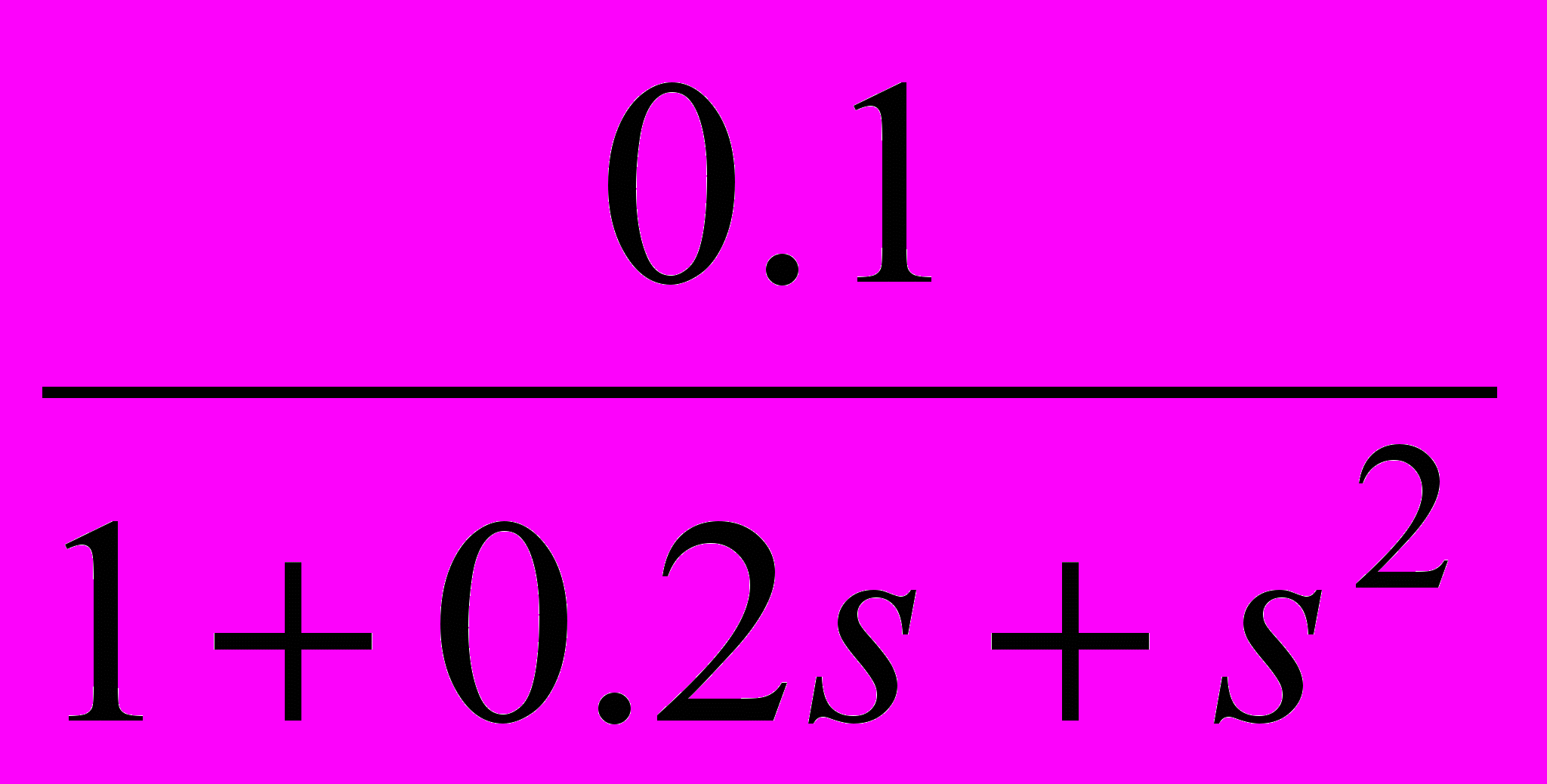
19


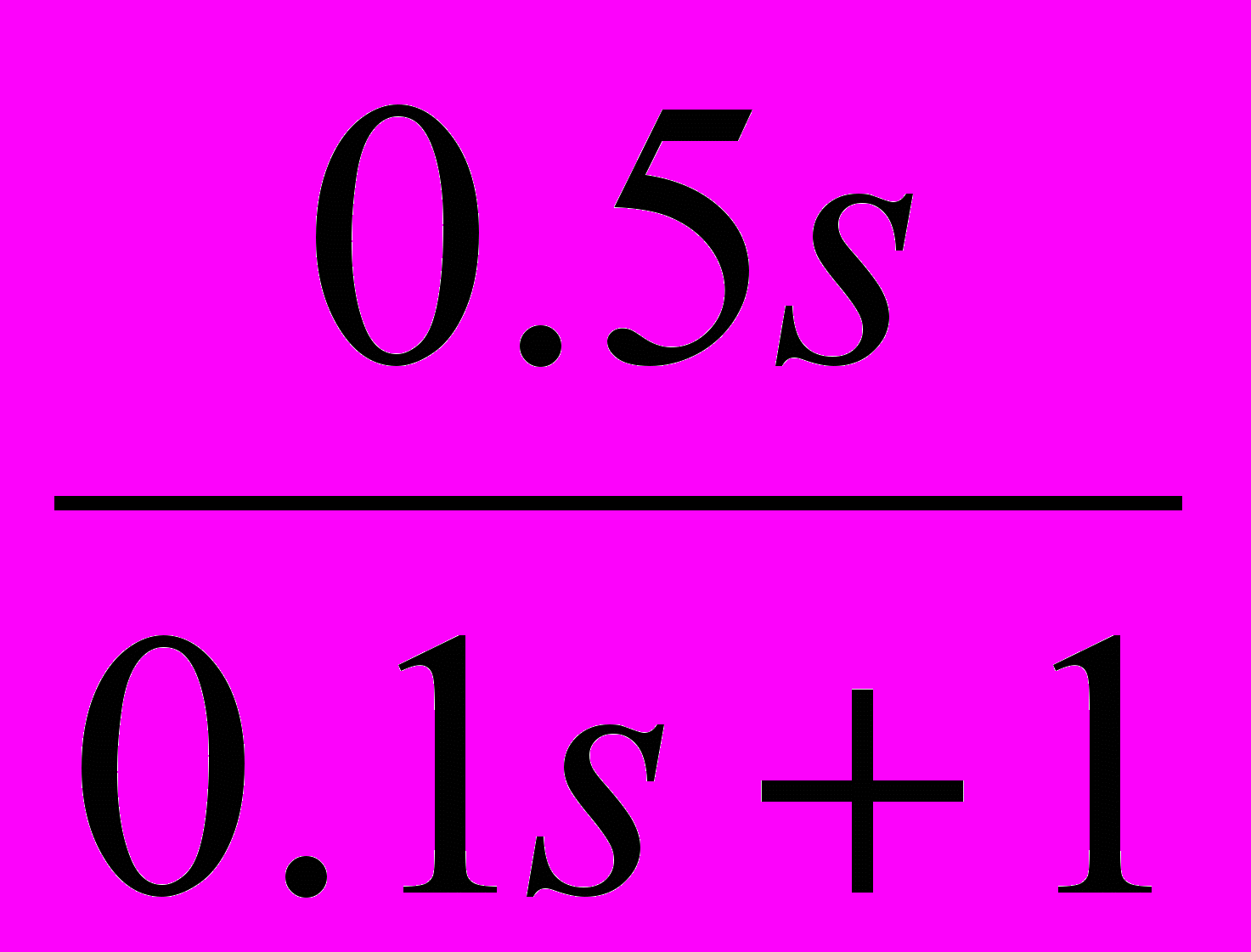
7


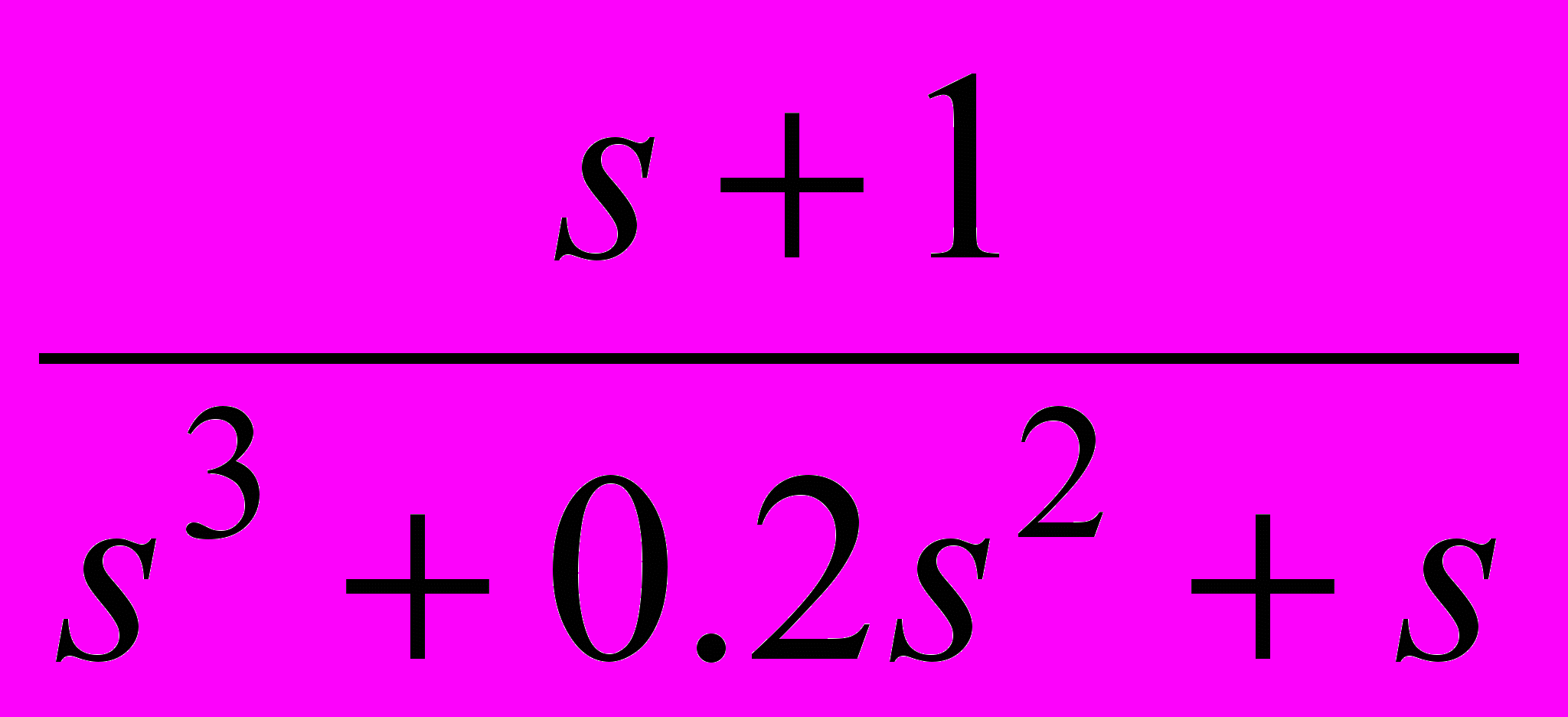
20


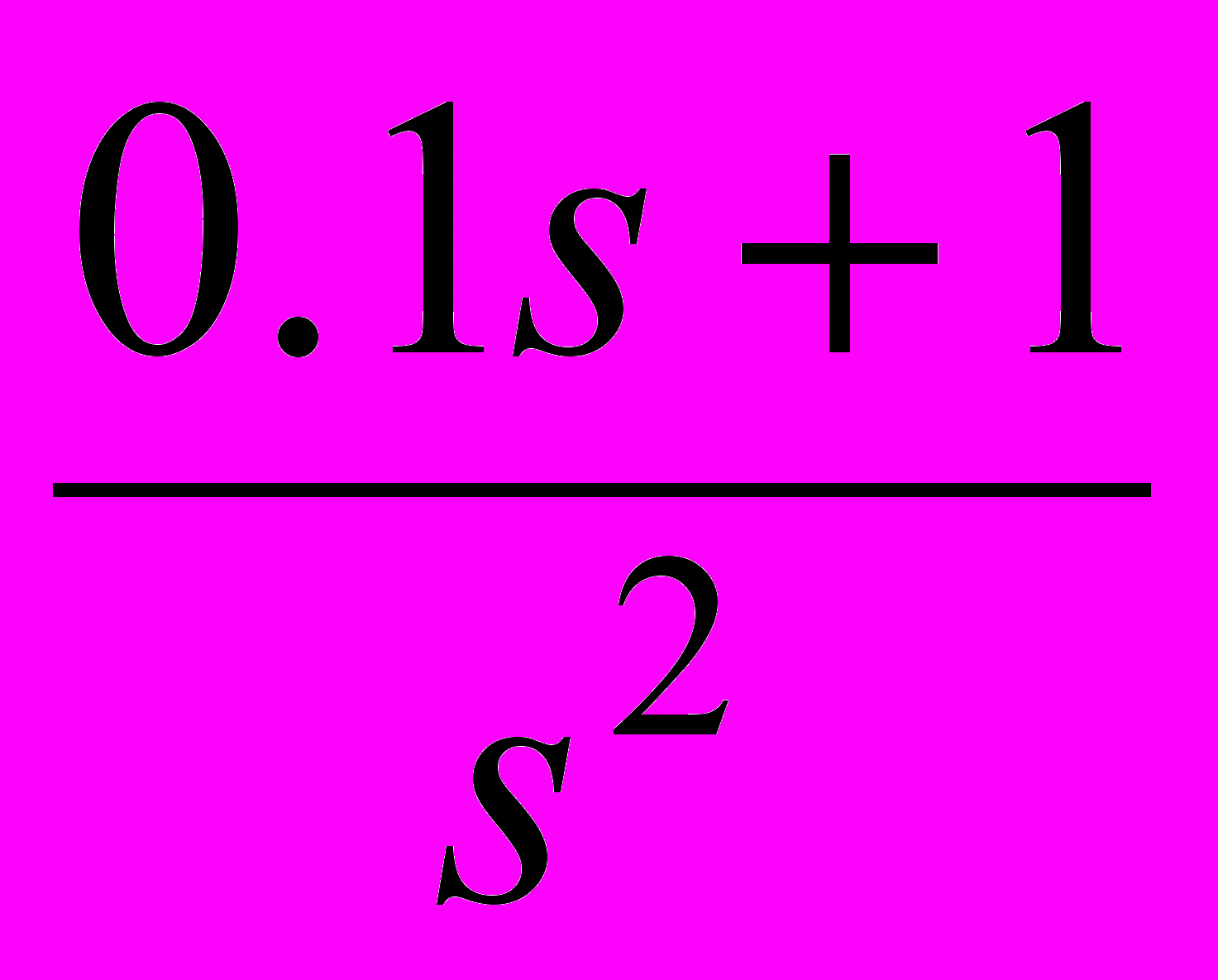
8


21


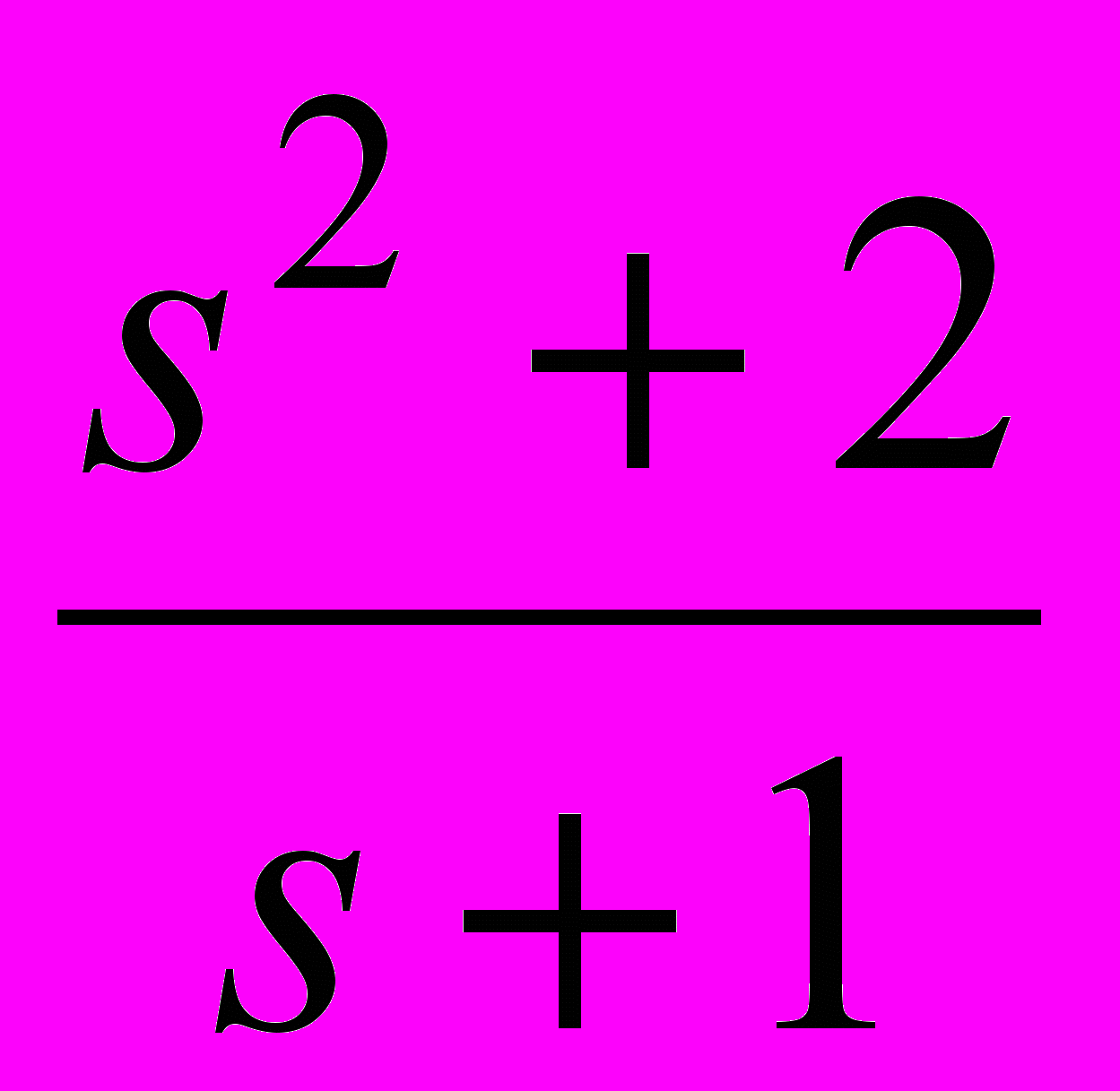
9


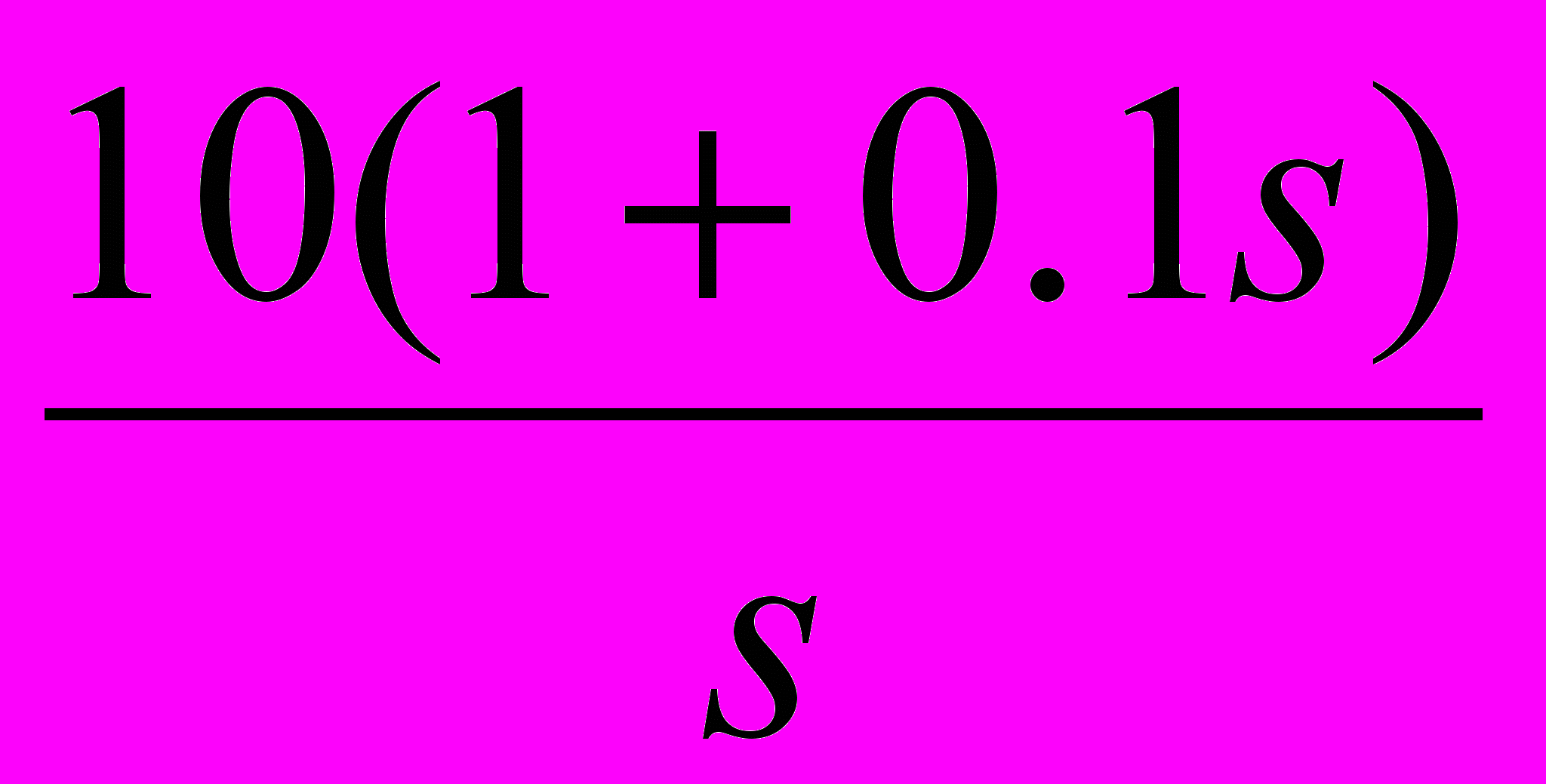
22


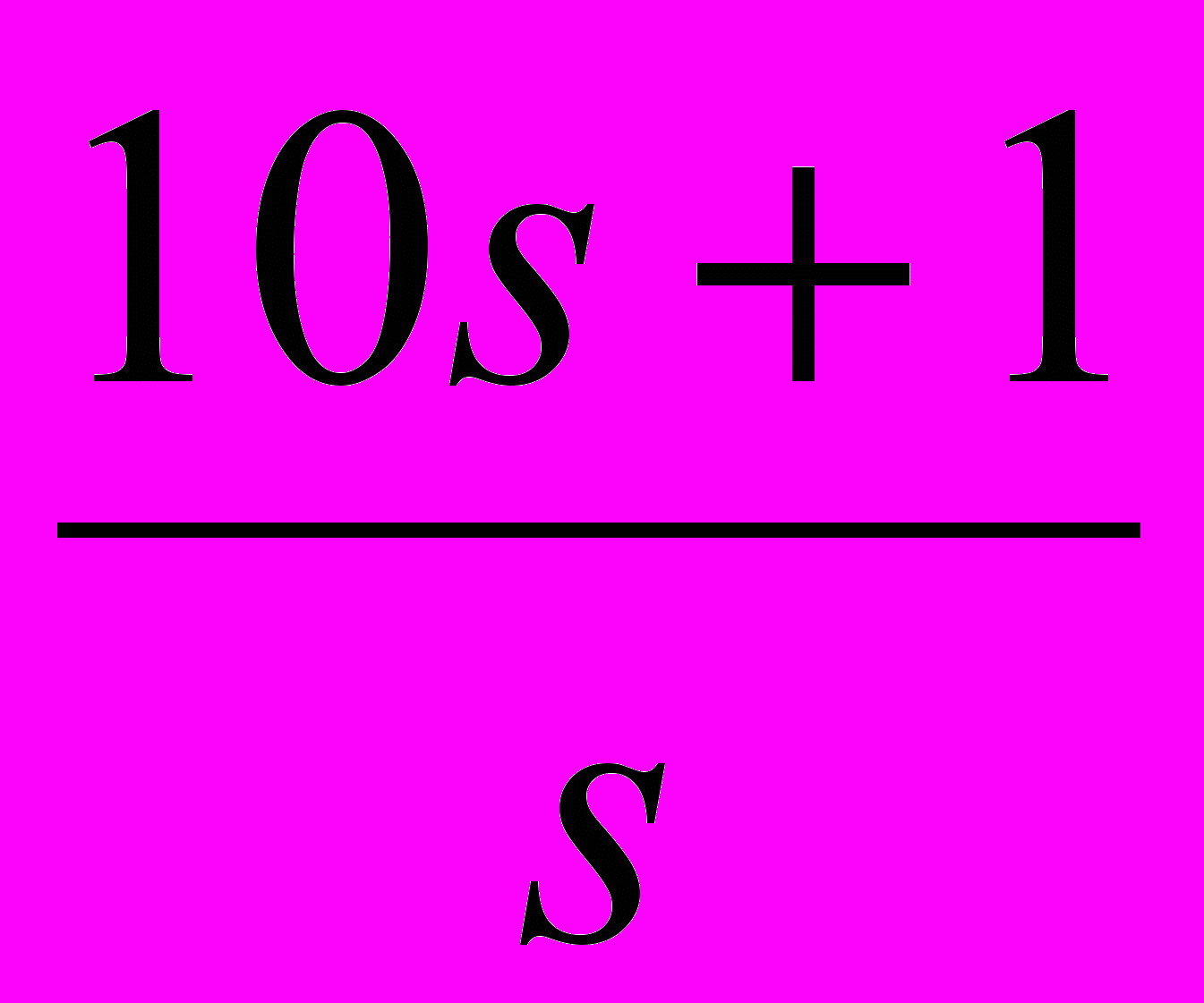
10


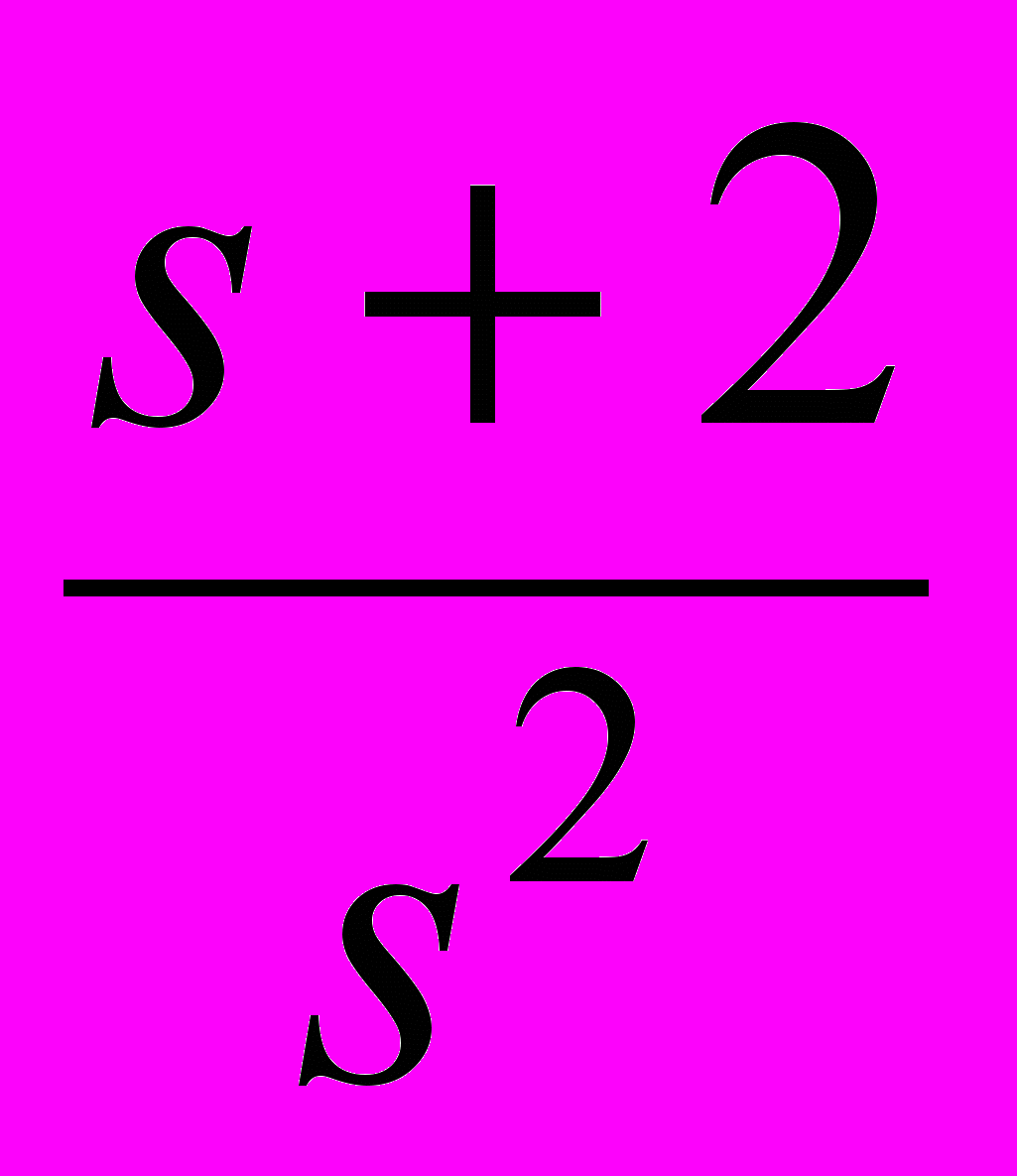
23


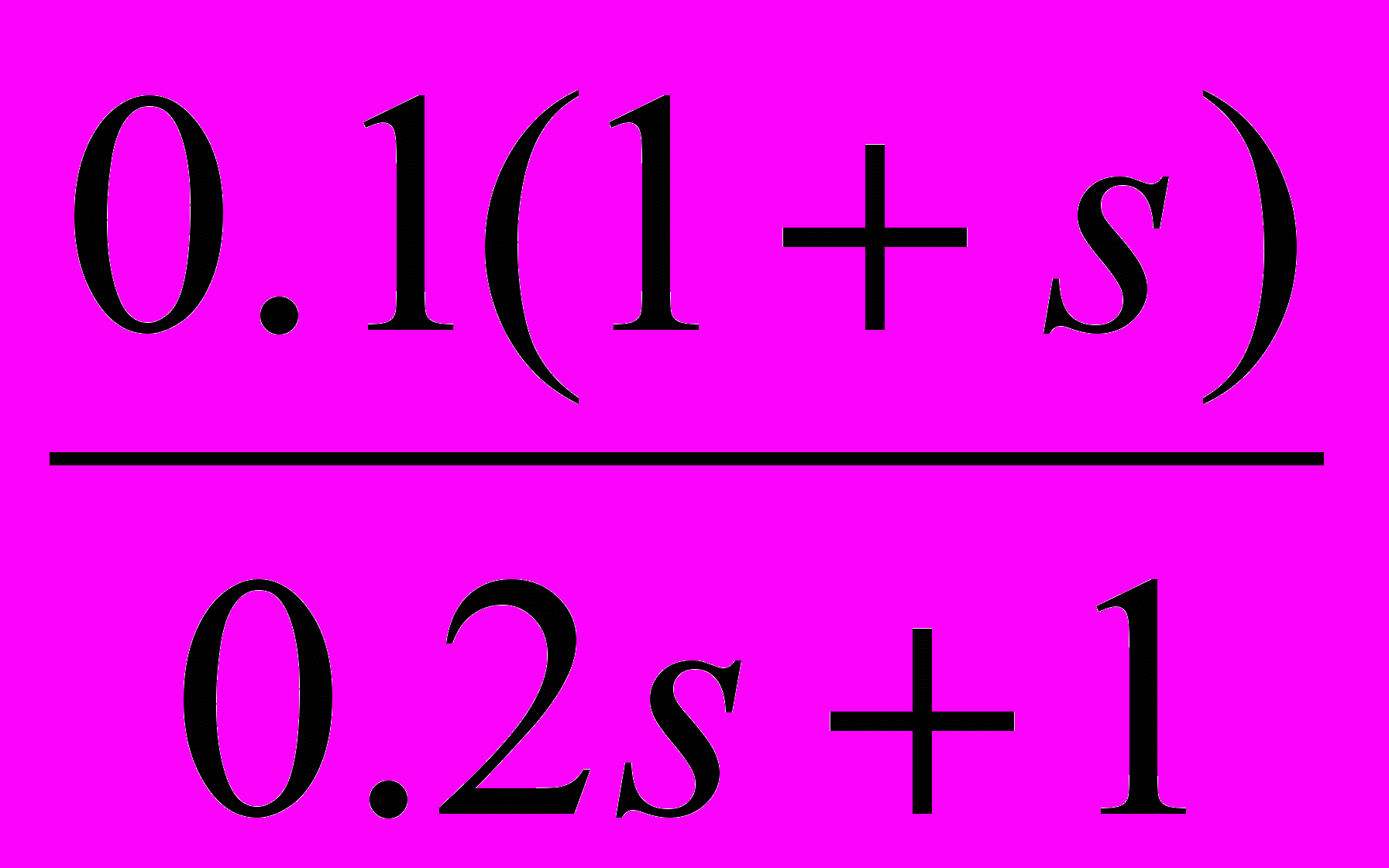
11


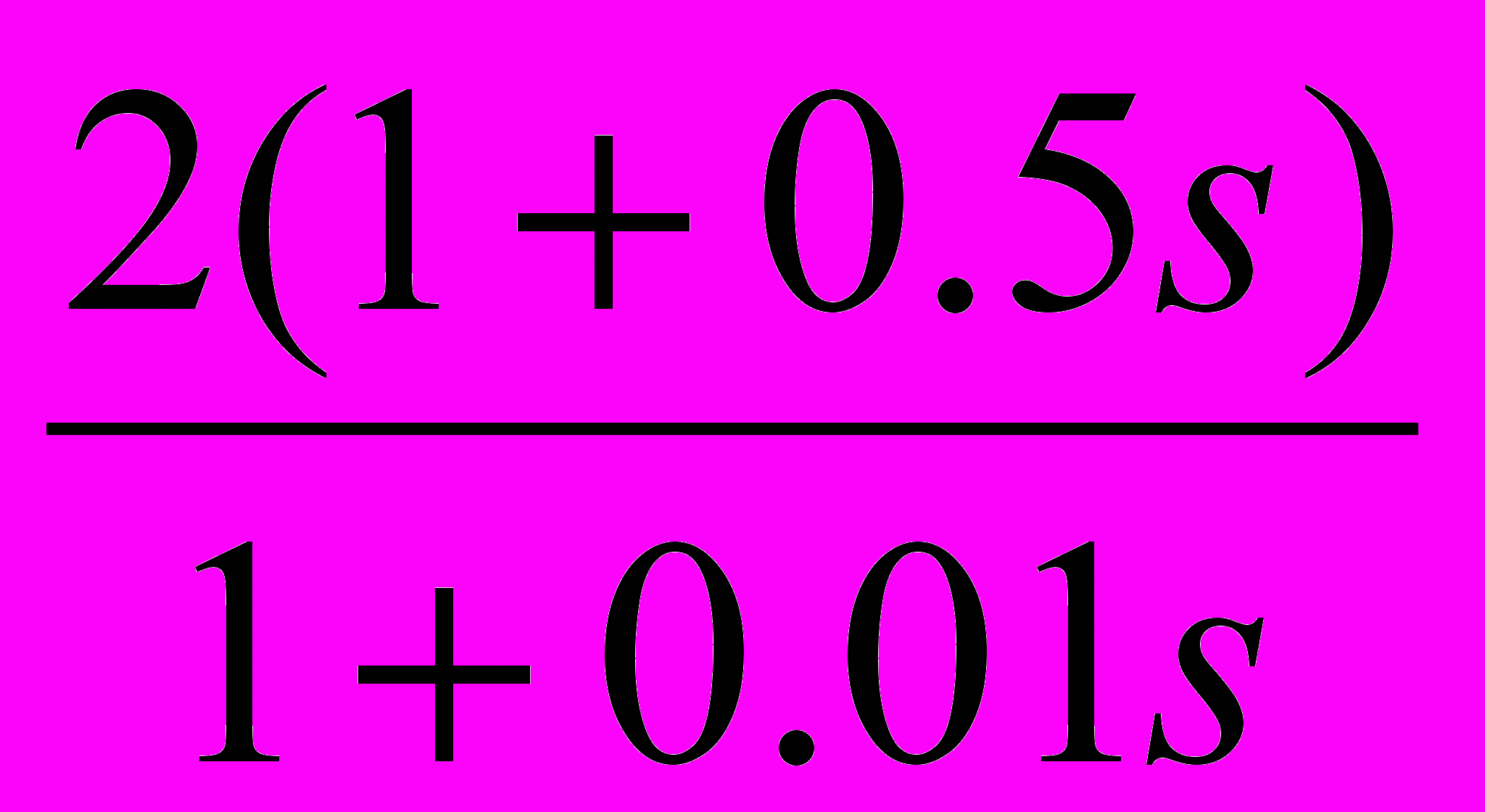
24


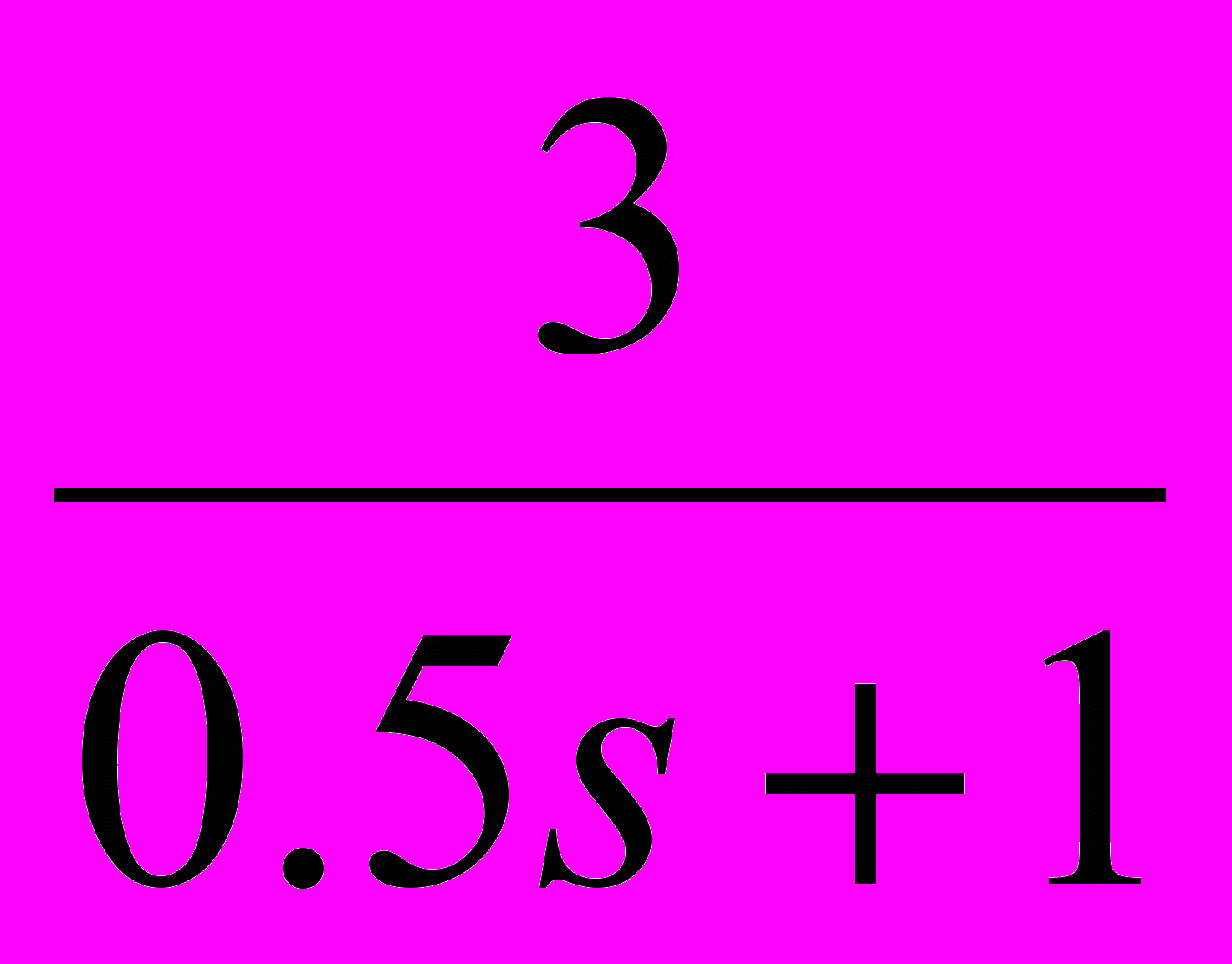
12


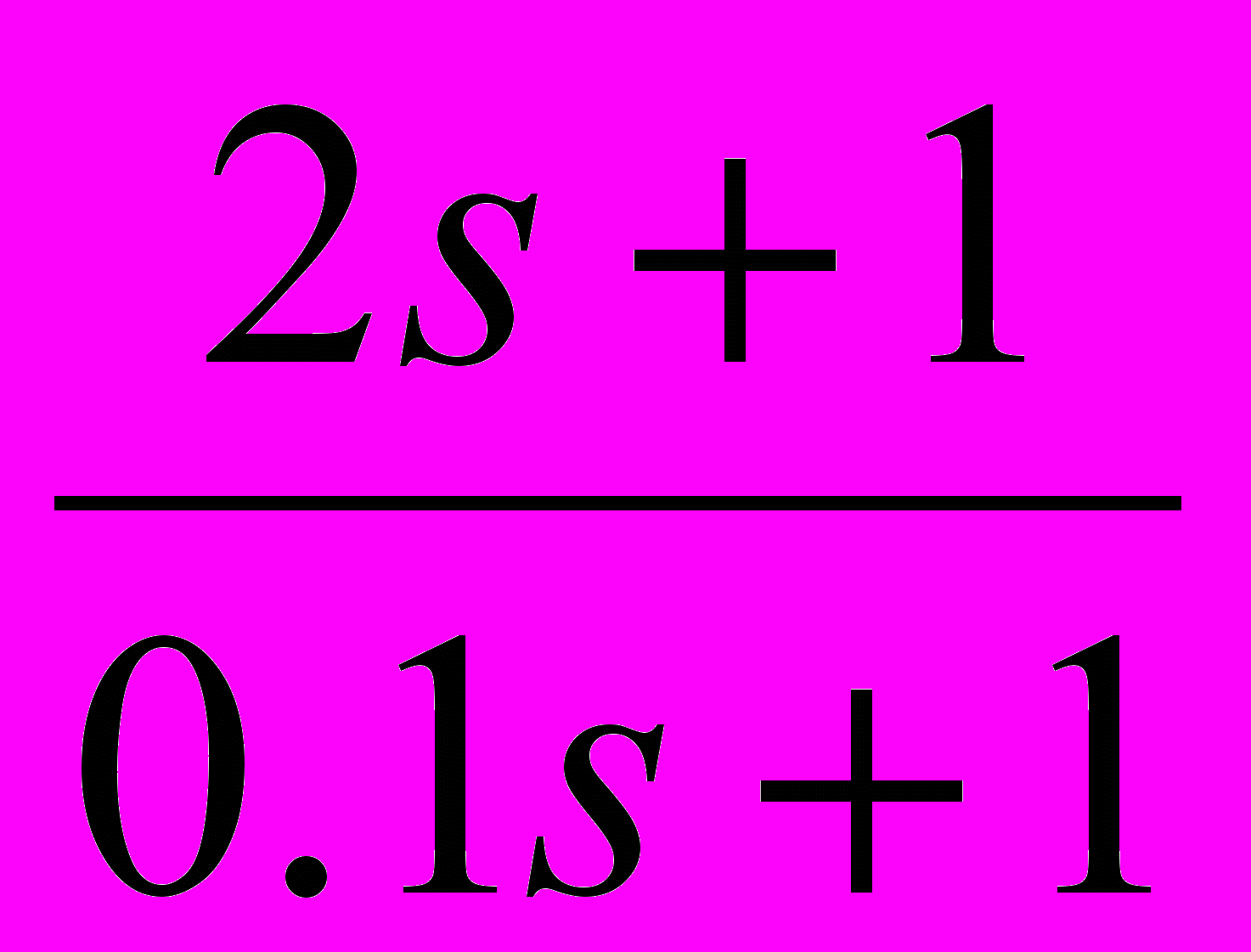
25


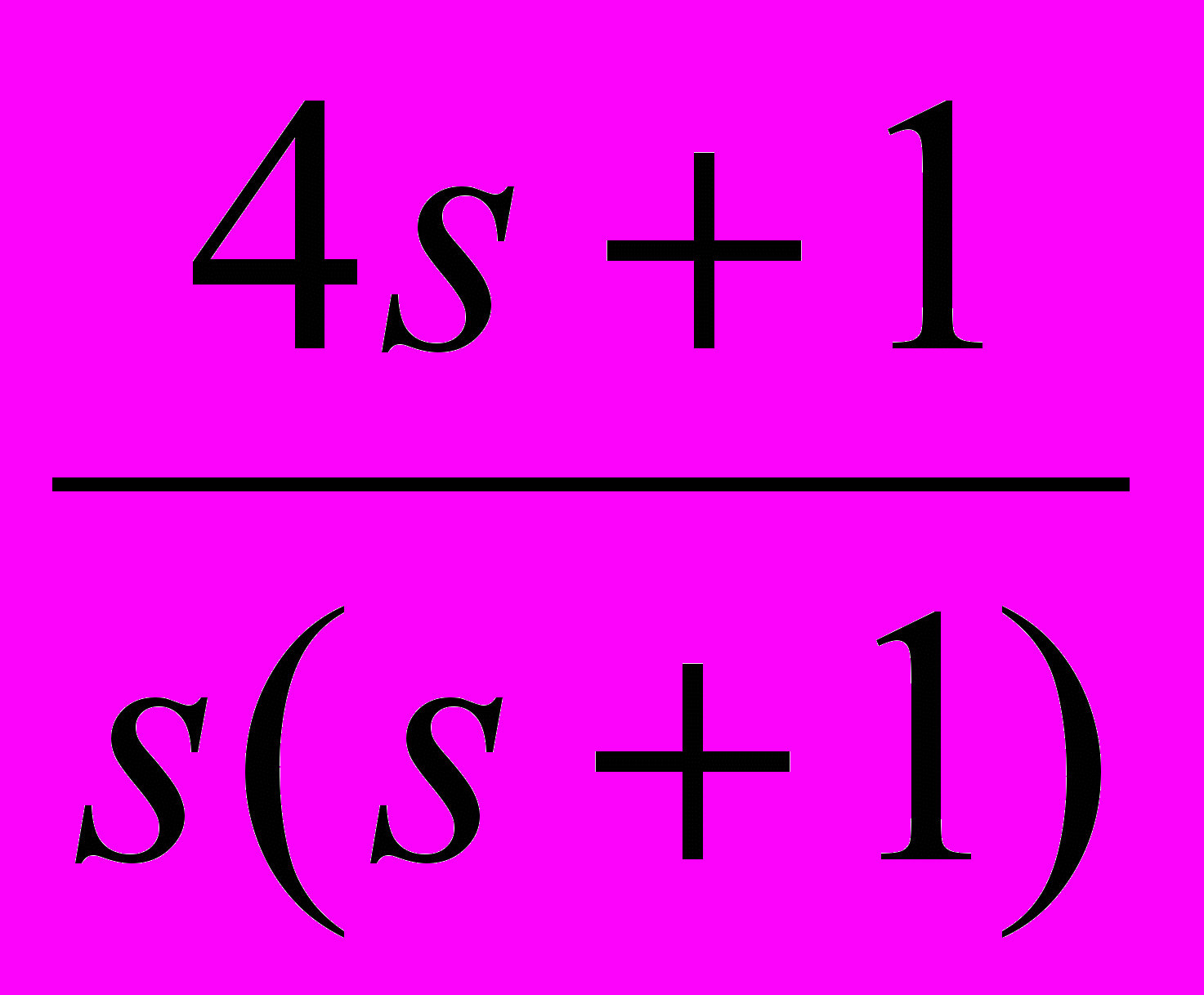
13


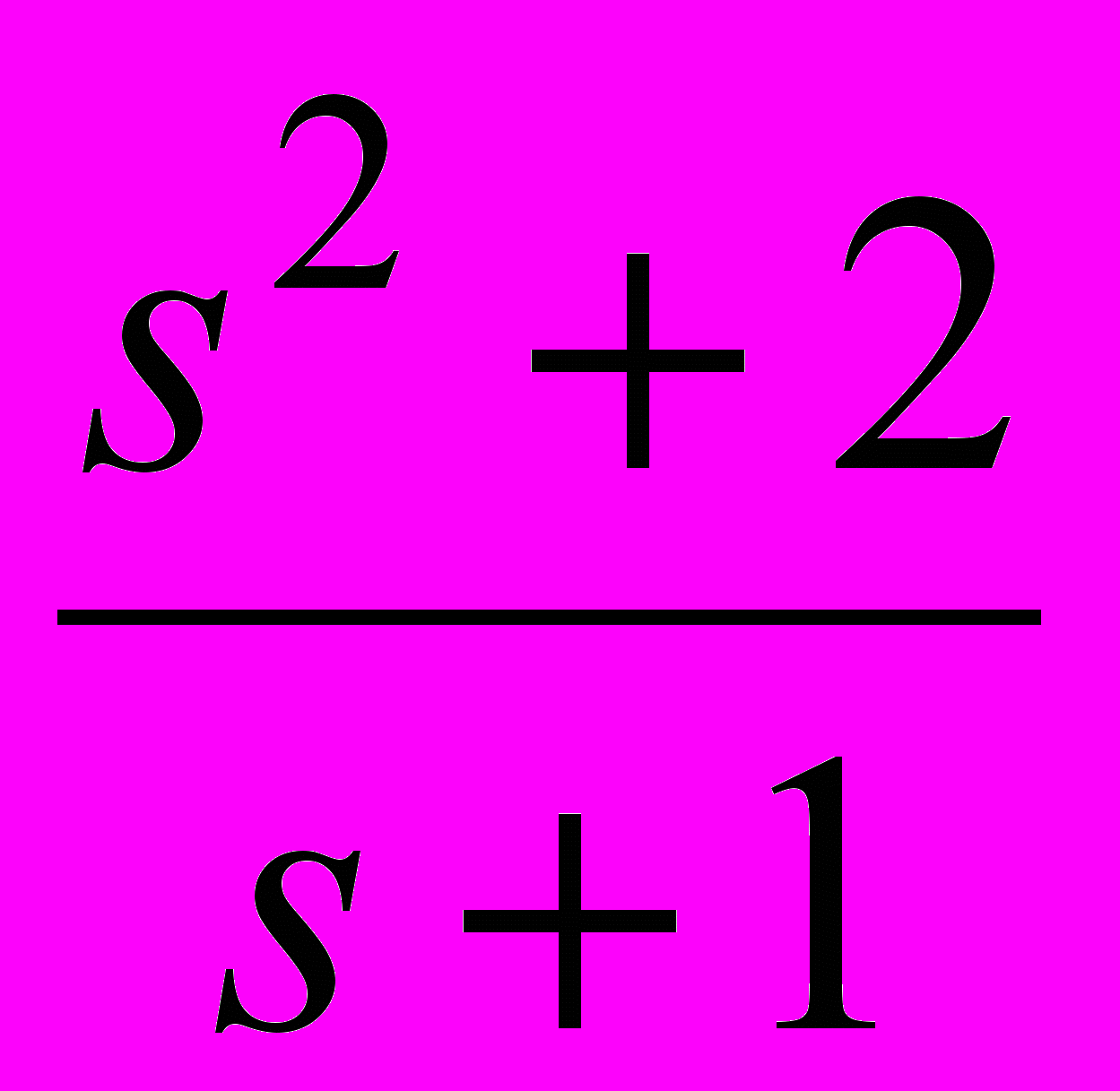
26



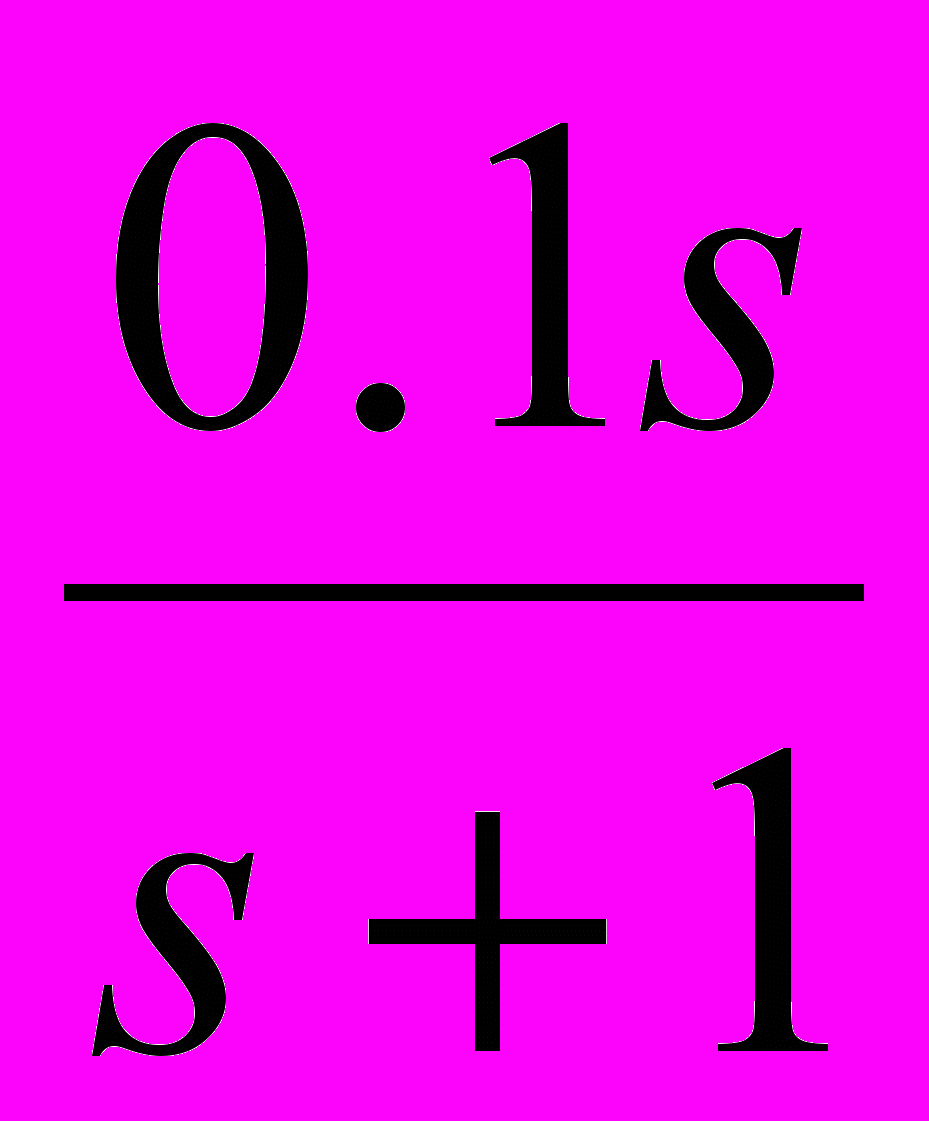
2. Оценить устойчивость замкнутой САУ, пользуясь критерием Рауса. Определить критическое значение коэффициента усиления усилителя Ку кр. Построить АФХ разомкнутой САУ и оценить устойчивость замкнутой системы, пользуясь критерием Найквиста. Оценить запасы устойчивости по модулю и по фазе. Пользуясь ЛАХ и ЛФХ разомкнутой САУ определить запасы устойчивости по модулю и по фазе и сравнить полученные результаты.

3. Построить кривые D-разбиения в плоскостях Ку(j) и Ку=(Тф). Определить диапазон изменения параметров Ку и Тф, обеспечивающих устойчивость исследуемой САУ.

4. Для исследуемой следящей системы определить установившиеся значения ошибки уст при заданных максимальных значениях скорости 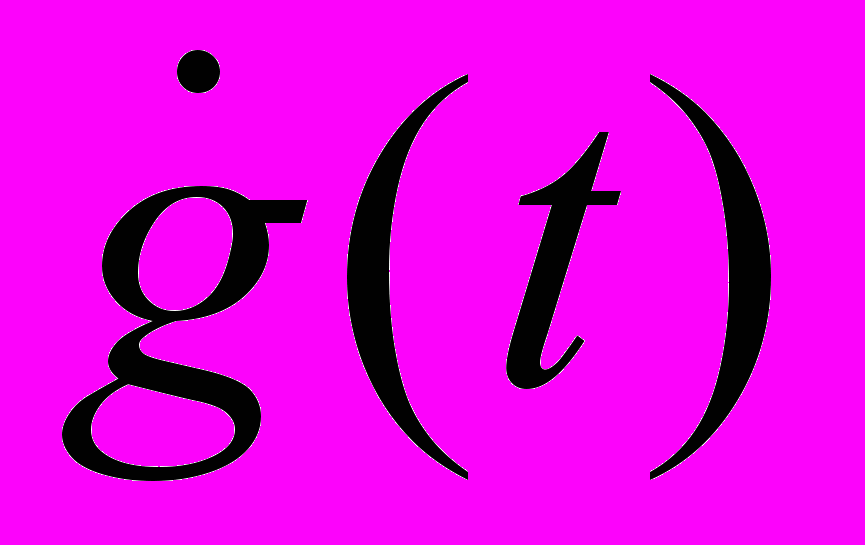max и ускорения 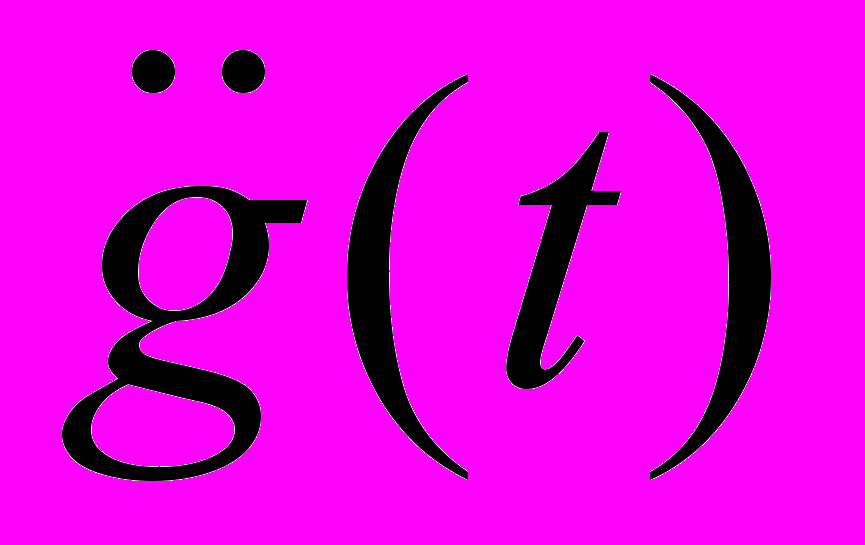max задающего воздействия g(t). Полученные результаты сравнить с допустимыми значениями ошибки уст доп= v+w для исследуемой системы, согласно таблице 1. Если расчетное значение установившейся ошибки превышает допустимые значения (уст доп= v+w), то необходимо определить значение коэффициента усиления разомкнутой цепи следящей системы К, при котором будут удовлетворяться требования к точности. Определить требуемое значение коэффициента усиления усилителя Кутр. Сравнить требуемое значение коэффициента усиления усилителя Ку тр с критическим значением и сделать вывод об устойчивости САУ, в которой выполнены требования к точности отработки задающего воздействия.

5. Если САУ с требуемым коэффициентом усиления разомкнутой цепи неустойчива, выбрать параметры Кос и ос корректирующей обратной связи (табл.2), обеспечивающие устойчивость замкнутой САУ, с корректирующим устройством, включенным согласно схеме, приведенной на рис.1. Для этого, пользуясь критерием Рауса, определить диапазон изменения коэффициентов Кос и ос, обеспечивающих устойчивость САУ. Сделать общий вывод о точности воспроизведения входного воздействия нескорректированной САУ, об устойчивости САУ с требуемым коэффициентом усиления и о рекомендациях по обеспечению устойчивости в системе с требуемым коэффициентом усиления.

6. Для исследуемой САУ построить амплитудно-частотную характеристику замкнутой САУ (). Определить частотный показатель колебательности М, резонансную частоту р, полосу пропускания п. Оценить по номограммам время переходного процесса, величину перерегулирования, время первого максимума.

7. Построить вещественную частотную характеристику замкнутой САУ P(). Используя свойства ВЧХ, оценить приближенно характер переходного процесса, время регулирования, величину перерегулирования, статическую ошибку. Используя ВЧХ, построить переходную характеристику исследуемой САУ. По ней определить прямые показатели качества:

tр - время регулирования;

 - величину перерегулирования;

t1max - время первого максимума;

т - частоту собственных затухающих колебаний;

характер переходного процесса.

8. Сделать вывод о качестве исследуемой системы по виду переходной функции. Сравнить между собой полученные оценки. Сделать вывод о степени приближения косвенных оценок к прямым.

Для варианта с последовательным корректирующим устройством.

1. Построить ЛАХ и ЛФХ разомкнутой САУ с требуемым коэффициентом усиления без корректирующей обратной связи. Определить запасы устойчивости по модулю и по фазе. Результаты сравнить с требуемыми показателями качества, приведенными в табл.3.

2. Исходя из заданных показателей качества обосновать выбор желаемой ЛАХ: низкочастотной части, среднечастотной, высокочастотной. Построить график желаемой ЛАХ совмещенный с графиком ЛАХ нескорректированной САУ (на листе миллиметровой бумаги по формату листа ПЗ). Вычитая из ординат желаемой ЛАХ ординаты нескорректированной ЛАХ, получить график ЛАХ последовательного корректирующего устройства. Вычислить запас устойчивости по фазе для желаемой ЛАХ.


Таблица 3 – Показатели качества

№ вар.
Запас по фазе
Время регулирования
Перере-гулиро-вание
№ вар.
Перере-гулиро-вание
Время первого максимума
Показатель колебат.




,град
tр,с
%



,%
t1max
M/р

1
45
-
-
14
35
0,7
-

2
60
-
-
15
25
0,8
-

3
50
-
-
16
25
0,6
-

4
40
-
-
17
30
0,4
-

5
35
-
-
18
20
0,5
-

6
60
-
-
19
40
0,6
-

7
45
-
-
20
25
0,3
-

8
50
-
-
21
30
0,5
-

9
-
2
15
22
-
-
1,6/9

10
-
1,5
40
23
-
-
1,4/12

11
-
0,9
25
24
-
-
1,5/8

12
-
1,6
20
25
-
-
1,8/7

13
-
0,8
30
26
-
-
1,25/10


3. Записать передаточную функцию корректирующего устройства. Записать передаточную функцию замкнутой скорректированной САУ и определить запас устойчивости по фазе.

4. Вычислить ВЧХ P() замкнутой скорректированной САУ и по ней приближенно оценить показатели качества САУ по tр, ,т и характеру переходного процесса.

5. Построить переходную характеристику h(t) для скорректированной замкнутой САУ, используя метод трапеций. Привести таблицу значений h(t) для каждой трапеции. Оценить полученное качество скорректированной САУ.

6. Сделать вывод о качественных показателях САУ и их соответствии заданным.


2 Теоретическая часть


2.1 Устойчивость САУ

Необходимое и достаточное условие устойчивости линеаризованных систем формулируется в теоремах А.М.Ляпунова [1,2].

Теорема 1. Если вещественные части всех корней характеристического уравнения первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво независимо от членов разложения выше первого порядка малости.

Теорема 2. Если среди корней характеристического уравнения первого приближения найдется по меньшей мере один с положительной вещественной частью, то невозмущенное движение неустойчиво, независимо от членов разложения выше первого порядка малости.

Так как при порядках характеристического уравнения n выше третьего определение корней представляет сложную задачу, то устойчивость реальных систем исследуют с помощью специально разработанных критериев

Критерием устойчивости называются правила, позволяющие исследовать устойчивость системы без непосредственного нахождения корней характеристического уравнения.

Пусть характеристическое уравнение замкнутой системы имеет вид

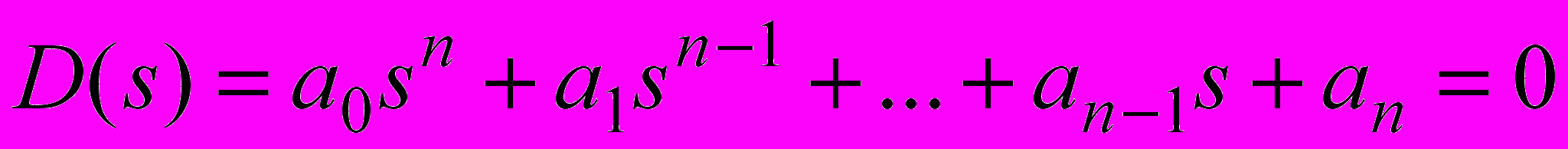. (1)

Тогда формулировки основных критериев устойчивости будут следующие.

Критерий Рауса – алгебраический критерий, позволяющий судить об устойчивости системы по коэффициентам уравнения (1).

Формулировка критерия: для устойчивости замкнутой системы необходимо и достаточно, чтобы все коэффициенты первого столбца таблицы Рауса были одного с а0 знака.

Таблица 4 – Таблица Рауса

а0
а2
а4
а6


а1
а3
а5
а7


C13
C23
C33




C14
C24
C34














C1,n+1
0
0
0
0


Таблица Рауса составляется по правилам:

а) в первой строке выписываются все коэффициенты с четными индексами, начиная с а0, во второй - с нечетными, начиная с а1, отсутствующие коэффициенты заменяются нулями;

б) коэффициенты третьей строки вычисляются по следующему алгоритму:

С13=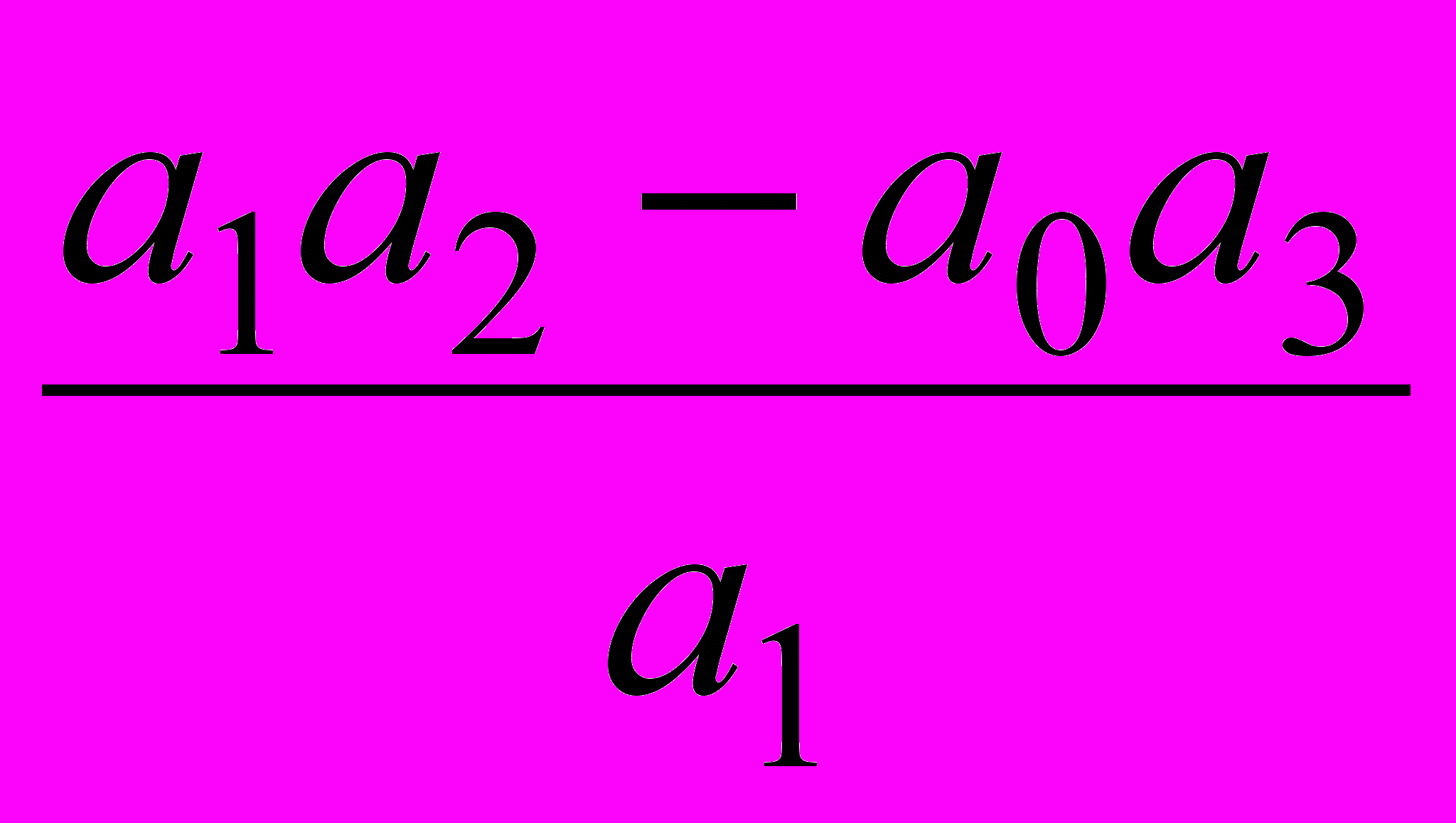; С23=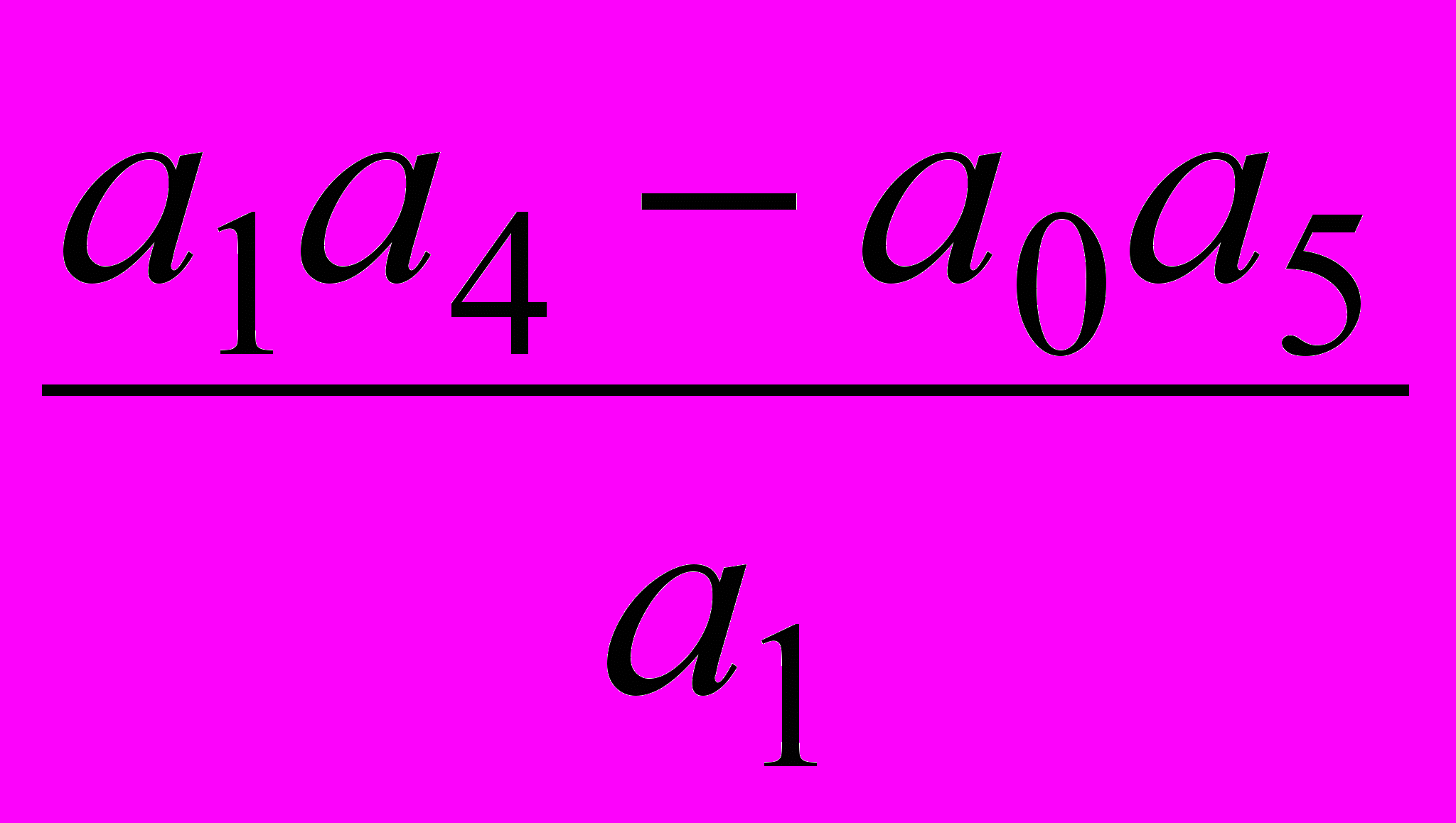; С33=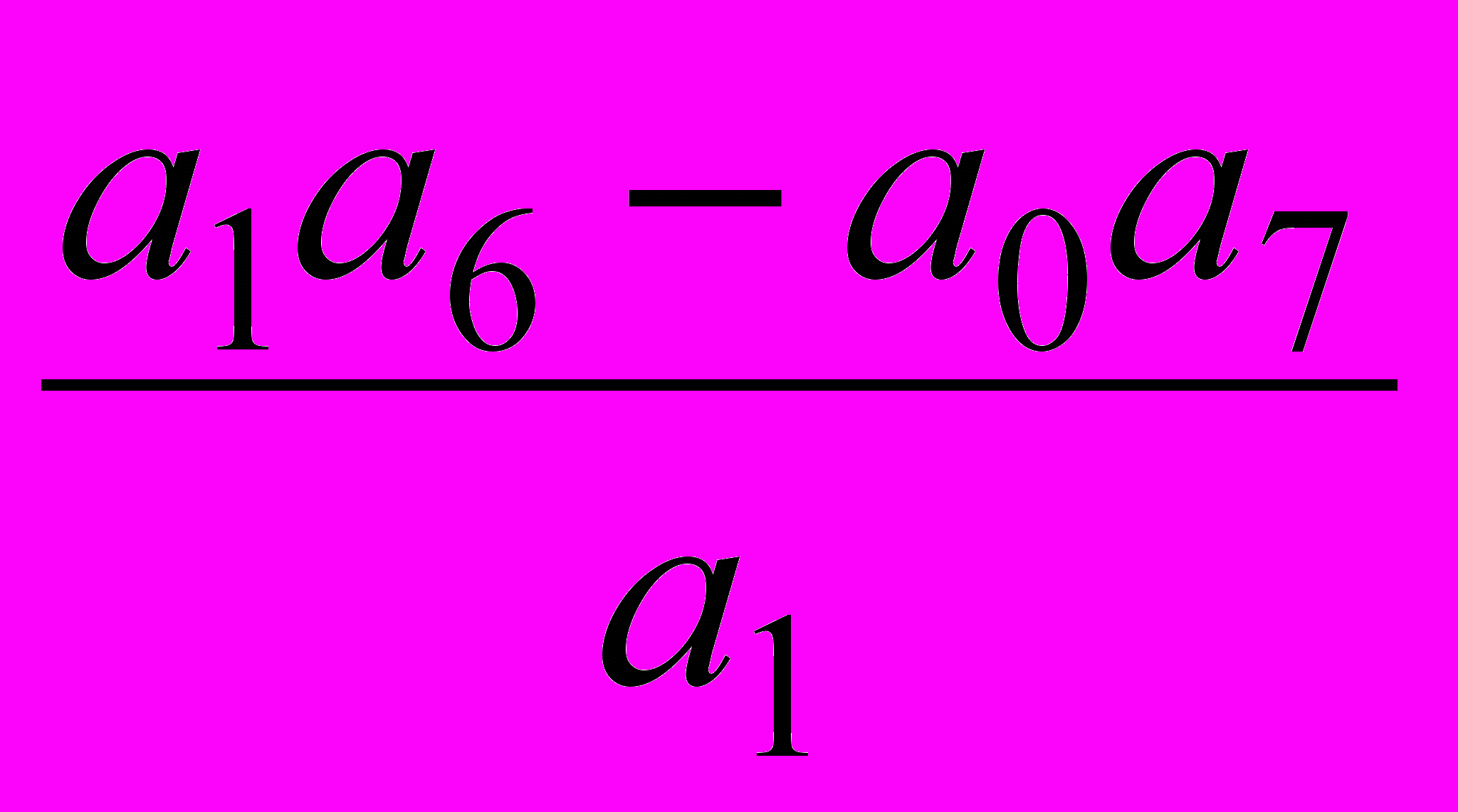 и т.д.

в) коэффициенты четвертой строки определяются по двум предыдущим строкам:

С14=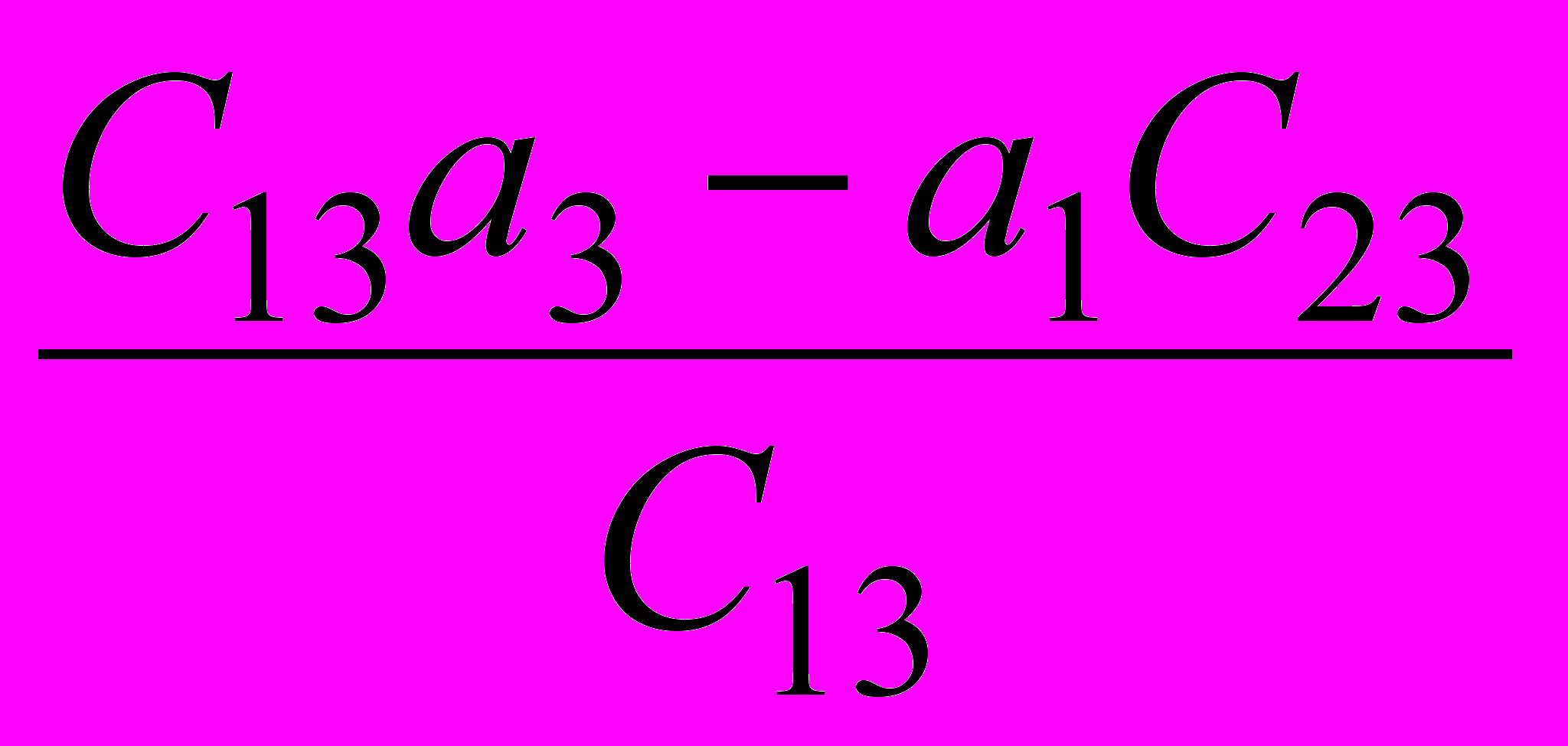; С24= 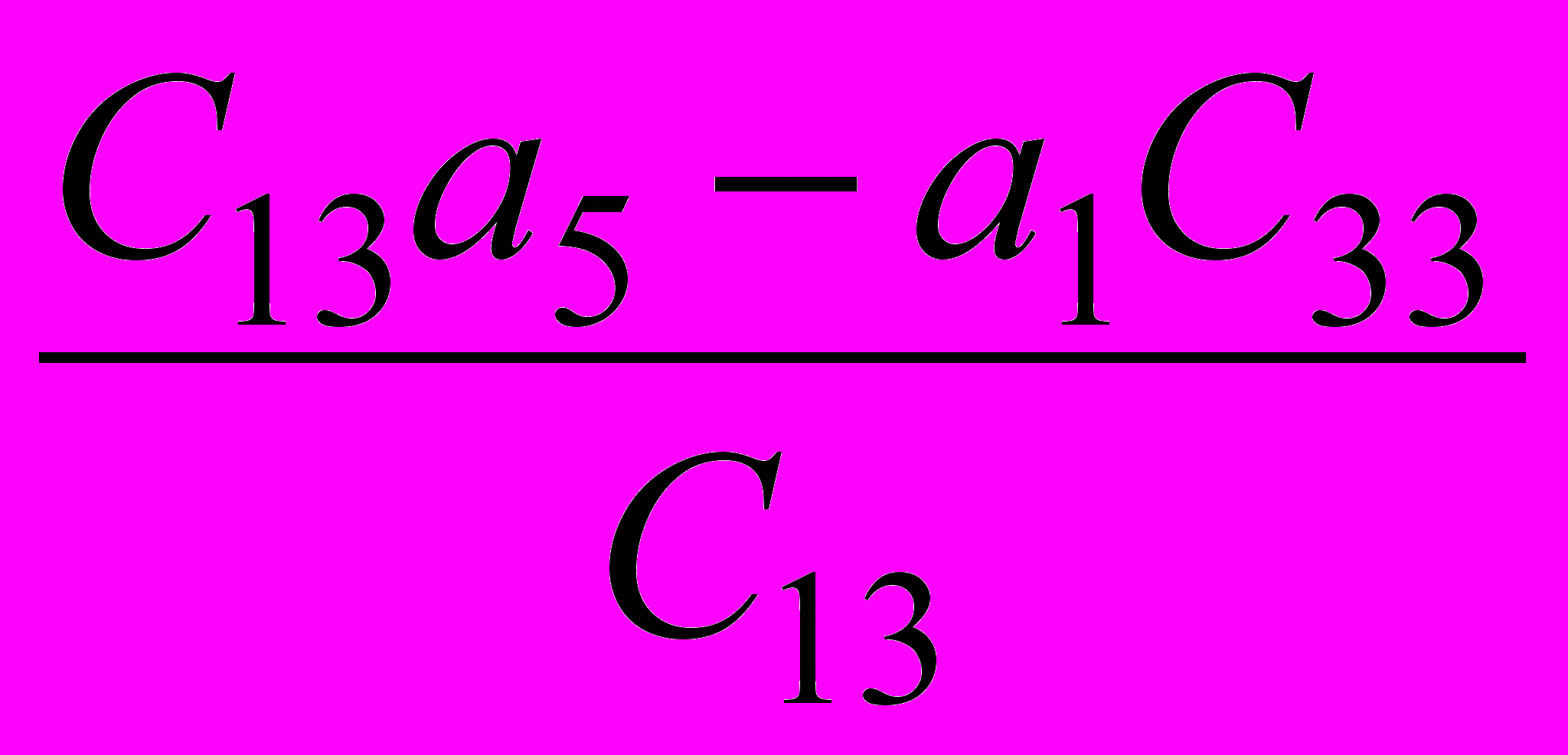и т.д.

Таблица Рауса имеет (n+1) строку и целое от 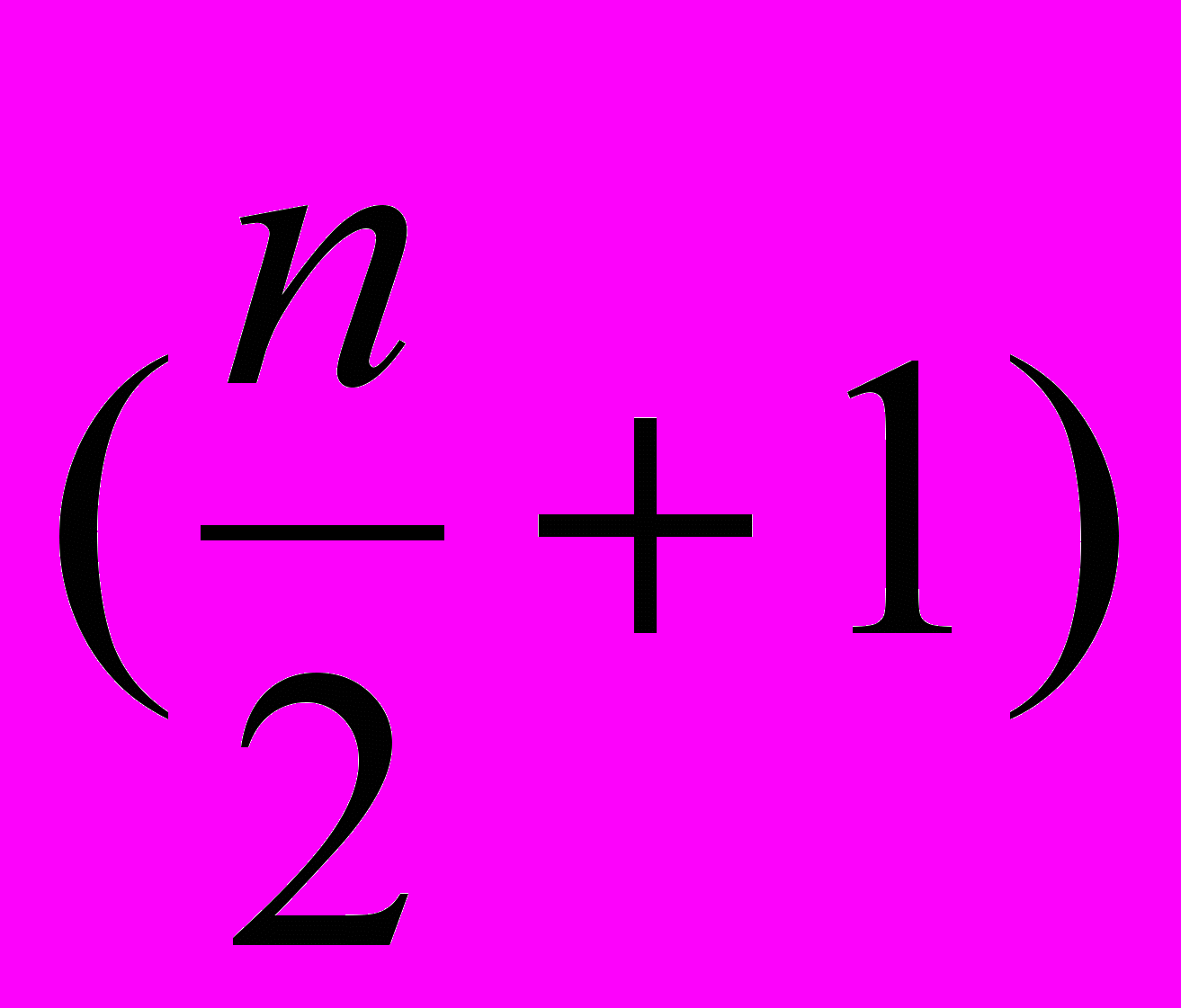число столбцов.

не обращаясь в нуль, т.е. согласно принципу аргумента

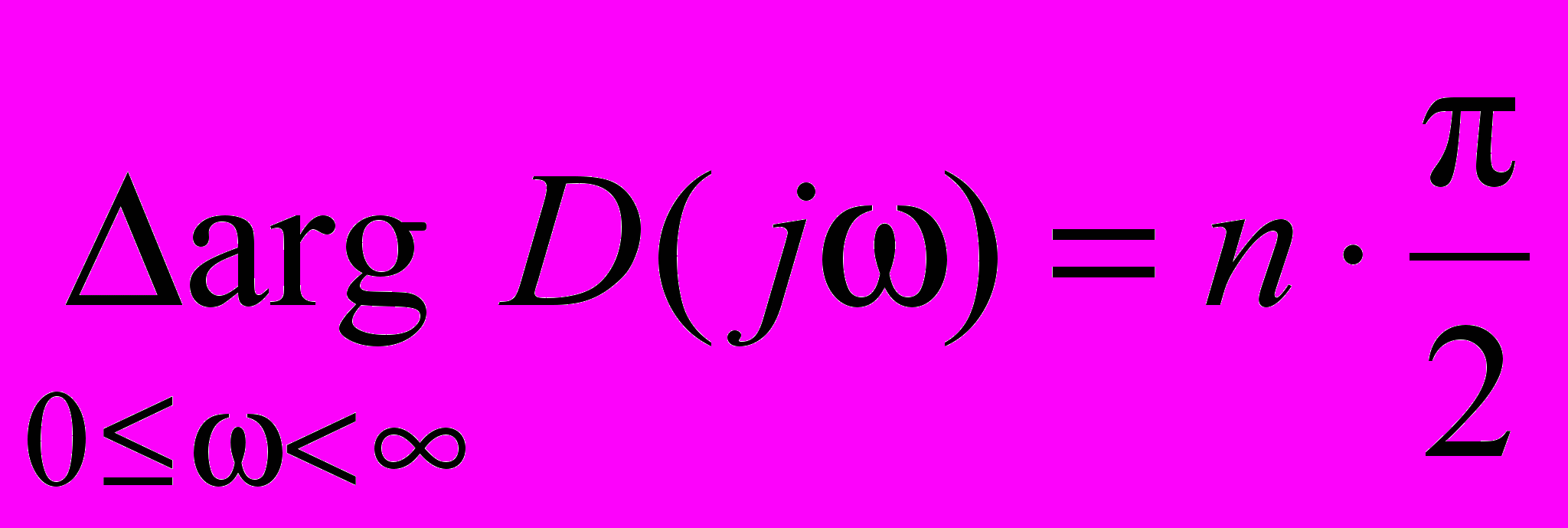. (2)

Критерий Найквиста – частотный критерий, позволяющий судить об устойчивости замкнутой системы с единичной обратной связью по виду амплитудно-фазовой характеристики разомкнутой системы.

Первая формулировка критерия: замкнутая система будет устойчива, если амплитудно-фазовая характеристика устойчивой разомкнутой системы не охватывает точку с координатами 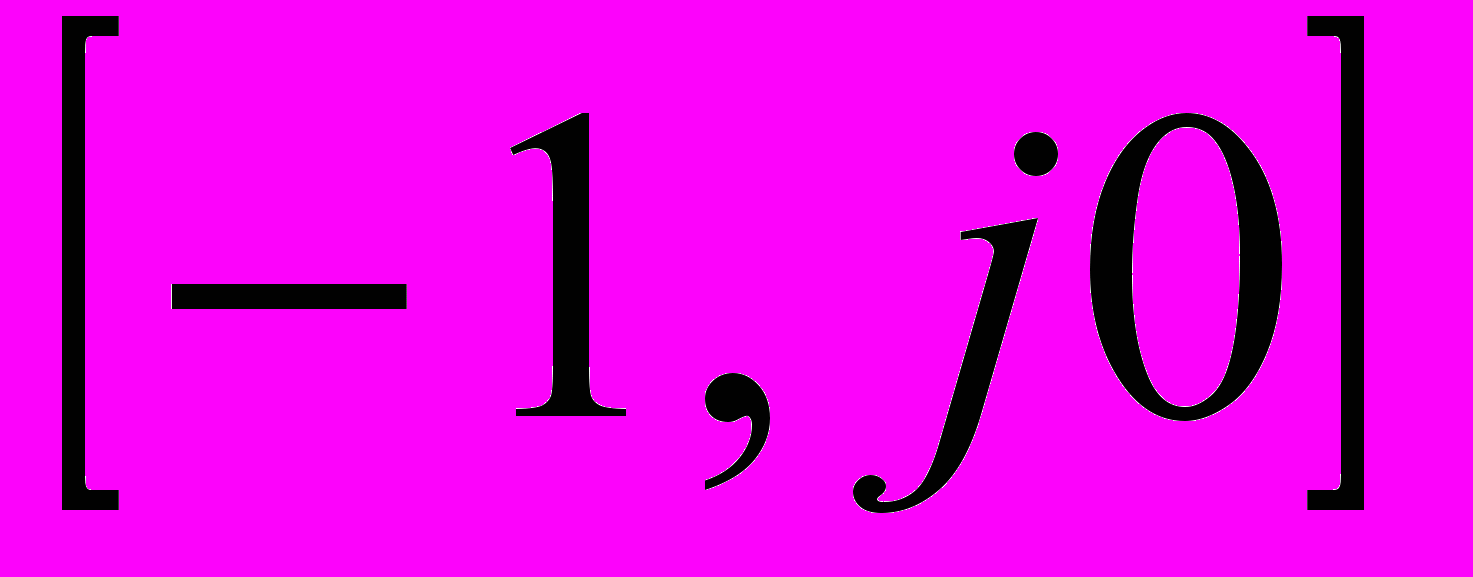, т.е. .

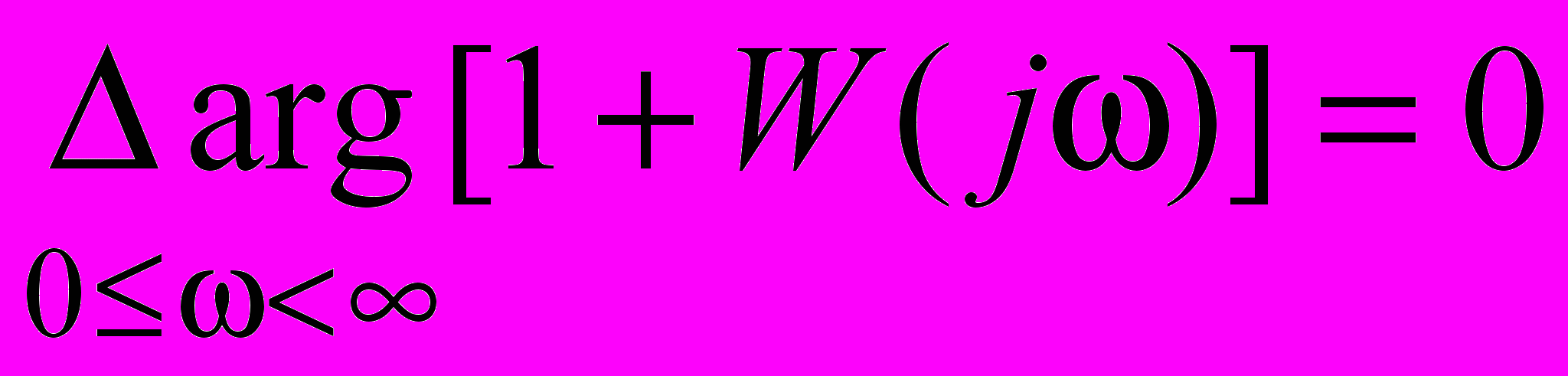Вторая формулировка критерия: если передаточная функция W(s) разомкнутой системы имеет 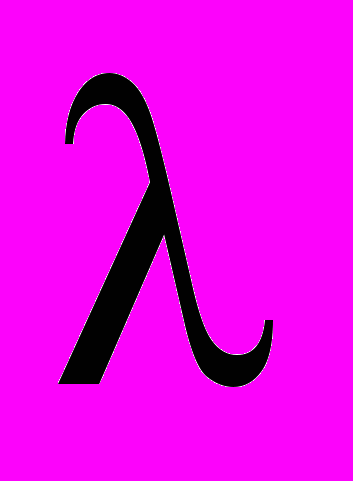правых корней, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы при изменении частоты от нуля до бесконечности охватывала точку с координатами (-1,) в положительном направлении (против часовой стрелки) 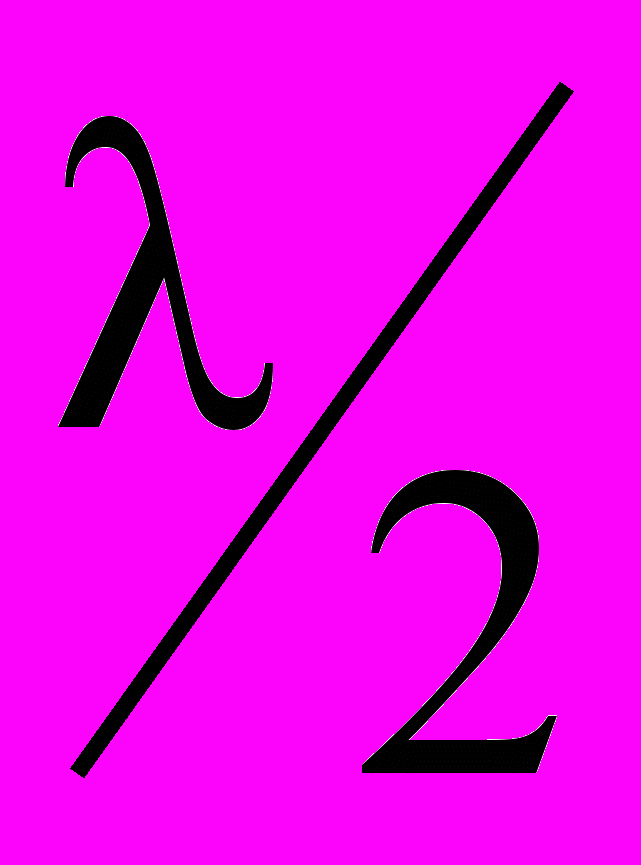раз, т.е..

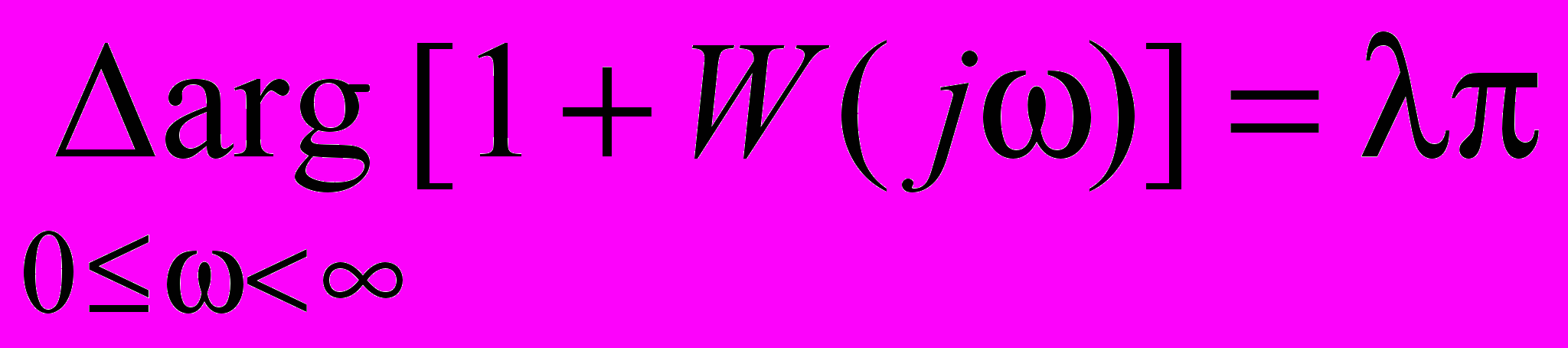Формулировка критерия для астатических систем: замкнутая система будет устойчива, если АФХ разомкнутой системы, дополненная дугой бесконечного радиуса до положительной вещественной полуоси, если число правых полюсов  передаточной функции W(s) равно нулю или четное, и до отрицательной вещественной полуоси, если  - нечетное число, при изменении частоты  от нуля до бесконечности охватывает точку с координатами 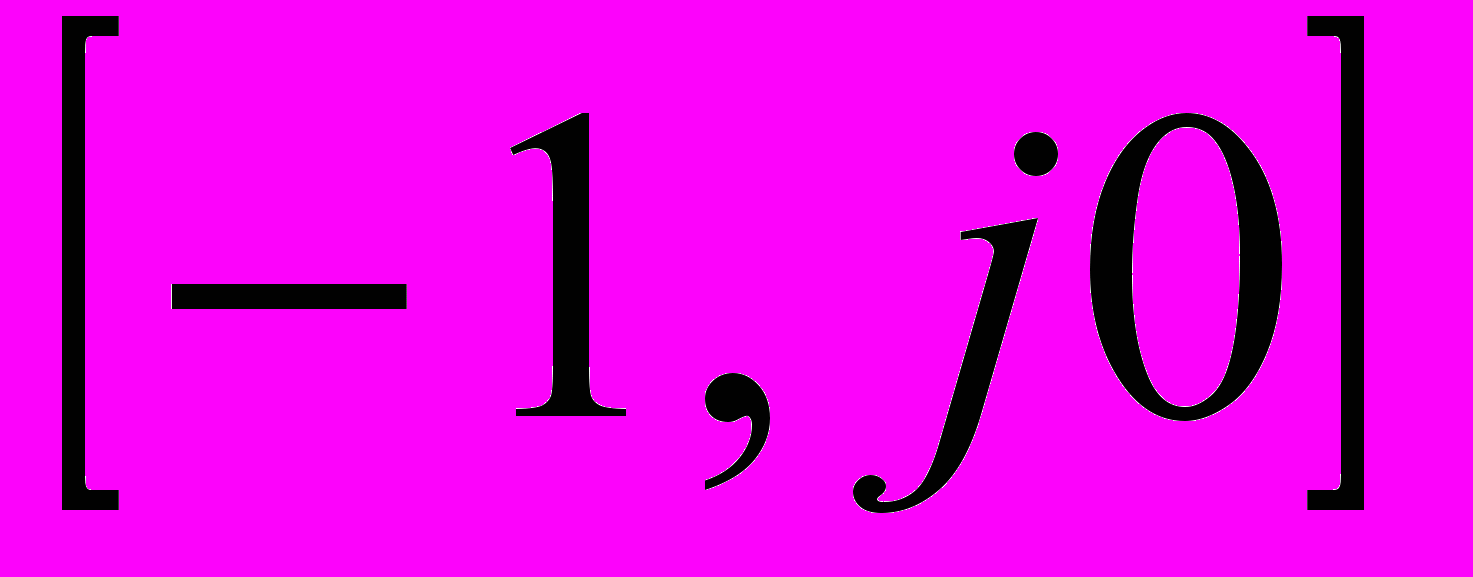в положительном направлении 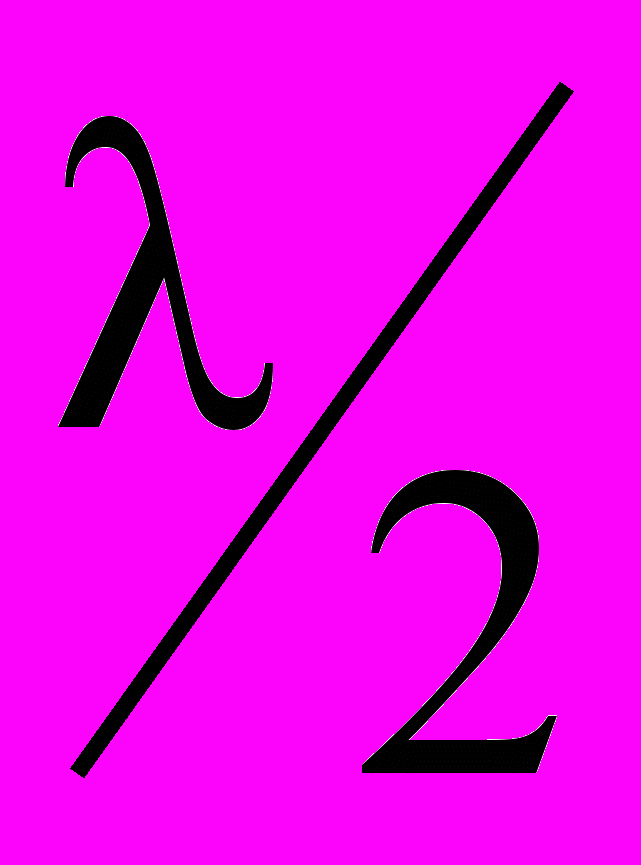раз.


2.2 Показатели качества работы САУ

Устойчивость является необходимым, но недостаточным условием работоспособности линейной САУ. Устойчивость означает, что переходные составляющие процессов затухают. Для практики этого недостаточно. Поэтому возникают определенные требования к времени затухания переходных составляющих, к характеру реакции системы на задающие и возмущающие воздействия, к точности отработки этих воздействий. Все эти стороны работоспособности системы обобщаются в понятии качества процесса управления. Качество процесса управления оценивается рядом показателей.

Существуют два вида установившихся (стационарных) режимов САУ: статический и динамический.

Статический стационарный режим характеризуется тем, что все внешние воздействия и параметры системы не меняются во времени (g(t)=x0=const, ).

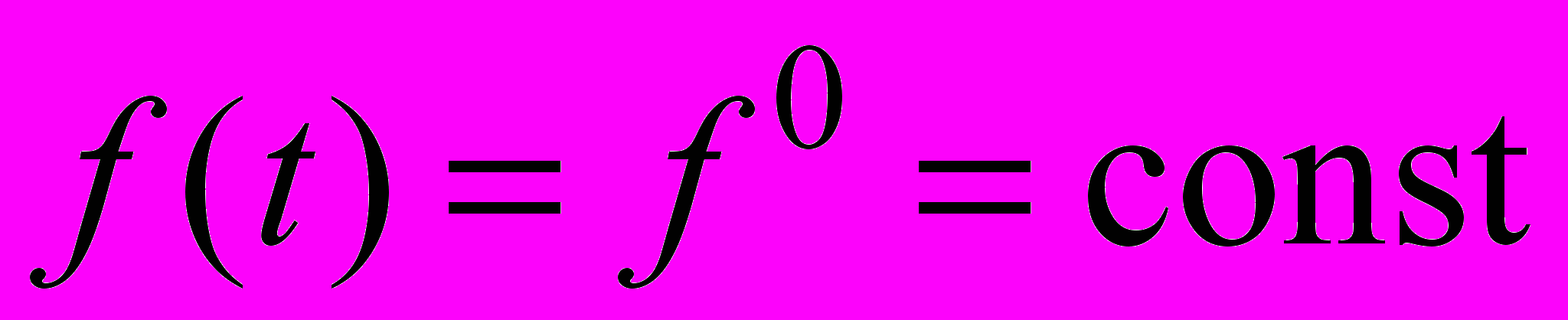Динамический стационарный режим – это режим, при котором приложенные к системе внешние воздействия (g(t), f(t)) изменяются по некоторому установившемуся закону, в результате чего в системе устанавливается режим вынужденного движения. Критерием качества работы в стационарном режиме служат ошибки (t), вызываемые действием детерминированных задающих g(t) и возмущающих f(t) воздействий.

Ошибки статического и динамического стационарных режимов называют соответственно статическими и динамическими.

Медленно меняющиеся входные воздействия – это такие детерминированные сигналы, которые за время действия весовой функции практически не успевают изменяться.

Вычисление установившейся ошибки (статической и динамической) можно производить либо с использованием теоремы Лапласа о конечном значении оригинала, если входное воздействие g(t) задано явно и является аналитической функцией времени:

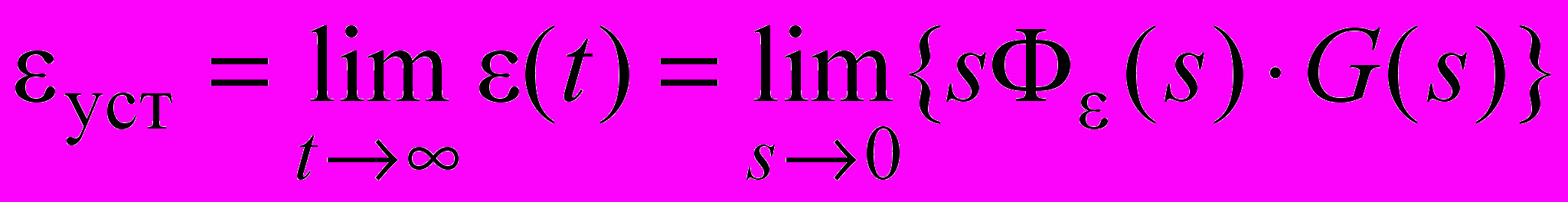, (3)

либо используя коэффициенты ошибок, если входное воздействие задано неявно

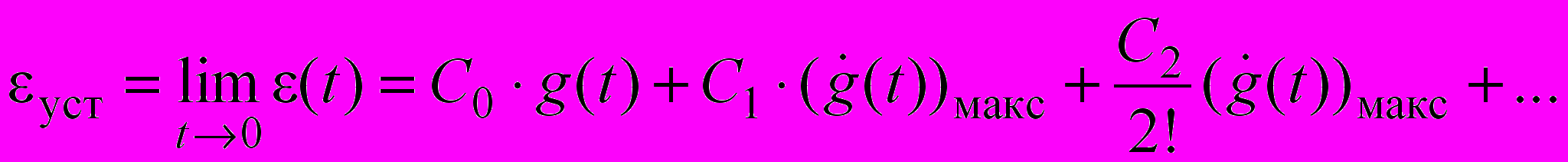, (4)

где 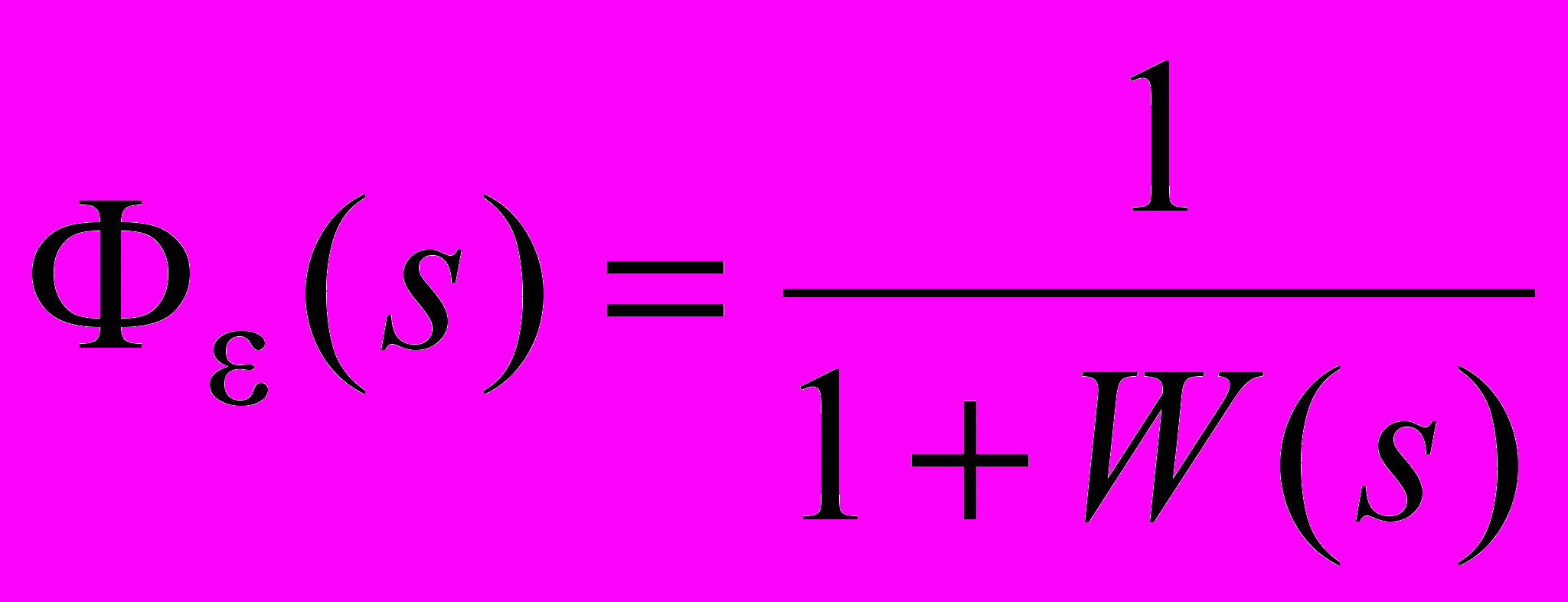– передаточная функция замкнутой системы по ошибке;

G(s) - изображение по Лапласу задающего воздействия g(t);

С0, С1, С2, - коэффициенты ошибок, являющиеся коэффициентами разложения функции Ф(s) в бесконечный степенной ряд

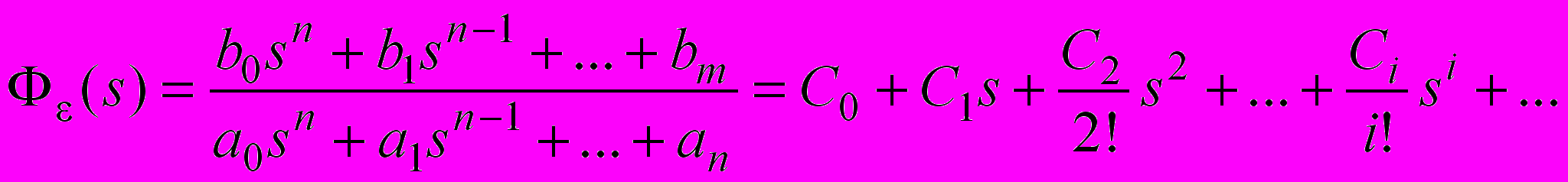, (5)

где 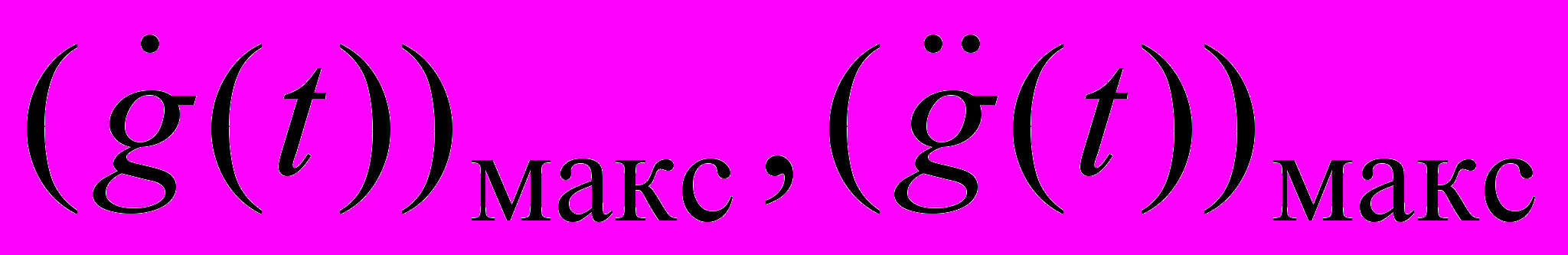– максимальные значения скорости и ускорения задающего воздействия g(t).

Статическая ошибка при g(t)=1(t) согласно (1) равна

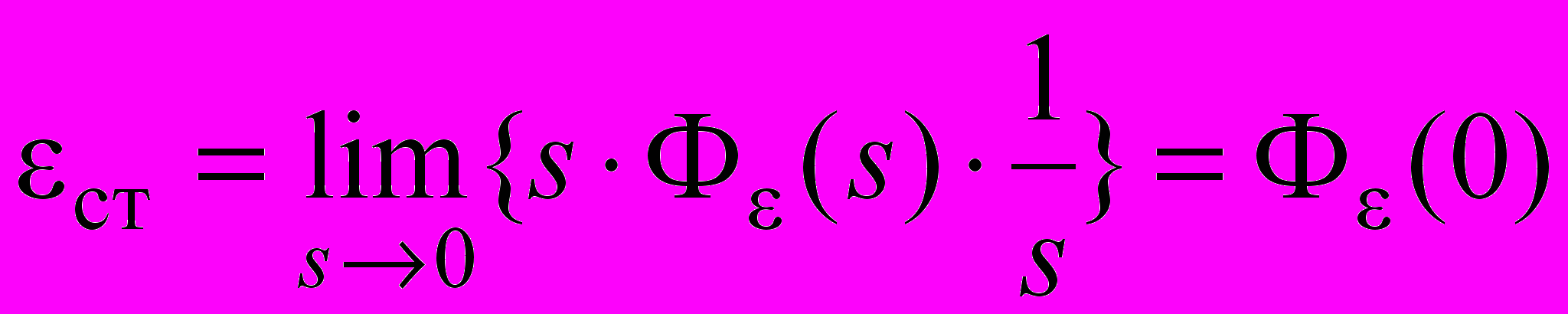. (6)

Если на систему одновременно действуют и задающее g(t) и возмущающее f(t) воздействия, то статическая ошибка системы определяется как

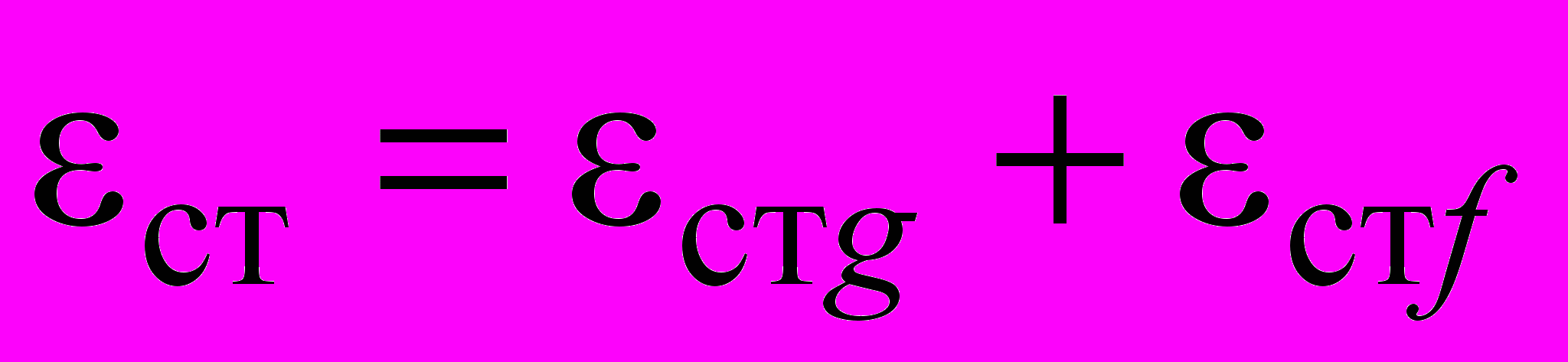, (7)

где 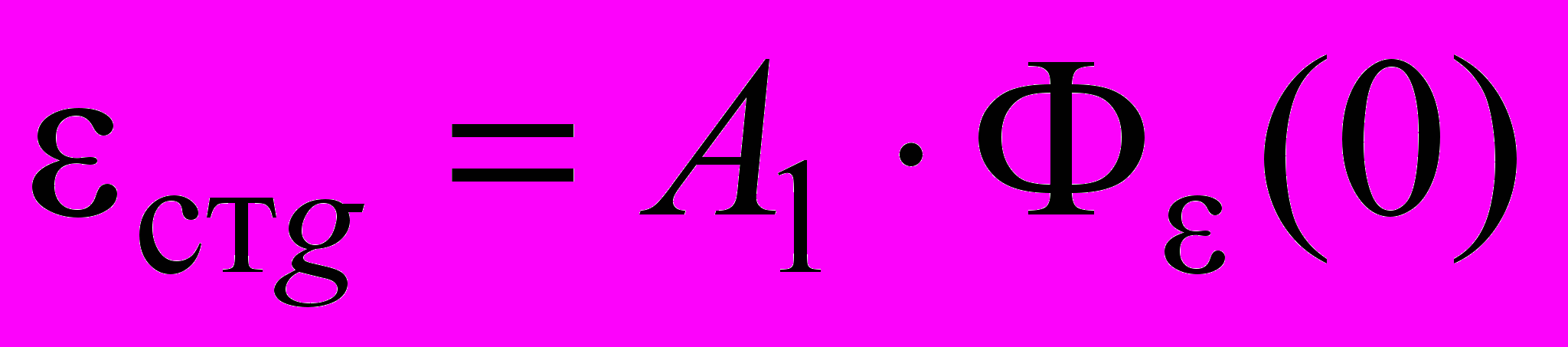согласно (6),

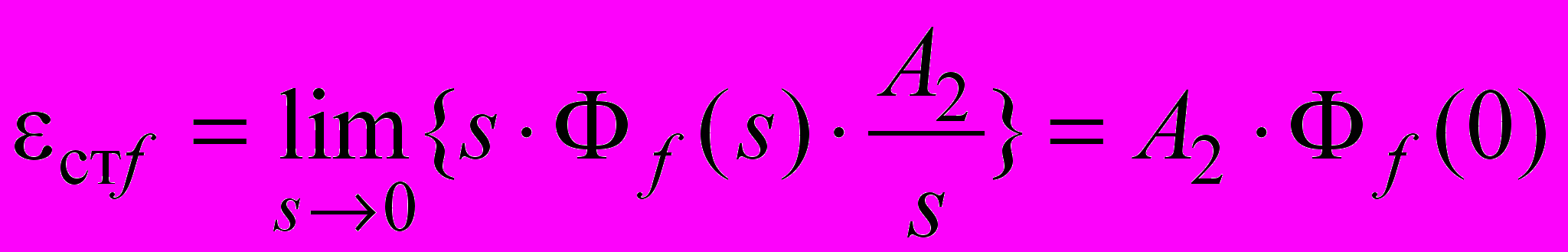, (8)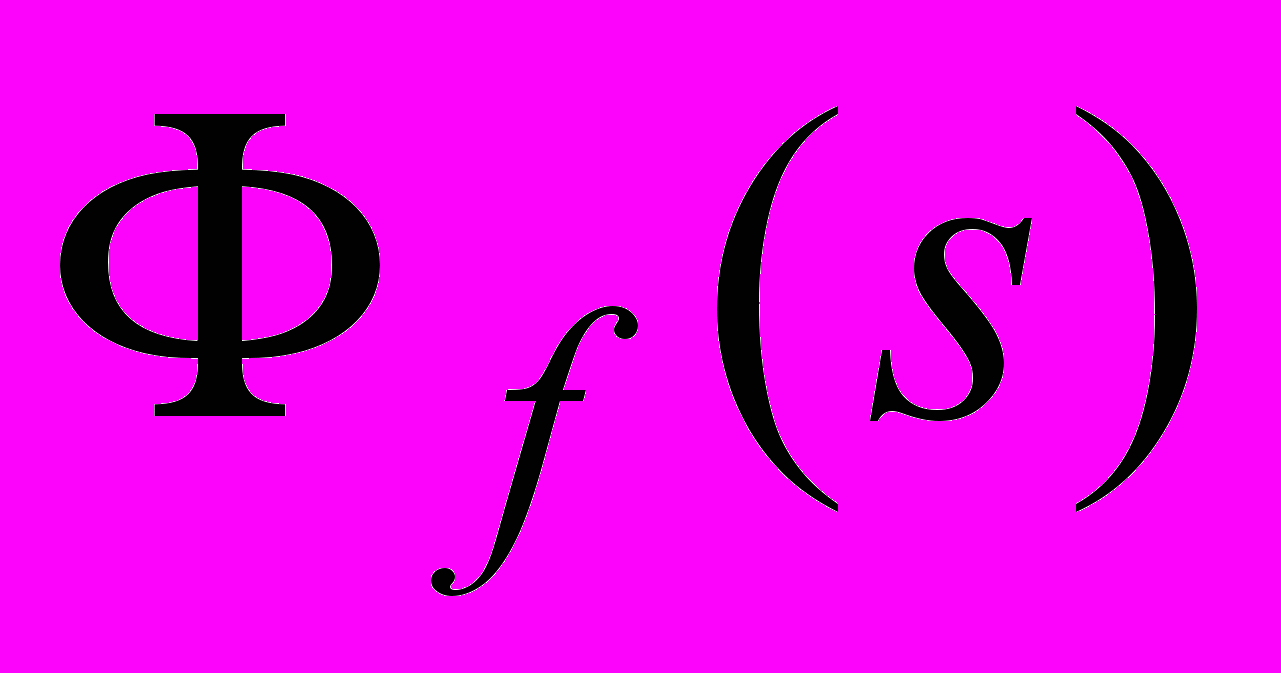

– передаточная функция замкнутой системы по возмущению, равная 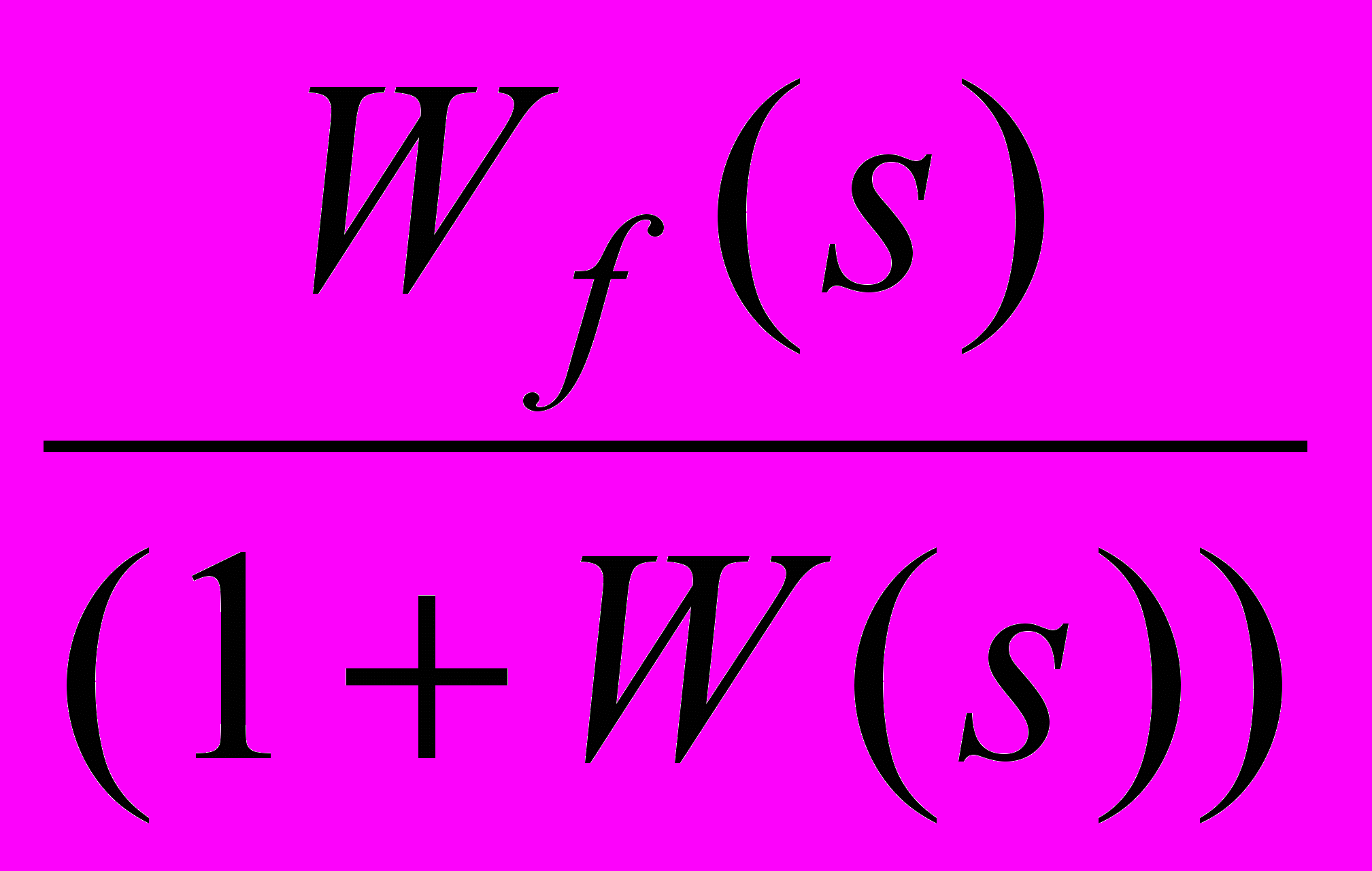. Здесь Wf(s) – передаточная функция участка цепи, заключенного между точкой приложения воздействия f(t) и выходной координатой x(t).

Все показатели качества можно разделить на прямые и косвенные. Прямые показатели качества определяются непосредственно по кривой переходного процесса h(t). Это:
  • ty - время переходного процесса, определяемое с заданной точностью ;
  • - величина перерегулирования, определяемая как
  • ;
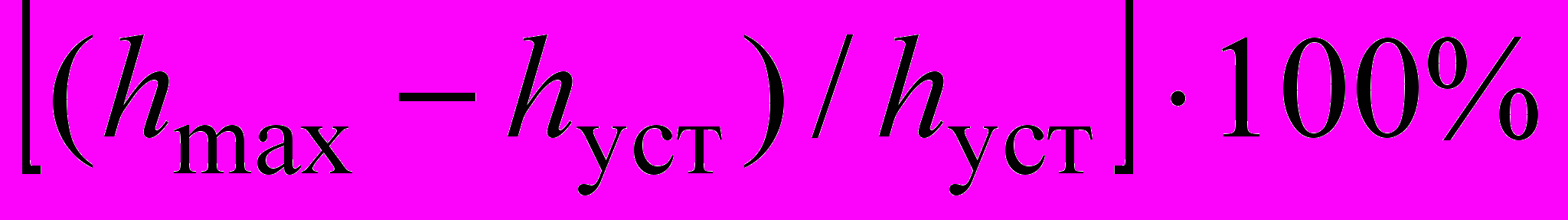  • t1max - время первого максимума;
  • ст – статическая ошибка системы, равная ;
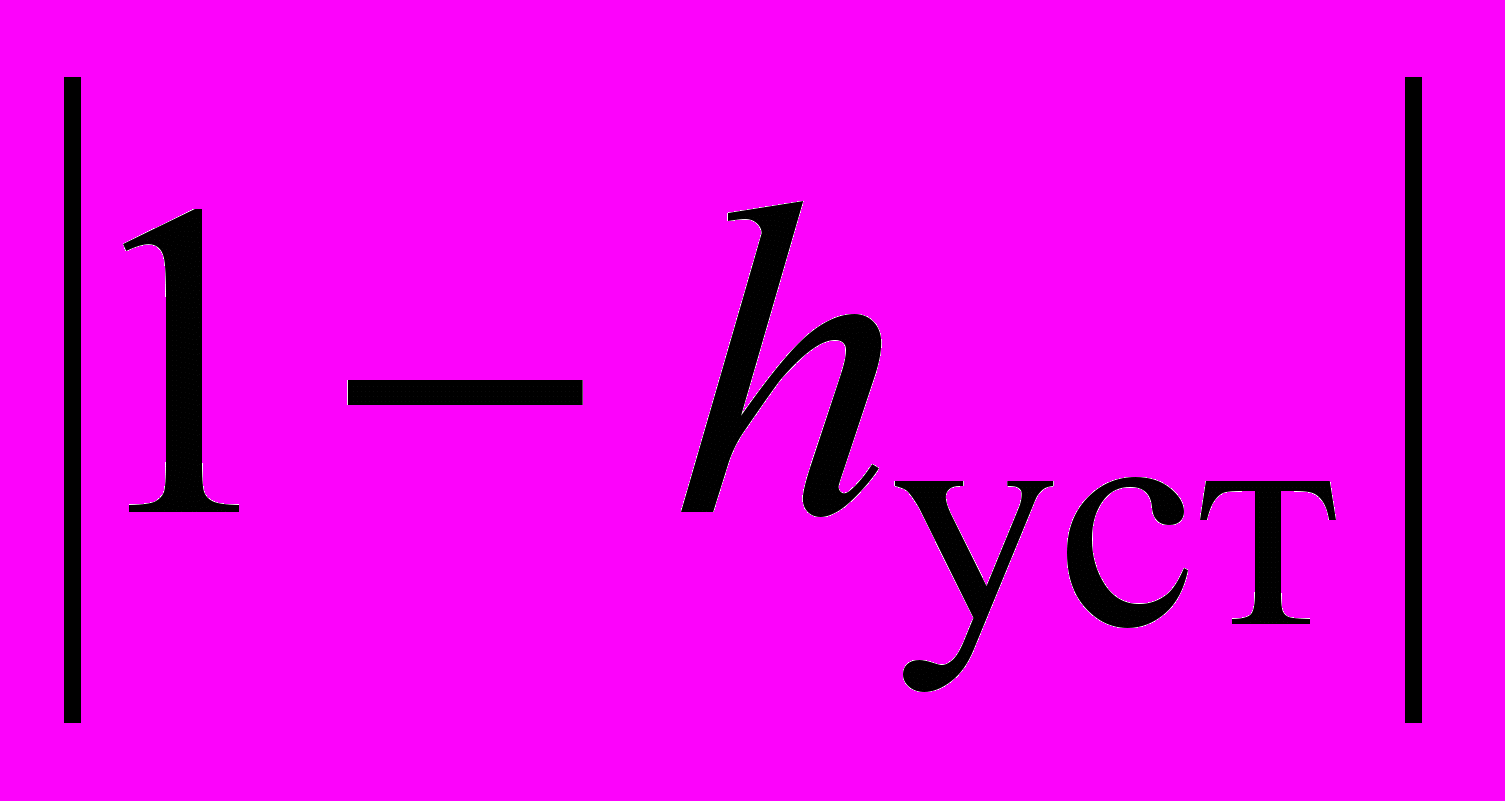  • характер переходного процесса.

Косвенные показатели качества подразделяются на частотные, корневые и интегральные.

Частотные показатели (критерии) качества позволяют оценивать качество процесса управления по отображению этого процесса из области времени t в область частоты . Частотные методы оценки показателей качества систем автоматического регулирования получили широкое распространение в инженерной практике. Математической основой этих методов является обратное преобразование Лапласа (или Фурье), которое однозначно связывает выходной сигнал и вещественную частотную характеристику замкнутой системы :

               (9)

При этом на входе системы действует , а начальные условия являются нулевыми.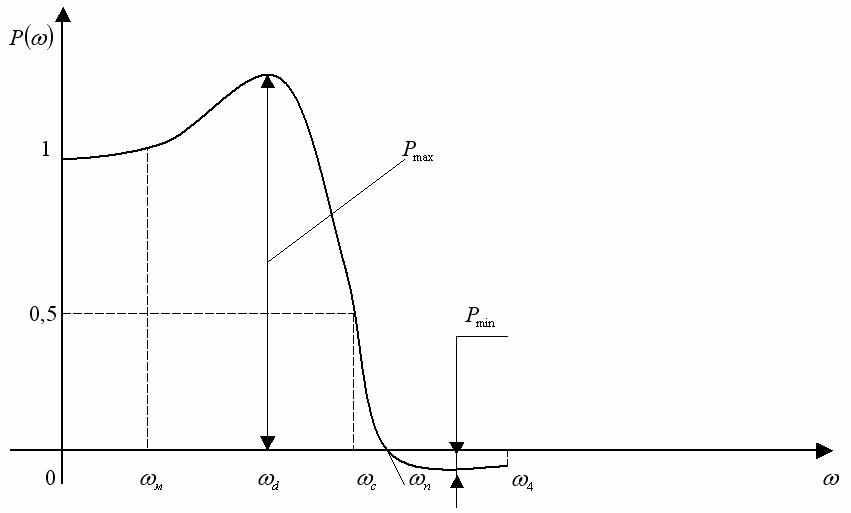



Рисунок 2 – АФЧХ вещественной части

К основным частотным критериям относятся:

а) вид амплитудно-фазовой характеристики W(j) или ЛАХ L() и ЛФХ () разомкнутой системы и характерные частоты (частота среза и т.п.);