Geum.ru

Методические указания к курсовой работе по дисциплине «Теория автоматического управления»

Вид материалаМетодические указания

Содержание


б) вид и характерные частоты амплитудно-частотной характеристики замкнутой системы Ф()
Подобный материал:
1   2   3   4

б) вид и характерные частоты амплитудно-частотной характеристики замкнутой системы Ф();


в) вид и характерные частоты вещественной частотной характеристики Р().

Так, если известна зависимость (рис. 2), то можно определить установившееся значение :

                                                                    .                                                  (10)

Зависимость и пик вещественной частотной характеристики замкнутой системы связаны следующим соотношение:                                          

.                                         (11)

Время переходного процесса зависит от длин интервала положительности :

,

т.е. если на интервале , то заведомо больше, чем .

Для большинства систем, у которых зависимость имеет вид, показанный на рисунке 2 (), показатели качества оценивают по номограммам В.В. Солодовникова (рис. 3):

;

.



Рисунок 3 – Номограммы В.В. Солодовникова


Вычисления в частотной области  обычно проще вычислений во временной области t, поэтому частотные критерия являются весьма эффективным и простым средством оценки качества процессов управления. С другой стороны, можно в некоторых случаях ограничиться только частотными оценками, такими как запасы устойчивости по модулю m и по фазе , показатель колебательности М и полоса пропускания п, не уточняя вопроса в области времени t. Так как во многих случаях частотные характеристики замкнутой системы близки к частотным характеристикам колебательного звена с коэффициентом затухания 0,5<<1, то это позволяет связать показатели переходной функции h(t) системы с ее частотными характеристиками.

Рекомендуемые нормы запасов устойчивости по модулю и фазе для систем с заданными показателями качества. Известно, что ВЧХ замкнутой системы и логарифмические частотные характеристики разомкнутой системы однозначно связаны. Следовательно, для каждой ЛАХ и ЛФХ существуют вполне определённые показатели качества переходного процесса.




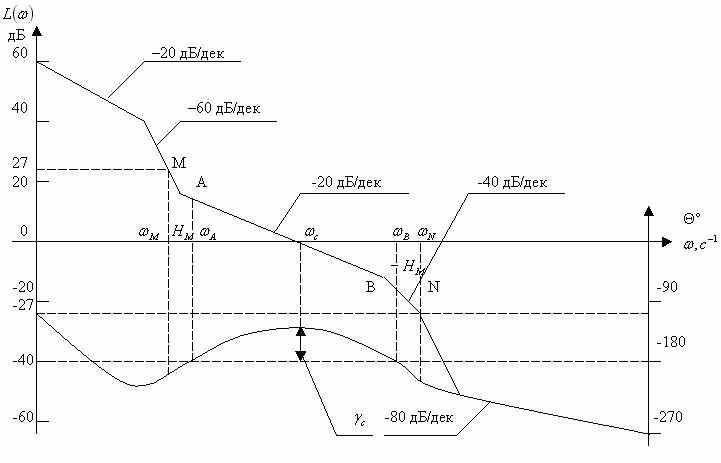
Рисунок 4 – ЛАХ и ЛФХ системы


Интервал частот от до (рис. 4), определяющий показатели качества системы, называется существенным. Он разделяет ЛАХ на три зоны: низкочастотную , среднечастотную и высокочастотную . Значения граничных частот и приближённо определяются выражениями:

Частоты и соответствуют запасу устойчивости по модулю и . В таблице 5 представлены нормы запасов устойчивости по модулю и фазе, гарантирующие показатели качества для длительно работающих систем автоматического регулирования.

При проектировании систем автоматического регулирования необходимо учитывать, что чем выше частота среза в системе, тем больше вероятность того, что не будут учтены малые постоянные времени объектов регулирования. Чтобы этого не случилось, необходимо увеличивать запасы устойчивости по фазе и модулю с ростом частоты среза. Сказанное отражено в таблице 5.


Таблица 5 - Нормы запасов устойчивости

Тип системы
Показатели устойчивости для диапазонов частот

От 0,01 до 100
От 100 до 1000
От 1000 до 10000
От 10000 и более

Для систем с высокими показателями качества



45
50
55
60

HМ, дБ
16
18
20
22

-HМ, дБ
14
16
18
20

Для систем с невысокими показателями качества



30
35
40
45

HМ, дБ
12
14
16
18

-HМ, дБ
10
12
14
16

 

Приведённые нормы запасов устойчивости справедливы как для внутренних контуров, так и для собственно систем автоматического регулирования.