Аналитическая статистика. Показатели вариации и анализ частотных распределений методические указания и решение типовых задач
| Вид материала | Методические указания |
- 1. теоретические аспекты применения показателей вариации в статистическом исследовании, 58.66kb.
- Н. П. Огарева Экономический факультет Кафедра статистики экономика и статистика фирм, 284.65kb.
- Н. П. Огарева Экономический факультет Кафедра статистики анализ временных рядов и прогнозирование, 191.07kb.
- Н. П. Огарева Экономический факультет Кафедра статистики демография и статистика населения, 143.09kb.
- Вопросы к экзамену по дисциплине "Статистика", 32.3kb.
- Методические указания и задачи для самостоятельной работы студентов по дисциплине «Математическая, 640.75kb.
- Вопросы по курсу «Допглавы эконометрики» Преподаватель : доцент, к ф. м н. Пяткина, 7.26kb.
- Методические указания к написанию лабораторных работ по учебным дисциплинам "Общая, 312.43kb.
- Статистика, 1361.62kb.
- Практикум: «Изучение процентов в школьном курсе математики», 90.4kb.
Контрольная работа N2. АНАЛИТИЧЕСКАЯ СТАТИСТИКА. ПОКАЗАТЕЛИ ВАРИАЦИИ И АНАЛИЗ ЧАСТОТНЫХ РАСПРЕДЕЛЕНИЙ
1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ И РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Исследование вариации в статистике и социально-экономических исследованиях имеет важное значение, так как величина вариации признака в статистической совокупности характеризует ее однородность.
В статистической практике для изучения и измерения вариации используются различные показатели (меры) вариации в зависимости от поставленных перед исследователем задач. К ним относятся размах вариации, среднее линейное отклонение, средний квадрат отклонений (дисперсия), среднее квадратическое отклонение и коэффициент вариации.
При изучении вопроса о вариации нужно четко представлять себе условия, порождающие вариацию признаков, а также сущность и значение измерения вариации признаков. Следует также усвоить, что изучение вариации признаков общественных явлений находится в прямой связи с группировками, в частности с рядами распределения. Очень важно научиться свободно исчислять все показатели вариации.
Способы вычисления показателей вариации.
Размах вариации (R) является наиболее простым измерителен вариации признака:
R=xmax-xmin ,
где xmax - наибольшее значенис варьирующего признака, xmin - наименьшее варьирующего признака.
Среднее линейное отклонение (
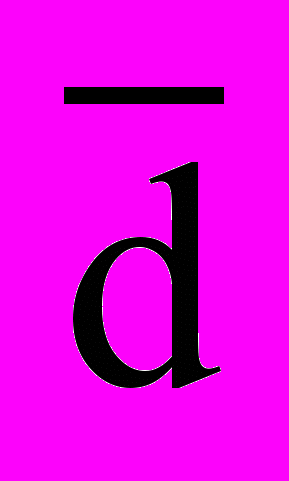 ) представляет собой среднюю величину из отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения:
) представляет собой среднюю величину из отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения: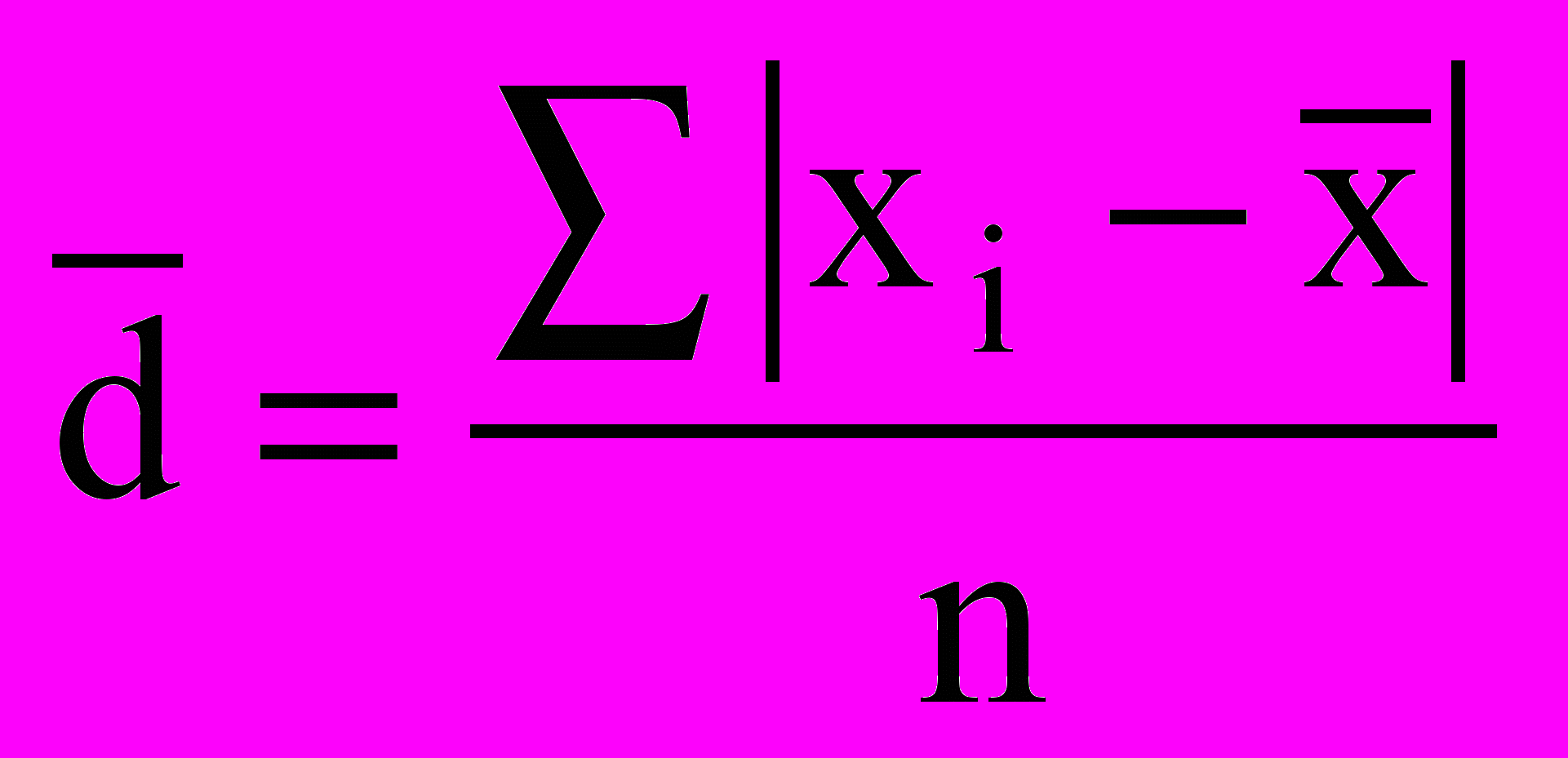 - невзвешенное среднее линейное отклонение;
- невзвешенное среднее линейное отклонение;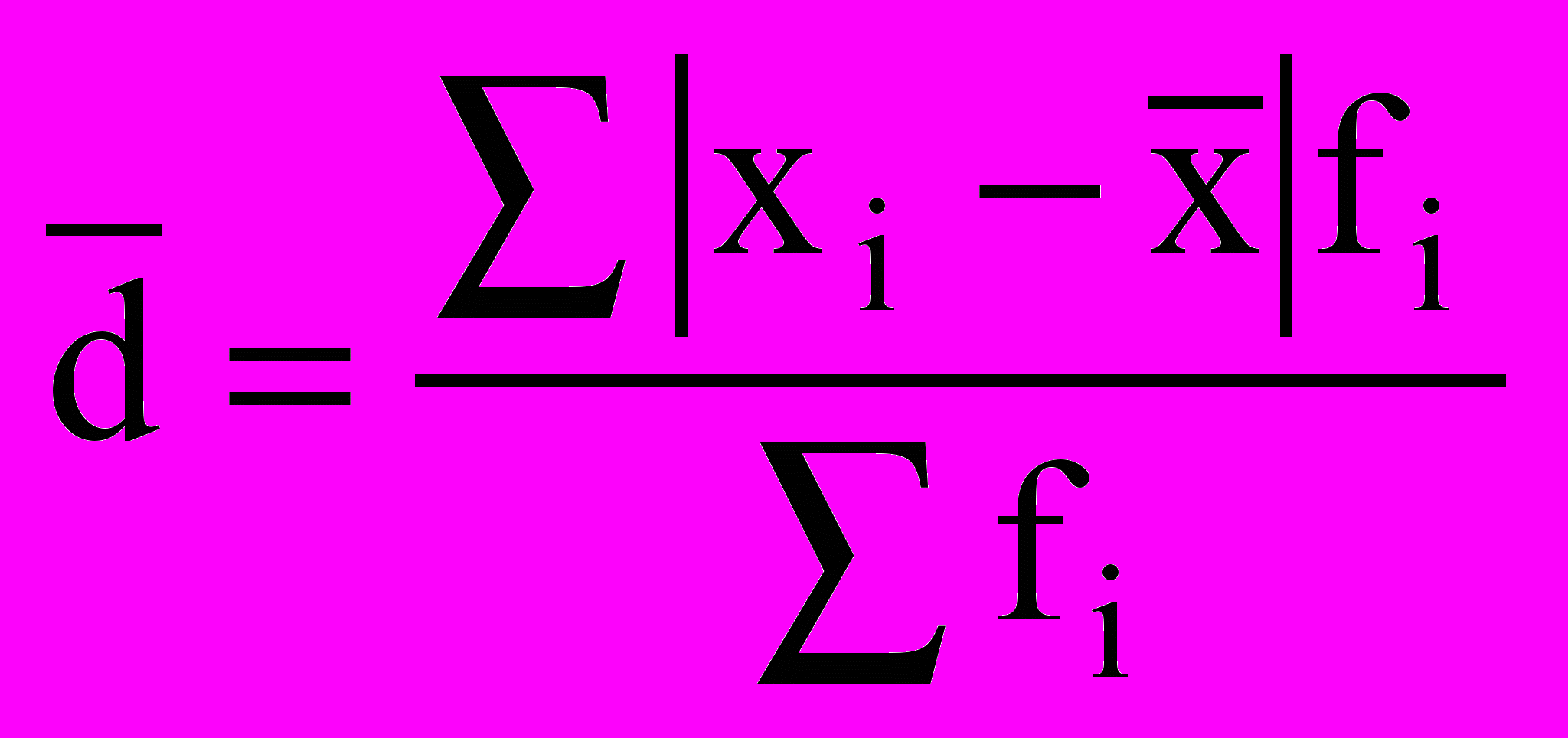 - взвешенное среднее линейное отклонение.
- взвешенное среднее линейное отклонение.Символы xi,
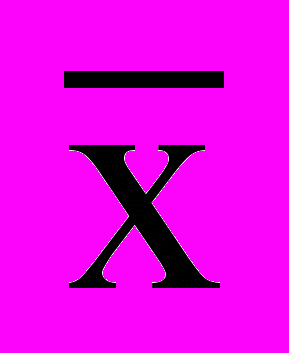 , fi , и n имеют то же значение, что и ранее (см. Контрольную работу 1). Рассмотренные выше показатели имеют ту же размерность, что и признак, для которого они вычисляются.
, fi , и n имеют то же значение, что и ранее (см. Контрольную работу 1). Рассмотренные выше показатели имеют ту же размерность, что и признак, для которого они вычисляются.Пример. На основе данных табл. 7.1 рассчитаем среднее линейное отклонение для дискретного ряда распределения.
Решение. Размах вариации стажа равен:
R = 12 - 8 = 4 года.
Результаты вспомогательных расчетов даны в графах 3-5 табл.1. Средний стаж работы определяем по формуле средней арифметической взвешенной:
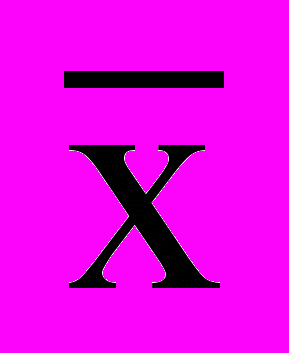 = 10 лет.
= 10 лет.Отклонения индивидуальных значений стажа от средней с учетом и без учета знака содержатся в графах 4 и 5, а произведения отклонений по модулю на соответствующие частоты - в гр. 6.
Таблица 1. Распределенне учителей средних школ по стажу работы
| Стаж работы, лет | Число учителей в % к итогу fi | xi fi | 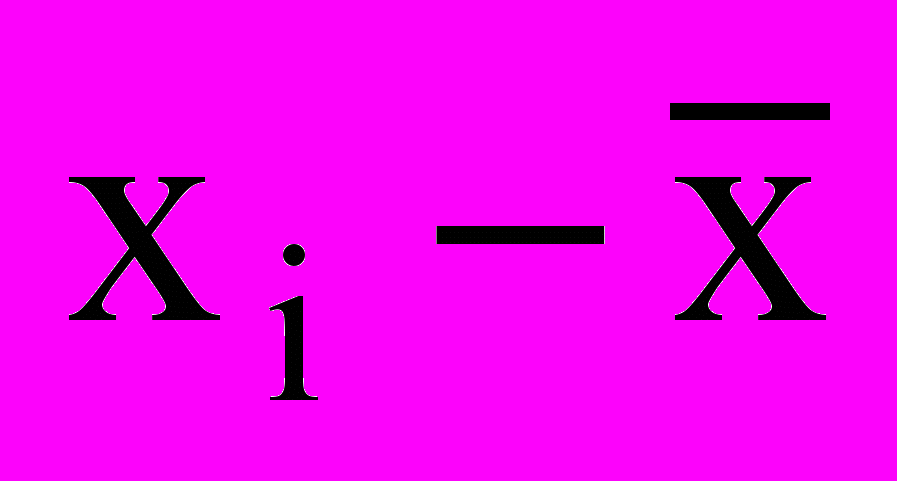 |  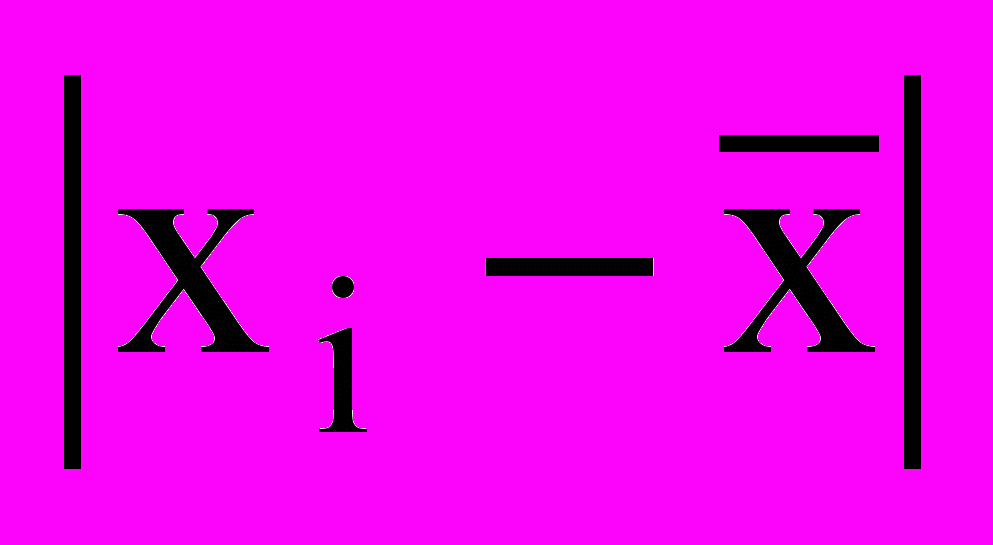 | 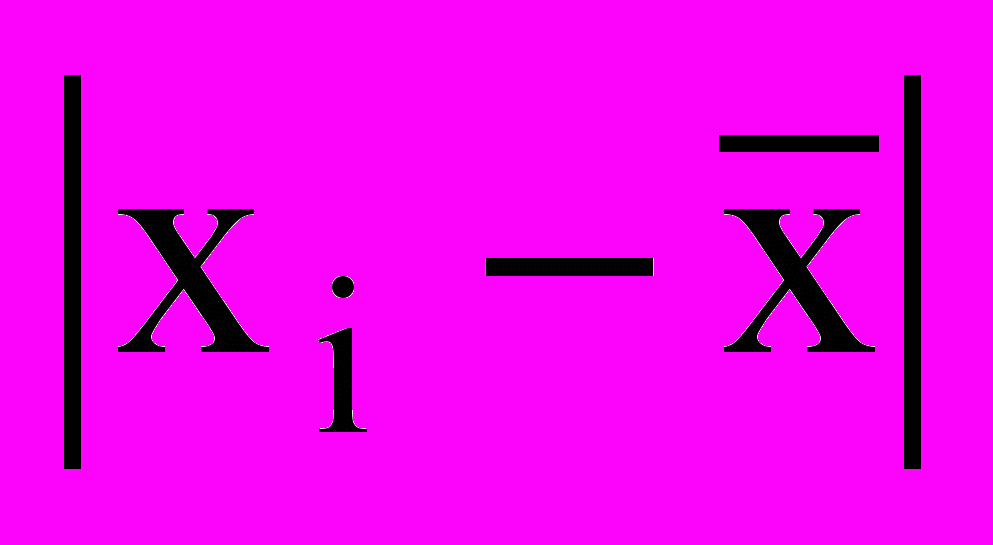 fi fi |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 8 | 14 | 112 | -2 | 2 | 28 |
| 9 | 20 | 180 | -1 | 1 | 20 |
| 10 | 30 | 300 | 0 | 0 | 0 |
| 11 | 24 | 264 | 1 | 1 | 24 |
| 12 | 12 | 144 | 2 | 2 | 24 |
| Итого | 100 | 1000 | 0 | - | 96 |
Среднее линейное отклонение стажа работы учителей средних школ района:
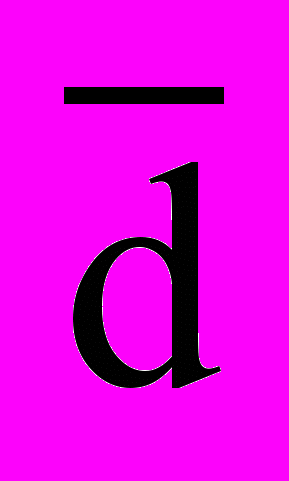 = 0,96 года.
= 0,96 года. Показатели дисперсии и среднего квадратического отклонения являются общепринятыми мерами в статистических исследованиях
Дисперсия вычисляется по формулам:
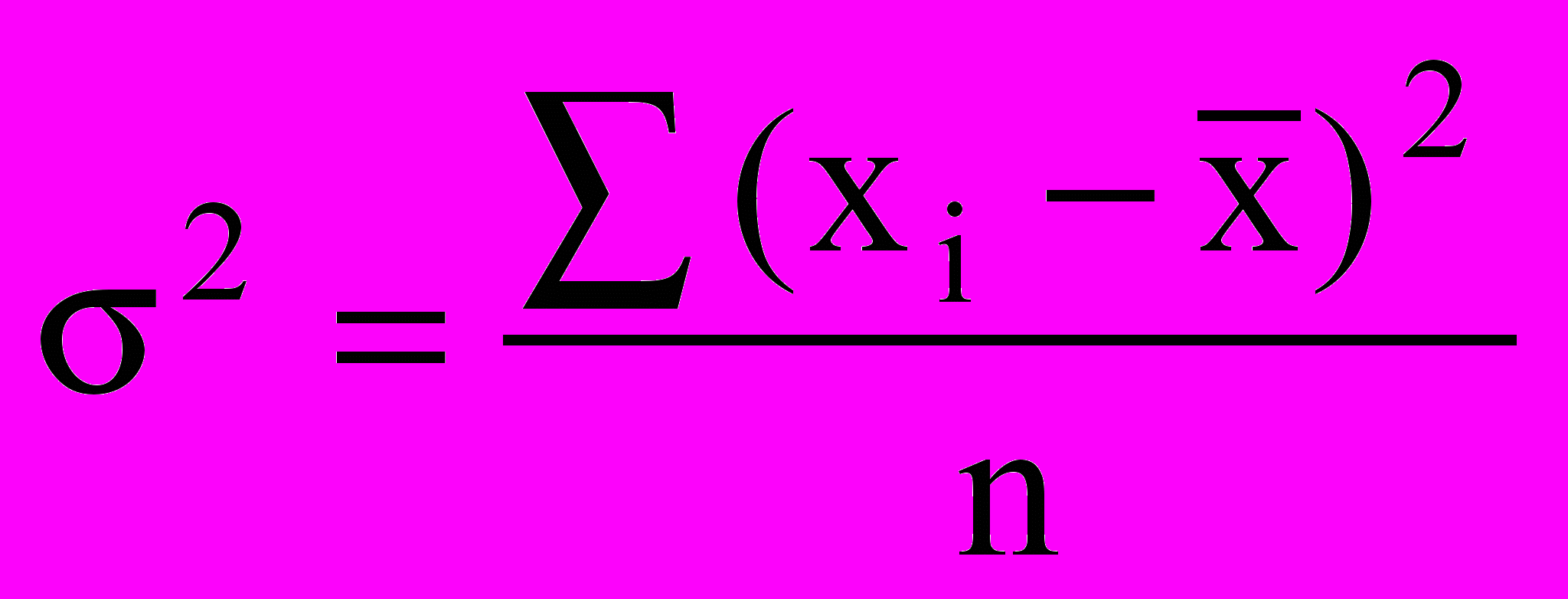 - невзвешенная;
- невзвешенная; 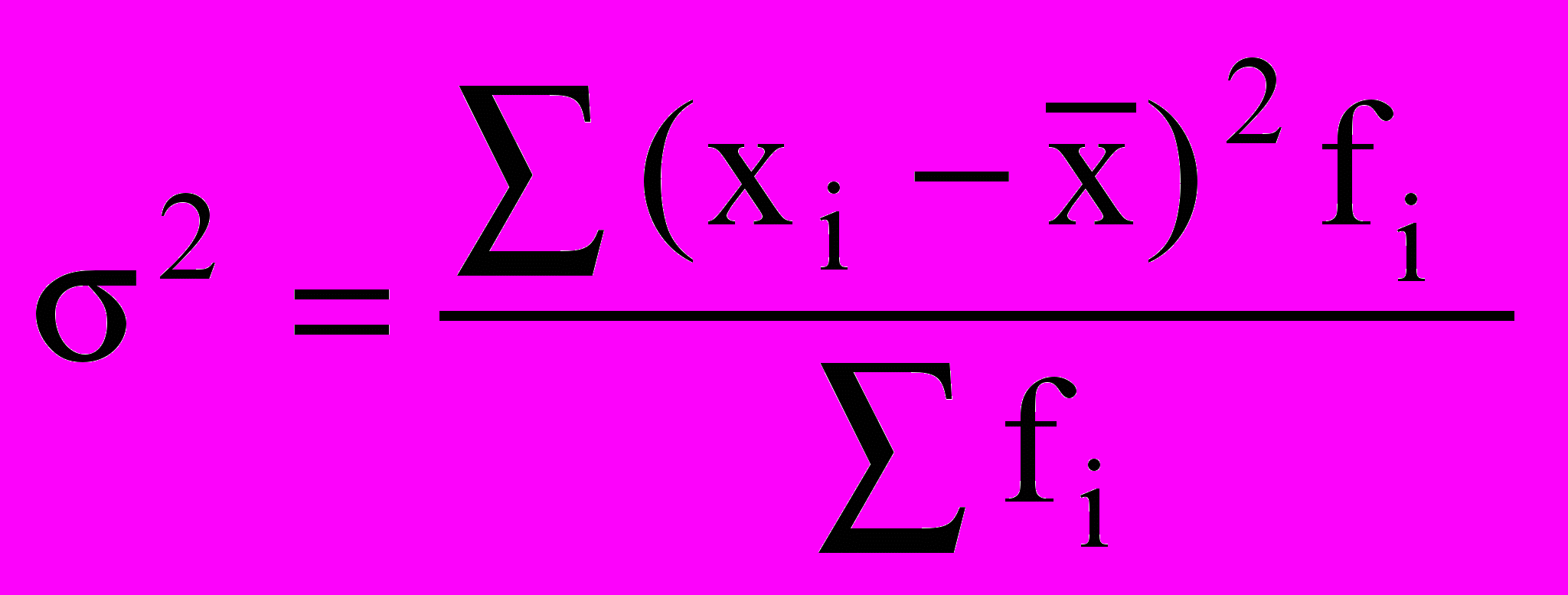 - взвешенная.
- взвешенная.Среднее квадратнческое отклюненне вычисляется по формулам:
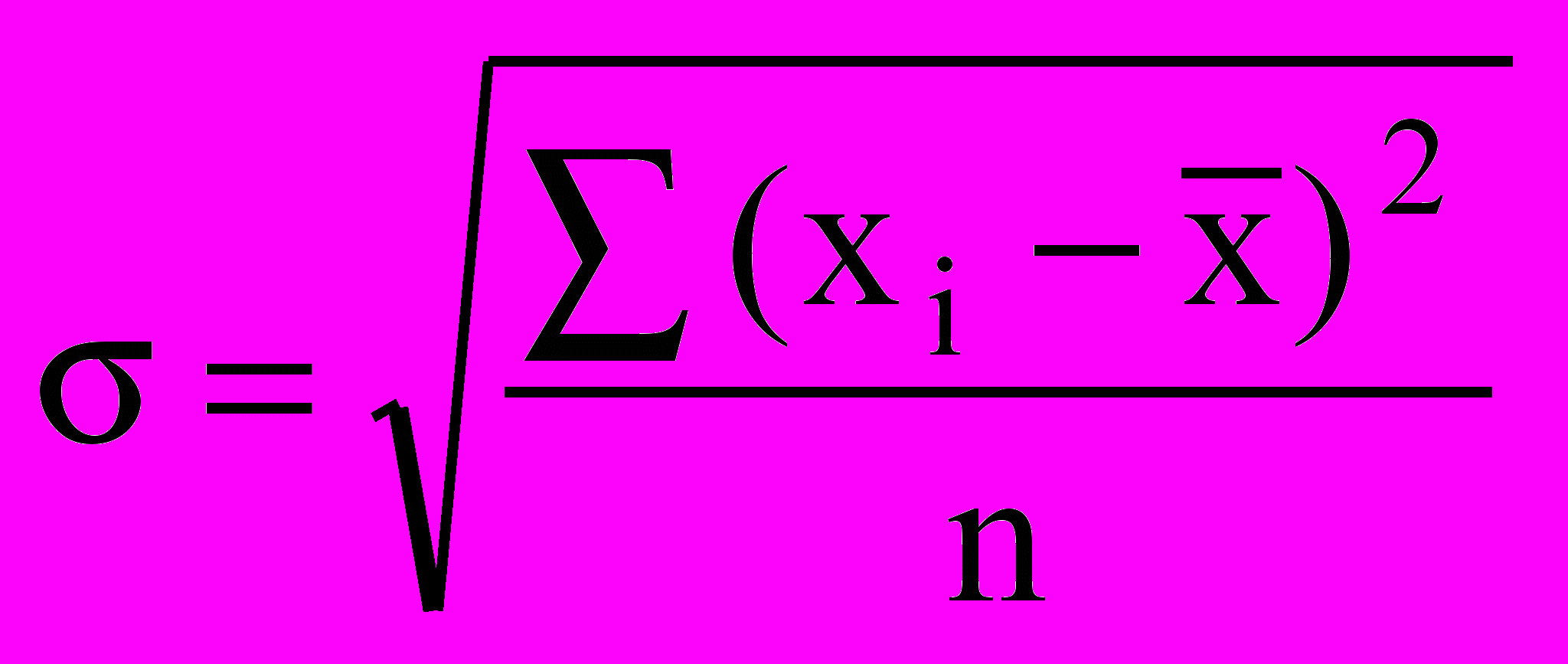 - невзвешенное,
- невзвешенное,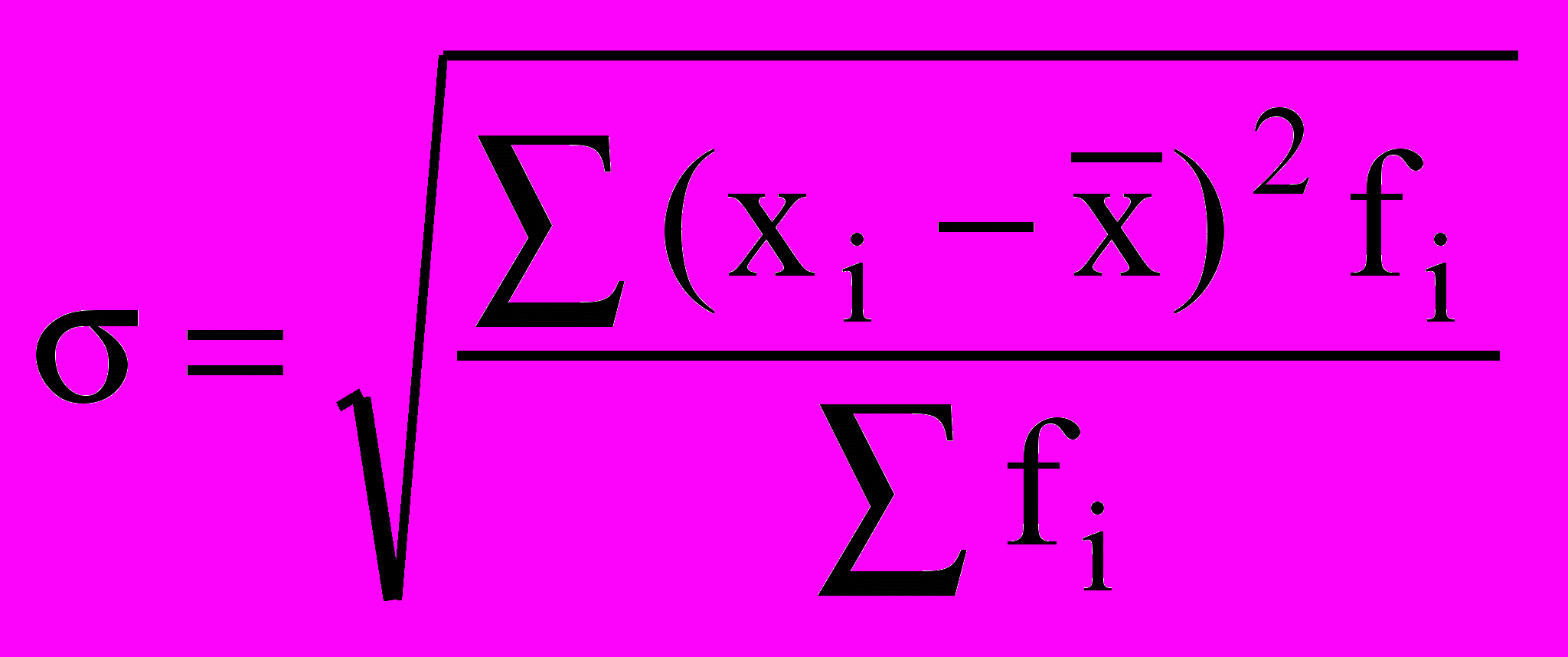 -взвешенное.
-взвешенное.Среднее квадратическое отклонение - величина именованная, имеет размерность осредняемого признака.
Пример. Рассчитаем дисперсию и среднее квадратическое отклонение для следующего ряда распределения (табл. 2).
Таблица 2. Распределение магазинов города по товарообороту во 2 КВАРТАЛЕ 1998 года
| Группы магазинов по величине товарооборота, тыс.$ | Число магазинов f, | Середина интервала, тыс. $. xi | xi fi | 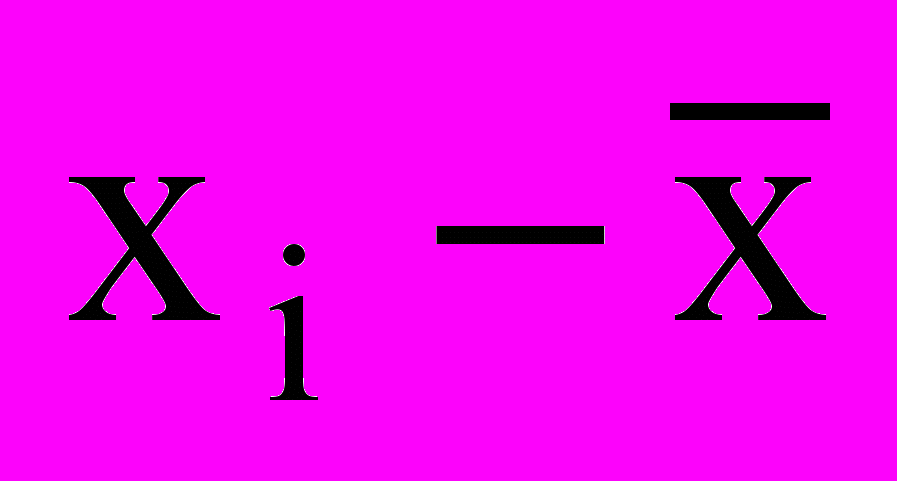 | 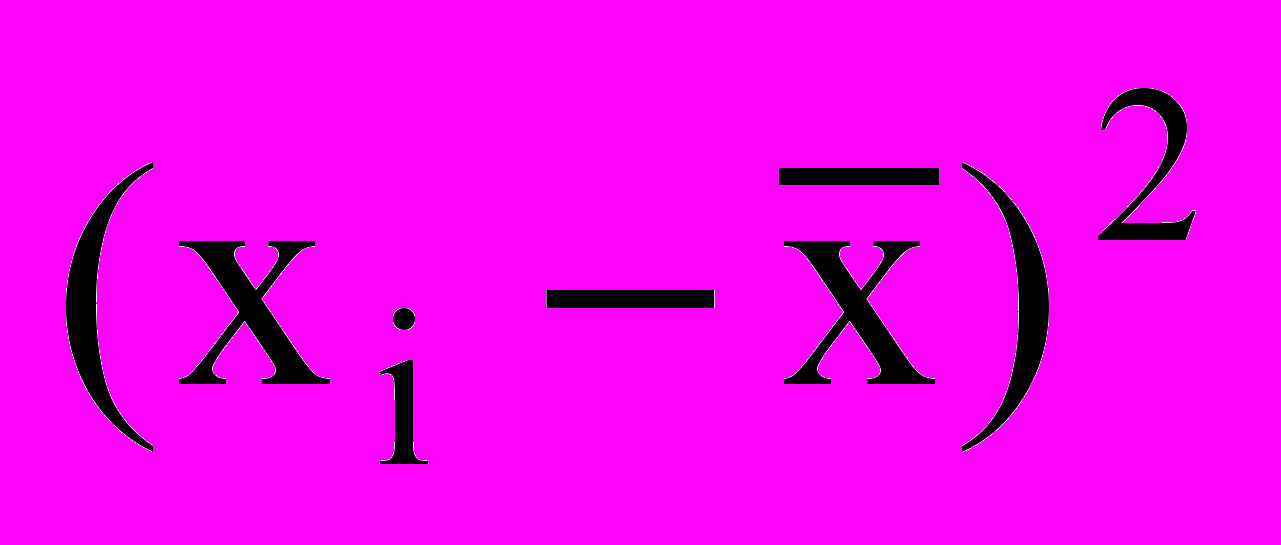 | 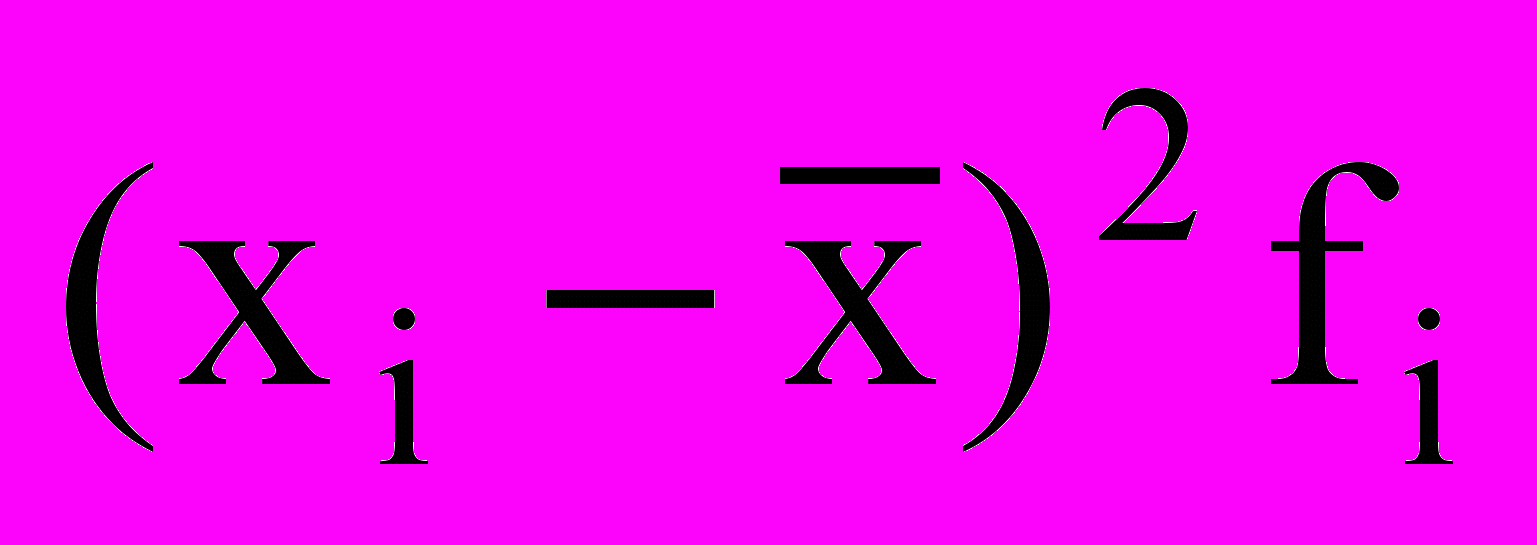 |
| А | 1 | 2 | 3 | 4 | 5 | 6 |
| 40-50 | 2 | 45 | 90 | -49,2 | 2420,64 | 4S41.28 |
| 50 -60 | 4 | 55 | 220 | -39,2 | 1536,64 | 6146,56 |
| 60-70 | 7 | 65 | 455 | -29,2 | 852,64 | 5968,48 |
| 70-80 | 10 | 75 | 750 | -19,2 | 368,64 | 3686,40 |
| 80-90 | 15 | 85 | 1275 | -9,2 | 84.64 | 1269,60 |
| 90 - 100 | 20 | 95 | 1900 | 0,8 | 0,64 | 12,80 |
| 100- 110 | 22 ' 105 | 2310 | 10,8 | 116,64 | 2566,08 | |
| 110- 120 | 11 | 115 | 1265 | 20.64 | 432,64 | 4759,04 |
| 120 - 130 | 6 | 125 | 750 | 30,8 | 948,64 | 5691,84 |
| 130 - 140 | П | 135 | 405 | 40,8 | 1664.64 | 4993,92 |
| Итого | 100 | 0 | 9420 | - | — | 39936,00 |
Решение. В приведенных ранее примерах мы имели дело с дискретными рядами. При расчете показателей вариации по интервальным рядам распределения (табл.2) необходимо сначала определить середины интервалов, а затем вести дальней. шие расчеты, рассматривая ряд середин интервалов как дискрет, ный ряд распределения. Результаты вспомогательных расчетов для определения дисперсии и среднего квадратического отклонения содержатся в груфах 2-6 табл. .2.
Средний размер товарооборота определяется по средней арифметической взвешенной и составляет:
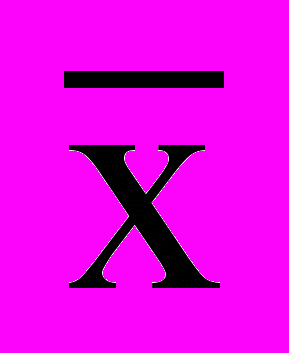 = 94,2 тыс. $.
= 94,2 тыс. $. Дисперсия товарооборота : 399,36.
Среднее квадратическое отклонение товарооборота определяется как корень квадратный из дисперсии:
=20 тыс. $.
Расчет дисперсии прямым способом в ряде случае трудоемок, поэтому логично, используя свойства дисперсии, упростить ее вычисления, например, используя расчет дисперсии по способу отсчета от условного нуля или способу моментов по общей формуле:
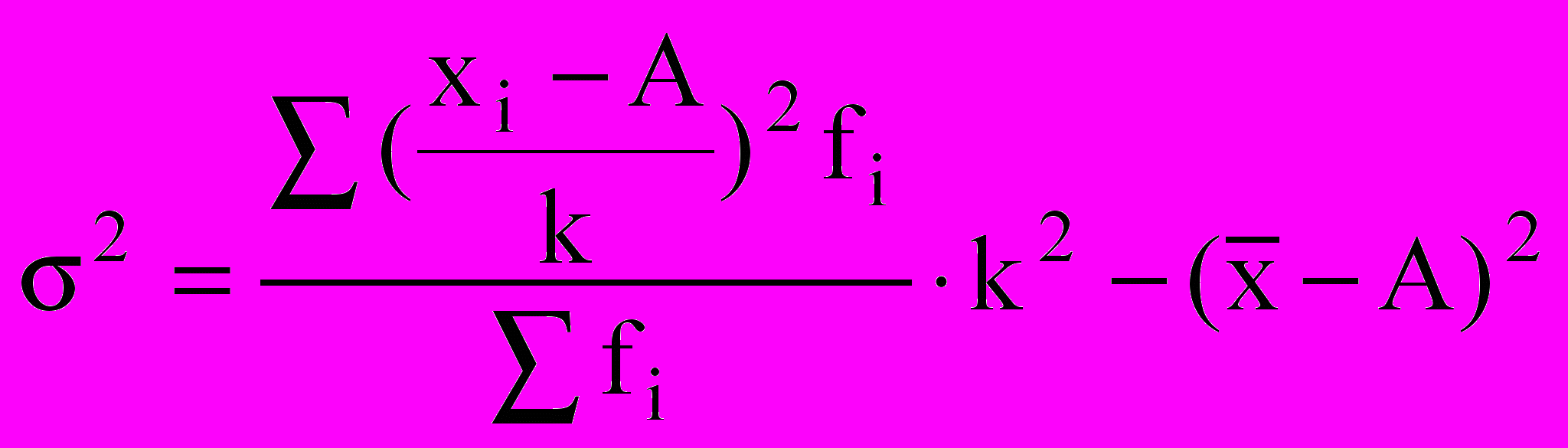
С использованием начальных моментов формула дисперсии по способу моментов имеет следующий вид:
=k2(m2-m1),
где k - величина интервала, А - условный нуль, в качестве которого удобно использовать середину интервала с наибольшей частотой,
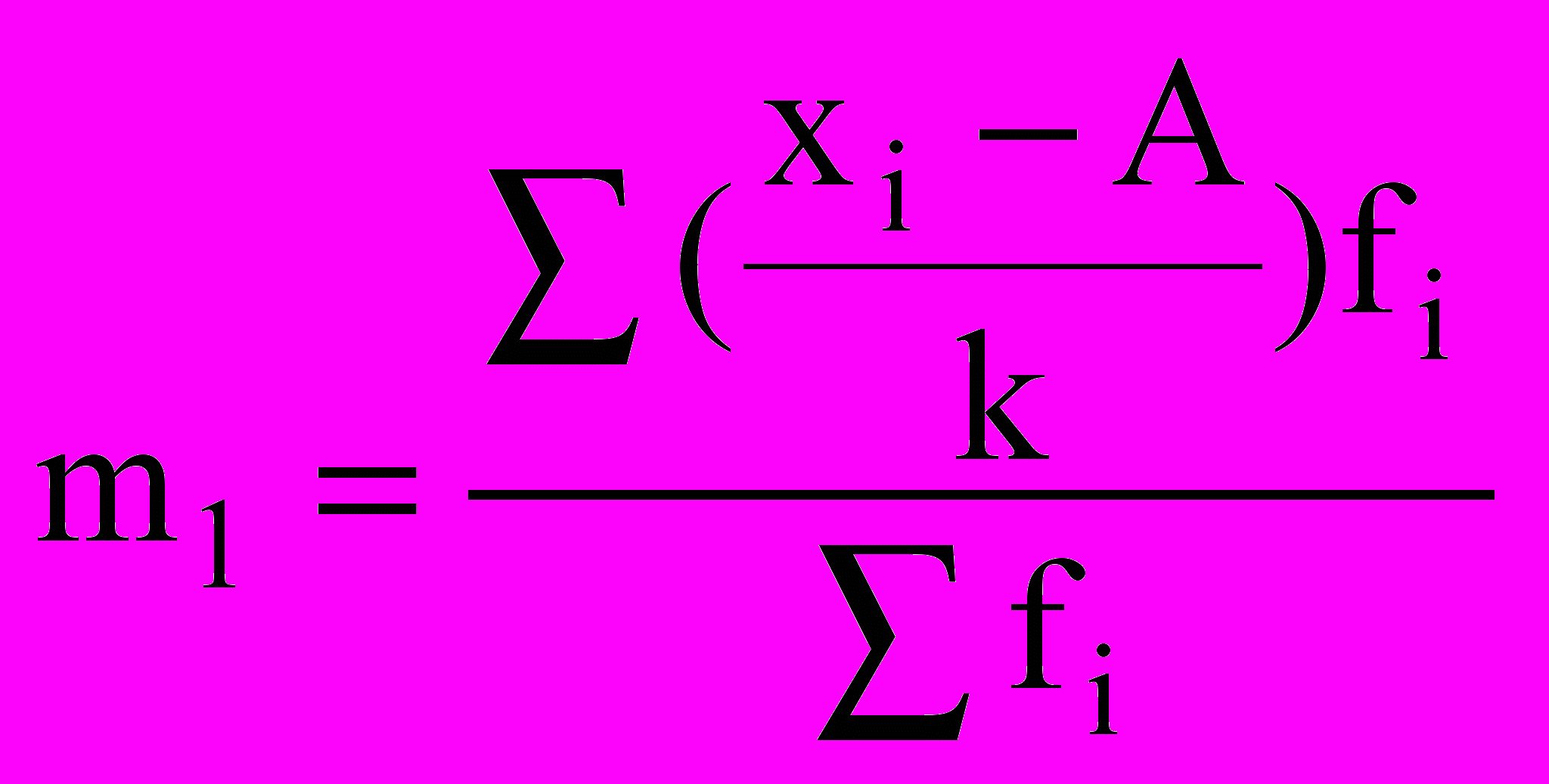 - начальный момент первого порядка;
- начальный момент первого порядка;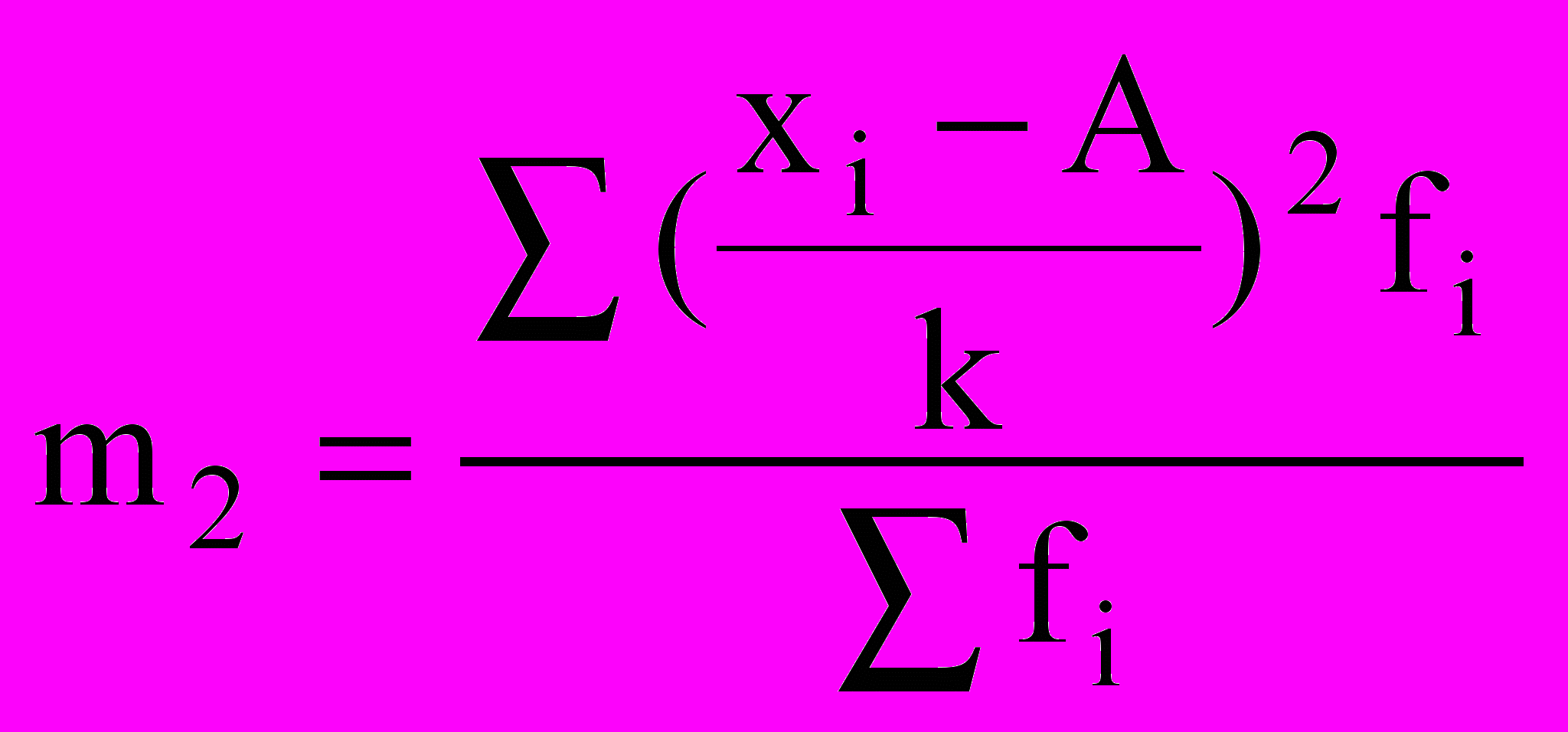 - начальный момент второго порядка.
- начальный момент второго порядка.В случае когда А приравнивается к нулю и, следовательно, не вычисляются отклонения, формула принимает вид:
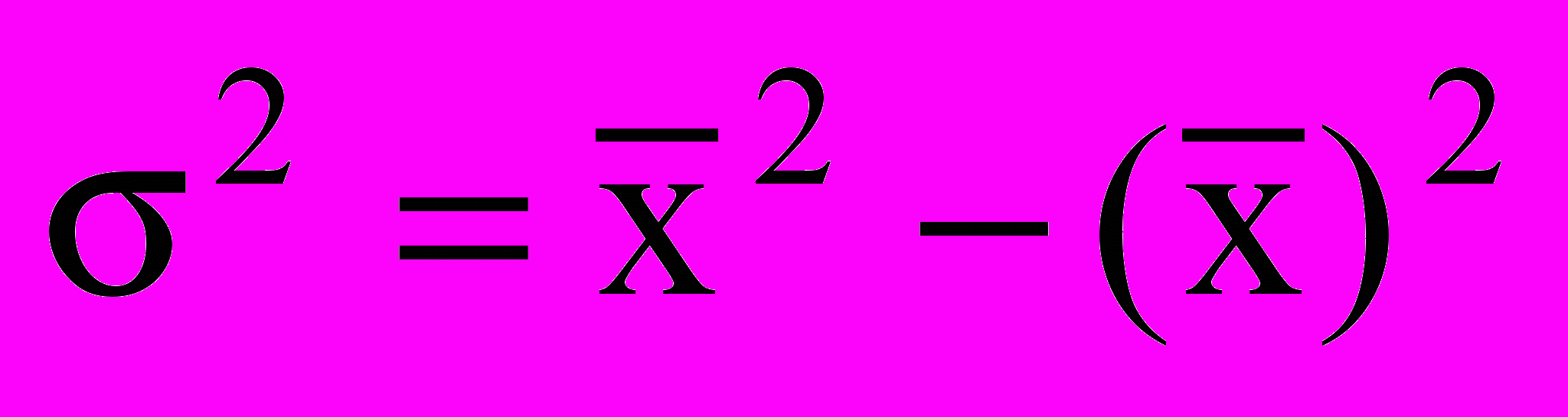 .
.Воспользуемся данными предыдущего примера и рассчитаем дисперсию по способу отсчета от условного нуля и способу моментов. Расчет произведем в табличной форме (табл..3).
Таблица .3
| Группы магазинов по товарообороту, тыс. $. | Число магазинов fi | Середина интервала, тыс. $. xi, | xi-A (А=95) | (xi-A)/k (k=10) | (xi-A)fi/k | (xi-A)2fi/k | xi2 | xi2fi |
| 40-50 | 2 | 45 | -50 | -5 | -10 | 50 | 2025 | 4050 |
| 50-60 | 4 | 55 | -40 | -4 | -16 | 64 | 3025 | 121100 |
| 60-70 | 7 | 65 | -30 | -3 | -21 | 63 | 4225 | 29575 |
| 70-80 | 10 | 75 | -20 | -2 | -20 | 40 | 5625 | 56250 |
| 80-90 | 15 | 85 | -10 | -1 | -15 | 15 | 7225 | 108375 |
| 90-100 | 20 | 95 | 1 | 0 | 0 | 0 | 9025 | 180500 |
| 100-110 | 22 | 105 | 10 | 1 | 22 | 22 | 11025 | 242550 |
| 110-120 | 11 | 115 | 20 | •> | 22 | 44 | 13225 | 145475 |
| 120-130 | 6 | 125 | 30 | 3 | 18 | 54 | 15625 | 91750 |
| 130-140 | 3 | 135 | 40 | 4 | 12 | 48 | 18225 | 54675 |
| Итого | 100 | - | - | - | -8 | 400 | - | 927730 |
По способу отсчета от условного нуля:
По способу моментов получаем:
По способу разности между средней квадратов вариантов признака и квадратом их средней величины
Результаты расчетов дисперсии по всем трем способам дают одну и ту же величину. Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях вычисляются относительные показатели вариации. Базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха, или среднего линейного отклонения, или среднего квадратического отклонения к средней арифметической. Чаще всего они выражаются в процентах и характеризуют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Различают следующие относительные показатели вариации (V):
Коэффициент осцилляции:
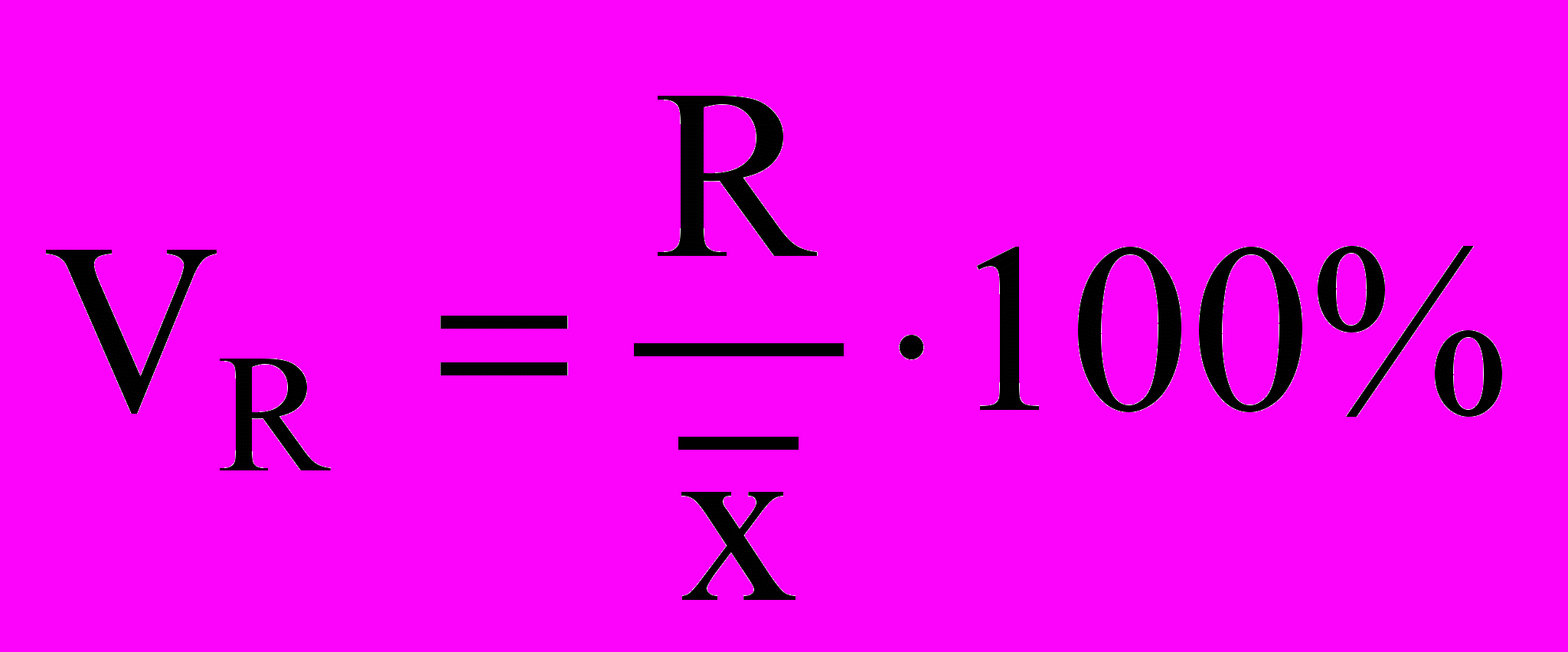 .
. Линейный коэффициент вариации:
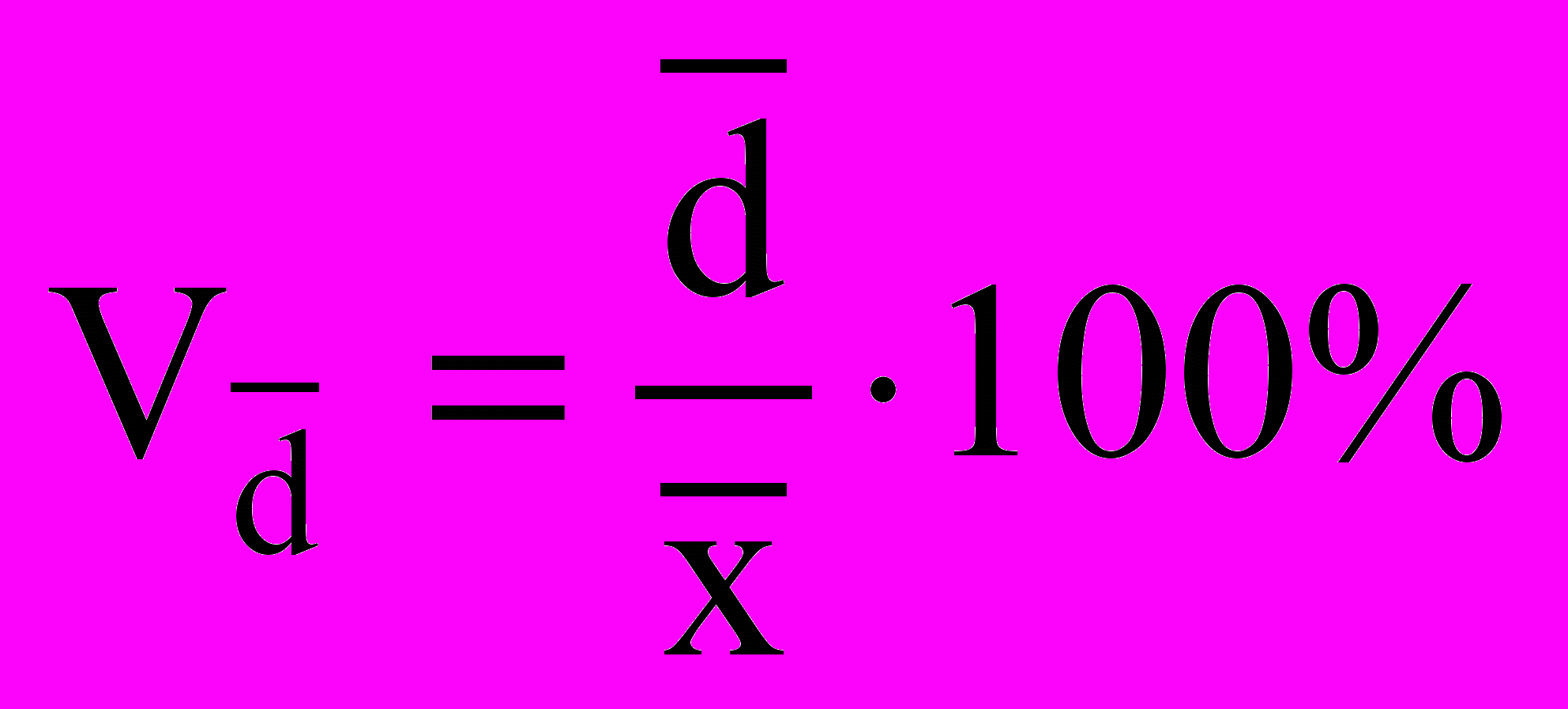 .
.Коэффициент вариации:
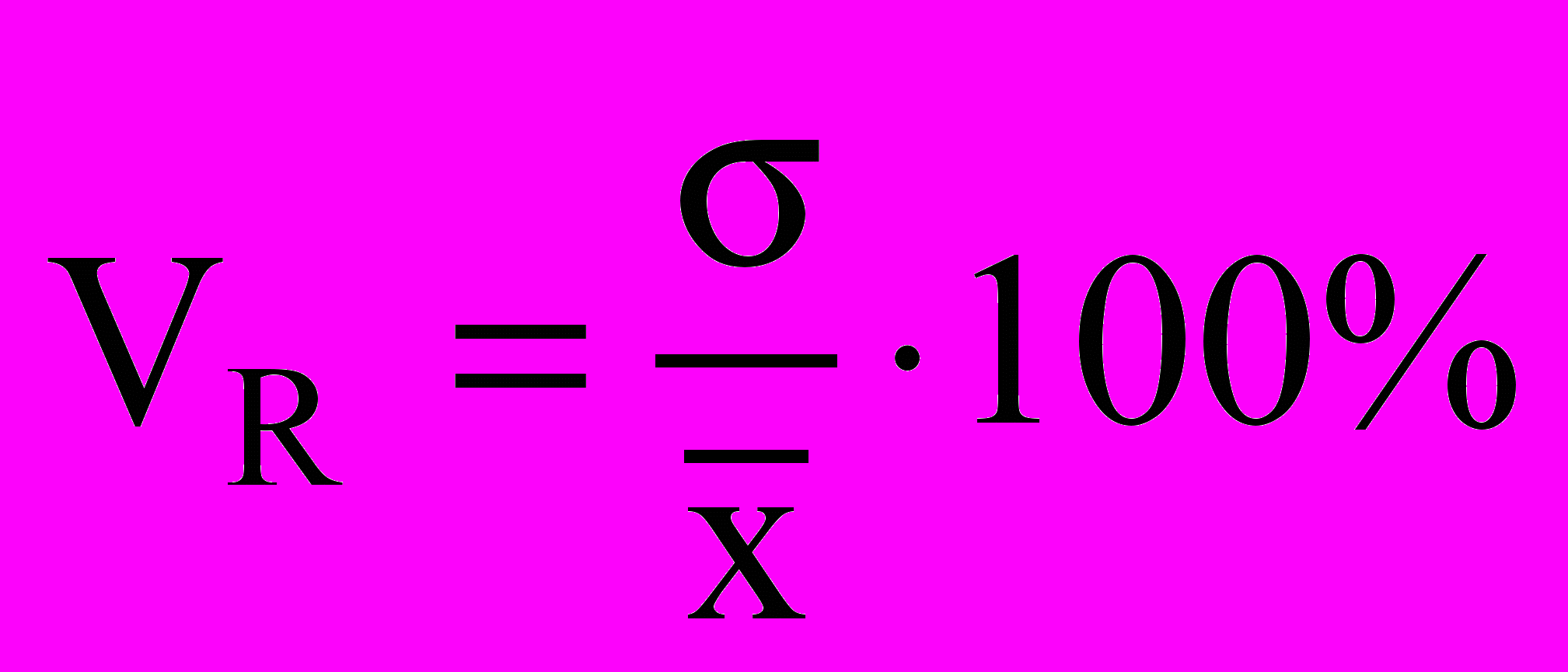
Наиболее часто в практических расчетах из этих трех показателей применяется коэффициент вариации.
Статистическое изучение вариации многих социально-экономических явлений проводится и при помощи дисперсии альтернативного признака, Обозначим наличие данного признака 1, отсутствие 0, долю вариантов, обладающих данным признаком, р, а не обладающих им q. Так как ряд р + q = 1, то средняя
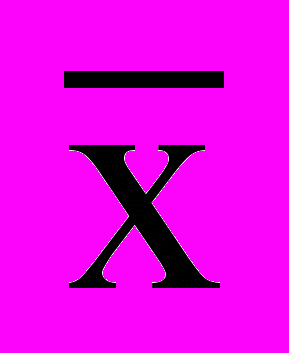 = р, а дисперсия альтернативного признака = pq, где р =m/n, n - число наблюдений, m - число единиц совокупности, обладающее данным признаком, q = 1 - р.
= р, а дисперсия альтернативного признака = pq, где р =m/n, n - число наблюдений, m - число единиц совокупности, обладающее данным признаком, q = 1 - р.Определим дисперсию альтернативного признака по следующим данным: налоговой инспекцией одного из районов города проверено 172 коммерческих киоска и в 146 обнаружены финансовые нарушения. Тогда
n= 172, m = 146; p=0.85: q = 1 - 0,85 = 0,15; = 0,85 • 0,15 = 0,1275.
Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.
Правило сложения дисперсий. Если данные представлены в виде аналитической группировки, то можно вычислить дисперсию общую межгрупповую и внутригрупповую.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов,, обусловливающих эту вариацию:
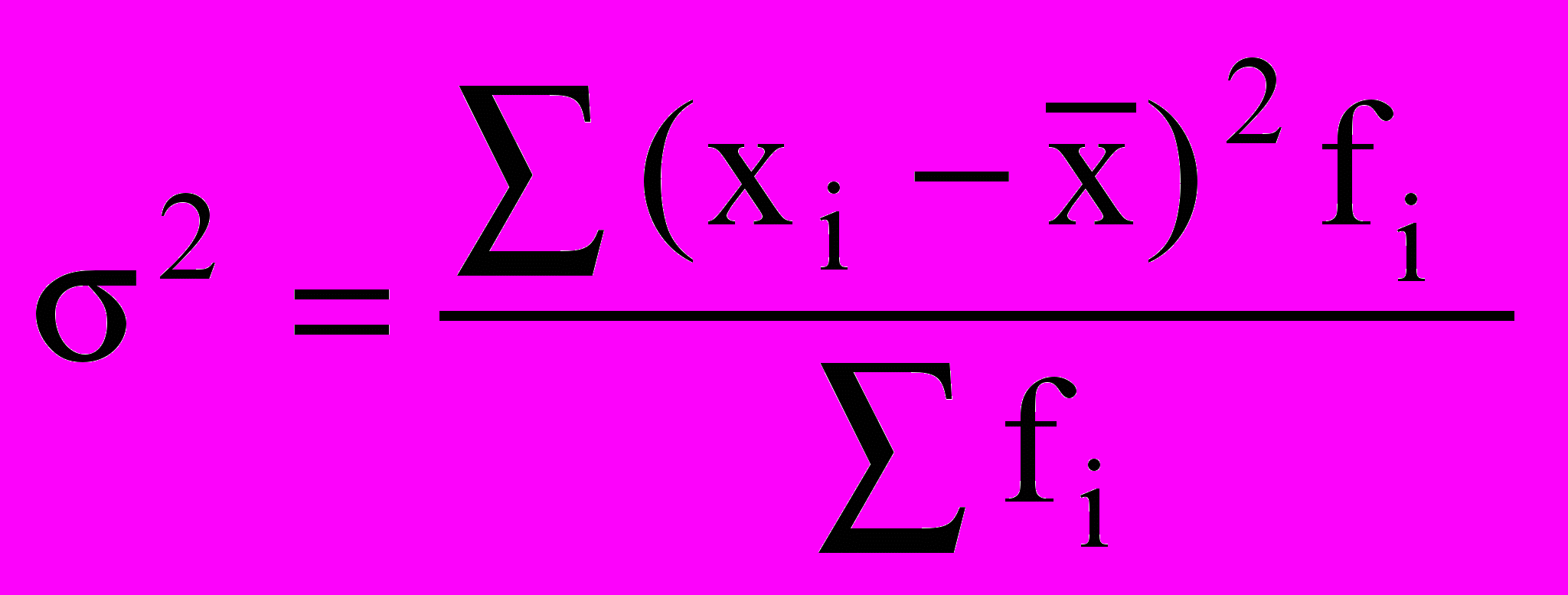
Межгрупповая дисперсия характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле:
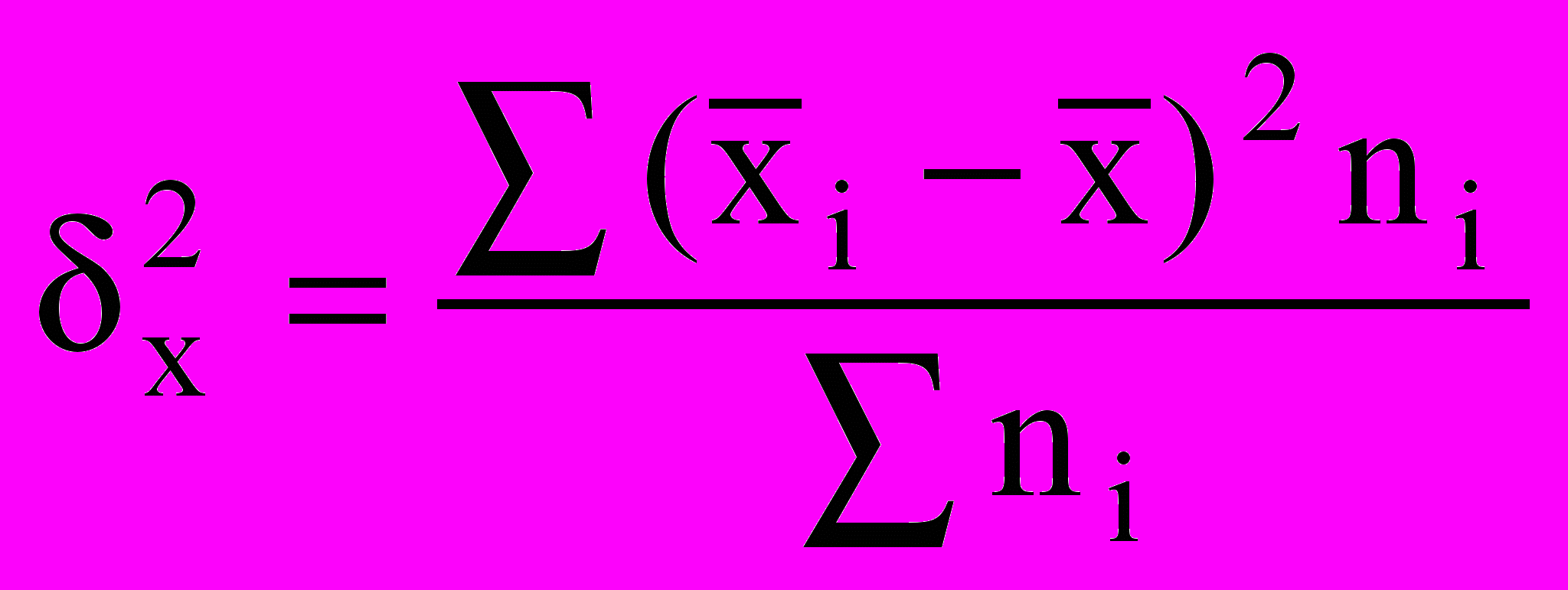 ,
,где
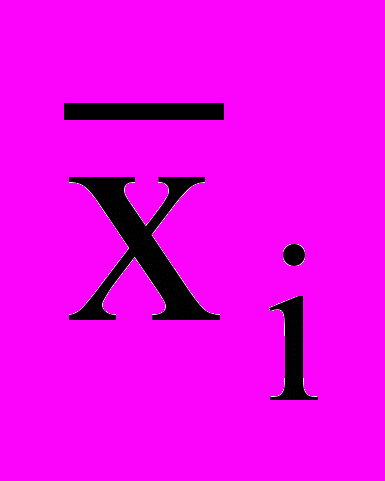 и ni - соответственно средние и численности по отдельным группам.
и ni - соответственно средние и численности по отдельным группам.Внутригрупповая дисперсия отражает случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она исчисляется следующим образом:
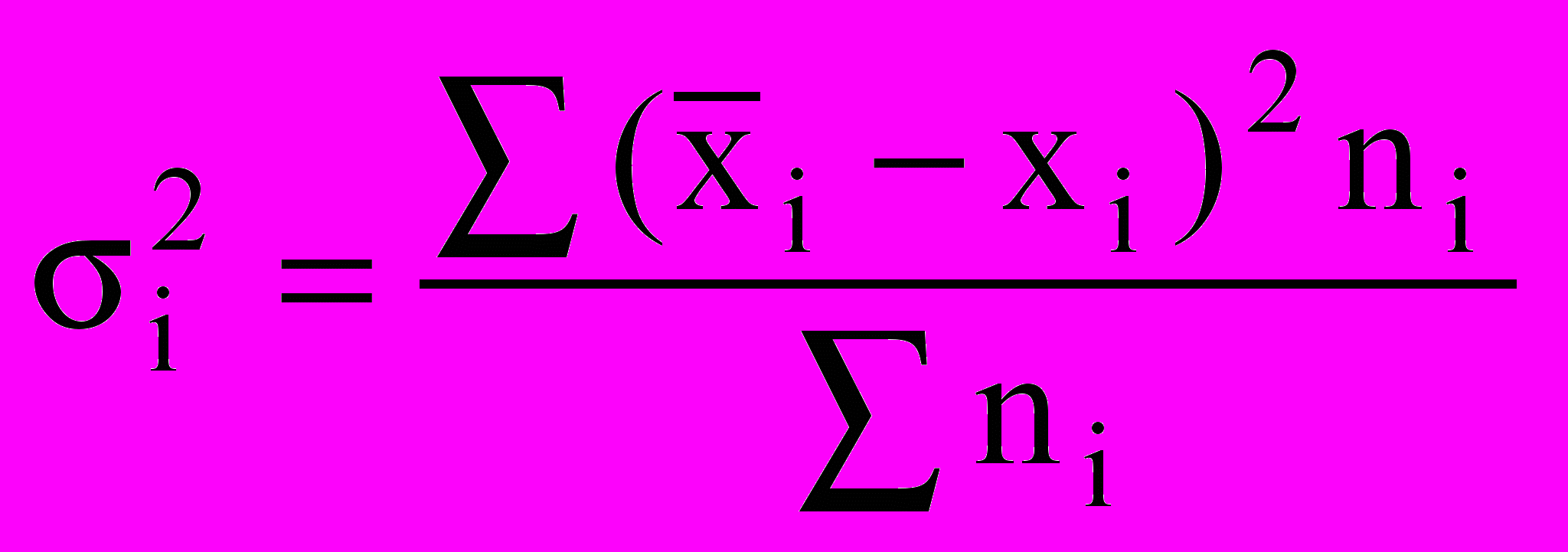 .
.Средняя из внутригрупповых дисперсии:
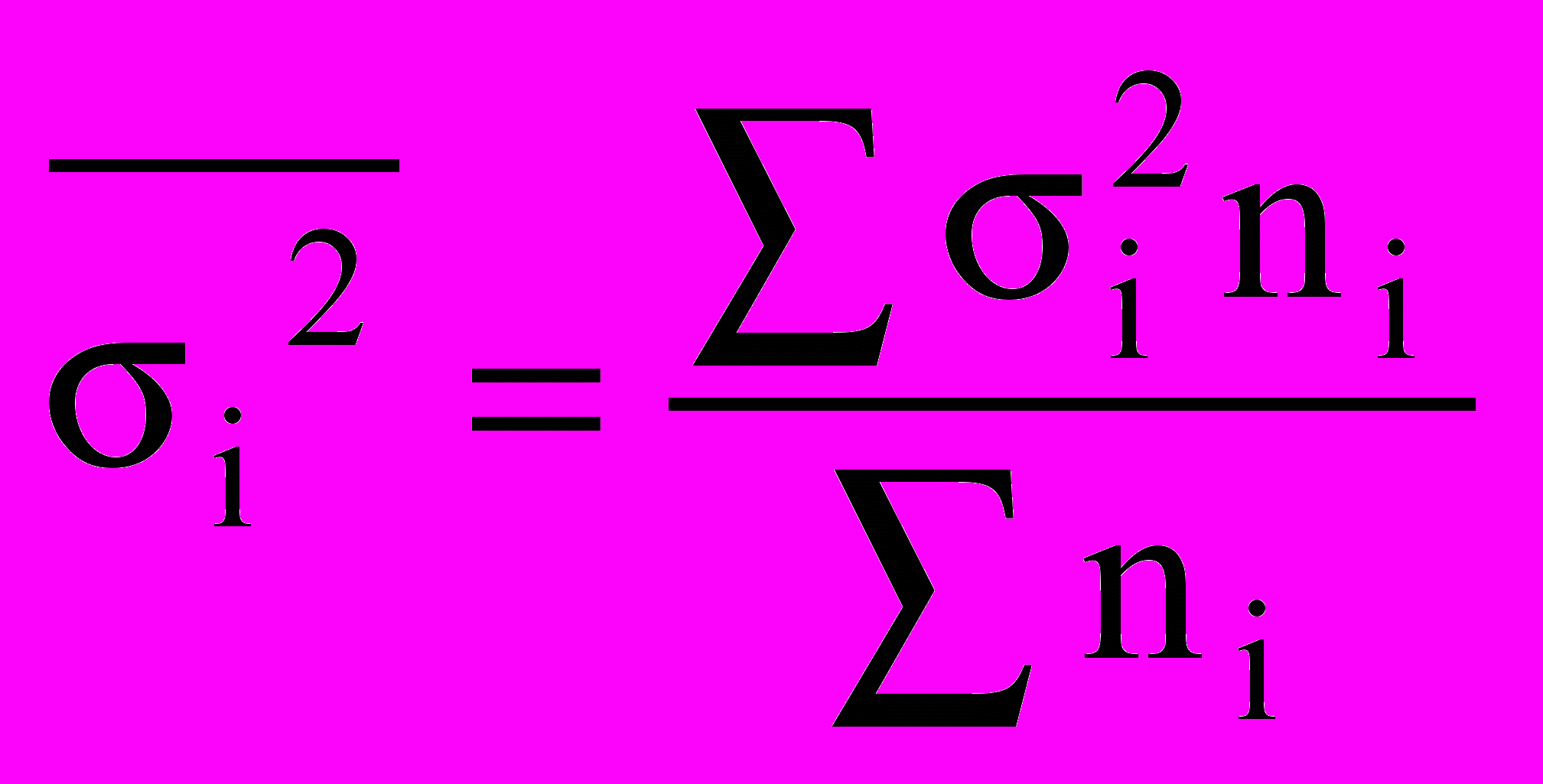
Существует закон, связывающий три вида дисперсий. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
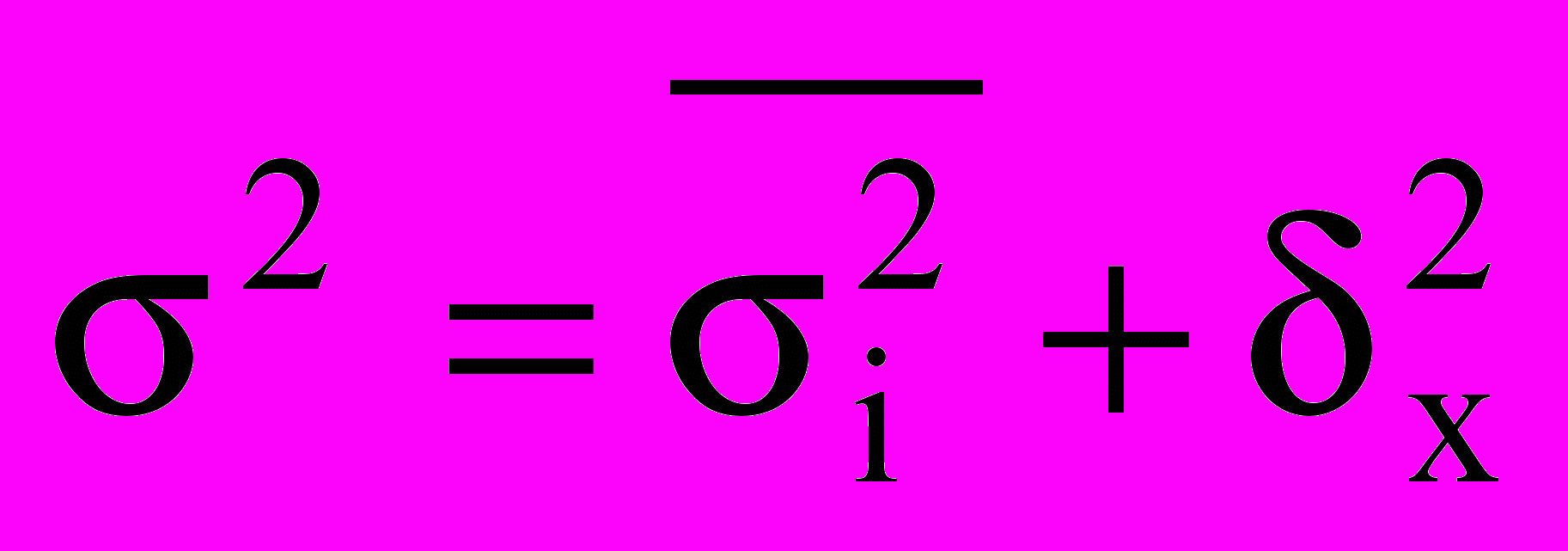 .
.Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих влиянием нием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.
Зная любые два вида дисперсий, можно определить или про ерить правильность расчета третьего вида.
Пример. Определим групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию по данным табл. 4.
Таблица 4 Производительность труда двух бригад рабочих-токарей
| 1-я бригада | 2-я бригада | ||||||
| № | Изготовлено деталей за час, шт. xi | | | № | Изготовлено деталей за час, шт. xi | | |
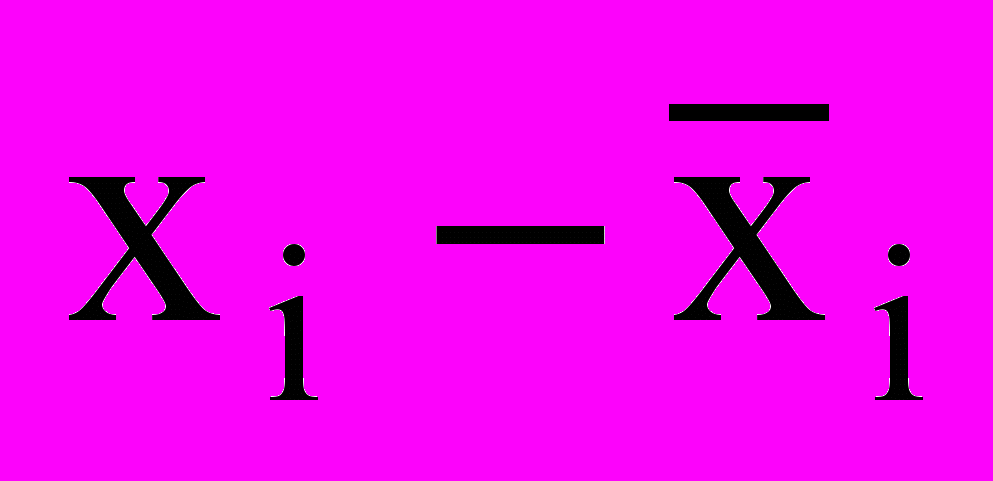 | 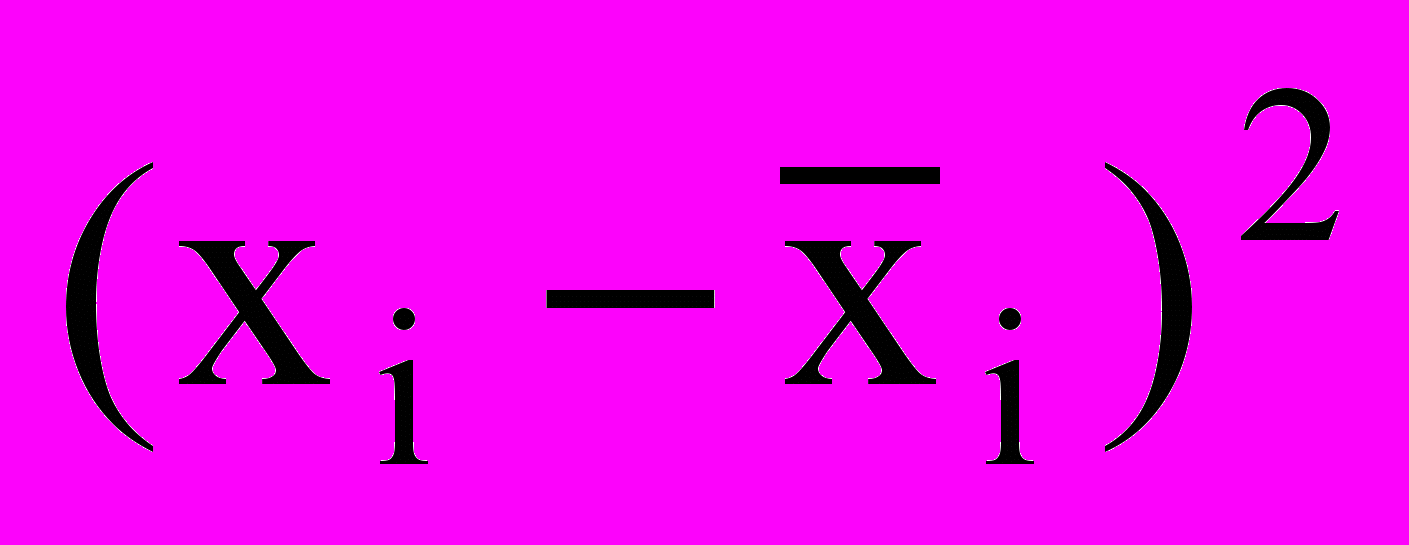 | 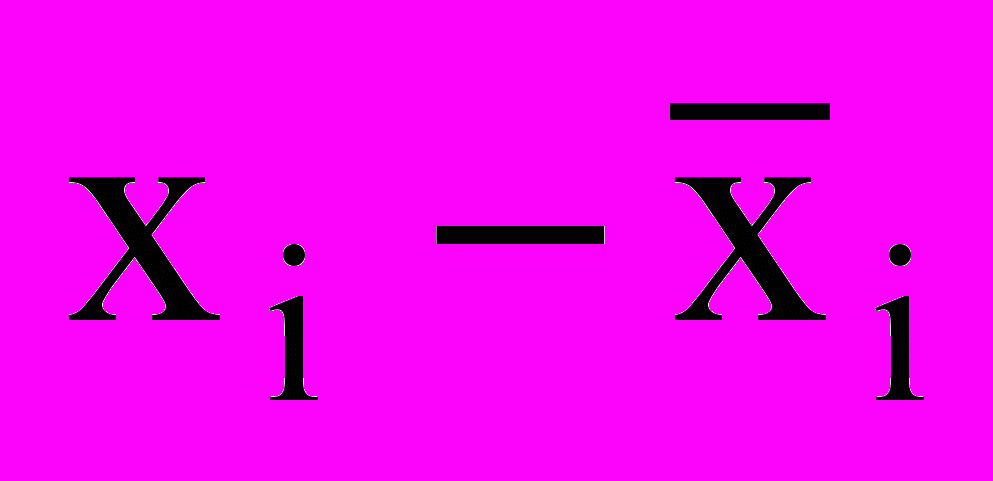 | 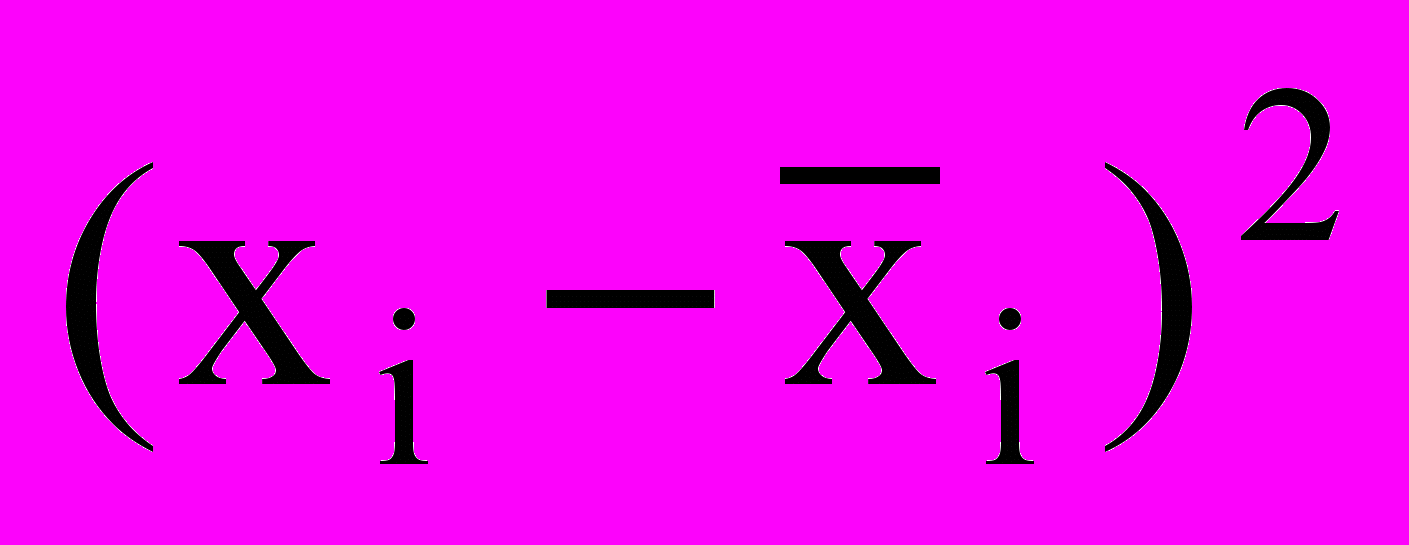 | ||||
| 1 | 13 | -2 | 4 | 7 | 18 | -3 | 9 |
| 2 | 14 | -1 | ] | 8 | 19 | -2 | 4 |
| 3 | 15 | 0 | 0 | 9 | 22 | 1 | 1 |
| 4 | 17 | 2 | 4 | 10 | 20 | -1 | 1 |
| 5 | 16 | 1 | 1 | 11 | 24 | 3 | 9 |
| 6 | 15 | 0 | 0 | 12 | 23 | 2 | 4 |
| 90 | | 10 | 126 | | 24 | ||
Решение.
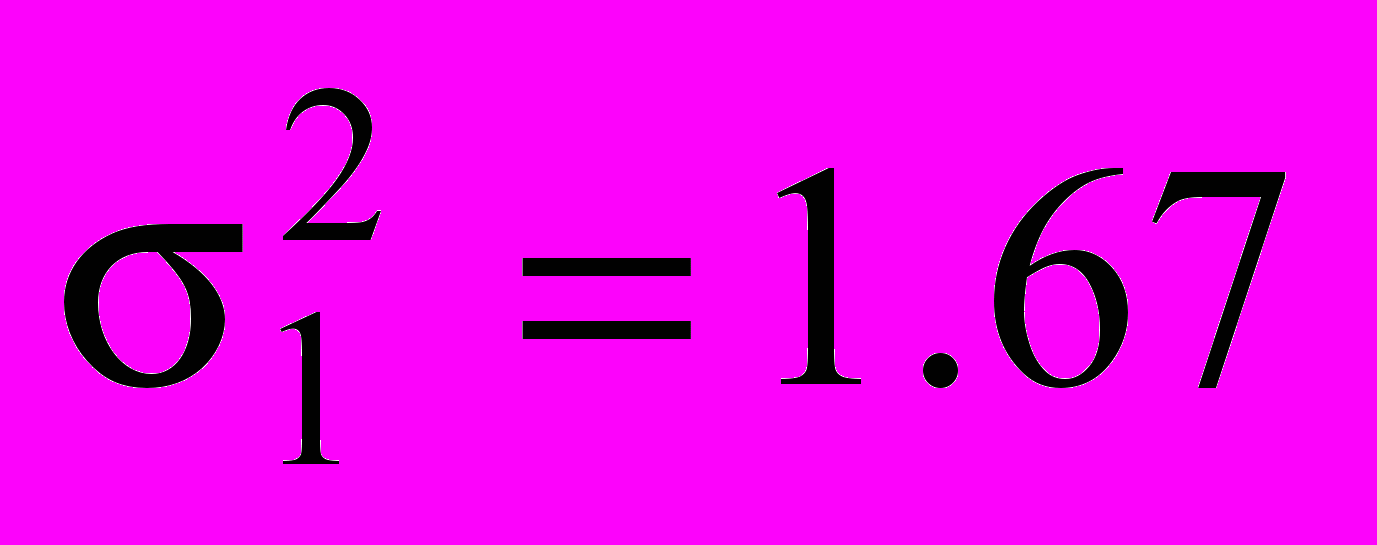 ;
; 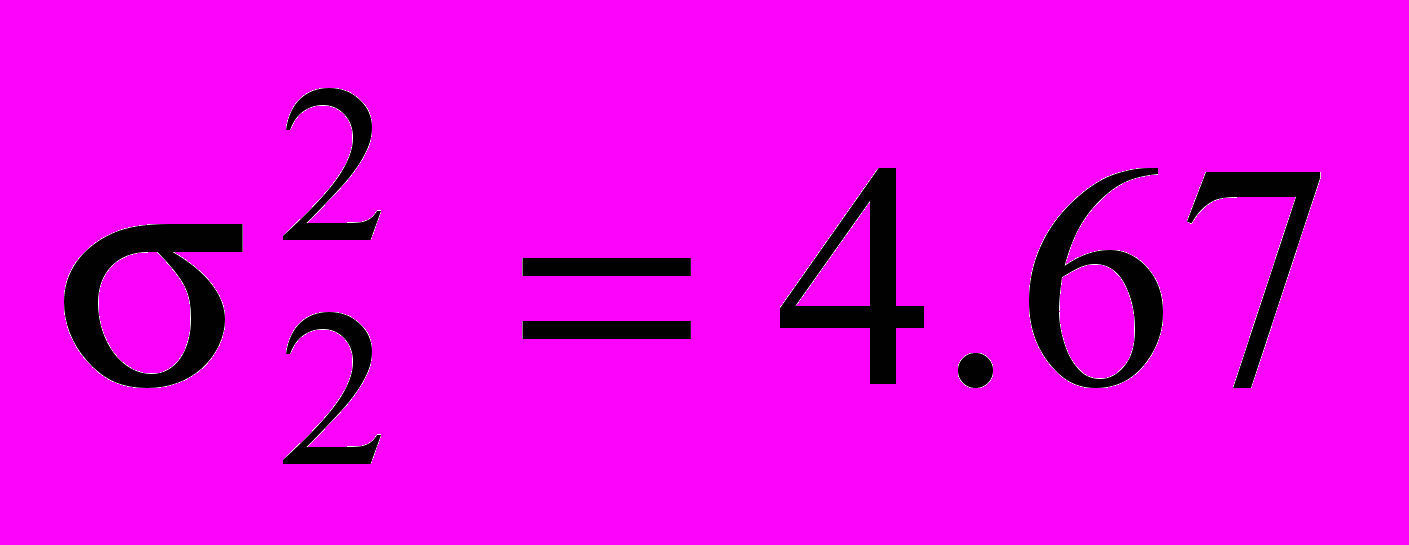 .
.Средняя из групповых дисперсий:
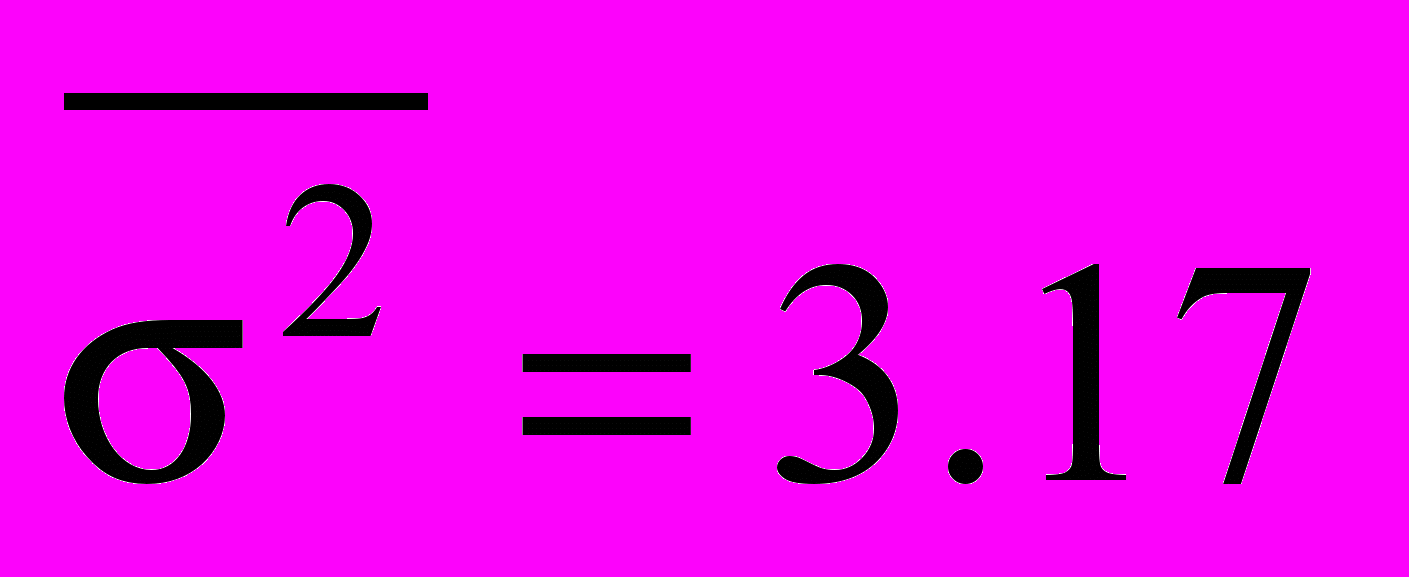 Затем рассчитаем межгрупповую дисперсию. Для этого предварительно определим общую среднюю как среднюю взвешенную из групповых средних и определим межгрупповую дисперсию:
Затем рассчитаем межгрупповую дисперсию. Для этого предварительно определим общую среднюю как среднюю взвешенную из групповых средних и определим межгрупповую дисперсию: 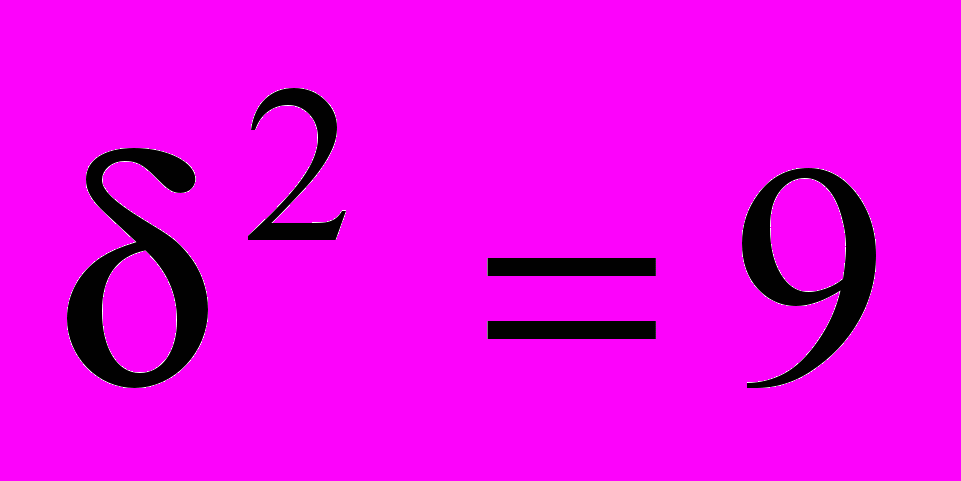 . Таким образом, общая дисперсия по правилу сложения дисперсии
. Таким образом, общая дисперсия по правилу сложения дисперсии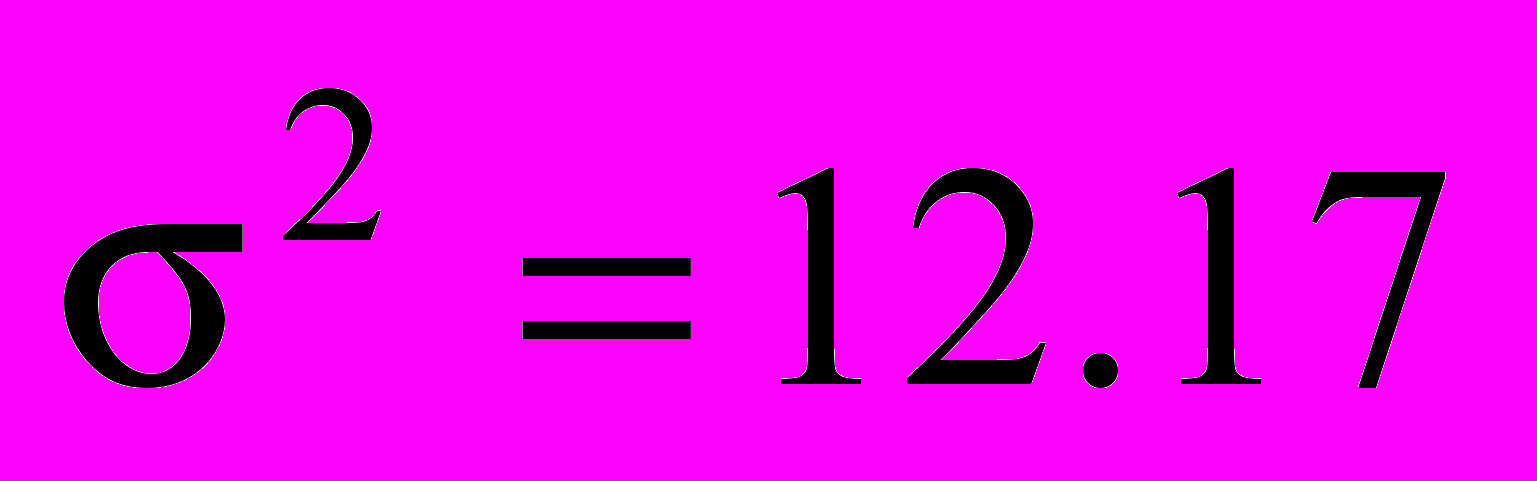 .
.На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результативным признаками. Он называется эмпирическим корреляционным отношением
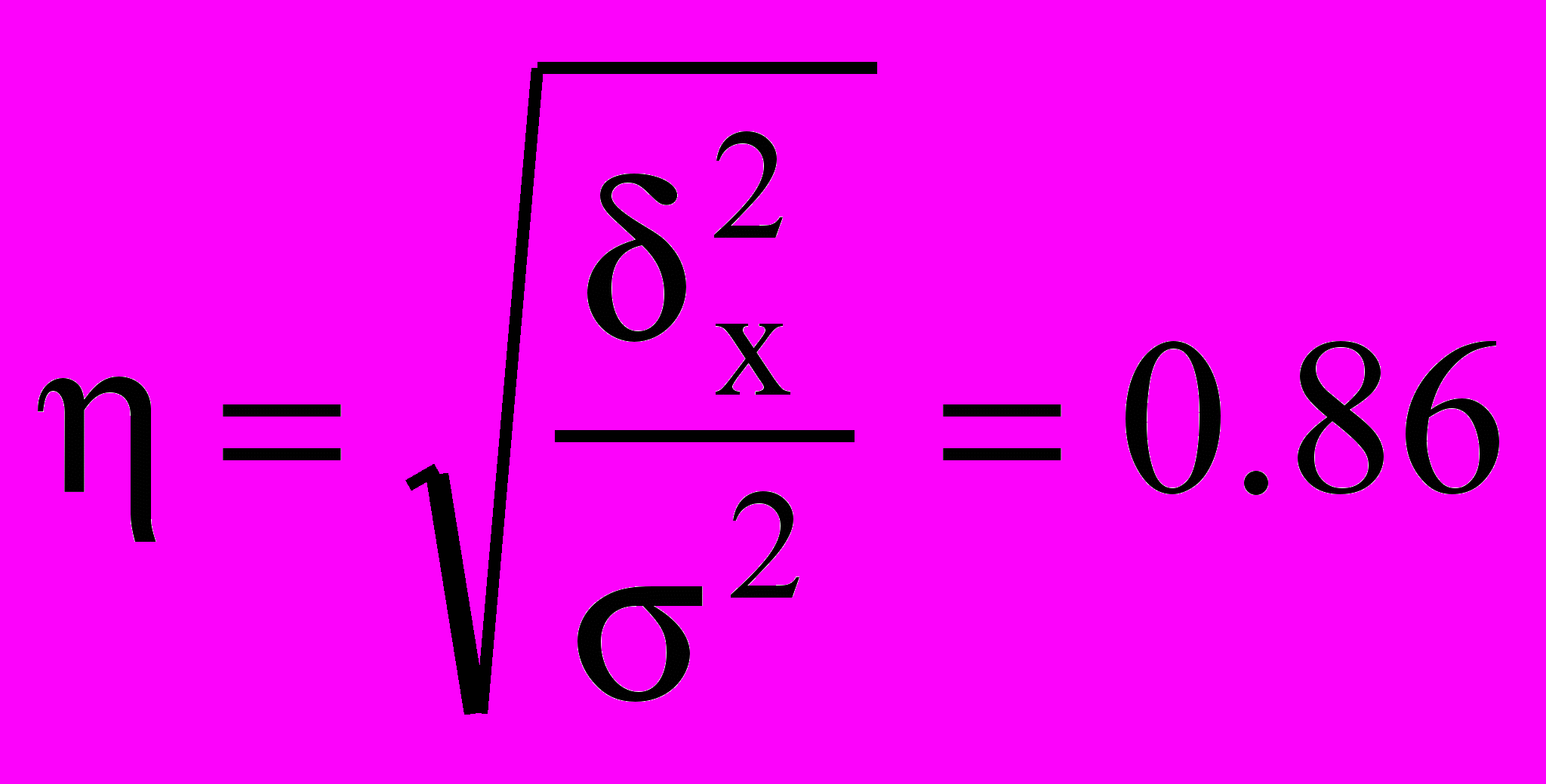 .
. Величина 0,86 характеризует существенную связь между группировочным и результативным признаками.
Наряду с вариацией индивидуальных значении признака вокруг средней может наблюдаться и вариация индивидуальных долей признаки вокруг средней доли. Такое изучение вариации достигается посредством вычисления и анализа следующих видов дисперсий.
Внутригрупповая дисперсия доли определяется по формуле
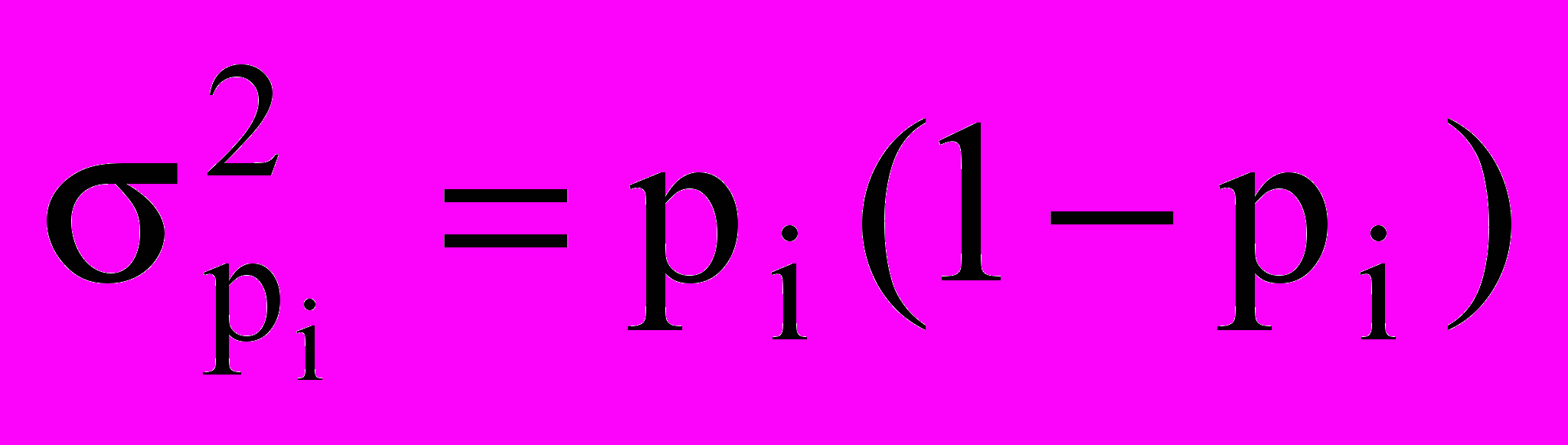 .
.Средняя из внутригрупповых дисперсий:
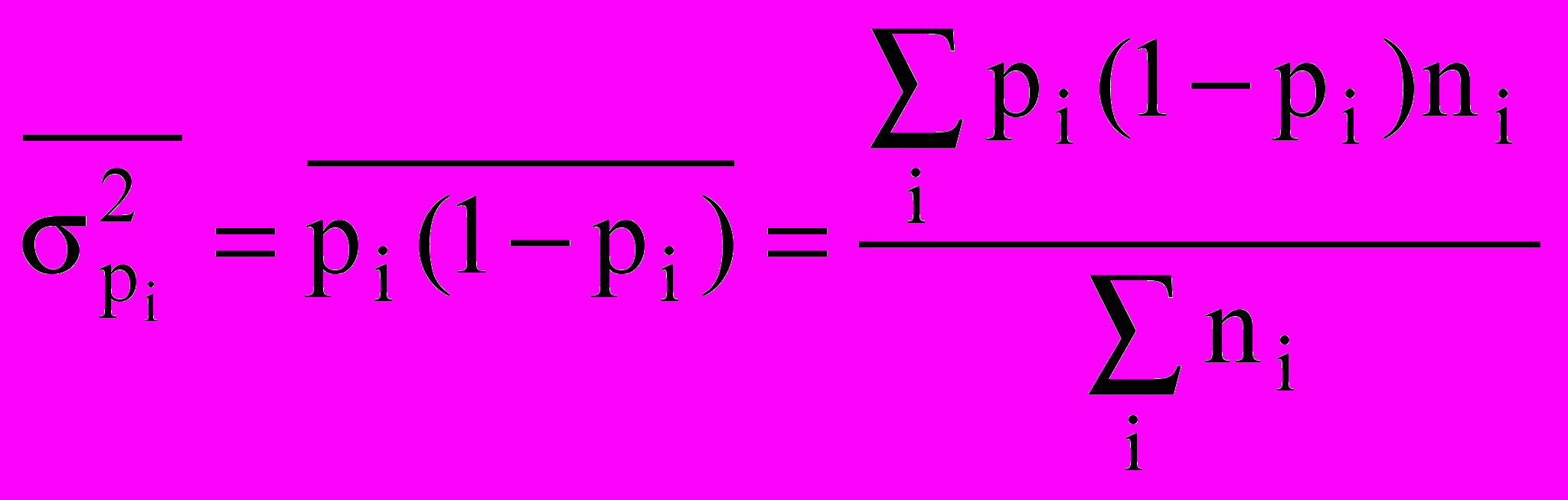 .
.Формула межгрупповой дисперсии имеет вид:
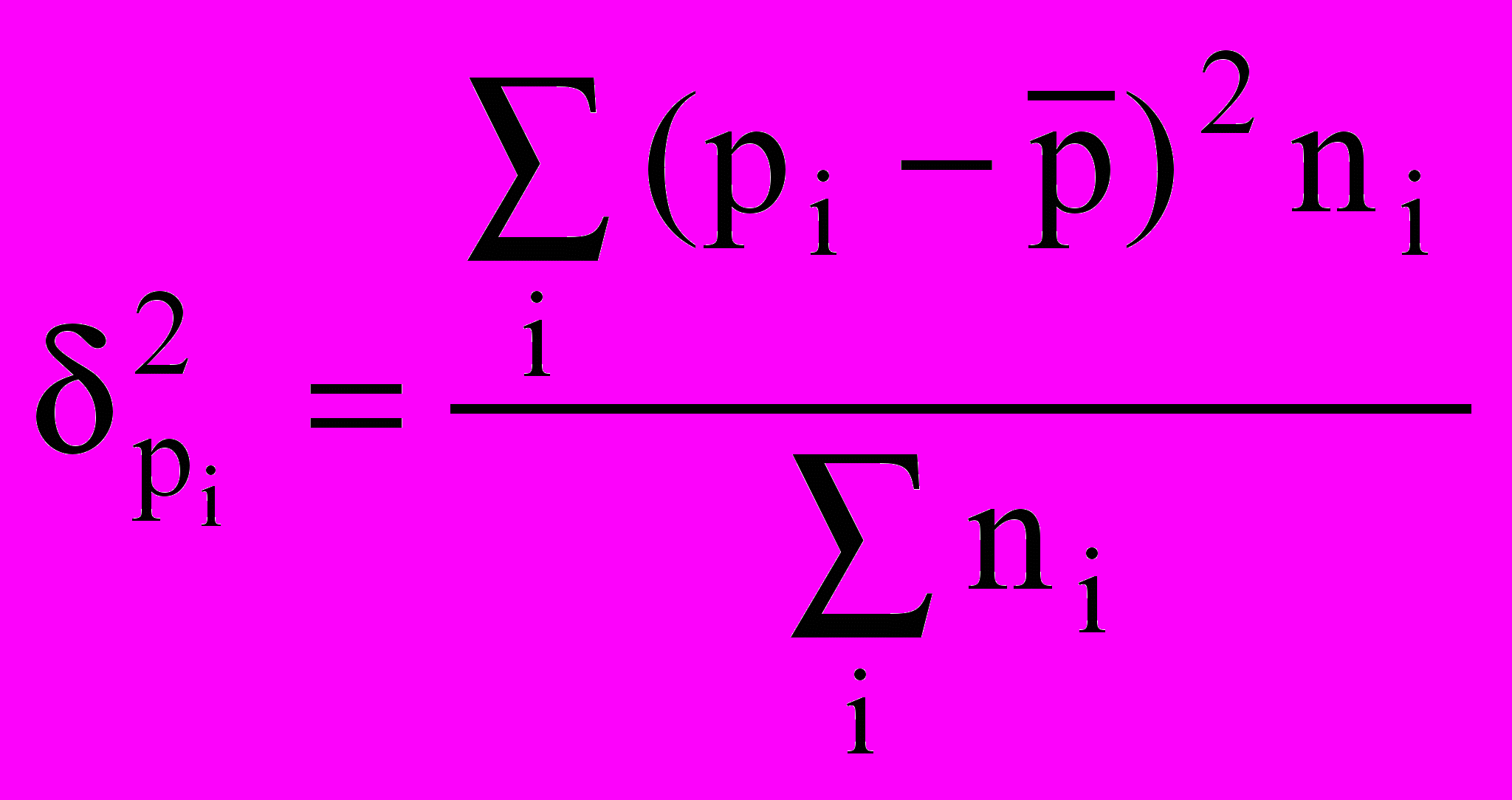
где ni - численность единиц в отдельных группах;
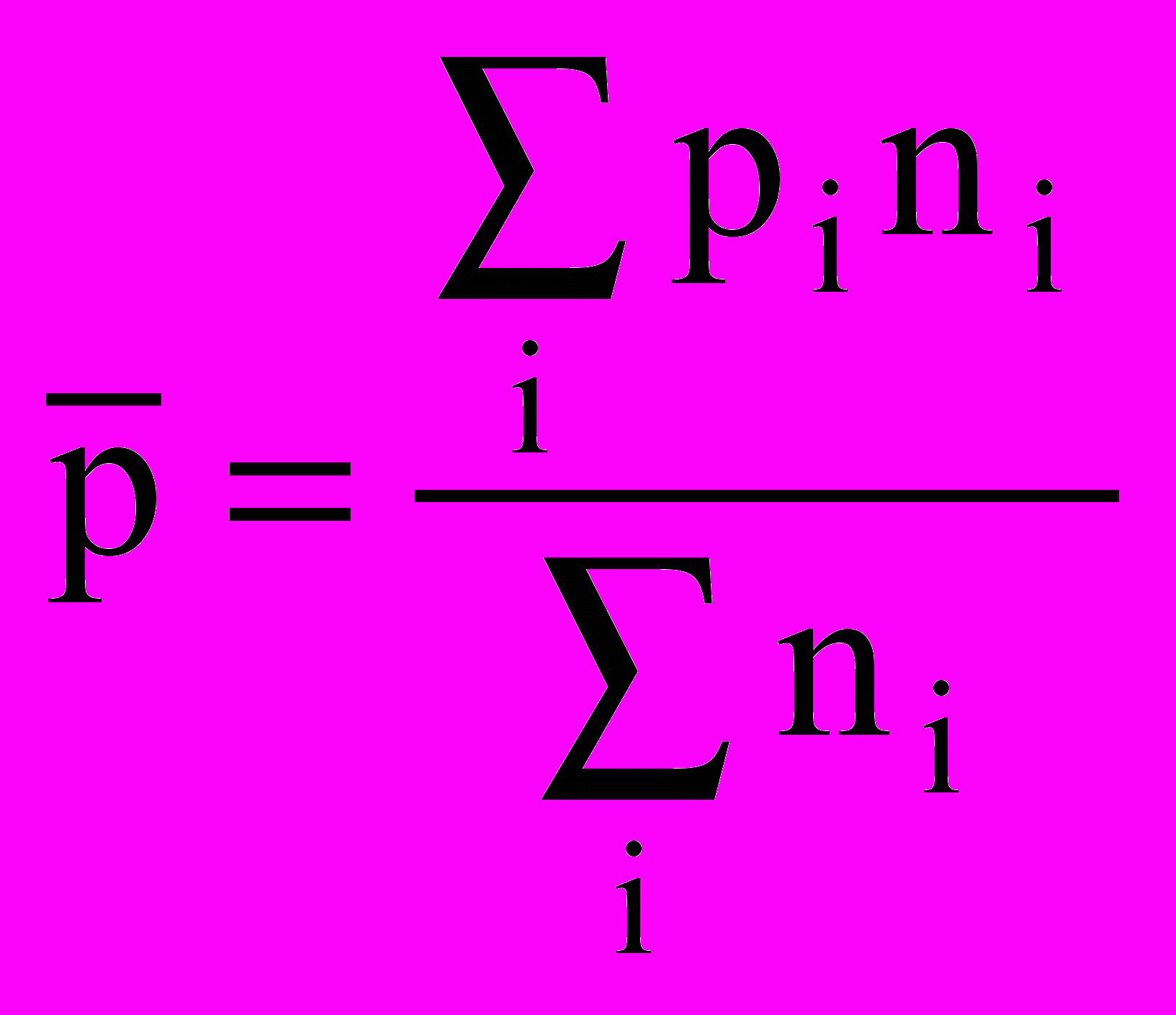
Общий дисперсия имеет вид;
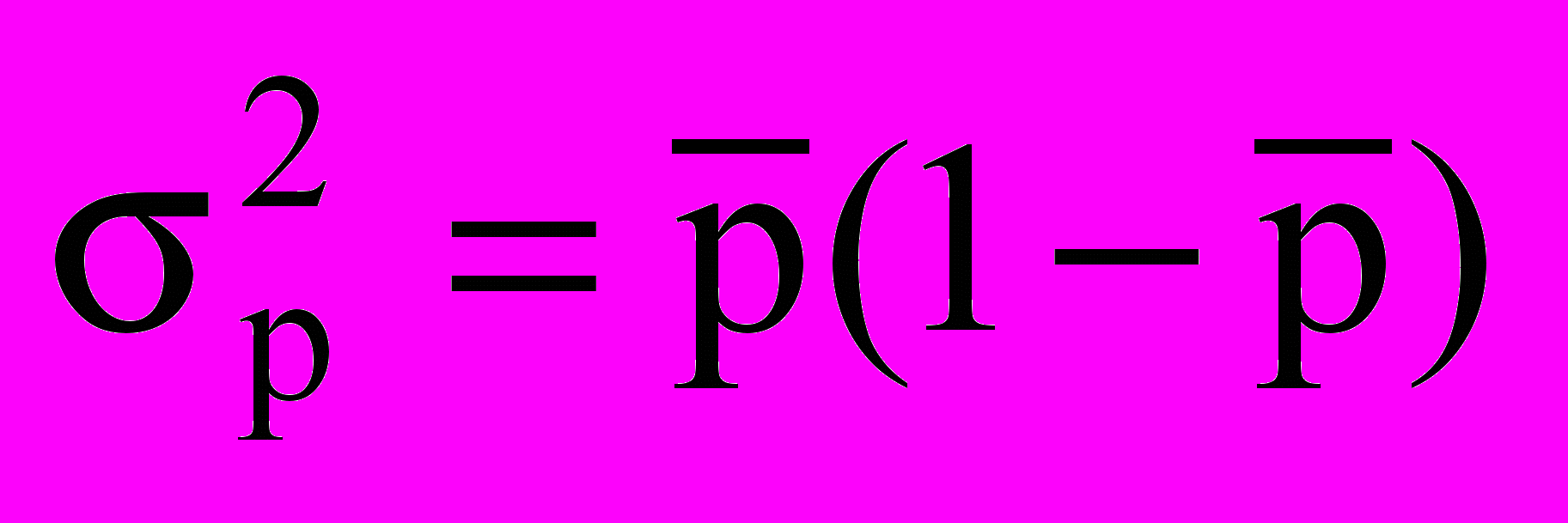 .
.Три вида дисперсии связаны между собой следующим образом:
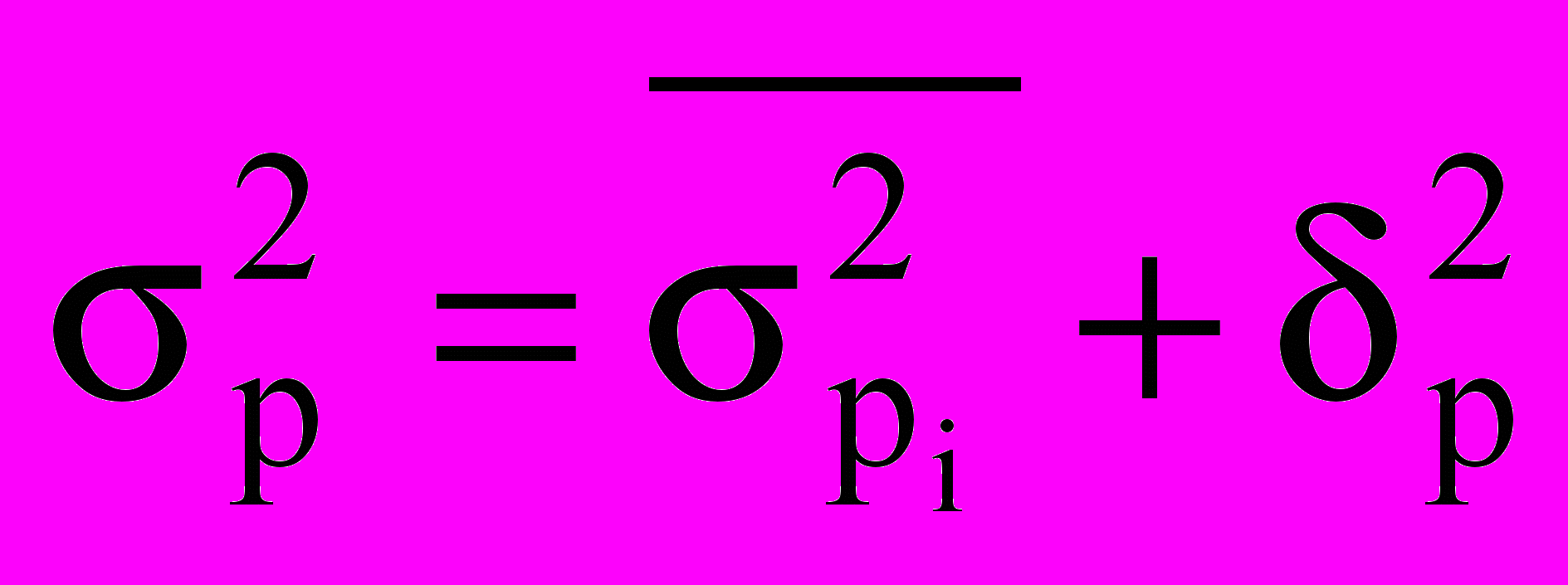
Данное соотношение дисперсий называется теоремой сложения дисперсии доли признака. Эта теорема широко используется в изучении колеблемости качественных признаков.
Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и оценку его симметричности, остро- или плосковсршинности. Симметричным называется распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. В статистике для характеристики асимметрии пользуются несколькими показателями.
Показатели асимметрии и эксцесса. Степень асимметрии может быть определена с помощью коэффициента асимметрии:
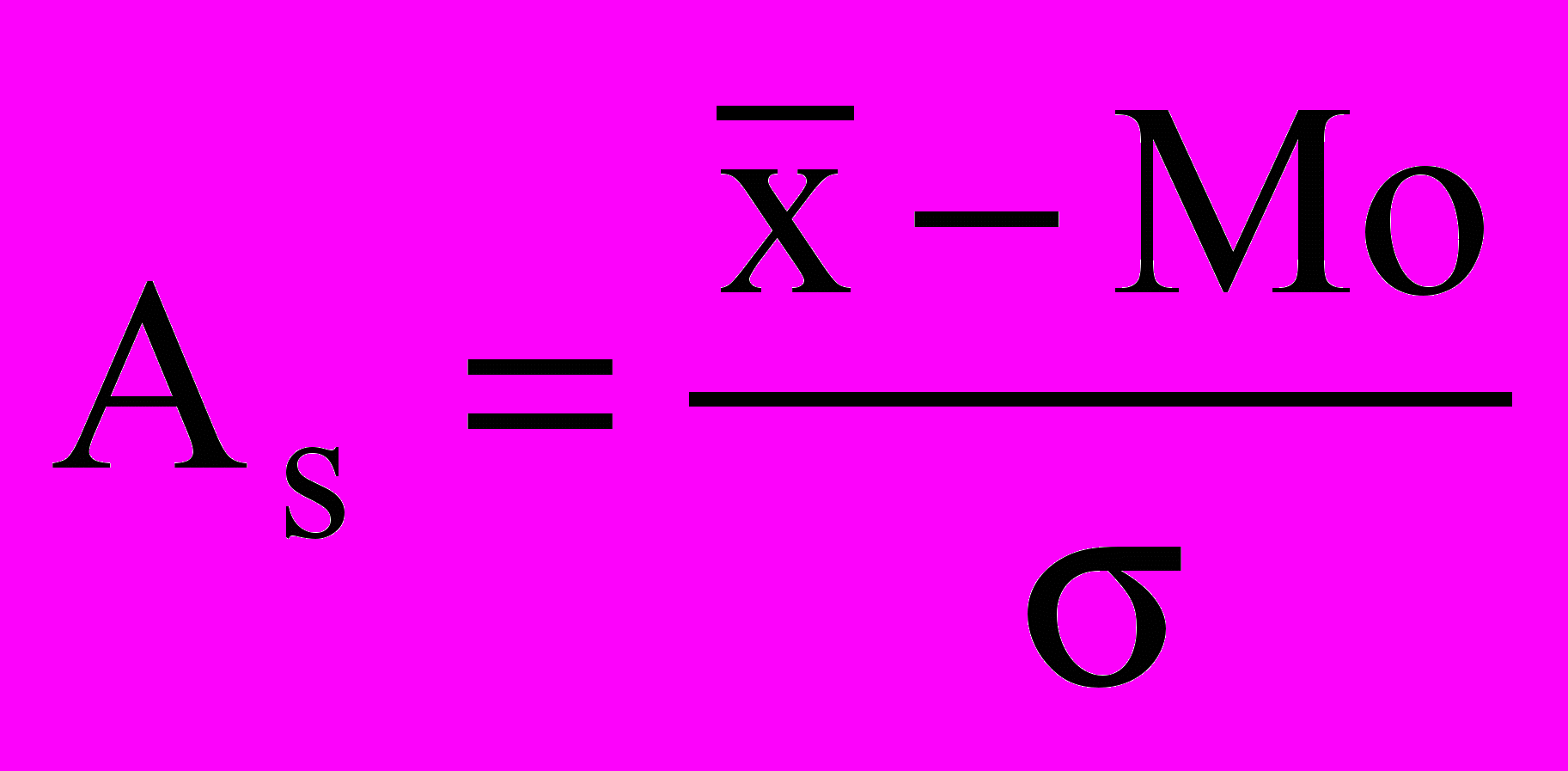 , где
, где 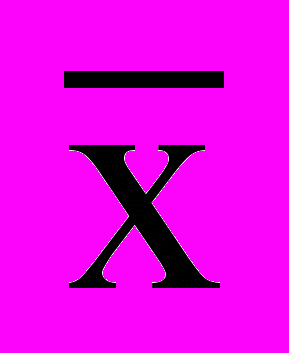 - средняя арифметическая ряда распределения; Мо - мода; - среднее квадрагическое отклонение.
- средняя арифметическая ряда распределения; Мо - мода; - среднее квадрагическое отклонение.При симметричном (нормальном) распределении
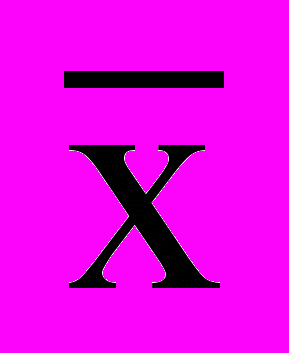 =Мо, следовательно, коэффициент асимметрии равен нулю. Если As > 0, то
=Мо, следовательно, коэффициент асимметрии равен нулю. Если As > 0, то 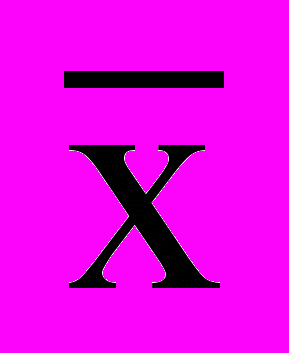 больше моды, следовательно, имеется правосторонняя асимметрия.
больше моды, следовательно, имеется правосторонняя асимметрия.Если As < 0, то
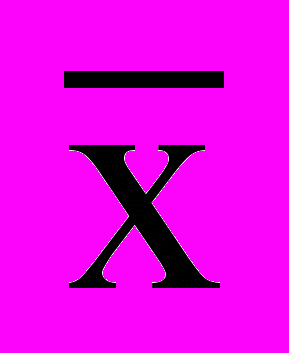 меньше моды, следовательно, имеется левосторонняя асимметрия. Коэффициент асимметрии может изменяться от -3 до +3.
меньше моды, следовательно, имеется левосторонняя асимметрия. Коэффициент асимметрии может изменяться от -3 до +3.В практических расчетах часто в качестве показателя асимметрии применяется отношение центрального момента третьего порядка к среднему квадратическому отклонению данного ряда
в кубе, т. е.
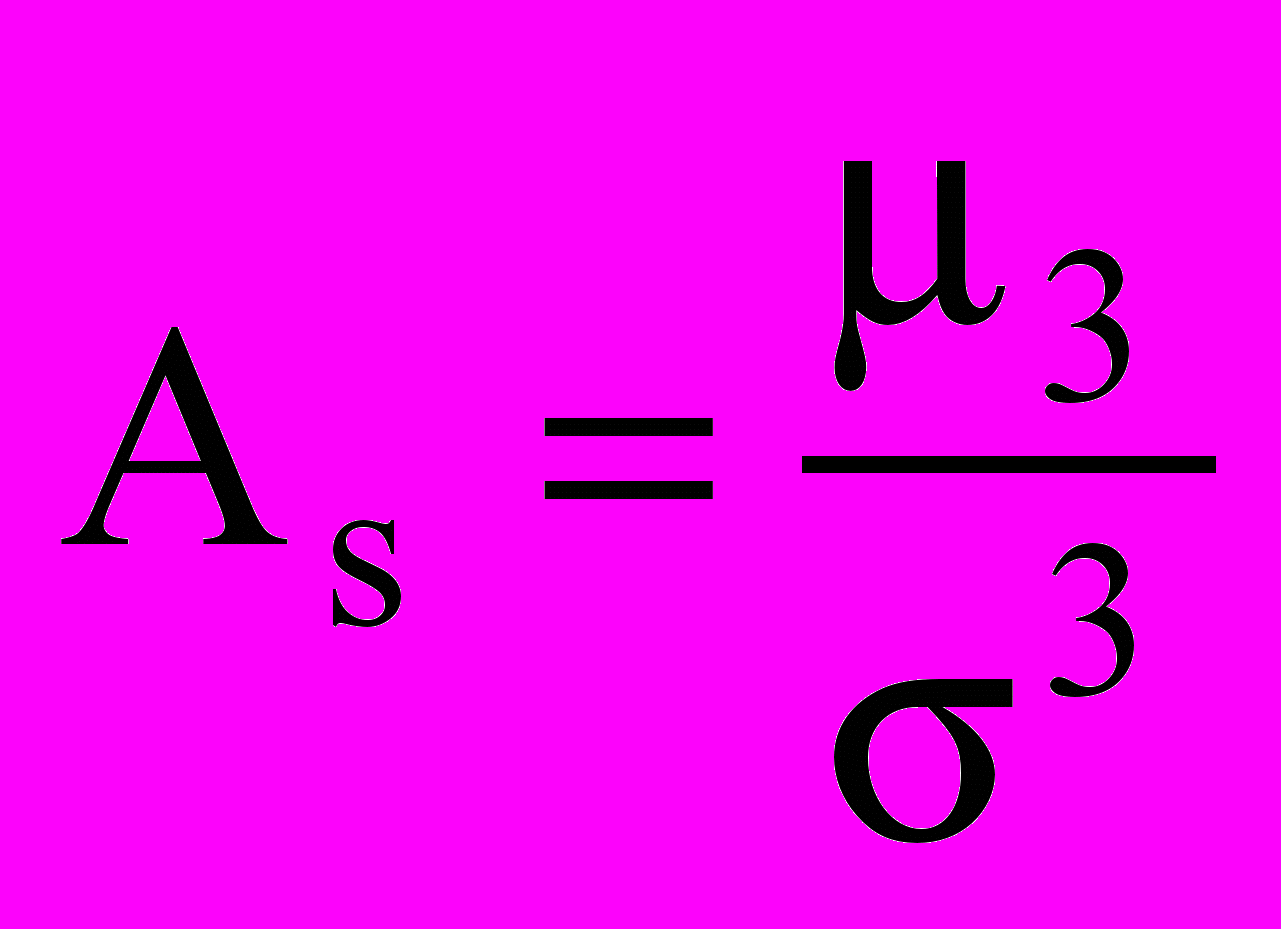 .
.Это дает возможность определить не только величину асимметрии, но и проверить наличие асимметрии в генеральной совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной. Асимметрия меньше 0,25 - незначительная.
Для симметричных распределений может быть также рассчитан показатель эксцесса:
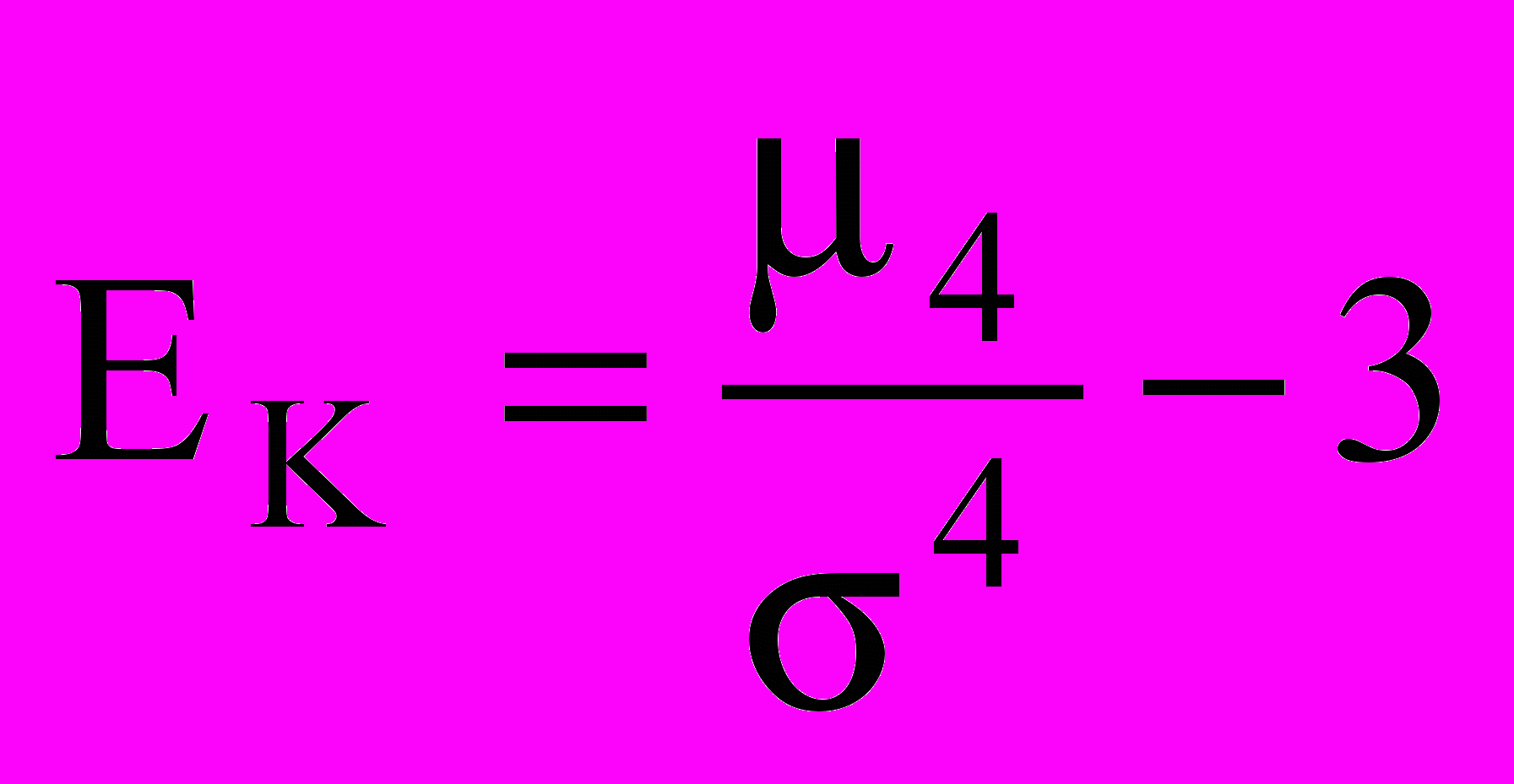
При симметричном распределении ЕK = 0. Если ЕK > 0, распределение является о стровершинным; если EK<0 - плосковершинным.
Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное эмпирическое распределение к типу нормального распределения.
Построение нормального распределения по эмпирическим данным. Имея дело с эмпирическим распределением, можно предположить, что данному распределению соответствует определенная, характерная для него теоретическая кривая. Выдвинув гипотезу о той или иной форме распределения, стремятся описать эмпирический ряд с помощью математической модели, выражающей некоторый теоретический закон распределения. Среди различных кривых распределения особое место занимает нормальное распределение.
Нормальное распределение чаще всего выражается следующей стандартизованной кривой нормального распределения:
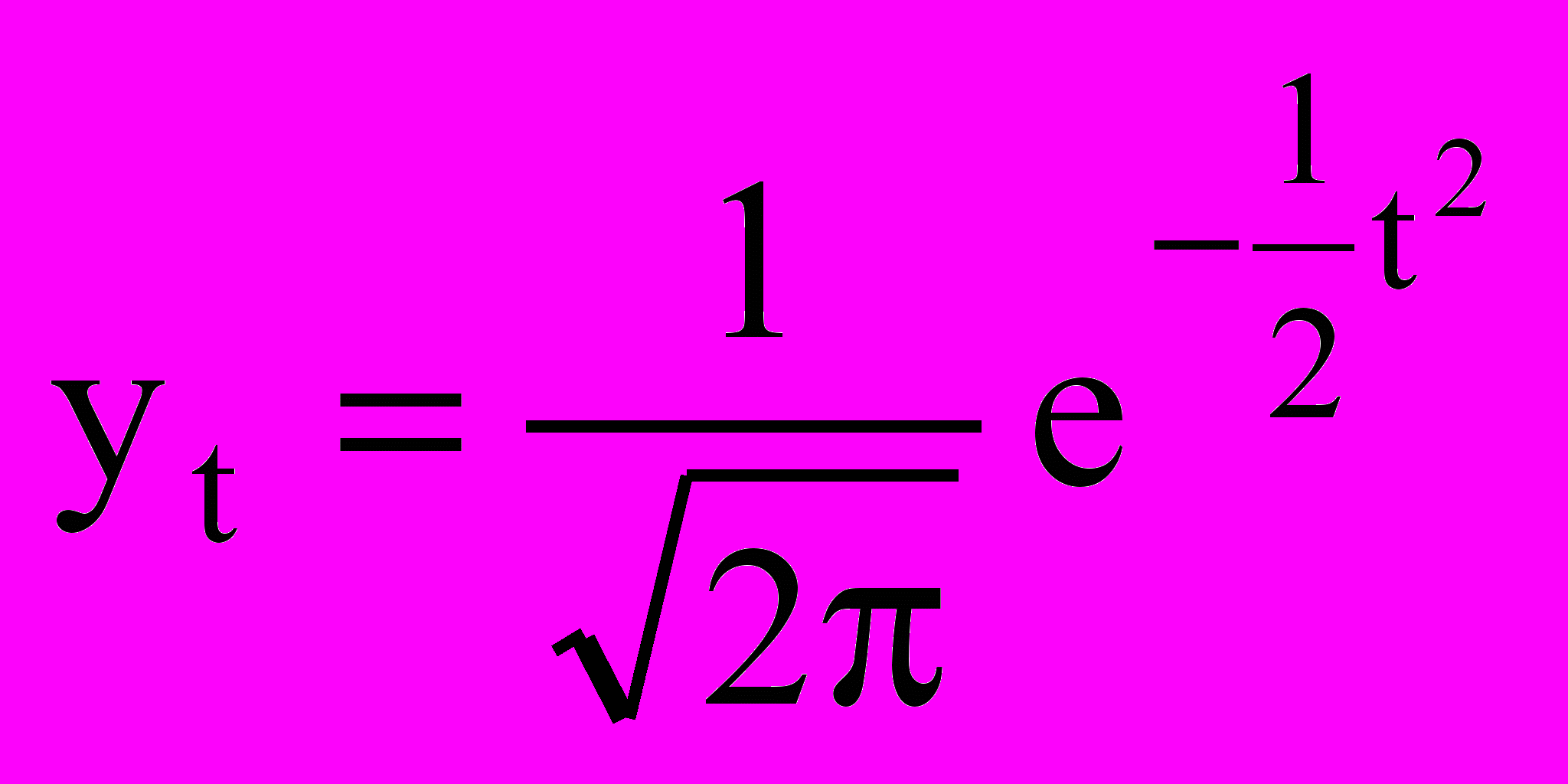 , где
, где 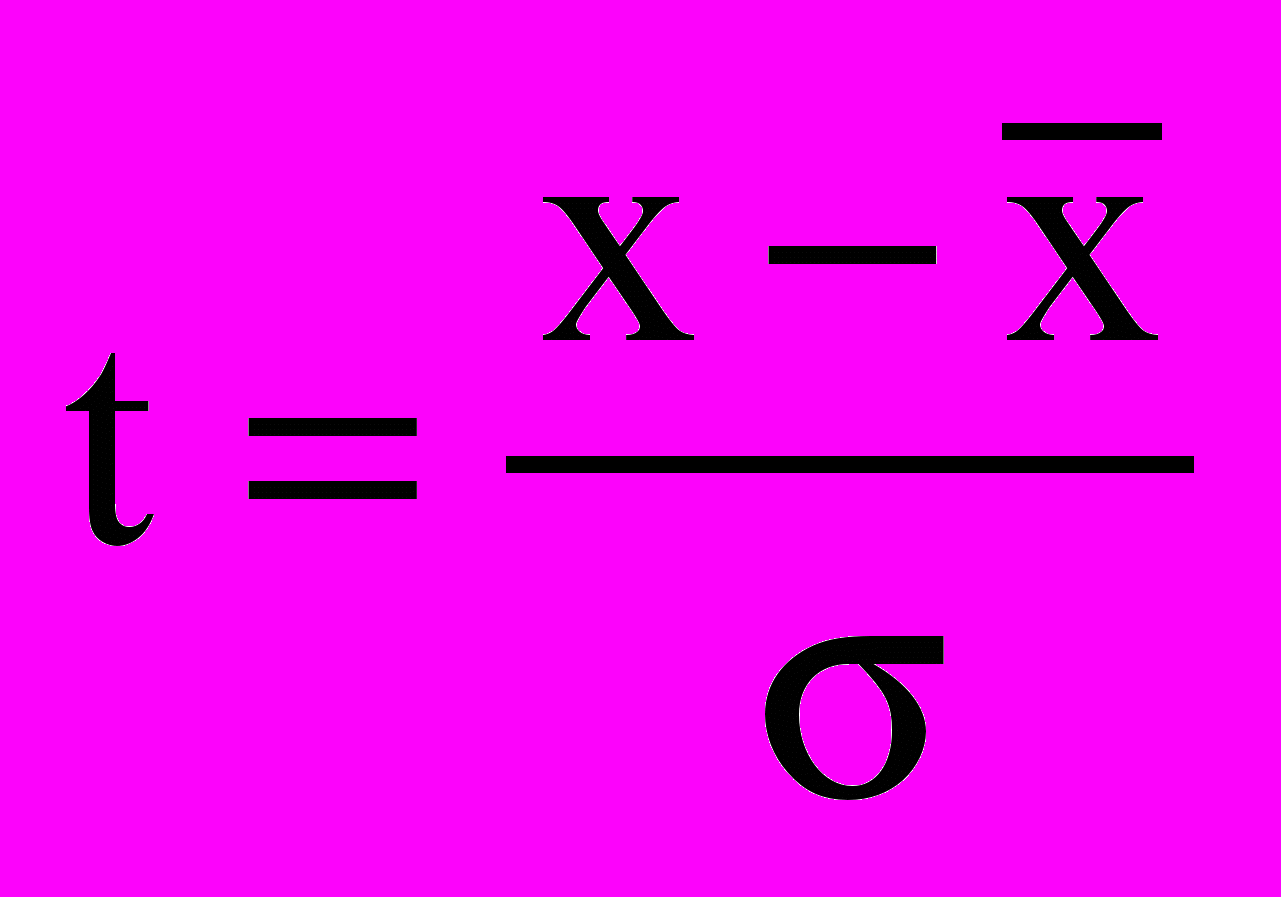 .
.Критерии согласия. Количественная характеристика соответствия может быть получена с помощью особых статистических показателей-критериев согласия. Известны критерии согласия К. Пирсона (хи-квадрат), В. И. Романовского, Б. С. Ястремского и А. Н. Колмогорова.
Критерий согласия Пирсона (
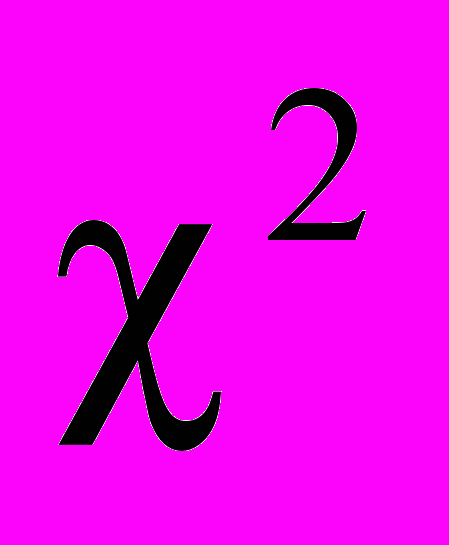 ) вычисляется по формуле:
) вычисляется по формуле: 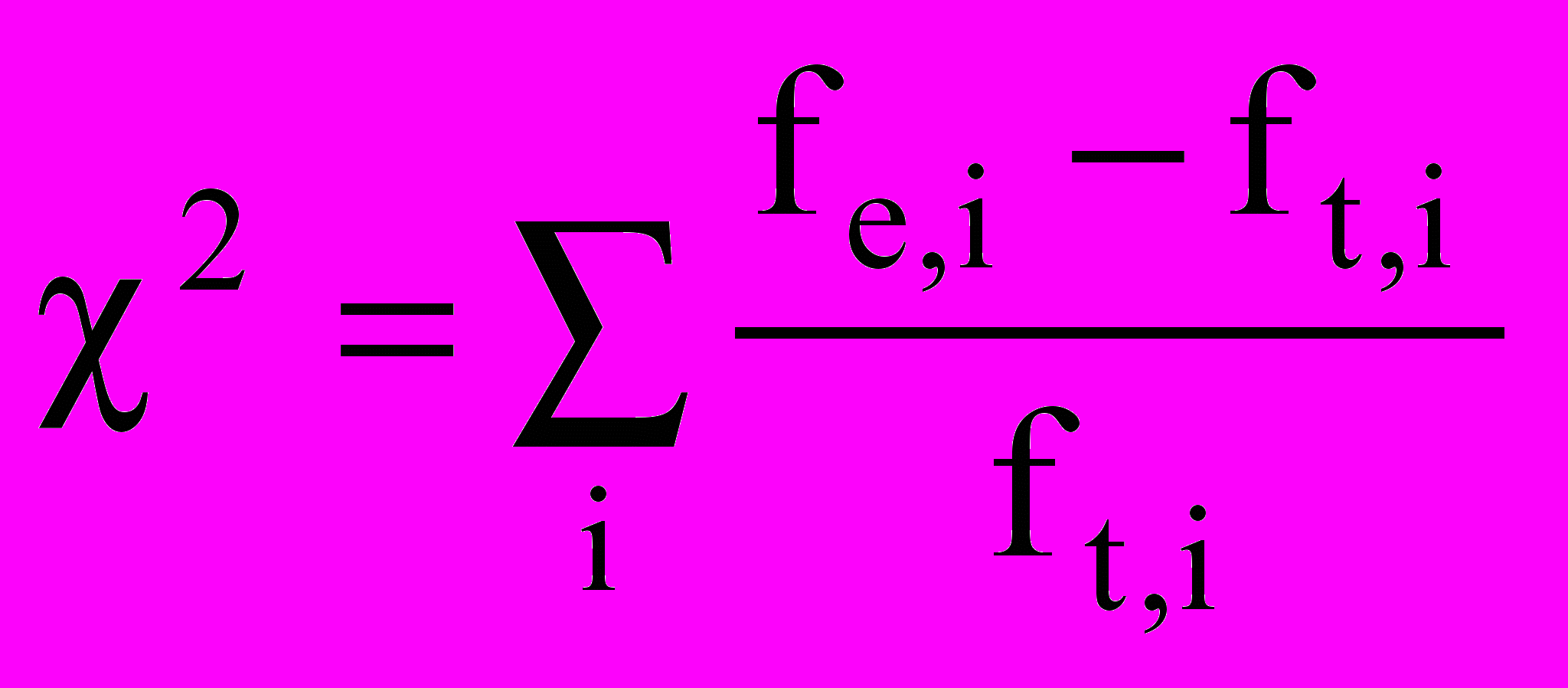
.
С помощью величины
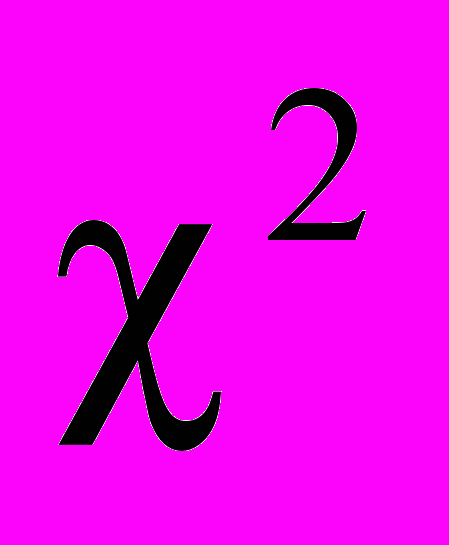 по специальным таблицам приложения определяется вероятность Р (
по специальным таблицам приложения определяется вероятность Р (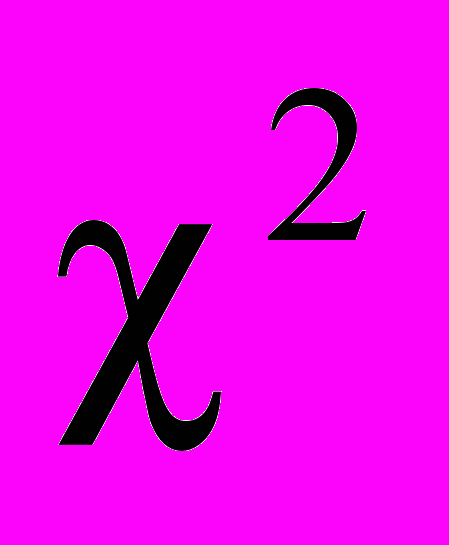 ). Входами в таблицу являются значения
). Входами в таблицу являются значения 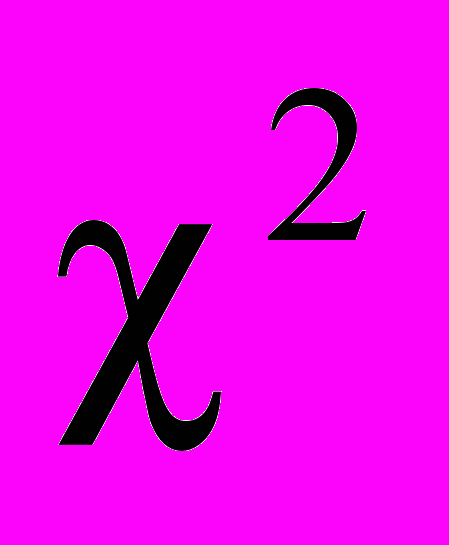 число степеней свободы = n - 1. На основе Р выносится суждение о существенности расхождения между эмпирическим и теоретическим распределениями. При Р > 0,5 считается, что эмпирическое и теоретическое распределения близки. При Р в интервале (0.2;0.5} совпадение между ними удовлетворительное, в остальных случаях недостаточное.
число степеней свободы = n - 1. На основе Р выносится суждение о существенности расхождения между эмпирическим и теоретическим распределениями. При Р > 0,5 считается, что эмпирическое и теоретическое распределения близки. При Р в интервале (0.2;0.5} совпадение между ними удовлетворительное, в остальных случаях недостаточное.Критерий Романовского (С), также используемый для при, верки близости эмпирического и теоретического распределении определяется следующим образом:
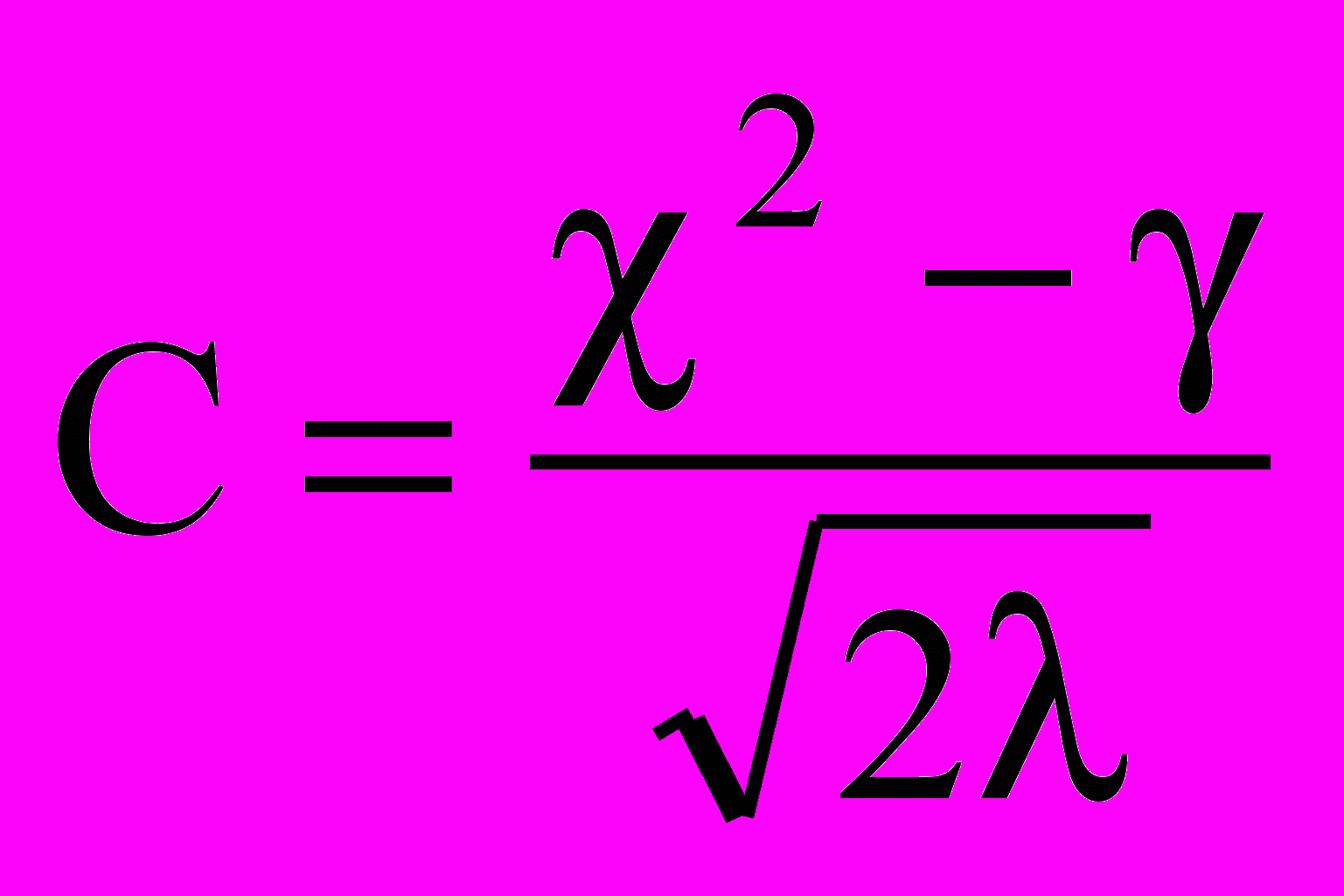 .
.При С < 3 различие несущественно, что позволяет считать эмпирическое распределение близким к нормальному.
Критерий Ястремского (L) может быть найден на основе следующего соотношения:
 , где N - объем совокупности; pq - дисперсия альтернативного признака;
, где N - объем совокупности; pq - дисперсия альтернативного признака;K - число вариантов или групп:, Q - принимает значение 0.6, при числе вариантов или групп от 8 до 20.
Если L < 3, то эмпирическое распределение соответствует теоретическому.
Критерий Колмогорова () вычисляется по формуле:
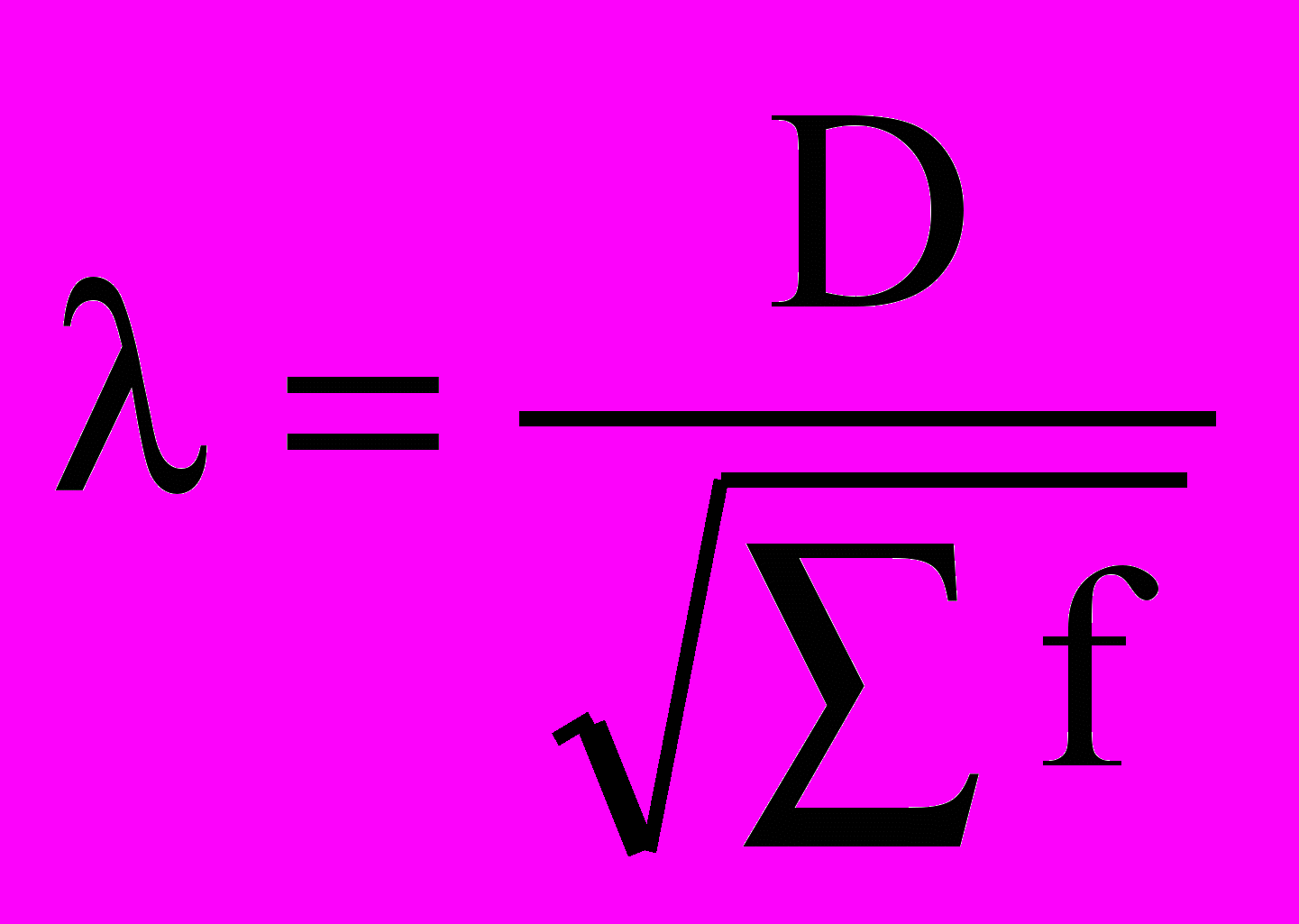 .
.где D - максимальное значение разности между накопленными эмпирическими и теоретическими частотами
Необходимым условием использования этого критерия является достаточно большее число наблюдений (не меньше 100).
Характеристики вариационного ряда.
Мода - значение признака, наиболее часто встречающееся в исследуемой совокупности.
Медиана - значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Для дискретных вариационных рядов модой будет значение варианта с наибольшей частотой. Вычисление медианы в дискретных рядах распределения имеет специфику. Если такой ряд распределения имеет нечетное число членов, то медианой будет вариант, находящийся в середине ранжированного ряда. Если ранжированный ряд распределения состоит из четного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда.
Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание продолжается до получения накопленной суммы частот, впервые превышающей половину.
Для интервальных вариационных рядов мода определяется по формуле
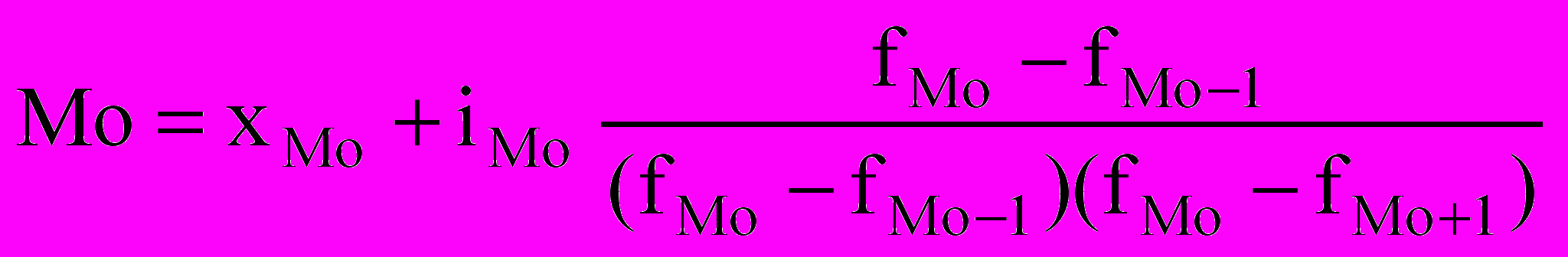
где хMo - нижняя граница значения интервала, содержащего моду; iMo - величина модального интервала;
fMo - частота модального интервала.
