Аналитическая статистика. Показатели вариации и анализ частотных распределений методические указания и решение типовых задач
| Вид материала | Методические указания |
- 1. теоретические аспекты применения показателей вариации в статистическом исследовании, 58.66kb.
- Н. П. Огарева Экономический факультет Кафедра статистики экономика и статистика фирм, 284.65kb.
- Н. П. Огарева Экономический факультет Кафедра статистики анализ временных рядов и прогнозирование, 191.07kb.
- Н. П. Огарева Экономический факультет Кафедра статистики демография и статистика населения, 143.09kb.
- Вопросы к экзамену по дисциплине "Статистика", 32.3kb.
- Методические указания и задачи для самостоятельной работы студентов по дисциплине «Математическая, 640.75kb.
- Вопросы по курсу «Допглавы эконометрики» Преподаватель : доцент, к ф. м н. Пяткина, 7.26kb.
- Методические указания к написанию лабораторных работ по учебным дисциплинам "Общая, 312.43kb.
- Статистика, 1361.62kb.
- Практикум: «Изучение процентов в школьном курсе математики», 90.4kb.
Медиана интервального ряда распределения определяется по формуле:
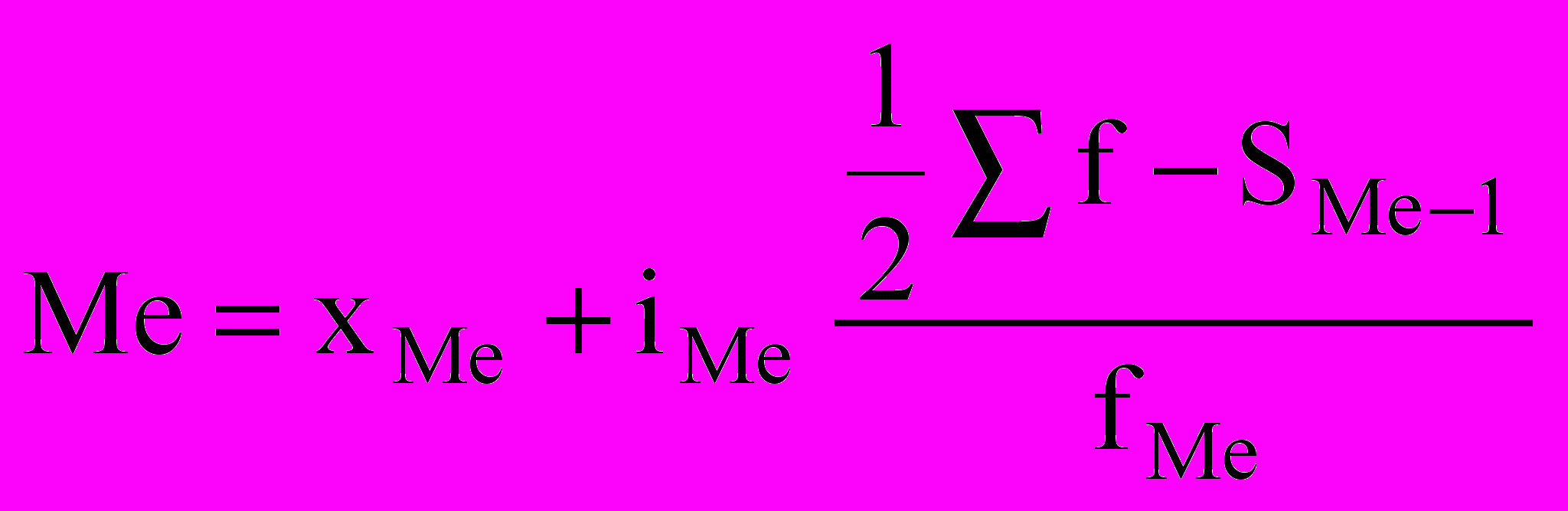 ,
, где хMe - нижняя граница значения нтгтервала, содержащего медиану; iMe – величина медианного интервала;
SMe-1 сумма накопленных частот предшествующих медианному интервалу; fМе - частота медианного интервала.
Пример. Рассчитаем моду и медиану по данным табл. 5. Mo=772 $. Следовательно, наибольшее число семей имеют среднедушевой доход 772 $. Me=780 $. Таким образом, половина семей города имеет среднедушевой доход менее 780 руб., остальные семьи - более 780 $.
Т а б л н ц а 5. Распределение сеней города по размеру средне-душевого
дохода в январе 1998 г.
| Группы семей по размеру дохода, $ | Число семей | Накопленные частоты | Накопленные частоты, % к итогу |
| До 500 | 600 | 600 | 6 |
| 500-600 | 700 | 1 300 | 13 |
| 600-700 | 1 700 | 3 000 | 30 |
| 700-800 | 2 500 | 5 500 | 55 |
| 800-900 | 2 200 | 7 700 | 77 |
| 900-1000 | 1 500 | 9 200 | 92 |
| Свыше 1000 | 800 | 10 000 | 100 |
| Итого | 10 000 | - | - |
Аналогично с нахождением медианы в вариационных рядах можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Например, можно найти значение признака у единиц, делящих ряд на четыре равные части, десять или сто частей. Эти величины называются «квартили», «децили» и «перцентили».
Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квартиль нижний (q1), отделяющий 1/4 часть совокупности с наименьшими значениями признака, и квартиль верхний (Q3), отсекающий 1/4 часть с наибольшими значениями признака. Средним квартилем Q2 является медиана.
Для расчета квартилей по интервальному вариационному ряду используют формулы:
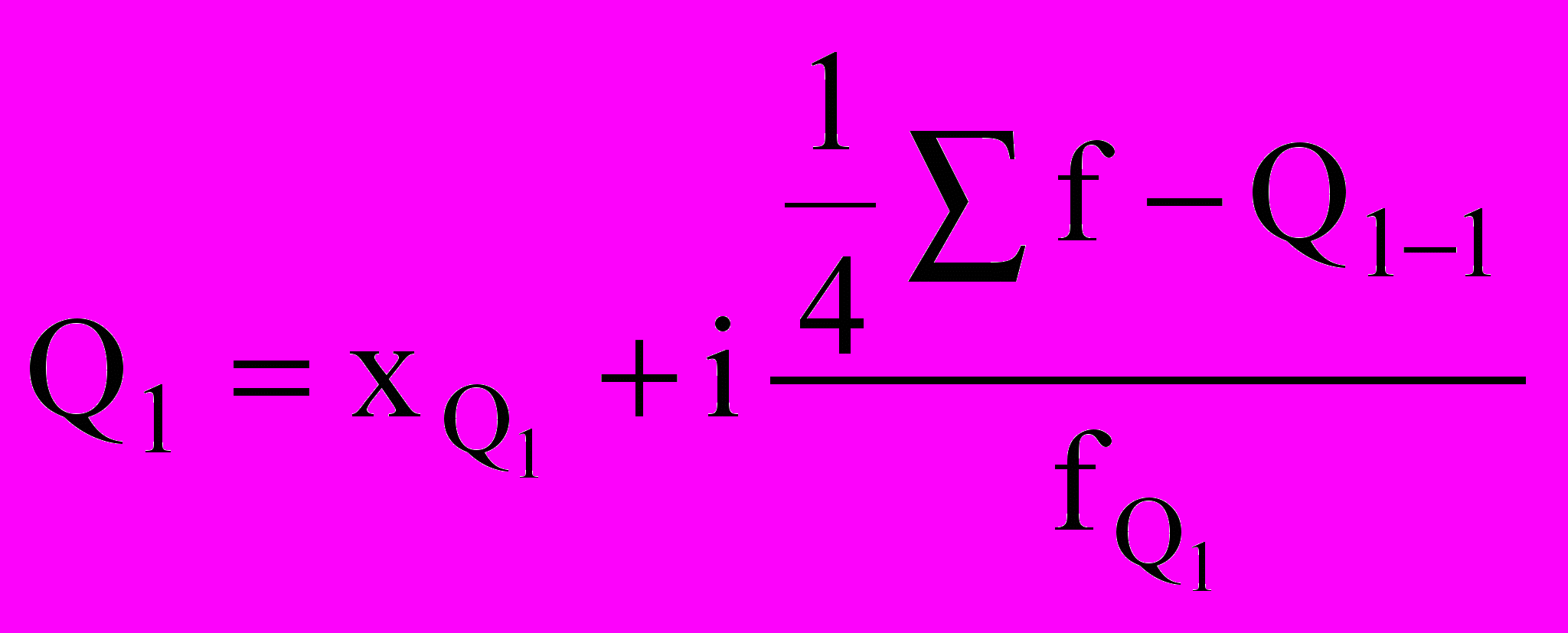 ,
, 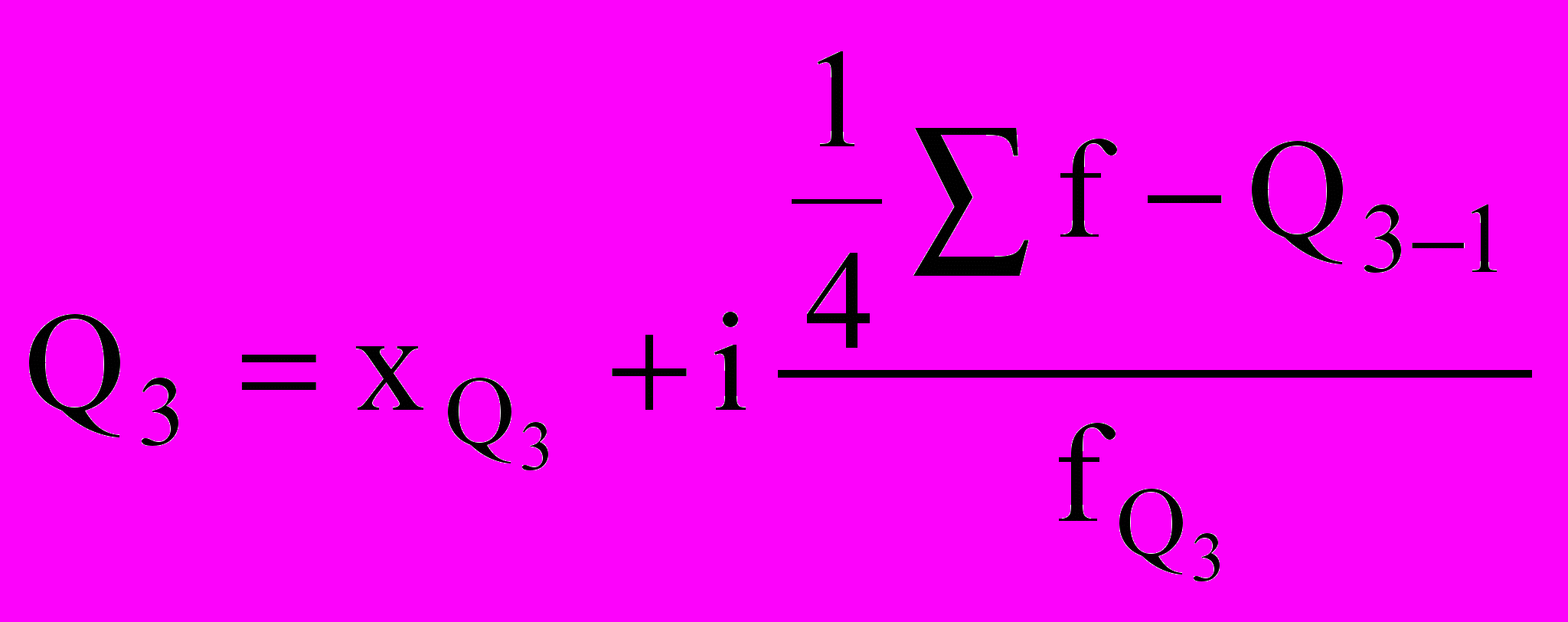 .
.|ЗАДАЧИ И УПРАЖНЕНИЯ
1. Распределение студентов одного из факультетов по возрасту характеризуется следующими данными:
| возраст студентов, лет | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | Всего |
| Число студентов | 20 | 80 | 90 | 110 | 130 | 170 | 90 | 60 | 750 |
Вычислите: а) размах вариации: б) среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; д) относ ительные показатели вариации возраста студентов.
2. Определите среднюю длину пробега автофургона торгово-посреднической фирмы и вычислите все показатели вариации, если известны:
| Длина пробега за один рейс. км | Число рейсов за квартал |
| 30-50 | 20 |
| 50-70 | 25 |
| 70-90 | 14 |
| 90-110 | 18 |
| 110-130 | 9 |
| 130-150 | 6 |
| Всего | 92 |
3. Имеется следующий ряд распределения телеграмм, принятых отделением связи, по числу слов:
| Количество слов | |
| в телеграмме | Число телеграмм |
| 12 | 18 |
| 13 | 22 |
| 14 | 34 |
| 15 | 26 |
| 16 | 20 |
| 17 | 13 |
| 18 | 7 |
| Итого | 140 |
Рассчитайте абсолютные и относительные показатели вариации.
4. Средняя урожайность зерновых культур в двух районах за 1991 - 1995 гг. Характеризуется следующими данными , ц/га
| | 1991 | 1992 | 1993 | 1994 | 1995 |
| 1 р-н | 30 | 20 | 23 | 16 | 22 |
| 2 р-н | 25 | 34 | 30 | 28 | 29 |
Рассчитайте все показатели вариации. Опеределите, в каком районе урожайность зерновых более устойчива
5. Имеются следующие данные выборочного исследования студентов одного из вузов
| Затраты времени на дорогу до института. ч | Число студентов, % к итогу |
| До 0,5 | 7 |
| 0.5-1,0 | 18 |
| 1,0-1,5 | 32 |
| 1.5-2.0 | 37 |
| Свыше 2,0 | 6 |
| Всего | 100 |
Вычислите абсолютные и относительные показатели вариации.
6. Имеются следующие данные о распределении скважин в одном из районов бурения по глубине:
| Группы скважин по глубине, м | Число скважин |
| До 500 | 4 |
| 500-1000 | 9 |
| 1000-1500 | 17 |
| 1500-2000 | 8 |
| Свыше 2000 | 2 |
| Итого | 40 |
Определите дисперсию и среднее квадратическое отклонение глубины скважин, применяя способ моментов и отсчета от условного нуля.
7. Акционерные общества области по среднесписочной численности работающих на 1 января 1998 г. распределялись следующим обпазом:
| Группы АО по средне списочной числен ности ра ботающих | до 400 | 400- 600 | 600- 800 | 800- 1000 | 1000- 1200 | 1200- 1400 | 1400- 1600 | 1600- 1800 | Итого |
| Количество АО | 11 | 23 | 36 | 42 | 28 | 17 | 9 | 4 | 170 |
Рассчитайте: а) среднее линейное отклонение; б) дисперсию; в) среднее квадрат и чес кое отклонение; г) коэффициент вариации.
8. По данным о распределении сельских населенных пунктов по числу дворов вычислите общую дисперсию тремя способами: а) обычным; б) упрощенным; в) по формуле
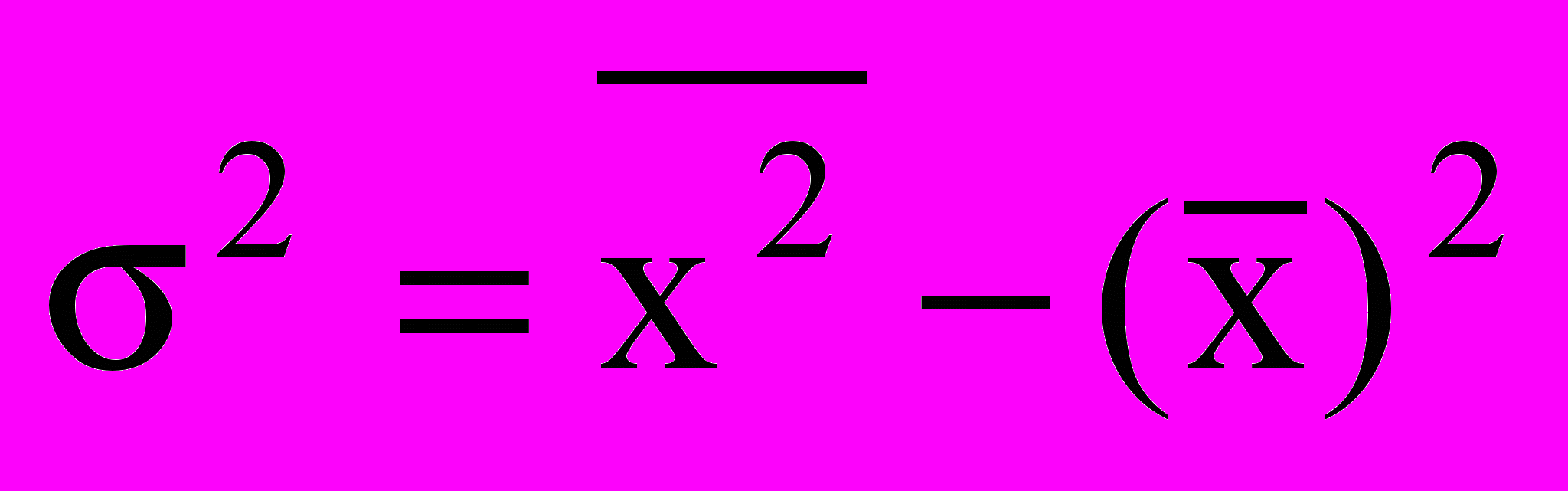 .
.| Населенные пункты по числу дворов | Число населенных пунктов, % к итогу |
| До 100 101-200 201-300 301-400 Свыше 400 | 15,5 28,6 21,7 20,3 13,9 |
| Итого | 100,0 |
9. Имеются следующие данные о распределении сотрудников коммерческого банка по среднемесячной заработной плате:
| Группы сотрудни ков по среднеме сячной заработной плате, тыс. руб. | Количество сотрудников, чел. |
| До 3 | 14 |
| 3-4 | 22 |
| 4-5 | 25 |
| 5-6 | 29 |
| 6-7 | 10 |
| 7-8 | 8 |
| 8-9 | 6 |
| 9-10 | 5 |
| Свыше 10 | 3 |
| Итого | 122 |
Определите общую дисперсию тремя способами: а) обычным;
б) упрощенным; в) по формуле
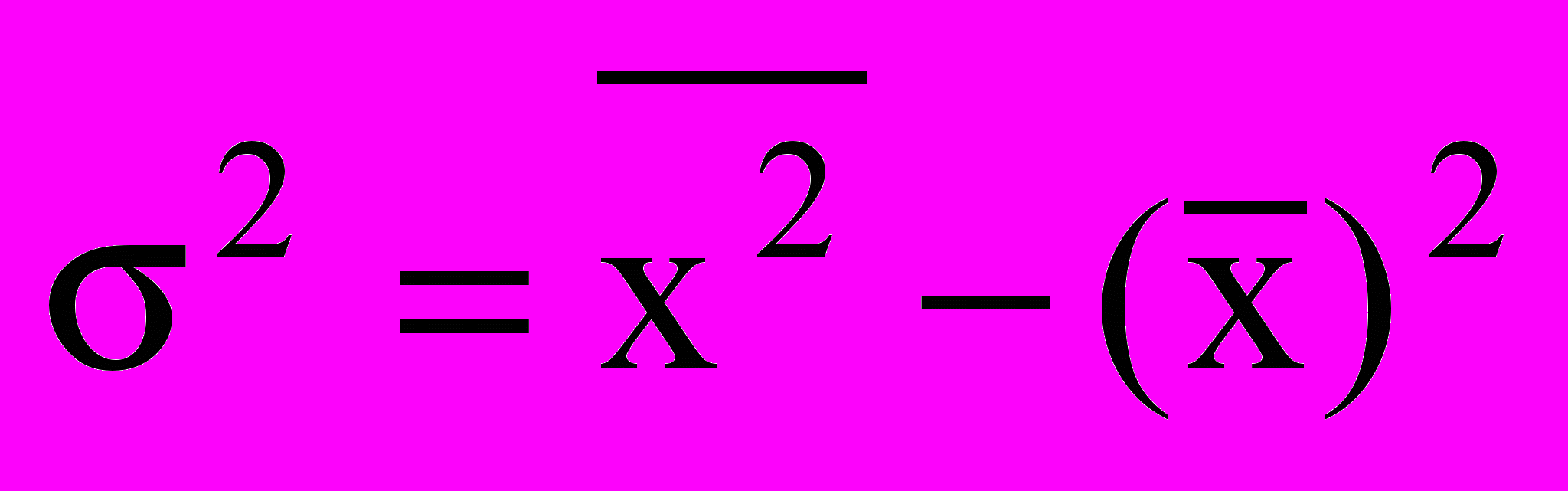
10. Средняя величина признака в совокупности равна 19, а средний квадрат индивидуальных значении этого признака - 397. Определите коэффициент вариации.
11. Дисперсия признака равна 9, средний квадрат индивидуальных его значений - 130. Чему равна средняя?
12. Средняя величина в совокупности равна 16, среднее квадратическое отклонение - 8. Определите средний квадрат индивидуальных значений этого признака.
13. Средний квадрат отклонений индивидуальных значений признака от их средней величины равен 100, а средняя - 15. Определите, чему равен средний квадрат отклонений индивидуальных значений признака от величины, равной 10 и 25.
14. Средняя величина признака равна 14, а дисперсия - 60. Определите средний квадрат отклонений вариантов признака от 1°.
15. Средний квадрат отклонений вариантов признака от произвольной величины равен 300, а сама произвольная величина равна 70 единицам. Определите дисперсию признака, если известно, что средняя величина его варианта равна 80.
16. Средний квадрат отклонений вариантов признака от некоторой произвольной величины равен 61. Средняя величина признака больше произвольной величины на 6 единиц и равна 10. Найдите коэффициент вариации.
17. Если дисперсия равна 20 000 единицам, а коэффициент вариации - 30%, то каков будет средний квадрат отклонений индивидуальных значений признака от величины, равной 250 единицам?
18. По данным таблицы о распределении пряжи по крепости нити вычислите все виды дисперсий. Определите общую дисперсию по правилу сложения дисперсий.
| 1 группа пряжи (менее крепкая) | II группа пряжи (балее крепкая) | ||
| Крепость нити, г | Число проб | Крепость нити, г | Число проб |
| 120-130 | 2 | 200-210 | 25 |
| 130-140 | 6 | 210-220 | 28 |
| 140-150 | 8 | 220-230 | 16 |
| 150-160 | 15 | 230-240 | 10 |
| 160-170 | 25 | 240-250 | 8 |
| 170-180 | 29 | 250-260 | 7 |
| 180-190 | 35 | 260-270 | 5 |
| 190-200 | 30 | | |
19. Товарооборот по предприятиям общественного питания на одного работника за квартал характеризуется следующими данными:
| Предприятие | Доля предприятий в общей численности работников, % | Товарооборот в расчете на одного работника, тыс. руб. | Дисперсия товарооборота в группе |
| Столовые Кафе, закусочные Рестораны | 35 50 15 | 13 20 26 | 3,29 36,00 9,00 |
Определите все виды дисперсии товарооборота предприятии общественного питания.
20. Имеются данные о распределении семей сотрудников финансовой корпорации по количеству детей:
| Число детей в семье | Число семей сотрудников по подразделениям | ||
| | первое | второе | третье |
| 0 | 4 | 7 | 5 |
| 1 | 6 | 10 | 13 |
| 2 | 3 | 3 | 3 |
| 3 | 2 | 1 | - |
Вычислите: а) внутригрупповые дисперсии; б) среднюю из внутригрупповых дисперсий; в) межгрупповую дисперсию; г) общую дисперсию. Проверьте правильность с помощью правила сложения дисперсий
21. Распределение основных фондов по малым предприятиям отрасли характеризуется следующими данными
| Группы предприятий по стоимости основных фондов. тыс. руб. | Число предприятий | Основные фонды в среднем на предприятии, тыс. руб. | Групповые дисперсии |
| 12-27 | 18 | 18 | 1,14 |
| 27-42 | 40 | 32 | 1,09 |
| 42-57 | 26 | 4S | 1,69 |
| 57-72 | 12 | 69 | 1.84 |
рассчитайте коэффициент детерминации и эмпирическое корреляционное отношение. Сделайте выводы.
