1. теоретические аспекты применения показателей вариации в статистическом исследовании

Вид материала

Документы

Содержание 2. определение коэффициента вариации

Подобный материал:

• За собой необходимость знания и применения на практике принципов и приемов маркетинга,, 39.09kb.
• 1. Теоретические аспекты применения контроллинга на предприятии, 591.37kb.
• 1. Понятие факторного и результативного признака, 404.74kb.
• «Налоги и налогообложение» 2010-2011уч, 123.84kb.
• Расчет показателей вариации в ms excel, 107.91kb.
• Планирование в исследовании систем управления, 48.03kb.
• Программа вступительных испытаний по менеджменту (3,5 года обучения на базе высшего, 14.32kb.
• Методологические проблемы применения естественнонаучных методов в историческом исследовании:, 825.64kb.
• Реферат «Возможности применения ит при исследовании языковой интерференции», 247.71kb.
• Вопросы для самоконтроля знаний студентов по дисциплине «Комплексный экономический, 39.33kb.

Применение показателей вариации в статистическом исследовании

Содержание

1. теоретические аспекты применения
показателей вариации в статистическом
исследовании

Для характеристики размера вариации признака используются абсолютные и относительные показатели. К абсолютным показателям вариации относятся:

• размах колебаний;

• среднее линейное отклонение;

• среднее квадратическое отклонение;

• дисперсия;

• квартильное отклонение.

Размах колебаний (размах вариации)



где x_mах , x_min - соответственно максимальное и минимальное значения признака. Величина показателя зависит от величины только двух крайних вариант и не учитывает степени колеблемости основной массы членов ряда.

Среднее линейное отклонение и среднее квадратическое отклонение (σ) показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения. Среднее линейное отклонение определяется по формулам:

а) для несгруппированных данных (первичного ряда)



б) для п вариационного ряда



Среднее квадратическое отклонение (σ) и дисперсия (σ²) определяются так:

а) для несгруппированных данных



б) для п вариационного ряда



Формула для расчета дисперсии может быть преобразована:



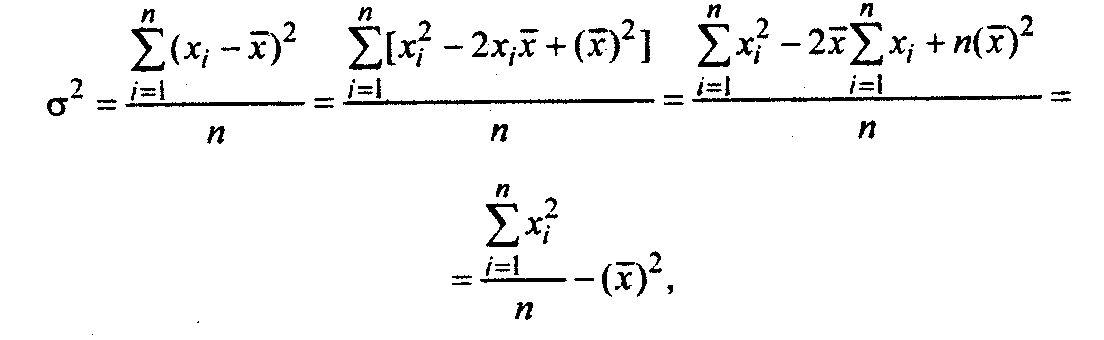
т. е. дисперсия равна средней из квадратов индивидуальных значений признака минус квадрат средней величины. Следовательно,



Среднее квадратическое отклонение по своей величине всегда превышает значение среднего линейного отклонения в соответствии со свойством мажорантности средних.

Квартильное отклонение (d_k) применяется вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений:



где Q₁ и Q₁ - соответственно третья и первая квартили распределения.

Квартиль - значения признака, которые делят ранжированный ряд на четыре равные по численности части. Таких величин будет три: первая квартиль (Q₁), вторая квартиль (Q₂), третья квартиль (Q₃). Вторая квартиль является медианой. Вычисление квартилей аналогично вычислению медианы.

Сначала определяют положение или место квартили:



Затем по накопленным частотам в дискретном ряду определяют численное значение.

В интервальном ряду распределения сначала указывают интервал, в котором лежит квартиль, затем определяют ее численное значение по формуле



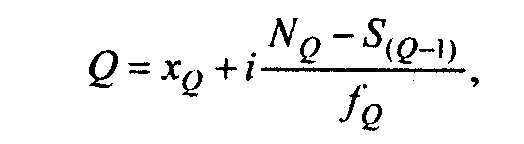
где Х_Q - нижняя граница интервала, в котором находится квартиль;

S_(Q-1) - накопленная частота интервала, предшествующего тому, в котором находится квартиль;

f_Q - частота интервала, в котором находится квартиль.

При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической используются относительные показатели вариации. Они вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане) и чаще всего выражаются в процентах.

Формулы расчета относительных показателей вариации следующие:



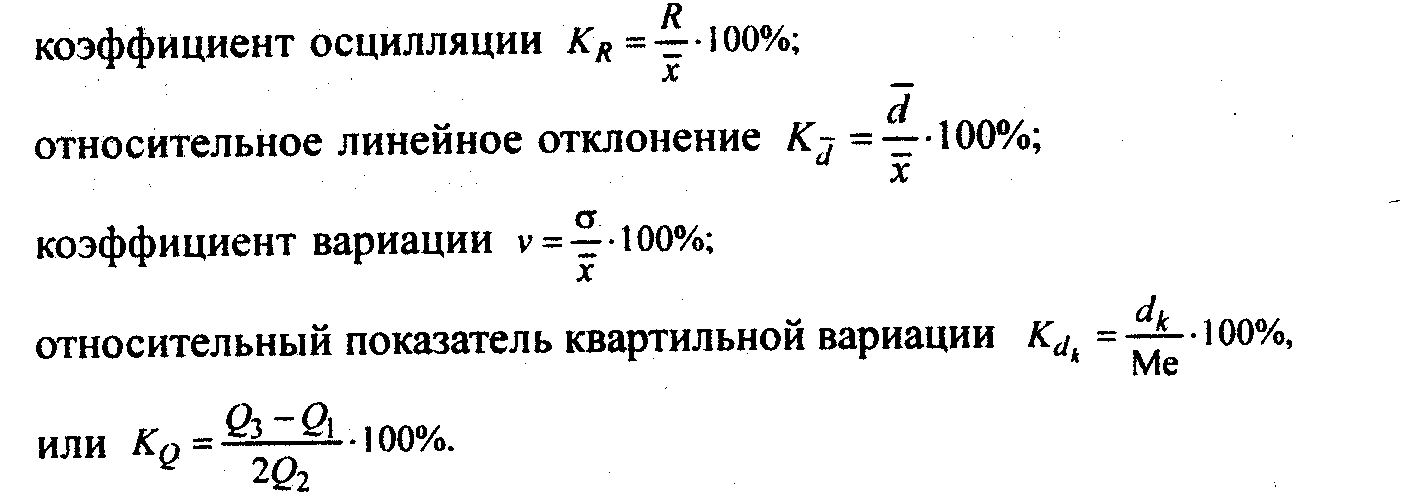
Наиболее часто применяется коэффициент вариации. Его применяют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).

2. определение коэффициента вариации

Пример 1. При определении коэффициента вариации по статистическому ряду распределения числа рабочих по разрядам будем использовать следующие формулы:

Среднее линейное отклонение рассчитывается по формуле:

.

Дисперсия определяется по формуле:

.

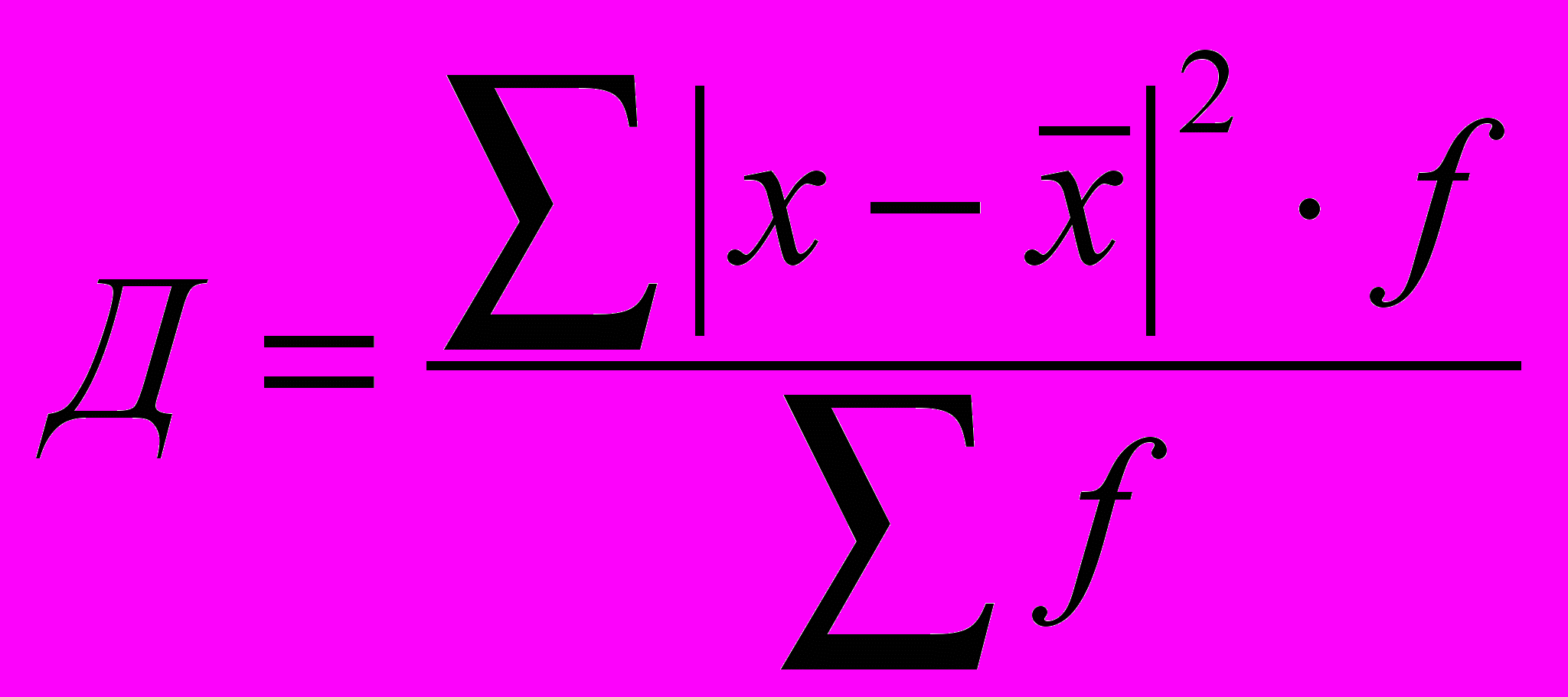Среднее квадратическое отклонение и коэффициент вариации:

;.


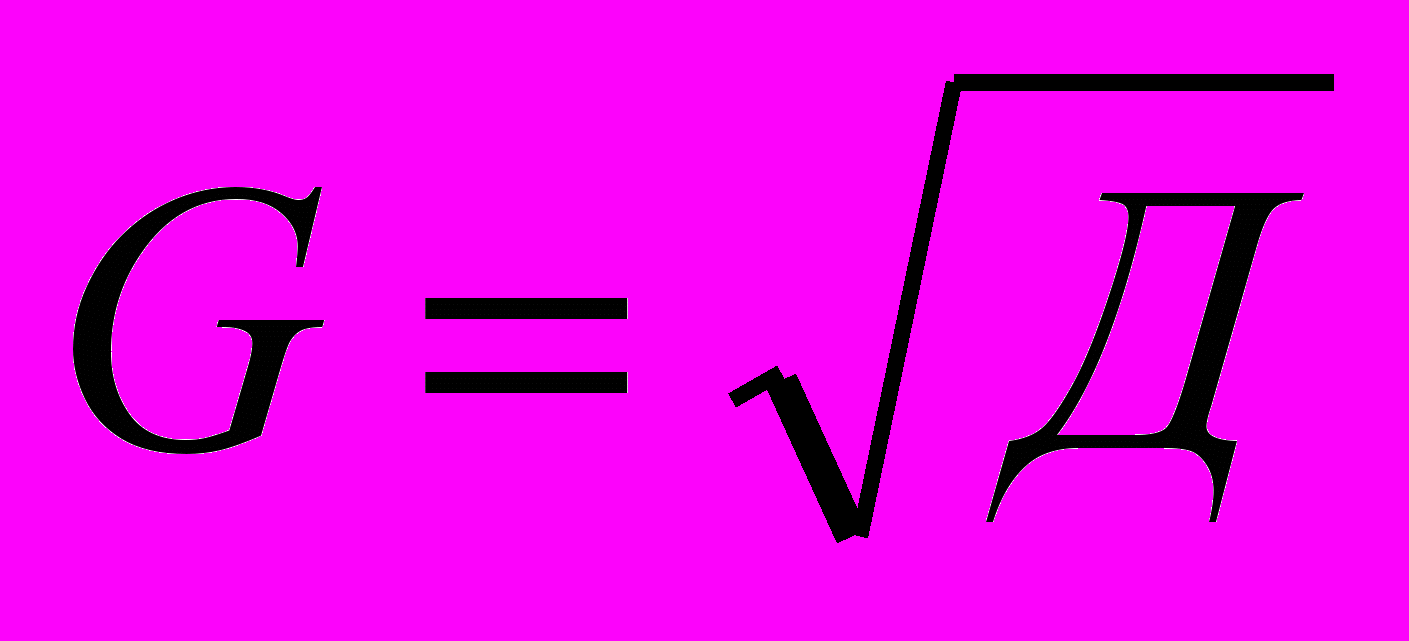Результаты расчетов представлены в таблице.


Таблица 1 – Распределение числа рабочих по тарифным разрядам и вспомогательные расчеты

Тарифный разряд (xi)	Число рабочих (fi)	xf
2	8	16	15,2	28,88
3	16	48	14,4	12,96
4	17	68	1,7	0,17
5	12	60	13,2	14,52
6	7	42	14,7	30,87
Всего	60	234	59,2	87,4

Среднее значение тарифного разряда определяется по формуле:



Среднее линейное отклонение равно:



Дисперсия:



Среднее квадратическое отклонение:



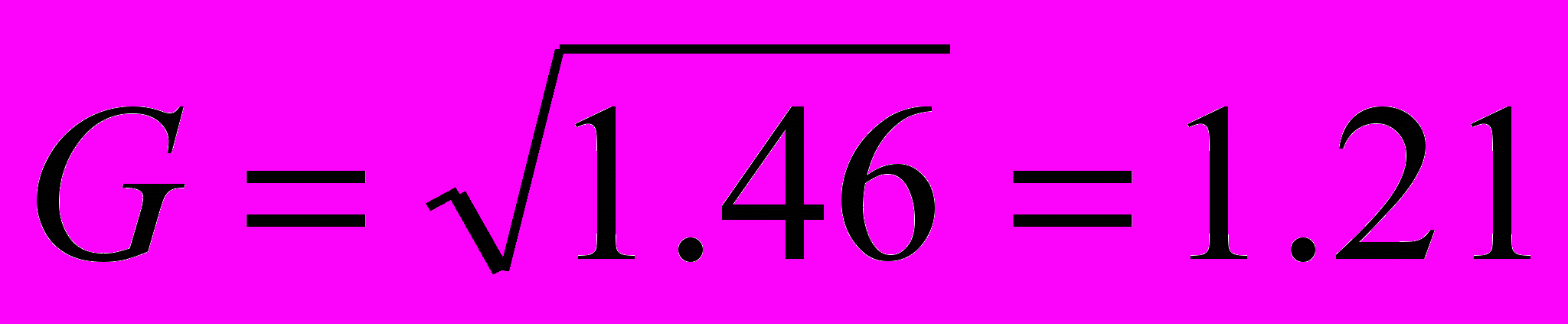
Коэффициент вариации:



Пример 2. Из урны, содержащей 8 белых, 6 черных шаров наугад извлекают 2 шара. Пусть Х – число вынутых черных шаров. Найдем коэффициент вариации этой случайной величины.

Ряд распределения случайной величины Х:

Хi	2	1	0
Рi	0,165	0,527	0,308

Если оба вынутых шара черные:








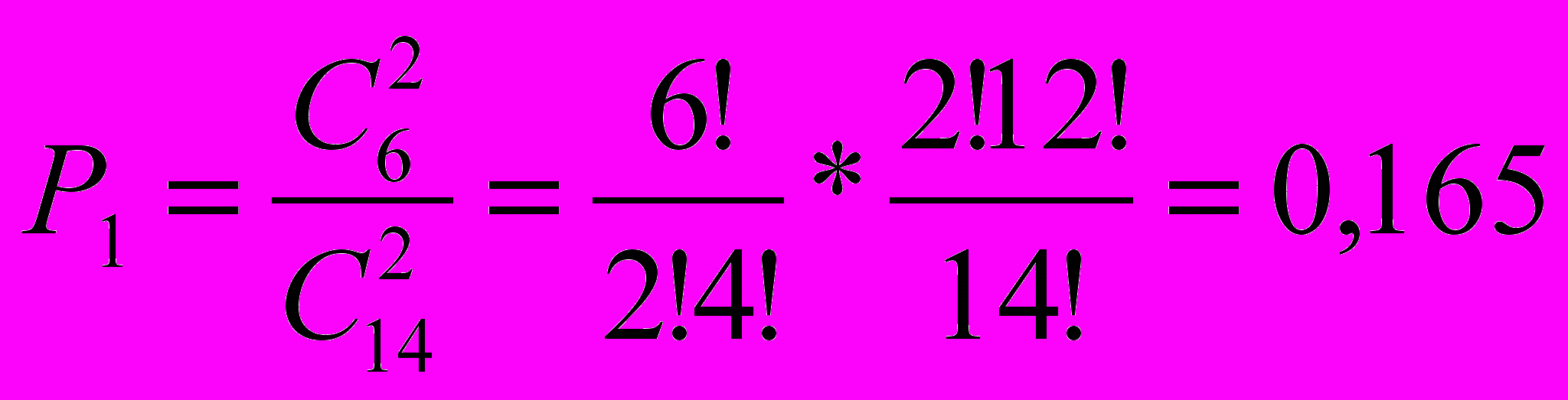
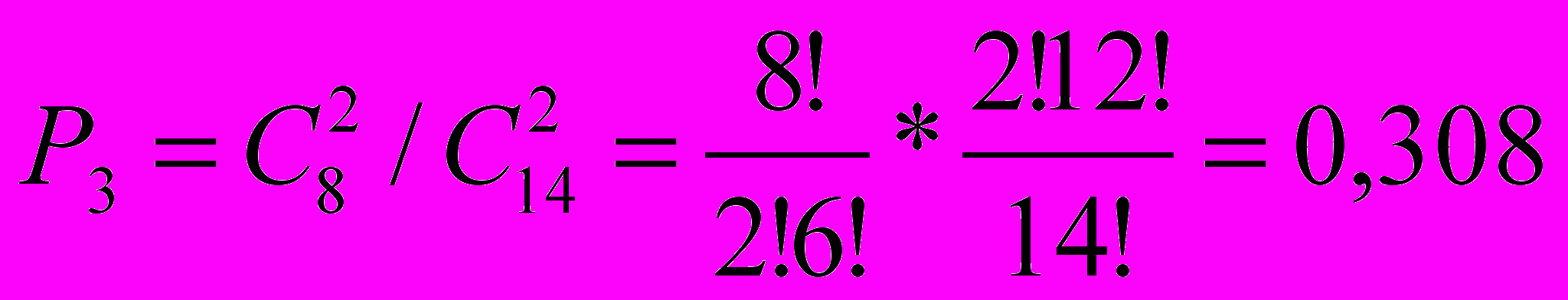
Функция распределения имеет вид:



Математическое ожидание:



Дисперсия:



Коэффициент вариации:

выводы

В лабораторной работе изучено применение показателей вариации в статистическом исследовании. Для этого рассмотрены теоретические аспекты применения показателей вариации в статистическом исследовании, определены коэффициенты вариации на двух условных примерах.

В результате определения коэффициента вариации по статистическому ряду распределения числа рабочих по разрядам получен коэффициент вариации, равный 31%, что свидетельствует об однородности совокупности.

Во втором примере нахождение коэффициента вариации числа вынутых из урны черных шаров дало его значение в размере 52,8%. Это свидетельствует о неоднородности совокупности, так как значение коэффициента вариации больше 33%.

список литературы

1. Статистика рынка товаров и услуг: Учебник / Под ред. И.К. Беляевского. – М.: Финансы и статистика, 1995. – 432с.
   
2. Экономическая статистика: учебник / Под ред. Ю.Н. Иванова. – М.: ИНФРА-М, 1998. – 480с.
   
3. Сиденко А.В., Попов Г.Ю., Матвеева В.М. Статистика: Учебник. – М.: Издательство „Дело и сервис”, 2000. – 464с.
   
4. Социально-экономическая статистика / Под ред. С.Р. Несторович. – Минск: БГЭУ, 2000.