1. Понятие факторного и результативного признака

Вид материала

Документы

Содержание Функциональная зависимость 3. Виды статистической связи. 2. Относительно своей аналитической формы 3. С точки зрения взаимодействующих факторов. Корреляционный анализ 5 Регрессионный анализ (эмпирическая линия регрессии). 6. Статистическое изучение корреляционной связи. 10 .Коэффициент корреляции 11. Эмпирическое корреляционное отношение. 12. Коэффициент Фехнера 13. Непараметрические показатели тесноты корреляционной связи. 14. Коэффициент корреляции рангов Спирмена 15. Коэффициенты ассоциации Юла и контингенции Пирсона 16. Коэффициент взаимной сопряженности Пирсона-Чупрова 17. Множественный коэффициент ранговой корреляции (коэффициент конкордации) 18. Построение модели связи(уравнения регрессии) 20. Этапы исследования множественной корреляции 21.Ряды динамики 22. Классификация рядов динамики 23. Сопоставимость и смыкание рядов динамики ... Полное содержание

Подобный материал:

• Методика факторного анализа: сущность, результативный показатель, понятие «фактора»., 30.47kb.
• Бизнес-план: понятие, строение. Виды смет. Понятие лигистического анализа. Модели детерминированного, 26.87kb.
• Дисперсионный анализ, 123.95kb.
• Тест. Вопросы/Варианты ответов Средняя величина представляет собой: а уровень признака, 121.7kb.
• По данным наблюдения провести корреляционно-регрессионный анализ (кра) зависимости, 134.2kb.
• Генетика человека, 33.55kb.
• Тематика дисциплины «Психогенетика» Вводная информация, 39.84kb.
• Литература 20 понятие государства и его сущность, 168.97kb.
• Применение Признака Паскаля. 9 Выводы. 10 Заключение. 10 Список используемой литературы., 93.57kb.
• Постановление Совета Министров Республики Беларусь 02. 02. 2011 n 119 Настоящим Положением,, 1528.36kb.

1. Понятие факторного и результативного признака.

Отличительная черта, свойство, качество, присущие единице совокупности и учитываемые при статистическом исследовании, называются признаком

Признаки по их значению делятся на 2 класса.

1. Результативные признаки – признаки, изменяющиеся под действием других связанных с ними признаков.

2. Факторные – признаки, обуславливающие изменения результативных признаков.


2.Функциональная и статистическая зависимость.

По характеру зависимости признаков различают функциональную (полную) связь и корреляционную (статистическую, неполную) связь.

Функциональная зависимость (жестоко детерминированная у=2х) – величине факторного признака строго соответствует одно или несколько значений результативного признака.

Статистическая – определенному значению факторного признака соответствует лишь среднее значение результативного признака. Стат. Связь не имеет ограничений и условий как в функциональной. Корреляционная связь явл. Частным случаем стат. Связи , состоит в том, что разным значениям одной переменной соответствуют различные средние значения др.


3. Виды статистической связи.

1. По направлению связи:

Положительная (прямая) – с увеличением (уменьш) одного признака в основном увелич. (уменьш) значения другого.

Отрицательная (обратная) – с увеличением (уменьш) одного признака в основном уменьшаются (увеличив) значения другого.


2. Относительно своей аналитической формы:

Линейная – между признаками в среднем проявляются линейные соотношения.

Нелинейная – выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно.


3. С точки зрения взаимодействующих факторов.

Парная – характеризуется связь 2 признаков.

Множественная – изучаются более чем 2 переменные.


Также подразделяется на сильную и слабую.


4. Корреляционный анализ. (корреляц. таблица, корреляц. поле).

В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются 2 группы методов, одна из которых включает в себя методы корреляционного анализа, а друга я – регрессионный анализ.


Корреляционный анализ – измерение тесноты связи между варьирующими признаками, определение неизвестных причинных связей и оценка факторов оказывающих наибольшее влияние на результативный признак.

Простейшим приемом выявления связи между 2 признаками является построение корреляционной таблицы.

В основу группировки положено 2 изучаемых во взаимосвязи признака – Х и У. Частоты f_ij показывают количество соответствующих сочетаний Х и У. Если f_ij расположены в таблице беспорядочно, то можно говорить об отсутствии связи между переменными. В случае образования какого-либо характерного сочетания f_ij допустимо утверждать о связи между Х и У. При этом если f_ij концентрируется около одной из двух диагоналей, имеет место прямая или обратная линейная связь. Наглядным изображением корреляционной таблице служит корреляционное поле. Оно представляет собой график, где на оси абсцисс откладывают значения Х, по оси координат – У, а точками показывается сочетание Х и У. По расположению точек, их концентрации в определенном направлении можно судить о наличии связи


Независимость Линейная зависимость


Прямая положит зависимость Прямая отриц зависимость


Криволинейная зависимость

5 Регрессионный анализ (эмпирическая линия регрессии).

Регрессионный анализ – установление формы зависимости, определение функции регрессии, использование уравнения для оценки неизвестных значений зависимой переменной.

В итогах корреляционной таблицы по строкам и столбцам приводятся 2 распределения – одно по х и другое по –У. Последовательность точек ( Х : _У¯) дает график, который иллюстрирует зависимость средн. значения результ. признака У от факторного Х, - эмпирическую линию регрессии, наглядно показывающую, как изменяется Х по мере изменения Х..

По существу , и корреляционная таблица, и корреляционное поле, и эмпирич. линия регрессии предварительно уже характеризует взаимосвязь, когда факторный и результ признаки и требуется сформулировать предположения о форме и направленности связи. В то же время количественная оценка тесноты связи требует дополнительных расчетов.


6. Статистическое изучение корреляционной связи.

При статистическом изучении корреляционной связи определяется влияние учтенных факторных признаков при отвлечении (абстрагировании) от прочих аргументов. Применяемый таким образом способ научной абстракции хотя и ведет к некоторому упрощению (аппроксимации) реального механизма связи, но делает возможным установления закономерностей взаимодействия изучаемых показателей. Это позволяет, не прибегая к экспериментированию, получать количественные характеристики корреляционной связи.

7. Проверка первичной информации на однородность и нормальность распределения.

Для оценки однородности совокупности используется коэффициент вариации по факторным признакам



Совокупность считается однородной, если коэффициент вариации не превышает 33%. Проверка нормальности распределения исследуемых факторных признаков (x₁, х₂, х₃, ... х_n) проводится с помощью правила “трех сигм”. Совокупность подчиняется закону нормального распределения, если значения попадают в следующие интервалы:

 - 68,3

 - 95,4

 - 99,7

 8. Установление факта наличия и направления корреляционной зависимости.

Установление факта наличия и направления корреляционной зависимости между результативным (у) и факторным (х) признаками. Основным методом выявления наличия корреляционной связи является метод аналитической группировки и определения групповых средних. Он заключается в том, что все единицы совокупности разбиваются на группы по величине признака-фактора и для каждой группы определяется средняя величина результативного признака. На основе данных аналитической группировки строится график эмпирической линии связи (линии регрессии), вид которой не только позволяет судить о возможном наличии связи, но и дает некоторое представление о форме корреляционной связи. Если эмпирическая линия связи по своему виду приближается к прямой линии, то можно предположить наличие прямолинейной корреляционной связи; если эмпирическая линия приближается к какой-либо кривой, то это связано с наличием криволинейной связи.

10 .Коэффициент корреляции

Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике — это мера линейной зависимости двух случайных величин.




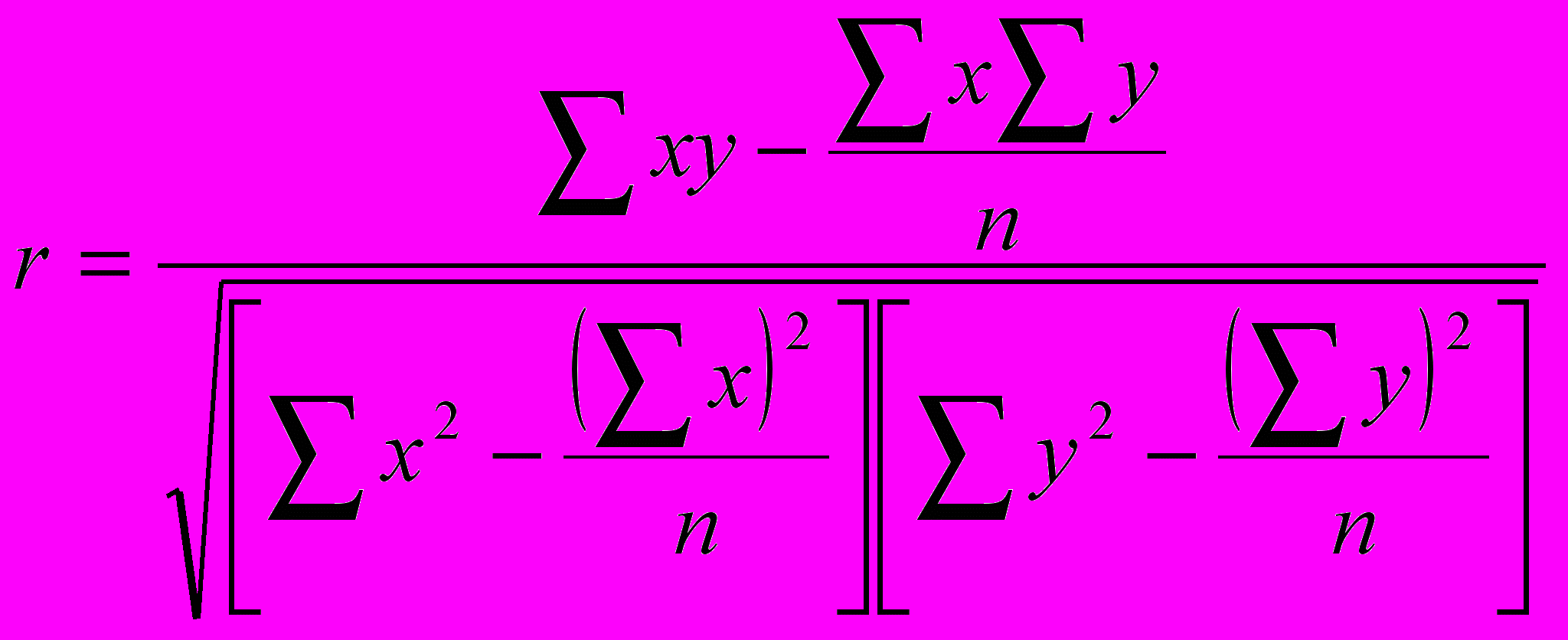
где

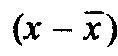- отклонения вариантов значений признака-фактора от их средней величины;

- отклонения вариантов значений результативного признака от их средней величины;

п - число единиц в совокупности;

Линейный коэффициент корреляции может принимать значения в пределах от -1 до +1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак при нем указывает направление связи: знак “+” соответствует прямой зависимости, знак “-” -обратной. Корреляционное отношение изменяется от 0 до 1: чем ближе к 1, тем связь теснее; направление связи он не показывает, оно устанавливается по данным групповой таблицы.


11. Эмпирическое корреляционное отношение.


Теснота корреляционной связи, как и любой другой, может быть измерена эмпирическим корреляционным отношением ηэ , когда δ2 (межгрупповая дисперсия) характеризует отклонения групповых средних результативного признака от общей средней:. Оно показывает тесноту связи между группировочными и результативными признаками. Эмпирическое корреляционное отношение, как и, может принимать значения от 0 до 1.

Коэффициент детерминации является наиболее конкретным показателем, так как он отвечает на вопрос о том, какая доля в общем результате зависит от фактора, положенного в основание группировки.


12. Коэффициент Фехнера

Элементарной характеристикой степени тесноты связи является коэффициент Фехнера. Коэффициент основан на сопоставлении знаков отклонений от средней и подсчете числа случаев совпадений и несовпадений знаков, а не на сопоставлении попарно размеров отклонений индивидуальных значений факторного и результативного признаков от средней




где na - количество совпадений знаков отклонении индивидуальных величин факторного признака х и результативного признака у от их средней арифметической величины (например, “плюс” и “плюс”, “минус” и “минус”, “отсутствие отклонения” и “отсутствие отклонения”);

nb - количество несовпадений знаков отклонений индивидуальных значений изучаемых признаков от значения их средней арифметической.

Коэффициент Фехнера целесообразно использовать для установления факта наличия связи при небольшом объеме исходной информации. Он изменяется в пределах - 1,0 < Кф < + 1,0. Чем ближе к 1, тем теснее связь.


13. Непараметрические показатели тесноты корреляционной связи.

Среди непараметрических показателей тесноты связи широко используются :

• коэффициент корреляции знаков (коэффициент основан на сопоставлении знаков отклонений от средней и подсчете числа случаев совпадений и несовпадений знаков)
  

• коэффициент ассоциации (Для исследования степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, может быть использован коэффициент ассоциации Д. Юла. Расчетная таблица в этом случае состоит из четырех ячеек (таблица “четырех полей”), статистическое сказуемое которой схематически может быть представлено в следующем виде:
  

Признаки	А (да)		Итого
В (да)	а	Ь	а+ b
В(нет)	с	d	c+d
Итого	а + с	b+d	П

a, b. с, d — частоты взаимного сочетания (комбинации) двух альтернативных

признаков

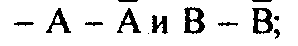
п - общая сумма частот.

Коэффициент ассоциации исчисляется по формуле

• взаимной сопряженности (применяется, когда требуется установить связь между качественными признаками, каждый из которых состоит из трех и более групп. Коэффициент взаимной сопряженности определяется по формуле
  

где φ2 - показатель средней квадратической сопряженности.



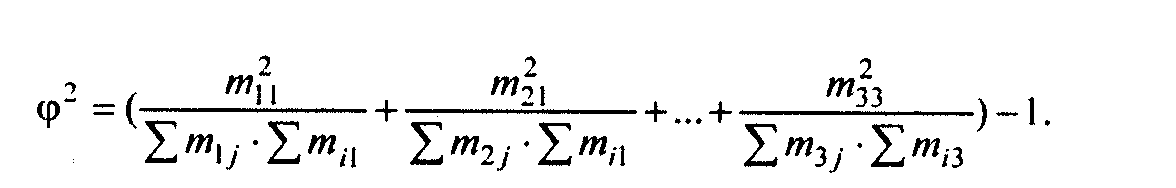
Коэффициент взаимной сопряженности изменяется от 0 до 1

• ранговые коэффициенты корреляции (Для определения тесноты связи как между количественными, так и между качественными признаками, при условии, что
  

значения этих признаков могут быть проранжированы по степени убывания или возрастания, используется коэффициент корреляции рангов Спирмэна



где di - разность между величинами рангов признака-фактора и результативного признака;

п - число показателей (рангов) изучаемого ряда.

Он варьирует в пределах от -1,0 до +1,0.


14. Коэффициент корреляции рангов Спирмена

Для определения тесноты связи как между количественными, так и между качественными признаками, при условии, что значения этих признаков могут быть проранжированы по степени убывания или возрастания, используется коэффициент корреляции рангов Спирмэна



где di - разность между величинами рангов признака-фактора и результативного признака;

п - число показателей (рангов) изучаемого ряда.

Он варьирует в пределах от -1,0 до +1,0.


15. Коэффициенты ассоциации Юла и контингенции Пирсона

Для исследования степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, может быть использован коэффициент ассоциации Д. Юла. Расчетная таблица в этом случае состоит из четырех ячеек (таблица “четырех полей”), статистическое сказуемое которой схематически может быть представлено в следующем виде:

Признаки	А (да)		Итого
В (да)	а	Ь	а+ b
В(нет)	с	d	c+d
Итого	а + с	b+d	П

a, b. с, d — частоты взаимного сочетания (комбинации) двух альтернативных

признаков

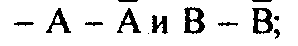
п - общая сумма частот.

Коэффициент ассоциации исчисляется по формуле




Коэффициент контингенции:



где а. Ь. с, d - числа в четырехклеточной таблице.

Коэффициент контингенции также изменяется от -1 до +1, но всегда его величина для тех же данных меньше коэффициента ассоциации.


16. Коэффициент взаимной сопряженности Пирсона-Чупрова

применяется, когда требуется установить связь между качественными признаками, каждый из которых состоит из трех и более групп. Коэффициент взаимной сопряженности определяется по формуле



где φ2 - показатель средней квадратической сопряженности.



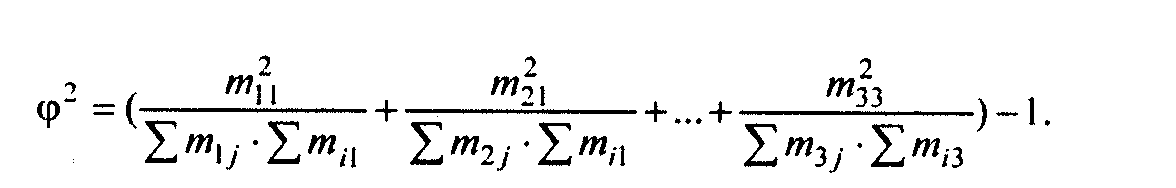
Коэффициент взаимной сопряженности изменяется от 0 до 1


17. Множественный коэффициент ранговой корреляции (коэффициент конкордации)


Для оценки степеней тесноты связи между несколькими признаками получил широкое распространение коэффициент конкордации, который вычисляется по формуле:




Где k – количество строк, n- количество столбцов, S – сумма квадратов отклонений сумм по строкам от их общего среднего значения. Данный коэффициент изменяется в пределах от 0 до 1.


18. Построение модели связи(уравнения регрессии)


После установления достаточной степени тесноты связи выполняется построение модели связи (уравнения регрессии). Тип модели выбирается на основе сочетания теоретического анализа и исследования эмпирических данных посредством построения эмпирической линии регрессии. Чаще всего используются следующие типы функций: а) линейная



б) гиперболическая



в) параболическая



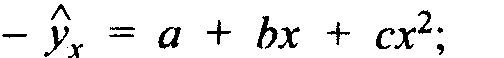
г) показательная



Для определения численных значений параметров уравнения связи (линии регрессии) используется метод наименьших квадратов и решается система нормальных уравнений.

Для определения параметров а и b уравнения прямолинейной корреляционной связи система нормальных уравнений (для несгруппированных данных) следующая:



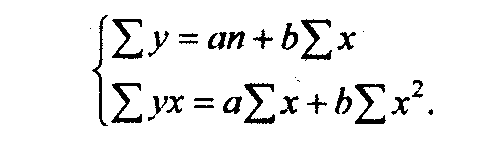
Решение указанной системы уравнений дает следующие формулы для расчета параметров а и b:



Для определения параметров гиперболической функции система нормальных уравнений следующая:



Для проверки возможности использования линейной функции определяется разность (η2 - г2); если она менее 0,1, то считается возможным применение линейной функции. Для решения

этой задачи можно использовать величину ω2, определяемую по формуле



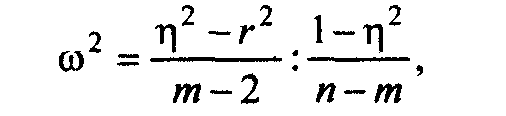
где т — число групп, на которое разделен диапазон значении факторного признака.

Если ω2 окажется меньше табличного значения F-критерия, то нулевая гипотеза о возможности использования в качестве уравнения регрессии линейной функции не опровергается. Значение F-критерия определяется по таблице в зависимости от уровня значимости а = 0,05 (вероятность Р = 0,95) и числа степеней свободы числителя (k1 = т - 2) и знаменателя (k2= п - т) (см. приложение 5).

В качестве меры достоверности уравнения корреляционной зависимости используется процентное отношение средней кварратической ошибки уравнения (Sе) к среднему уровню результативного признака (у):



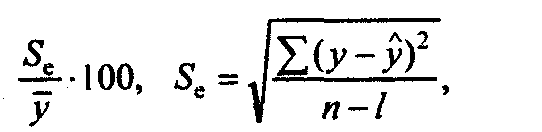
где у - фактические значения результативного признака;

- значения результативного признака, рассчитанные по уравнению регрессии;

i - число параметров в уравнении регрессии.

Если это отношение не превышает 10 - 15%, то следует считать, что уравнение регрессии достаточно хорошо отображает изучаемую взаимосвязь.


20. Этапы исследования множественной корреляции

Множественный, или совокупный, коэффициент корреляции для случая трех признаков, один из которых — результативный (с номером 1) и два—факторных (с порядковыми номерами 2 и 3) рассчитывается по формуле (Для расчетов используется такая формула



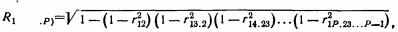
пригодная для случаев, когда число признаков, совокупное влияние которых исследуется, превосходит два. Существуют стандартные программы, вычисляющие R1(23...P))



где подстрочные индексы при r показывают номера признаков, связь между которыми оценивается этим коэффициентом корреляции.

Множественный коэффициент корреляции является показателем тесноты линейной связи между результативным признаком и совокупностью факторных признаков.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1. Равенство его нулю говорит об отсутствии линейной связи, равенство единице—о функциональной связи. Указаний на то, является ли связь прямой или обратной, коэффициент не дает.


21.Ряды динамики

Ряд динамики – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Всякий ряд динамики включает два обязательных элемента: время, конкретное значение показателя, ил уровень ряда. Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными,

относительными или средними величинами.


22. Классификация рядов динамики

Ряды динамики различаются по следующим признаками.

1. По времени:
   

- моментные ряды (если уровень ряда показывает фактическое наличие изучаемого явления в конкретный момент времени, то совокупность уровней образует моментный ряд динамики. Примерами моментных рядов могут быть последовательности показателей численности населения на начало года, величины запаса какого-либо материала на начало периода и т.д)

- интервальный ряд динамики – последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени. Таковы, например, ряды показателей объема продукции по месяцам года, количества отработанных человеко-дней по отдельным периодам..

2. По форме представления уровней:

- ряды абсолютных величин

- ряды относительных величин

- ряды средних величин

3. По расстоянию между датами или интервалами времени:
   

- полные хронологические ряды ( имеют место, когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами. Это равностоящие ряды динамики)

- неполные хронологические ряды – когда принцип равных интервалов не соблюдается

3. По числу показателей:
   

- изолированные ряды динамики ( если ведется анализ во времени одного показателя)

- комплексные ряды динамики ( получается в том случае, когда в хронологической последовательности дается система показателей, связанных между собой единством процесса или явления)


23. Сопоставимость и смыкание рядов динамики

Важнейшим условием правильного построения ряда динамики является сопоставимость всех входящих в него входящих в него уровней. Данное условие решается либо в процессе сбора и обработки данных, либо путем их пересчета.
   Несопоставимость уровней ряда может возникнуть вследствие изменения единиц измерения или единиц счета.
   На сопоставимость уровней ряда динамики непосредственно влияет методология учета или расчета показателей.
   Условием сопоставимости уровней ряда динамики является периодизация динамики. В процессе развития во времени прежде всего приосходят количественные изменения явлений, а затем на определенных ступенях совершаются качественные скачки, приводящие к изменению закономерности явления. Поэтому научный подход к изучению рядов динамики заключается в том, чтобы ряды, охватывающие большие периоды времени, расчленять на такие, которые бы объединяли лишь однокачественные периоды развития совокупности, характеризующейся одной закономерностью развития.
   Процесс выделения однородных этапов развития носит название периодизации динамики.
   Важно также, чтобы в ряду динамики интервалы или моменты, по которым определены уровни, имели одинаковый экономический смысл..
   Уровни ряда динамики могут оказаться несопоставимыми по кругу охватываемых объектов вследствие перехода ряда объектов из одного подчинения в другое.
   Для того чтобы привести уровни ряда динамики к сопоставимому виду, иногда приходится прибегать к приему, который называется «смыкание рядов динамики». Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или разным территориальным границам. Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах).


24. Требования, предъявляемые к рядам динамики

1. Сопоставимость статистических данных. Основным условием для получения правильных выводов при анализе рядов динамики является сопоставимость его элементов.

2. Величины временных интервалов должны соответствовать интенсивности изучаемых процессов. Чем больше вариация уровней во времени, тем чаще следует делать замеры. Соответственно для стабильных процессов интервалы можно увеличить.

3. Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.


25. Показатели ряда динамики.

Цепные и базисные показатели:

1. Абсолютные приросты.

Абсолютный прирост определяется как разность между двумя уровнями динамического ряда и показывает на сколько данный уровень ряда превышает уровень, принятый за базу сравнения:

= yi- yi-1, или = yi- y0

где - абсолютный прирост;

yi - уровень сравниваемого периода;

где yi-1 - уровень непосредственно предшествующего периода.

y0 - уровень базисного периода.

2,Коэффициент роста (снижения)

показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы).

При сравнении с постоянной базой Ki= yi/ y0

При сравнении с переменной базой Ki= yi/ yi-1

3. Темп роста

Если коэффициенты роста выражают в процентах, то их называют темпами роста: Тр = К*100%.

Темп роста всегда представляет собой положительное число.

4. Темп прироста.

Темп прироста (сокращения) показывает на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения.

Тn= Тp- 100%

5. Коэффициенты опережения (отстаивания).

При сопоставлении динамики развития двух явлений можно использовать показатели, представляющие собой отношения темпов роста или темпов прироста за одинаковые отрезки времени по двум динамическим рядам Эти показатели называют коэффициентами опережения.

KOn= Tp' / Tp''

или

KOn= Tn' / Tn''

где Tp', Tp'' и Tn', T_n'' - соответственно темпы роста и темпы прироста сравниваемых динамических рядов.

6.Абсолютное значение одного процента прироста.

Аi рассчитывают как отношение абсолютного прироста к темпу прироста (в %) за тот же период времени.

Ai= (yi- уi-1) / Tni / i-1.

7. Пункты роста (отстаивания).


26. Изучение тенденции развития рядов динамики.


Всякий ряд динамики теоретически м.б представлен в виде след составляющих:

Тренд – основная тенденция развития динамическогоряда(к увеличению либо снижению его уровней)

Циклические (периодические) колебания, в том числе сезонные.

Случайные колебания.


Изучение тренда включает 2 основных этапа:

1. ряд динамики проверяется на наличие тренда.
   
2. Производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.
   

27. Методы выявления тенденции в целом, методы выявления тенденции по видам.

Методы выявления тенденции в целом, в рядах динамики.

Кумулятивный Т-критерий.

С помощью данного метода выявляется не только сама тенденция, но и её математическое выражение – тренд. Выдвигается гипотеза об отсутствии тенденции в исходном ряду динамики. Гипотеза проверяется на основе кумулятивного Т-критерия, расчетное значение которого определяется по формуле следующего вида

ааааааааааааааа

Z_n-накопленный итог отклонений эмпирических значений признака от среднего уровня исходного ряда динамики.

Если Т расчетное больше Т критического (a,n) то гипотеза об отсутствии тенденции отвергается, следовательно ряду динамики существует тенденция, сл-но существует и тренд. Т.к Т расчетное больше Т критического, то гипотеза об отсутствии тенденции в исходном ряду динамики отвергается, сл-но, тенденция существует, сл-но, существует тренд.


Методы выявления тенденции по видам.

В прогностики различают тенденцию 3-х видов:

1. Тенденцию среднего уровня аналитически выражается в виде некоторой функции вокруг которой варьируют эмпирические значения признака.

2. Тенденцию дисперсии – это изменение отклонений эмпирических значений признакаот среднего уровня исходного ряда динамики.

3.Тенденцию автокорреляции – это изменение корреляционной зависимости между последовательными уровнями исходного ряда динамики.

Методы определения основного направления развития явления.

Весь исходный ряд динамики разбивается на 2, примерно равные части, каждая их кот-х рассматривается как самостоятельная независимая нормально распределенная совокупность. Если исходный ряд имеет тенденцию, то средние вычисленные для 2-х совокупностей должны существенно и значимо различаться между собой. Если расхождение между средними не значимо и случайно, то в ряду динамики отсутствует тенденция среднего уровня. Выдвигается гипотеза ррррррррррррррррто о равенстве средних двух нормально распределенных совокупностей. Проверка гипотезы осуществляется на основе расчета и анализа t-критерия Стьюдента, расчетное значение которого осуществляется по формуле:


Если t расчетное больше t критического, то гипотеза о равенстве средних двух нормально распределенных совокупностей отвергается, сл-но, средние различаются существенно, сл-но сущ тенденция средней, и сл-но сущ тренд. С помощью данного метода проверяется гипотеза Н о равенстве дисперсий 2-х нормально распределенных совокупностей. Данная гипотеза означает, что если дисперсии, вычисленные для двух совокупностей существенно различаются между собой, то в целом в ряду динамики сущ тенденция дисперсии и сл-но, сущ тренд. Проверка гипотезы осущ на основе F-критерия Фишера, расчетное значение которого определяется по формуле.


Если Fрасчетное больше F критического, то гипотеза о равенстве дисперсий 2-х нормально распределенных совокупностей отвергается, сл-но в ряду динамики сущ тенденция дисперсии,сл-но сущ тренд.


Метод Фостера-Стюарта.

С помощью данного метода можно определить наличие тенденции средней и дисперсии в исходном ряду динамики. В основе реализации метода лежит принцип сравнения каждого след значения исходного ряда динамики со значением всех предыд уровней. Рассчитываются 2 величины: U_{t и} e_t. Величина U_t принимает значение 1, если значение каждого след уровня ряда динамики больше всех предыдущих значений и 0 во всех остальных случаях. Величина e_t. Принимает значение 1, если значение каждого след уровня меньше значения всех предыд и 0 во всех остальных случаях.

На основе этих величин определяется их сумма S и разность D. С помощью S проверяется гипотеза об отсутствии тенденции в дисперсиях, а D – об отсутствии тенденции средней. Проверка гипотезы осущ на основе расчета и анализа t- критерия Стьюдента, расчетное значение которого определяется по формулам:


Где математическое ожидание

Среднеквадратическая ошибка величины S -среднеквадратическая ошибка величины D

-табличные числа.

28. Непосредственное выделение средней.

1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину аждого интервала (одновременно уменьшается кол-во интервалов).

2. Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Интервал может быть нечетным (3, 5 точек) или четным.

При нечетном сглаживании полученное среднее арифмет значение закрепляют за серединой расчетного интервала, при четном этого делать нельзя. Поэтому при обработке ряда четными интервалами их искусственно делают нечетными, для чего образуют ближайший большой нечетный интервал, но из крайних его уровней берут только 50%.

Недостаток методики сглаживания скользящими средними состоит в условности определения сглаженных уровней для точек в начале и конце ряда. Получают их спец приемами –расчетом средн арифм взвешенной.

3.Аналитическое выравнивание. Под эти понимают определение основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает перед исследователем как бы в зависимости только от течения времени. В итоге выравнивания временного ряда получают наибольший суммарный проявляющийся во времени результат действия все причинных факторов. Отклонение конкретных уровней ряда от уровней соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. В результате приходят к трендовой модели. Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f_t. На практике по имеющемуся временному ряду задают вид и находят параметры функции f_t, а затем анализируют поведение отклонений от тенденции. Функцию f_t выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.


30. Сглаживание динамического ряда методом скользящей средней

Скользящая средняя - это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Если, предположим, продолжительность периода равна 3, то скользящие средние рассчитываются следующим образом:





и т.д.


Первую рассчитанную среднюю относят ко второму периоду, вторую - к третьему, третью - к четвертому и т.д. По сравнению с фактическим сглаженный ряд становится короче на (m - 1)/2, где m - число уровней интервала.


31. Аналитическое выравнивание динамических рядов (выбор трендовой модели)

Важнейшим способом количественного выражения общей тенденции изменения уровней динамического ряда является аналитическое выравнивание ряда динамики, которое позволяет получить описание плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями, которые рассчитываются на основе определенной кривой, где уравнение рассматривается как функция времени. Вид уравнения зависит от конкретного характера динамики развития. Его можно определить как теоретически, так и практически. Теоретический анализ основывается на рассчитанных показателях динамики. Практический анализ - на исследовании линейной диаграммы.

Задачей аналитического выравнивания является определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами. Способ определения неизвестных значений внутри динамического ряда называют интерполяцией. Эти неизвестные значения можно определить: 1) используя полусумму уровней, расположенных рядом с интерполируемыми; 2) по среднему абсолютному приросту; 3) по темпу роста. В результате аналитического выравнивания получают следующую трендовую модель:





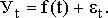
где f(t) – уровень, определяемый тенденцией развития; e_t – случайное и циклическое отклонение от тенденции.

Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t). На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.


32 Выравнивание ряда динамики прямой линией

. Чаще всего при выравнивании используются следующие зависимости:

Л
инейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.

Параболическая зависимость используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.

Экспоненциальные зависимости применяются, если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, – устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или темпов роста и т.п.).

Оценка параметров (a0, a1, a2, ...) осуществляется следующими методами:

1) методом избранных точек,

2) методом наименьших расстояний,

3) методом наименьших квадратов (МНК).

В большинстве расчетов используют метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выравненных:





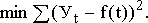
Для линейной зависимости (f(t)=a₀+a₁t) параметр а₀ обычно интерпретации не имеет, но иногда его рассматривают как обобщенный начальный уровень ряда; а₁ – сила связи, т.е. параметр, показывающий, насколько изменится результат при изменении времени на единицу. Таким образом, а можно представить как постоянный теоретический абсолютный прирост.

33 Точечное прогнозирование.

Для точечного прогноза нужно составить уравнение зависимости.

В общем виде оно выглядит так:




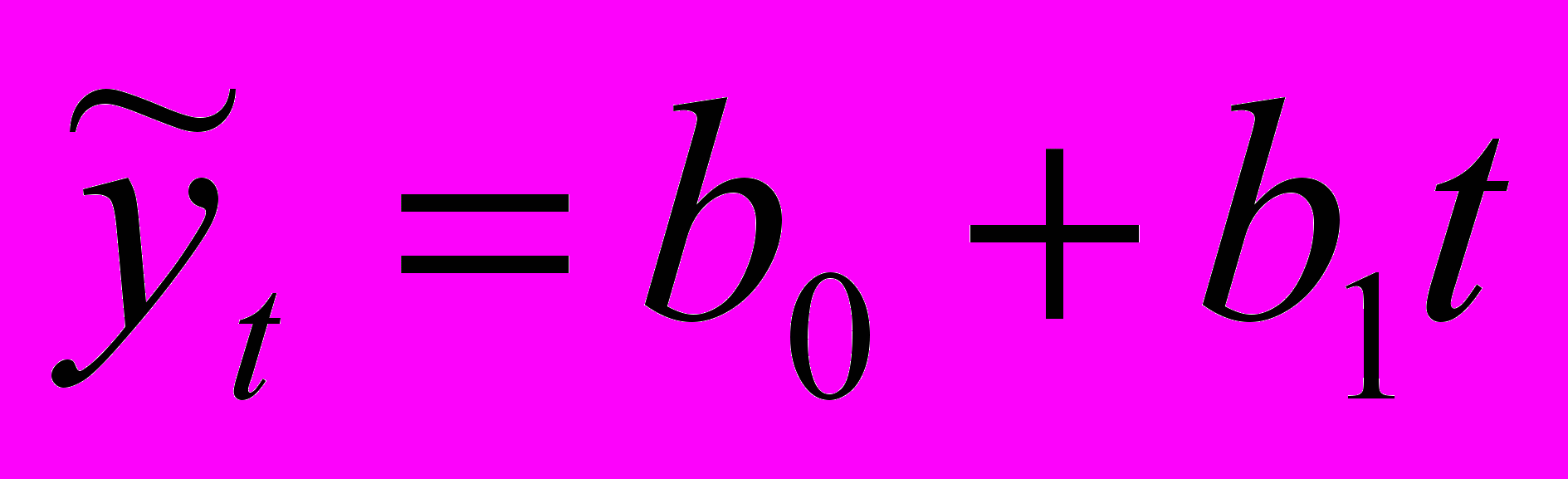
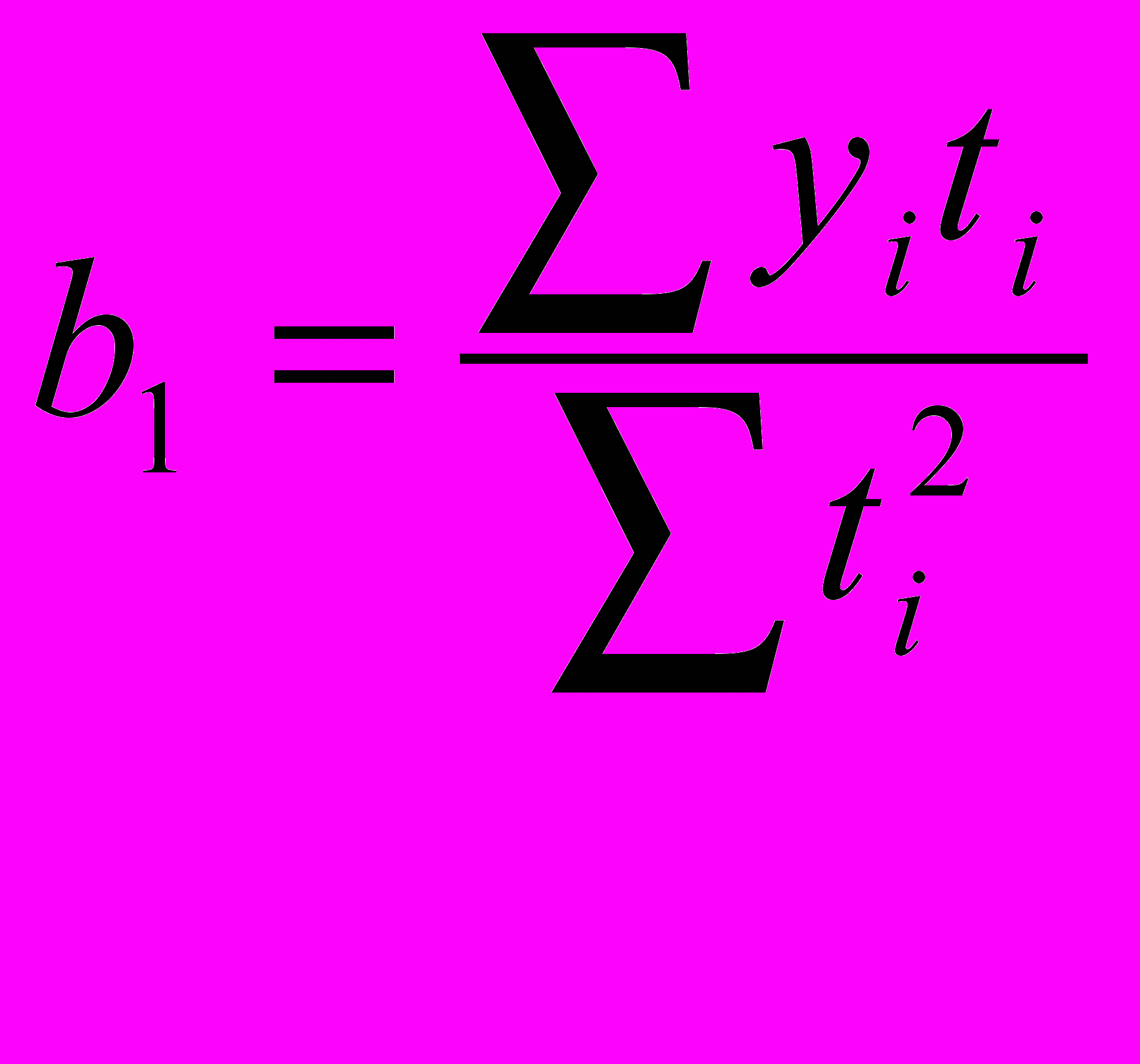
Подставив все значения в уравнение получаем точечный прогноз.


34. Интервальный прогнозирование.


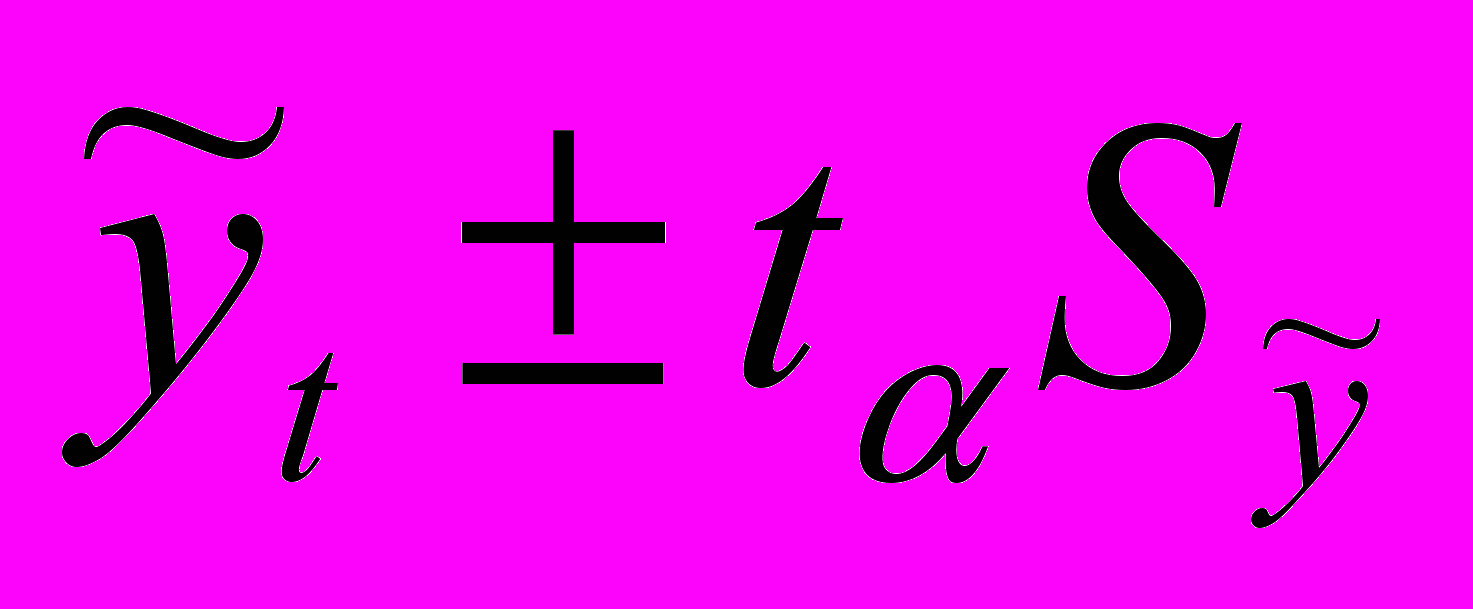- необходимо найти интервалы в которых будет находится прогнозируемое значение.




35. С
татистическое изучение сезонных колебаний

Анализ рядов динамики предполагает и исследование сезонной неравномерности (сезонных колебаний), под которыми понимают устойчивые внутригодовые колебания, причиной которых являются многочисленные факторы, в том числе и природно-климатические. Сезонные колебания измеряются с помощью индексов сезонности, которые рассчитываются двумя способами в зависимости от характера динамического развития.

36 Методы абсолютных и относительных разностей.

Сезонность – изменение динамических рядов имеющих внутригодичную цикличность, зависящую от календарного периода года, явлений природы, праздников и тд.

Для измерения сезонных колебаний используются 3 метода:

1. Метод абсолютных разностей
   

При его использовании определяется абсолютное отклонение уровней ряда по периодам от среднего уровня ряда. Если тренда нет или он незначителен, то для каждого месяца(квартала) индекс рассчитывается по формуле: , где

- средний уровень ряда, полученный в результате осреднения уровня ряда за одноименные периоды времени.

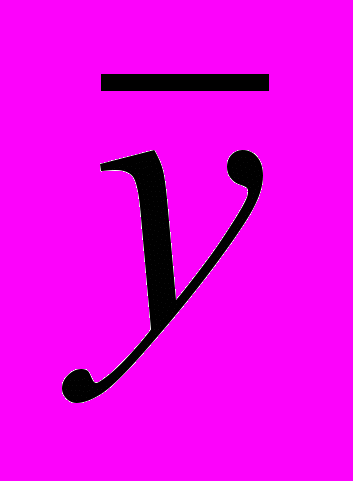- общий средний уровень ряда за все время наблюдения.

2. Метод относительных раностей.
   

При его использовании рассчитывают отношение абсолютных отклонений и среднего уровня ряда. Ряд динамики имеет общую тенденцию и она определена либо методом скользящего среднего, либо методом аналитического выравнивания.



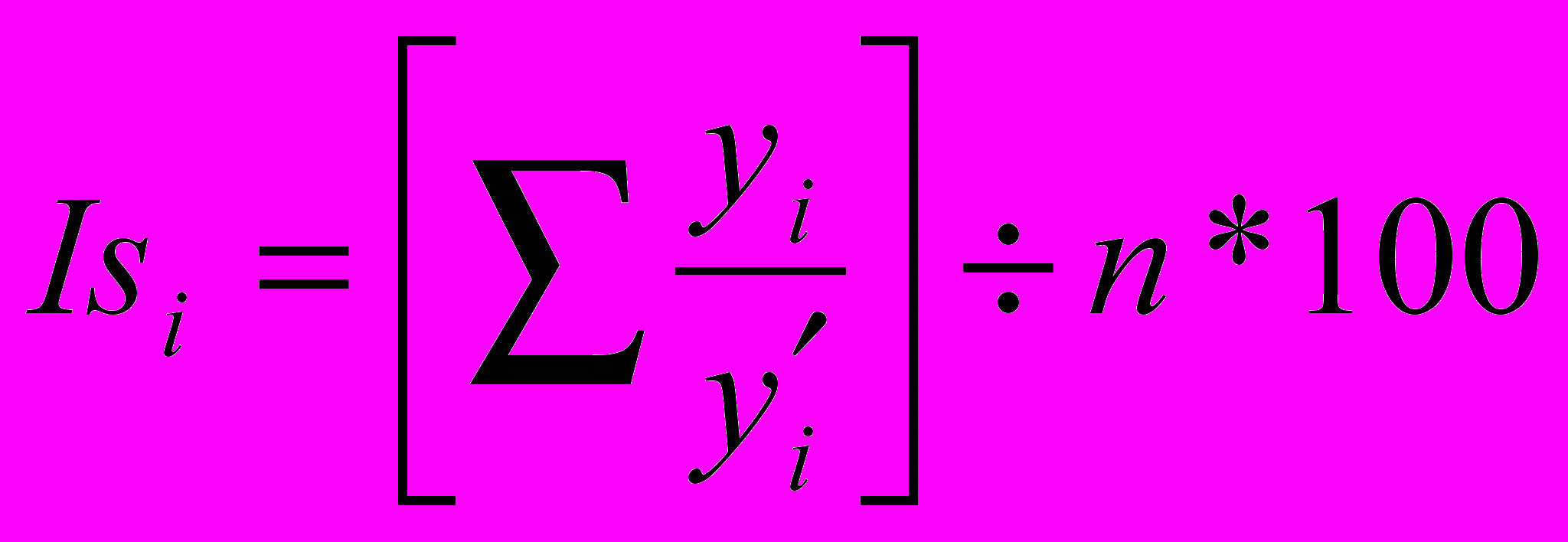
- исходные уровни ряда

- уровни ряда, полученные в результате определения скользящих средних для тех же периодов времени, что и исходные данные.

i – номер месяца или квартала, для которого определяется индекс сезонности

n – число лет наблюдения за процессом.

Обощающим показателем силы колеблемости динамического ряда из-за переодичности служит среднее отклонение индексов сезонности в процентах от 100%.





Is – индекс сезонности для каждого периода

n – количество периодов.


37. Индексы сезонности

При относительно неизменном годовом уровне явления индекс сезонности можно рассчитать как процентное отношение средней величины из фактических уровней одноименных месяцев к общему среднему уровню за исследуемый период:





В условиях изменчивости годового уровня индекс сезонности определяется как процентное отношение средней величины из фактических уровней одноименных месяцев к средней величине из выровненных уровней одноименных месяцев:





В простейших случаях для характеристики взаимосвязи двух или более рядов их приводят к общему основанию, для чего берут в качестве базисных уровни за один и тот же период и исчисляют коэффициенты опережения по темпам роста или прироста. Коэффициенты опережения по темпам роста – это отношение темпов роста (цепных или базисных) одного ряда к соответствующим по времени темпам роста (также цепным или базисным) другого ряда. Аналогично находятся и коэффициенты опережения по темпам прироста.

Временной лаг - экономический показатель, показывающий отставание или опережение одного экономического явления по сравнению с другим, связанным с ним явлением.