Тест. Вопросы/Варианты ответов Средняя величина представляет собой: а уровень признака в расчете на единицу совокупности
| Вид материала | Документы |
- А внимательно прочитайте вопросы и варианты ответов, 85.91kb.
- А внимательно прочитайте вопросы и варианты ответов, 66.8kb.
- Экзаменационный тест вступительного испытания по Литературе, 71.75kb.
- Статья-тест Как узнать самостоятельно, без помощи специалиста, готов ли ребенок к школе?, 171.2kb.
- Тест основан на расчете d статистики:, Расчетная величина, 57.24kb.
- Сущность и значение средних величин, 161.2kb.
- Тест по теме: «Периодическая система химических элементов. Строение атома. Химическая, 132.64kb.
- Вкачестве дополнения к тесту можно предложить комплекс вопросов Охарактеризуем технологии, 56.53kb.
- Измерить какую-нибудь величину значит узнать, сколько раз в ней заключается однородная, 246.88kb.
- Микроклимат практикум-тест №5 Вопросы Варианты ответа, 53.12kb.
| № п/п | ТЕСТ. Вопросы/Варианты ответов |
| | Средняя величина представляет собой: а) уровень признака в расчете на единицу совокупности; б) наиболее распространенное значение признака; в) значение признака, находящееся в середине ранжированной совокупности. |
| | Совокупность по которой рассчитывается средняя, должна быть: а) упорядоченной; б) однородной; в) подчиняться закону нормального распределения. |
| | Средняя величина отражает: а) типичный уровень признака в совокупности; б) индивидуальные особенности всех значений признака; в) отклонения значений признака от типичного уровня. |
| | Исходное соотношение средней представляет собой: а) отношение объема признака к объему совокупности; б) отношение объема совокупности к объему признака; в) разность между объемом признака и объемом совокупности. |
| | Объем признака представляет собой: а) максимальное значение признака в совокупности; б) суммарную величину всех значений признака; в) число единиц совокупности. |
| | К степенным средним относятся: а) средняя квадратическая, кубическая и т.п.; б) названные выше средние, а также средняя гармоническая и средняя геометрическая; в) названные выше средние, а также средняя арифметическая. |
| | Взвешанные средние используются в тех случаях, когда: а) частоты всех вариантов признака равны; б) все без исключения варианты значений признака повторяются; в) все или отдельные варианты значений признака повторяются. |
| | Могут ли веса средней быть выражены относительными показателями? а) могут; б) не могут. |
| | |
| | Сумма отклонений индивидуальных значений признака от средней арифметической равна: а) нулю; б) единице; в) любой положительной величине. |
| | Изменится ли средняя величина, если все варианты увеличить на 10%? а) изменится; б) не изменится. |
| | Изменится ли средняя величина, если все веса уменьшить на некоторую постоянную величину? а) изменится; б) не изменится. |
| | Возможны ли случаи, когда взвешенные и невзвешенные средние приводят к одному и тому же результату? а) возможны; б) нет. |
| | Может ли одно и то же исходное соотношение быть реализовано на основе различных форм средней? а) может; б) не может. |
| | Как изменится средняя величина, если все варианты признака уменьшить в 1,5 раза, а все веса в 1,5 раза увеличить? а) не изменится; б) уменьшится; в) возрастет. |
| | Можно ли вместо средней арифметической невзвешенной использовать среднюю гармоническую невзвешенную? а) нельзя; б) можно при отсутствии весов; в) можно при равенстве весов. |
| | Для определения среднего значения признака, индивидуальные значения которого выражены обратными показателями следует применять формулу средней: а) гармонической; б) арифметической; в) геометрической. |
| | Средняя величина является обобщающей характеристикой варьирующего признака: а) только в качественно однородной совокупности; б) в любой совокупности; в) в совокупности, состоящей из случайных величин. |
| | Значение средней величины зависит: а) от индивидуальных значений признака; б) от максимального и минимального значений признака; в) от индивидуальных значений признака и их весомости. |
| | Средняя величина является величиной типичной: а) для качественно однородной совокупности; б) для любой совокупности; в) качественно неоднородной совокупности. |
| | Имеются следующие данные о выпуске годовой продукции по цехам предприятия (млн. руб.) за месяц: 126,138,132,141,150. Для определения среднего выпуска готовой продукции в целом по предприятию за месяц следует применять формулу средней: а) арифметической простой; б) арифметической взвешанной; в) гармонической простой; г) гармонической взвешанной. |
| | Какой величине равна сумма отклонений индивидуальных значений признака от средней: а) нулю; б) больше нуля; в) меньше нуля. |
| | Если осредняемые значения признака уменьшить ил увеличить на постоянное число А, то средняя арифметическая соответственно: а) уменьшится или увеличится на ту же величину; б) останется неизменной; в) предсказать изменение средней нельзя. |
| | Если все индивидуальные значения признака увеличить в 3 раза, а частоты уменьшить в 3 раза, то средняя арифметическая соответственно: а) не изменится; б) уменьшится в 3 раза; в) увеличится в 3 раза. |
| | Если частоты всех значений признака уменьшить в 5 раз, а значения признака оставить без изменения, то средняя арифметическая: а) увеличится в 5 раз; б) уменьшится в 5 раз; в) не изменится. |
| | Мода в ряду распределения – это: а) наиболее распространенное значение признака; б) наибольшая частота; в) наименее распространенное значение признака. |
| | Значение моды: а) зависит от крайних значений признака; б) не зависит; в) иной ответ. |
| | Медиана в ряду распределения – это: а) наиболее распространенное значение признака; б) значение признака, делящее ряд распределения на две равные части; в) значение признака, делящее ряд распределения на четыре равные части. |
| | Значение медианы совпадает со значение средней: а) в ассиметричном распределении; б) в симметричном распределении; в) если данные не сгруппированы. |
| | Средние значения признака в двух совокупностях одинаковые. Может ли быть разной вариация в этих совокупностях? а) да; б) нет; в) иной ответ. |
| | |
| | |
| | Могут ли мода, медиана и средняя арифметическая совпадать? а) могут; б) могут совпадать только средняя и медиана; в) не могут. |
| | Может ли ряд распределения характеризоваться двумя и более модами? а) не может; б) может только двумя; в) может двумя и более. |
| | Установите содержание задачи, решаемой путем анализа рядов динамики: а) измерение уровня вариации явлений; б) анализ территориальных пропорций; в) анализ процесса развития явления во времени; г) иная задача. |
| | В числе нижеприведенных динамических рядов выделите интервальный ряд: а) численность поголовья крупного рогатого скота на начало каждого года; б) размер основных фондов на 1-ое июля каждого года, млн. руб.; в) валовой сбор зерна за ряд лет, млн. руб. г) число крестьянских фермерских хозяйств на конец каждого года, единиц. |
| | Укажите правильный ответ расчета темпа прироста фондовооруженности труда по одной из машиностроительных фирм в 2004 году по сравнению с 2003 годом, если фондовооруженность труда в 2003году составила 14,3 тыс. руб., а в 2004 году – 15,7 тыс. руб.: а) 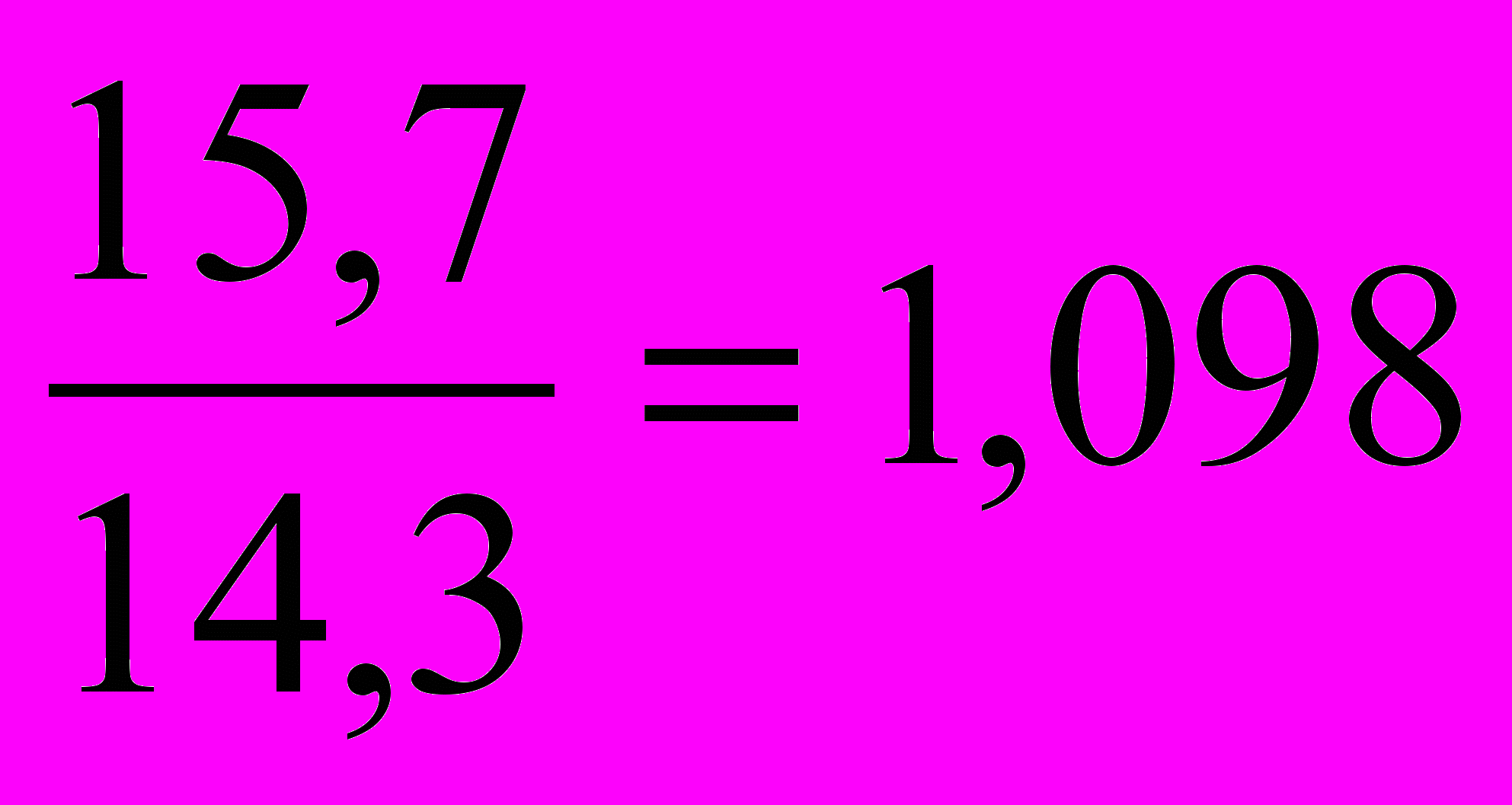 или 109,8%; или 109,8%;б) 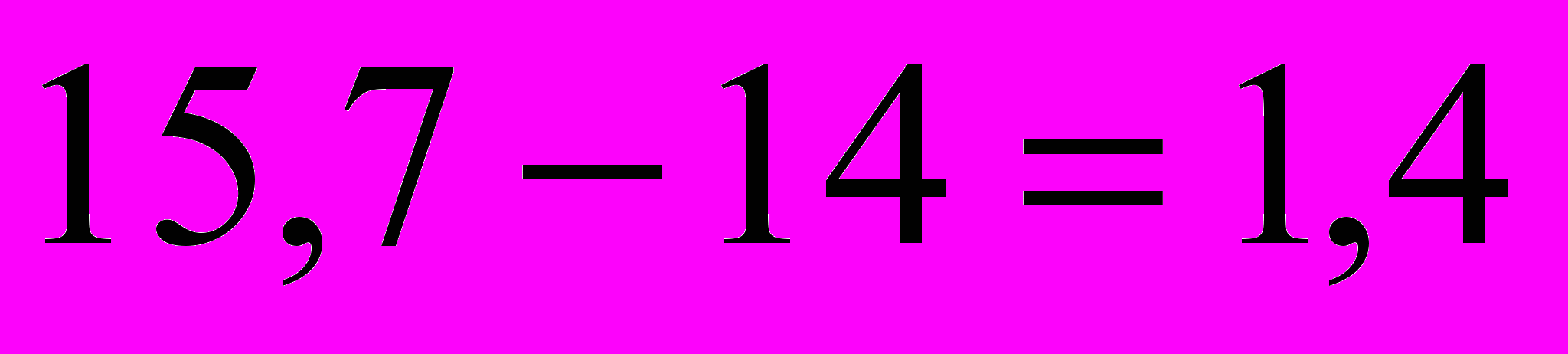 ; ;в) 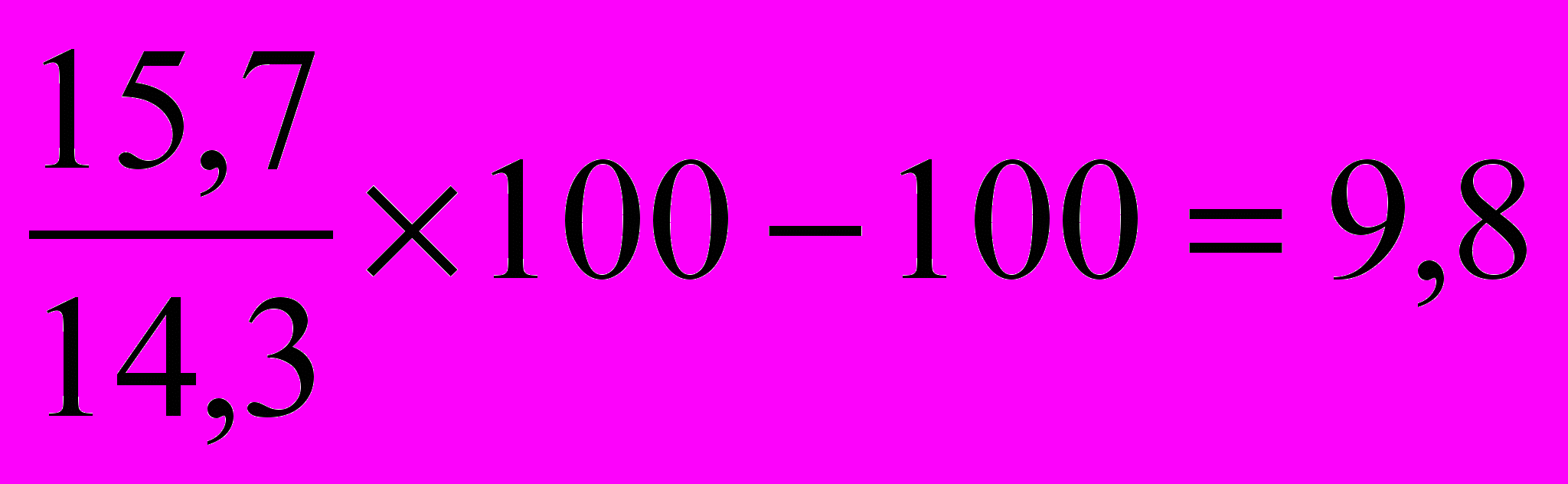 ; ;г) 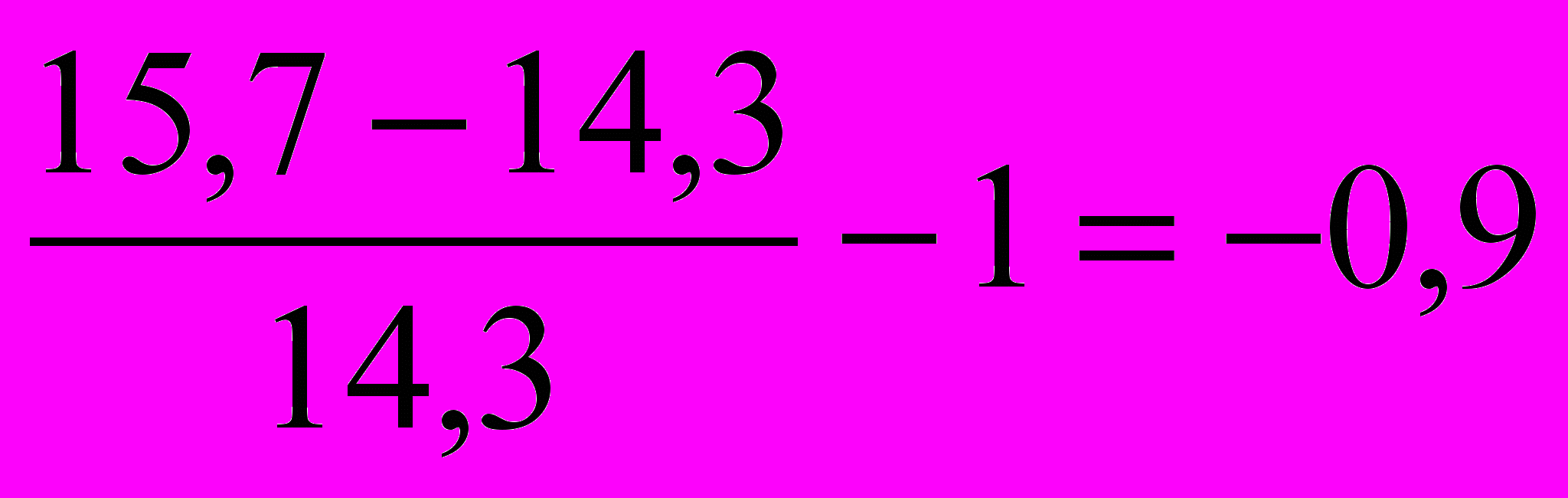 . . |
| | Укажите правильный ответ расчета цепного показателя абсолютного прироста, если известна динамика среднегодовой численности работников предприятия: 2000 г. – 1180 чел, 2001 г. – 1250 чел., 2002 г. – 1243 чел., 2003 г. – 1315 чел., 2004 г. – 1396чел. а) 1315 - 1180 = 135; б) 1396 - 1250 = 146; в) 1396 – 1315 = 81; г) 1243 - 1180 = 63. |
| | Укажите правильный ответ расчета цепного темпа роста ввода в действе жилых домов предприятиями всех форм собственности региона, если известны следующие данные (млн. м2 общей площади): 2001 г. – 21, 2002 г. – 20, 2003 г. – 22, 2004 г. – 23: а) 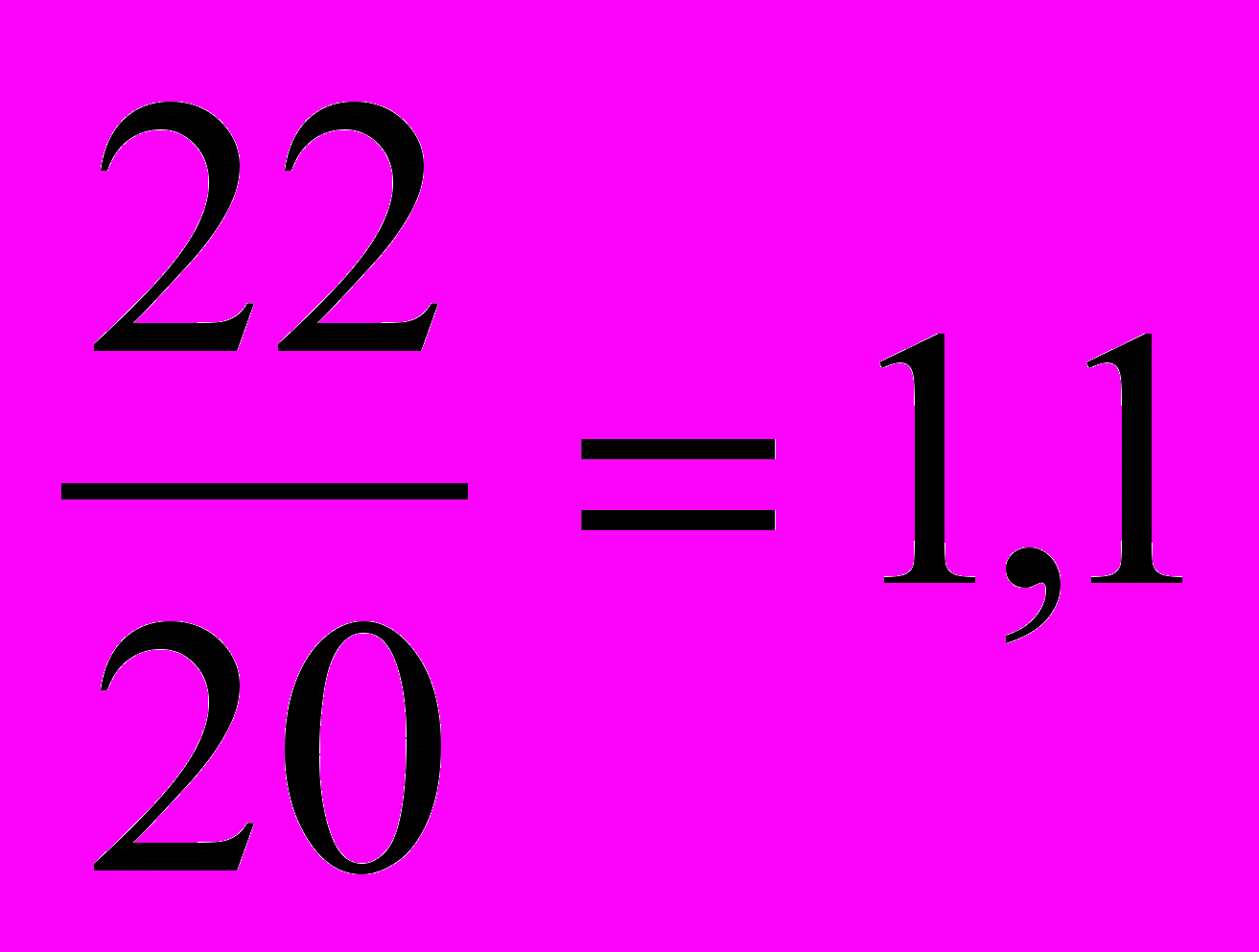 или110%; или110%;б) 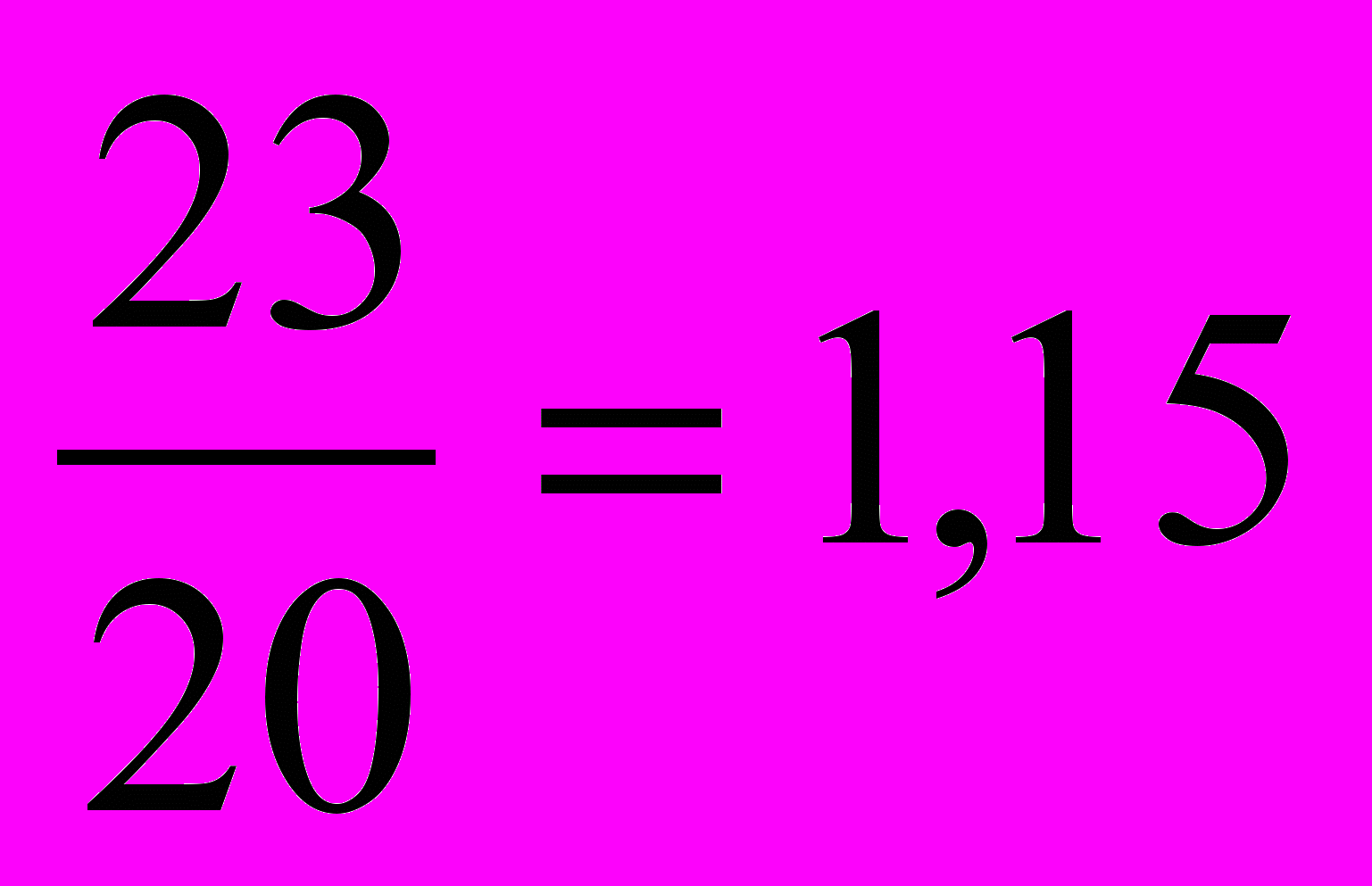 или 115%; или 115%;в) 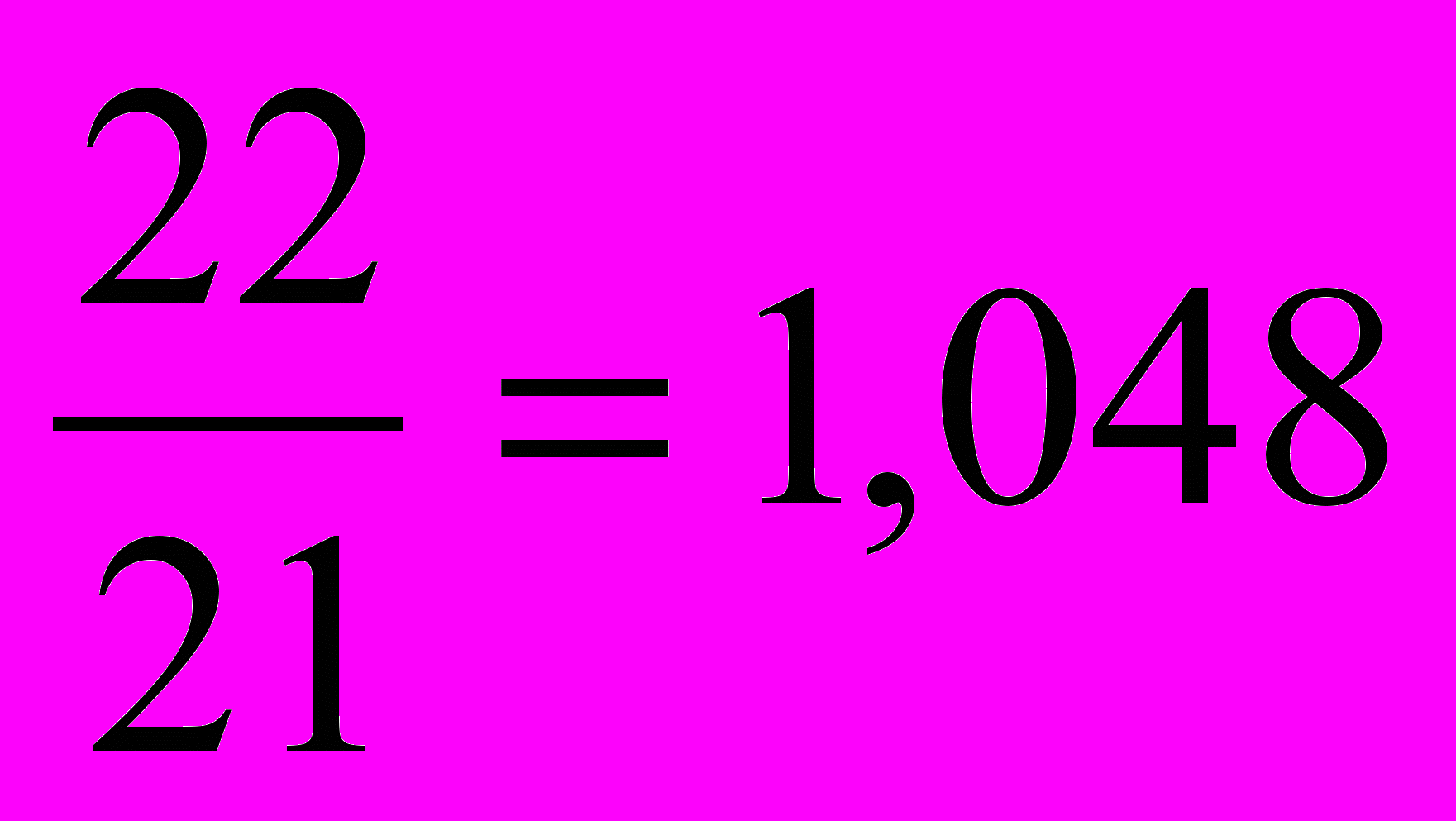 или 104,8%; или 104,8%;г) 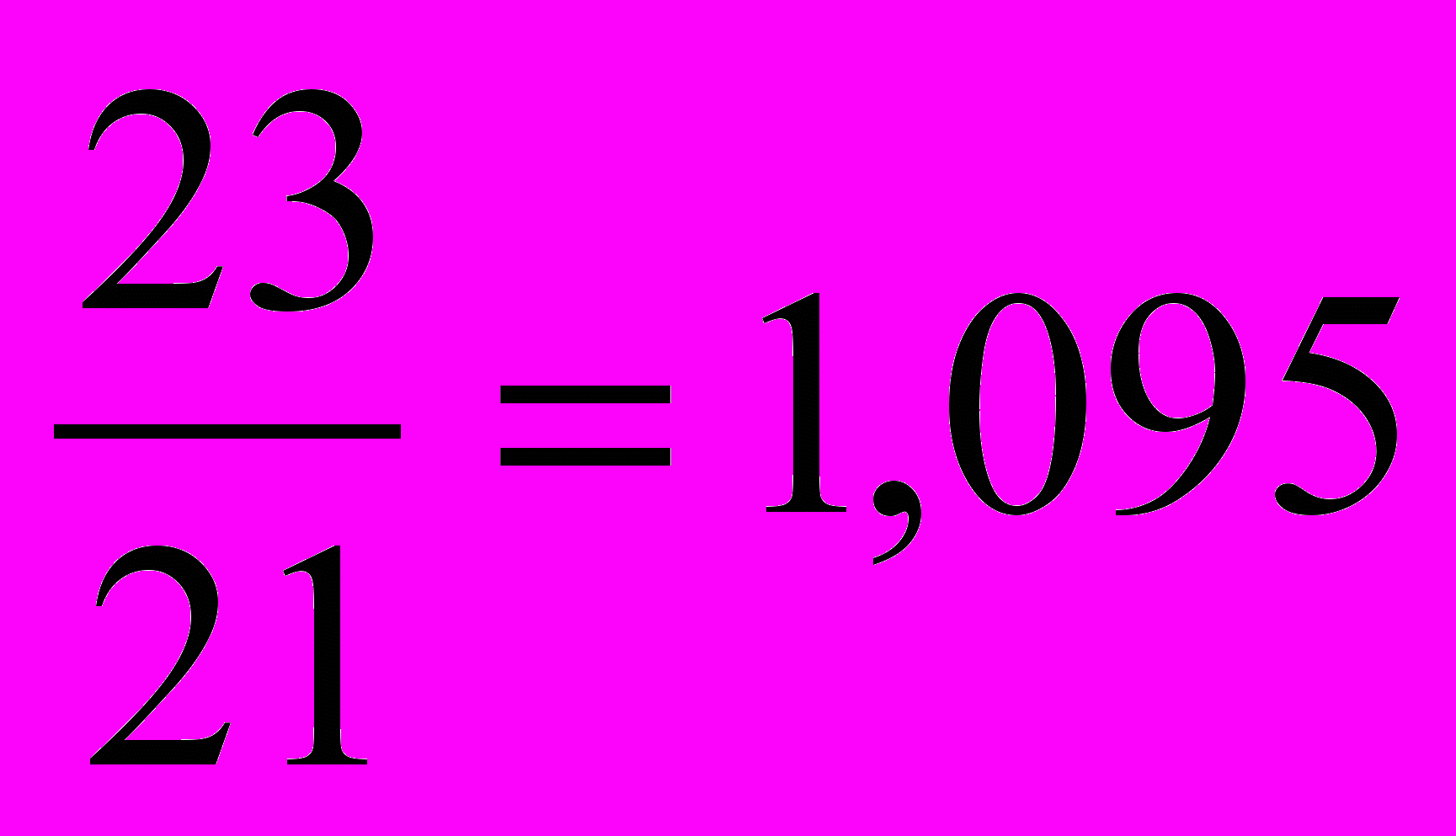 или 104,5%. или 104,5%. |
| | Укажите правильный ответ расчета абсолютного значения одного процента прироста производства автомобилей в регионе по данным за 2003 г. – 1602 тыс. шт., в 2004 г. – 1846 тыс. шт.: а) 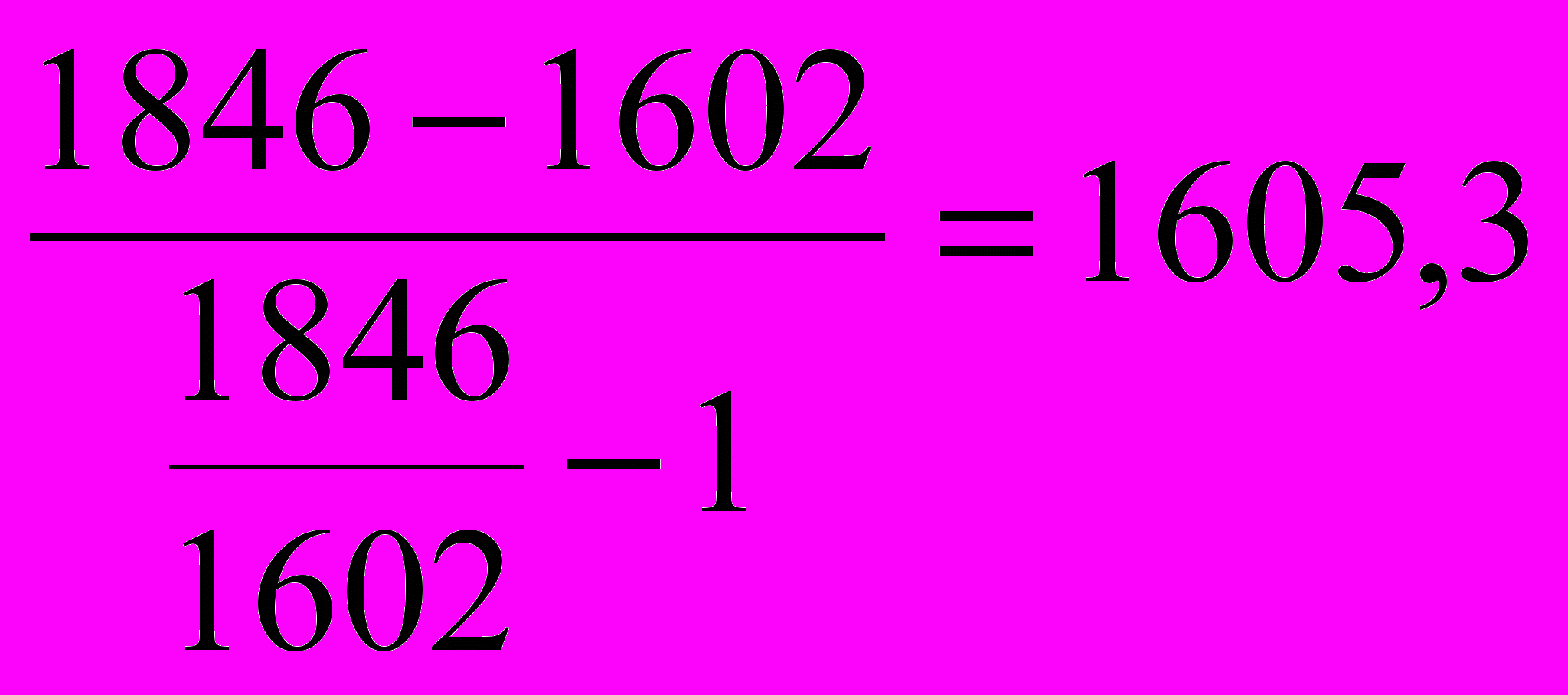 ; ;б) 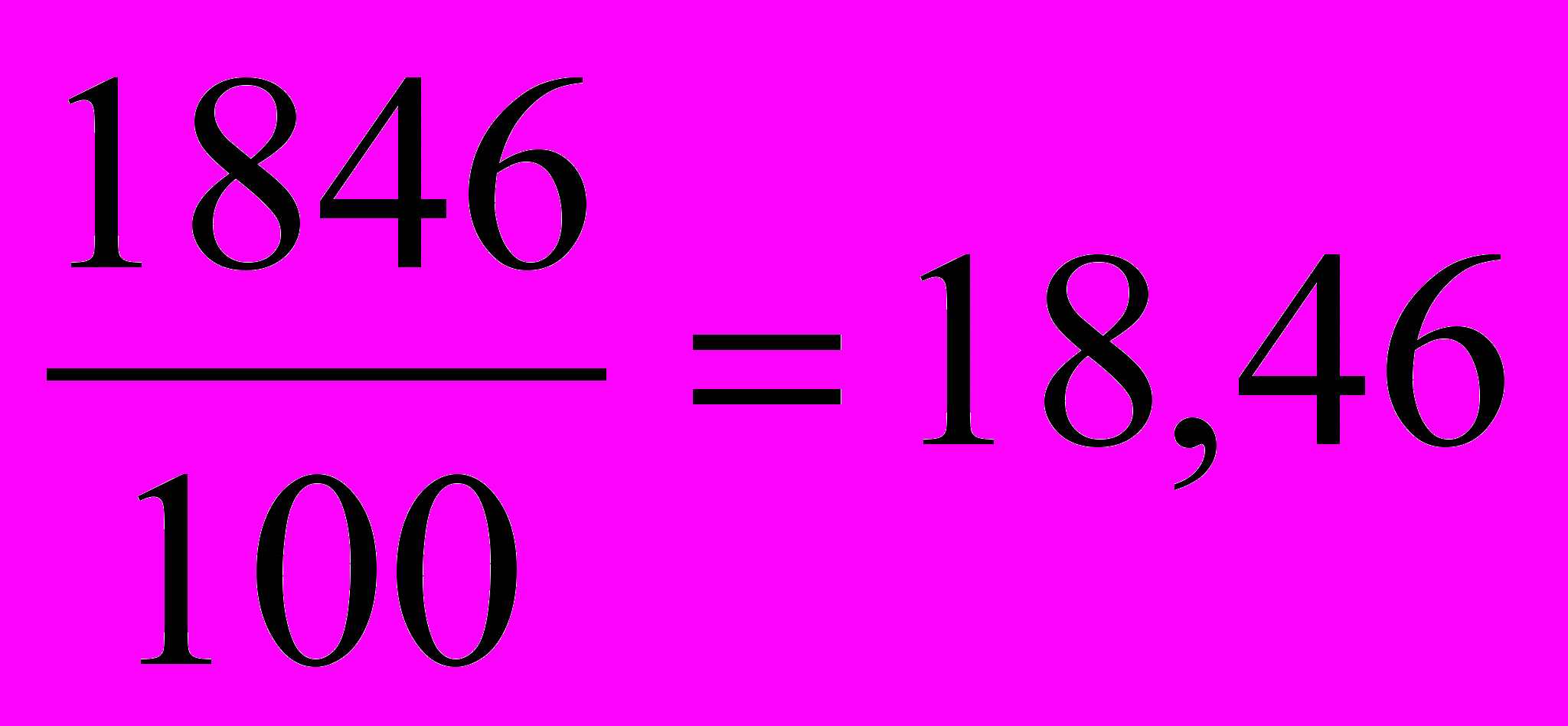 ; ;в) 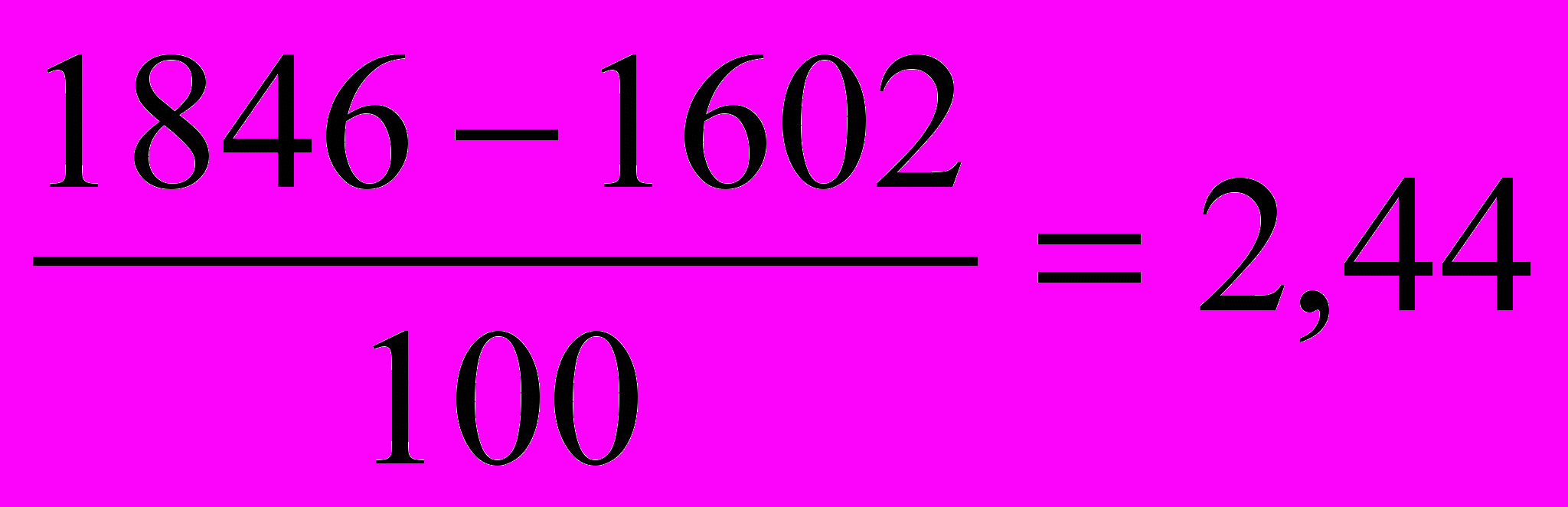 ; ;г) 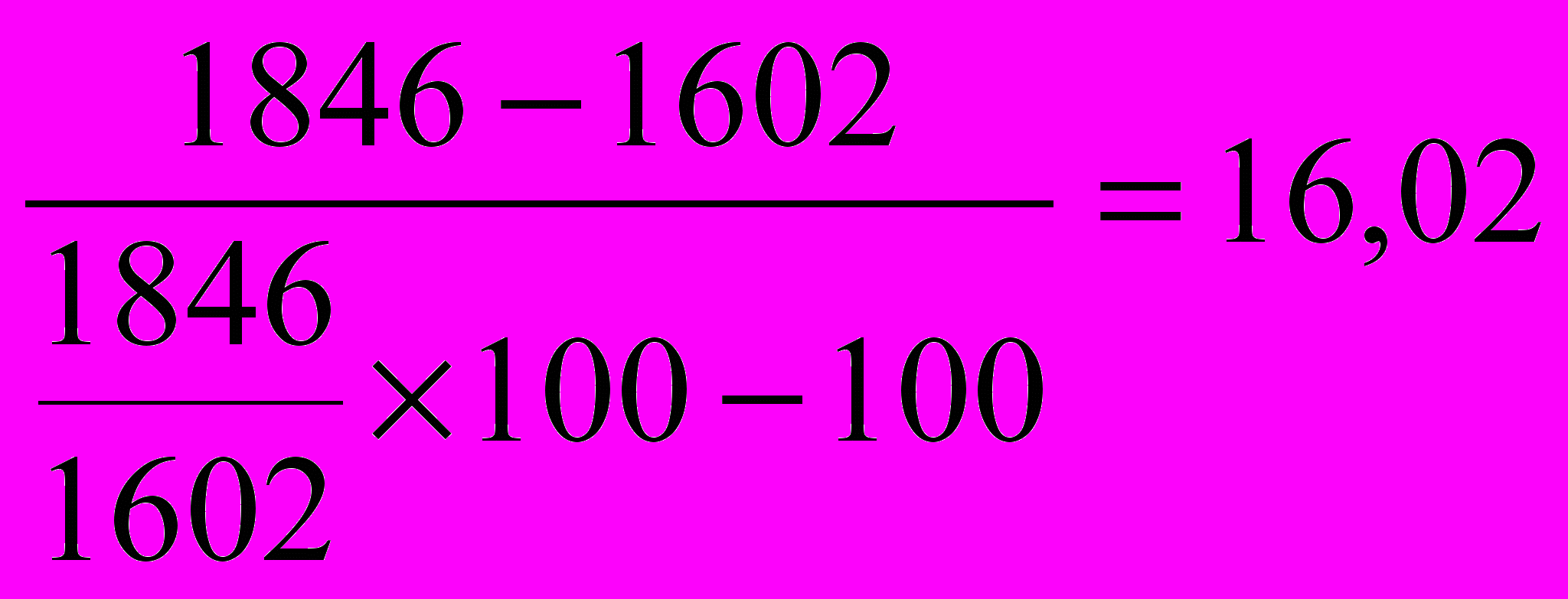 . . |
| | Определите правильный способ вычисления среднего темпа роста численности работников предприятия, если известна динамика среднегодовой численности работников предприятия: 2000 г. – 1180 чел, 2001 г. – 1250 чел., 2002 г. – 1243 чел., 2003 г. – 1315 чел., 2004 г. – 1396чел. а) 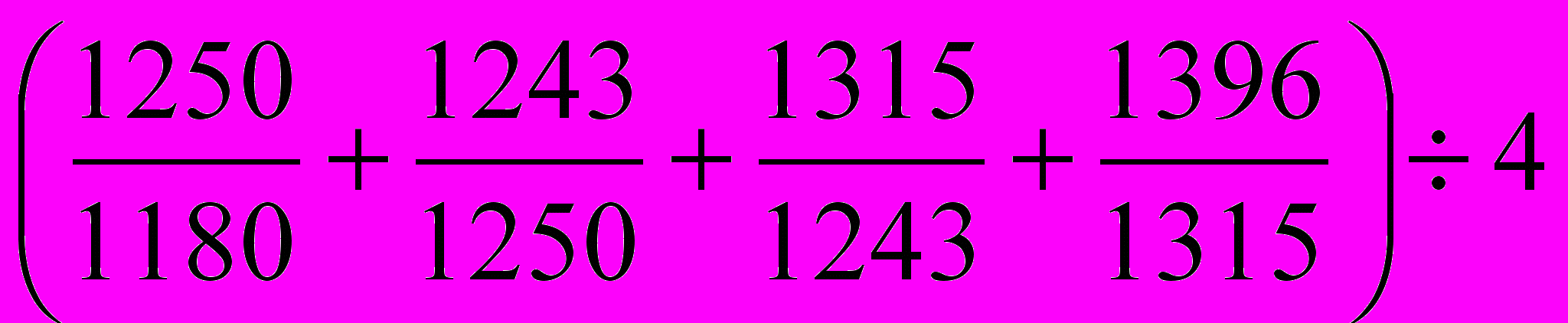 ; ;б) 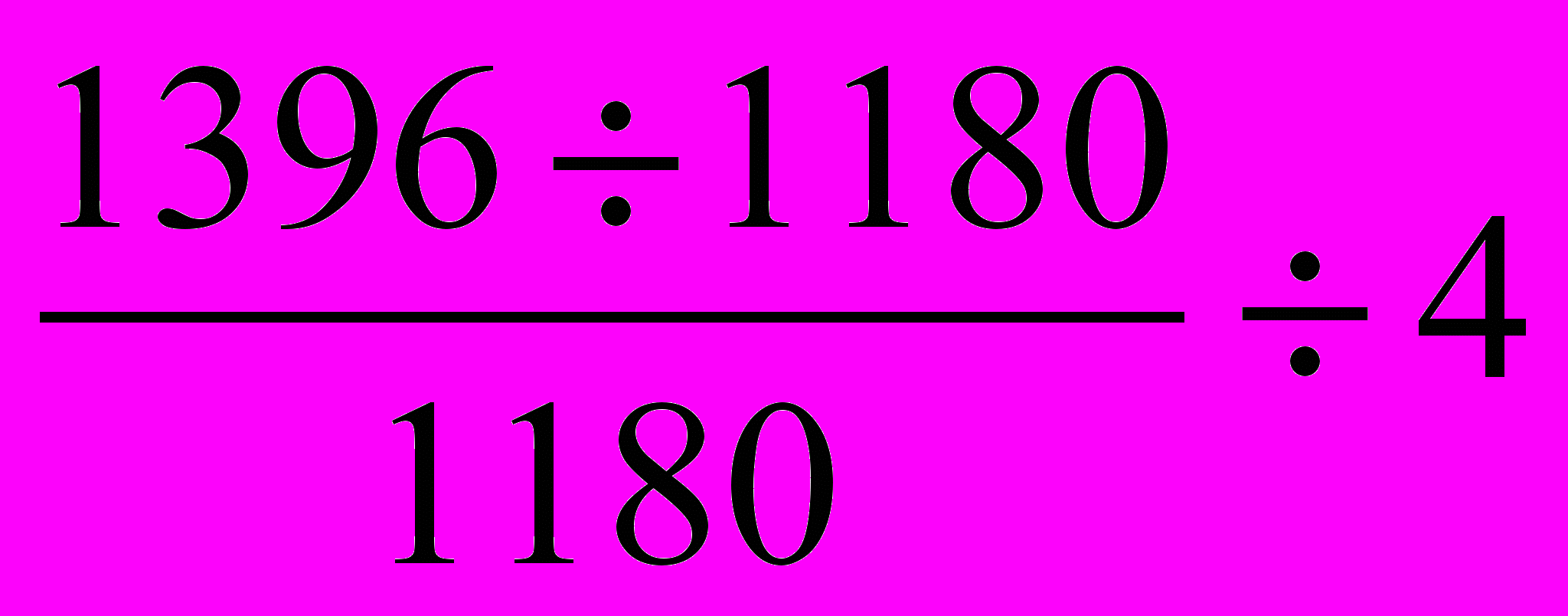 ; ;в) 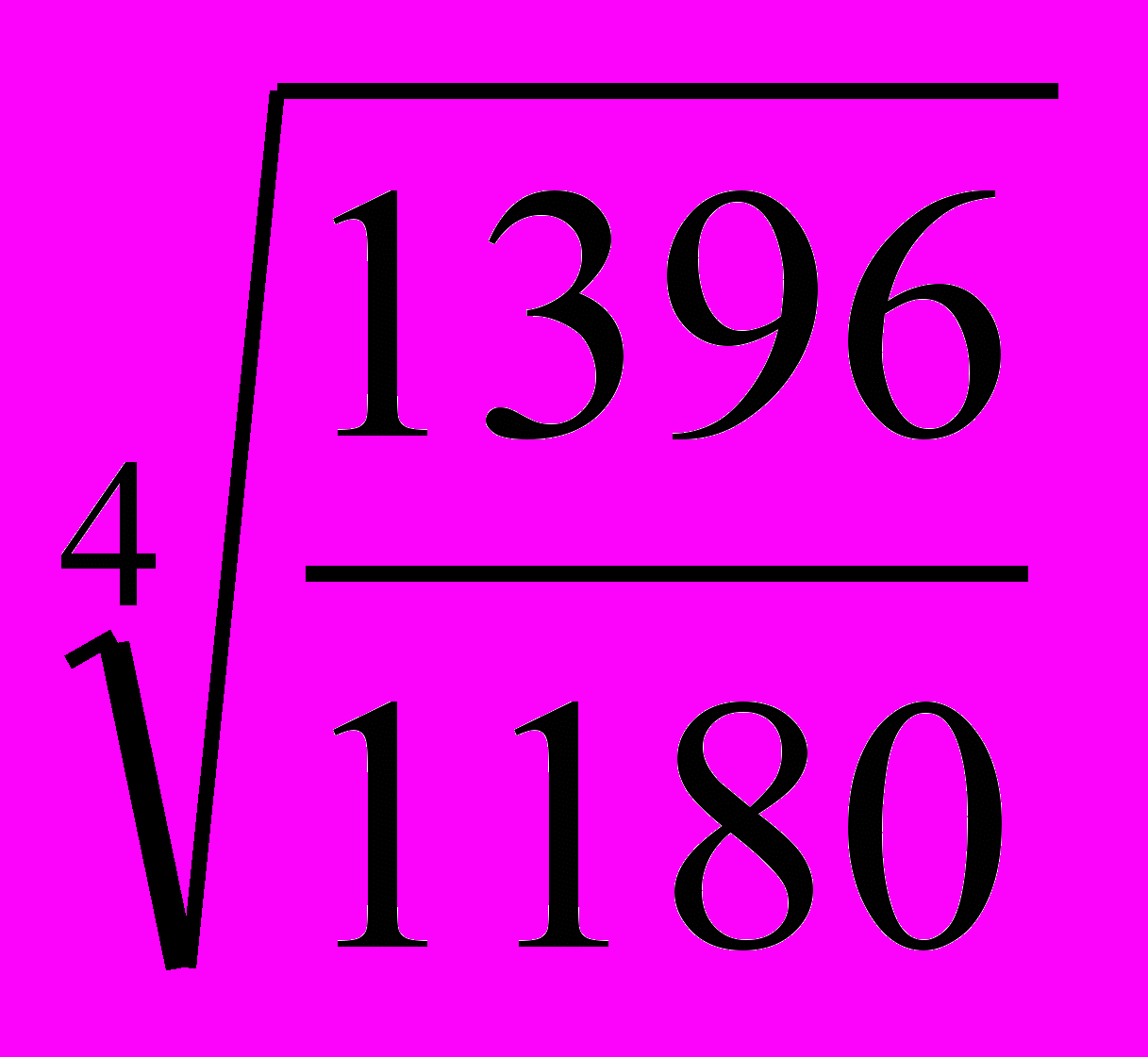 ; ;г) 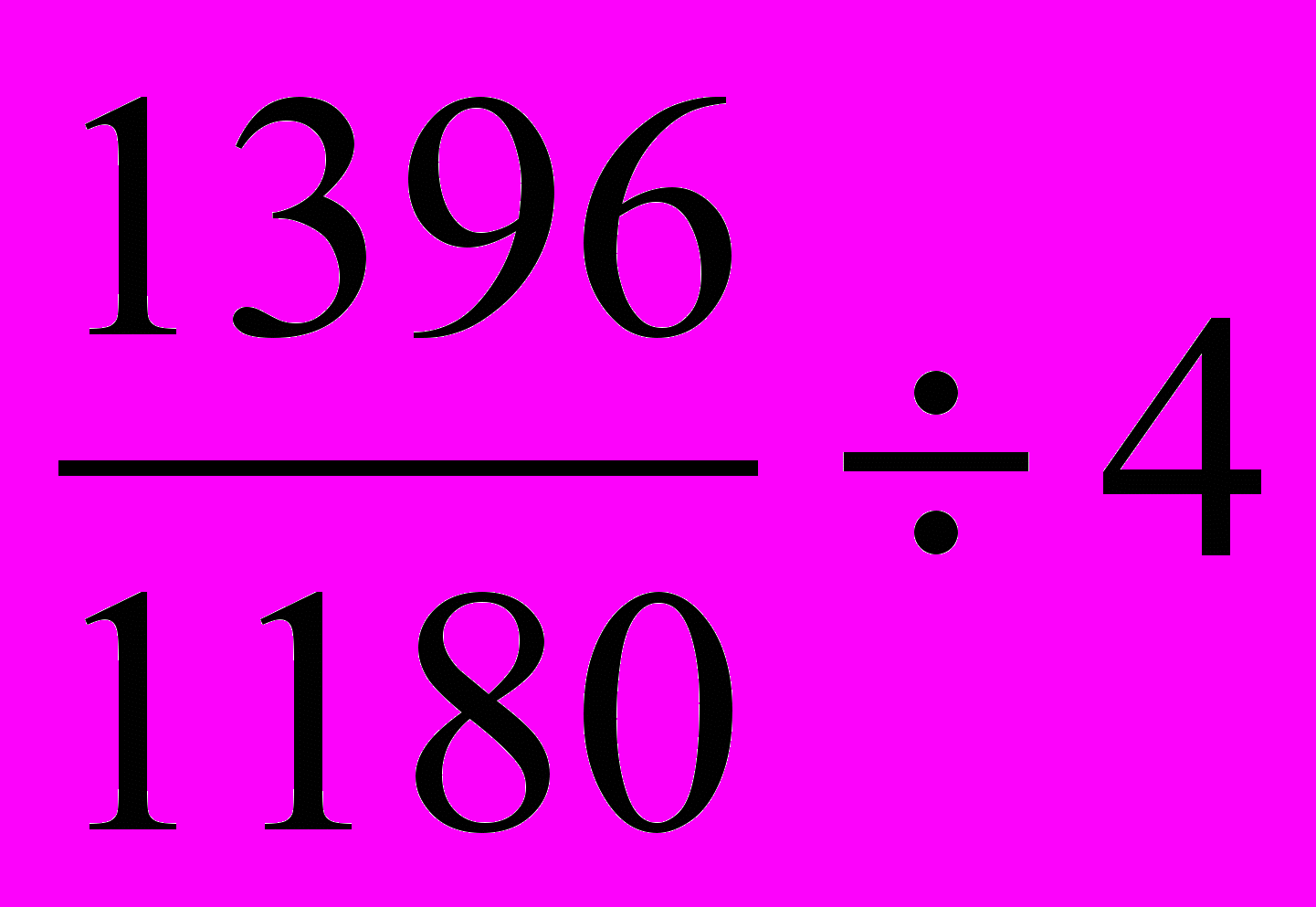 . . |
| | |
| | Какой из способов вычисления среднегодовой численности установленного оборудования методически является наиболее обоснованным, если задан ряд динамики о численности единиц установленных в цехе шлифовальных станков на начало каждого месяца: а) 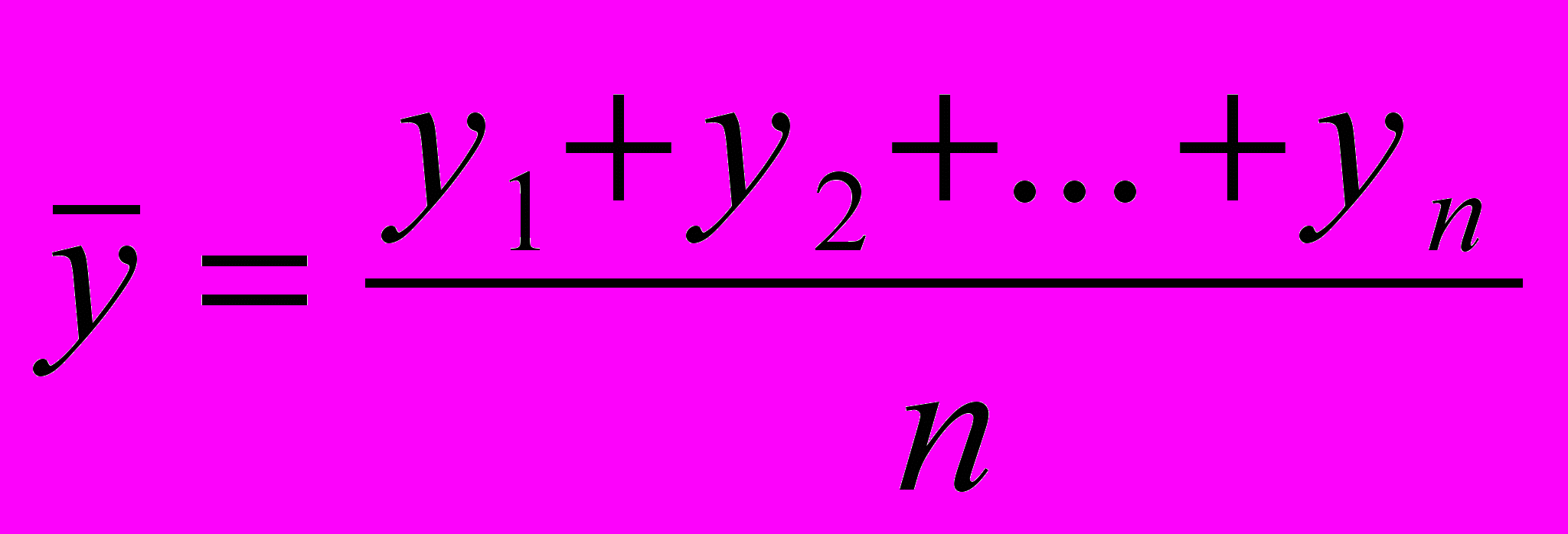 ; ;б) 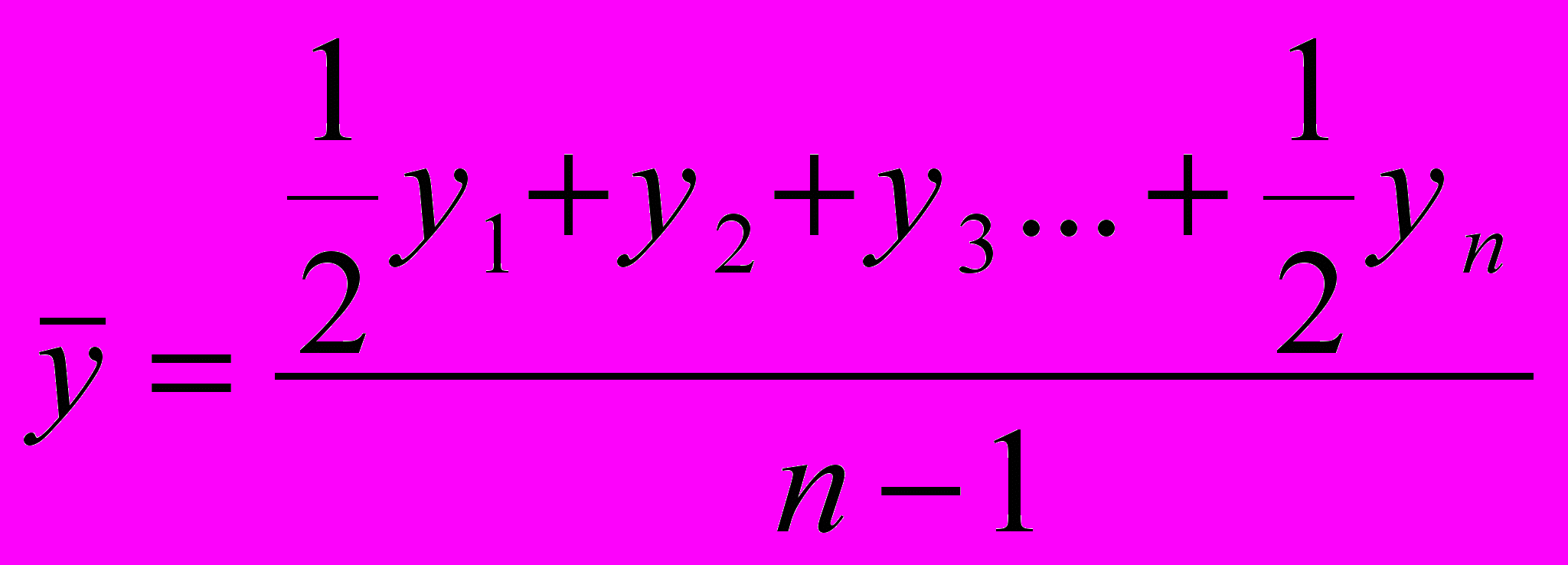 ; ;в) 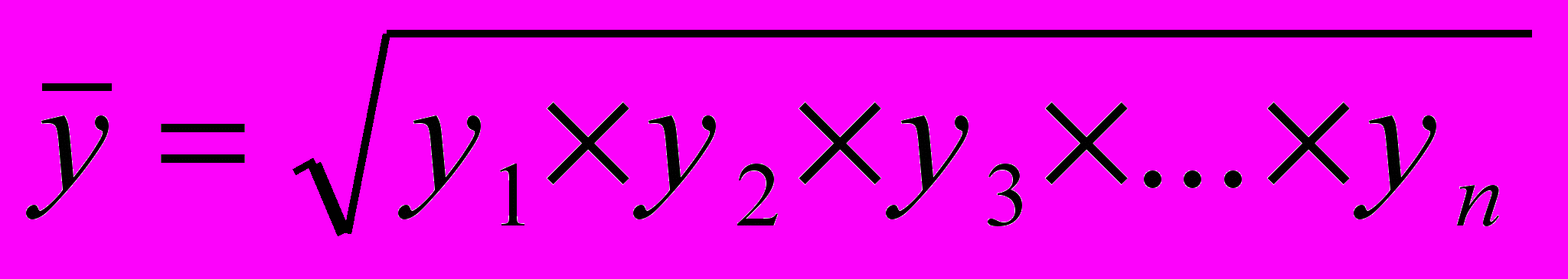 ; ;г) 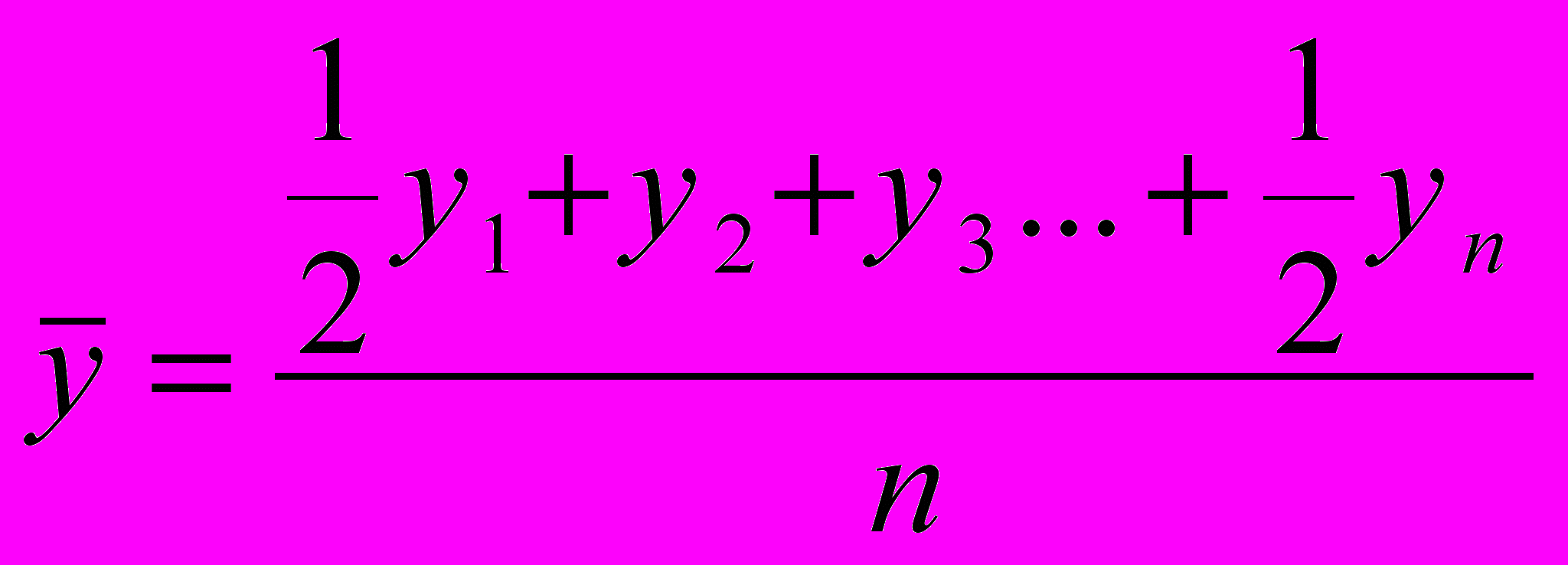 . . |
| | Индексы позволяют соизмерить социально-экономические явления: а) в пространстве; б) во времени; в) в пространстве и во времени. |
| | Можно ли утверждать, что индивидуальные индексы динамики по методологии исчисления адекватны темпам роста? а) можно; б) нельзя. |
| | Сводные индексы позволяют получить обобщающую оценку изменения: а) по товарной группе; б) одного товара за несколько периодов. |
| | Является ли средней арифметической индекс разновидностью агрегатной формы индексов? а) является; б) не является. |
| | Может ли в отдельных случаях средний гармонический индекс рассчитываться по средней гармонической невзвешанной? а) может; б) не может. |
| | В составе следующих выражений укажите наличие расчета индекса цен в среднегармонической форме: а) 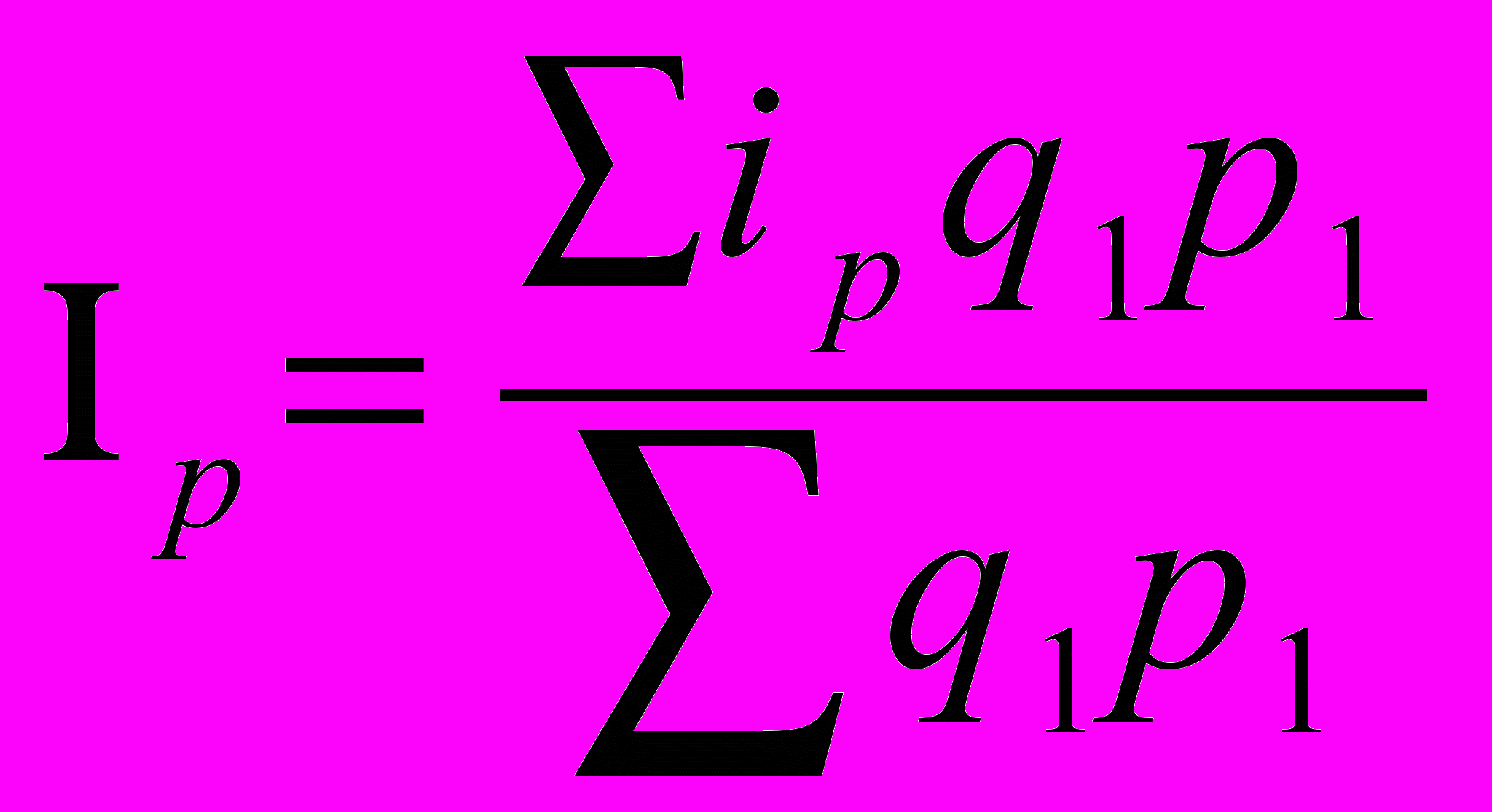 ; ;б) 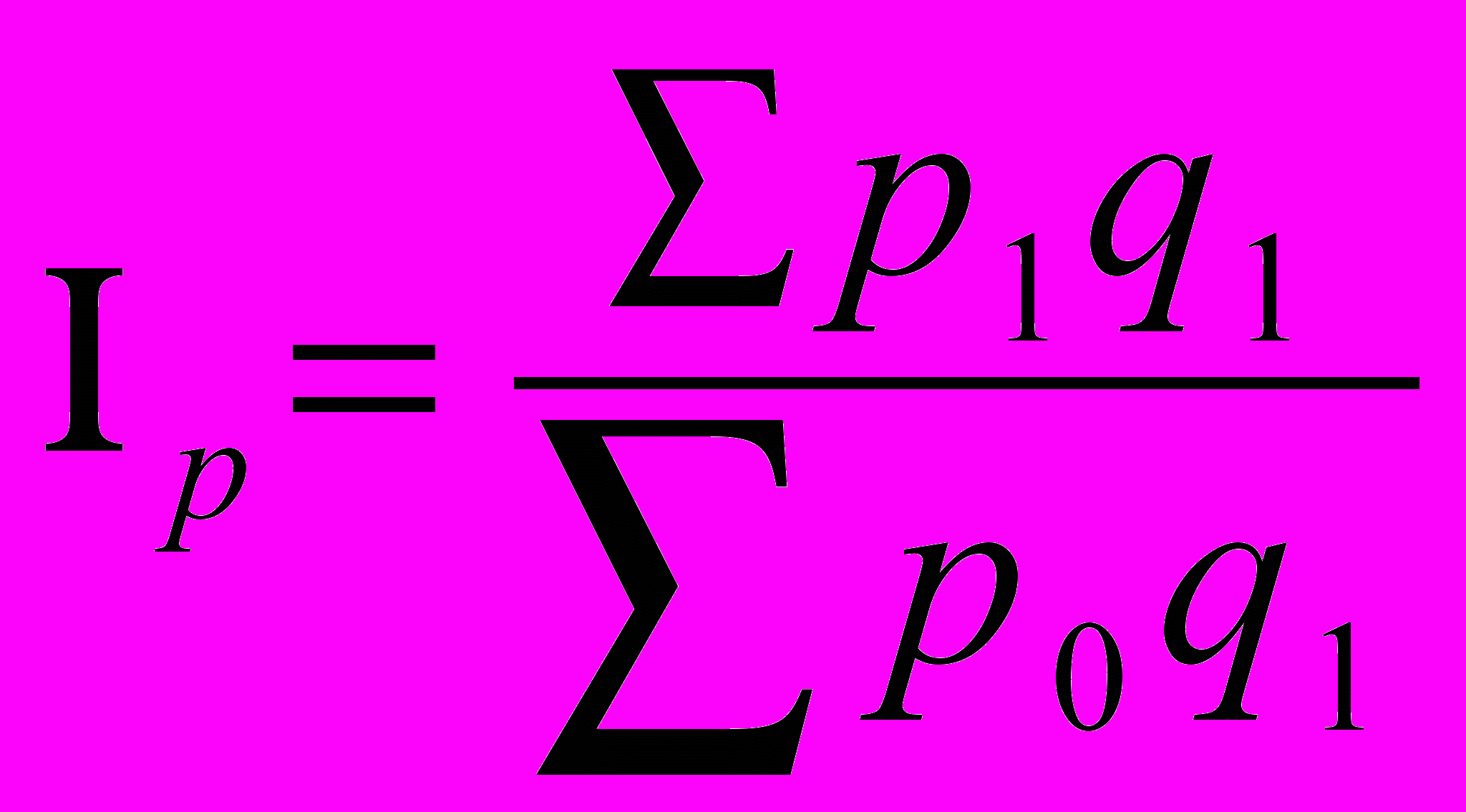 ; ;в) 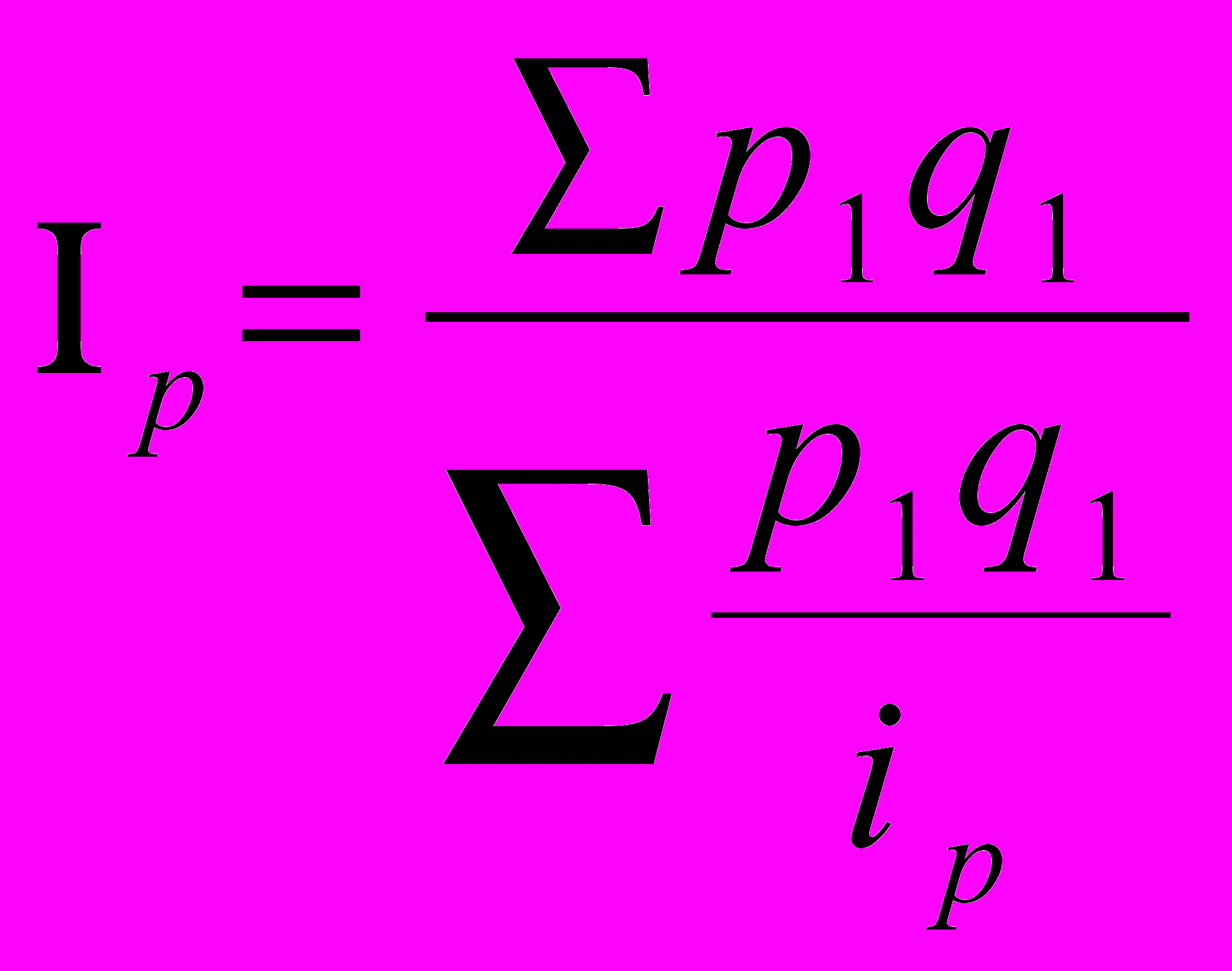 ; ;г) иное выражение. |
| | Укажите, какой из формул необходимо воспользоваться для вычисления индекса физического объема реализации при наличии данных об индексе товарооборота и индекса цен: а) 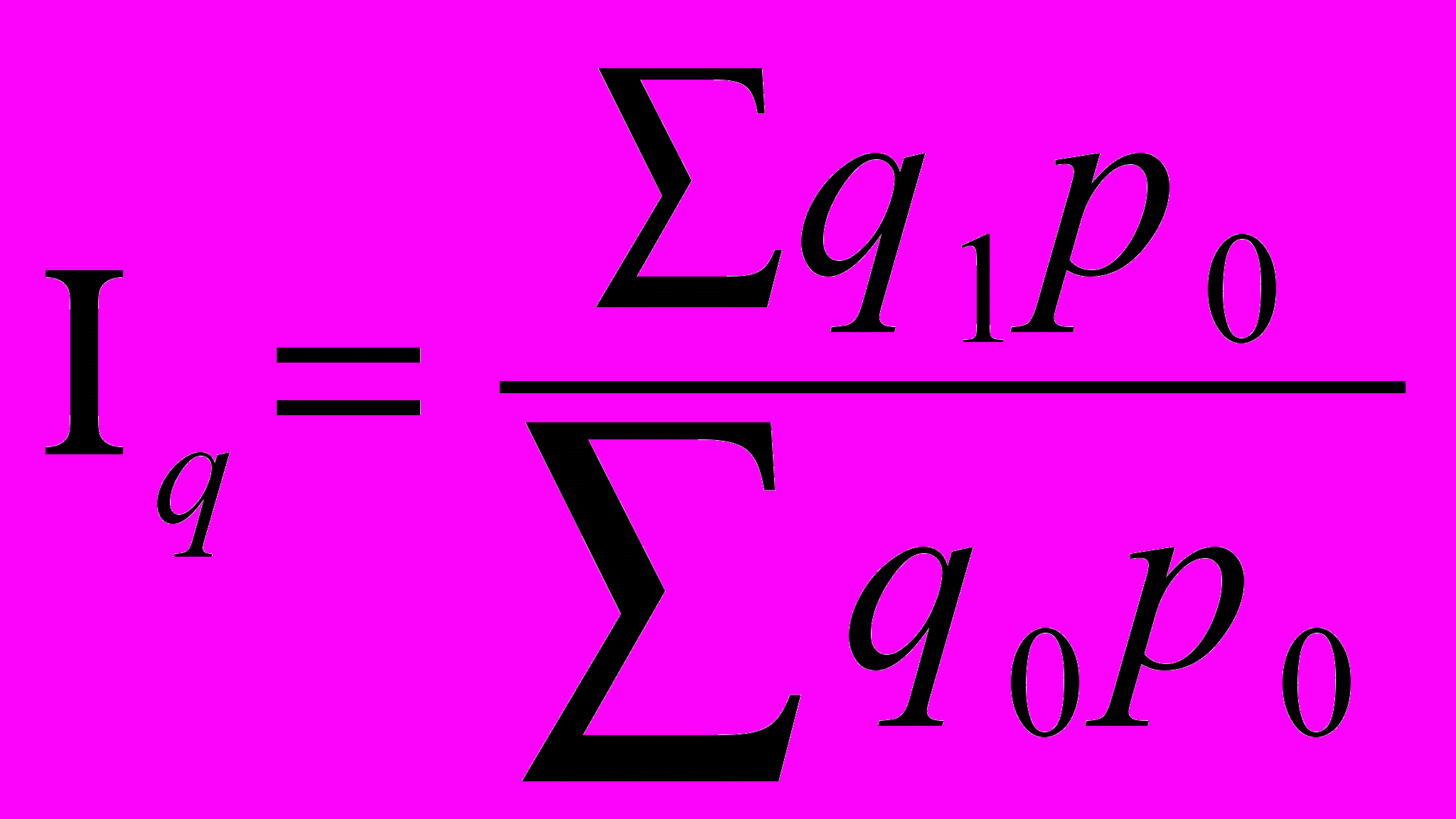 ; ;б) 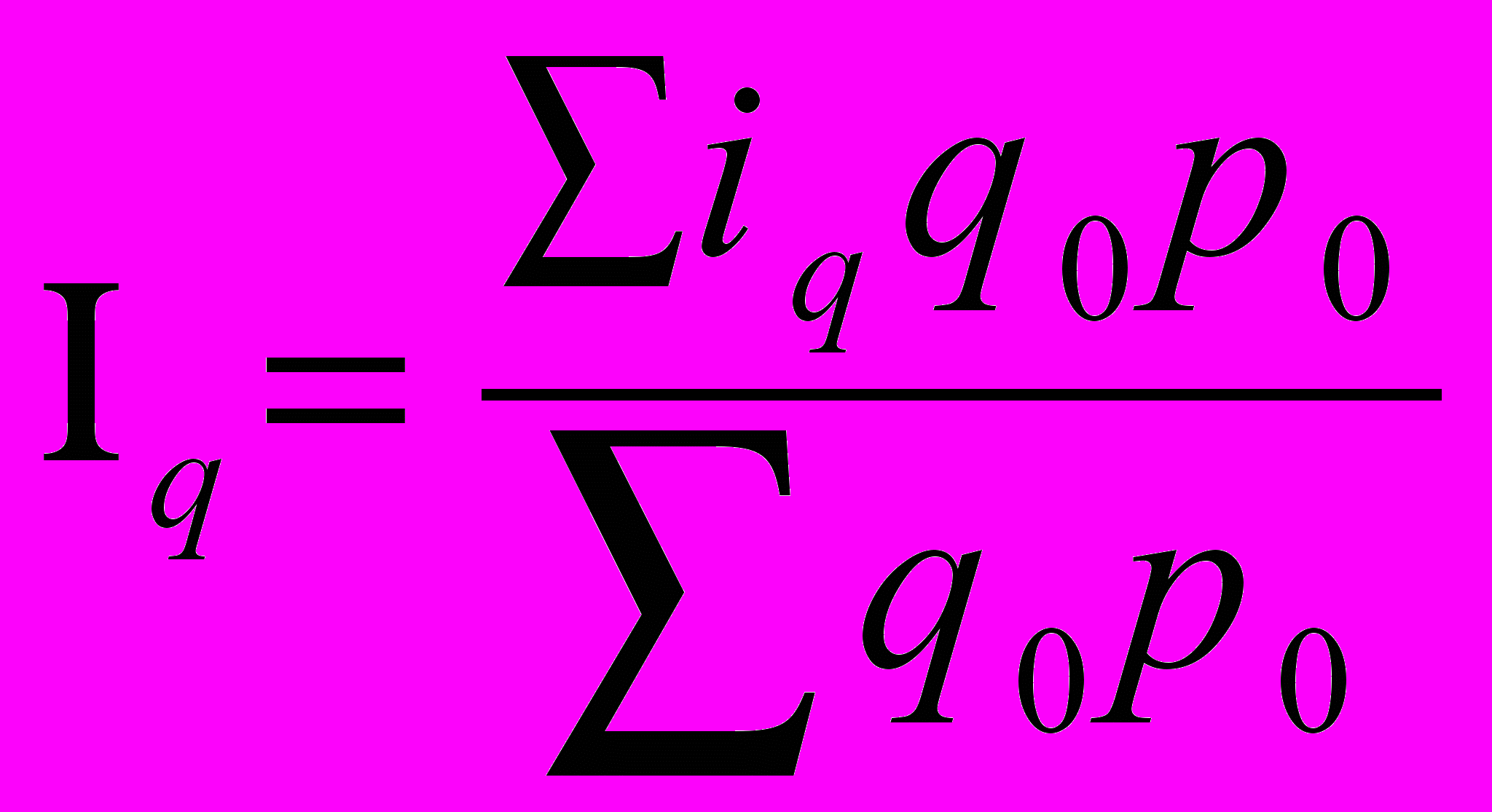 ; ;в) 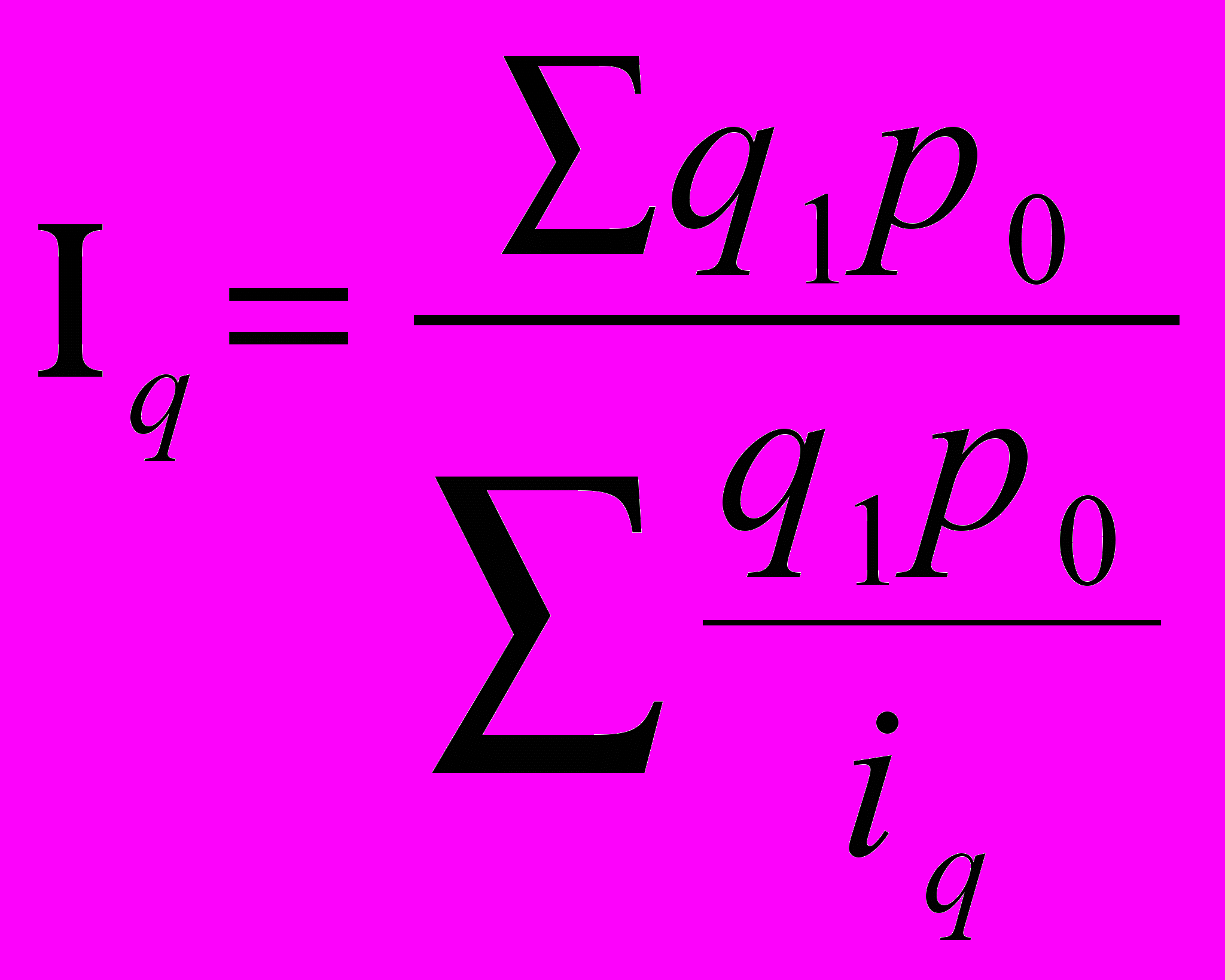 ; ;г) 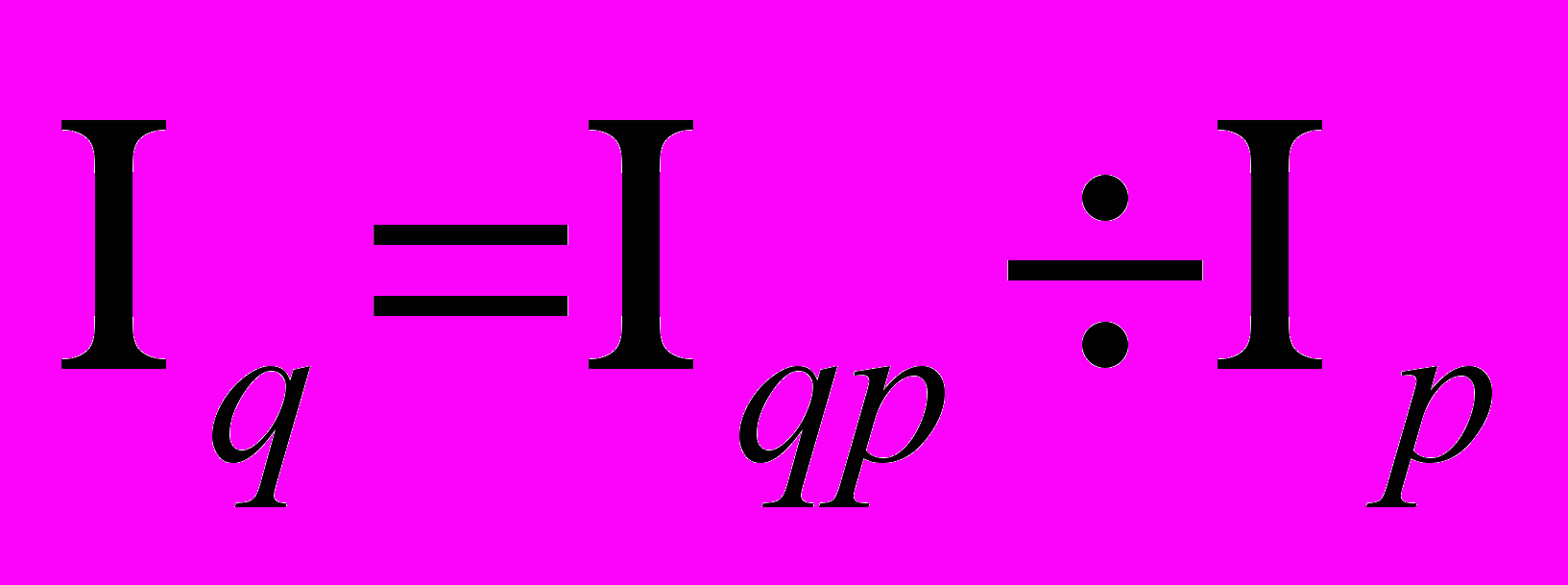 . . |
