Geum.ru

Тест основан на расчете d  статистики:, Расчетная величина

Вид материалаДокументы

Содержание


Тест серий (Бреуша-Годфри)
Тест Бокса-Пирса
Тест Бокса-Льюинга
Методы устранения автокорреляции
2. Метод Кохрана—Оркатта
3. Метод Хилдрета—Лу
Подобный материал:
Статистика Дарбина-Уотсона


Статистика Дарбина-Уотсона предназначена для обнаружения автокорреляции первого порядка. Кроме того, уравнение регрессии должно иметь постоянный член и не содержать лаговую зависимую переменную в качестве факторной переменной

Тест основан на расчете d статистики: ,

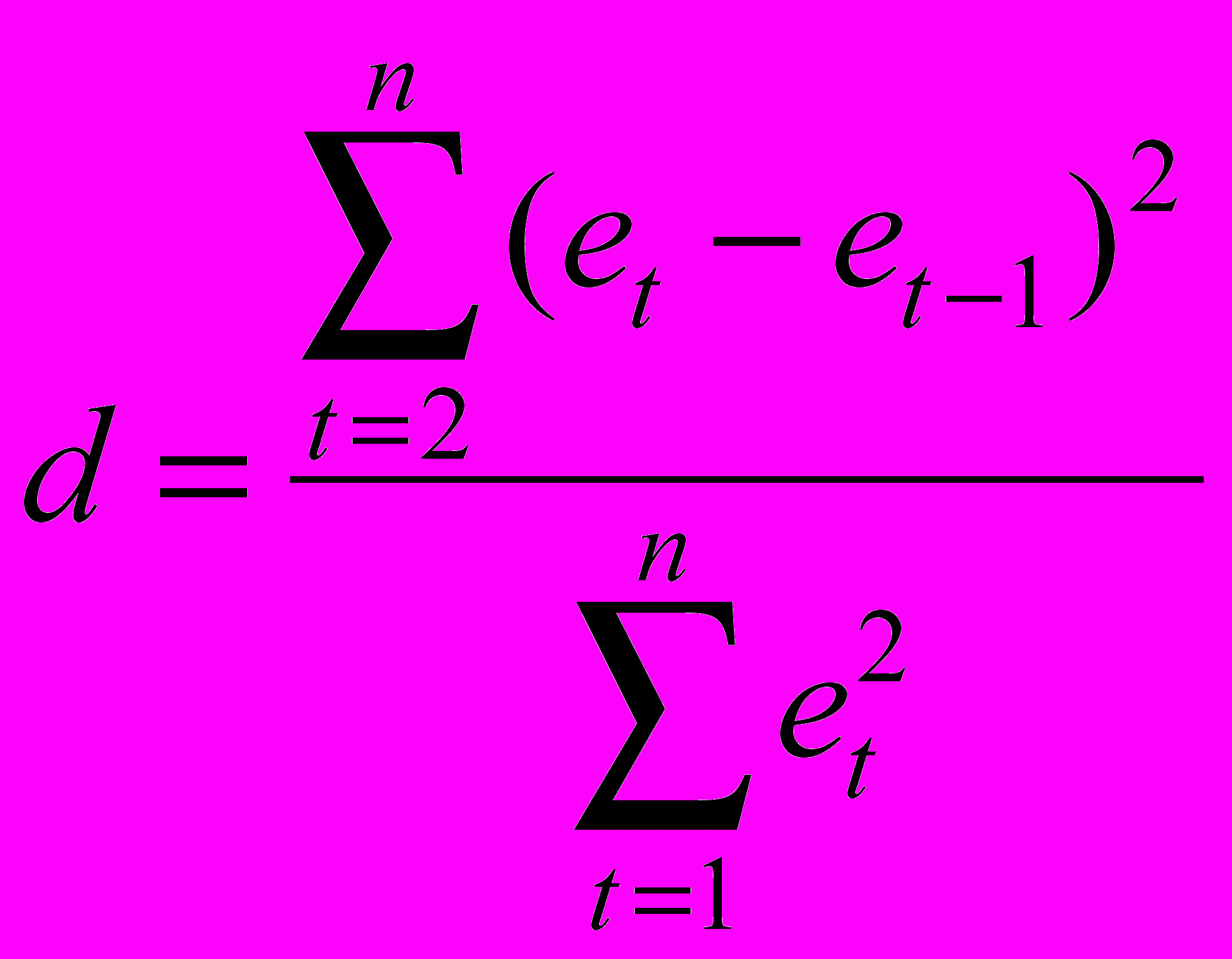Расчетная величина d сравнивается с двумя табличными уровнями d1 и d2

Возможные случаи

Величина статистики D
Результат



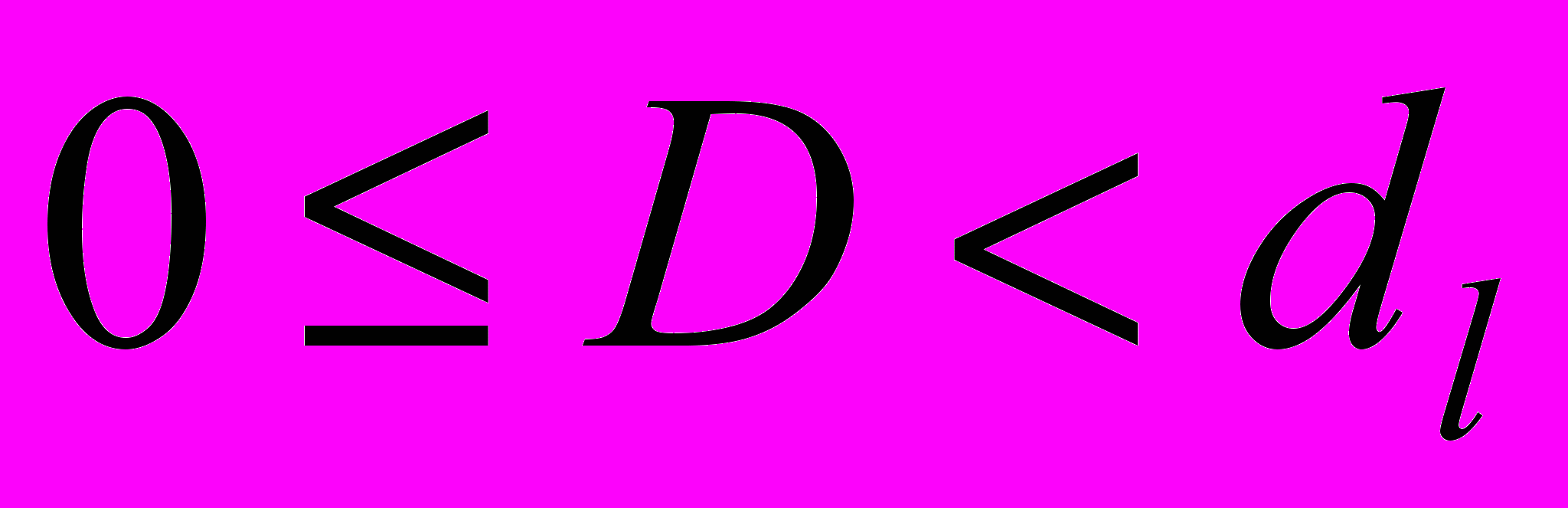Присутствует положительная автокорреляция



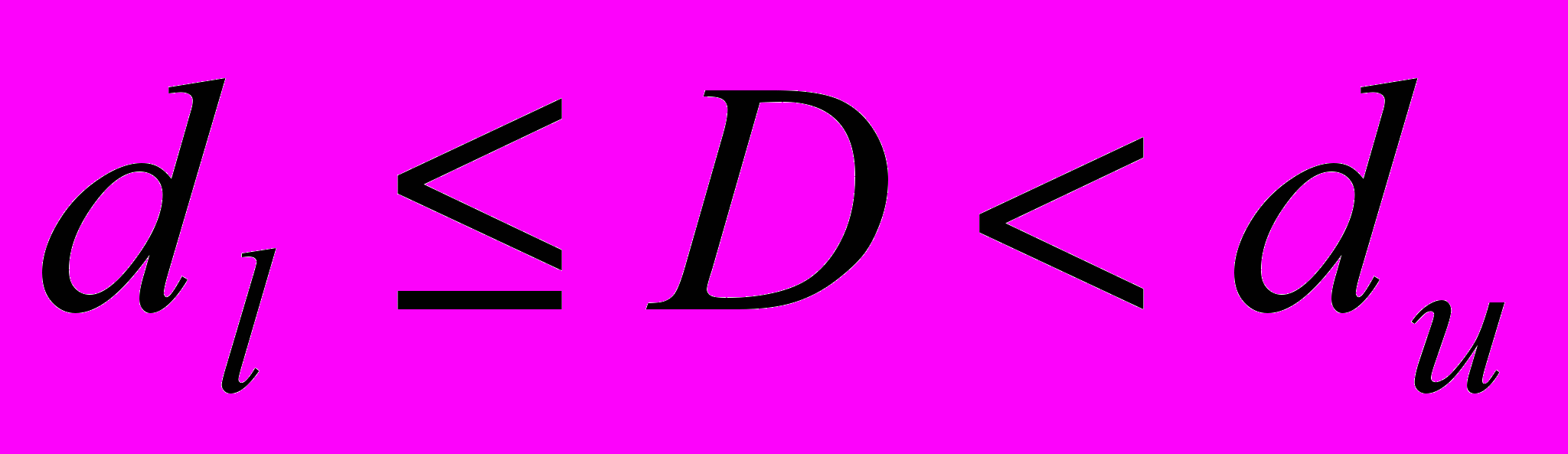Результат неопределенный.



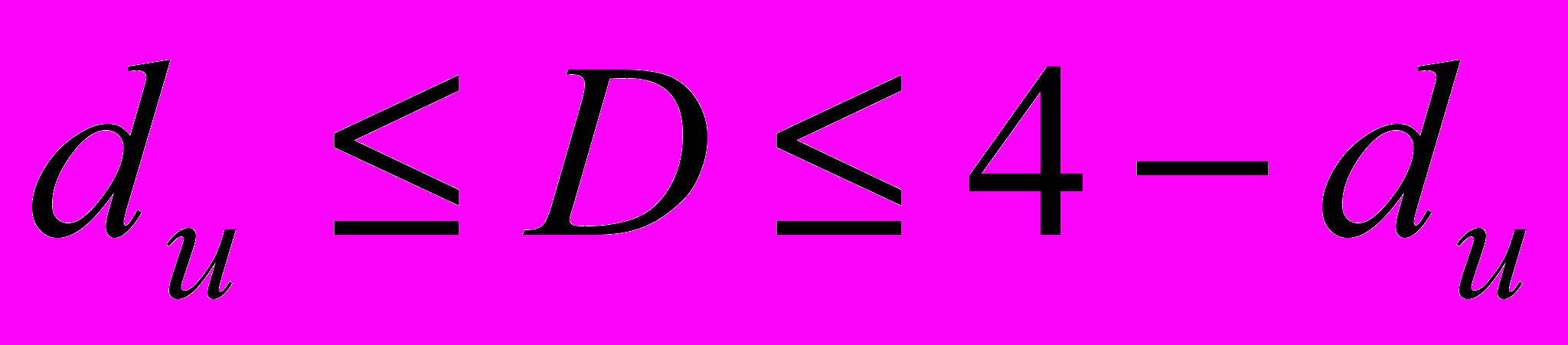Автокорреляция отсутствует



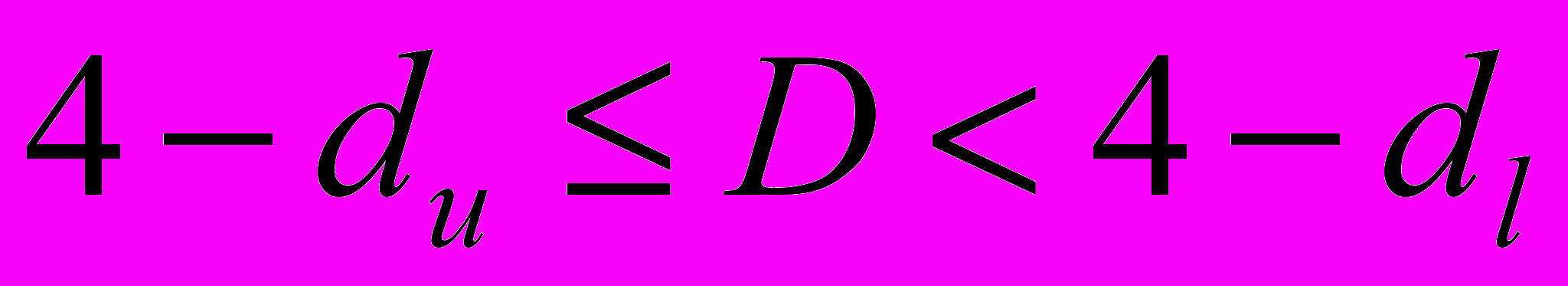Результат неопределенный



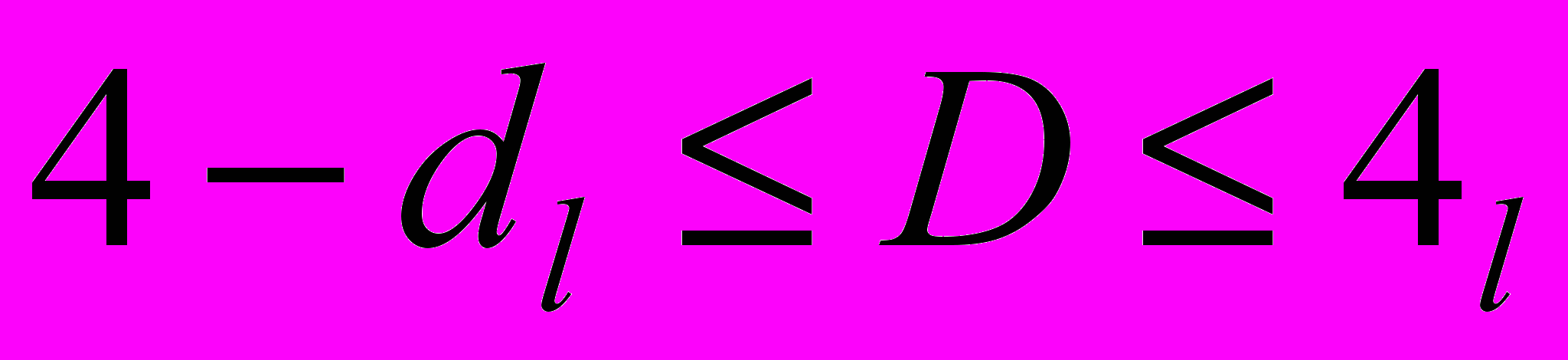Присутствует отрицательная автокорреляция



Тест серий (Бреуша-Годфри)


Тест основан на следующей идее: если имеется корреляция между соседними наблюдениями, то естественно ожидать, что в уравнении

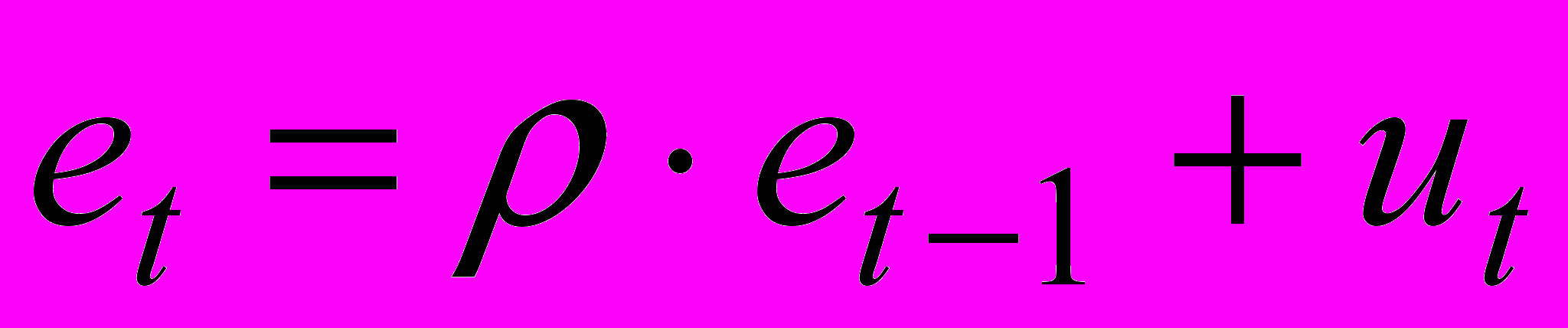, где 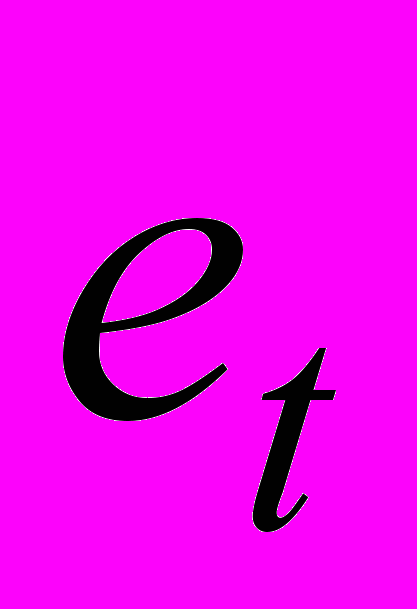- остатки, полученные обычным МНК, коэффициент окажется статистически значимым.

Преимуществом этого теста является возможность обобщения : в число регрессоров могут быть включены не только остатки с лагом 1, но с лагом 2,3 и т.д. Критерий может быть применен при попадании в зону неопределенноси критерия Дарбина-Уотсона.

Тест Бокса-Пирса

Проверяет гипотезу о совместном равенстве нулю всех коэффициентов автокорреляции временного ряда до порядка т включительно, т.е. гипотезу 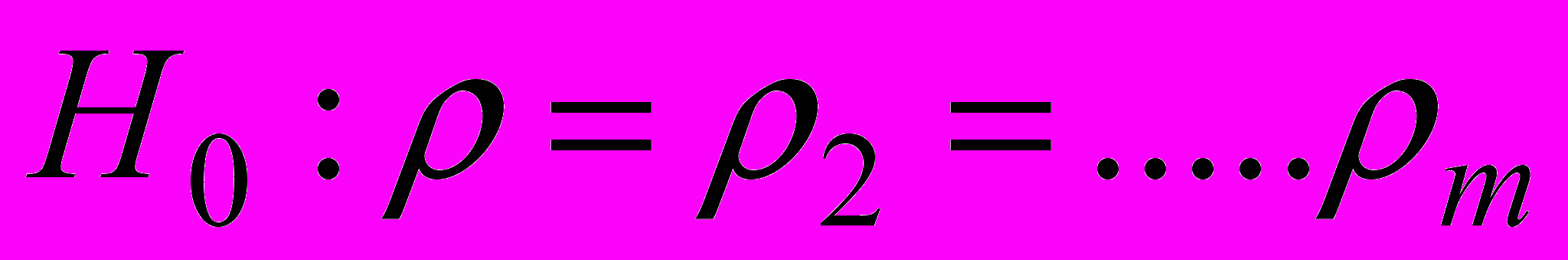против альтернативной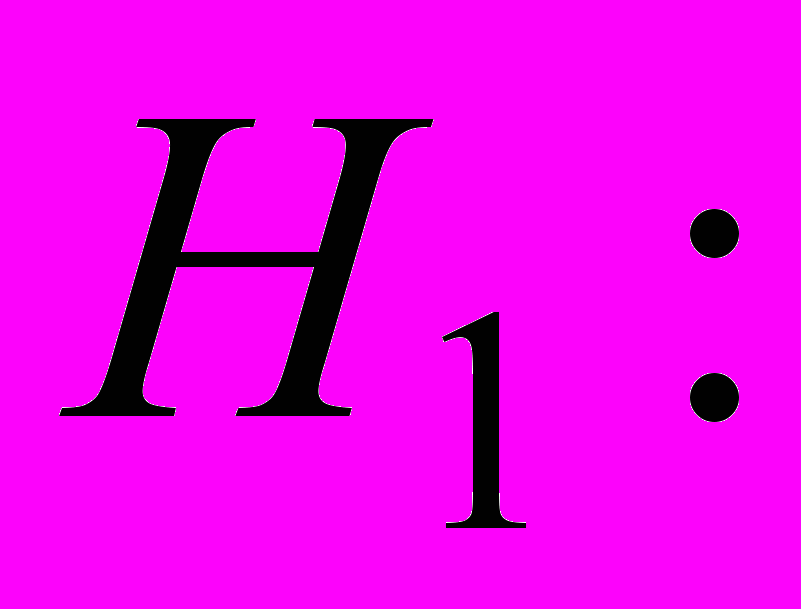

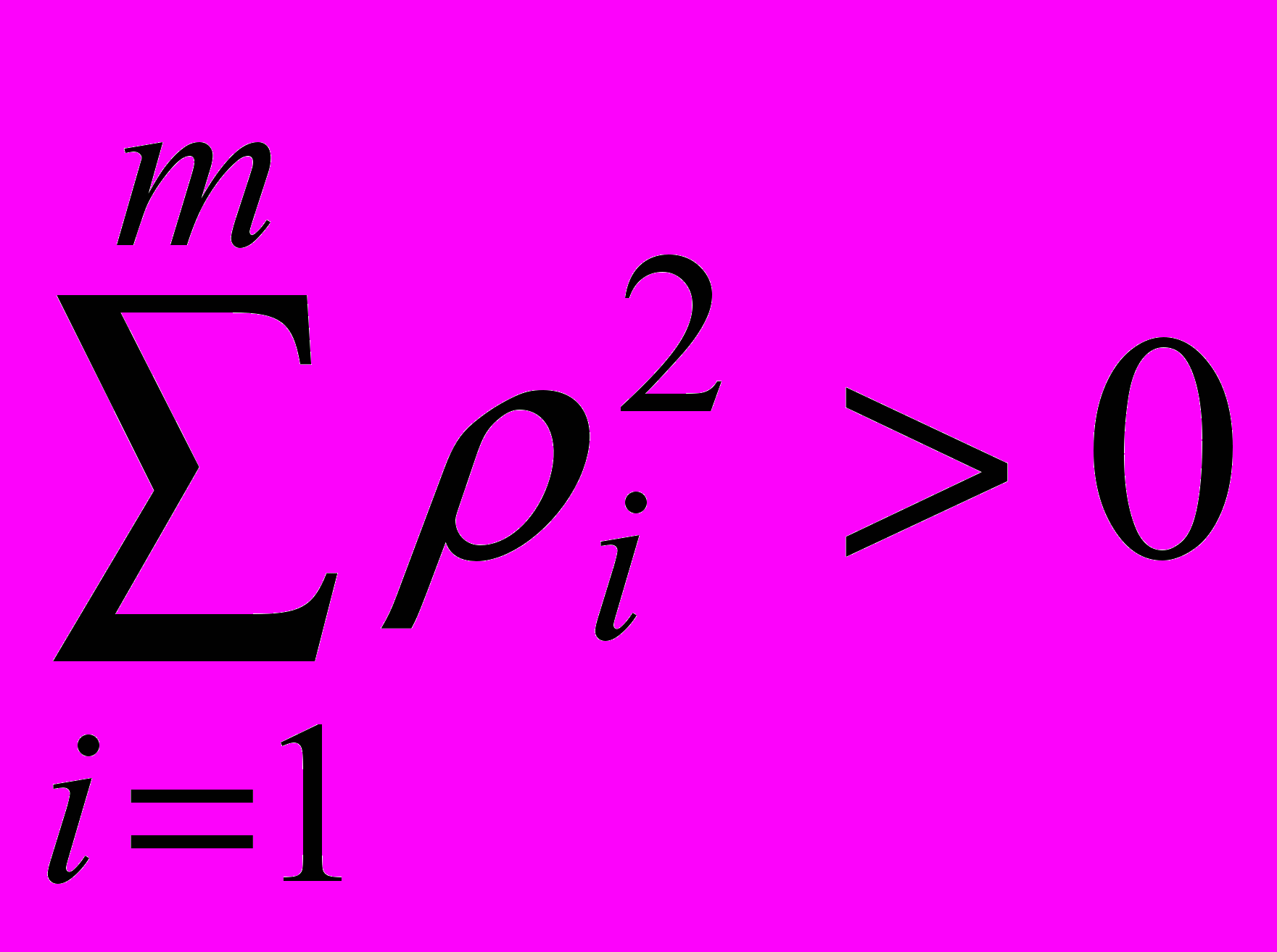
Рассчитывается статистика 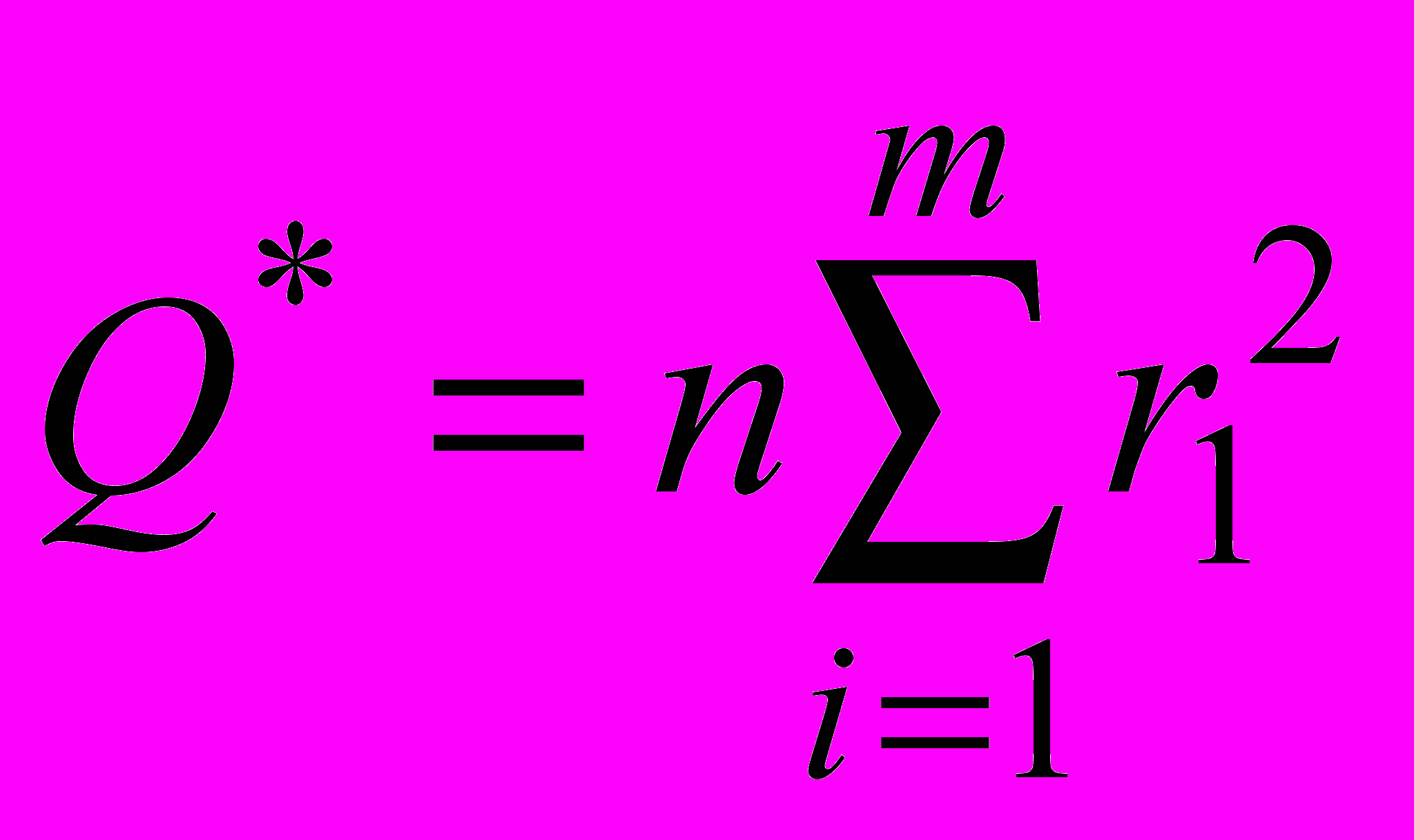,где 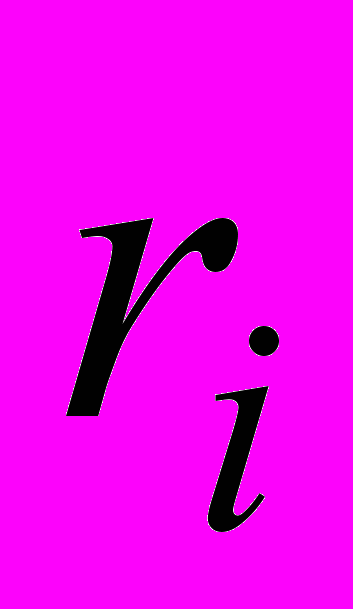- выборочные коэффициенты автокорреляции

Доказано, что при увеличении длины выборки статистика имеет асимптотическое распределение 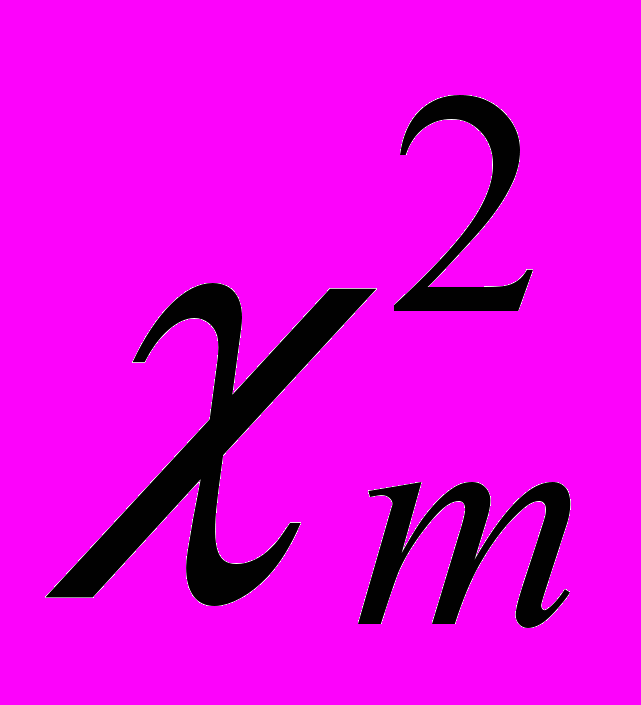. Если 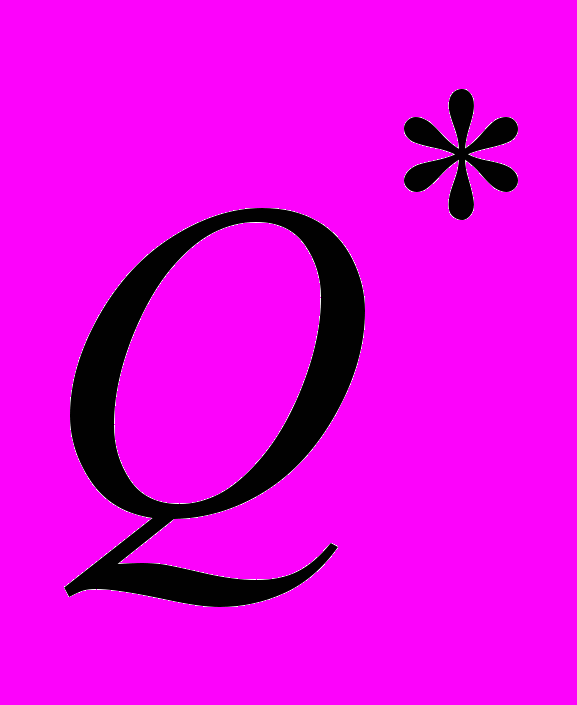превосходит критическое значение 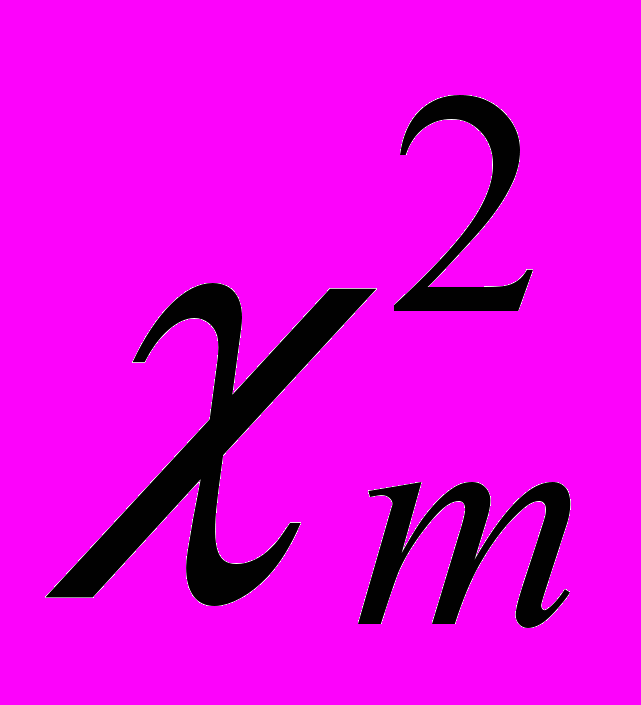, то нулевая гипотеза отвергается и ряд остатков автокоррелирован.

Тест Бокса-Льюинга


Рассчитывается статистика

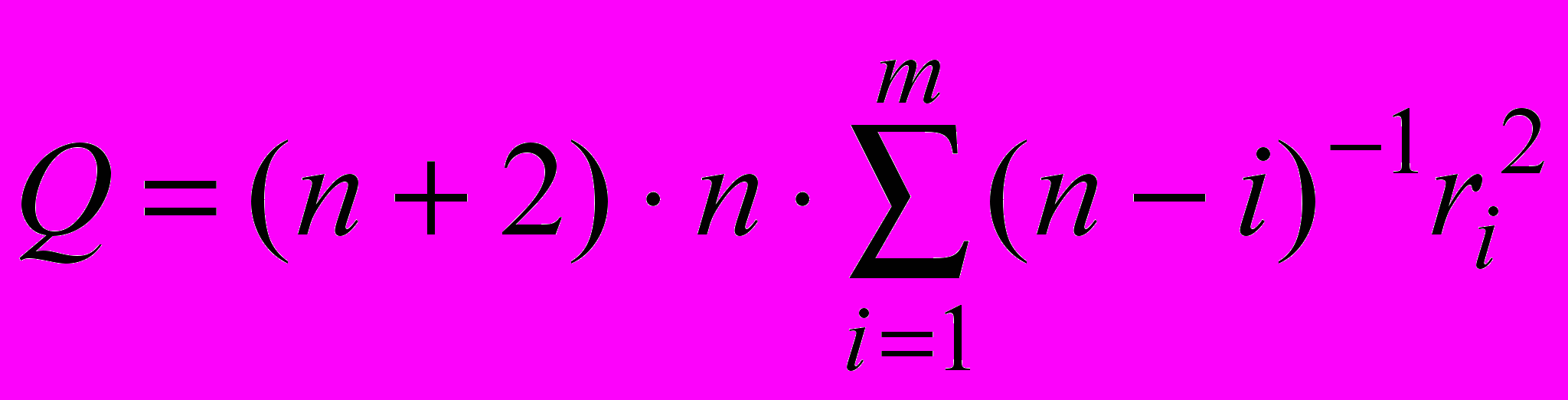
По сравнению со статистикой Бокса-Пирса различным слагаемым приданы разные веса. Доказано, что эта статистика имеет также асимптотическое распределение 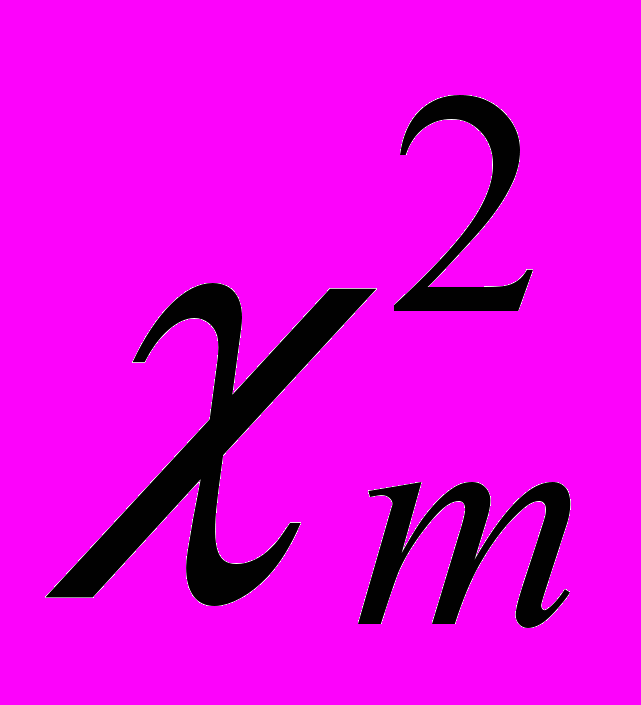, но лучше им аппроксимируется при конечном числе наблюдений.

Если расчетное значение статистики Бокса и Льюнга превосходит критическое значение 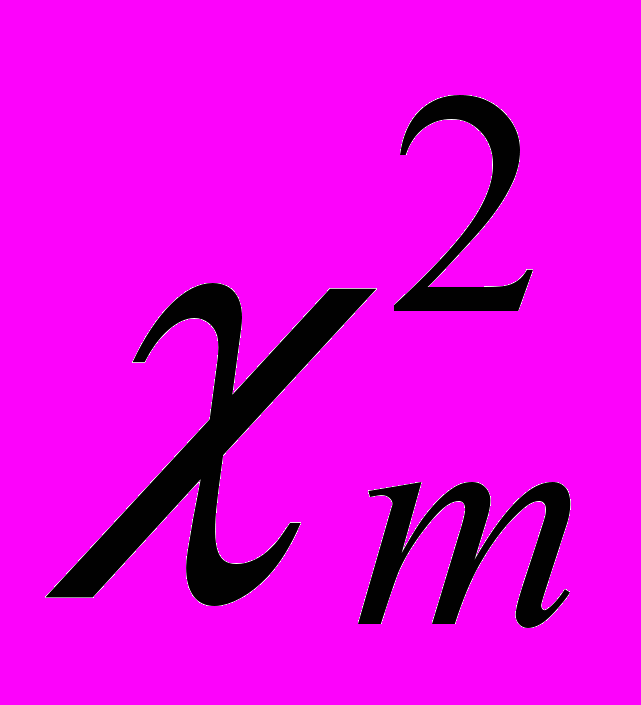, то признается наличие автокорреляции (до 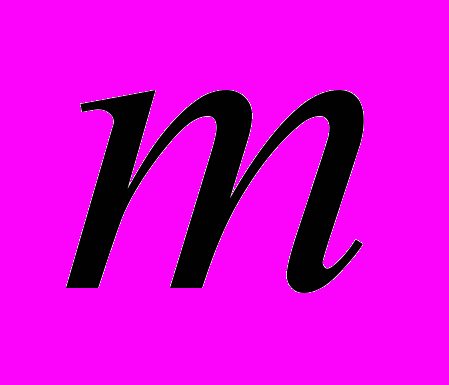-го порядка) в ряду остатков.

Метод множителей Лагранжа
  • Методом МНК строится обычная регрессия вида

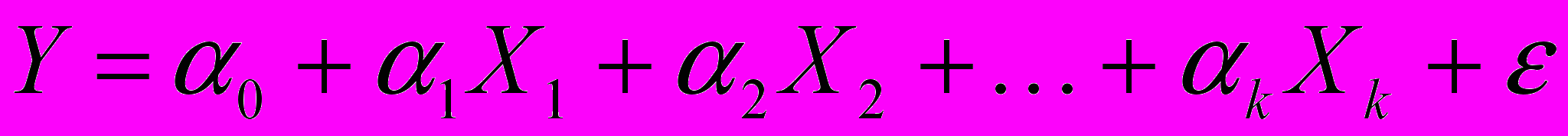. Обозначим остатки ее оценочной модели через .
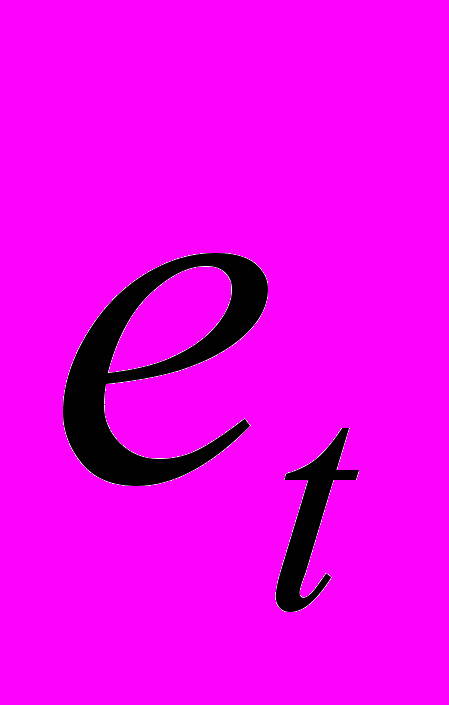  • Строится регрессия либо той же объясняемой переменной 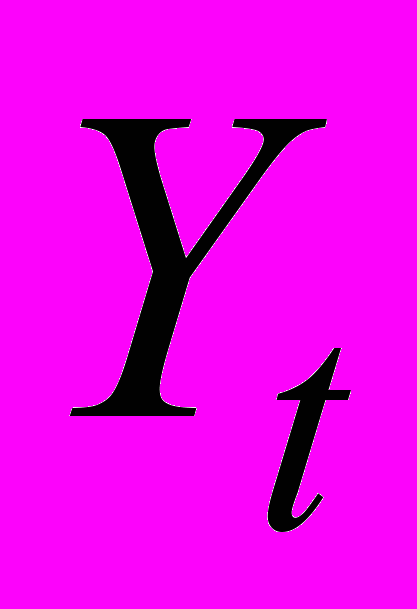, либо остатков 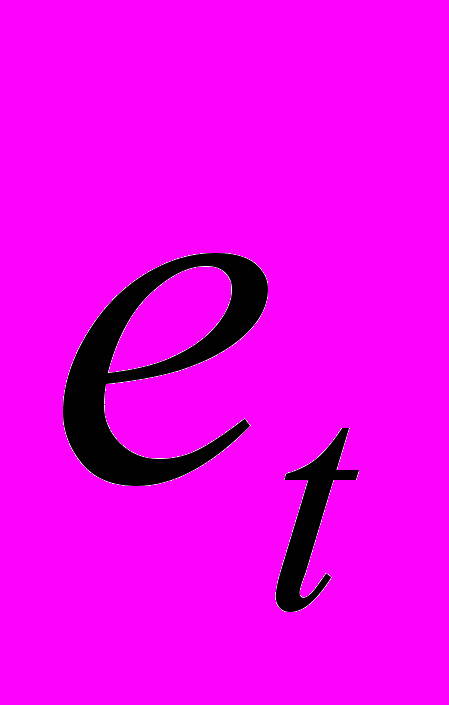на старые регрессоры и остатки с лагом до р включительно (то есть в качестве дополнительных объясняющих переменных используем ()
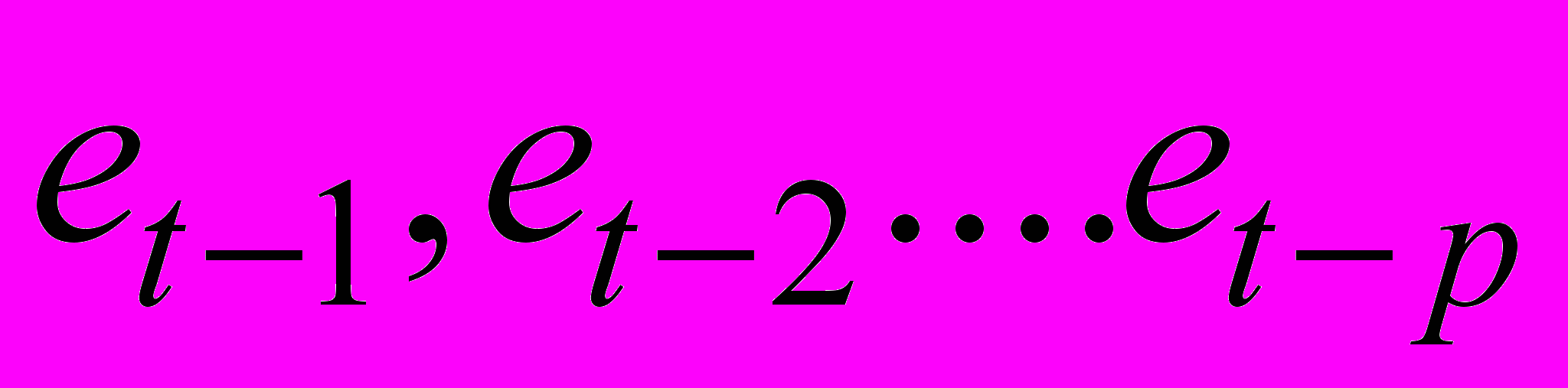  • Проверяется гипотеза о том, что группа дополнительных переменных является излишней,
  • Если в качестве объясняемой переменной используются остатки, то статистика U= где - число наблюдений, a — коэффициент множественной детерминации имеет асимптотическое (при увеличении числа наблюдений) распределение с р степенями свободы.

Если то гипотеза об отсутствии автокорреляции отвергается

Для проверки гипотезы о равенстве нулю группы переменных можно использовать F-

статистику, но только при нормальном распределении случайного члена.

Применение же теста множителей Лагранжа не требует нормальности распределения.


Методы устранения автокорреляции

Воспользуемся авторегрессионным преобразованием. В линейной регрессионной модели либо в моделях, сводящихся к линейной, наиболее целесообразным и простым преобразованием является авторегрессионная схема первого порядка AR(1).

Для простоты изложения AR(1) рассмотрим модель парной линейной регрессии. (1)

Тогда наблюдениям 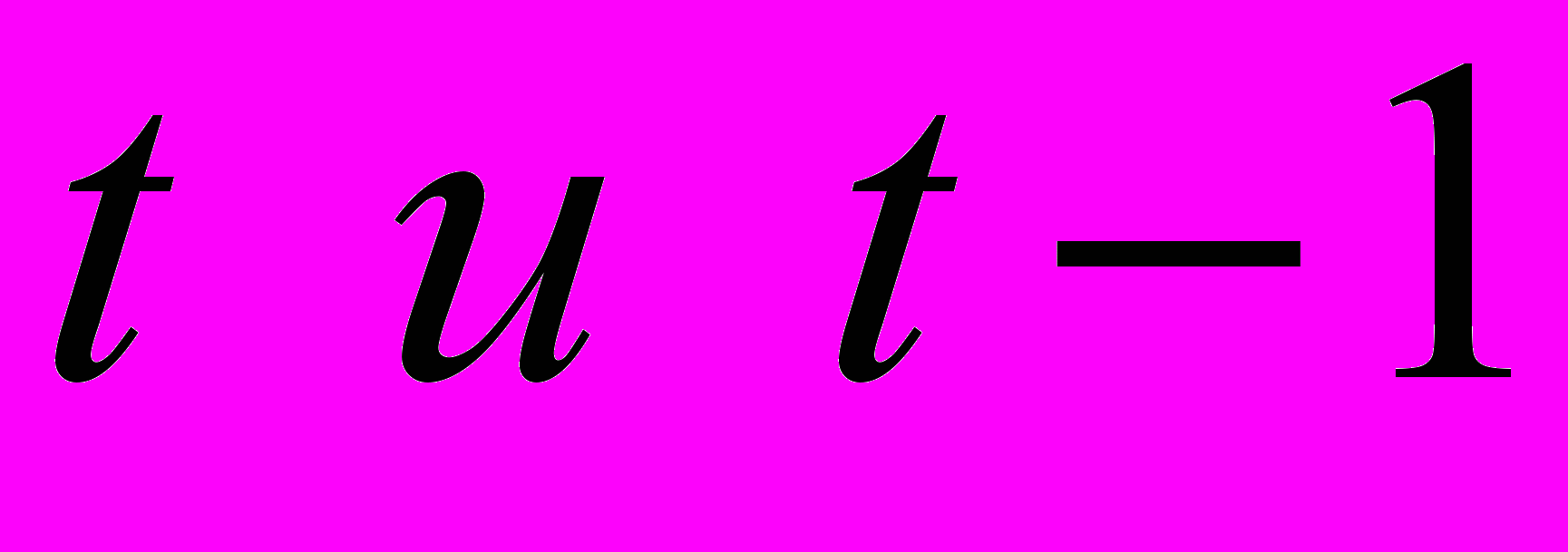соответствуют уравнения:

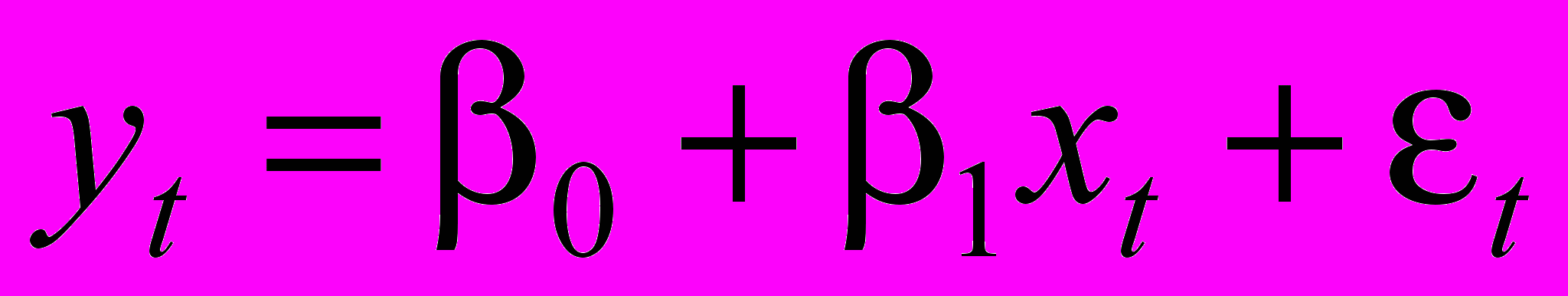(2)

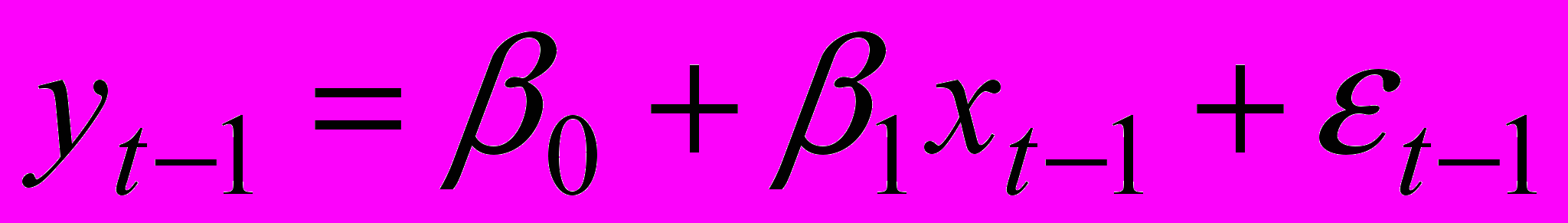(3)

Пусть случайные отклонения подвержены воздействию авторегрессии первого порядка:

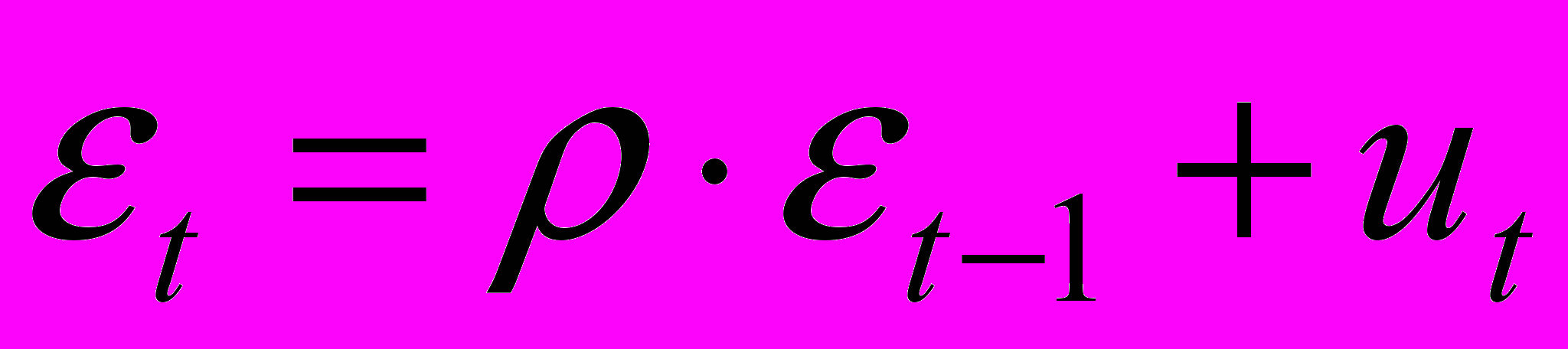(4)

где 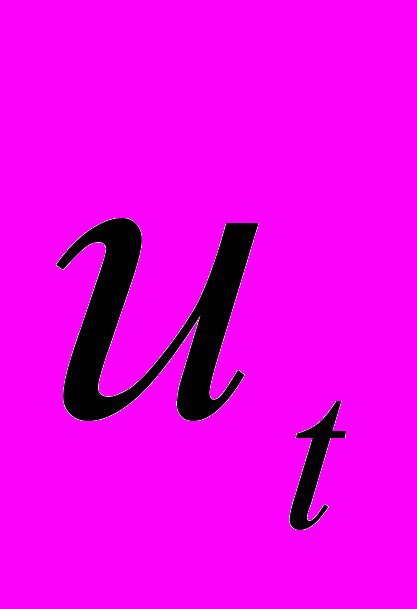— случайные отклонения, удовлетворяющие всем условиям Гаусса-Марка, а коэффициент известен.

Вычтем из (2) соотношение (3), умноженное на :

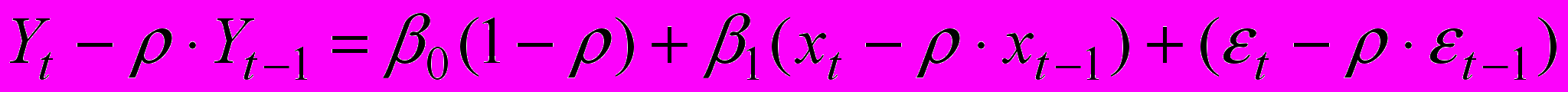(5)

Сделаем замену переменных, положив:





.

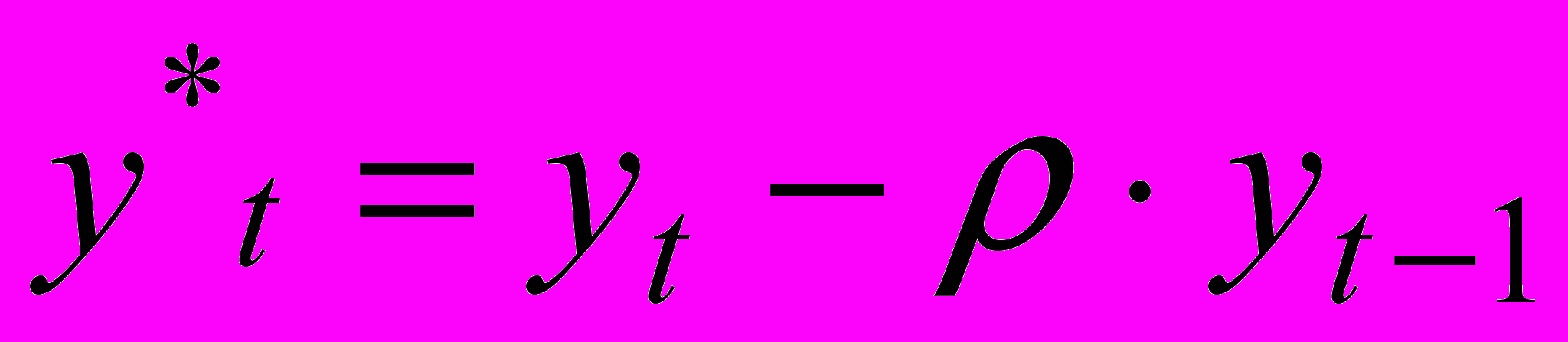
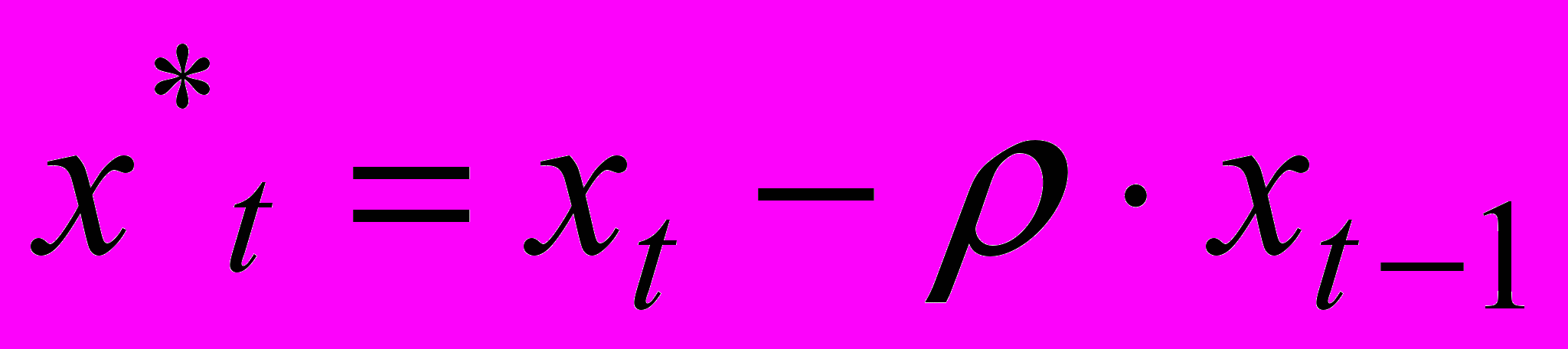
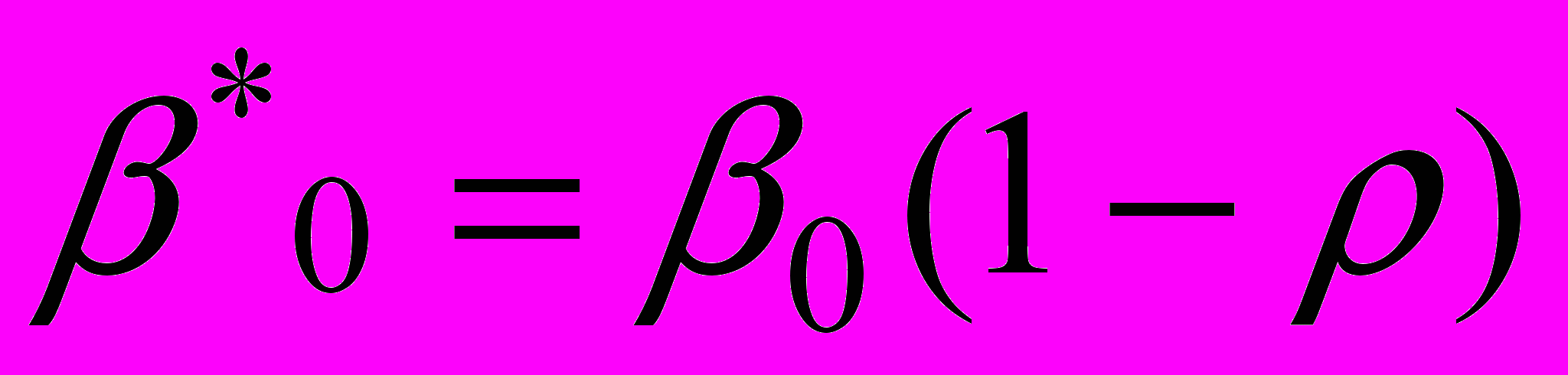Получим

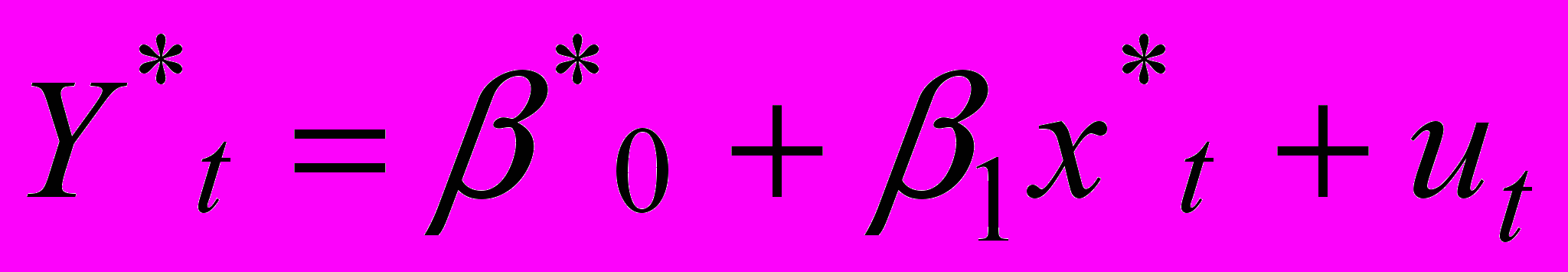
В силу того что случайные отклонения 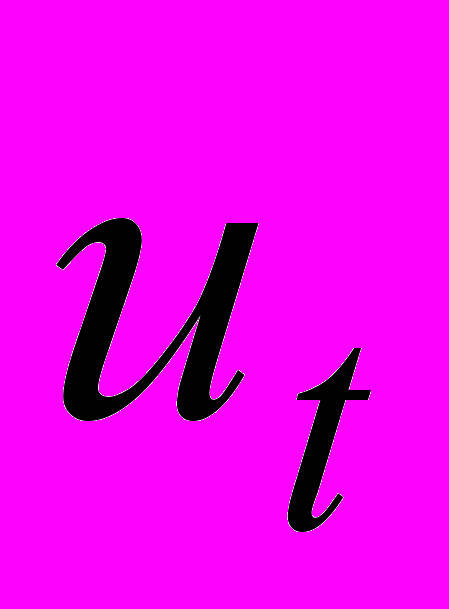удовлетворяют условиям Гаусса-Маркова оценки 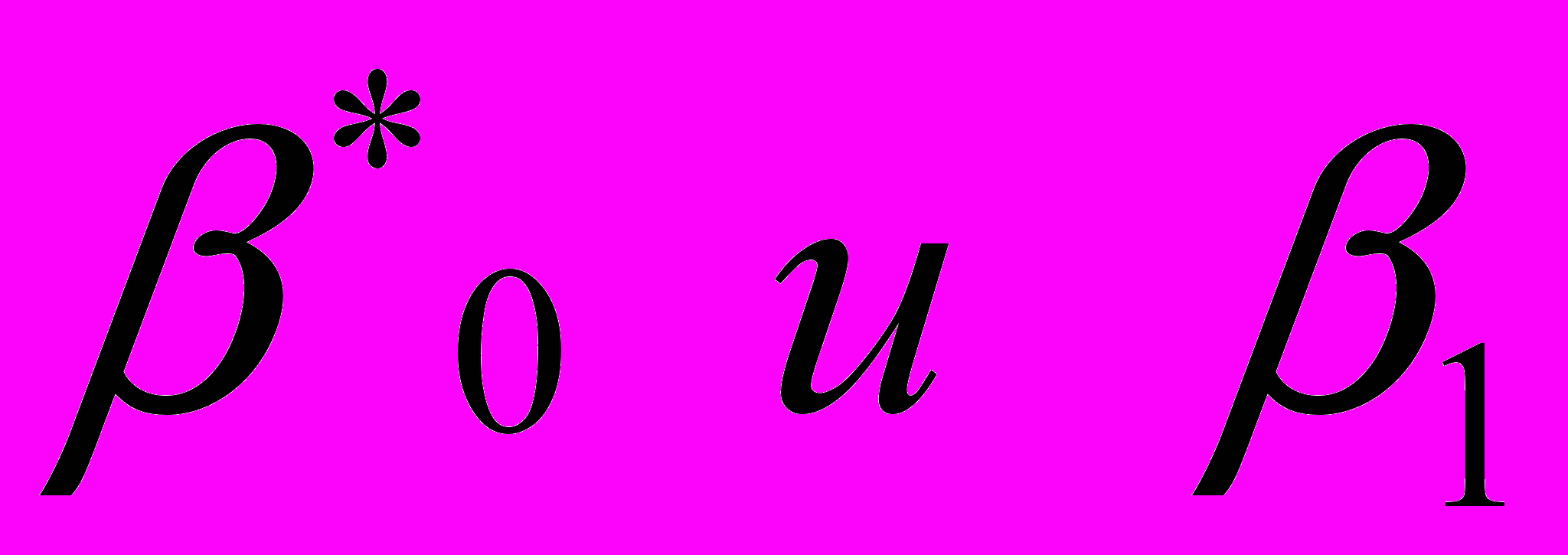будут обладать свойствами наилучших линейных несмещенных оценок и автокорреляции не будет

Однако способ вычисления 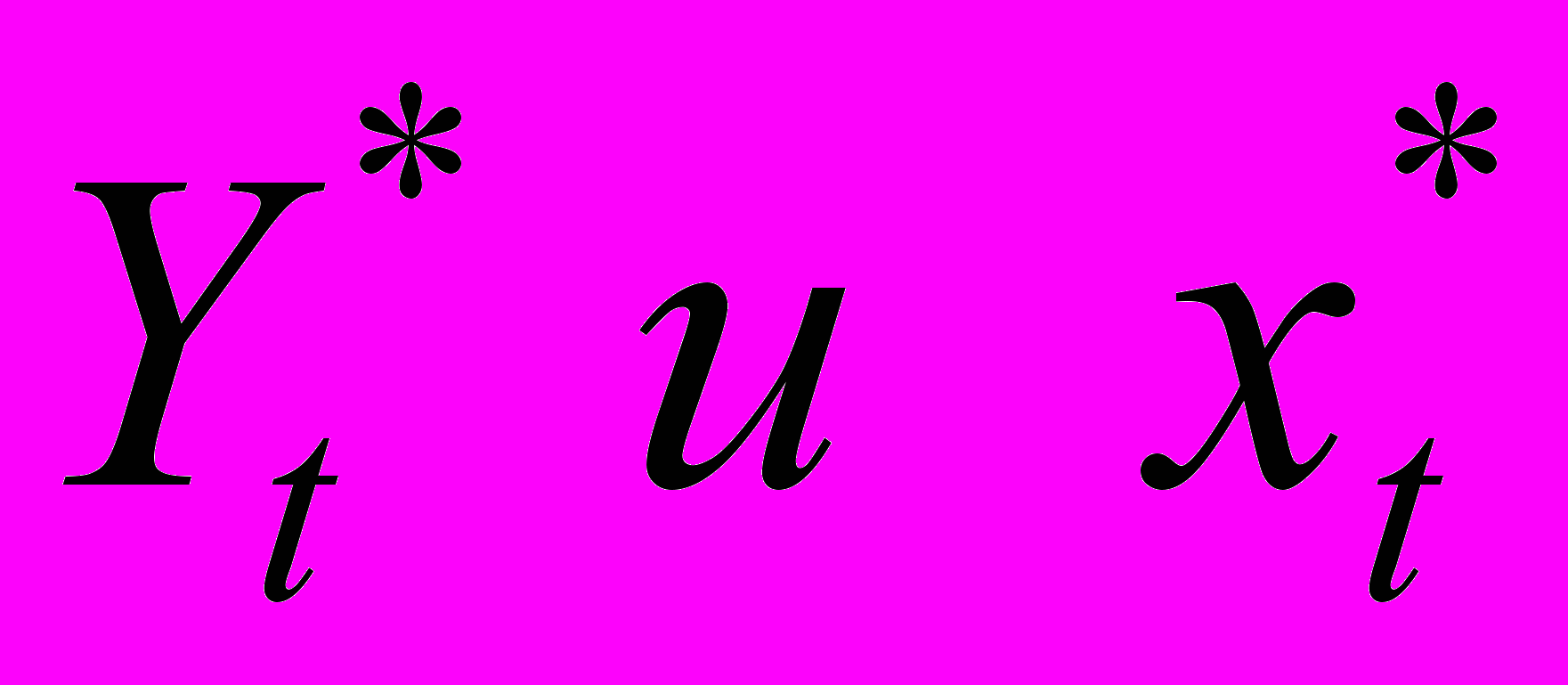приводит к потере первого наблюдения Число степеней свободы уменьшится на единицу, что при больших выборках не так существенно, но при малых выборках может привести к потере эффективности. Эта проблема обычно преодолевается с помощью поправки Прайса—Винстена:


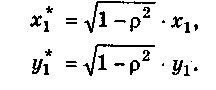(6)

Отметим, что авторегрессионное преобразование может быть обобщено на произвольное число объясняющих переменных, т.е. использовано для уравнения множественной регрессии.

Авторегрессионное преобразование первого порядка AR(1) может быть обобщено на преобразования более высоких порядков AR(2), AR(3) и т.д.:

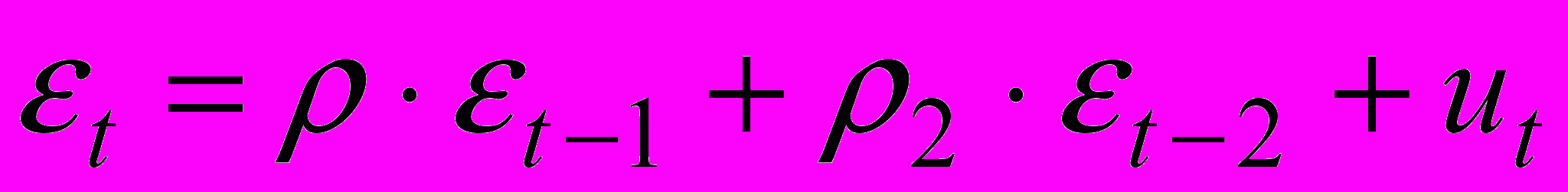и т.д.

Однако на практике значение коэффициента обычно неизвестно и его необходимо оценивать. Существует целый ряд методов оценивания. Приведем наиболее употребляемые.

2. Метод Кохрана—Оркатта


Это иттеративный процесс. Опишем его на примере парной регрессии :

(1)

и авторегрессионной схемы первого порядка .

1. Оценивается по МНК регрессия и для нее определяются оценки 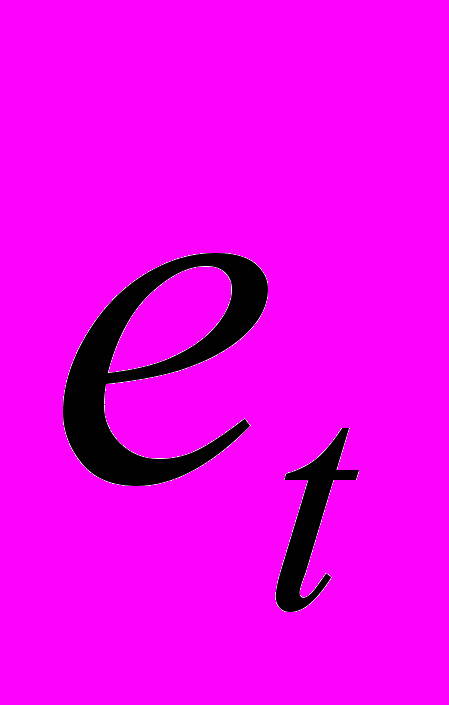отклонений ,

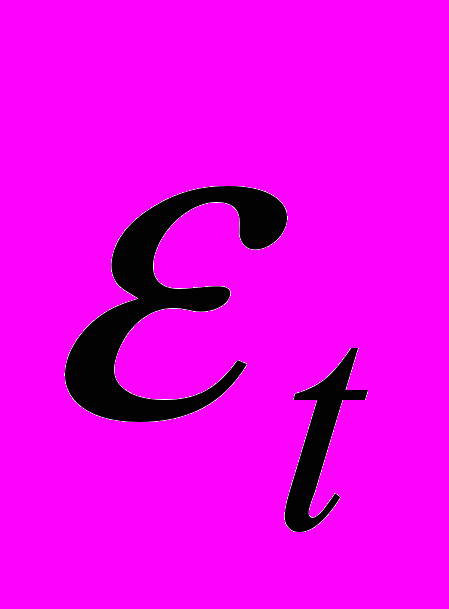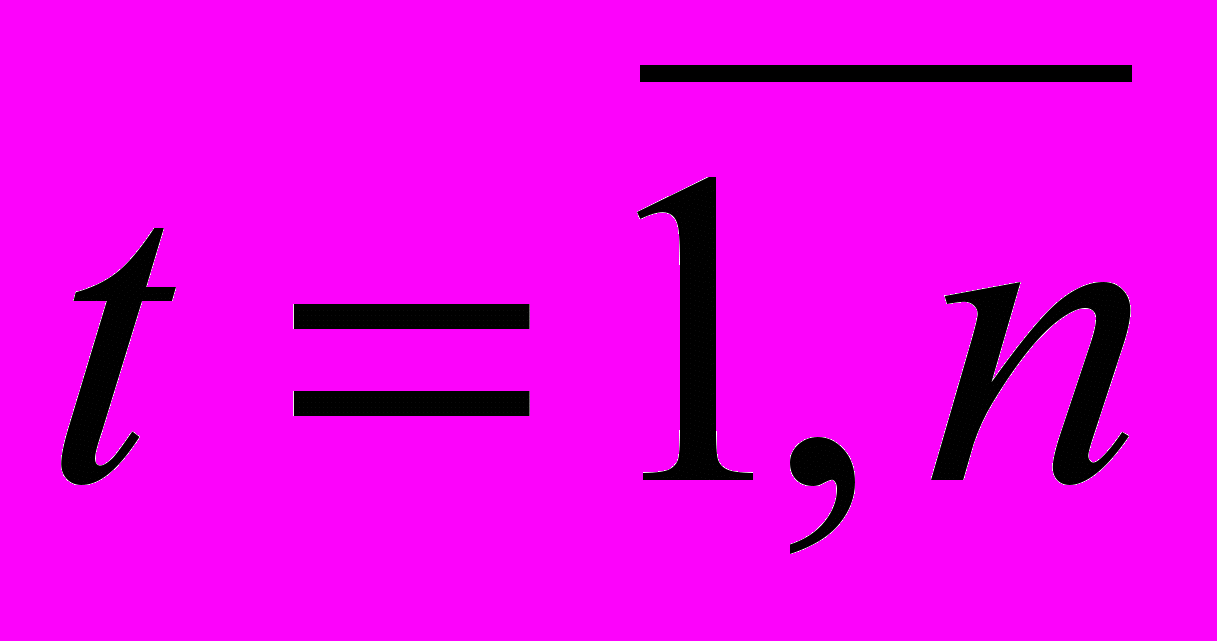
2. Оценивается регрессионная зависимость 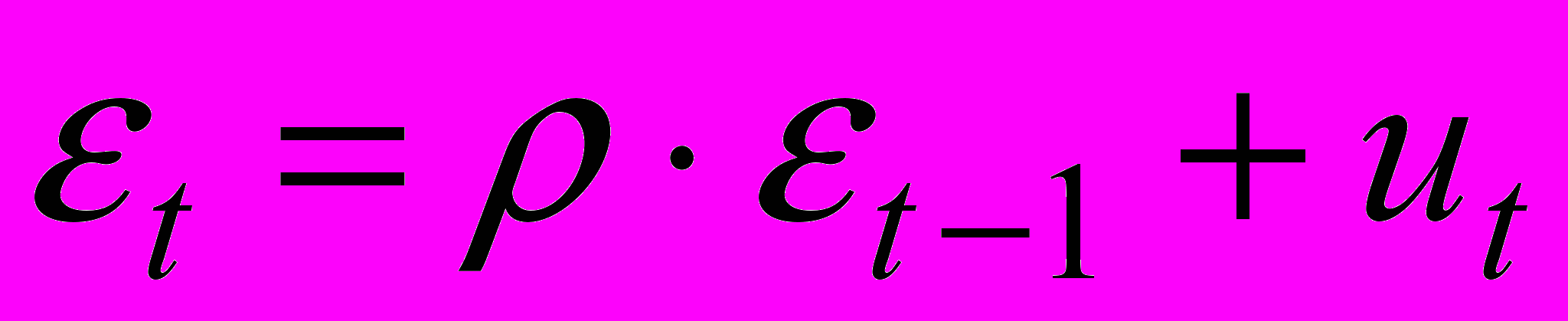, и в качестве приближенного значения берется его МНК оценка .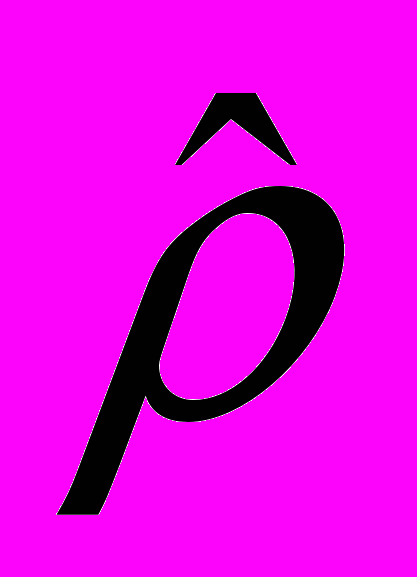

3. На основе этой оценки строится уравнение:

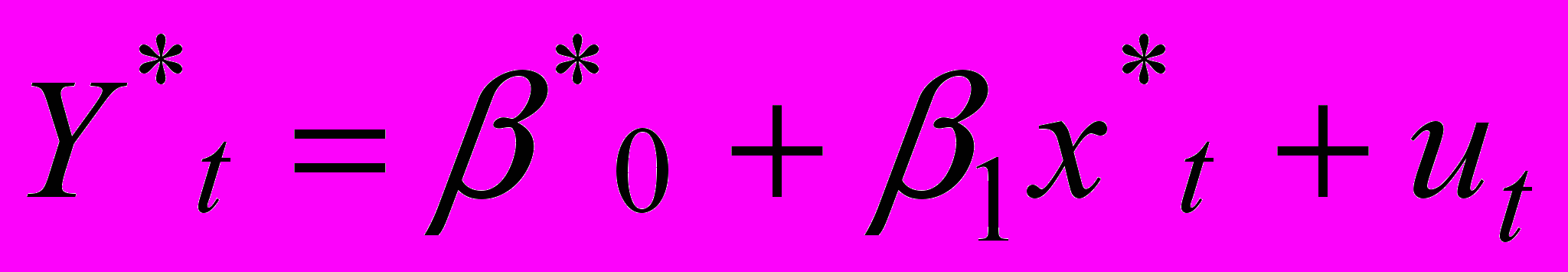, (2), где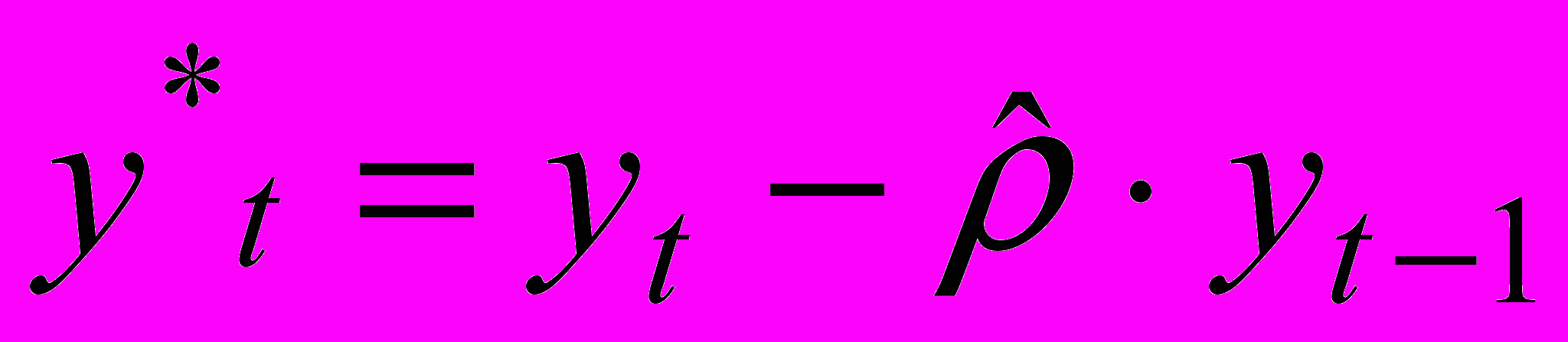





.

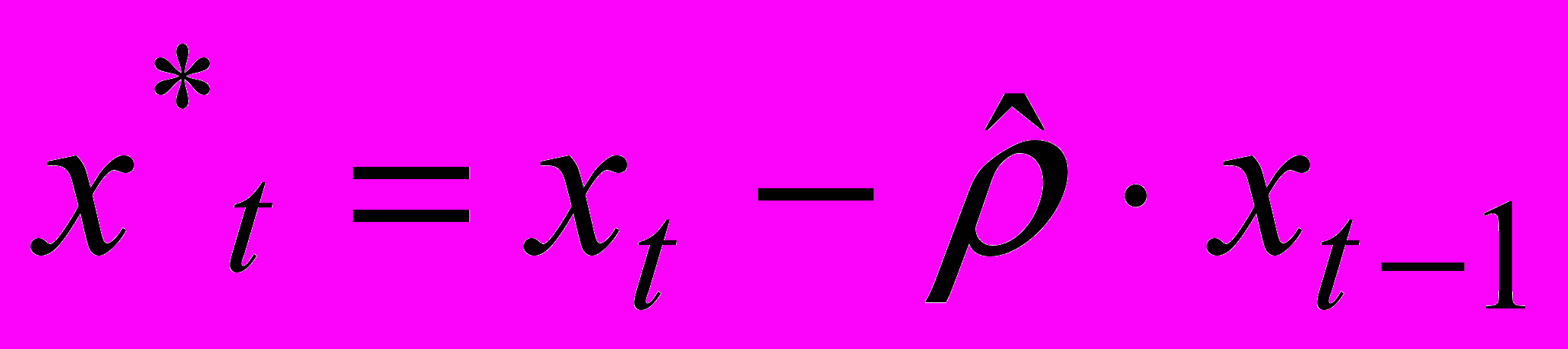
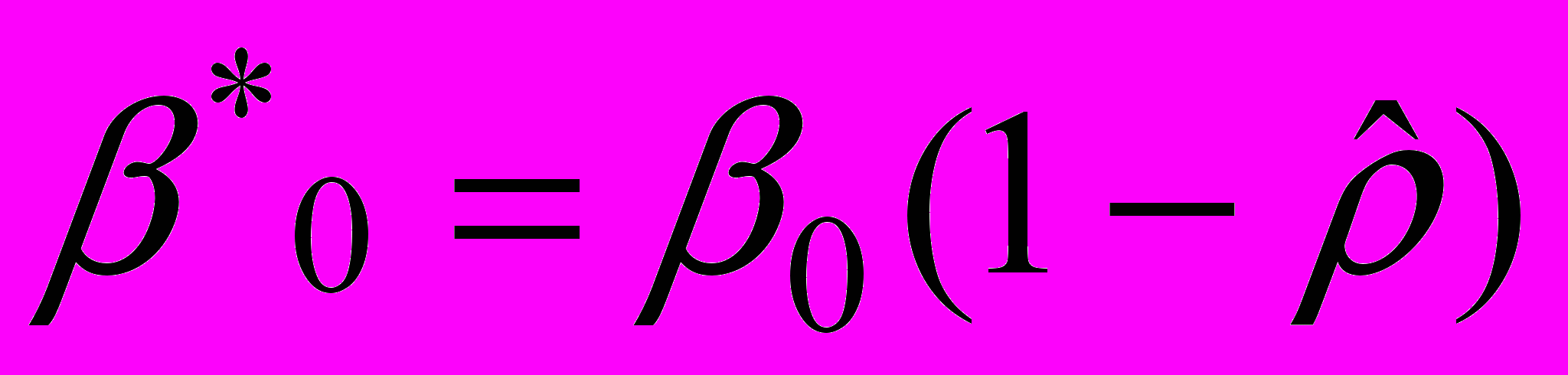С помощью уравнения (2) оцениваются коэффициенты 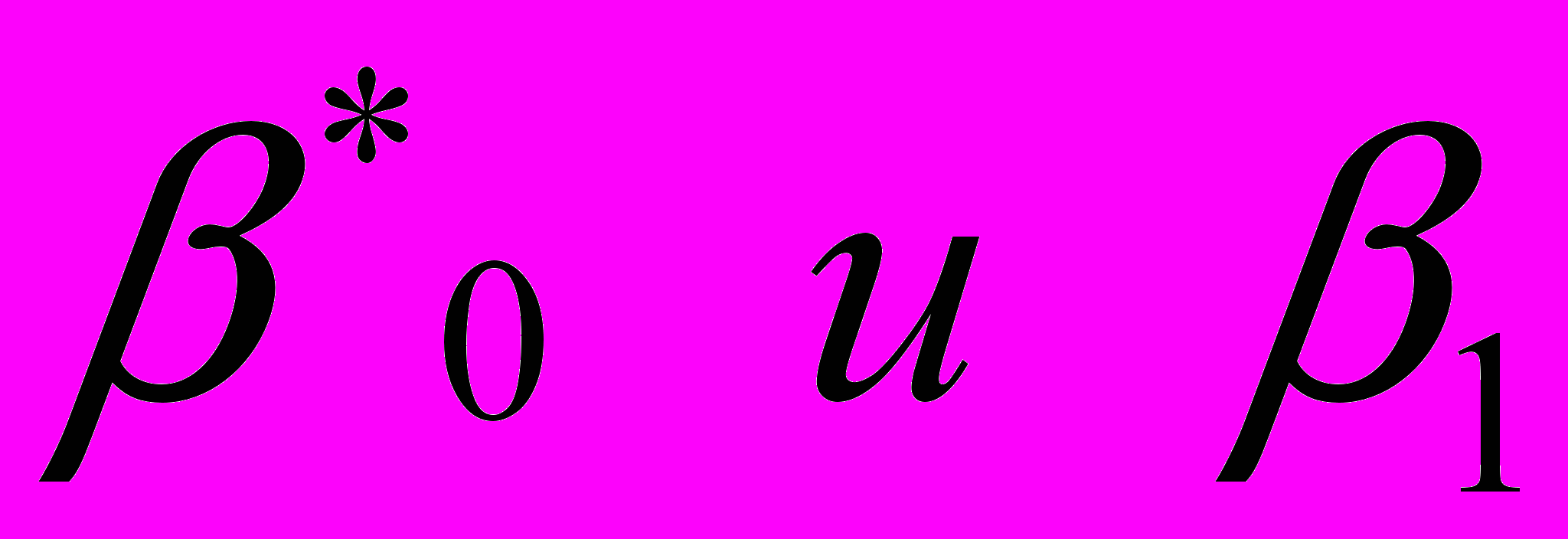(в этом случае значение 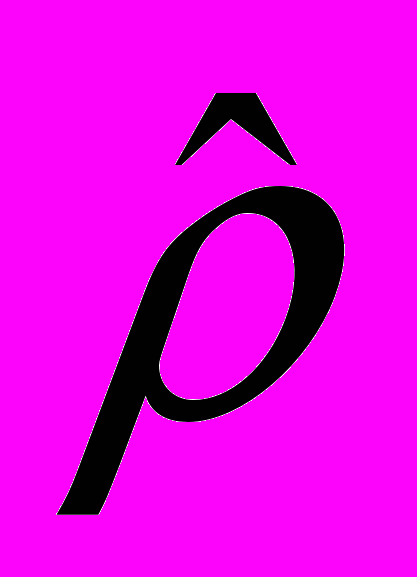известно).

4. Значения 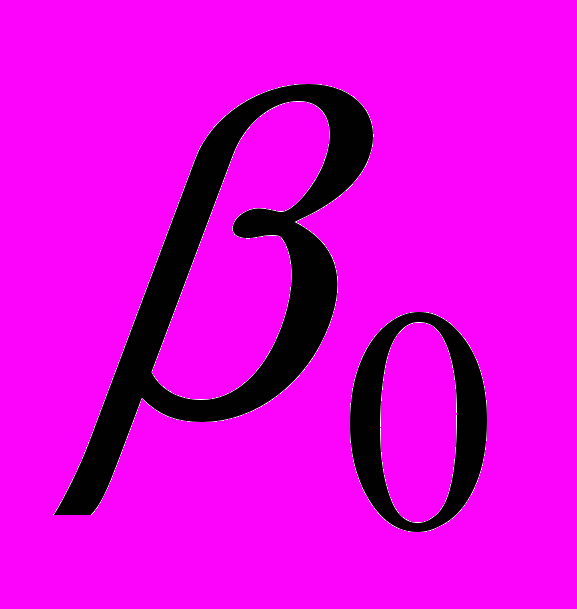и 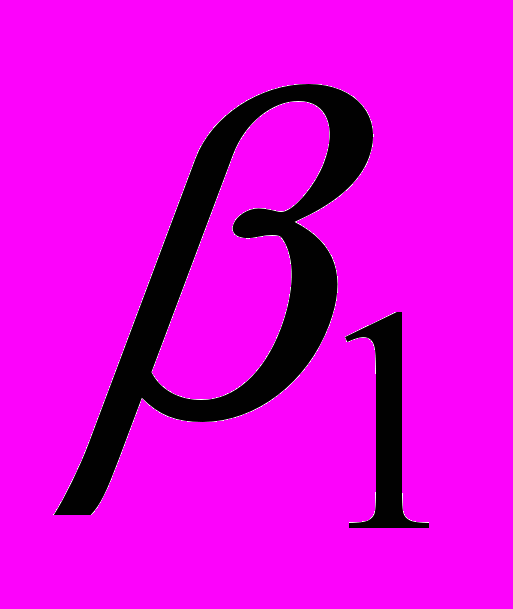подставляются в (7)и вновь вычисляются оценки 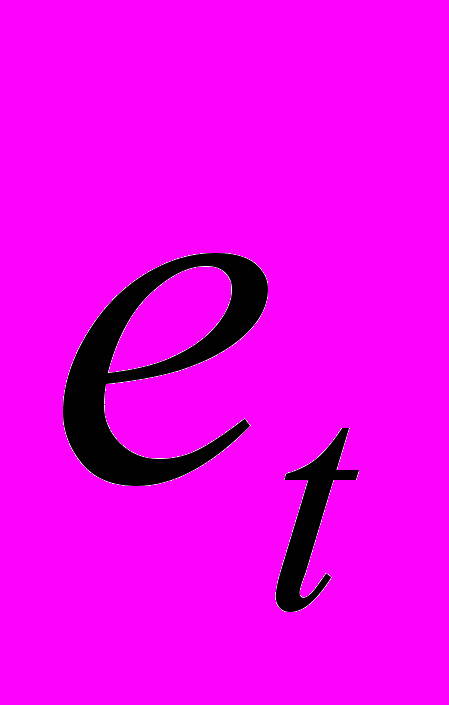отклонений и процесс возвращается к этапу 2.

Чередование этапов осуществляется до тех пор, пока не будет достигнута требуемая точность, т.е. пока разность между предыдущей и последующей оценками не станет меньше заданной точности.

3. Метод Хилдрета—Лу


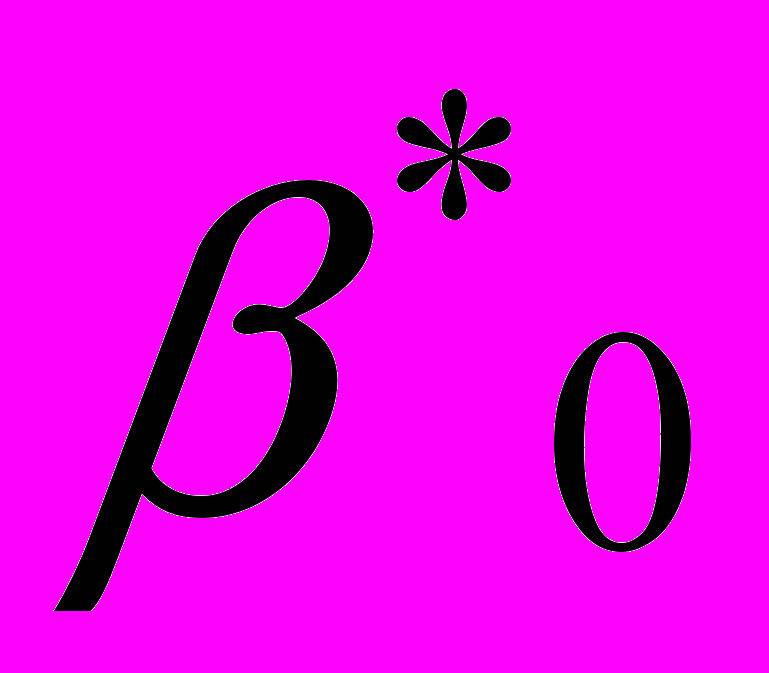По данному методу регрессия оценивается для каждого возможного значения из отрезка [-1, 1] с любым шагом (например, 0,001; 0,01 и т.д.). Величина , дающая наименьшую стандартную ошибку регрессии, принимается в качестве оценки коэффициента . Значения и 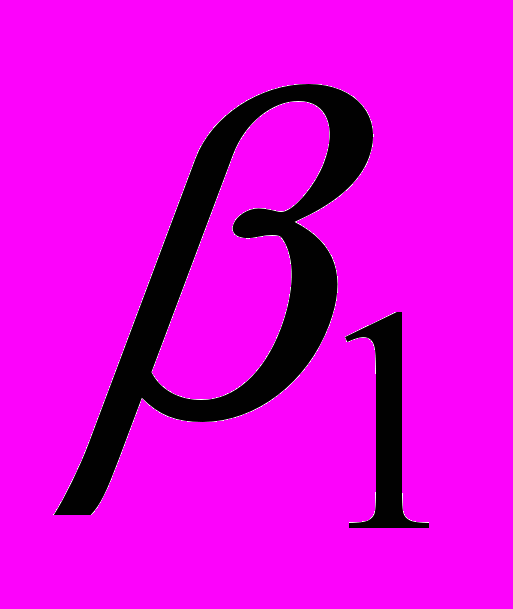оцениваются из уравнения регрессии именно с данным значением .

Этот итерационный метод широко используется в пакетах прикладных программ.