Geum.ru

Студентка Борщёва Елена Валерьевна группы зму 237 пояснительная записка

Вид материалаПояснительная записка

Содержание


2.1. Сводка и группировка статистических данных
Таблица 1. Распределение регионов по численности безработных Выводы.
2.2. Расчет относительных и средних величин
2.3. Показатели вариации
2.4. Корреляционно-регрессионный анализ
Подобный материал:
1   2   3   4   5   6   7
Глава 2. Расчет и анализ статистических показателей, характеризующих занятость и безработицу

2.1. Сводка и группировка статистических данных



Группы регионов по численности безработных
Число регионов
Центр интервала
Накопленная частота

f
x



0,6-9,8
37
5,2
37

9,8-19,0
28
14,4
65

19,0-28,2
10
23,6
75

28,2-37,4
5
32,8
80

37,4-46,6
2
42
82

46,6-55,8
2
51,2
84

55,8-65,0
1
60,4
85




85





Имеются данные о численности безработных (тыс.чел.) по 85 регионам страны. Необходимо построить статистический ряд распределения регионов по численности безработных, образовав необходимое число групп с равными интервалами.

Построим статистический ряд распределения регионов по признаку "численность безработных", образовав при этом 7 групп с равными интервалами. Число 7 нашли из формулы Стерджесса:


k = 1 + 1,44 ∙ ln(n) = 1 + 1,44 + ln (85)  7,41  7.

Таблица 1.

Распределение регионов по численности безработных


Выводы. Как видим из таблицы распределение по регионам однородное. Больше всего регионов с небольшой численностью безработных от 0,6 до 9,8 тыс. чел. – 37 регионов, а меньше всего с численностью свыше 28,2 тыс. чел. На эти регионы приходится 4 группы, а число регионов всего (5+2+2+1) = 10 регионам. То есть можно отметить, что большая часть регионов (85 – 10 = 75) Российской Федерации в 2007 г. имеет численность безработных по официальным данным от 0,6 до 28,2 тыс. чел на регион. То есть если считать, что на регион в среднем приходится 1 647 тыс. чел, то средний уровень безработицы в этих 75 регионах не превышает 1,7%.

2.2. Расчет относительных и средних величин


Проанализируем относительные величины численности населения за 2007 год по г. Омску. Имеются следующие данные по региону, тыс. человек:

На начало 2007 года



численность населения
1028,5

численность населения в трудоспособном возрасте
596,53

численность неработающих инвалидов



в трудоспособном возрасте
8,21

численность занятого населения
480,0

численность работающих пенсионеров и подростков до 16 лет
25,48

численность работающих лиц, прибывших из других регионов
5,10

численность трудоспособного населения данного региона, работающего за его пределами
7,2

численность официально зарегистрированных безработных
4,1

численность ищущих работу самостоятельно
30,3

В течение 2007 года



вступило в трудоспособный возраст трудоспособного населения
18,5

вовлечено для работы в отраслях экономики региона пенсионеров и подростков до 16 лет
5,4

прибыло из других регионов трудоспособного населения в трудоспособном возрасте
2,8

выбыло из состава трудовых ресурсов по разным причинам
12,6

выбыло трудоспособного населения в трудоспособном возрасте в другие области
1,7



Определите:
  1. на начало года:
  • численность трудовых ресурсов;
  • численность трудовых ресурсов с учетом механического движения;
  • численность экономически активного населения;
  • коэффициенты занятости и безработицы населения, трудовых ресурсов, населения трудоспособного возраста, экономически активного населения;
  • уровень официальной безработицы;
  • коэффициент экономической нагрузки на одного экономически активного;
  • коэффициент экономической активности населения;
  1. на конец года: численность трудовых ресурсов;
  2. среднегодовую численность трудовых ресурсов;
  3. коэффициенты естественного, механического и общего прироста трудовых ресурсов.

Определим
    • численность трудовых ресурсов:

596,53 – 8,21 +25,48 = 613,8 тыс. чел.
    • численность трудовых ресурсов с учетом механического движения:

613,8 – 5,1 + 7,2 = 615,9 тыс. чел.
    • численность экономически активного населения:

480 + 4,1 +30,3 = 514,4 тыс. чел.
    • коэффициенты занятости и безработицы населения, трудовых ресурсов, населения трудоспособного возраста, экономически активного населения:

480 : 1028,5  1000 = 466,7 ‰ коэффициент занятости населения

480 : 613,8  1000 = 782,0 ‰ коэффициент занятости трудовых ресурсов

480 : 596,53  1000 = 804,7 ‰ – коэффициент занятости населения трудоспособного возраста,

480 : 514,4  1000 = 933,1 ‰ коэффициент занятости экономически активного населения.

34,4 : 1028,5  100 = 3,34% коэффициент безработицы населения

34,4 : 613,8  100 = 5,60% коэффициент безработицы трудовых ресурсов

34,4 : 596,53  100 = 5,77% коэффициент безработицы населения трудоспособного возраста

34,4 : 514,4  100 = 6,69% коэффициент безработицы экономически активного населения.
    • уровень официальной безработицы:

4,1 : 514,4  100 = 0,80%
    • коэффициент экономической нагрузки на одного экономически активного:

1028,5 : 514,4 = 1,99
    • коэффициент экономической активности населения:

514,4 : 1028,5  100 = 50,01%

На конец года: численность трудовых ресурсов:

613,8 +18,5 – 12,6 + 5,4 = 625,1 тыс. чел.

С учетом механического движения:

615,9 +2,8 – 1,7 = 617,0 тыс.чел.

Среднегодовая численность трудовых ресурсов:

(613,8 + 625,1) : 2 = 619,45 тыс. чел.

Найдем коэффициенты естественного, механического и общего прироста трудовых ресурсов.

(625,1 – 613,8) : 619,45 = 11,3 : 619,45 = 18,24 – коэффициент естественного прироста трудовых ресурсов.

(617,0 – 615,9) : 619,45 = 1,1 : 619,45 = 1,78 – коэффициент механического прироста трудовых ресурсов.

(11,3 +1,1) : 619,45 = 20,02 – коэффициент общего прироста трудовых ресурсов.

Существуют различные виды средних рассчитаем среднюю простую арифметическую, среднюю взвешенную, моду и медиану, используя полученные данные в табл. 2.


Группы регионов по численности безработных
Число регионов
Центр интер-вала
Накоп-ленная частота
Расчетные значения

xf
x-x
(x-x)2
(x-x)2f

f
x



0,6-9,8
37
5,2
37
192,4
-9,4
88,7
3280,8

9,8-19,0
28
14,4
65
403,2
-0,2
0,0
1,3

19,0-28,2
10
23,6
75
236
9,0
80,7
807,0

28,2-37,4
5
32,8
80
164
18,2
330,6
1653,2

37,4-46,6
2
42
82
84
27,4
749,9
1499,7

46,6-55,8
2
51,2
84
102,4
36,6
1338,4
2676,7

55,8-65,0
1
60,4
85
60,4
45,8
2096,1
2096,1




85






1242,4






12014,897



Таблица 2

Вычислим среднюю арифметическую по исходным данным, то есть нужно найти среднюю арифметическую простую:

Хср = (1491,6 – 312,4) : 85 = 13,873 тыс. чел.


Средняя арифметическая взвешенная:

x = 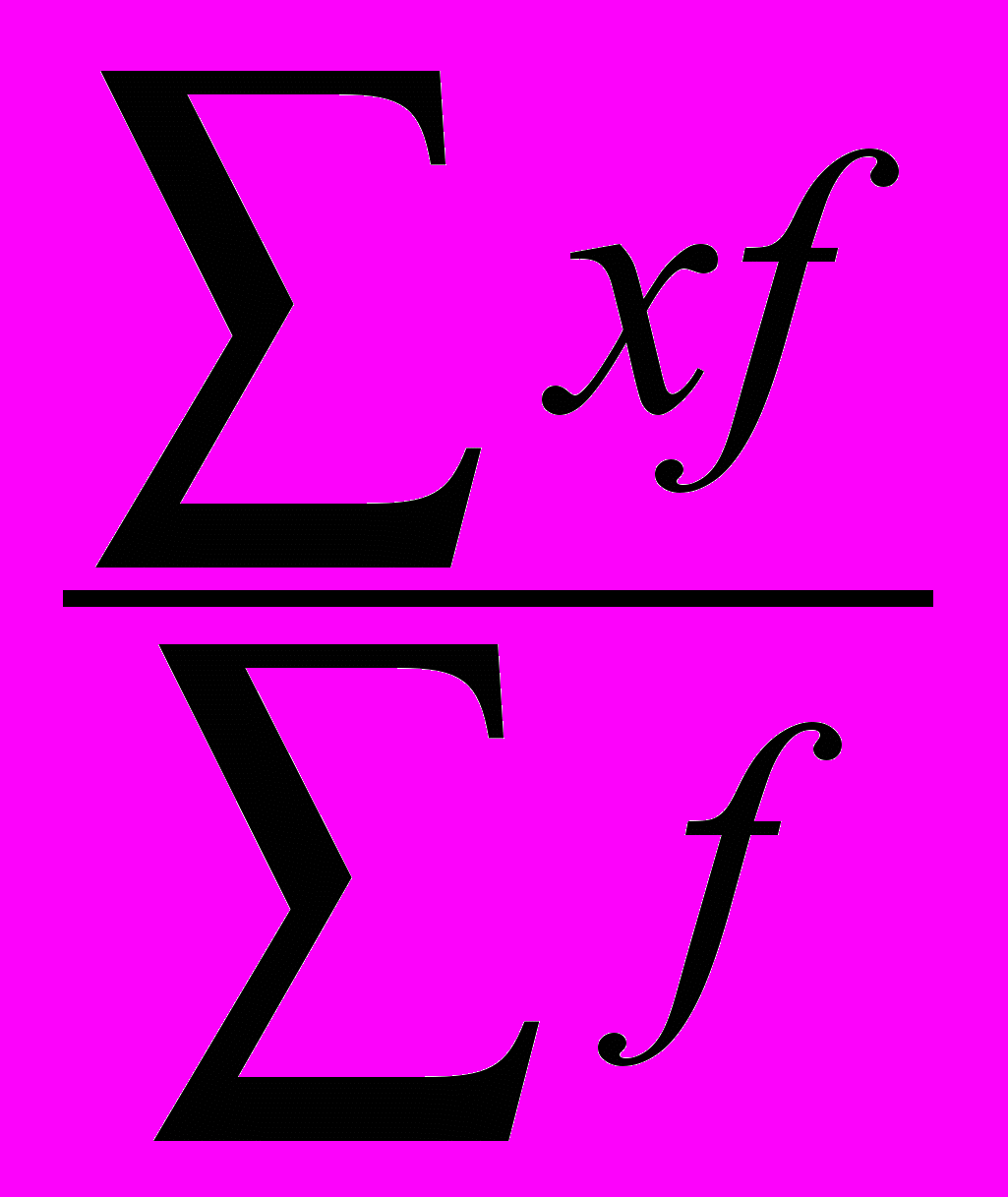= 1242,4 : 85 = 14,617 тыс. чел.

Мода – это наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака. На практике моду и медиану находят, как правило, по сгруппированным данным. Моду определим по формуле



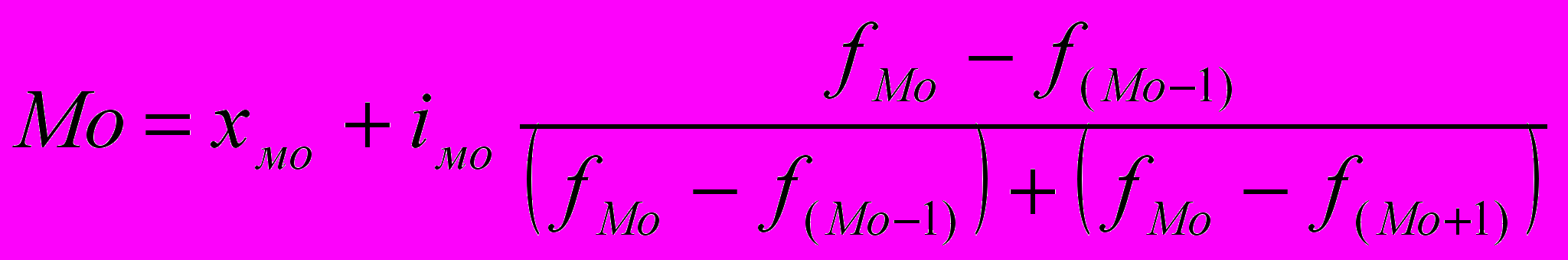
где 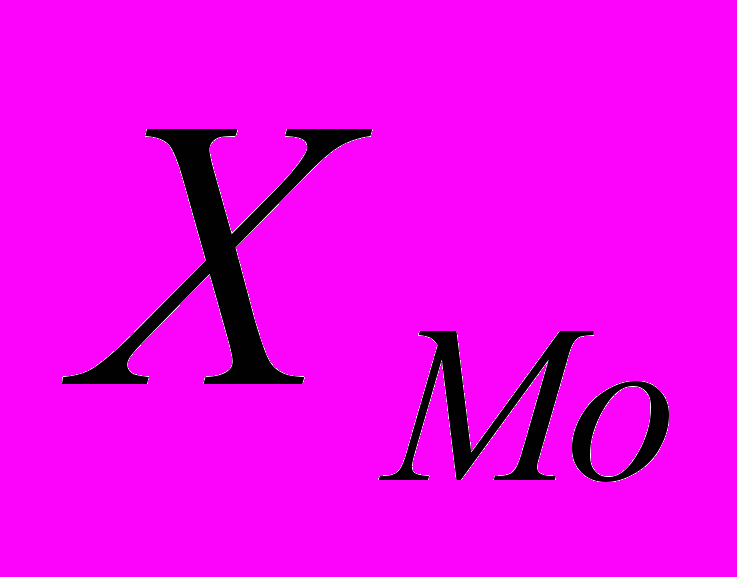– начальное значение интервала, содержащего моду;

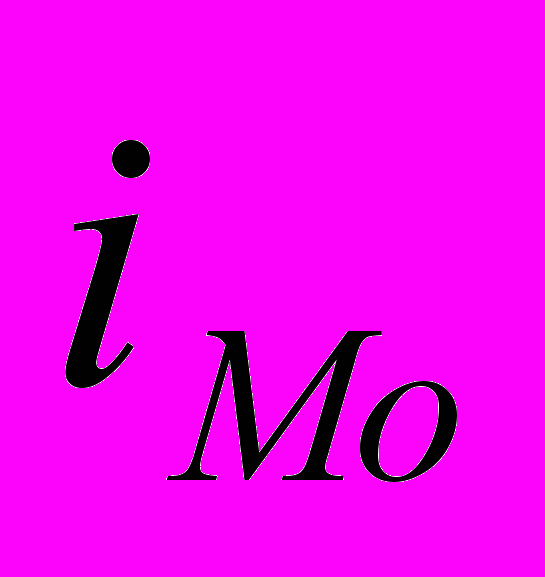– величина модального интервала;

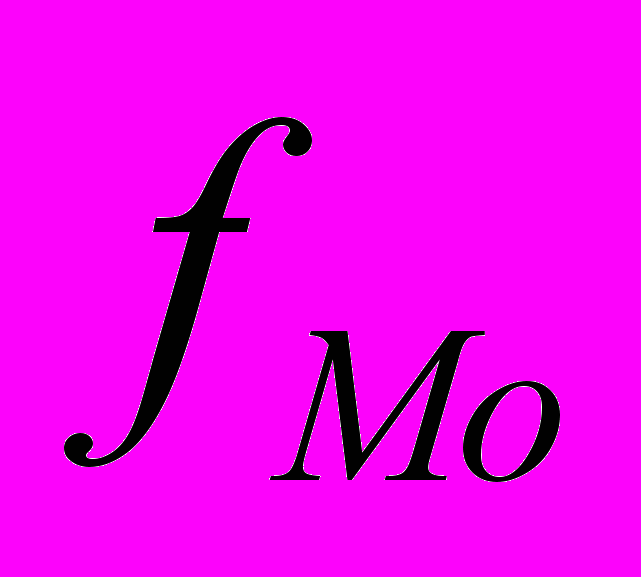– частота модального интервала;

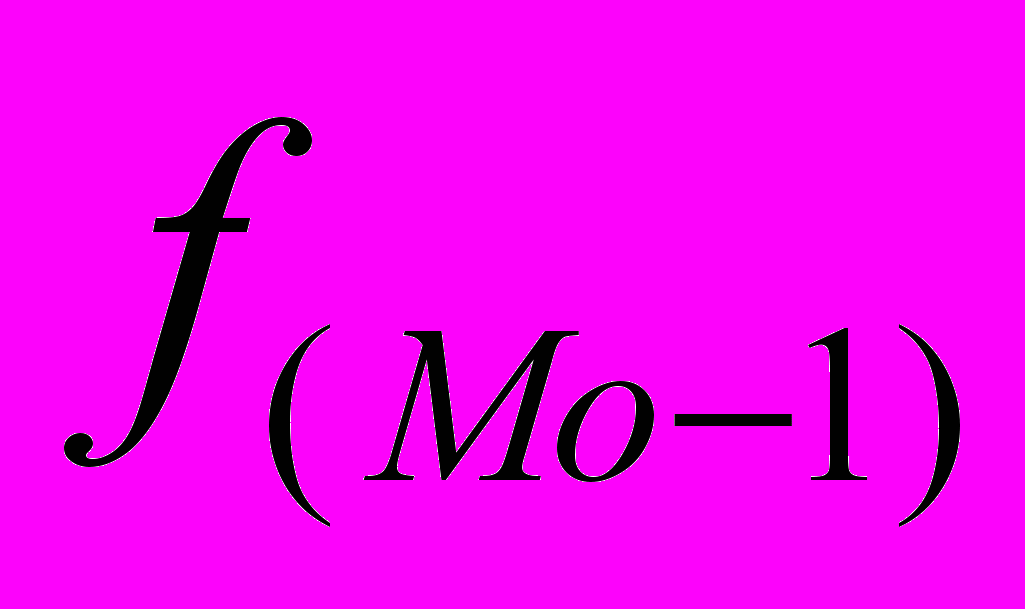– частота интервала, предшествующего модальному;

– частота интервала, следующего за модальным.

Первоначально по наибольшей частоте признака определим модальный интервал. Наибольшее число регионов – 37 – имеют численности безработных от 0,6 до 9,8 тыс. чел. Это интервал и является модальным, значит:


M0 =0,6 + 9,2 ∙ 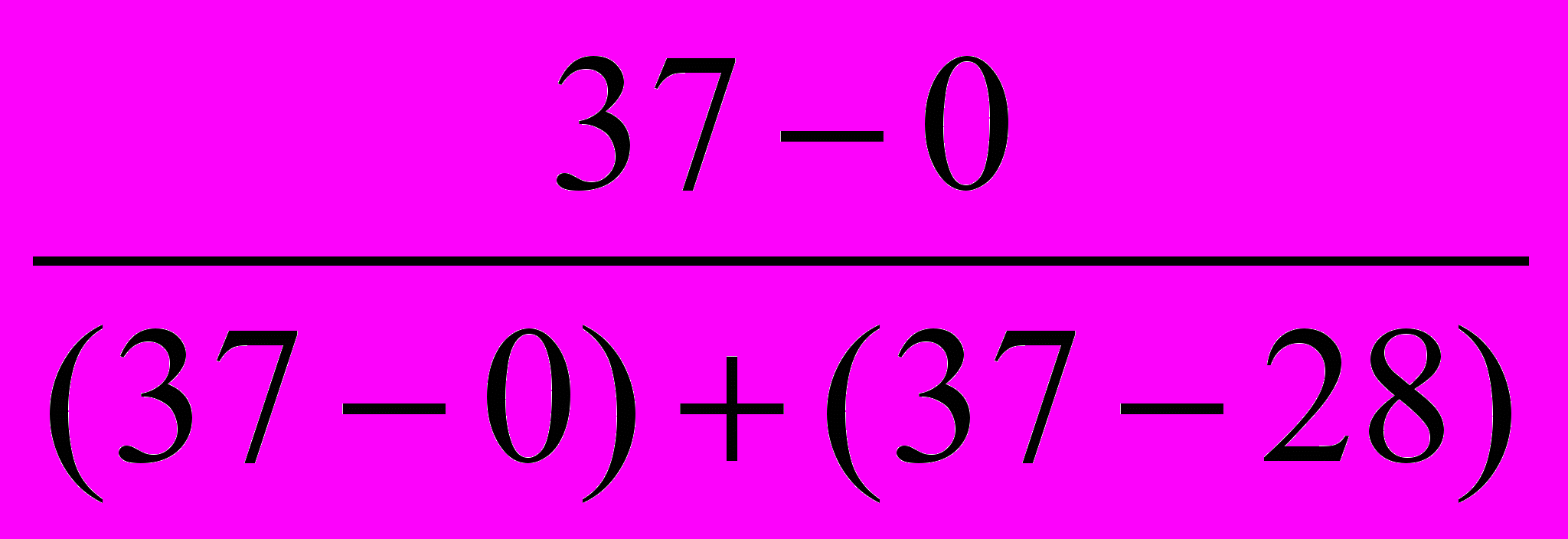= 8 тыс. чел.

Медиана – вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части, таким образом, что половина единиц совокупности имеют значения признака меньше, чем медиана, а половина – больше, чем медиана.

В интервальном ряду медиана определяется по формуле:





где хМе – начало медианного интервала,

iMe – величина медианного интервала, f – сумма частот вариационного ряда,

fMe – частота медианного интервала,

SMe-1 – сумма частотных интервалов в домедианном интервале.

Определим медианный интервал. Для этого подсчитаем сумму частот накопленным итогом до числа, превышающего половину объема совокупности (85 : 2 = 42,5). В графе "накопленная частота" (табл. 1) значение 28 соответствует интервалу [9,8 ; 19,2]. Это и есть медианный интервал.

Значит:


Me = 9,8 +9,2 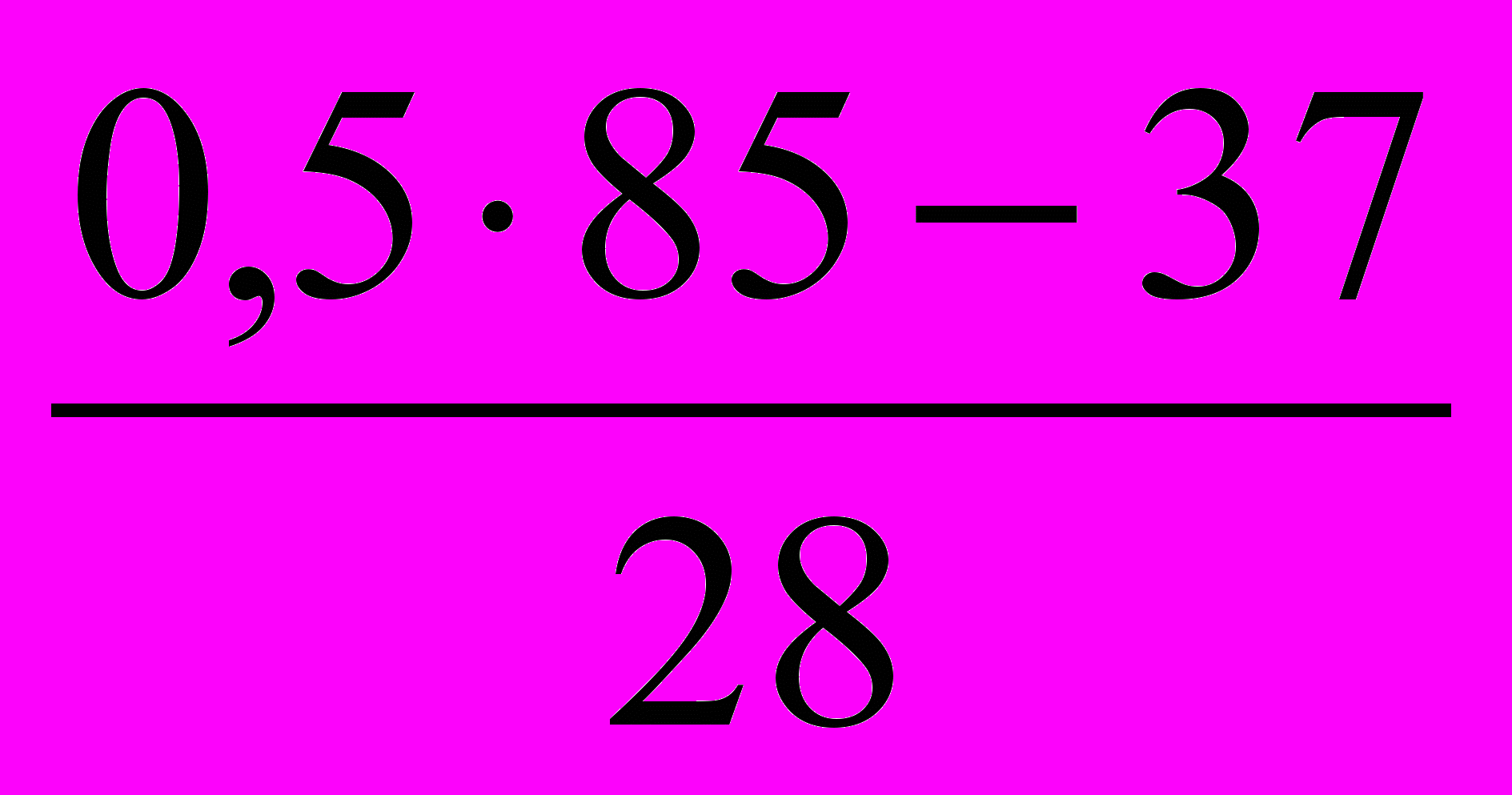 ≈ 11,61 тыс. чел.


Выводы. Как можно видеть, средние арифметические, посчитанные двумя разными способами разошлись: средняя взвешенная равна 14,617 тыс. чел. оказалась больше средней арифметической простой, равной 13,873 тыс. чел.

Другие средние: медиана равна 11,61 тыс. чел., а мода 8 тыс. чел., что говорит о том, что не выполняется одно из условий симметричности распределения.


2.3. Показатели вариации


При характеристике колеблемости признака используют систему абсолютных и относительных показателей.

Абсолютные показатели вариации:
  • Размах вариации R = xmax – xmin;
  • Среднее линейное отклонение
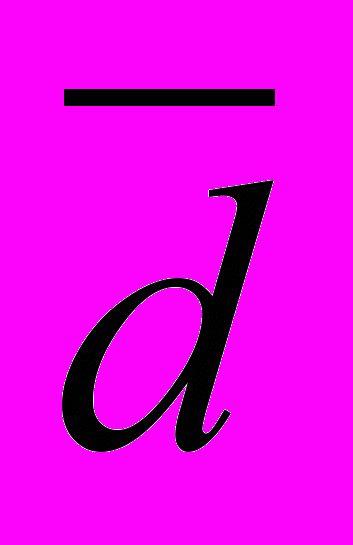
  • Дисперсия σ 2
  • Среднеквадратическое отклонение σ

Абсолютные показатели, кроме дисперсии, измеряются в тех же единицах, что и сам признак.

Относительные показатели вариации:
  • Коэффициент осцилляции
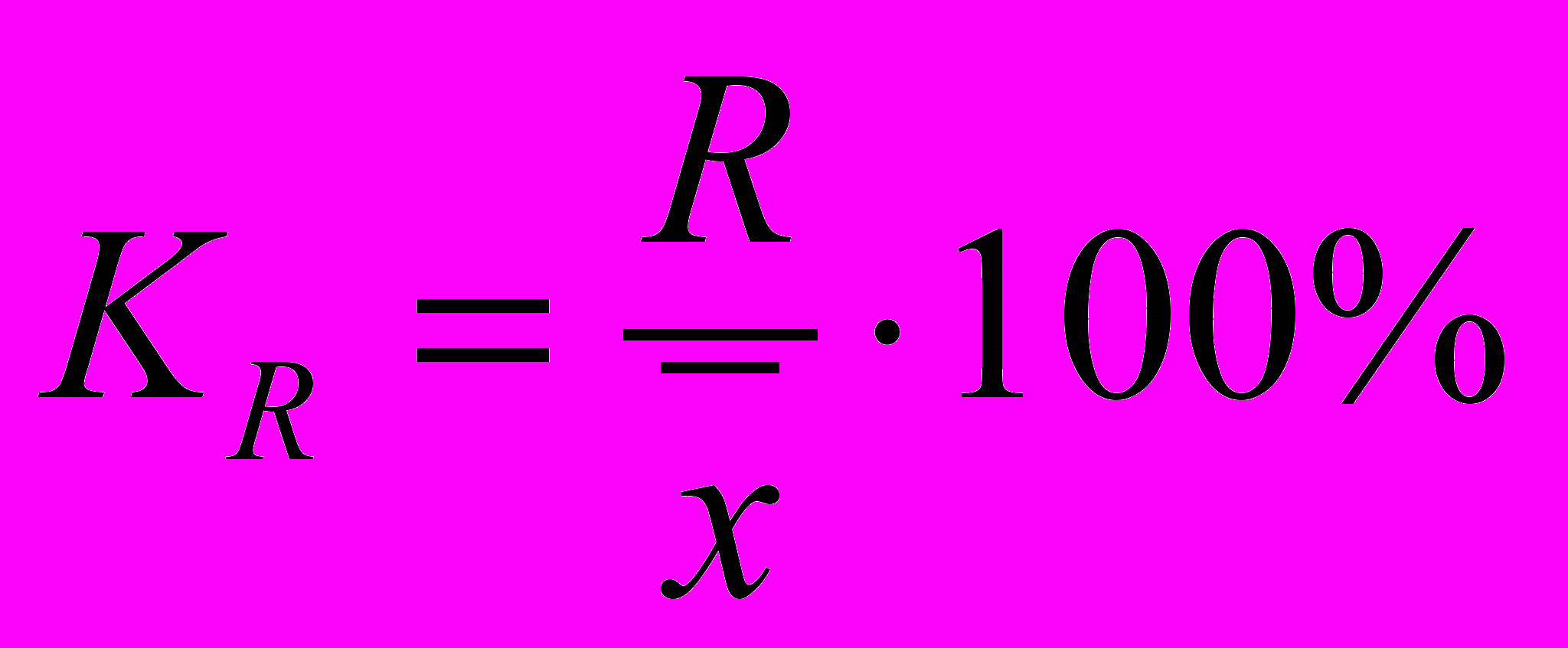
  • Относительное линейное отклонение
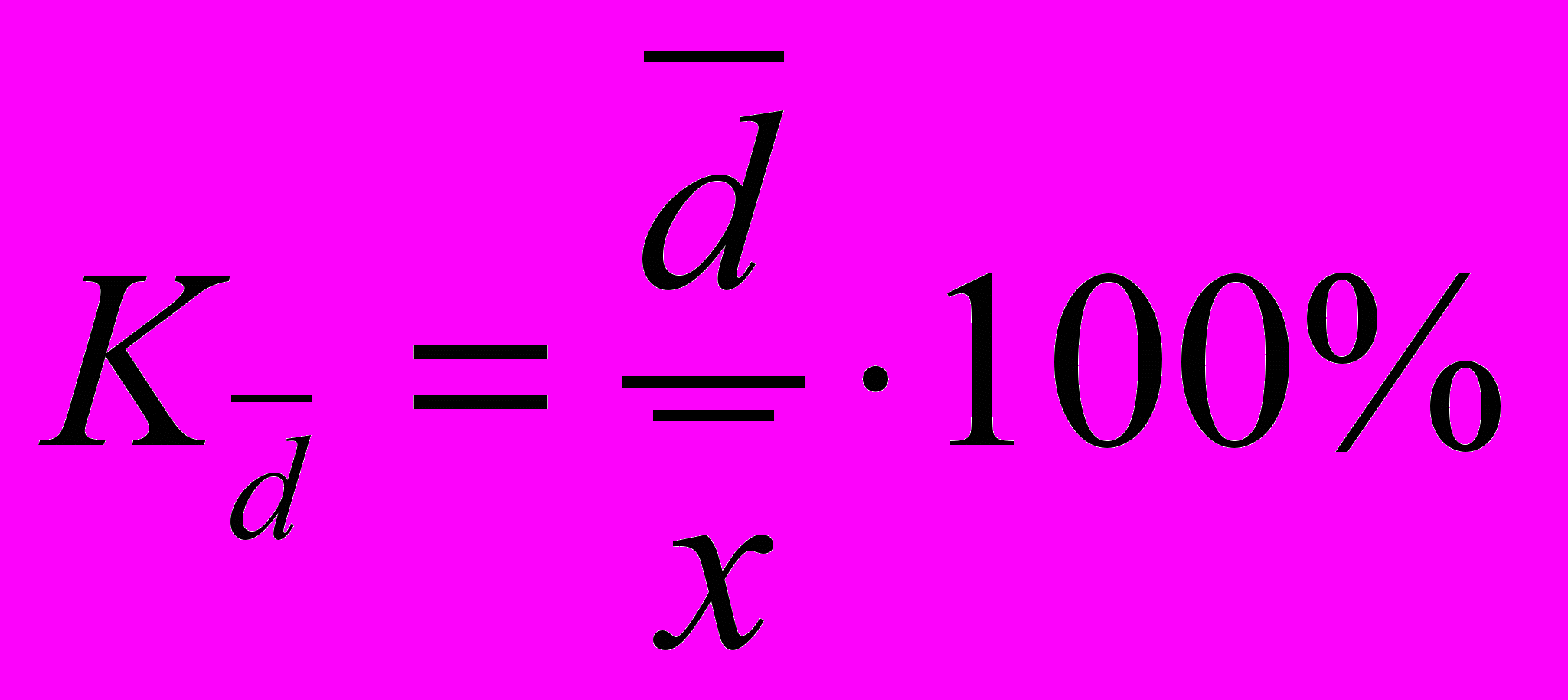
  • Коэффициент вариации

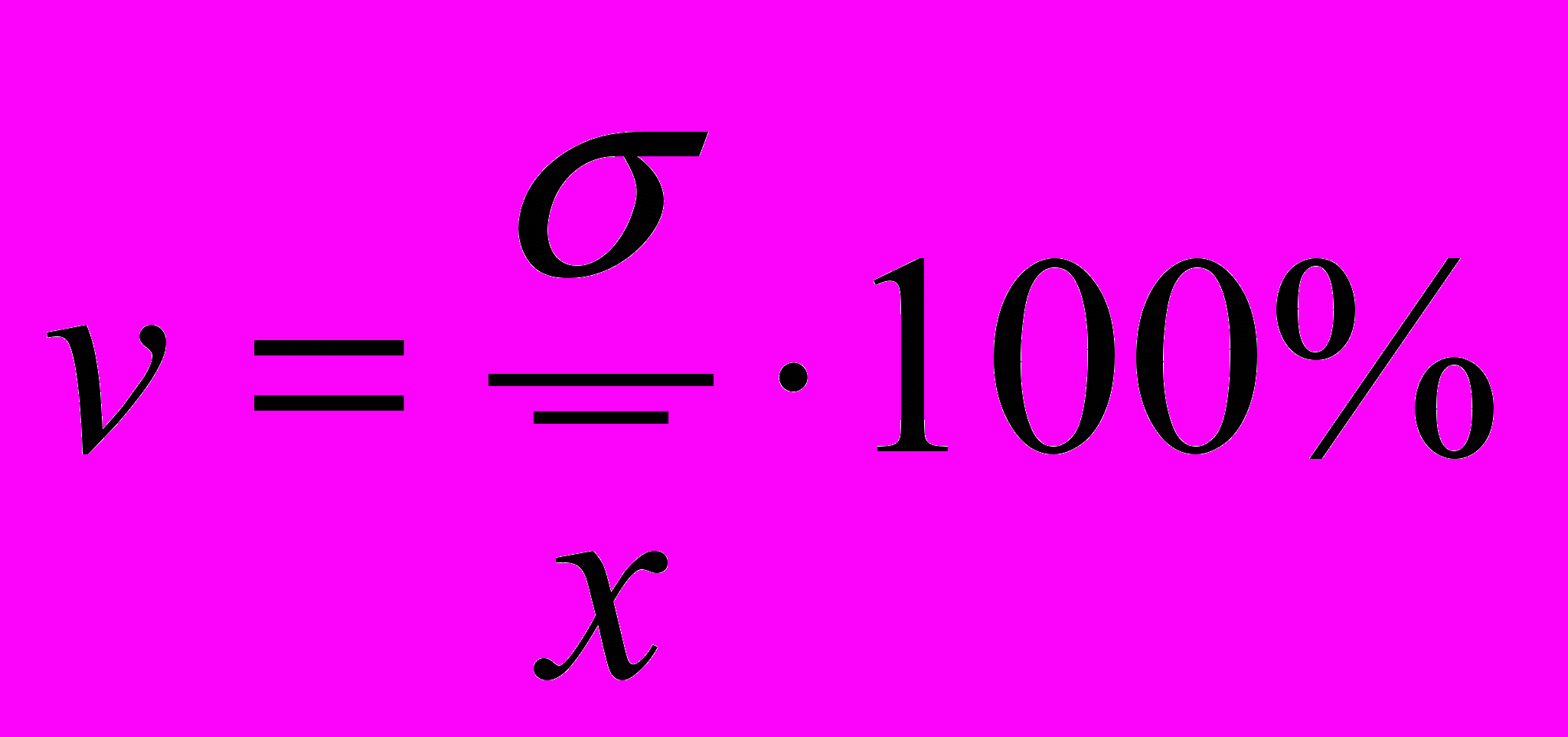
Относительные показатели чаще всего выражаются в процентах

Рассчитаем эти показатели.

Абсолютные показатели вариации:

Размах вариации R = xmax – xmin = 65 – 0,6 = 64,4 тыс. чел.

Среднее линейное отклонение = =

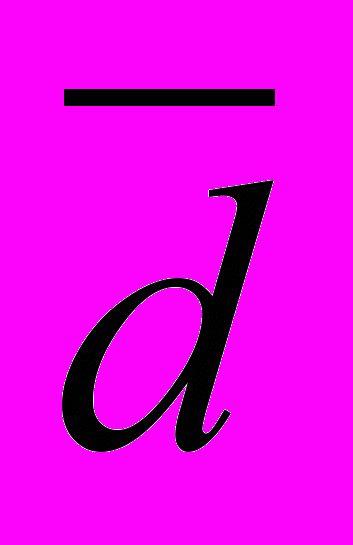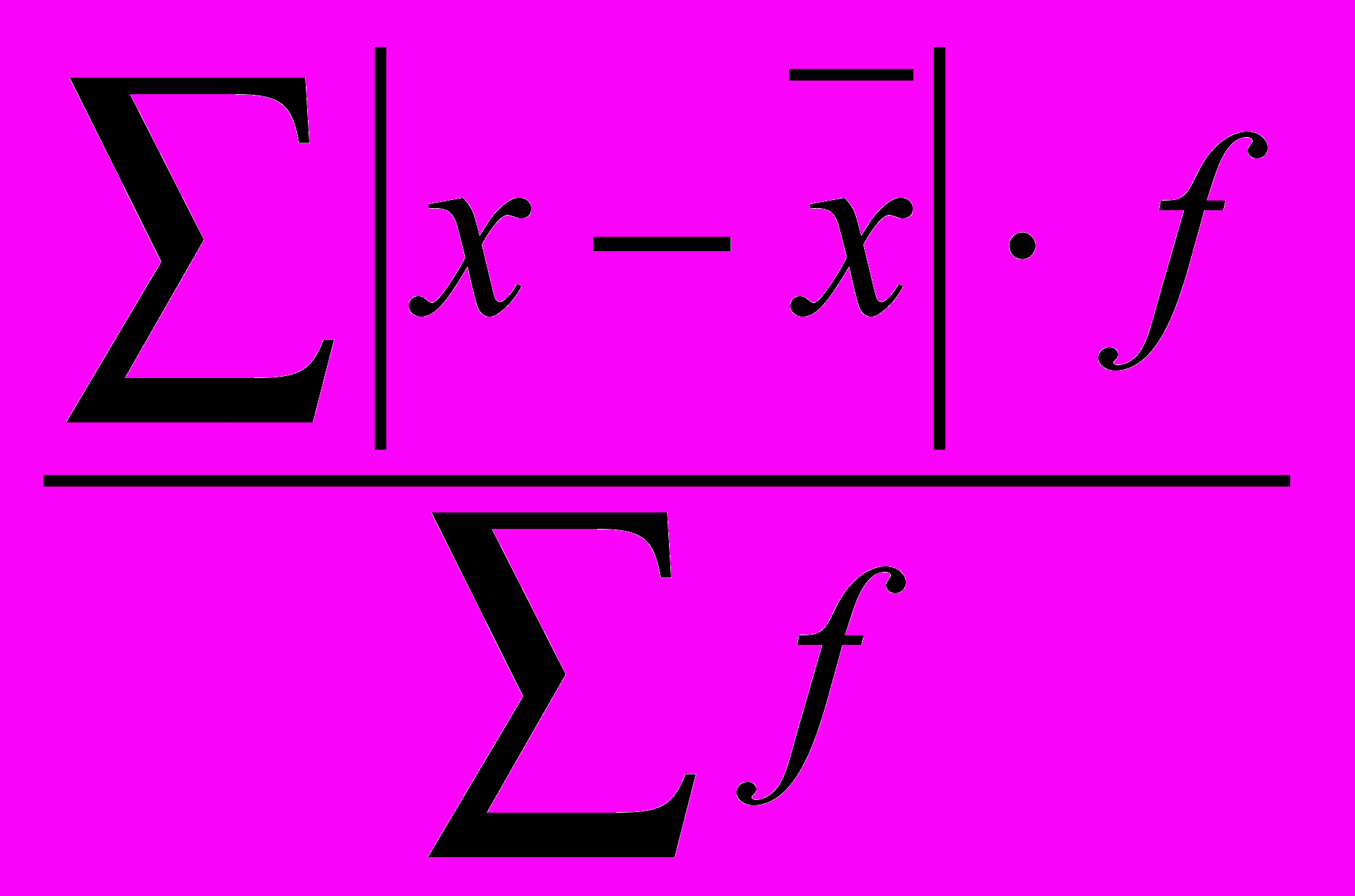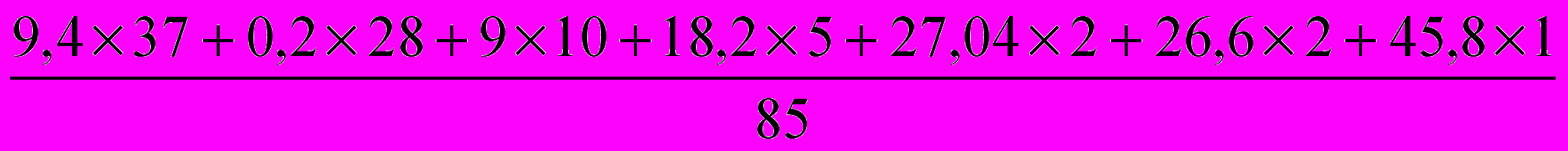= 8,34 тыс. чел.

Дисперсия (из табл. 1) 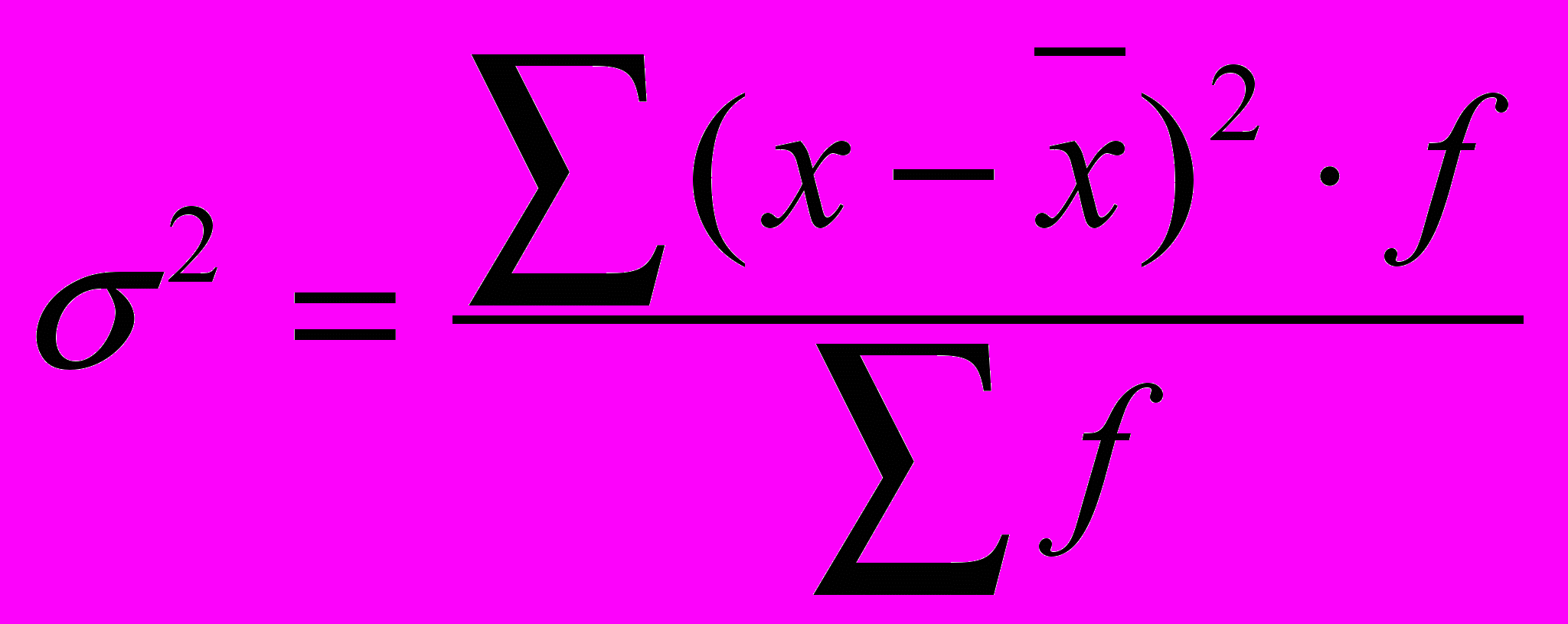= 12014,897 : 85 = 141,352

Среднеквадратическое отклонение σ = 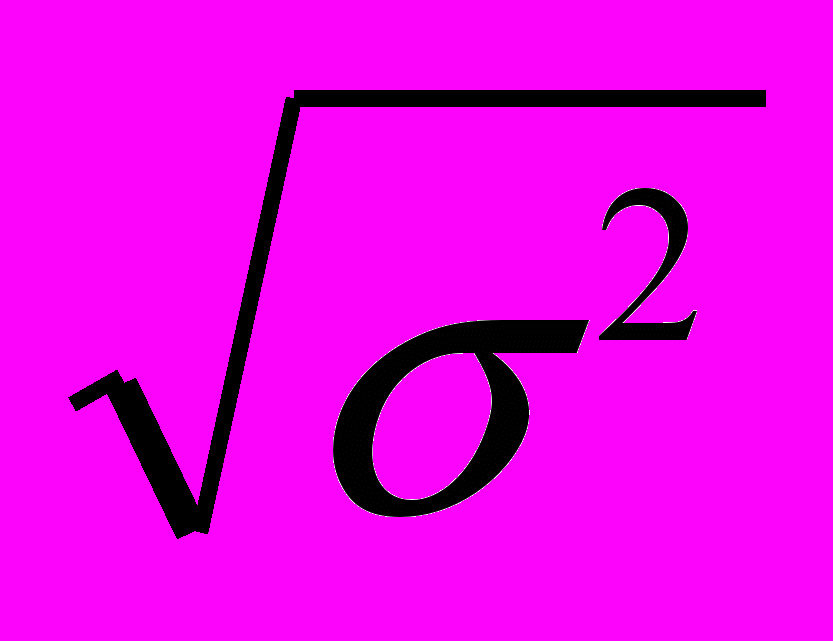= √ 141,352  11,889 тыс. чел.

Относительные показатели вариации:

Коэффициент осцилляции 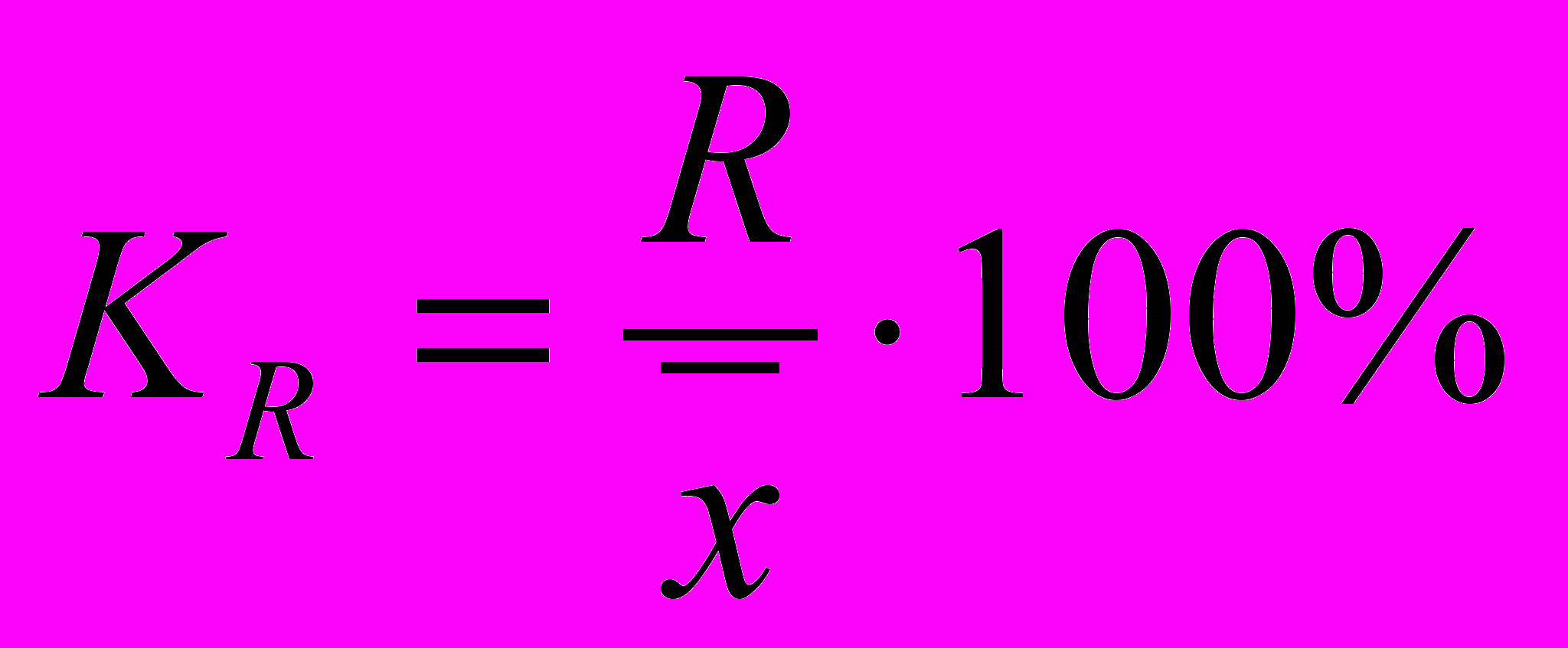= 64,4 : 14,617 ∙ 100 = 440,6%

Относительное линейное отклонение 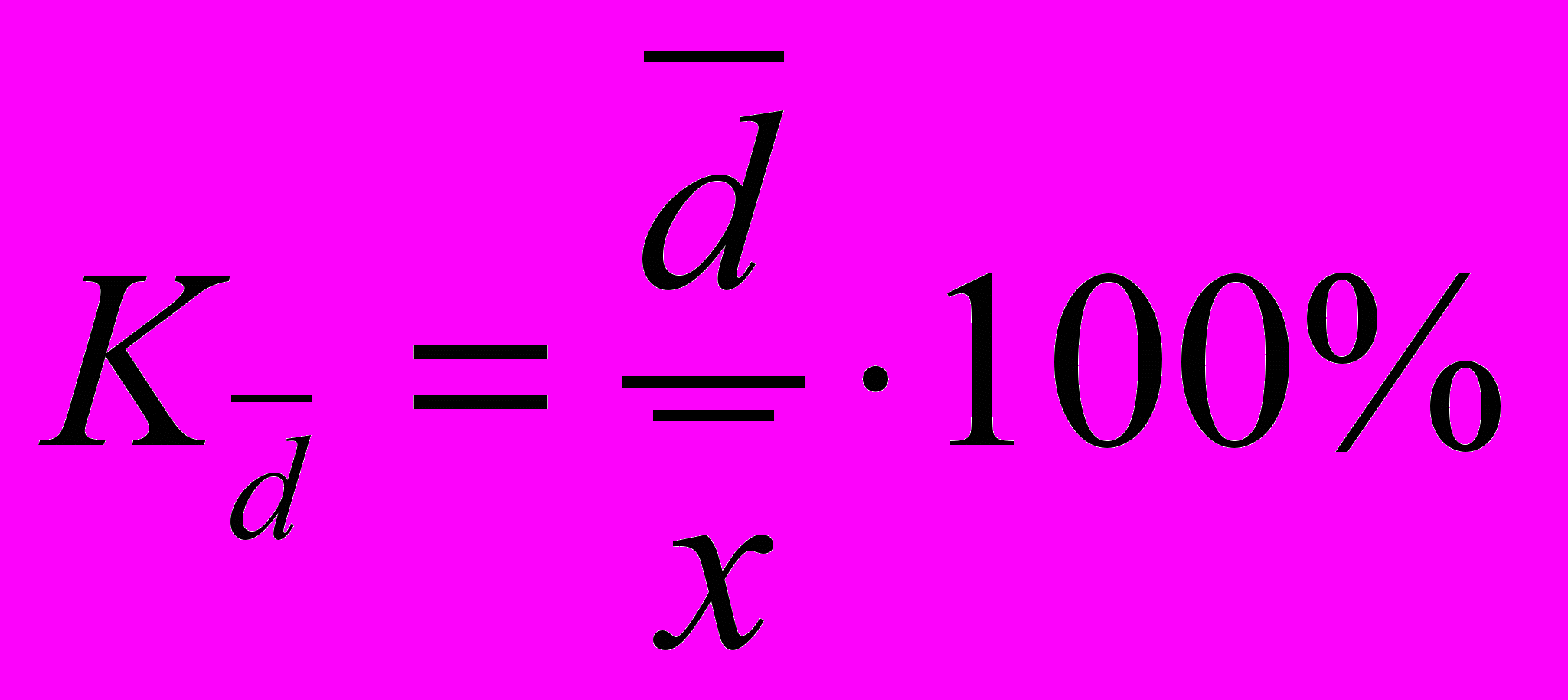= 8,34 : 14,617 ∙ 100 = 57,06%

Коэффициент вариации 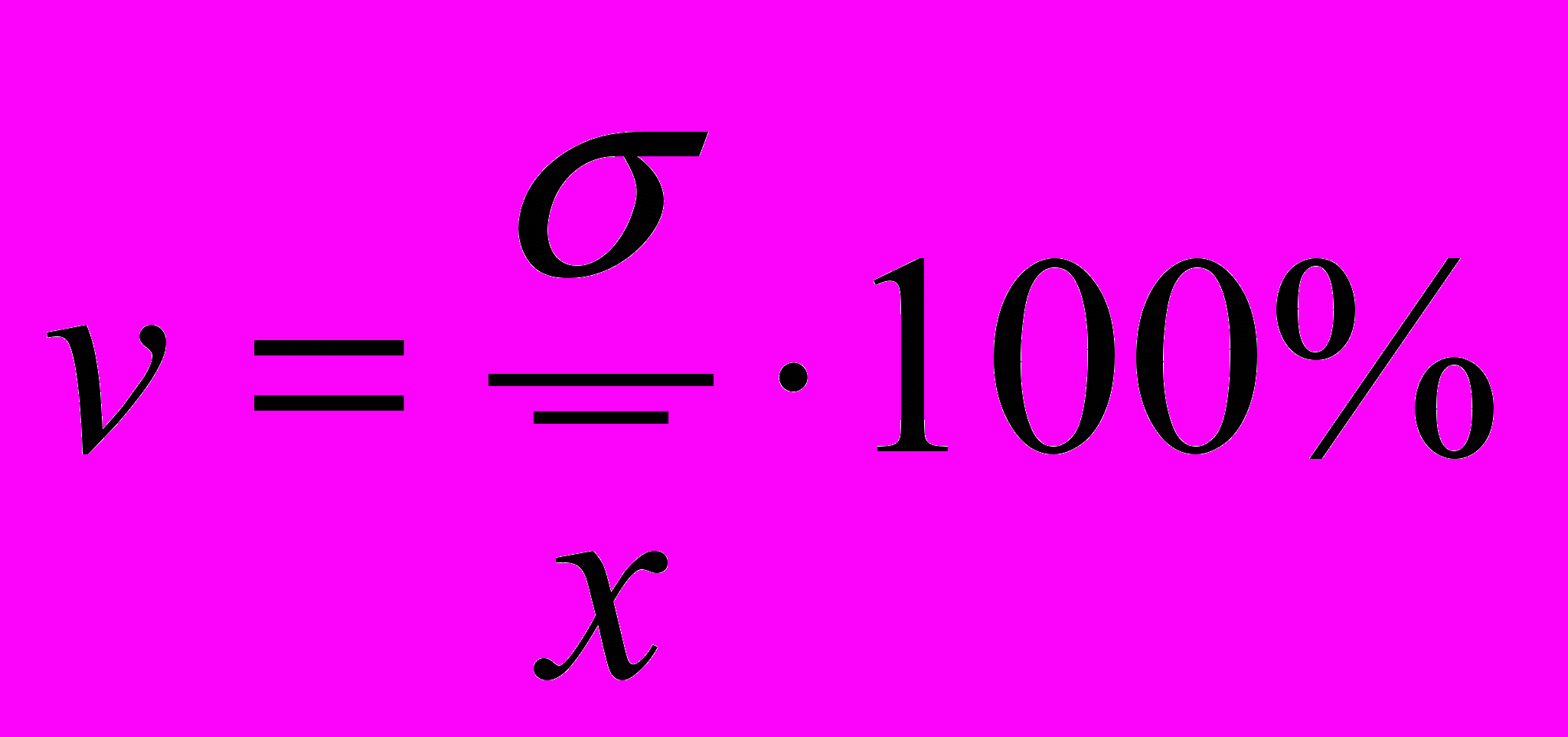= 11,89 : 14,617 ∙ 100 = 81,34 %

Выводы. Наиболее точными при анализе вариации являются среднее квадратическое отклонение и коэффициент вариации. Среднее квадратическое отклонение составило 11,89 тыс. чел. – это довольно большое значение, указывающее, что от среднего значения равного 14,62 тыс. чел. показатель по регионам может отклоняться на величину чуть меньшую средней.

Коэффициент вариации, равный 81,34% показывает, что численность безработных является неоднородной последовательностью, так как его значение намного больше 33%.

2.4. Корреляционно-регрессионный анализ

Таблица 3

Численность экономически активного населения, занятых и безработных в Российской Федерации в 2001-2008 годах

Годы
Число экономически активного населения, млн. чел.
Численность безработных, млн. чел.
Численность занятых, млн. чел.

1999
72,18
9,09
63,08

2000
71,46
7,00
64,47

2001
71,41
6,41
65,00

2002
72,42
6,82
65,60

2003
72,84
6,83
66,00

2004
72,91
6,51
66,40

2006
73,81
7,01
66,80

2008
74,19
6,99
67,20