Методические указания по выполнению практических занятий для студентов специальности 100403 "Организация перевозок и управления на транспорте"
| Вид материала | Методические указания |
- Методические указания для студентов по выполнению практических занятий по дисциплине, 1393.58kb.
- Методические указания для практических занятий для студентов специальности 060600 «Мировая, 422.63kb.
- Методические указания и контрольные задания для студентов-заочников образовательных, 984.59kb.
- Методические указания к выполнению практических работ по дисциплине "Организация предпринимательской, 669.56kb.
- Методические указания к проведению практических занятий по курсу «Архитектура гражданских, 272.14kb.
- Методические указания к выполнению практических занятий по курсу "Мониторинг и контроль, 263.92kb.
- Программа по специальности 190701 «Организация перевозок и управление на транспорте, 240.55kb.
- Методические указания к выполнению практических занятий для студентов специальности, 271.69kb.
- Учебно-методический комплекс по дисциплине грузоведение для специальности (направления), 289.45kb.
- Методические указания к выполнению практических занятий по дисциплине "Осложнения, 1155.63kb.
математическое МОДЕЛИРОВАНИЕ СИСТЕМ
План практического занятия
- Понятие о линейном программировании: задача программирования, классификация задач программирования, определение линейного программирования.
- Формулировка моделей линейного программирования.
Литература: [5], [8].
Методические указания
После изучения темы Вы должны:
| Знать | → | классификацию задач математического программирования |
| → | основные понятия математического программирования | |
| → | этапы построения линейной модели | |
| → | примеры задач линейного программирования |
| Уметь | → | определять множество технологических процессов |
| → | определять: систему ингредиентов, которые потребляются или производятся технологическими процессами, коэффициенты затрат-выпуска | |
| → | составлять уравнения материального баланса |
Ключевые понятия: целевая функция, системы линейных уравнений и неравенств, транспортная задача, аддитивность, план для системы.
Рассмотрим примеры задач линейного программирования.
Известная загрузка каждого цеха aij (оцениваемое в данном случае в процентах) при изготовлении любого из изделий и прибыль от реализации ci. Нужно определить, сколько изделий каждого вида следует делать при возможно полной загрузке цехов, чтобы получить за период, который рассматривается максимальную прибыль.
| Изделие, i | Цех, j | Прибыль от реализации i-го изделия | ||
| 1 | 2 | 3 | ||
| 1 | 5% | 1,6% | 2,9% | 240 у.е. |
| 2 | 4% | 6,4% | 5,8% | 320 у.е. |
| Максимальная загрузка | 100% | 100% | 100% | |
Целевая функция в данном случае будет иметь вид:
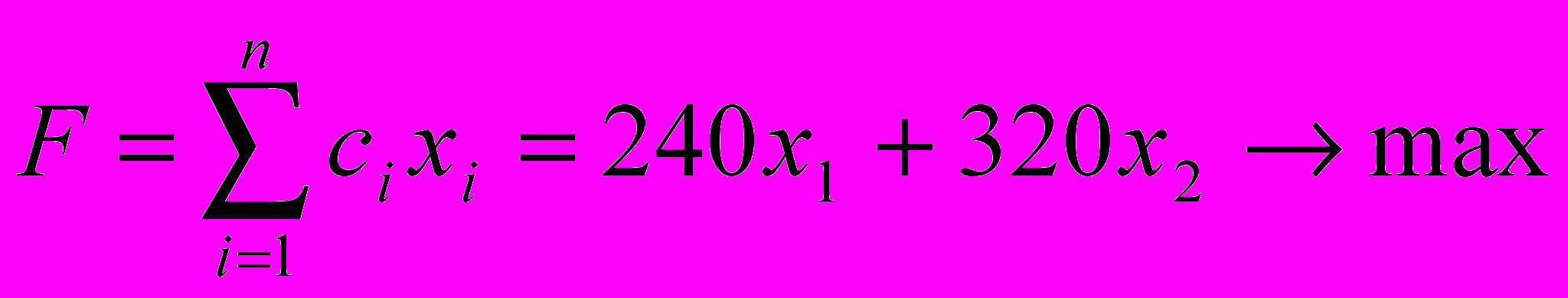
а ряд ограничений (в данном случае определяются возможностями цехов, то есть их граничной 100% загрузкой):
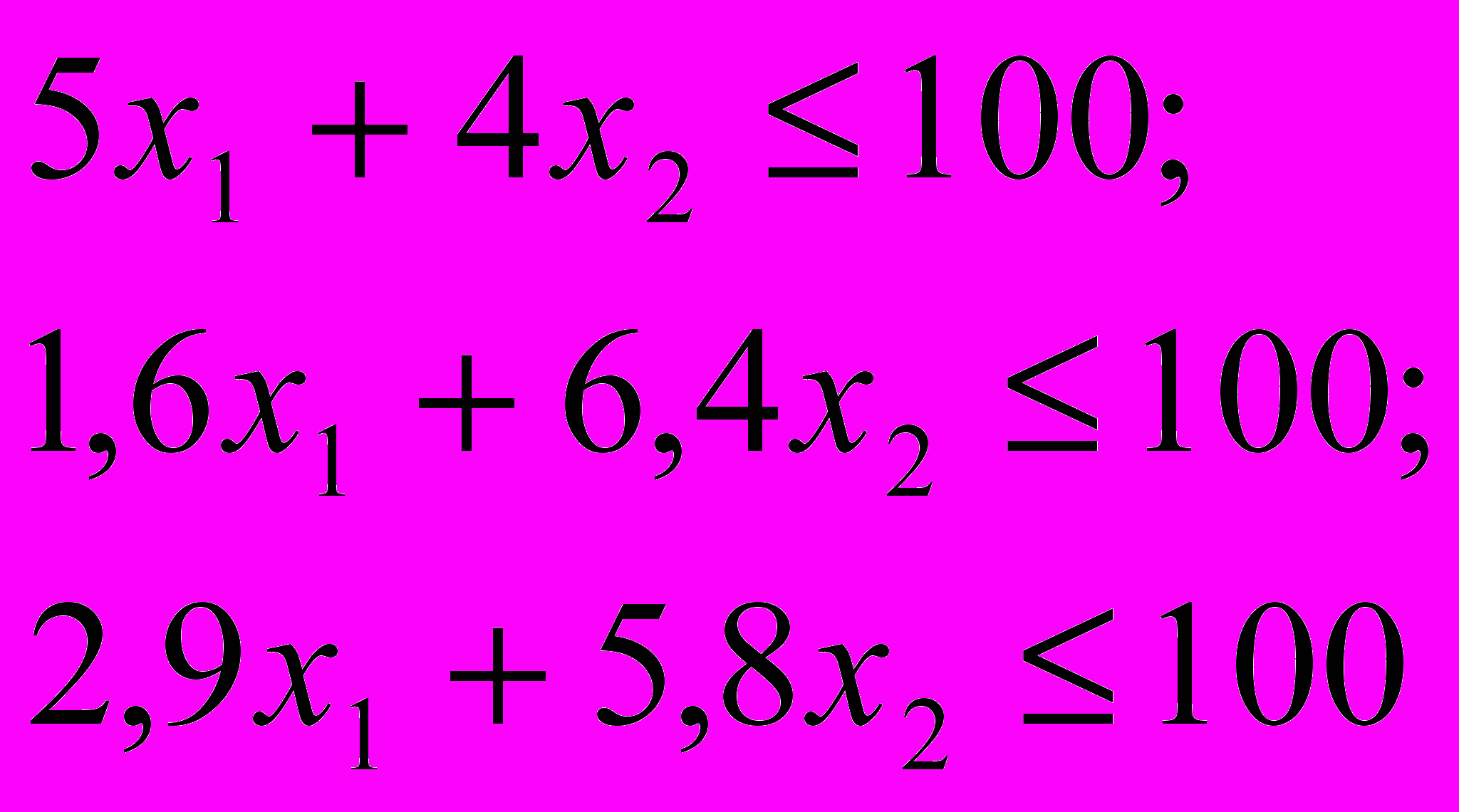
или в общем виде:
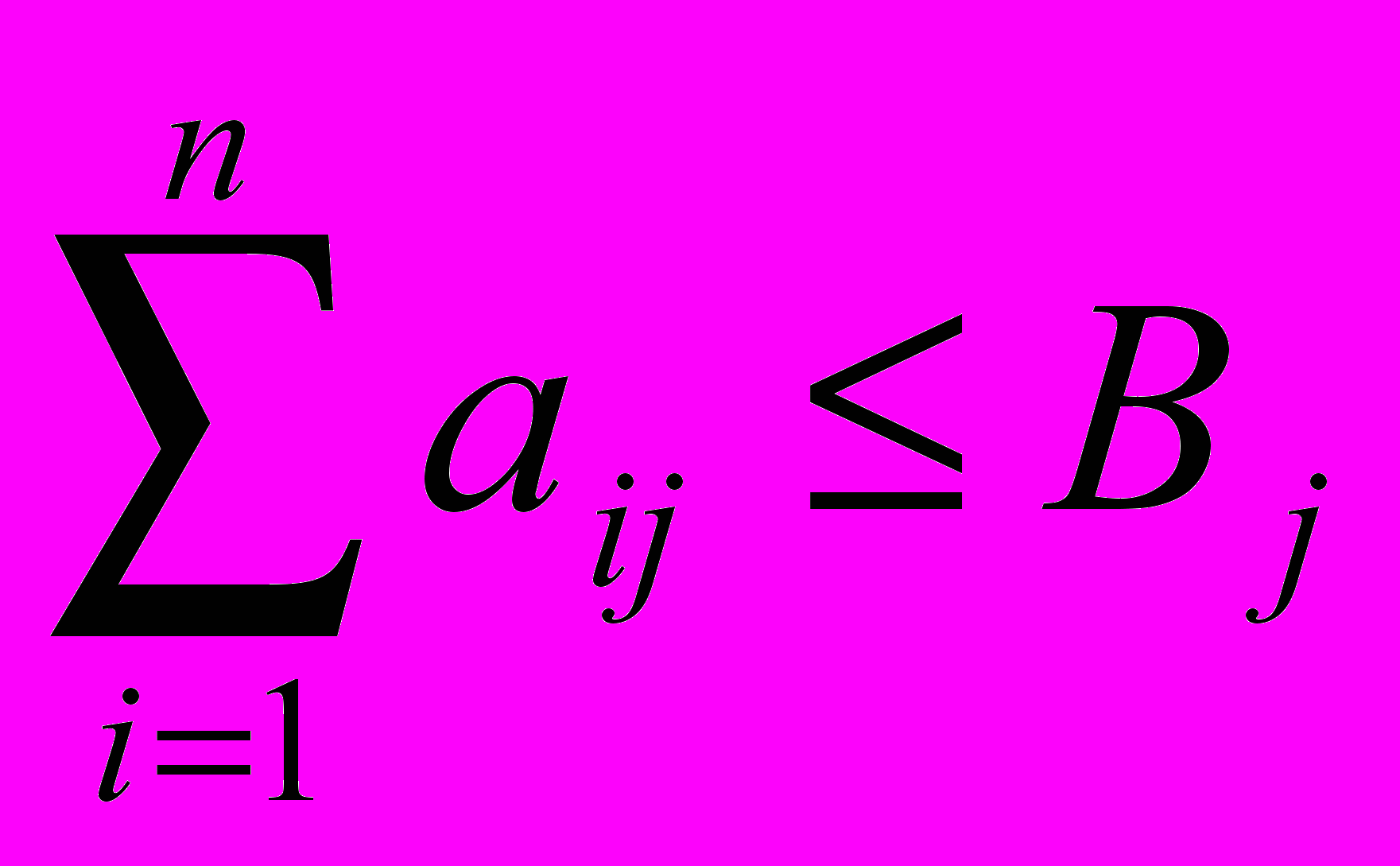
Задача про банк.
Пусть собственные средства банка в суме с депозитами составляет 100 млн. дол. Часть этих средств, но не меньше 35 млн. дол. должна находится в кредитах. Кредиты есть неликвидными активами банка, потому что в случае непредвиденной потребности в наличных обратить кредиты в деньги без существенных трат невозможно. Существует правило, соответственно с которым коммерческие банки должны покупать в определенной пропорции ликвидные активы, которые компенсируют неликвидность кредитов. В данном примере ликвидные активы должны составлять не менее 30% средств, размещенных в кредитах и ценных бумагах.
Пусть x – средства (млн. дол.), размещенные в кредитах, y – средства, вложенные в ценные бумаги.
Имеем следующую систему линейных ограничений:
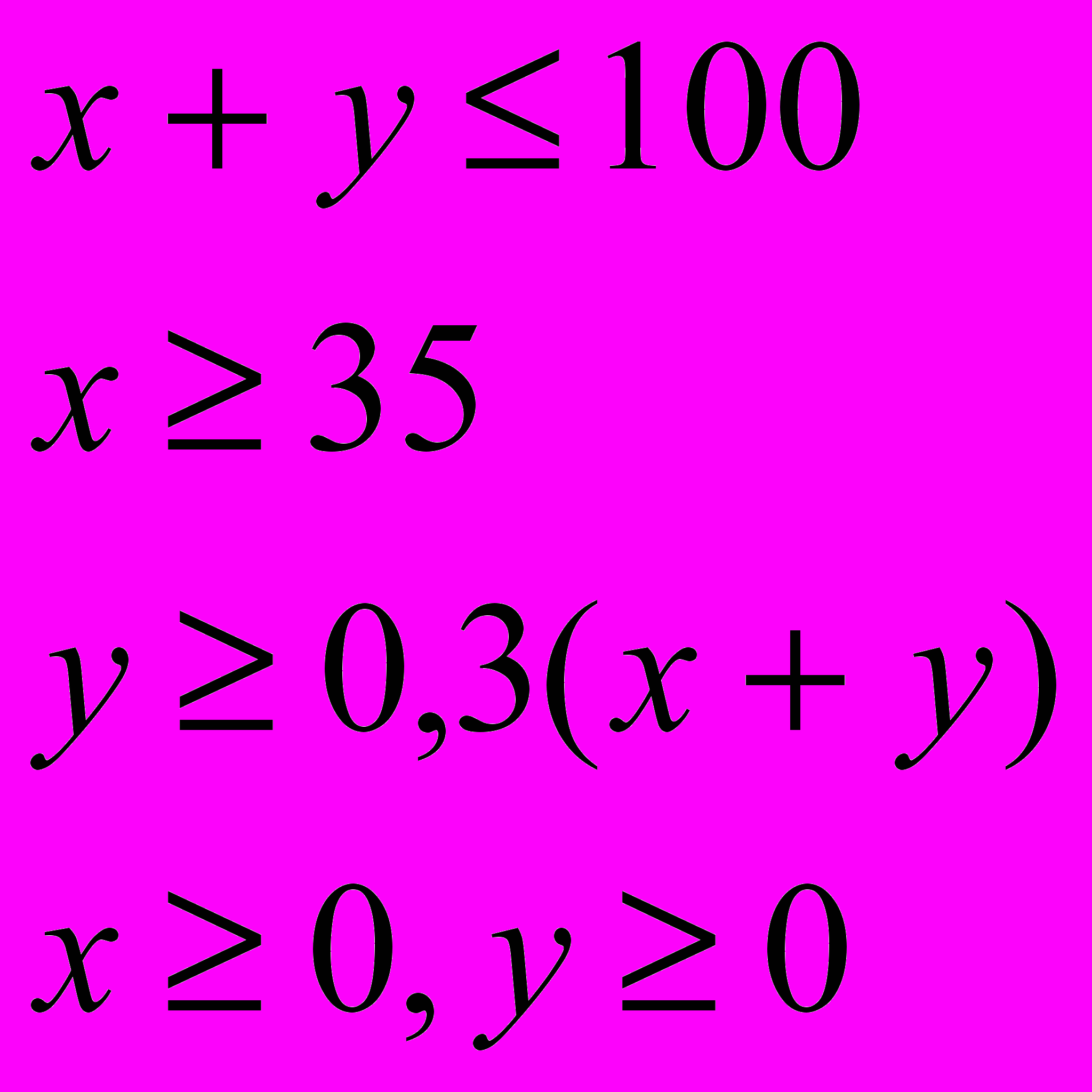
Цель банка состоит в том, чтобы достать максимальную прибыль от кредитов и ценных бумаг:
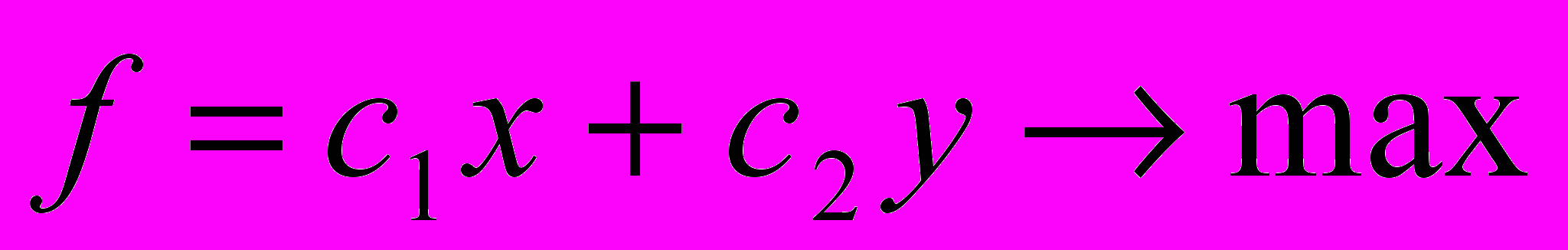,где з1 – прибыльность кредитов, з2 – прибыльность ценных бумаг.
Задача про диету.
С имеемых в нашем распоряжении продуктов необходимо сложить такую диету, которая б с одной стороны, удовлетворяла минимальные потребности организма в питательных веществах (белках, жирах, углеводах, минеральных солях, витаминах), с другой стороны - требовала б наименьших затрат.
Рассмотрим простую математическую модель этой задачи.
Пусть имеются два вида продуктов: П1 і П2 , которые содержат питательные вещества А, У, С. В 1 кг продуктов П1 и П2 содержится определенное количество питательных того или иного вида:
| | А | У | З |
| В 1 кг П1 | a1 | b1 | c1 |
| В 1 кг П2 | a2 | b2 | c2 |
Кроме этих данных нам известны: a, b, c – суточные потребности организма в питательных веществах А, У, С и s1, s2 – стоимость 1 кг продуктов П1 и П2. Необходимо рассчитать количество х1 продукта П1 и х2 продукта П2 так, что бы обеспечить необходимое количество питательных веществ при минимальных затратах на продукты. Очевидно, общая стоимость продуктов будет
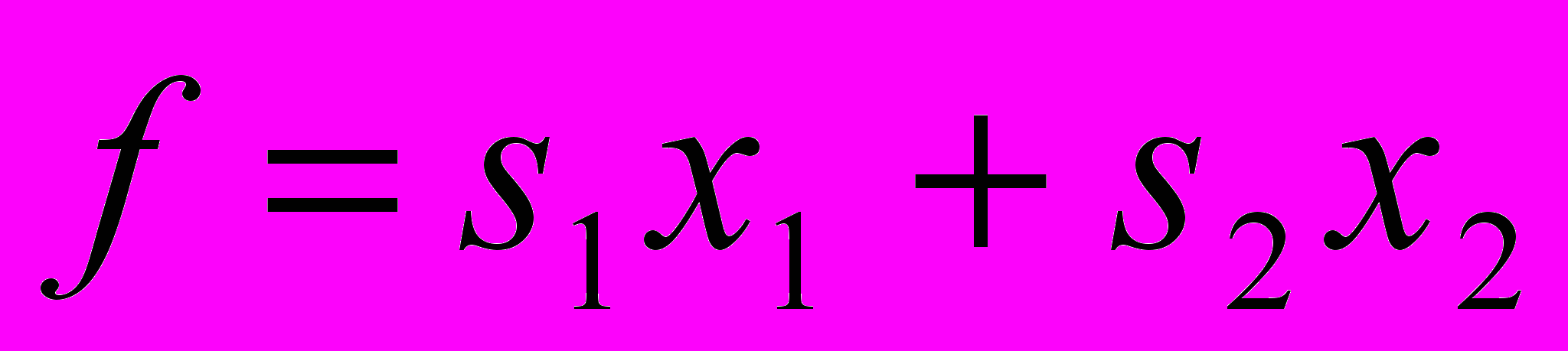.Общее количество веществ А в обоих видах продуктах равняется
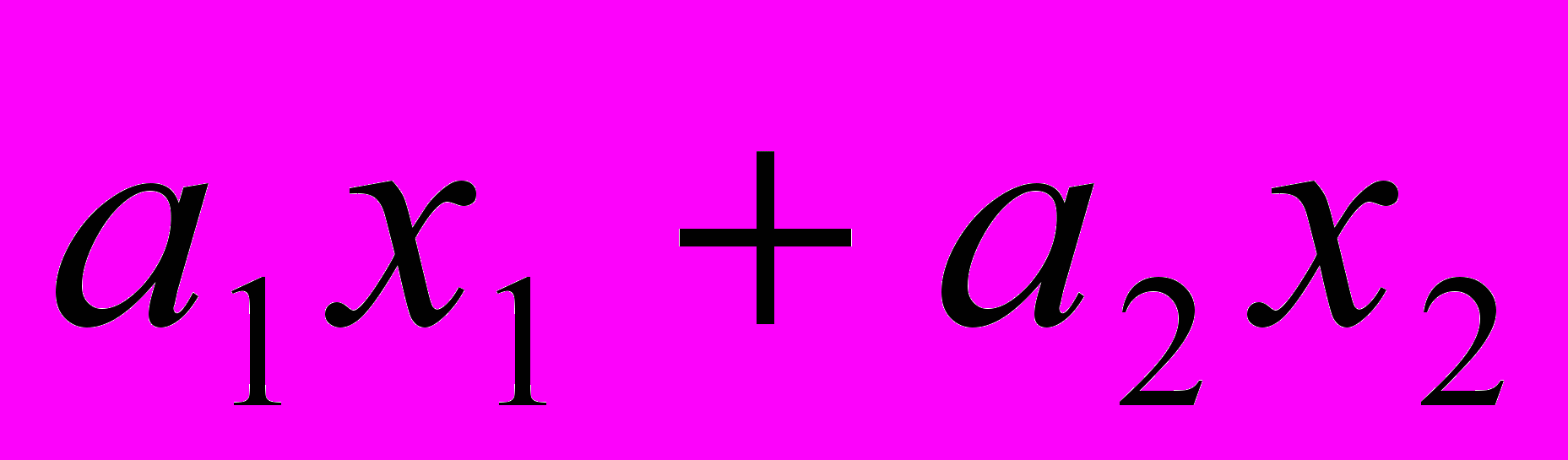. Оно должно быть не менее а: 
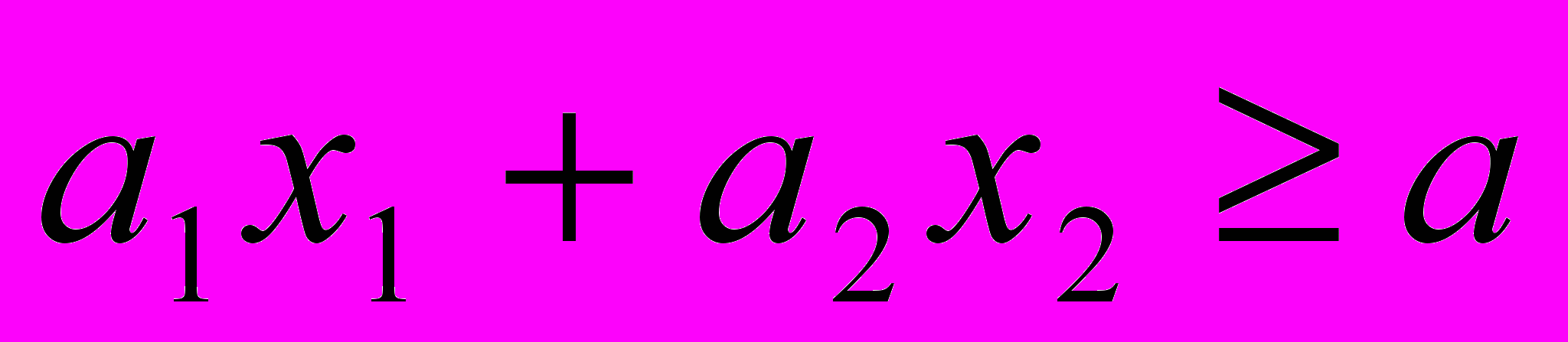.Аналогичные неравенства должны выполнятся для В и С. Таким образом, перед нами задача линейного программирования.
Дано систему
Необходимо выбрать такое количество х1 продукта П1 и х2 продукта П2, при котором функция
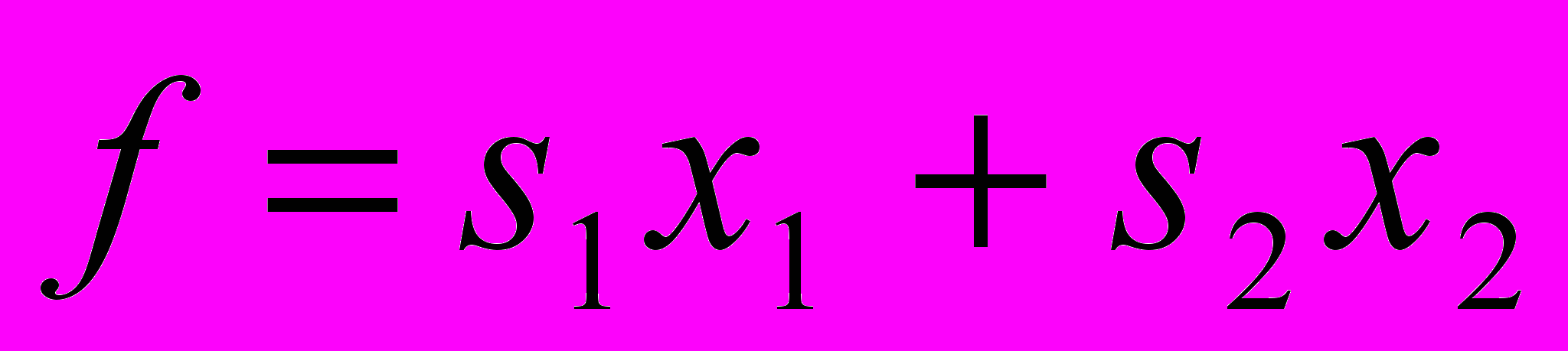достигает наименьшего значения.Задача об использовании ресурсов.
Предприятие имеет в своем распоряжении определенное количество ресурсов: рабочую силу, деньги, сырье, оборудование, производственные ресурсы, площади и т.п. Допустим, ресурсы трех видов R1, R2, R3 имеются в количестве соответственно b1, b2, b3 у.е. Предприятие выпускает два вида товаров T1, T2. Причем известно, сколько единиц каждого ресурса необходимо для производства единицы каждого товара. Пусть
- число единиц ресурса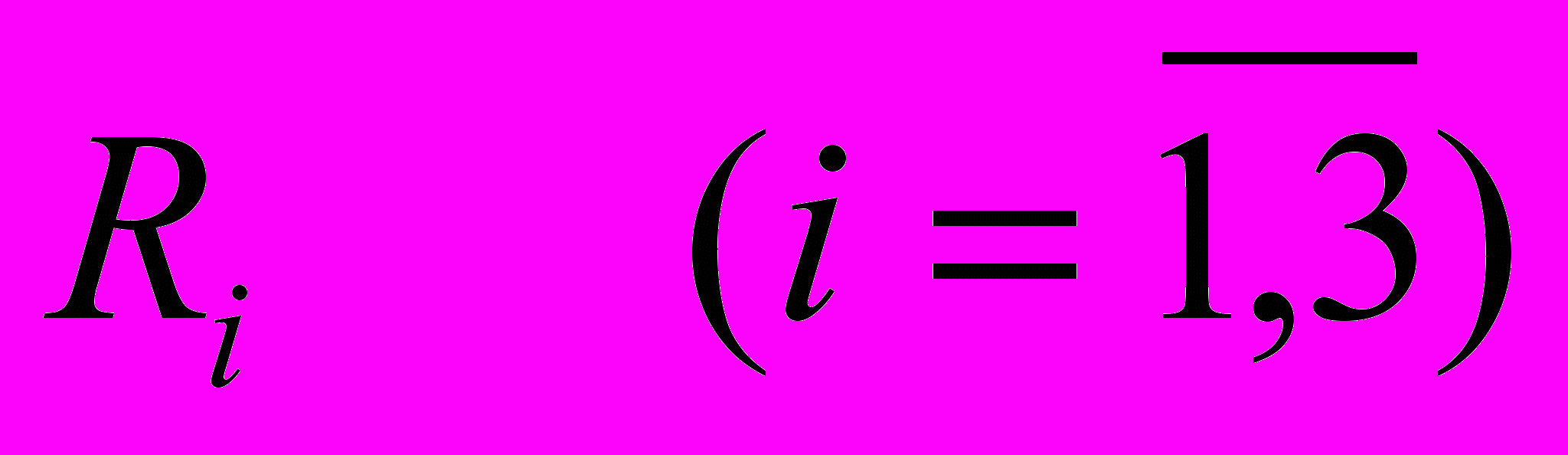 
, необходимое для производства единицы товара 
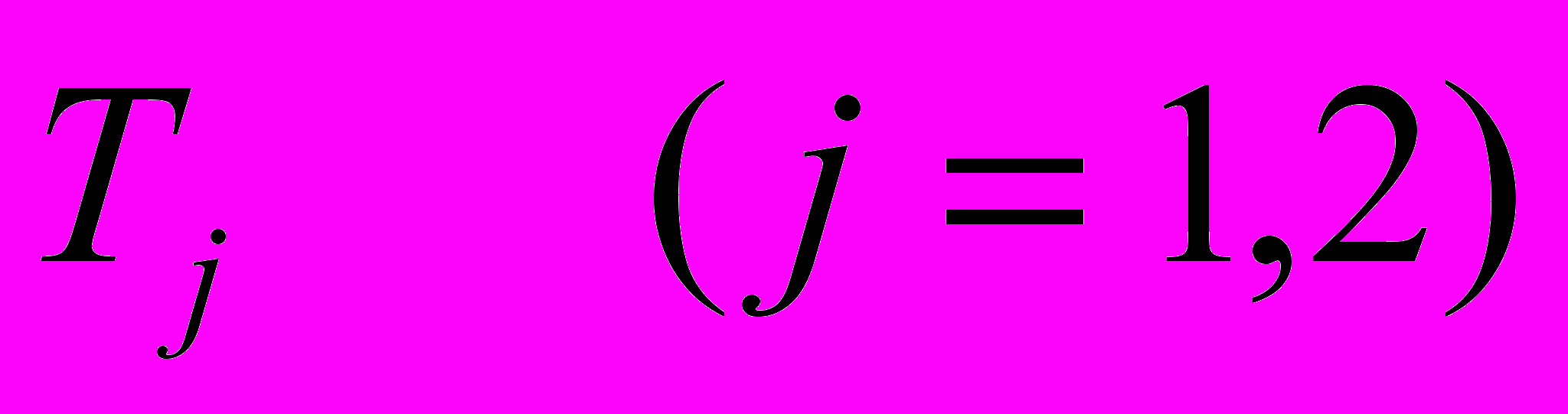. Доход, получаемый предприятием от единицы каждого вида товаров, соответственно равняется с1, с2. Необходимо при данных ресурсах выпустить такую комбинацию товаров, при которой доход предприятия оказался бы максимальным.Обозначим через х1 и х2 соответственно количество товаров T1, T2. Очевидно, доход предприятия
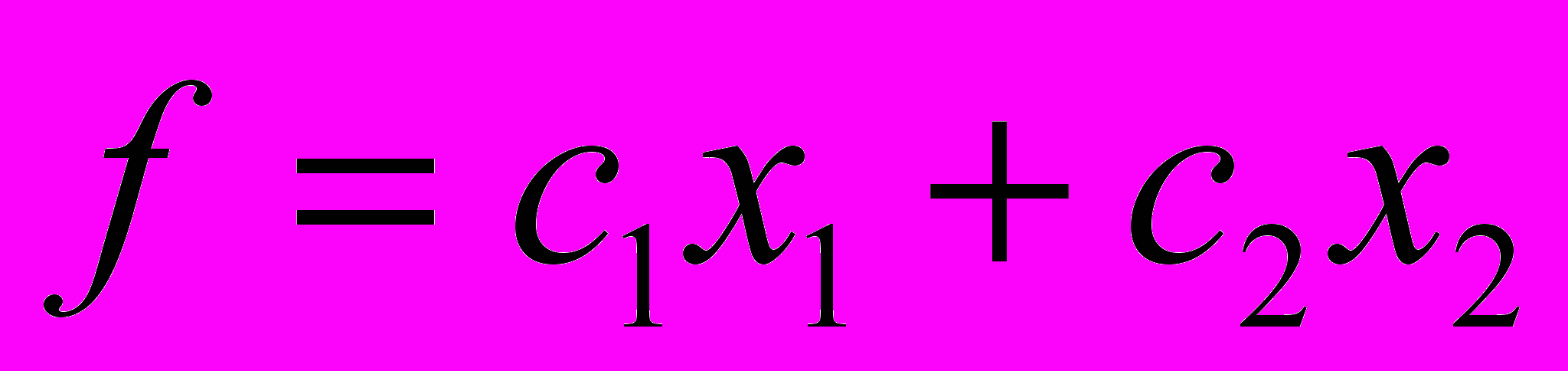.Итак, математическая задача об использовании ресурсов складывается в определении значений неизвестных х1 и х2 , что удовлетворяют условиям:
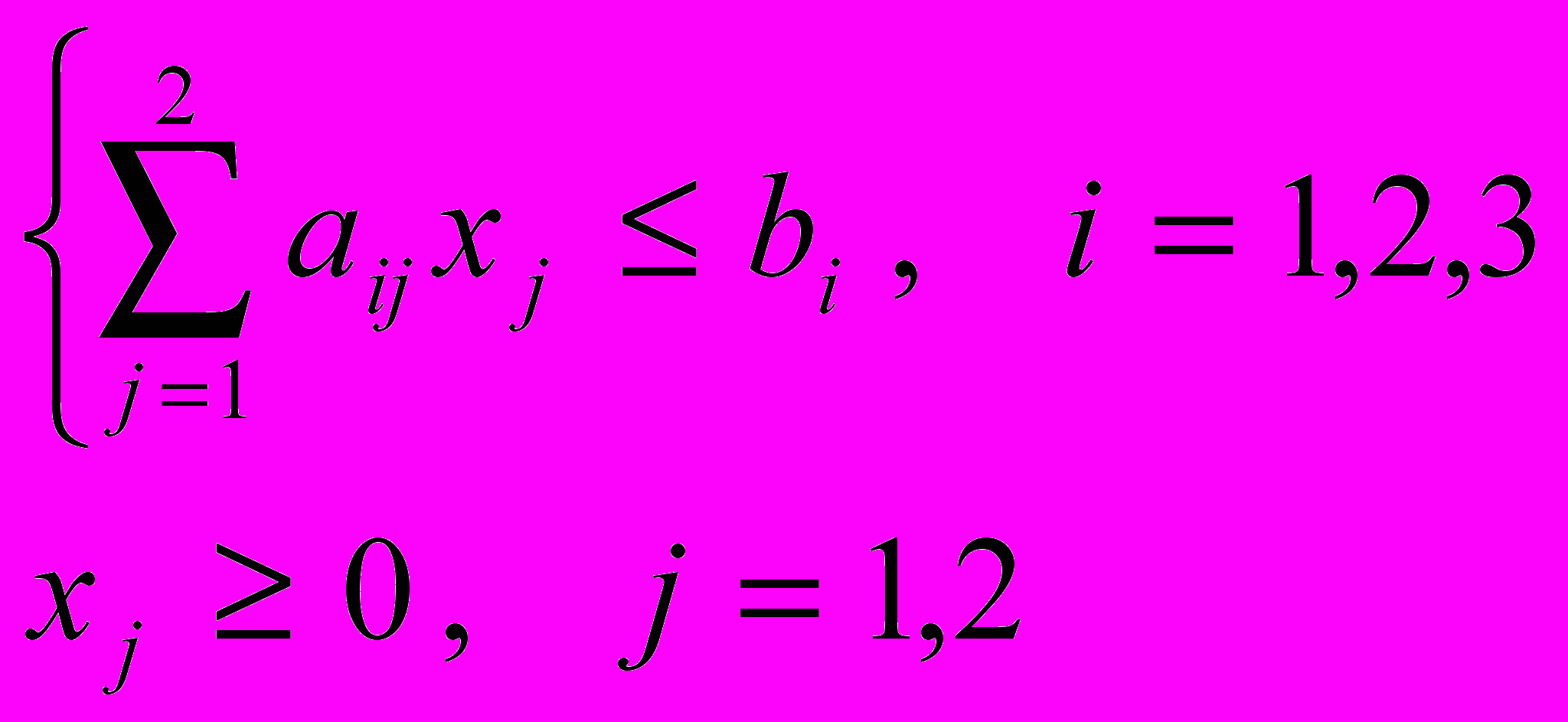
и максимизирующих функцию
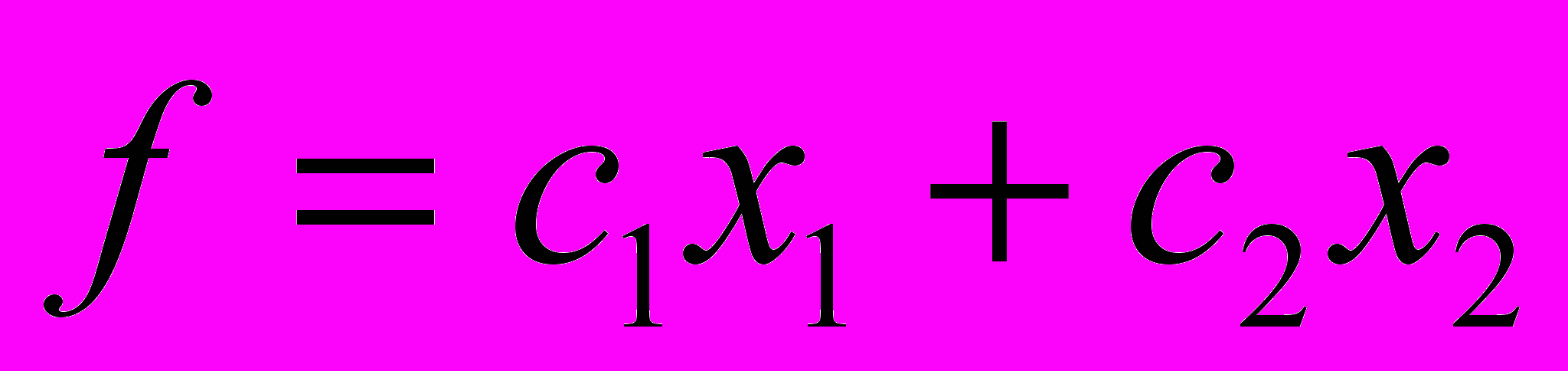.Задание для проверки знаний
Составьте математические модели задач 1, 2
Задача 1.
В трех пунктах отправления сосредоточен однородный груз в количествах, соответственно равных 420, 380 и 400 т. Этот груз необходимо перевезти в три пункта назначения в количествах, соответственно равных 260, 520 и 420 т. Стоимости перевозок 1 т груза из каждого пункта отправления в каждый пункт назначения есть известными величинами и задаются матрицей
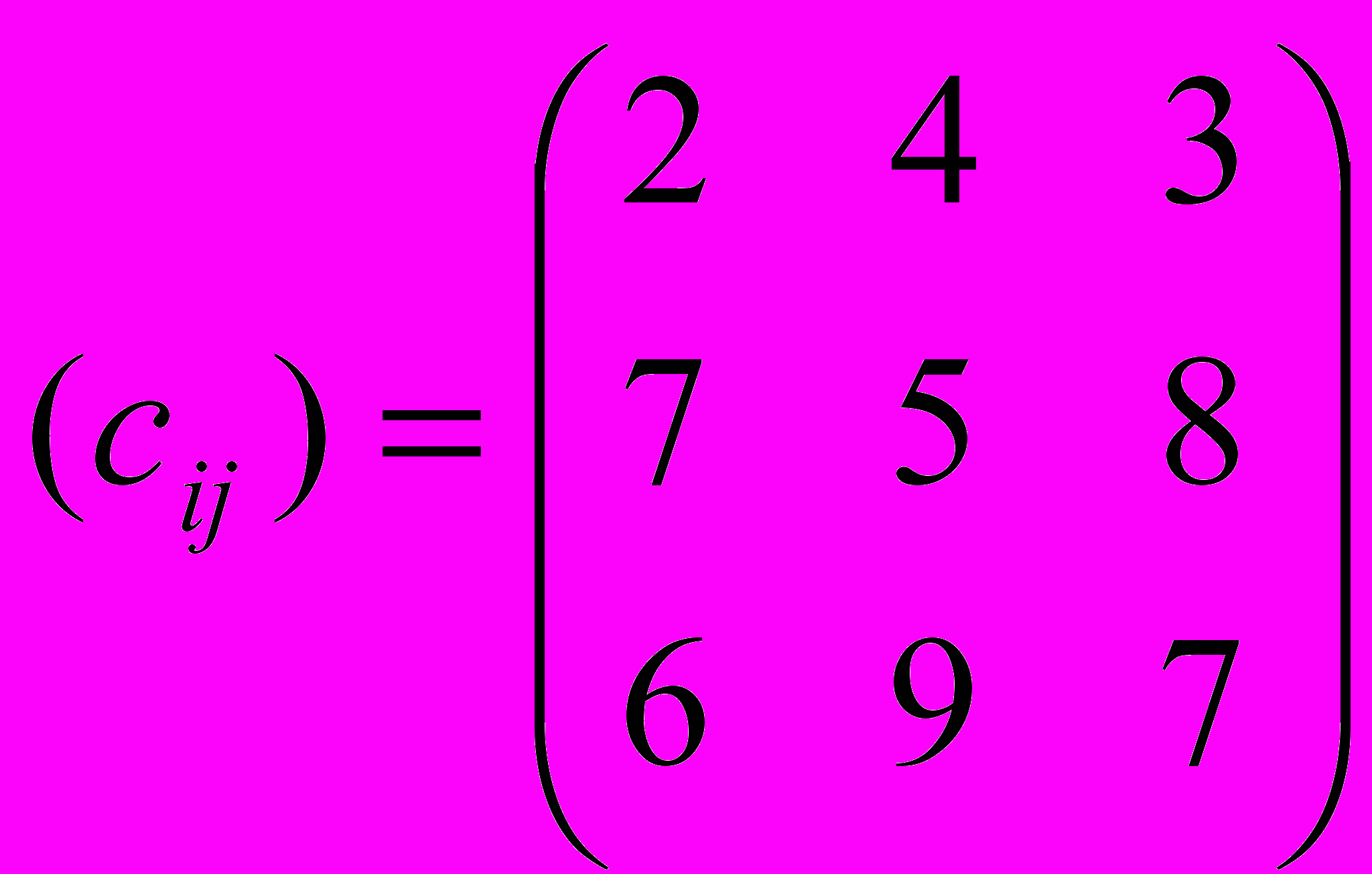. Найти план перевозок, который обеспечивает вывоз имеющегося в пунктах отправления и завозки необходимого в пунктах назначения груза при минимальной общей стоимости перевозок.
Задача 2.
Кондитерская фабрика для производства трех видов карамели А, В и С использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Нормы затраты сырья каждого вида на производство 1 т карамели данного вида приведенные в таблице.
В ней же указанное общее количество сырья каждого вида, которое может быть использовано фабрикой, а также наведена прибыль от реализации 1 т карамели данного вида.
Найти план производства карамели, который обеспечивает максимальную прибыль от ее реализации.
| Вид сырья | Нормы трат сырья (т) на 1 т карамели | Общее количество сырья (т) | ||
| а | в | с | | |
| Сахарный песок | 0,8 | 0,5 | 0,6 | 800 |
| Патока | 0,4 | 0,4 | 0,3 | 600 |
| Фруктовое пюре | - | 0,1 | 0,1 | 120 |
| Прибыль от реализации 1 т продукции, у.е. | 108 | 112 | 126 | |
Практическое занятие № 7
ОСОБЕННОСТИ МЕТОДОЛОГИЙ СИСТЕМНОГО АНАЛИЗА
План практического занятия
- Содержание системных методологий решение сложных проблем.
- Анализ методологий системного решения проблем.
- Прикладные применения методологий системного анализа.
Литература: [1-3], [6], [9].