Методические указания к выполнению практических занятий для студентов специальности 150405. 65 «Машины и оборудование лесного комплекса»

Вид материала

Содержание

Основы теории
Общие положения
Общие понятия и терминология
2. Основные виды и показатели надежности
N — начальное число работающих изделий; п
N, то в конце наблюдения число работоспособных изделий и вероятность безотказной работы будут равны нулю: N
N (наблюдений, измерений) опытное значение λ
Нормальный закон
Экспоненциальный закон.
Закон Вейбулла.

Подобный материал:

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Тихоокеанский государственный университет»

Утверждаю в печать

Ректор университета

д.т. н., проф. _______С. Н. Иванченко

«___»____________________ 2010 г.

ОСНОВЫ ТЕОРИИ

НАДЕЖНОСТИ МАШИН

Методические указания к выполнению практических занятий

для студентов специальности 150405.65

«Машины и оборудование лесного комплекса»

Рассмотрена и рекомендована к изданию кафедрой

«Машины и оборудование лесного комплекса»

Зав. кафедрой, профессор В.А. Иванов

«___»______________ 201__ г.

Рассмотрена и рекомендована к изданию методическим советом института природопользования и экологии

Председатель совета ИПЭ, профессор П.Б. Рябухин

«___»______________ 201__ г.

Нормоконтроль, доцент С.П. Захарычев

Хабаровск

Издательство ТОГУ

2011

ОСНОВЫ ТЕОРИИ

НАДЕЖНОСТИ МАШИН

Хабаровск 2011

УДК 634.03 (075)

Основы теории надежности машин: Методические указания к выполнению практических занятий для студентов специальности 150405.65 «Машины и оборудование лесного комплекса»./ Сост. С.П. Захарычев. – Хабаровск: Изд-во Тихоокеан. гос. ун-та, 2011. – 48 с.

Методические указания разработаны на кафедре «Машины и оборудование лесного комплекса» применительно к учебному плану специальности 150405.65 для изучения дисциплины «Основы теории надежности машин».

Приведены теоретические положения и изложены основные методические рекомендации для решения задач по оценке надежности основных агрегатов и машин, позволяющие в дальнейшем планировать организацию технического обслуживания машин при эксплуатации их в реальных природно-климатических условиях Дальнего Востока.

Печатается в соответствии с решениями кафедры «Машины и оборудование лесного комплекса» и методического совета Института природопользования и экологии.

© Тихоокеанский государственный

университет, 2011

ОБЩИЕ ПОЛОЖЕНИЯ

В методических указаниях изложены основные теоретические модели и применяемые вероятностные и статистические методы расчетов основных показателей надежности различных агрегатов и машин, лимитирующих их сроки применения и себестоимость эксплуатации и ремонта.

Проблема надежности в последнее время приобрела исключительно важное значение. Недостаточный уровень надежности машин вызывает большой материальный ущерб, а иногда и человеческие жертвы.

Основные направления научно-техничекого прогресса в области машиностроения связаны с непрерывным ростом сложности используемых машин, вызываемой интенсификацией и усложнением работ, выполняемых современными машинами. Растет энерговооруженность машин, скорость выполнения ими требуемых операций, уровень их автоматизации.

Процесс создания машин непрерывно связан с повышением их качества и надежности. Под качеством понимается совокупность свойств машины, определяющих степень ее пригодности к выполнению заданных функций при использовании по назначению. К основным качественным свойствам машины относятся: грузоподъемность, производительность, надежность, топливная экономичность, динамичность, комфортабельность и др. [1]. Большинство качественных свойств машины ухудшается в процессе ее эксплуатации. Связано это, прежде всего с тем, что элементы машин, связаны между собой неподвижными и подвижными соединениями в виде различных кинематических пар. Они выполняют требуемые перемещения и испытывают переменные внешние и внутренние нагрузки. Скорость перемещений и величины внешних нагрузок в современных машинах постоянно растут. Соответственно, растут амплитуды и частоты переменных напряжений в опасных сечениях деталей машин. Это приводит к усталости материалов, возникновению усталостных трещин и к усталостным поломкам. Кроме того, машины и их детали работают в различных условиях физического трения, вызывающего износ трущихся поверхностей кинематических пар (подшипников, направляющих, колес). Все это сокращает срок службы и вызывает со временем отказы машин – неспособность выполнять требуемую работу.

ОБЩИЕ ПОНЯТИЯ И ТЕРМИНОЛОГИЯ

Основные термины и определения, используемые в теории надежности, регламентированы ГОСТ 13377-75 [2].

Надежность – свойство технического объекта выполнять заданные функции, сохраняя во времени значения установленных эксплуатационных показателей в требуемых пределах, соответствующим заданным режимам и условиям использования, технического обслуживания (ТО), ремонта, хранения и транспортирования. Под техническим объектом здесь понимается предмет определенного целевого назначения, например, машина или ее части: агрегаты, узлы, отдельные детали.

Надежность является комплексным свойством, которое в зависимости от назначения машины и условий ее эксплуатации может включать сочетание свойств безотказности, долговечности, ремонтопригодности и сохраняемости как для всего объекта, так и для его частей – деталей, узлов, агрегатов.

Безотказность – свойство объекта непрерывно сохранять работоспособность в течение некоторого времени или наработки.

Долговечность – свойство объекта сохранять работоспособность до наступления предельного состояния при установленной системе технического обслуживания и ремонтов.

Ремонтопригодность – свойство объекта, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения его отказов и устранению их последствий путем проведения ремонтов и технического обслуживания.

Сохраняемость – свойство объекта непрерывно сохранять исправное и работоспособное состояние в течение и после хранения и транспортирования.

Перечисленные свойства имеют разную значимость в зависимости от вида технического объекта и условий его эксплуатации. Все объекты делятся на ремонтируемые, неремонтируемые, восстанавливаемые и невосстанавливаемые. Термины «восстанавливаемый» и «невосстанавливаемый» объект не заменяют собой понятия «ремонтируемый» и «неремонтируемый» объект. Первые характеризуют условия восстановления объекта в конкретных условиях эксплуатации, а вторые – свойства объектов, т.е. возможность устранения повреждений и отказов путем ремонтов. Такое деление объектов носит условный характер и может меняться в зависимости от конкретных условий.

Для некоторых неремонтируемых объектов (поршневые кольца ДВС, электрические лампочки и др.) определяющим свойством является безотказность. Для машин кратковременного или сезонного действия (лесопосадочные машины) важное значение приобретают сохраняемость и безотказность. Для ремонтируемых объектов длительного пользования одним из важнейших свойств надежности является их ремонтопригодность.

Все объекты с точки зрения надежности могут находиться в исправном, неисправном, работоспособном, неработоспособном и предельном состояниях.

Исправное состояние – это состояние, при котором объект соответствует всем требованиям, установленным нормативно-технической документацией (НТД).

Неисправное состояние – это такое состояние, при котором объект не соответствует хотя бы одному из требований НТД.

Работоспособное состояние – состояние объекта, при котором он способен выполнять заданные функции, сохраняя значение заданных параметров в пределах, установленных НТД.

Неработоспособное состояние – состояние объекта, при котором значение хотя бы одного заданного параметра не соответствует требованиям НТД.

Предельное состояние – состояние объекта, при котором его дальнейшая эксплуатация должна быть прекращена из-за неустранимого нарушения требований безопасности, или неустранимого ухода заданных параметров за пределы требований НТД. Понятие исправность шире, чем понятие работоспособность. Работоспособный объект может быть неисправным, однако его неисправность при этом не настолько существенна, чтобы нарушить нормальную работу (вмятины на облицовке, царапины на лакокрасочном покрытии и др.).

Исходными понятиями надежности являются понятия повреждения и отказа.

Повреждения – это событие, заключающееся в нарушении исправности объекта или его составных частей вследствие влияния внешних воздействий, превышающих уровни параметров, установленных в НТД для объекта. Повреждение может быть существенным и несущественным, при котором работоспособность объекта сохраняется.

Отказ – событие, заключающееся в нарушении работоспособности объекта. Признаки (критерии) отказов должны устанавливаться в НТД. Отказ является более узким понятием, чем повреждение.

Нарушение работоспособности машин в процессе эксплуатации происходит в результате появления отказов, которые имеют разнообразный характер и причины. При анализе отказов используют их классификацию по целому ряду признаков.

Различают:

внезапный отказ – отказ, характеризующийся скачкообразным изменением одного или нескольких заданных параметров объекта;
постепенный отказ, характеризующийся постепенным изменением одного или нескольких заданных параметров объекта;
независимый отказ – отказ элемента объекта, необусловленный повреждением или отказами других элементов объектов;
зависимый отказ – отказ элемента объекта, обусловленный повреждением или отказами других элементов объектов;
сбой – самоустраняющийся отказ, приводящий к кратковременному нарушению работоспособности объекта;
перемежающийся отказ – многократно возникающий сбой одного и того же характера;
конструкционный отказ – отказ, возникающий в результате нарушения установленных правил и норм конструирования;
производственный отказ – отказ, возникший в результате нарушения установленного процесса изготовления или ремонта объекта;
эксплуатационный отказ – отказ, возникший в результате нарушения установленных правил и норм эксплуатации объекта;
систематический отказ – многократно повторяющийся отказ, обусловленный дефектами конструкции объекта, нарушением процесса его изготовления, низким качеством используемых материалов и др.;
частичный отказ – отказ, после возникновения которого объект может быть использован по назначению, но с меньшей эффективностью;
полный отказ – отказ, после возникновения которого объект не может быть использован по назначению;

Применительно к отказу и повреждению рассматривают критерий, причину, признаки, характер и последствия.

Критериями отказа являются признаки позволяющие установить факт нарушения работоспособного состояния. Наиболее распространенными критериями отказов машин являются трещины, износ, нарушения регулировок и т.д.

Причинами отказов являются непосредственные или косвенные воздействия, нарушения правил или норм, допущенные при конструировании, производстве и эксплуатации машин, ремонте объектов, а также естественные процессы изнашивания и старения материалов деталей.

Кроме общей классификации отказов, единой для всех технических систем, для отдельных групп машин в зависимости от их назначения и характера работы применяется дополнительно классификация отказов по сложности их устранения. Для лесозаготовительных машин и оборудования все отказы по сложности их устранения объединяют в три группы. При этом учитывают такие факторы, как способ устранения, необходимость разборки и трудоемкость устранения отказов – табл. 1.

Таблица 1. Группы сложности отказов лесных машин т оборудования

Группа слож- ности	Способ устранения отказа	Место устранения отказа	Место распо- ложения	Необходи-мость разборки	Трудоем-кость, чел.-ч.
I II III	Частичная регулировка, прочистка или замена Регулировка, ремонт, замена детали Ремонт, замена узла или агрегата	На месте эксплуата-ции с использованием индивидуального ЗИП^٭ На месте эксплуата-ции или в РММ^٭ с использованием группового ЗИП и табельных средств ТО В специальных условиях с использованием ремонтного ЗИП	Снаружи узлов или агрегатов Снаружи и внутри узлов (легкая доступность) Внутри узлов и агрегатов (доступность затруднена)	Без раз- борки Частичная разборка Разборка и расчленение основных агрегатов	≤ 1 ≤ 8 > 8

Признаками отказов называются непосредственные или косвенные воздействия на органы чувств наблюдателя явлений, характерных для неработоспособного состояния объектов (падение давления масла, появление стуков, изменение температурного режима и т.д.). Характером отказа (повреждения) являются конкретные изменения в объекте, связанные с возникновением отказа (обрыв провода, деформация или поломка детали). К последствиям отказа относятся явления, процессы и события, возникшие после отказа и в непосредственной причинной связи с ним (остановка двигателя, вынужденный простой машины по техническим причинам).

2. ОСНОВНЫЕ ВИДЫ И ПОКАЗАТЕЛИ НАДЕЖНОСТИ

2.1. Безотказность

Вероятность безотказной работы Р(t) есть вероятность того, что в пределах заданной наработки отказ объекта не возникнет. Изделие проработает с начала эксплуатации время Т, большее некоторого заданного времени t

Р(t) = Р(Т > t).

На основе статистических данных вероятность безотказной работы определяется по приближенной формуле

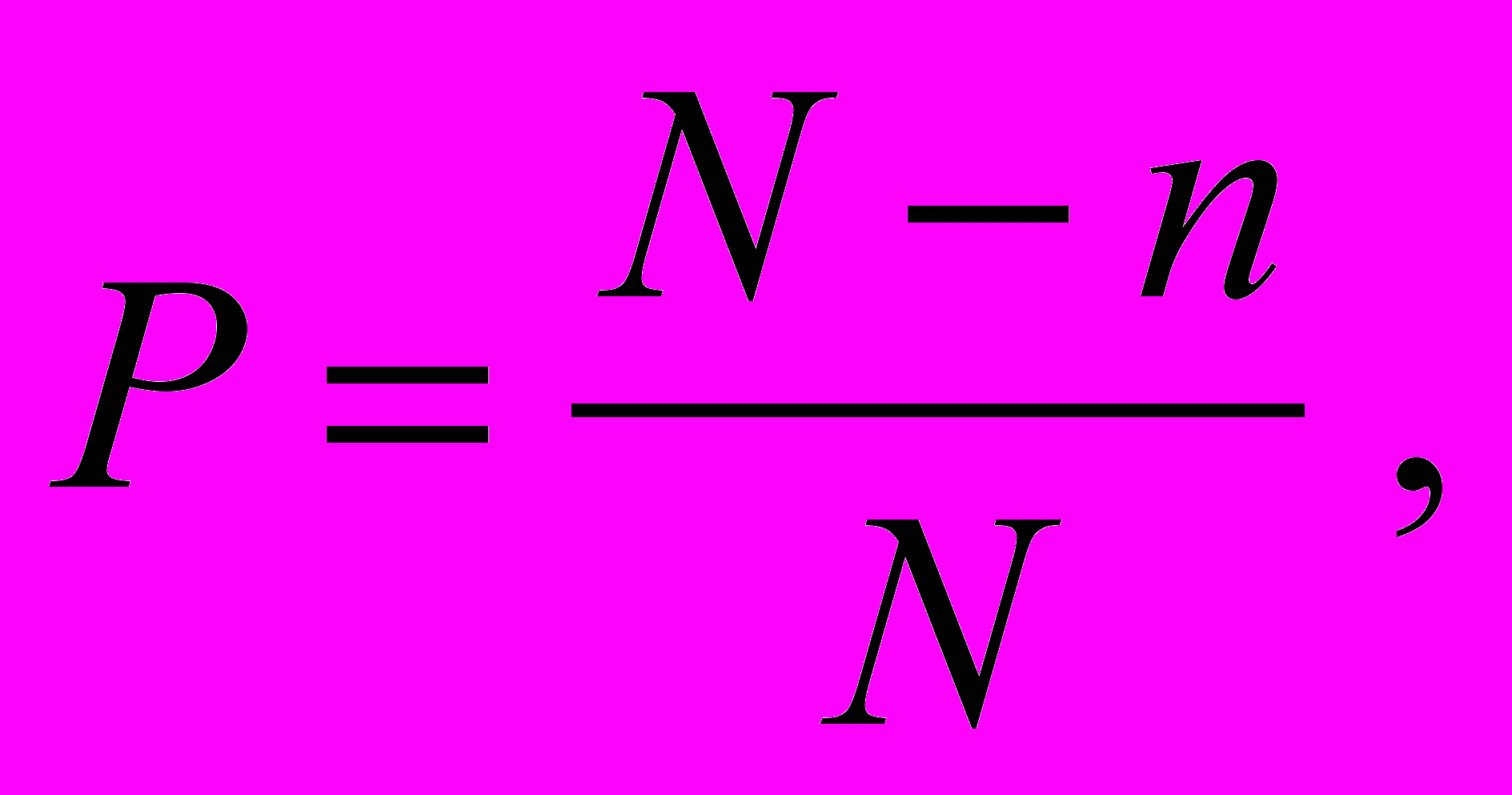(1)

где N — начальное число работающих изделий; п — число отказавших изделий за период времени t.

Частота случайного события при неограниченном увеличении числа опытов приближается к его вероятности с увеличением числа опытов или времени наблюдения за техническими объектами или изделиями, т.е. Р приближается к Р(t). Эта функция является монотонно убывающей: при t = 0: Р(t) = 1, а при t → ∞ Р(t) → 0.

Если испытания изделий проводятся до отказа всех работающих объектов N, то в конце наблюдения число работоспособных изделий и вероятность безотказной работы будут равны нулю: N(t)=0, P(t)=0.

Статистически вероятность безотказной работы можно определить отношением числа объектов, безотказно проработавших до момента времени t, к числу объектов, работоспособных в начальный момент времени наблюдения

Вероятность отказа - это событие, противоположное для вероятности безотказной работы

(2)

В отличие от Р(t) вероятность отказа представляет собой вероятность того, что время исправной работы изделия Т будет меньше некоторого заданного времени t.

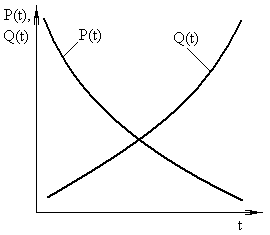
Рис. 1. Изменение вероятности безотказной работы Р(t)

и вероятности появления отказов Q(t) от времени наработки t.

Из теории вероятностей следует, что вероятность суммы двух несовместимых противоположных событий равна единице, и функция вероятности появления отказов будет монотонно возрастать от нуля до единицы – рис. 1.

Из (2) следует

(3)

где N – N(t) – число отказавших объектов (изделий) к моменту времени t.

Продифференцировав Q(t), получим плотность распределения вероятности времени исправной работы до отказа f(t) (дифференциальную функцию)

(4)

При построении опытной гистограммы плотность распределения вероятности времени исправной работы по оси абсцисс обычно откладывают интервалы времени Δt (разряды), а по оси ординат – частоту отказов ΔN за промежуток времени Δt.

Тогда

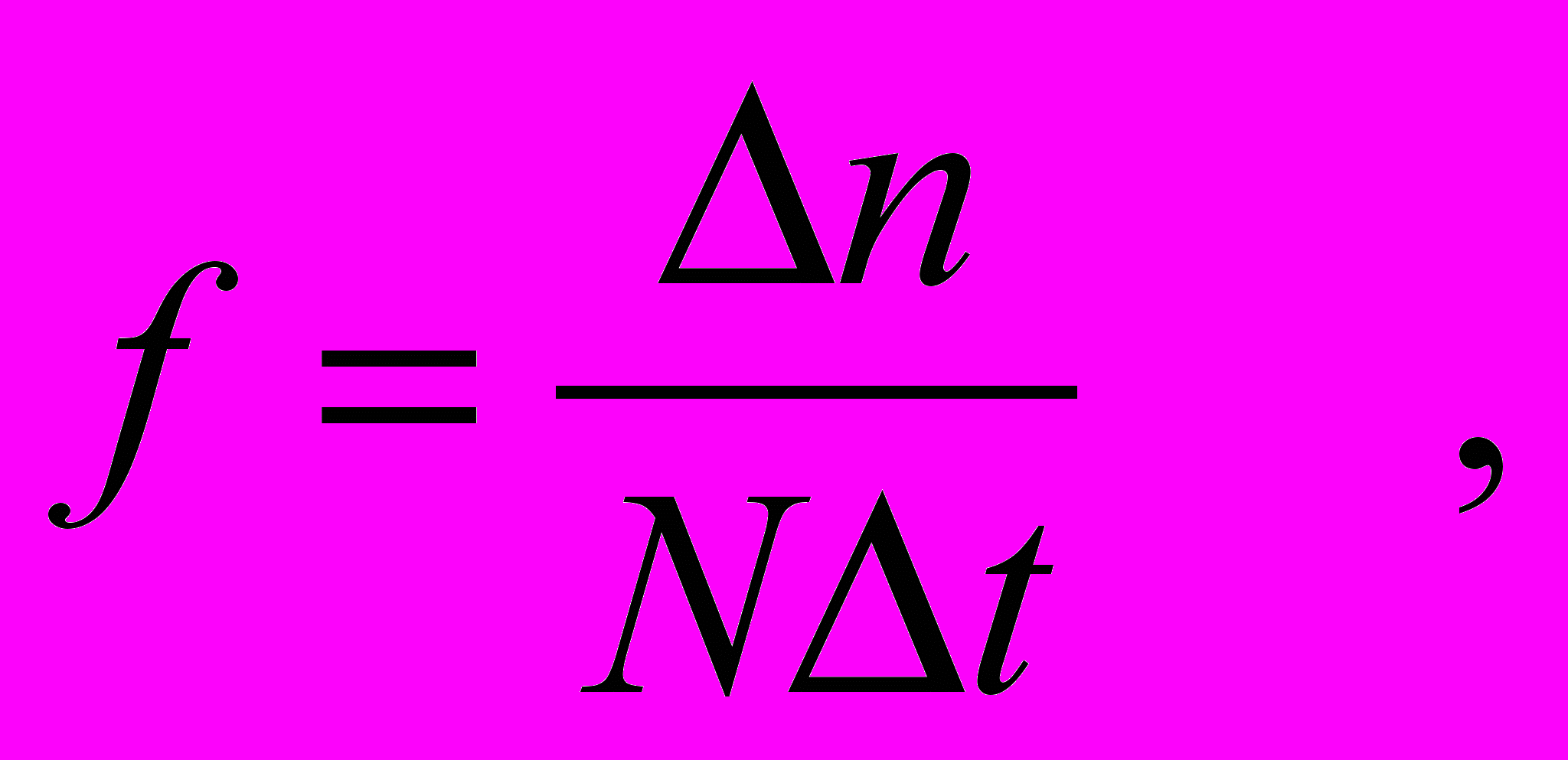(5)

где Δn - число отказавших изделий за время Δt;

N – число первоначально работавших изделий.

Пользуясь формулами (2) и (4), нетрудно установить связь между рассмотренными величинами

(6)

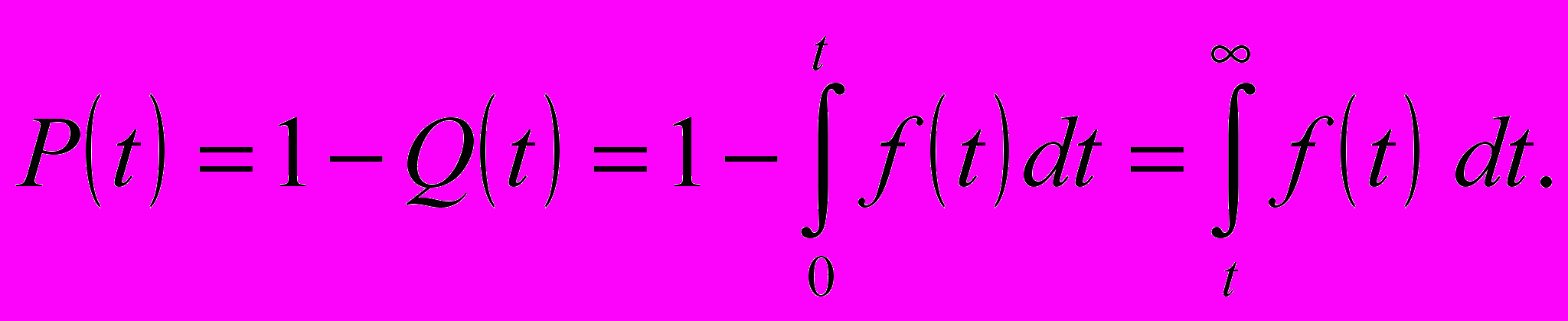
Одной из наиболее полных характеристик надежности неремонтируемых изделий является интенсивность отказов. Под интенсивностью отказов понимается число отказов в единицу времени, отнесенное к числу элементов, оставшихся исправными к началу рассматриваемого промежутка времени.

Используя статистические данные о работе изделий, можно построить гистограмму интенсивности отказов λ для промежутков времени Δt согласно следующему выражению

(7)

где Δn — число отказов за время Δt; N — начальное число испытанных изделий; п — число отказавших изделий от начала испытаний до конца периода Δt.

Между ранее рассмотренными характеристиками надежности и интенсивностью отказов существует связь. Разделив числитель и знаменатель формулы (7) на NΔt, получим

(8)

При увеличении числа изделий N (наблюдений, измерений) опытное значение λ стремится к λ(t) и зависимость (8) принимает вид

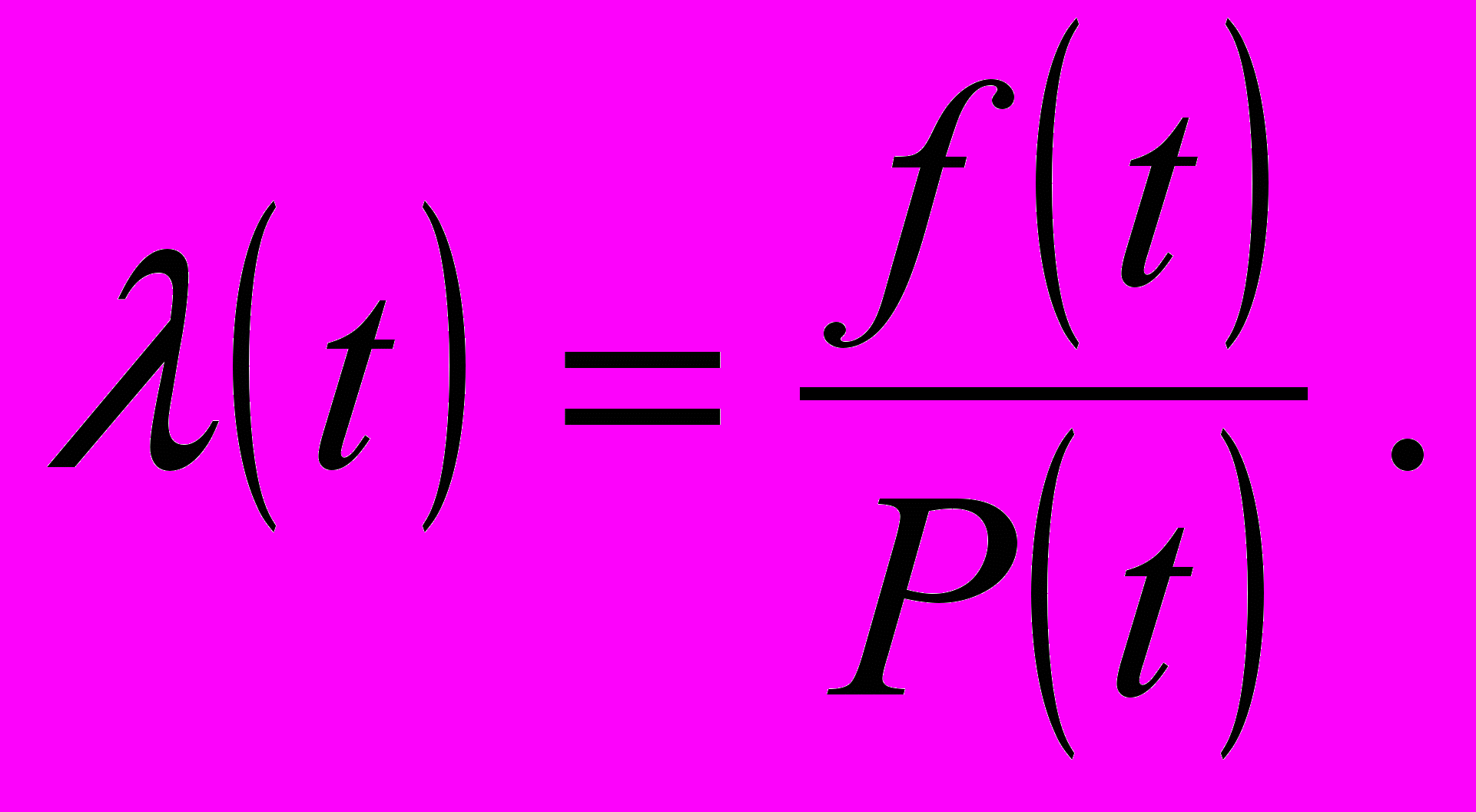(9)

Используя формулу (4), можем представить связь λ(t) с Р(t) в следующем виде

(10)

Интегрируя зависимость (10), получим уравнение связи между вероятностью безотказной работы и интенсивностью отказов

(11)

или

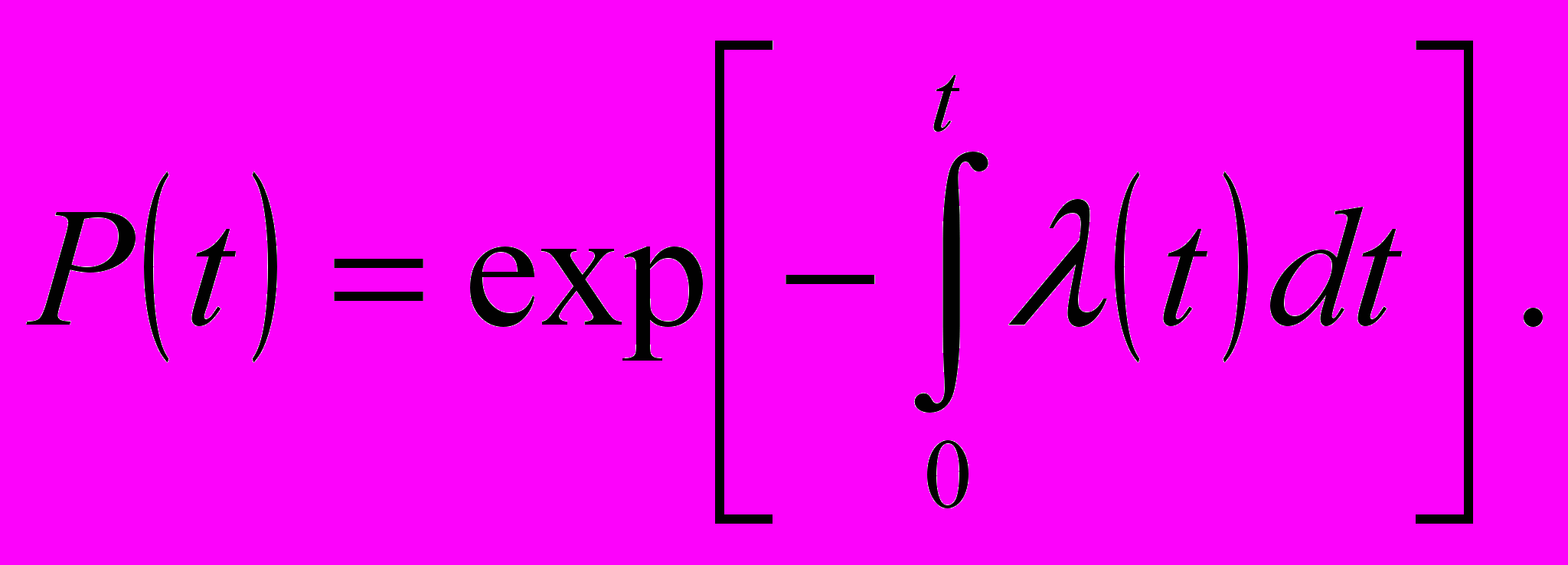(12)

Интенсивность отказов является функцией времени и наглядно характеризует основные периоды работы изделия.

Надежность неремонтируемых изделий может быть охарактеризована средним временем безотказной работы, представляющим собой математическое ожидание времени безотказной работы

(13)

Учитывая, что время отрицательным быть не может и используя зависимость (4), после интегрирования по частям получают уравнение связи Т_ср с вероятностью безотказной работы

Так как Р(t) = 1, а Р (∞) = 0 и Р (t) → 0 быстрее, чем t → ∞ , то tP (t) |₀^∞ = 0.

Следовательно,

(14)

Приведенные выше уравнения являются общими: они пригодны для любых законов распределения наработки до отказа.

2.2. Характеристики случайных величин

1. Среднее арифметическое – это частное от деления суммы значений случайной величины на число слагаемых этой суммы

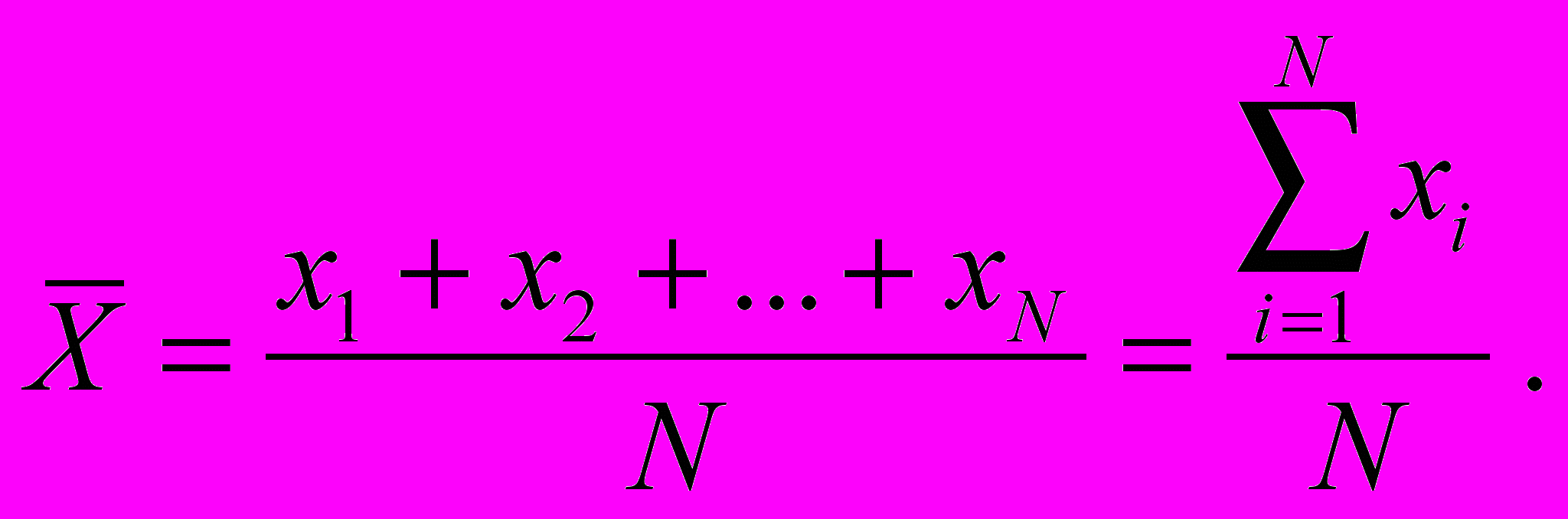(15)

2. Математическое ожидание – сумма произведений всех возможных значений случайной величины на вероятности этих значений – поз. 3 на рис. 2.

(16)

3. Мода случайной величины – наиболее вероятное ее значение, т.е. значение, которому соответствует наибольшая частота. Графически – моде соответствует наибольшая ордината кривой распределения – поз. 2 на рис. 2.

Рис. 2. Плотность вероятности и числовые характеристики центра группирования случайной величины: 1 — медиана; 2 — мода; 3 — математическое ожидание

4. Медиана случайной величины (первый центральный момент) – это такое ее значение, для которого наиболее вероятно – окажется ли случайная величина больше или меньше медианы. Геометрически медиана определяет абсциссу точки, ордината которой делит пополам площадь, ограниченную кривой распределения – поз. 1 на рис. 2.

Для симметричных распределений среднее арифметическое, мода и медиана совпадают.

5. Размах рассеивания случайной величины – это разность между максимальным и минимальным ее значениями, полученными в результате испытаний

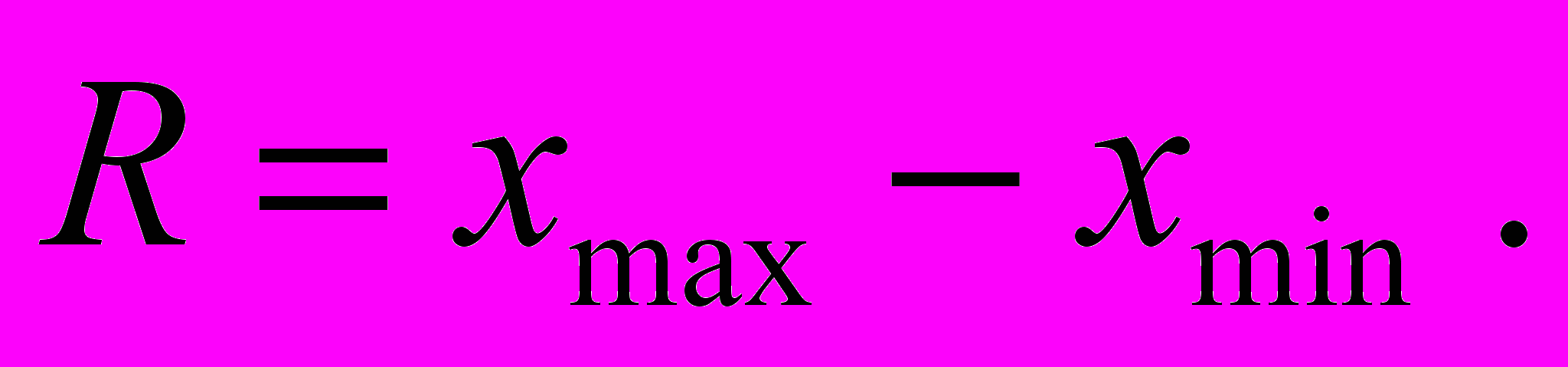(17)

При малом числе наблюдений (N<10) размах служит мерой рассеивания.

6. Дисперсия (второй центральный момент) является одной из основных характеристик рассеивания случайной величины около ее среднего арифметического значения. Величина ее определяется по формуле

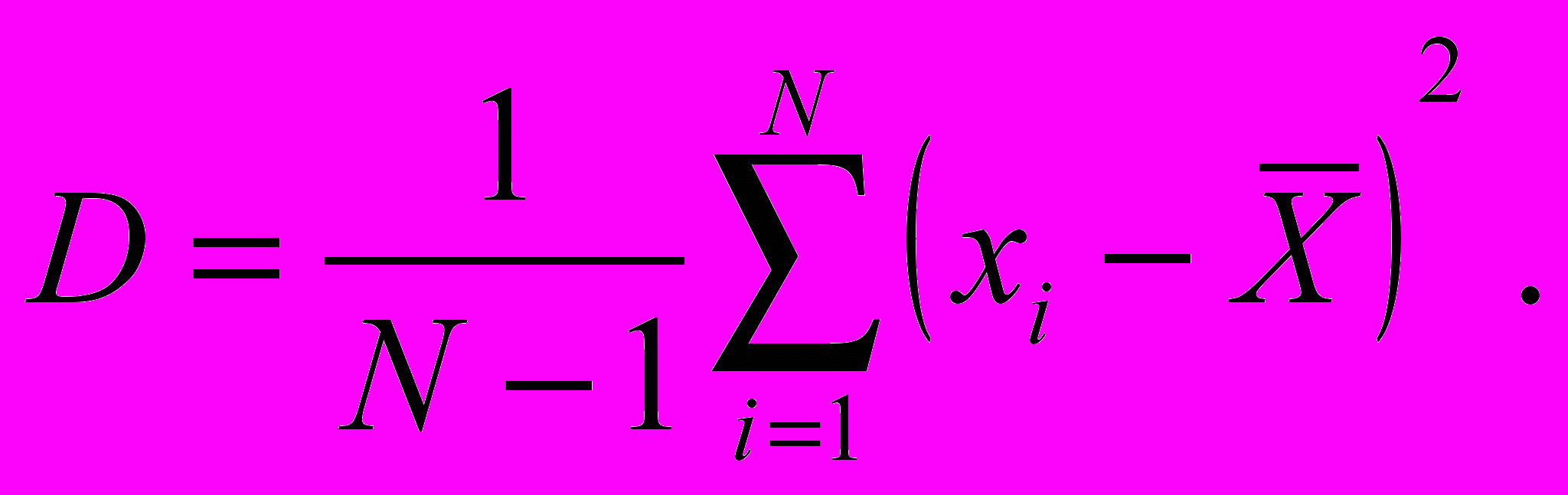(18)

7. Среднее квадратичное отклонение также является мерой рассеивания и равно корню квадратному из дисперсии

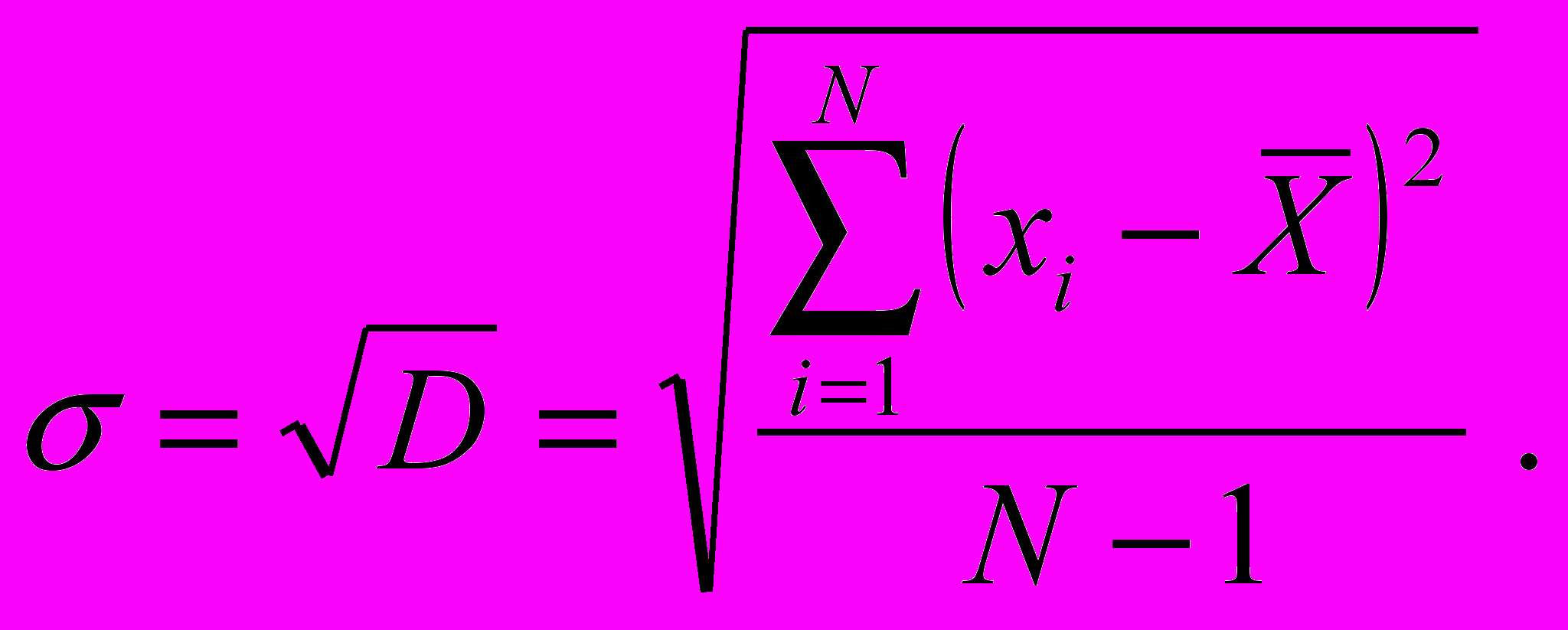(19)

Поскольку среднее квадратичное отклонение имеет размерность случайной величины, пользоваться им удобнее, чем дисперсией.

Среднее квадратичное отклонение называют также стандартом, основной ошибкой или основным отклонением. Среднее квадратичное отклонение, выраженное в долях среднего арифметического, носит название коэффициента вариации V

(20)

Введение коэффициента вариации необходимо для сравнения величин, имеющих разную размерность. Для этой цели среднее квадратичное отклонение непригодно, так как имеет размерность случайной величины.

При исследовании надежности работы неремонтируемых деталей машин важнейшим является вопрос об установлении законов распределения случайных величин и соответствия их теоретическим.

2.3. Основные законы распределения случайных величин

Случайная величина, представленная совокупностью отдельных значений, может иметь тот или закон распределения. Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. В теории надежности и практике чаще всего используются следующие законы распределения: нормальный (Гаусса), логарифмически нормальный, Вейбулла, экспоненциальный и др.

Интегральная функция распределения имеет вид

(21)

Дифференциальная функция распределения, или плотность распределения, есть производная от интегральной функции

(22)

Нормальный закон распределения встречается довольно часто. Случайная величина х распределена по нормальному закону, если плотность распределения имеет вид

(23)

где m – математическое ожидание; σ – среднее квадратическое отклонение случайной величины (в других источниках – обозначается как S); е – основание натуральных логарифмов. Постоянные m и σ – больше нуля и могут быть любыми. Плотность распределения f(x) вычисляют по статистическим данным испытаний, обозначая случайную величину t через х и заменяя математическое ожидание m на среднее арифметическое

, а формула принимает вид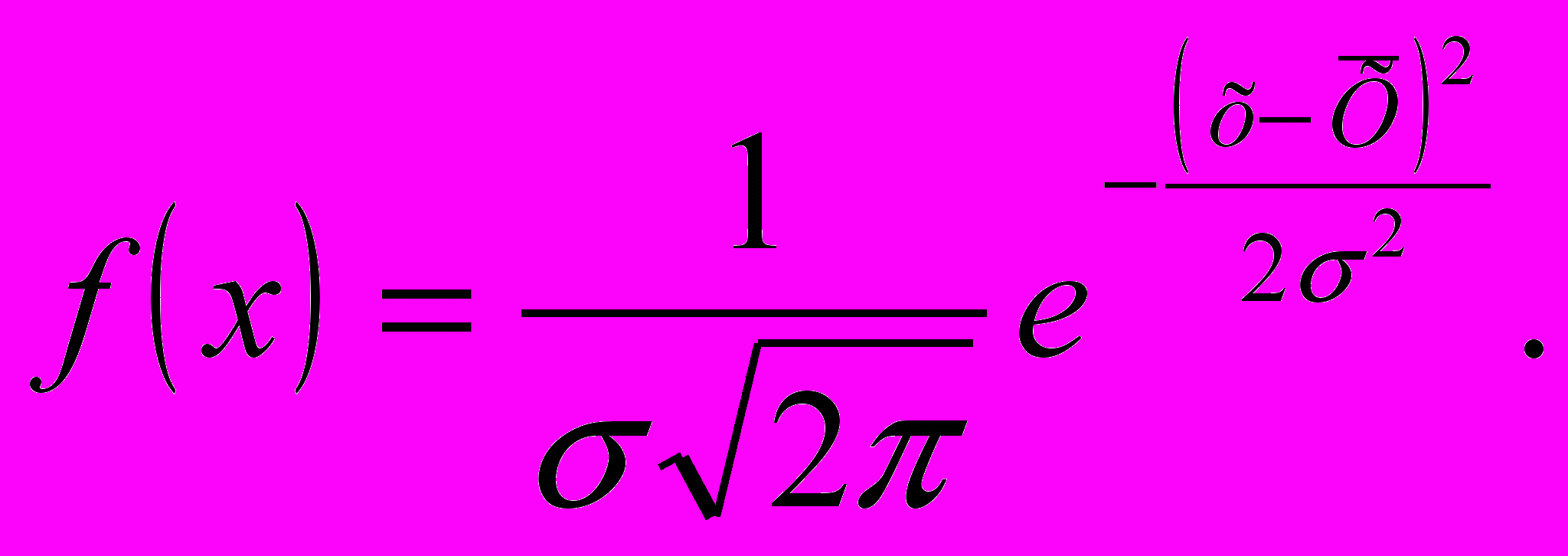

(24)

Величина

(среднее арифметическое) показывает смещение кривой f(x) вдоль оси абсцисс без изменения ее формы, т.е расстояние от начала координат до абсциссы с максимальной ординатой (рис. 2).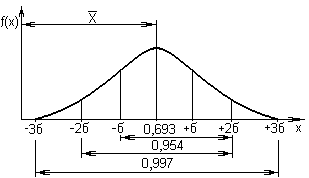

Рис. 3. Нормальный закон распределения

Величина среднего квадратичного отклонения σ показывает разброс отдельных значений случайной величины х относительно среднего арифметического

. На участке кривой, ограниченной ординатами +σ и -σ расположено 68,3% значений случайной величины; на интервале от +2σ до -2σ – 95,4%; на участке между ординатами +3σ и -3σ расположено 99,7%. На этом основано правило трех сигм: вероятность того, что случайная величина х лежит в пределах ±3σ, близка к единице или к 100%.

Если в качестве аргумента в формуле (24) принять безразмерную переменную

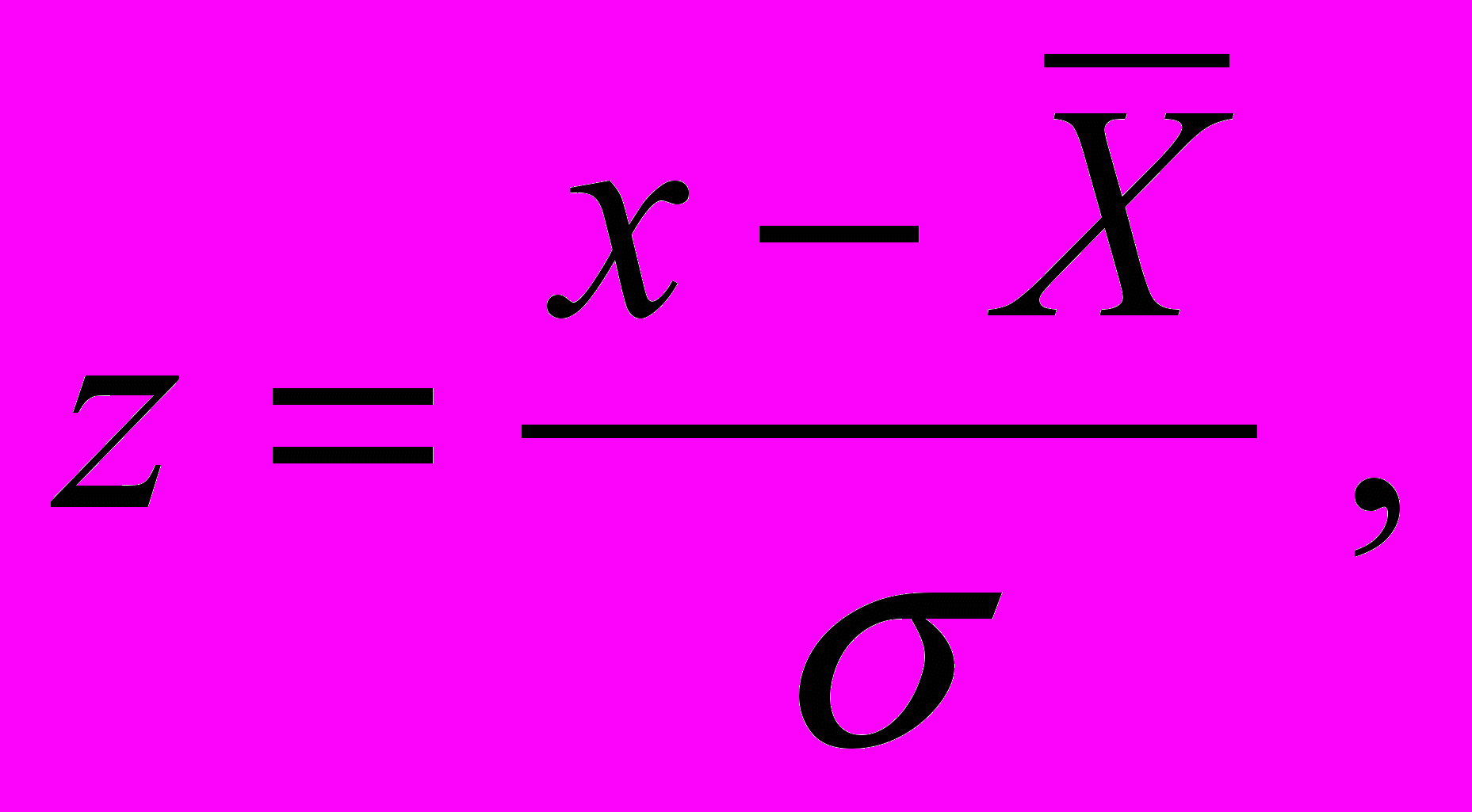(25)

то получим стандартный закон нормального распределения

(26)

Нормальный закон соблюдается в тех многочисленных случаях, когда на измеряемую случайную величину действуют разнообразные факторы, не связанные между собой и равнозначно действующие на случайную величину (например, размеры и износы деталей, наработки на отказ и до предельного состояния, причинами которых являются износы и т.д.).

Значения параметров m и σ оценивают по результатам испытаний или наблюдений по статистическим формулам

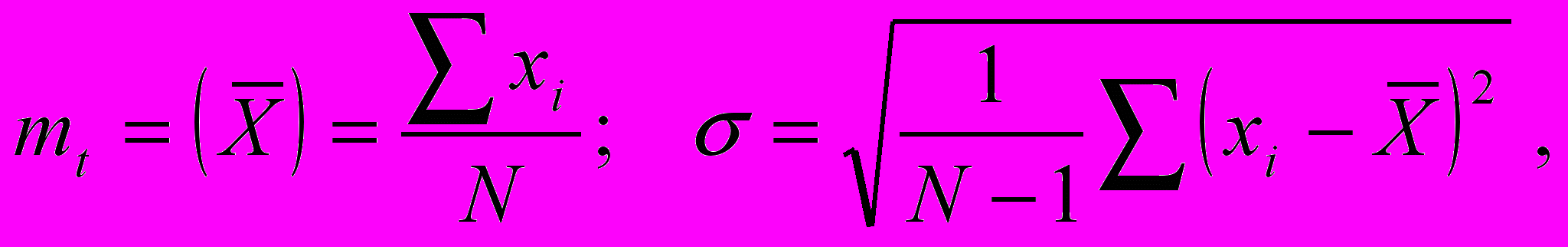(27)

где m (

) и σ – математическое ожидание и среднеквадратическое отклонение средней наработки до отказа; N – общее число наблюдений (измерений); х_i – наработка на отказ i –го объекта наблюдения.

Операции с нормальным распределением проще, чем с другими, поэтому им часто заменяют другие распределения. При малых коэффициентах вариации (V= σ /m) нормальное распределение хорошо заменяет биноминальное, пуассoново и логарифмически нормальное.

На практике функции нормального распределения вычисляют с помощью квантилей нормированного нормального распределения U_P (U_P = (х – m/σ)), каждому значению которых соответствует величина вероятности безотказной работы и плотности распределения, выбираемые по таблицам.

Например:

U_P 0 1 2 3 4

f_O(x) 0,3989 0,2420 0,0540 0,0044 0,0001

F_O(x) 0,5 0,8413 0,9772 0,9986 0,9999

Значения квантилей задаются в таблицах в зависимости от требуемой вероятности. Например:

P(t) 0,5 0,90 0,95 0,99 0,999 0,9999

U_P 0 -1,282 -1,645 -2,326 -3,090 -3,719

Логарифмически нормальный закон выполняется тогда, когда десятичный логарифм случайной величины у распределяется по нормальному закону, при этом в формуле (24): х = log y.

Экспоненциальный закон. Случайная величина t экспоненциально распределена, если ее функция распределения описывается уравнением

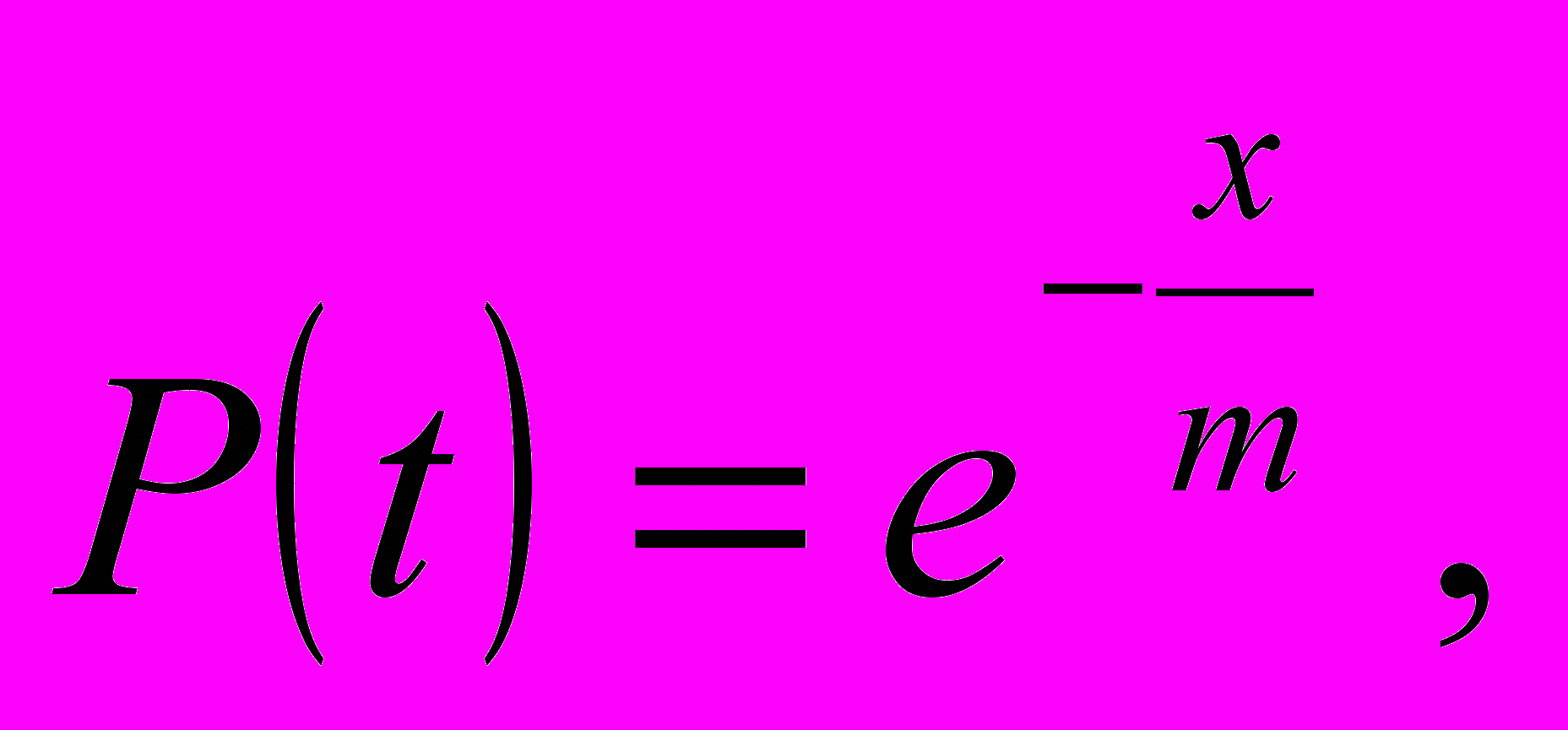(28)

где m – математическое ожидание случайной величины х.

Время безотказной работы подчиняется этому закону, если отказы возникают в результате воздействия большого количества случайно действующих факторов.

Дифференциальная функция (плотность распределения) экспоненциального закона имеет вид

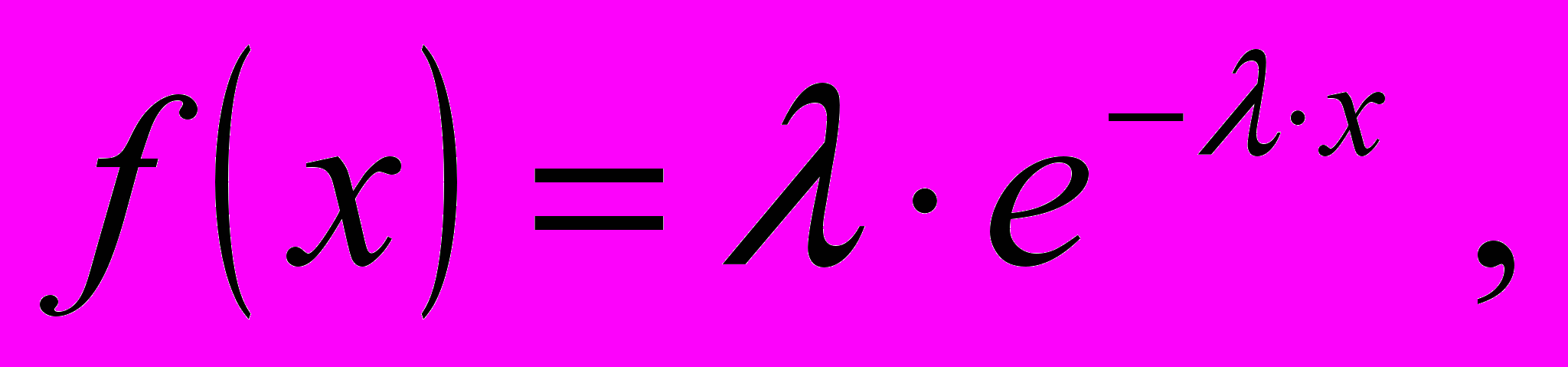(29)

где λ – параметр распределения (постоянный коэффициент).

Рис. 4. Плотность распределения экспоненциального закона

У экспоненциального закона распределения математическое ожидание и среднее квадратичное отклонение одинаковы

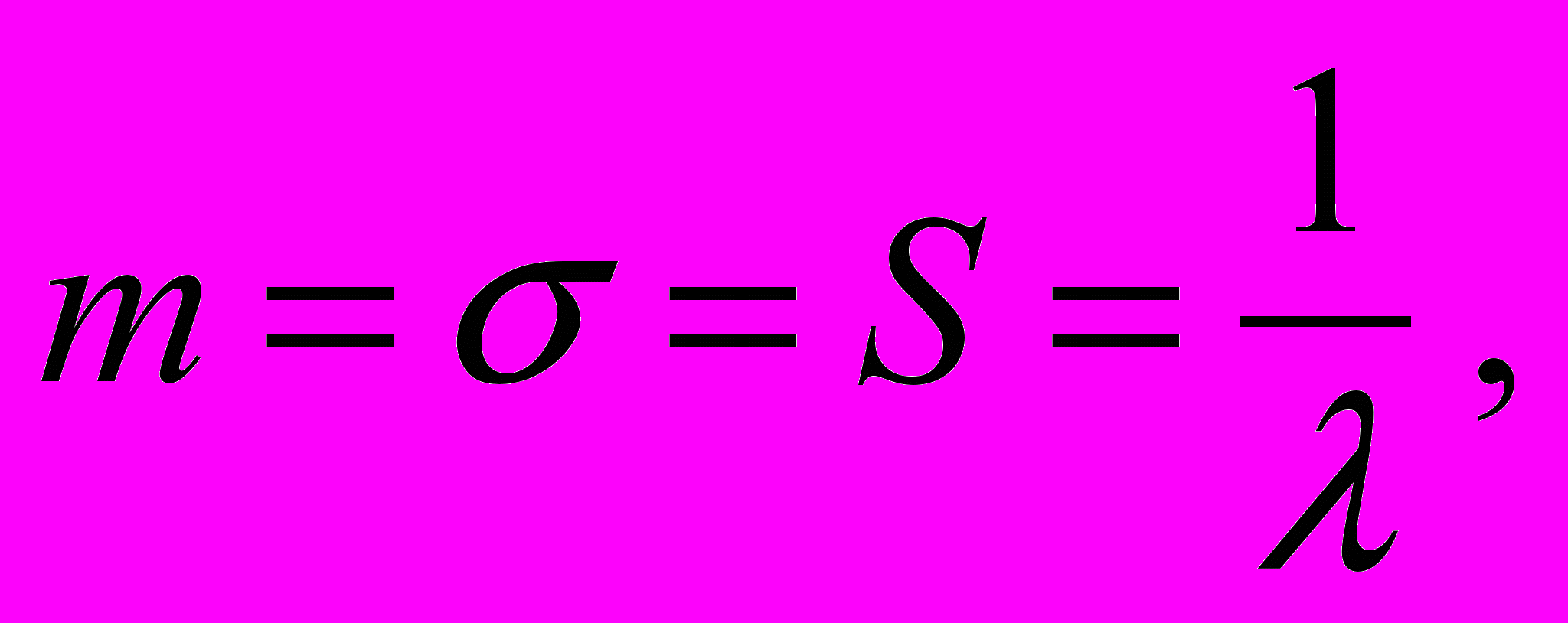(30)

поэтому коэффициент вариации здесь равен единице: V=1.

Экспоненциальный закон распределения — один из основных законов распределения — используется при определении показателей надежности в период нормальной эксплуатации, т. е. в период после окончания приработки изделия и до существенного проявления постепенных отказов. В этот период постепенные отказы еще не проявляются, и надежность характеризуется внезапными отказами. В качестве основного параметра экспоненциального распределения принимается интенсивность отказов X(t) для невосстанавливаемых изделий или параметр потока отказов λ(t) для восстанавливаемых. У невосстанавливаемых изделий рассматриваются первичные отказы, a у восстанавливаемых — первичные и вторичные.

Процесс функционирования восстанавливаемого изделия можно описать как последовательность чередующихся интервалов работоспособности и простоя, вызванного ремонтом и профилактикой. При замене старых элементов изделия новыми образуется поток отказов, параметры которых не зависят от t и равняются интенсивности λ, т. е. λ(t) = λ = const. При этом поток внезапных отказов предполагают стационарным (ординарным), т. е. среднее число отказов в единицу времени постоянно, и одновременно возникает не более одного отказа, и без последствия, что означает взаимную независимость появления отказов в разные промежутки времени.

Для стационарного (ординарного) потока интенсивность отказов: λ(t) = λ =1/Т, где Т — средняя наработка между отказами.

В сложных изделиях (системах) параметр потока отказов рассматривается как сумма параметров потоков отказов. Составляющие потоки можно рассматривать по узлам
(элементам) или по типам устройств, например, механическим, гидравлическим, электрическим и другим

λ(t)=λ₁(t)++ λ₂(t)+ λ₃(t)+...

Средняя наработка между отказами изделия

Т =1/ λ(t) или 1/T=1/T₁ + 1/T₂ + ...

В табл. 1 приведены основные показатели надежности элемента для экспоненциальных законов распределения наработки до отказа F(t) = 1–е^-λ^t и времени восстановления G(t) = 1 – e^-μ^t .

Таблица 1

Экспоненциальный закон распределения наработки между отказами

Показатели	Точное значение	Приближенное значение
Вероятность безотказной работы в интервале времени от 0 до t₀- P(t₀)	-	1-λt₀
Вероятность отказа элемента в интервале времени от 0 до t₀	Р(О)=1–е^-λ^t^о	λt₀^!
Средняя наработка между отказами Т		-
Среднее время восстановления - τ		-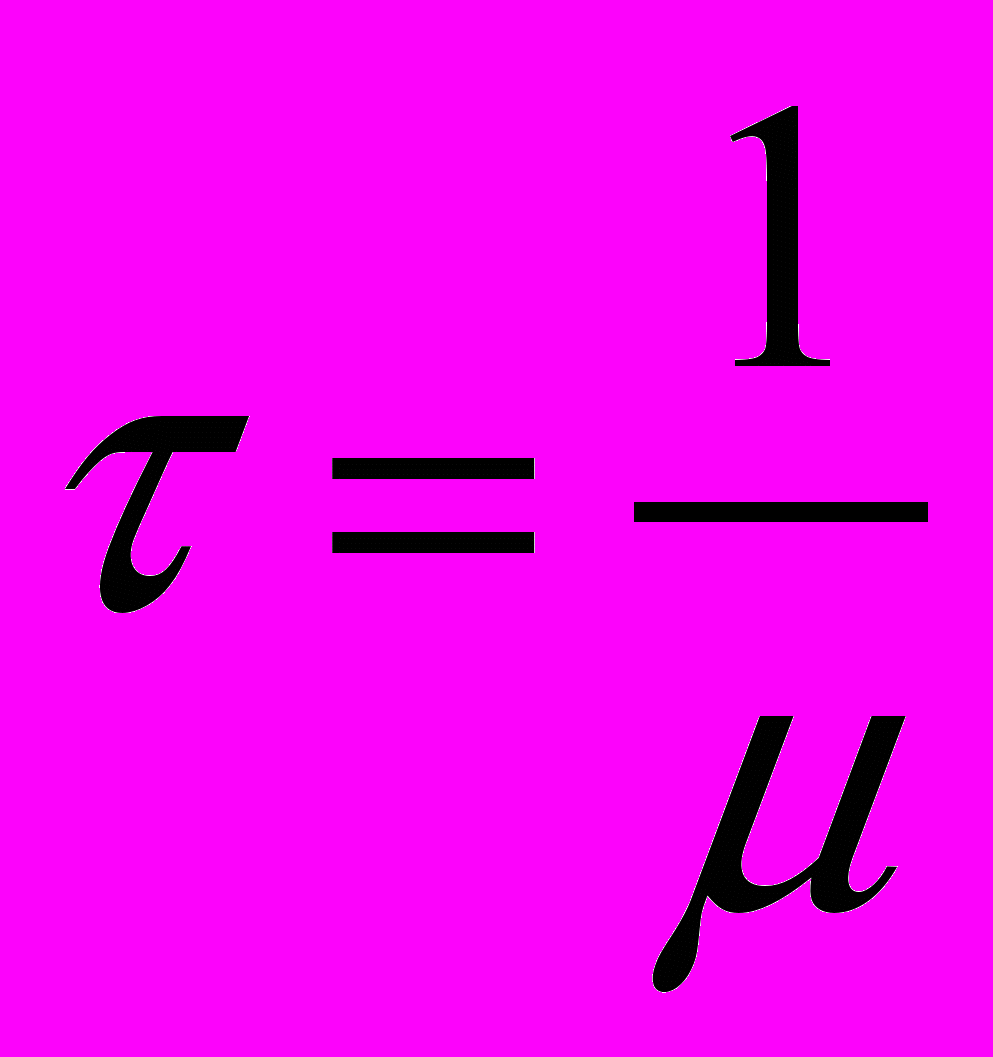
Коэффициент оперативной готовности К		1 – γ

Здесь: N – общее число наблюдений.

Приближенные значения показателей приведены для условий

λ t₀<< 1 и γ = λ /μ<<1,

где λ – математическое ожидание числа отказов изделия с восстановлением в единицу времени для установившегося процесса эксплуатации (вероятное определение) или среднее число отказов изделия с восстановлением в единицу времени (статистическое определение). λ выражается числом отказов в час и, как правило, составляет малую дробь; μ — интенсивность восстановления объекта в момент времени t, отсчитываемом от момента начала восстановления.

Используя экспоненциальный закон распределения, несложно определить среднее число объектов n, которые выйдут из строя к заданному моменту времени, и среднее число объектов (изделий), которые останутся работоспособными. Этот закон характерен для распределения случайных величин, изменение которых обусловлено влиянием какого-то доминирующего фактора. Он используется при рассмотрении внезапных отказов деталей в тех случаях, когда изнашивание и усталость материалов выражены настолько слабо, что ими пренебречь (например, наработка до отказа многих невосстанавливаемых изделий).

Закон Вейбулла. Случайная величина t имеет распределение Вейбулла, если функция распределения описывается уравнением

(31)

где m – математическое ожидание случайной величины; n – показатель степени, определяющий крутизну кривой по сравнению с экспоненциальным распределением.

Закон распределения Вейбулла описывается дифференциальной функцией плотности распределения

(32)

где m и а – параметры распределения Вейбулла.

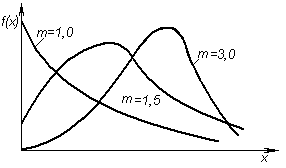
Рис. 5. Плотность распределения по закону Вейбулла

Значение параметра m зависит от коэффициента вариации и определяется по таблицам [1, 2], расчетом или графоаналитическим путем. Величина его влияет на форму дифференциальной кривой – рис. 5.

Таблица 2

Вероятность безотказной работы для нормального распределения

и значения коэффициентов b_m и c_m для распределения Вейбулла

Нормальное распределение				Распределение Вейбулла
Кван- тиль, U_p	Вероят- ность безот- казной работы, P(t)	Кван- тиль, U_p	Вероят- ность безот- казной работы, P(t)	Пара- метр фор- мы, m	1/m	b_m	c_m	Коэффи-циент вариа-ции, V=c_m/b_m
0,000 -0,1 -0,126 -0,2 -0,253 -0,3 -0,385 -0,4 -0,5 -0,524 -0,6 -0,674 -0,7 -0,8 -0,842 -0,9 -1,0 -1,036 -1,1 -1,2 -1,282 -1,3 -1,4 -1,5 -1,6 -1,645 -1,7 -1,751 -1,8 -1,881 -2,0	0,5000 0,5398 0,55 0,5793 0,60 0,6179 0,65 0,6554 0,6915 0,70 0,7257 0,75 0,7580 0,7881 0,80 0,8159 0,8413 0,85 0,8643 0,8849 0,90 0,9032 0,9192 0,9332 0,9452 0,95 0,9554 0,96 0,9641 0,97 0,9772	-2,054 -2,1 -2,170 -2,2 -2,3 -2,326 -2,4 -2,409 -2,5 -2,576 -2,6 -2,652 -2,7 -2,748 -2,8 -2,878 -2,9 -3,0 -3,090 -3,291 -3,5 -3,719	0,98 0,9821 0,985 0,9861 0,9893 0,99 0,9918 0,992 0,9938 0,995 0,9953 0,996 0,9965 0,997 0,9974 0,998 0,9981 0,9986 0,999 0,9995 0,9998 0,9999	0,400 0,417 0,435 0,455 0,476 0,500 0,526 0,556 0,588 0,625 0,667 0,714 0,769 0,833 0,909 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5	2,5 2,4 2,3 2,2 2,1 2,0 1,9 1,8 1,7 1,6 1,5 1,4 1,3 1,2 1,1 1,0 0,909 0,833 0,769 0,714 0,667 0,625 0,588 0,556 0,526 0,500 0,476 0,455 0,435 0,417 0,400	3,32 2,98 2,68 2,42 2,20 2,00 1,83 1,68 1,54 1,43 1,33 1,24 1,17 1,10 1,05 1,00 0,965 0,941 0,924 0,911 0,903 0,897 0,892 0,889 0,887 0,886 0,886 0,886 0,886 0,887 0,008	10,4 8,74 7,38 6,22 5,27 4,47 3,81 3,26 2,78 2,39 2,06 1,78 1,54 1,33 1,15 1,00 0,878 0,787 0,716 0,659 0,615 0,574 0,540 0,512 0,485 0,463 0,439 0,425 0,409 0,394 0,380	3,14 2,93 2,75 2,57 2,40 2,24 2,08 1,94 1,80 1,67 1,55 1,43 1,32 1,21 1,10 1,00 0,910 0,837 0,775 0,723 0,681 0,640 0,605 0,575 0,547 0,523 0,496 0,480 0,461 0,444 0,428

При m=1 распределение Вейбулла преобразуется в экспоненциальное, при m=2,5–3,5 и V=0,3–0,4 – приближается к нормальному распределению.

Распределение Вейбулла применяется при расчете показателей надежности при исследовании усталостной прочности и долговечности деталей. Этому закону хорошо подчиняются распределения предела упругости ряда металлов, характеристики прочности и усталостной долговечности деталей (подшипники качения, напряженные оси, валы и др.).

Blog

Методические указания к выполнению практических занятий для студентов специальности 150405. 65 «Машины и оборудование лесного комплекса»

Содержание

«Тихоокеанский государственный университет»