Методические указания по курсовому проектированию санкт-петербург

Вид материала

Методические указания

Содержание Теория механизмов и машин Рычажного механизма Ii. динамическое исследование движения системы Проектирование маховика Iii. кинетостатический расчет рычажного механизма с учетом ускорения J – приведенный момент инерции системы в расчетном положении, кгм; J Список литературы Основные принятые обозначения

Подобный материал:

• М. А. Бонч-Бруевича Методические указания к курсовому проектированию предварительных, 789.79kb.
• Методические указания к курсовому проектированию по учебной дисциплине, 1609.55kb.
• Методические указания к курсовому проектированию по учебной дисциплине «Управленческие, 1355.04kb.
• Методические указания по курсовому проектированию по дисциплине «страхование» для студентов, 1442.66kb.
• Методические указания по курсовому проектированию по дисциплине «страхование» для студентов, 1282.26kb.
• Методические указания к курсовому проектированию по дисциплине "антикризисное управление", 137.98kb.
• Методические указания к курсовому проектированию по дисциплине «экономика организации», 560.98kb.
• Методические указания к курсовому проектированию по учебной дисциплине «инновационный, 378.33kb.
• Методические указания к курсовому проектированию по курсу "Базы данных" Москва, 654.27kb.
• Методические указания к курсовому проектированию по дисциплине «Прикладное программирование», 474.71kb.

Федеральное агентство по образованию


Государственное образовательное учреждение

высшего профессионального образования

Санкт-Петербургский государственный горный институт им. Г. В. Плеханова

(технический университет)

Кафедра конструирования горных машин и

технологии машиностроения


ТЕОРИЯ МЕХАНИЗМОВ И МАШИН


Методические указания по курсовому проектированию

САНКТ-ПЕТЕРБУРГ

2006


УДК 621.01.001 (075.83)


ТЕОРИЯ МЕХАНИЗМОВ И МАШИН: Методические указания по курсовому проектированию / Санкт-Петербургский государственный горный ин-т.

Сост.: А.В. Большунов, В.В. Денегин, Г.В. Соколова. СПб, 2006. 27 c.


Изложены методические указания по выполнению курсового проекта и требования к его оформлению. Представлены типовые схемы механизмов с вариантами заданий для курсового проектирования по дисциплине «Теория механизмов и машин». Методические указания предназначены для студентов всех форм обучения специальностей 170100  (150402)   «Горные машины и оборудование», 170300 (150404) «Металлургические машины и оборудование» и 090700 (130501) «Проектирование, сооружение и эксплуатация газонефтепроводов и газонефтехранилищ».


Научный редактор проф. И.П. Тимофеев


Библиогр.: 7 назв.


 Санкт-Петербургский горный

институт имени Г.В. Плеханова, 2006 г.




ВВЕДЕНИЕ


Курсовое проектирование по теории механизмов и машин является заключительным этапом изучения дисциплины, способствующим закреплению, углублению и обобщению теоретических знаний, полученных студентами, и применению этих знаний к комплексному решению задачи динамического исследования механизма.

Курсовой проект содержит пояснительную записку и графические построения (схемы, чертежи). Графические построения к каждому разделу проекта выполняются на отдельных листах формата А1 с соблюдением всех требований ЕСКД. На чертежах следует сохранять все вспомогательные построения, проставлять принятые масштабы и соответствующие надписи. Каждый лист проекта должен иметь угловой штамп. Допускается компьютерный вариант выполнения чертежей с применением графических редакторов КОМПАС-3D.8V или AutoCAD 2005.

Пояснительная записка должна содержать титульный лист, аннотацию, содержание, список использованной литературы. В пояснительной записке следует привести схему механизма с исходными данными к проекту и расшифровкой обозначений величин.

Количество положений в цикле движения механизма следует принимать равным 12; для механизма четырехтактного двигателя внутреннего сгорания - 24. При выполнении расчетов следует записать исходную формулу, при необходимости преобразовать ее к удобному виду, подставить численные значения и указать результат. Обязательно указывать единицы измерения всех исходных и полученных в результате расчета величин. Расчеты для всех положений механизма рационально представлять в табличной форме.

Если студент ранее выполнял расчетно-графическую работу по кинематическому исследованию рычажного механизма, ее следует приложить к проекту и дать соответствующую ссылку в пояснительной записке.

При защите проекта студент, должен дать исчерпывающие объяснения по всем вопросам, связанным с методами исследования механизмов и приемами графических построений.

I. КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ

РЫЧАЖНОГО МЕХАНИЗМА

Целью кинематического исследования механизма является определение положений механизма в различные моменты времени, траекторий характерных точек звеньев механизма, включая центры масс звеньев, а так же величины и направления линейных скоростей и ускорений этих точек и угловых скоростей и ускорений звеньев.

Определение перечисленных кинематических характеристик производится в пределах одного периода (цикла) установившегося движения механизма, что соответствует одному полному обороту ведущего звена.

Кинематическое исследование механизма с одной степенью подвижности производят в предположении, что ведущее звено имеет постоянную угловую скорость.

В масштабе _S [м/мм] строят план 12 равноотстоящих по времени положений механизма за один цикл его работы. Масштаб плана положений принимают равным отношению


,


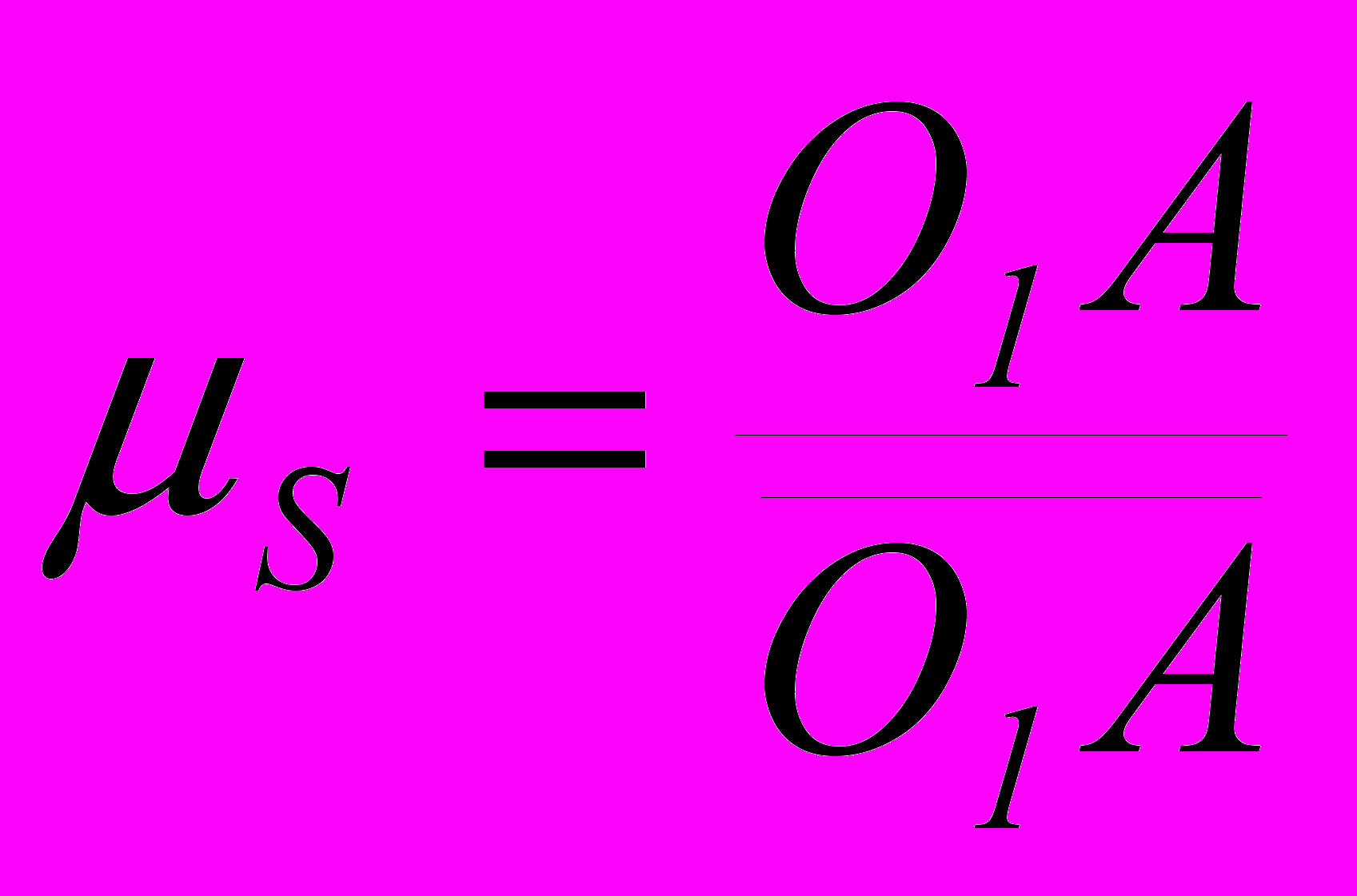где O₁A – действительная длина ведущего звена, м; O₁A – чертежное изображение ведущего звена, принимаемое равным не менее 50 мм.

Нулевым (исходным) в цикле движения считают положение соответствующее началу холостого хода выходного звена механизма технологической машины или началу рабочего хода выходного звена энергетической машины. В тактах рабочего и холостого хода выделяют контурными линиями по одному положению механизма (номера положений студент выбирает самостоятельно).

В последовательности присоединения структурных групп и с учетом их особенностей графическим решением векторных уравнений скоростей и ускорений строят масштабные планы скоростей и ускорений. Планы скоростей строят для всех 12 фиксированных положений механизма, планы ускорений – для двух ранее выделенных. Для определения масштабных коэффициентов планов скоростей _ [м/(смм)] и планов ускорений _a [м/(с²мм)] задают изображения линейной скорости и ускорения кривошипной точки ведущего звена не менее 50 мм.

По построенным планам вычисляют линейные скорости и ускорения для всех характерных подвижных точек звеньев механизма, включая центры масс звеньев, а также угловые скорости и ускорения звеньев. Результаты вычислений представляют в табличной форме.

Планы скоростей и ускорений оформляют на чертеже как отдельные изображения с подрисуночными надписями с обязательным указанием соответствующих масштабных коэффициентов _S, _ и _a.

По результатам решений планов скоростей строят масштабный график скоростей выходного звена механизма за цикл движения. При этом в такте холостого хода скорости выходного звена принимают направленными вверх, а в такте рабочего хода – вниз.

График перемещений выходного звена в функции угла поворота кривошипа строят методом графического интегрирования графика скоростей. При этом площадь между кривой скоростей и осью абсцисс на каждом участке интегрирования заменяют равновеликим прямоугольником. Получаемые горизонтальные стороны сносят на ось ординат и из точек пересечения проводят лучи в полюс интегрирования, расположенный на продолжении оси абсцисс. На поле графика перемещений последовательно пристраивают хорды будущей кривой на интегрируемых участках, параллельные соответствующим лучам, проведенным в полюс интегрирования скоростей. По полученным точкам строят лекальную кривую графика перемещений. При этом масштабный коэффициент графика перемещений _S [м/мм] вычисляют по следующей зависимости:


,


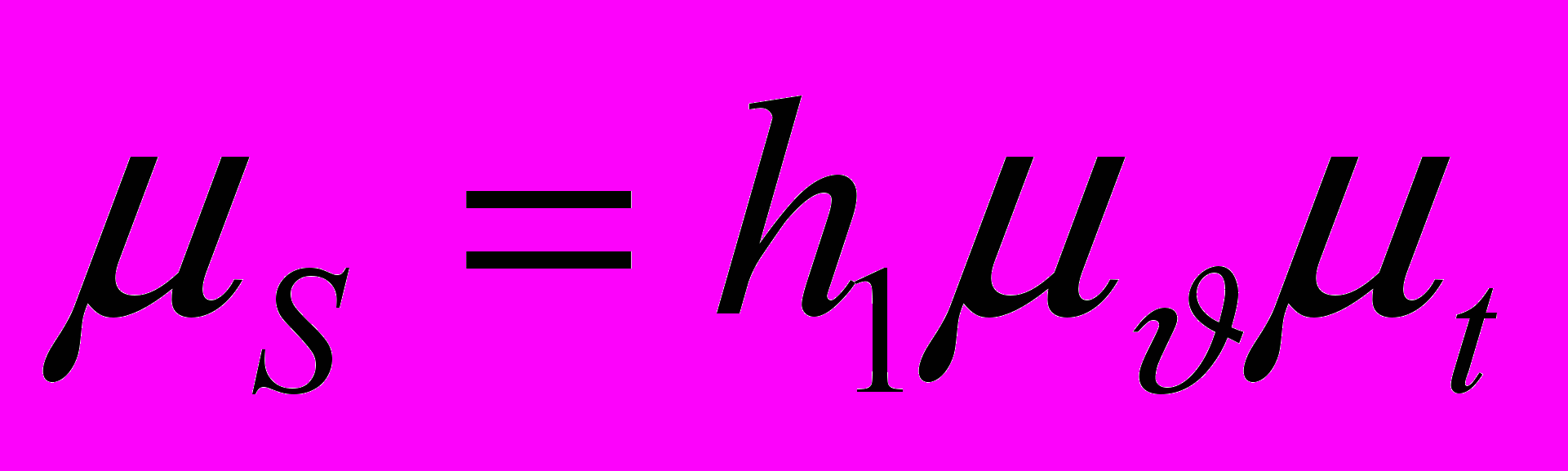где h₁ – полюсное расстояние для интегрирования, мм; _ – масштабный коэффициент графика скоростей, м/(смм); _t – масштабный коэффициент времени, с/мм.




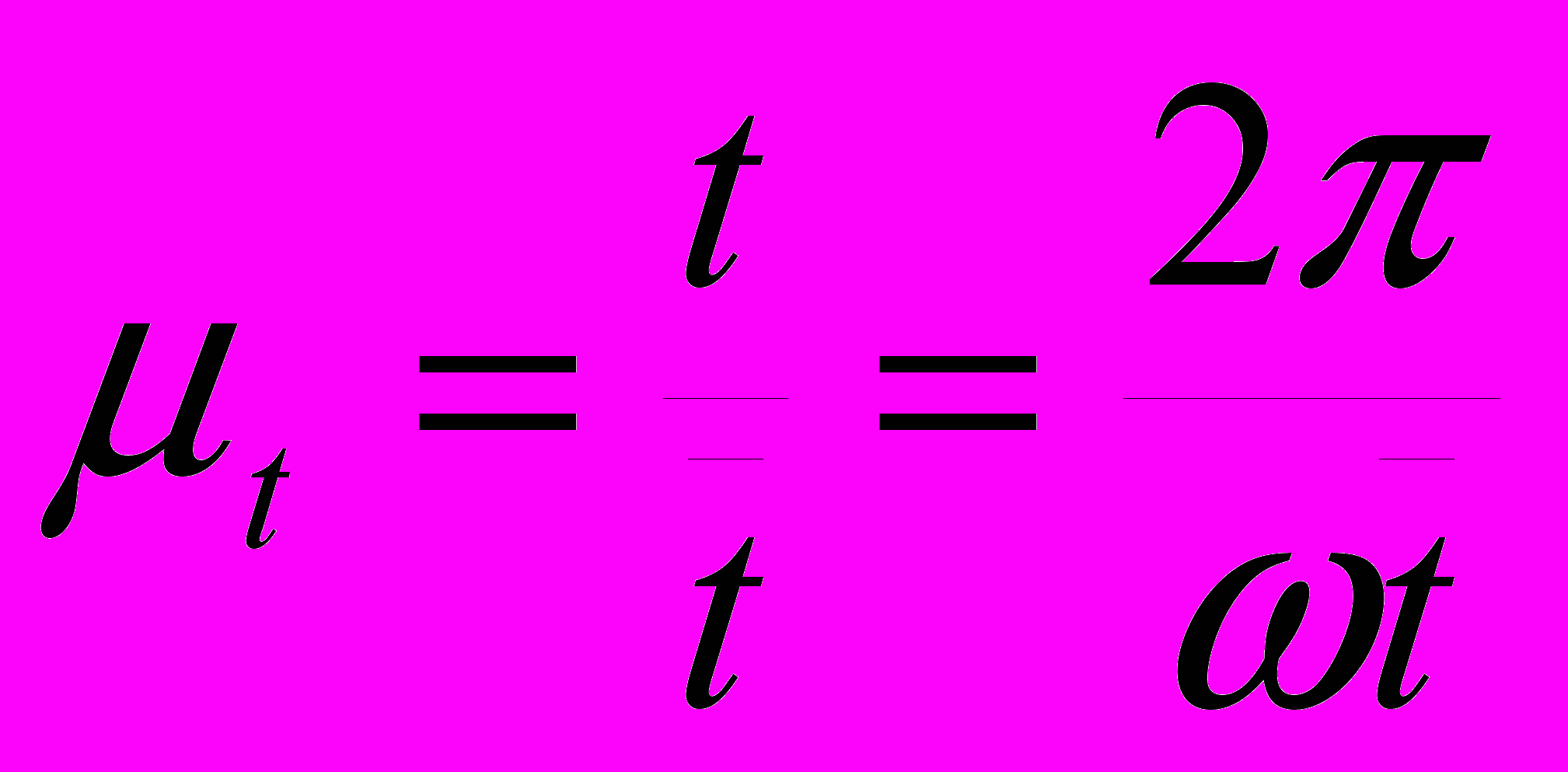
где  – заданная угловая скорость ведущего звена, с^-1; t – время цикла работы механизма, с; 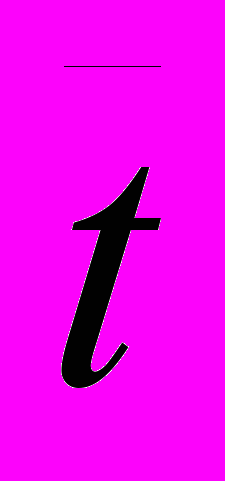– чертежное изображение времени цикла работы механизма, мм. Значение 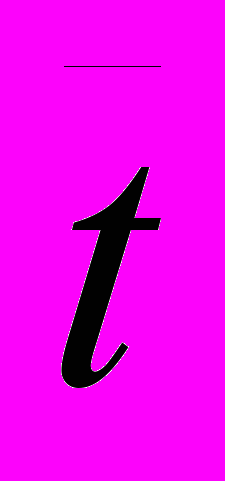принимают кратным 12 (180 мм, 240 мм и т.п.).

График ускорений получают методом графического дифференцирования скоростей выходного звена. Для чего на каждом участке дифференцирования проводят хорды кривой скорости. На продолжении оси абсцисс будущего графика ускорений откладывают полюсное расстояние h₂ [мм]. Из полученного полюса проводят лучи параллельные соответствующим хордам графика скоростей. Через точки пересечения лучей с осью ординат на каждом участке проводят отрезки параллельные оси абсцисс и далее проводят окончательную кривую ускорения выходного звена.

Масштабный коэффициент ускорений _a [м/(с²мм)] определяют из метрического соответствия графиков скоростей и ускорений


.


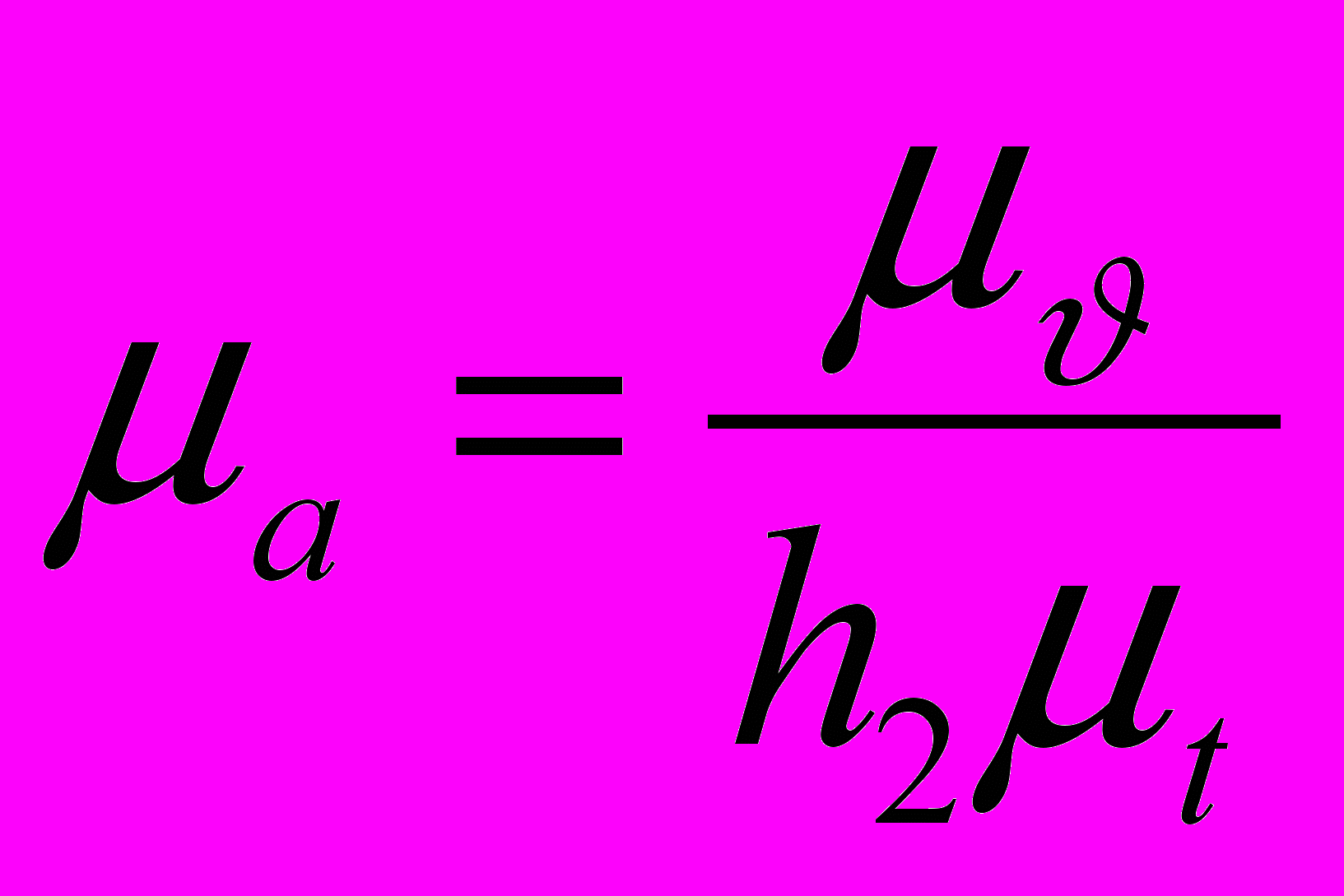Для двух выбранных в кинематическом исследовании положений механизма по полученным графикам вычисляют перемещения и ускорения выходного звена, которые сравнивают с соответствующими перемещениями и ускорениями, рассчитанными по планам положений и ускорений, и оценивают погрешность вычислений в процентах.

II. ДИНАМИЧЕСКОЕ ИССЛЕДОВАНИЕ ДВИЖЕНИЯ СИСТЕМЫ


Для определения истинного закона движения механизма достаточно установить закон движения ведущего звена механизма под действием заданных сил и моментов сил. При этом действующие силы и моменты, а также массы и моменты инерции звеньев следует привести к ведущему звену механизма, называемому звеном приведения.

Уравнение приведенного момента сил сопротивления или движущих сил (в зависимости от типа машины) с учетом сил тяжести звеньев в общем виде в каждом расчетном положении имеет вид


,


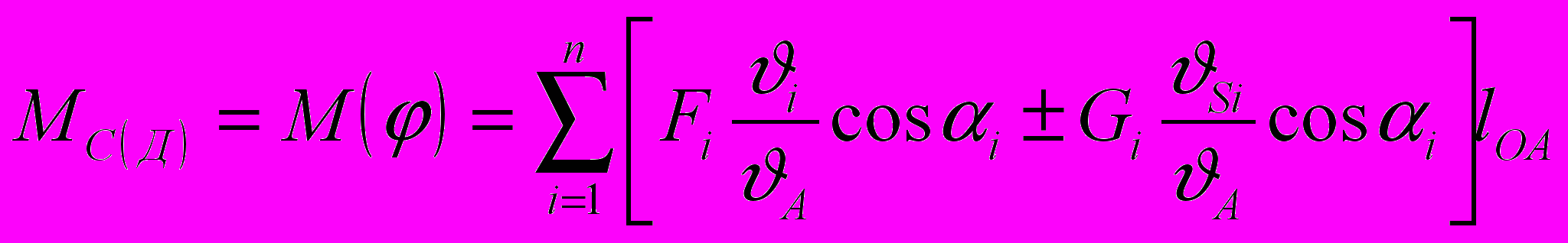где M_C – приведенный момент сил сопротивления, Нм; M_Д – приведенный момент движущих сил, Нм;  – угол положения начального звена; i – номер звена; F_i – сила сопротивления (F_С) или движущая сила (F_Д), Н;   – скорость точки приложения силы F_i, м/c; _i – угол между линией действия силы F_i и вектором скорости ; – скорость кривошипной точки A, м/с; l_OA – радиус кривошипа, м; G_i – сила тяжести i-го звена, Н; 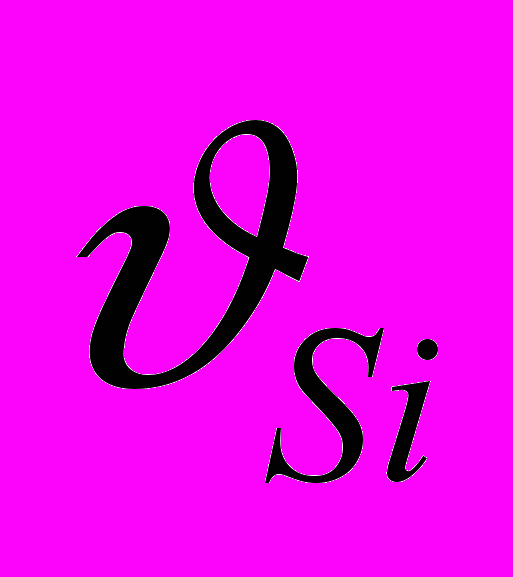– линейная скорость центра масс i-го звена, м/с.

Для упрощения расчетов рационально в представленном уравнении заменить линейные скорости (,,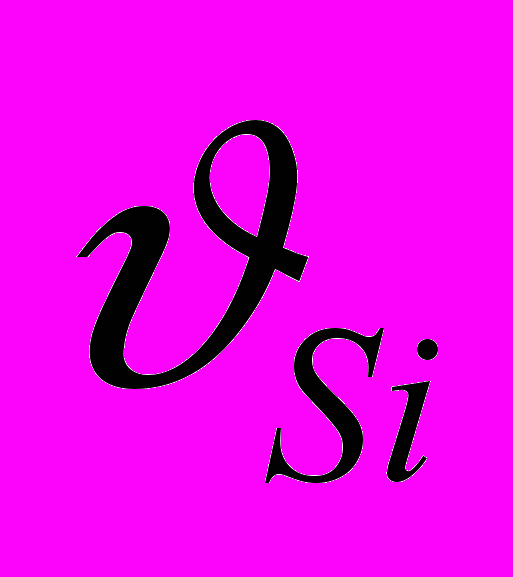) их изображениями на планах скоростей. Тогда расчетные формулы приведенного момента сил сопротивления M_C или движущих сил M_Д имеют вид


,




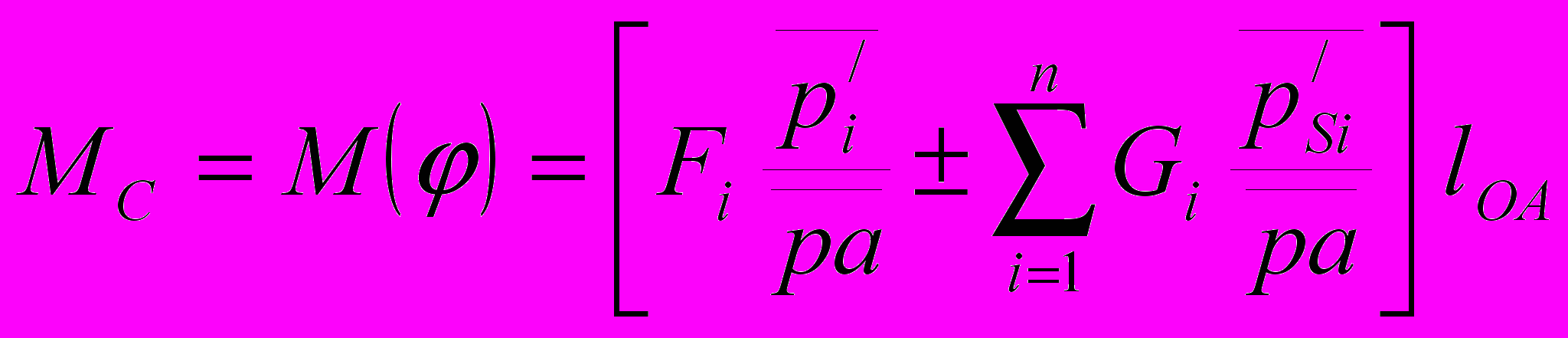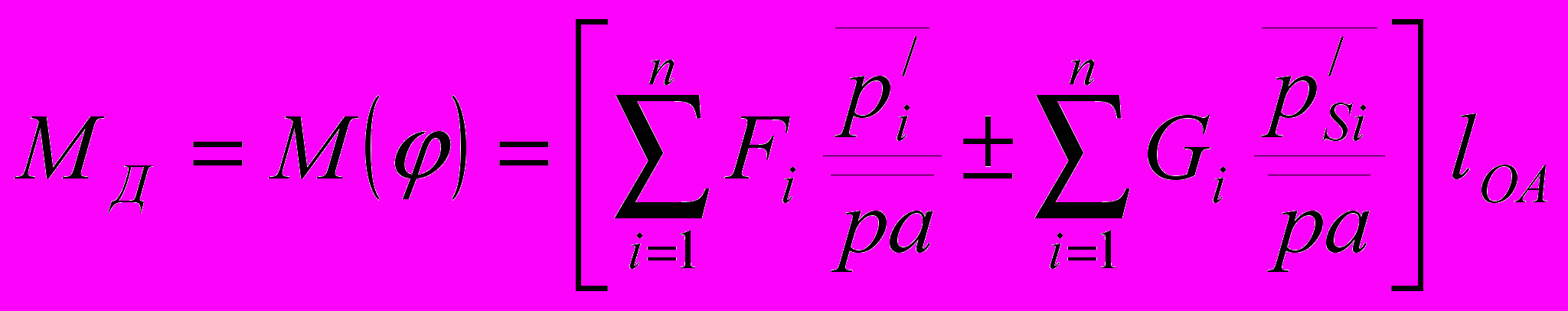
где 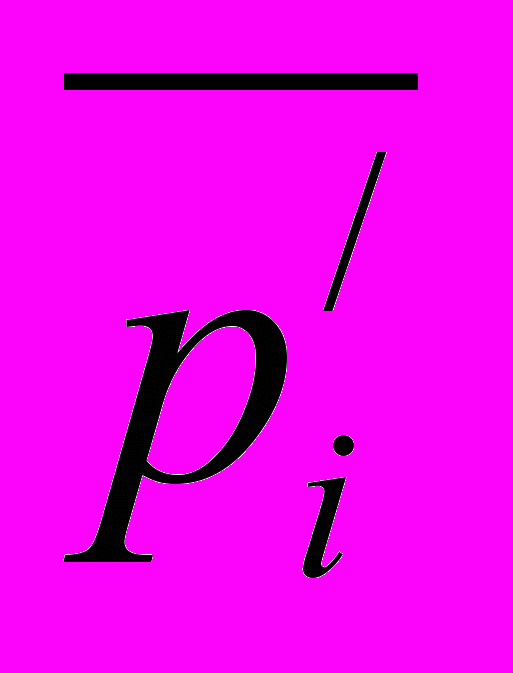, 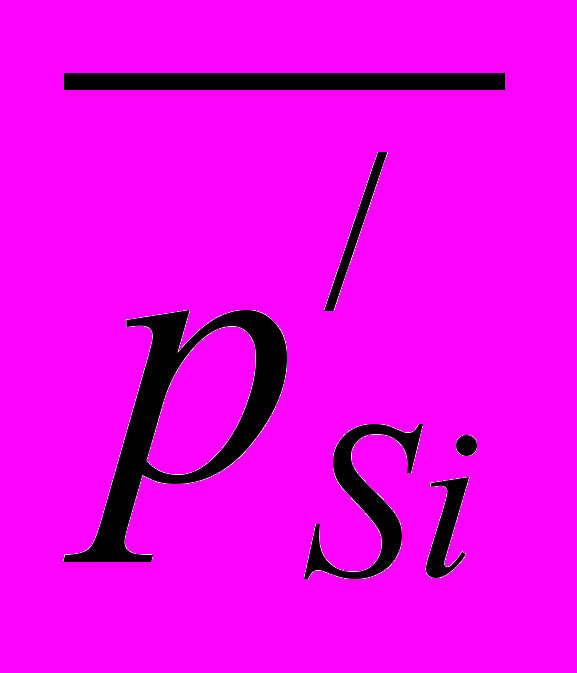– чертежные изображения проекций векторов скоростей и 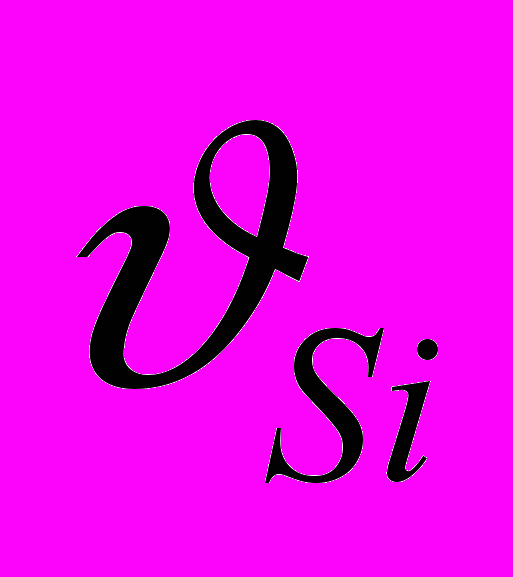на линии действия соответствующих сил на плане скоростей, мм; 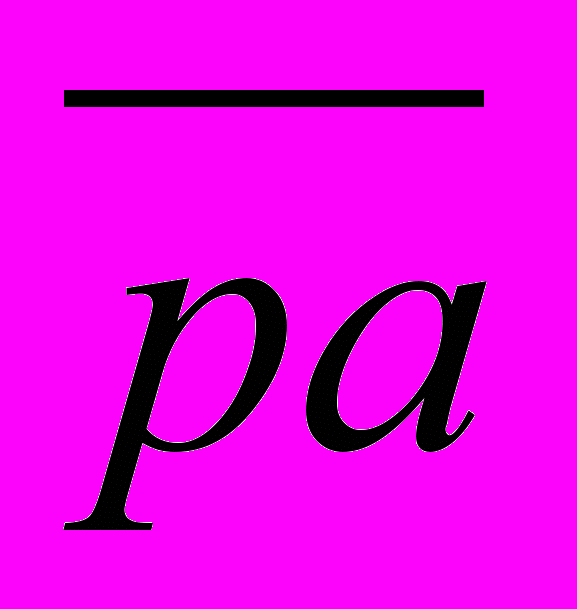– чертежное изображение вектора скорости кривошипной точки А на плане скоростей, мм.

Окончательный вид расчетной формулы определяется схемой механизма и исходными данными к ней.

В расчетах приведенного момента сил сопротивлений при составляющих от сил тяжести знак «плюс» соответствует положениям механизма, в которых вертикальные проекции скоростей 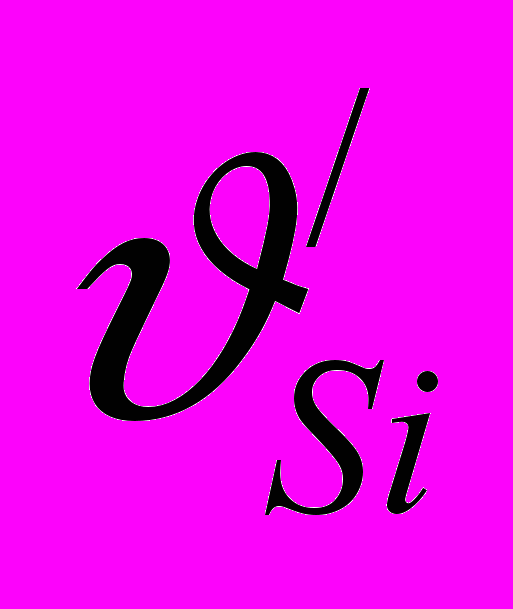направлены вверх, а знак «минус» – при направлении этих проекций вниз. В расчетах приведенного момента движущих сил знаки при составляющих от сил тяжести противоположны предыдущим: плюс при направлении векторов 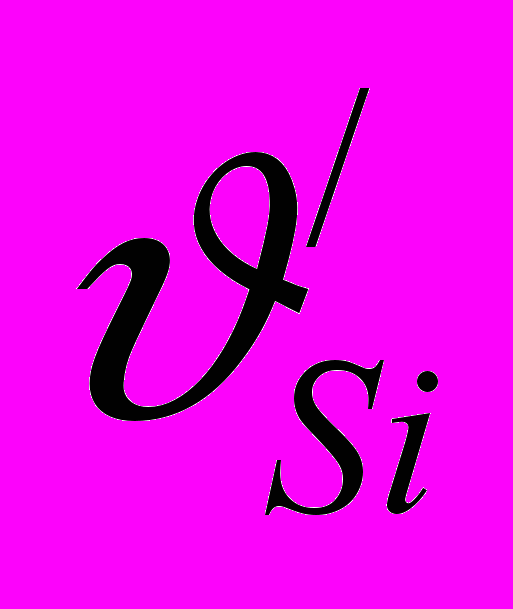вниз и минус, если эти векторы направлены вверх.

Рассчитывают М_С (М_Д) за цикл движения механизма. По результатам вычислений в масштабе _M [Нм/мм] строят график моментов сил сопротивлений или движущих сил M = f().

Интегрированием графика приведенного момента сил в функции угла положения начального звена получают масштабный график работ приведенных сил A = f(). Интегрирование выполняют ранее освоенным методом хорд, при этом предварительно задаются величиной полюсного расстояния h [мм]. Масштабный коэффициент _A [Дж/мм] графика работ вычисляют по зависимости





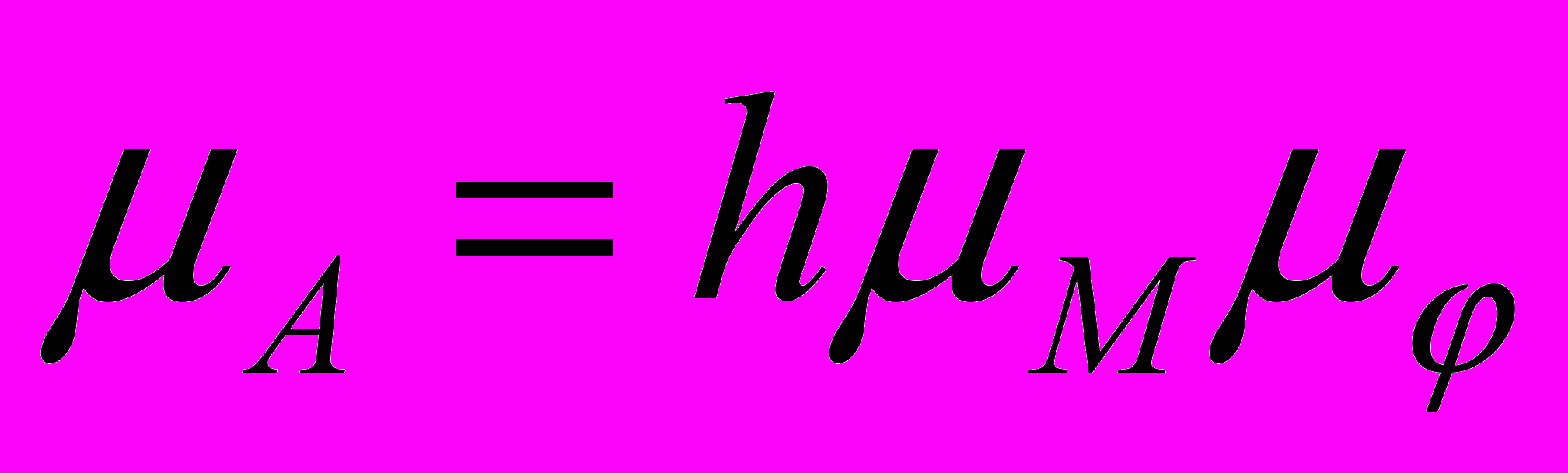
где h – полюсное расстояние, мм; _M – масштабный коэффициент графика моментов сил, Нм/мм; _ – масштабный коэффициент углов положения начального звена, рад/мм.


,

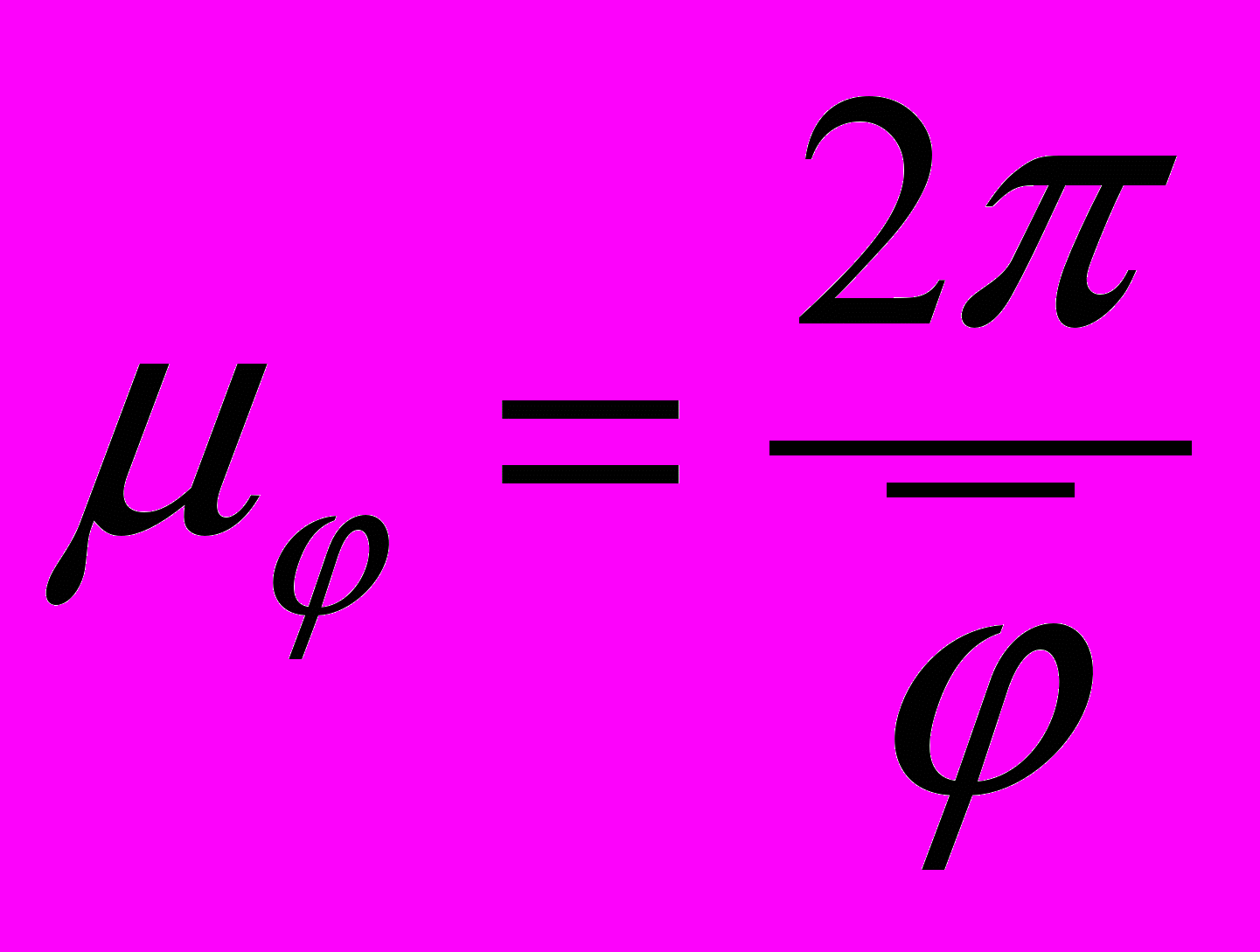где – чертежное изображение угла поворота кривошип, мм. Принимают равным значению кратному 12 (180 мм, 240 мм и т.п.).

Учитывая, что за цикл установившегося движения системы сумма работ сил сопротивлений и движущих сил равна нулю, строят прямолинейный график работ движущих сил A_Д = f() для технологической машины или график работ сил сопротивлений A_С = f() для энергетической машины.

Алгебраическим суммированием ординат графиков работ сил сопротивлений A_С = f() и движущих сил A_Д = f() строят масштабный график избыточной энергии T = f() рассматриваемой системы. При этом масштабный коэффициент _T [Дж/мм] графика T = f() принимают равным масштабному коэффициенту графика работ _A. Если амплитуда графика T = f() оказывается незначительной, то масштабный коэффициент следует уменьшить в 2÷3 раза и принять его равным _T = _A/(2÷3).

Для всех положений механизма за цикл движения рассчитывают избыточную энергию T [Дж], равную


,


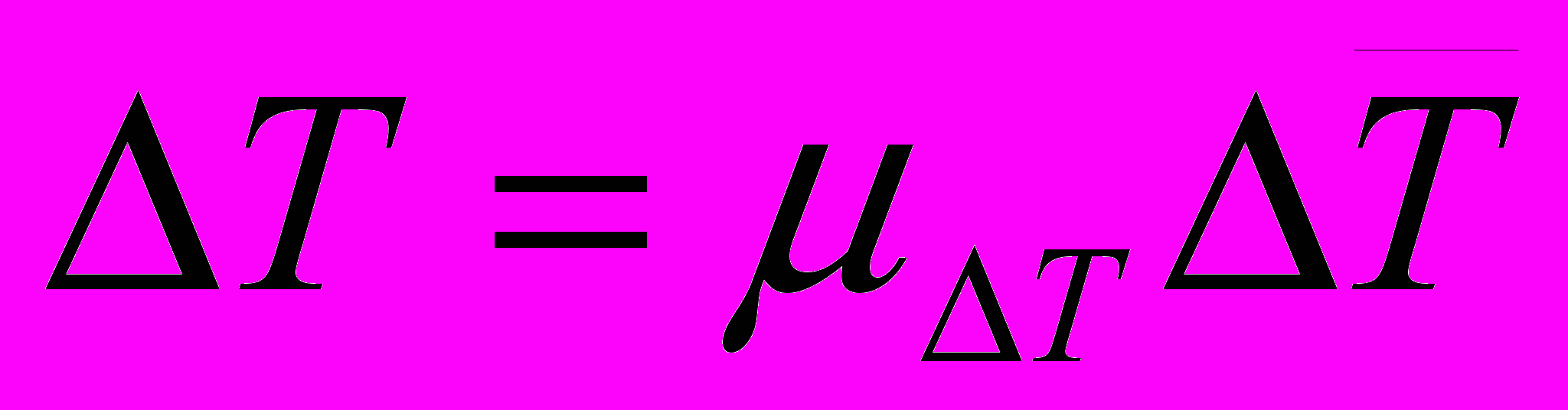где – изображение избыточной энергии на графике T = f(), мм.

Результаты вычислений T за цикл движения механизма следует представить в табличной форме.

Составляют расчетную формулу приведенного к начальному звену момента инерции системы в функции угла положения. Окончательный вид расчетной формулы зависит от схемы механизма и исходных данных к ней.

Приведенный момент инерции системы равен


,

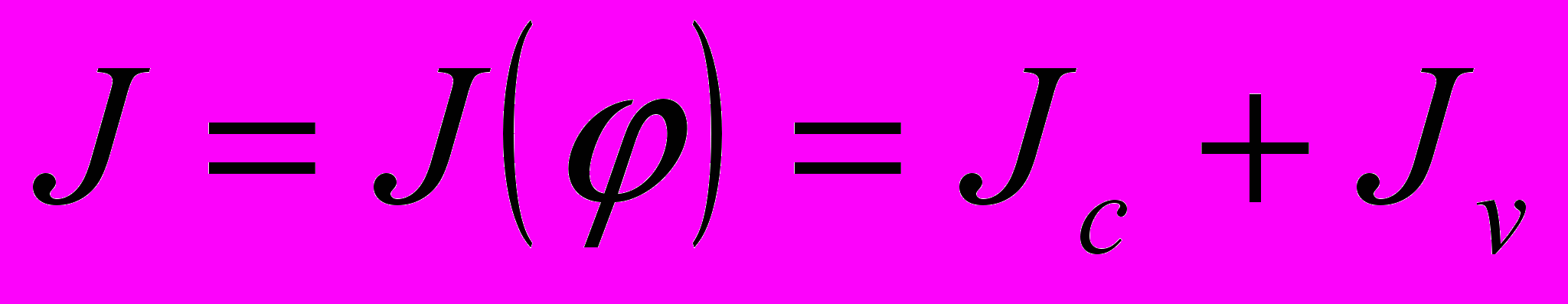где J_c – постоянная часть приведенного момента инерции, кгм²; J_v – переменная часть приведенного момента инерции, кгм².


,


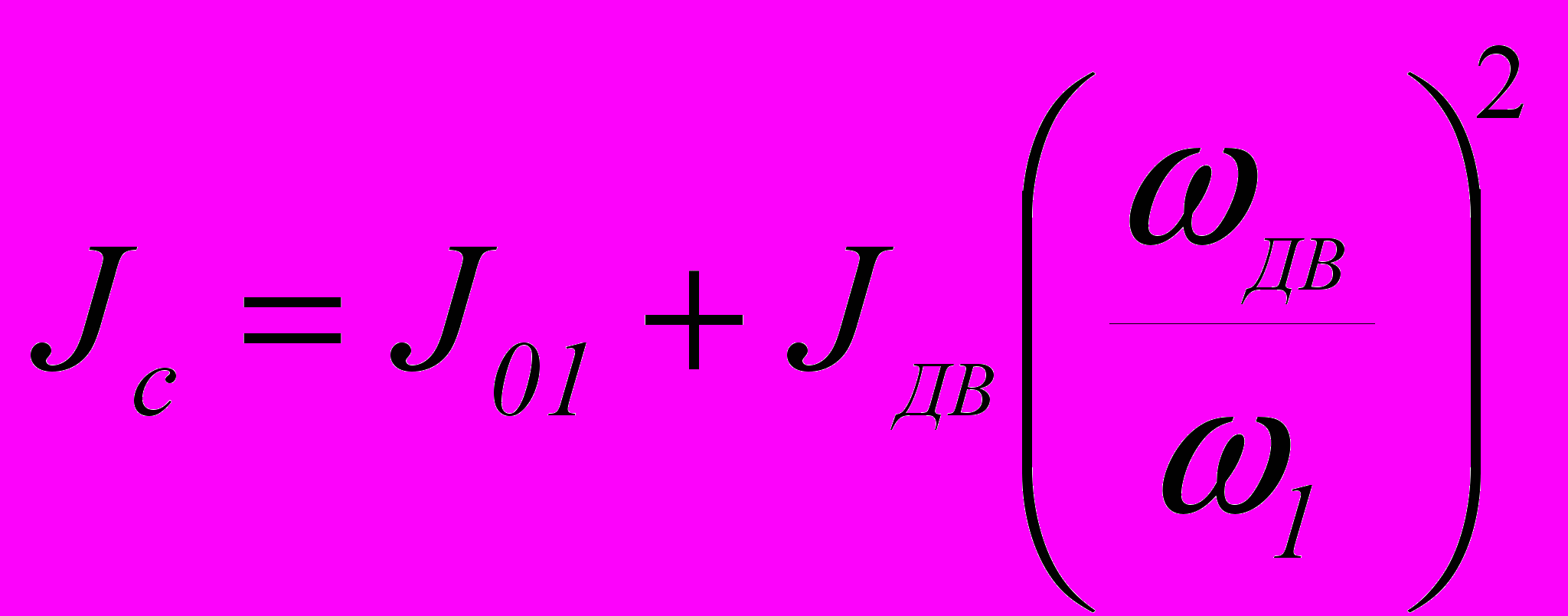где J₀₁ – момент инерции начального звена относительно оси, проходящей через его центр масс, кгм²; J_ДВ – момент инерции ротора двигателя, кгм²; ₁ – угловая скорость начального звена, с^-1; _ДВ – угловая скорость ротора двигателя, с^-1.


,


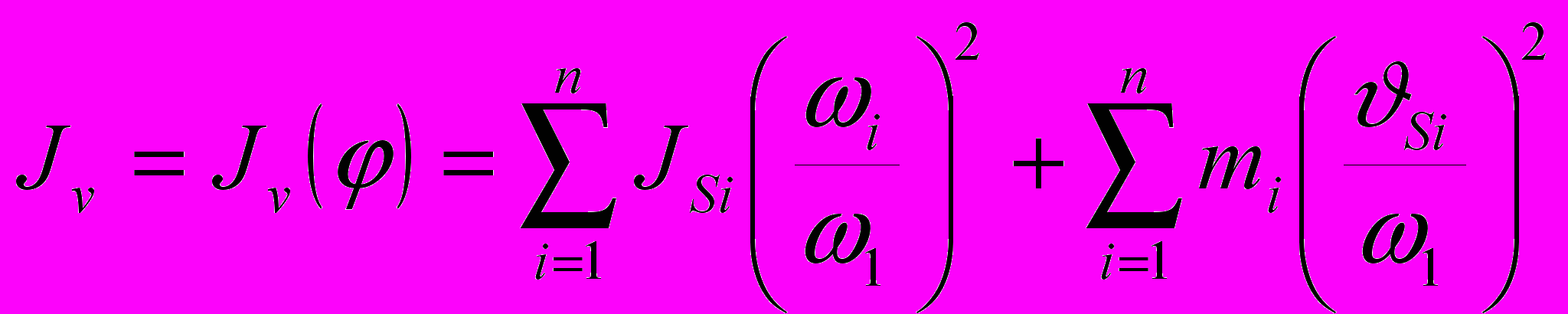где J_Si – момент инерции i-го звена относительно оси, проходящей через центр масс звена, кгм²; _i – угловая скорость i-го звена, с^-1; m_i – масса i-го звена, кг; 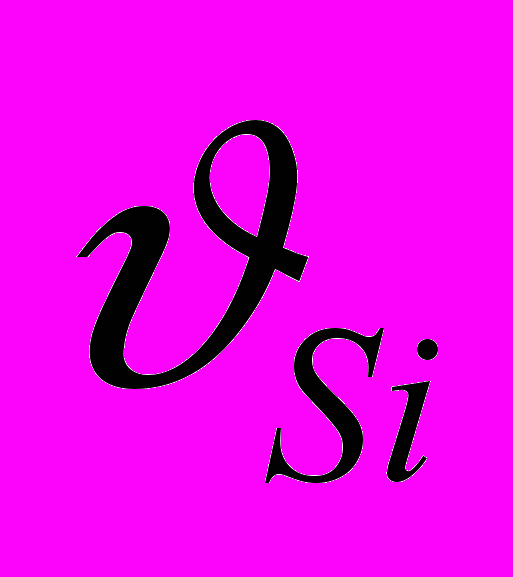– линейная скорость центра масс i-го звена, м/с.

Рассчитывают приведенный момент инерции системы за цикл движения механизма. По результатам вычислений в масштабе _J [кгм²/мм] строят график приведенного момента инерции системы в функции угла положения начального механизма J = f().

Учитывая последующую необходимость исключения углового параметра , оси координат графика J = f() располагают повернутыми на 90⁰ по часовой стрелке с размещением его на чертеже вверху справа от сетки предыдущих графиков M = f(), A = f(), T = f().

Решением дифференциального уравнения движения системы получают расчетную формулу скорости начального звена в функции угла положения


,


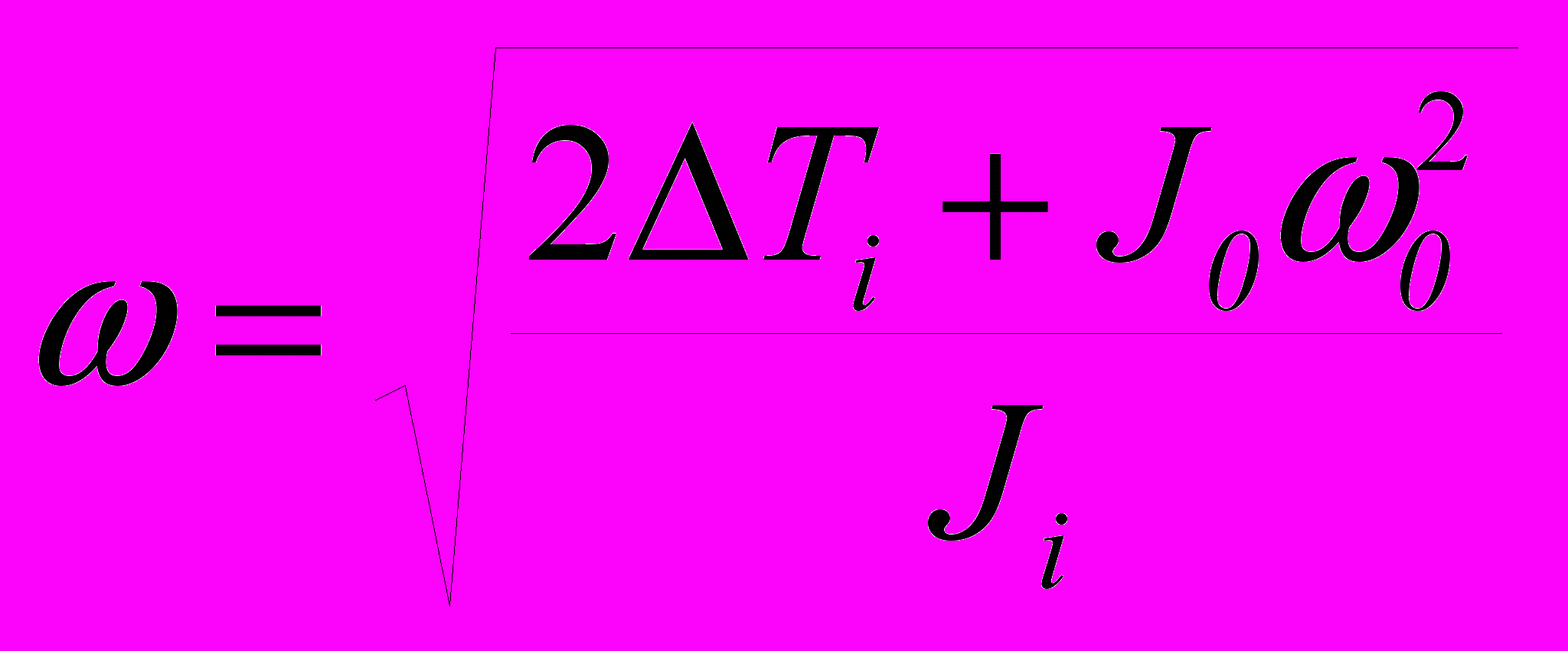где  – угловая скорость начального звена в каждом расчетном положении механизма, c^-1; J₀ – приведенный момент инерции системы в начале цикла, кгм²; ₀ – угловая скорость звена приведения в начале цикла, с^-1; J_i – приведенный момент инерции системы в каждом расчетном положении, кгм².

По результатам вычислений строят масштабный график угловой скорости звена приведения  = f(), рассчитывают среднюю скорость _ср за цикл движения и определяют фактический коэффициент неравномерности движения  системы


,


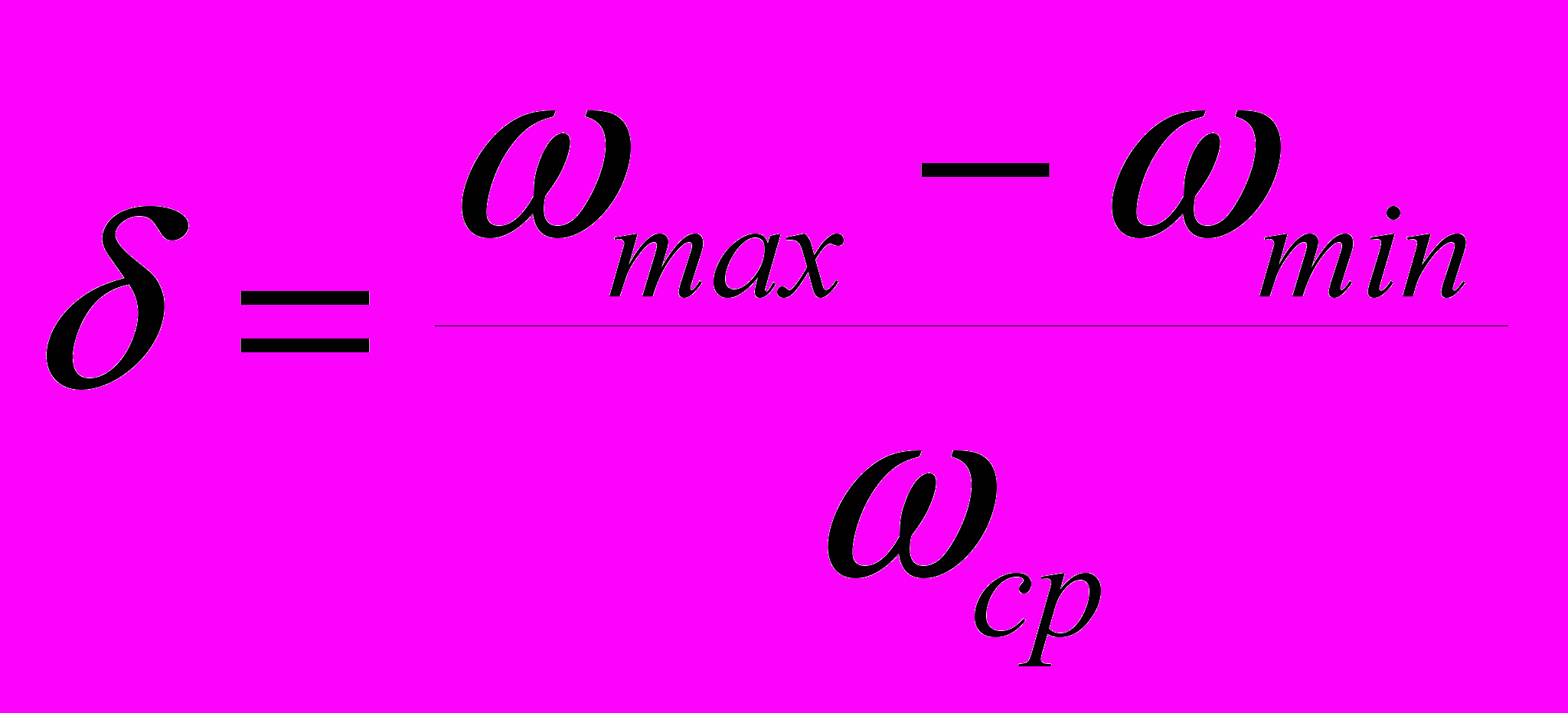где _max – максимальная скорость ведущего звена, с^-1; _min – минимальная скорость ведущего звена, с^-1; _ср – средняя скорость ведущего звена, с^-1.

Если расчетный коэффициент неравномерности оказывается больше заданного допустимого значения, следует перейти к проектированию маховика – регулятора движения системы.


Проектирование маховика – регулятора

движения системы


Совместным решением зависимостей T = f() и J = f() при исключении углового параметра  получают функцию T = f(J), графически представляемую диаграммой Ф. Виттенбауэра (кривая энерго-масс).

При заданной средней скорости звена приведения рассчитывают углы наклона _min и _max внешних касательных к указанной кривой

,


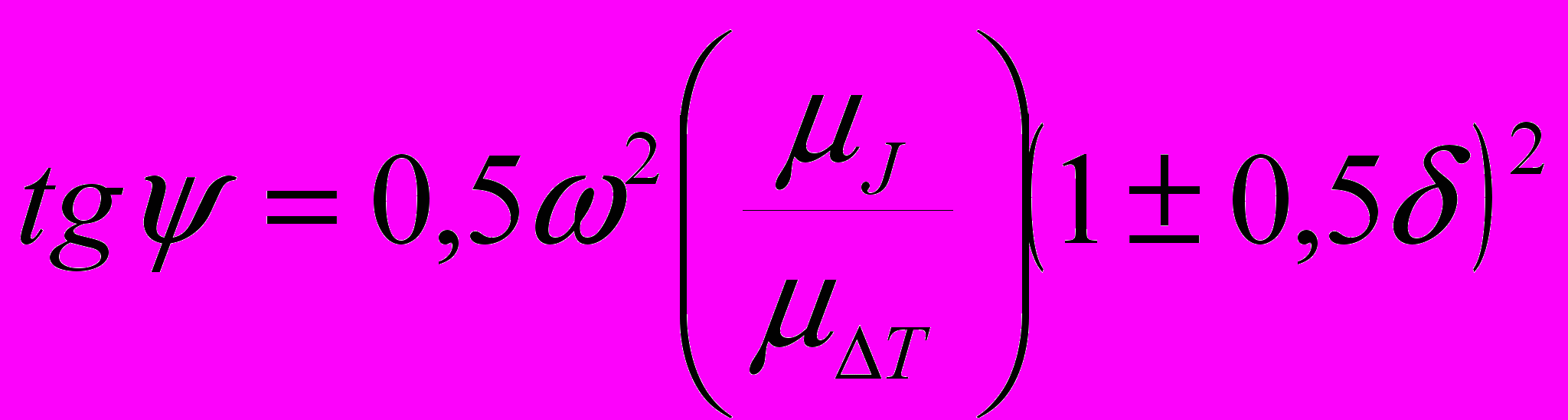где _J – масштабный коэффициент момента инерции, кгм²/мм; _T – масштабный коэффициент энергии, Дж/мм;  – заданный коэффициент неравномерности движения.

Знак «плюс» используют при расчете _max , знак «минус» – _min.

К кривой Ф. Виттенбауэра строят внешние касательные с наклонами к оси моментов инерции под углами _max и _min.

На оси T определяют отрезок 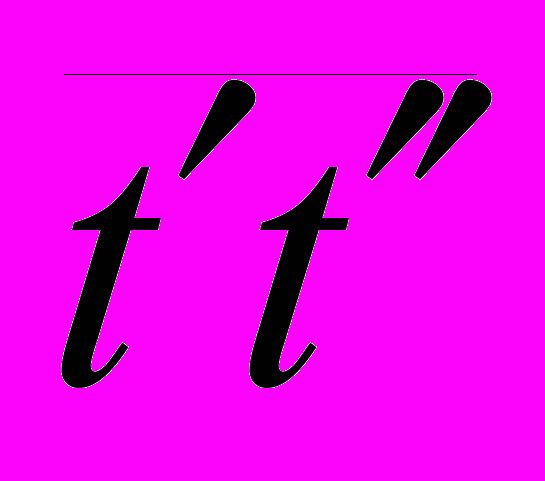, являющийся изображением в мм части избыточной энергии аккумулируемой маховиком. Момент инерции маховика J_м [кгм²] определяют по зависимости


,


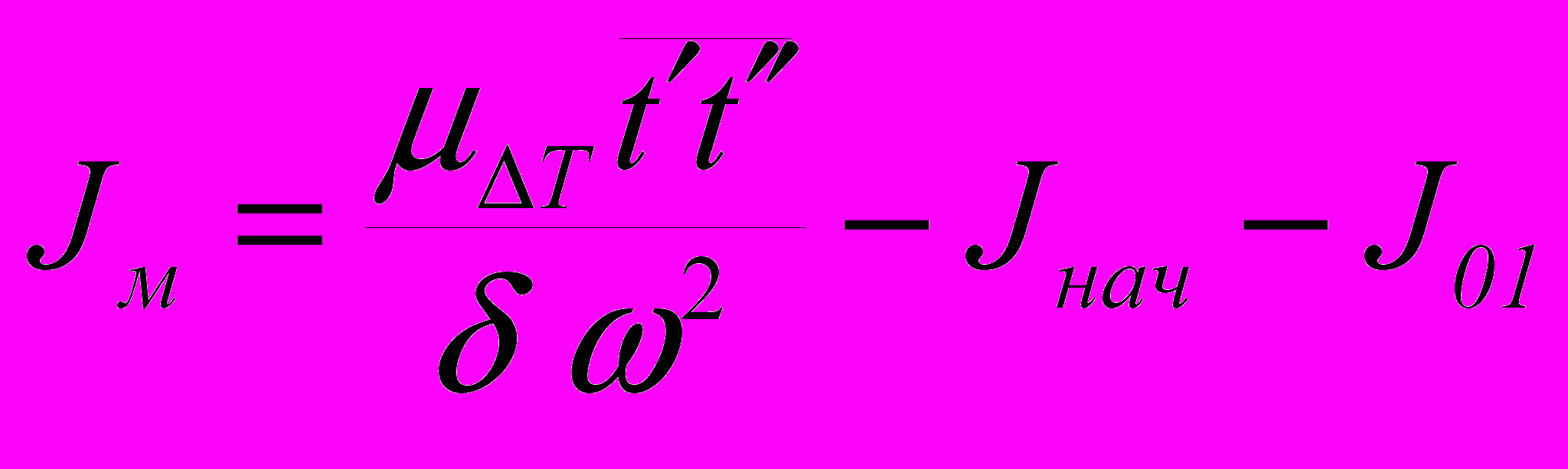где J_нач – момент инерции системы в начале цикла, кгм²; J₀₁ – момент инерции кривошипа, кгм².

Далее выделяют часть момента инерции моховика, относящуюся к его ободу J_об = (0,85…0,95)J_м и рассчитывают размеры поперечного сечения обода.

Расчетный диаметр маховика в первоначальном варианте принимают равным D_м = 10l_OA .

Масса обода маховика m_об [кг]


,


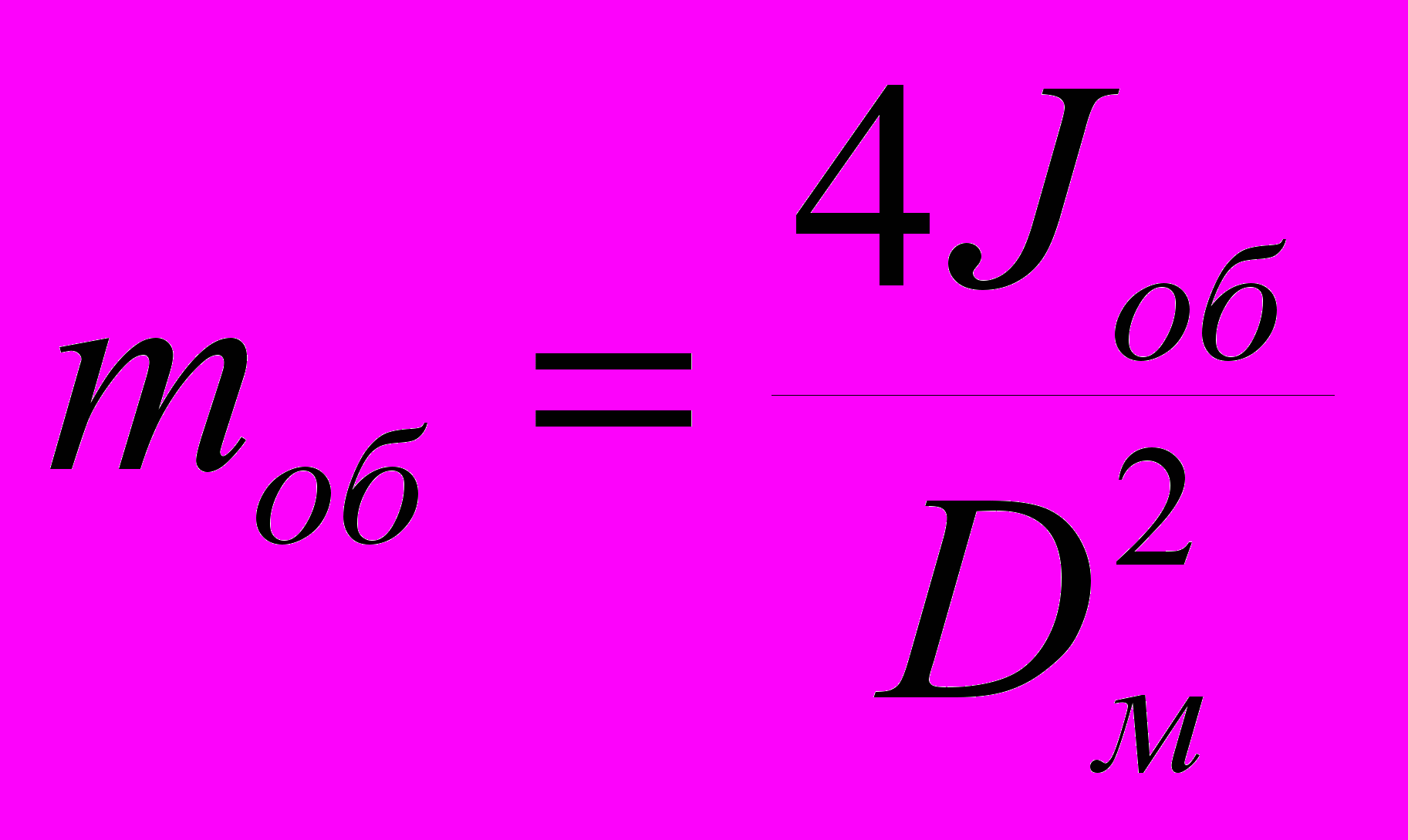С учетом принятого диаметра D_м и удельного веса материала маховика  масса обода маховика равна


,

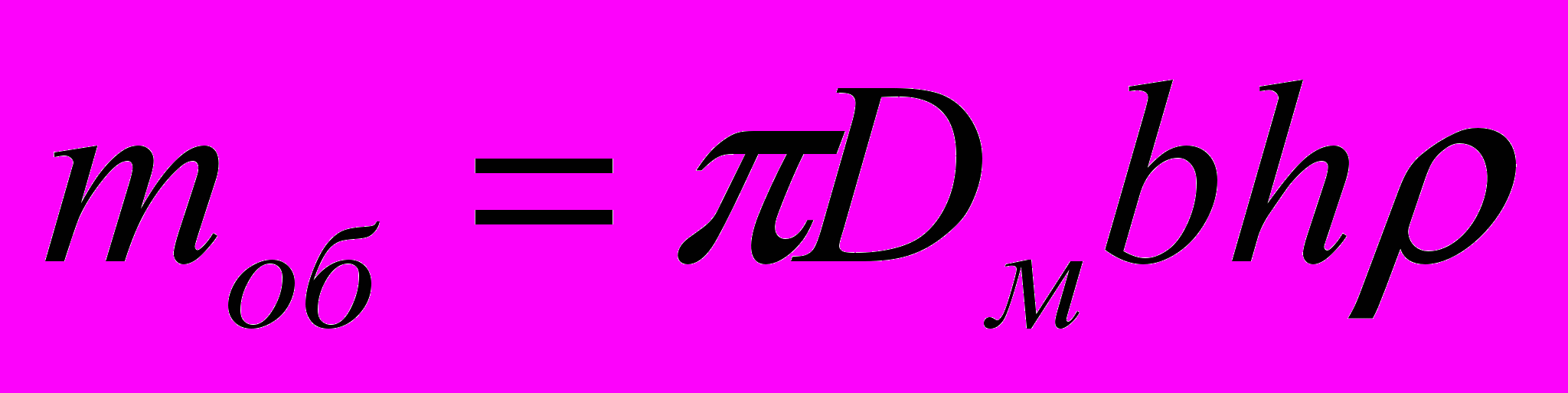где b – ширина обода маховика, м; h – высота обода маховика, м;  – удельный вес материала маховика (для серого чугуна  = 7100 – 7300 кг/м³).

Отношение b/h принимают равным 1,4…1,6.

В полученные размеры сечения обода вносят коррективы изменением диаметра D_м. Следует рассмотреть несколько вариантов (2  3) и принять оптимальный.

При этом следует проверить маховик на непревышение его ободом критической скорости 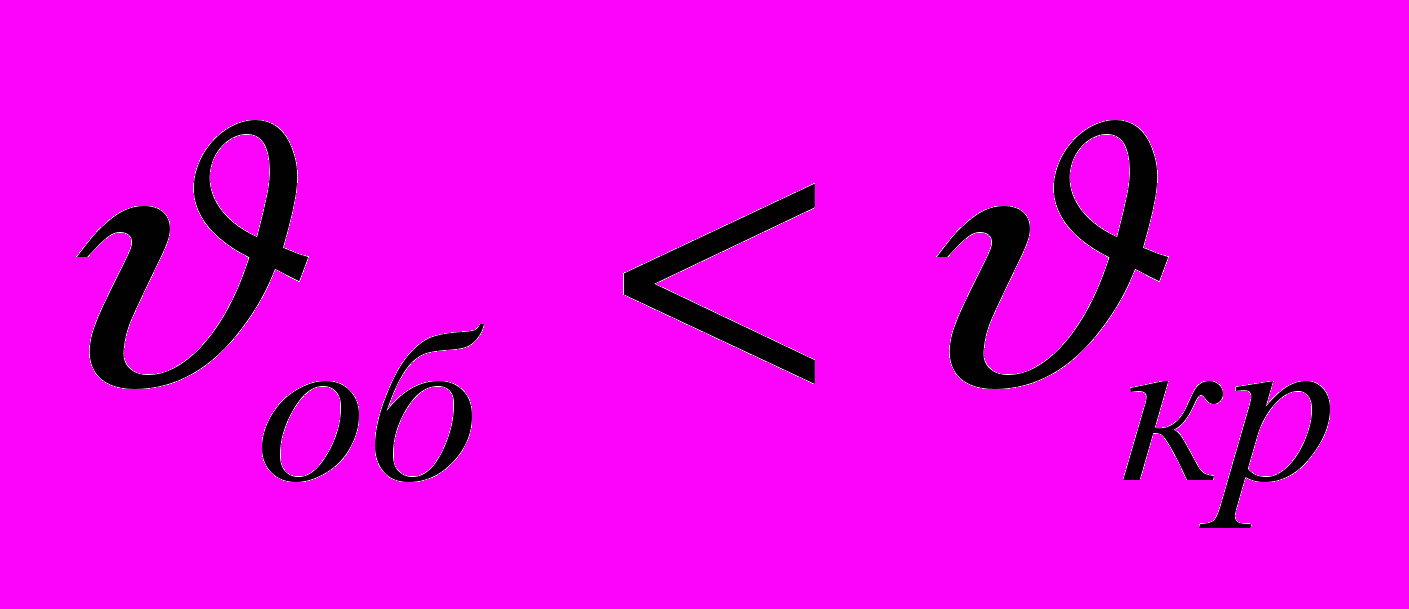. Для серого чугуна критическая скорость равняется .





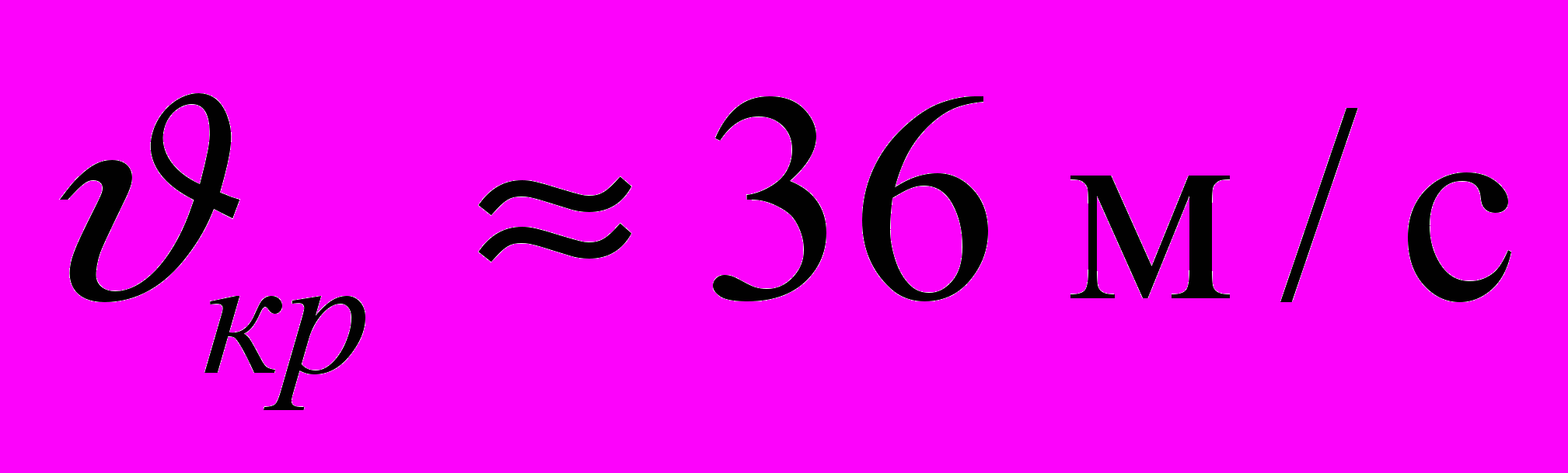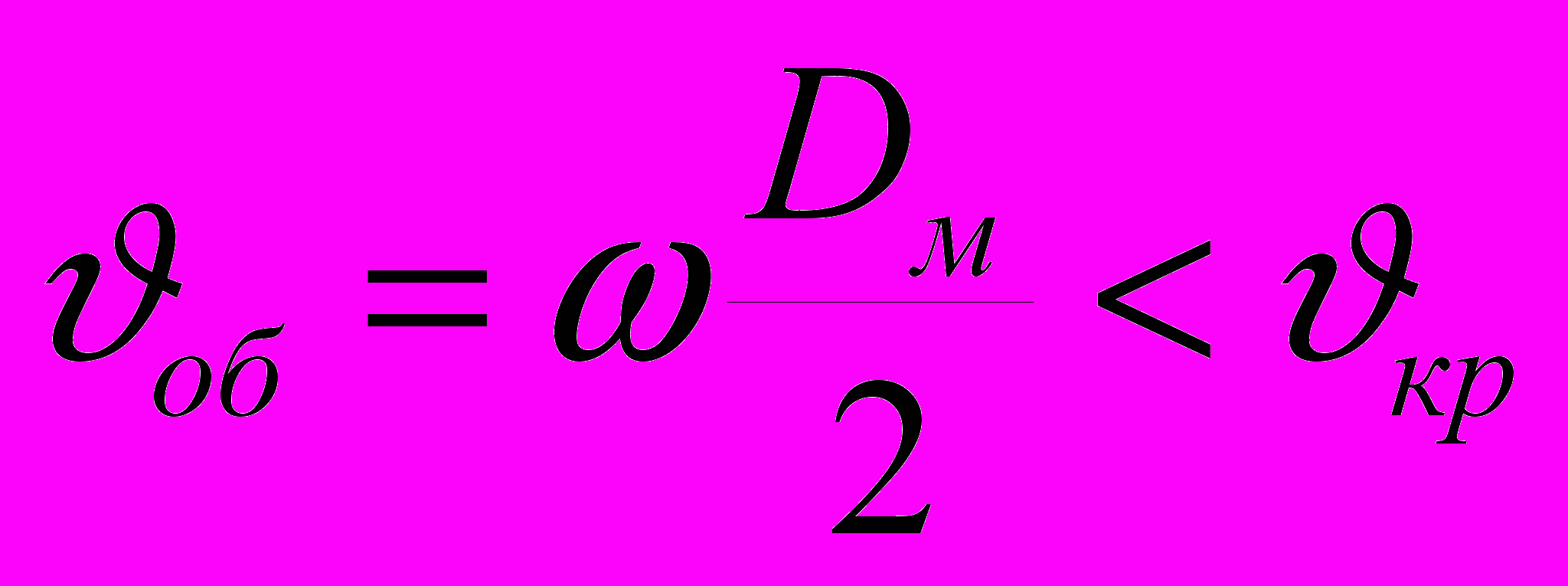
III. КИНЕТОСТАТИЧЕСКИЙ РАСЧЕТ РЫЧАЖНОГО МЕХАНИЗМА С УЧЕТОМ УСКОРЕНИЯ

НАЧАЛЬНОГО ЗВЕНА


Кинетостатический расчет механизма выполняют для одного положения, относящегося к такту раюочего хода механизма. Рассчитывают угловое ускорение начального звена  [с^-2] с учетом момента инерции маховика по дифференциальному уравнению движения системы


,


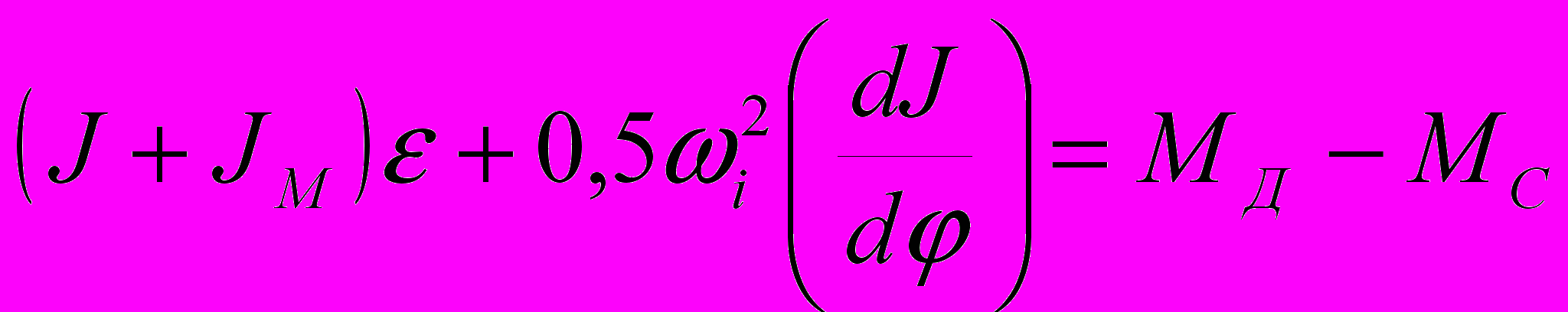где для расчетного положения _i – угловая скорость звена приведения, вычисляемая с учетом момента инерции маховика, с^-1; 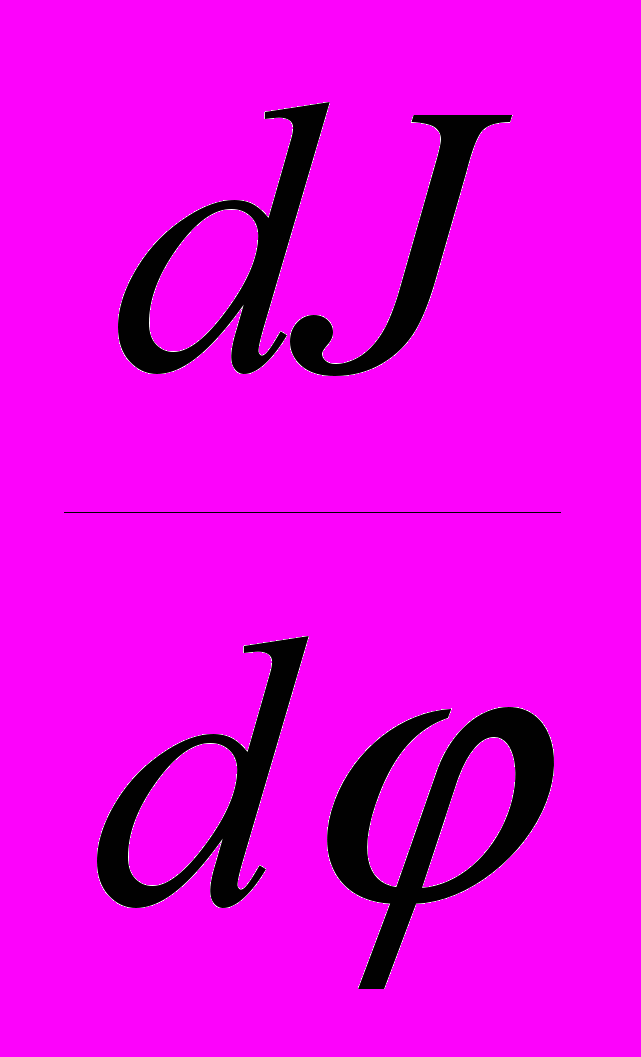– значение производной приведенного момента инерции, кгм²; J – приведенный момент инерции системы в расчетном положении, кгм²; J_М – момент инерции маховика, кгм².

Для нахождения значения 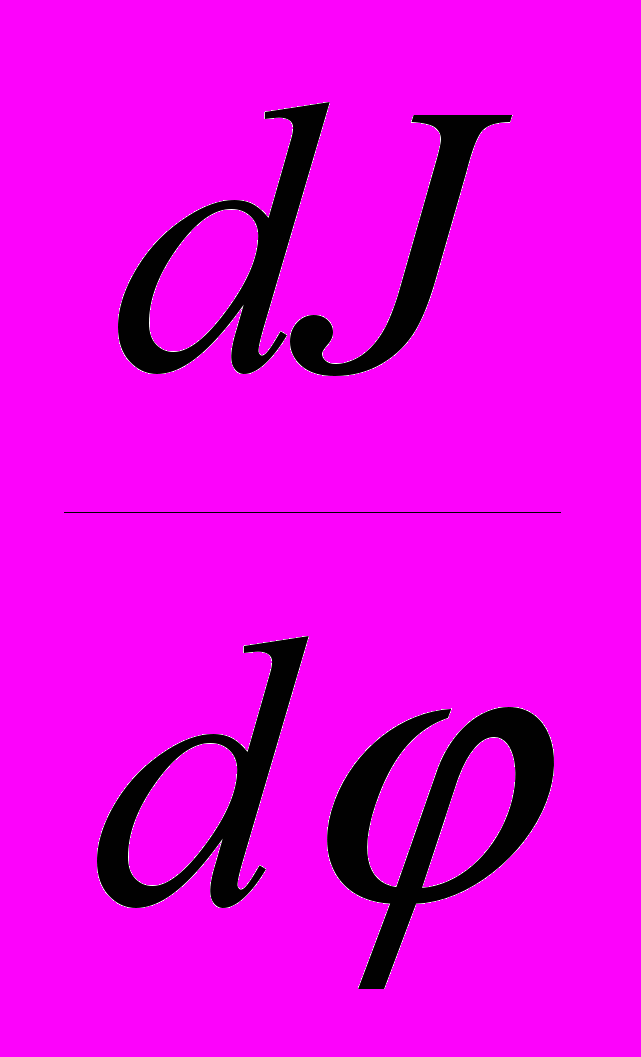графически дифференцируют кривую приведенного момента инерции системы J = f() на нескольких участках. Так, если расчетным является седьмое положение, то кривую J = f() дифференцируют на двух участках до расчетного положения (5, 6) и двух – после (8, 9).

Окончательное значение производной


; ,


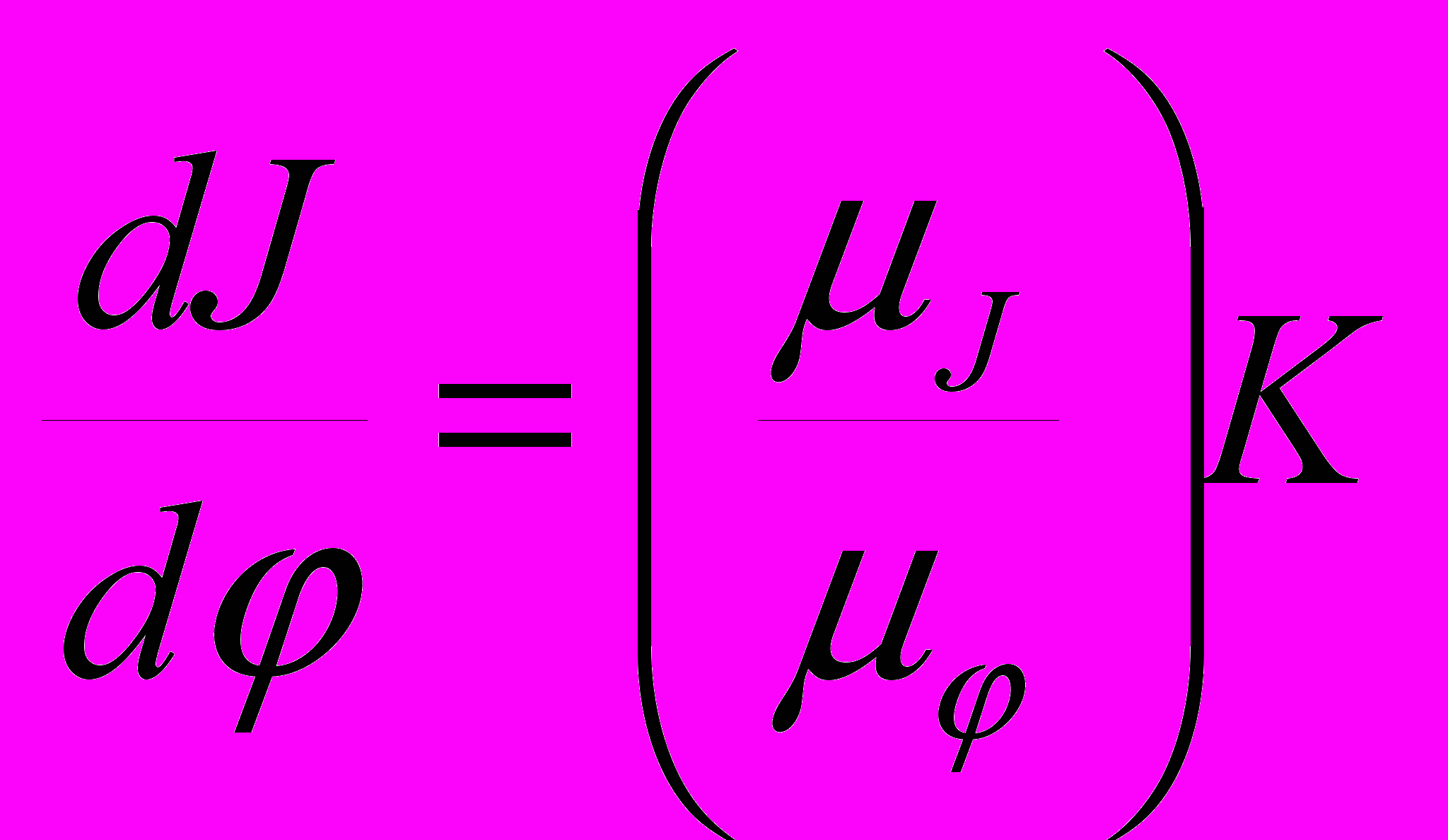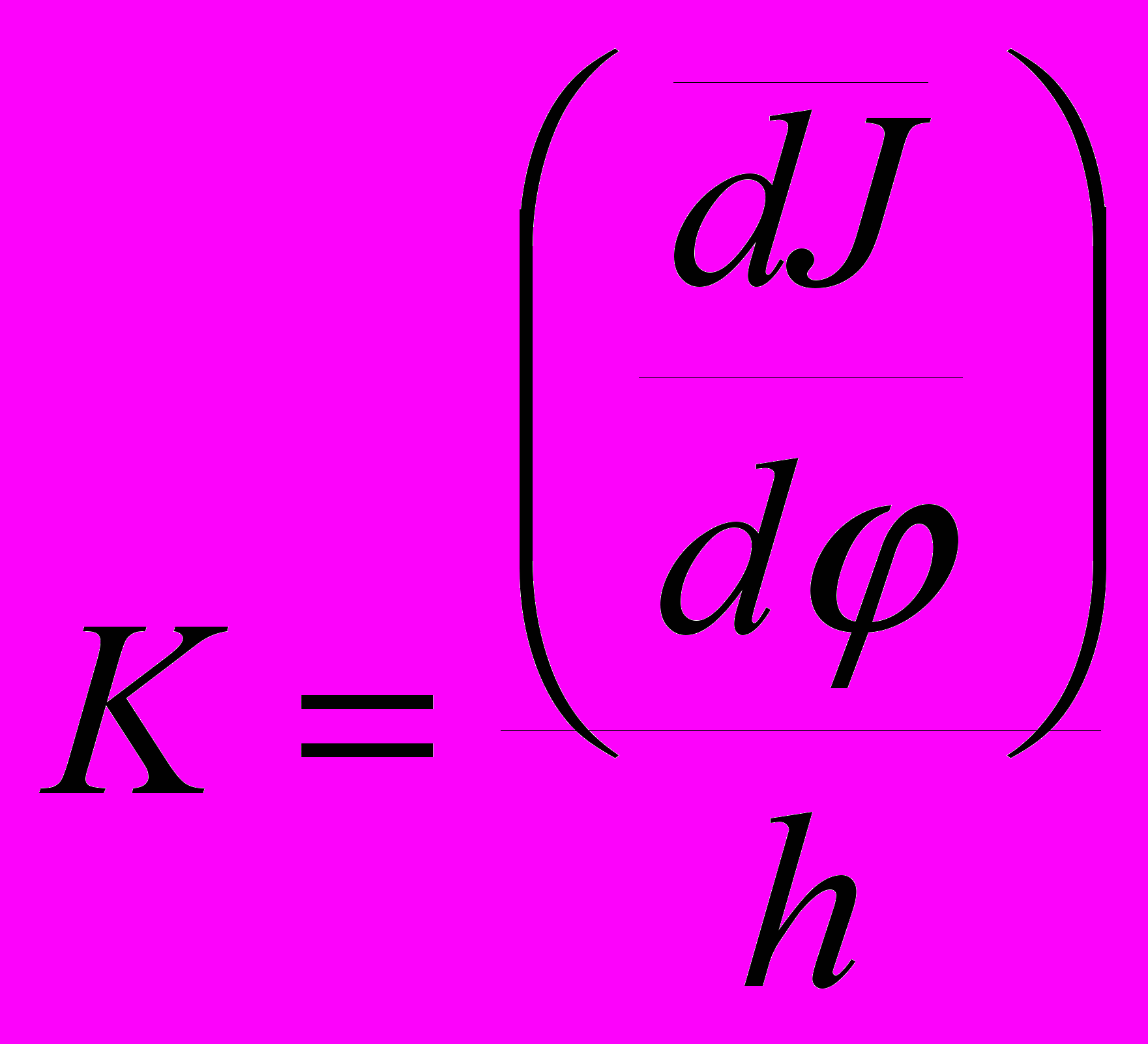где 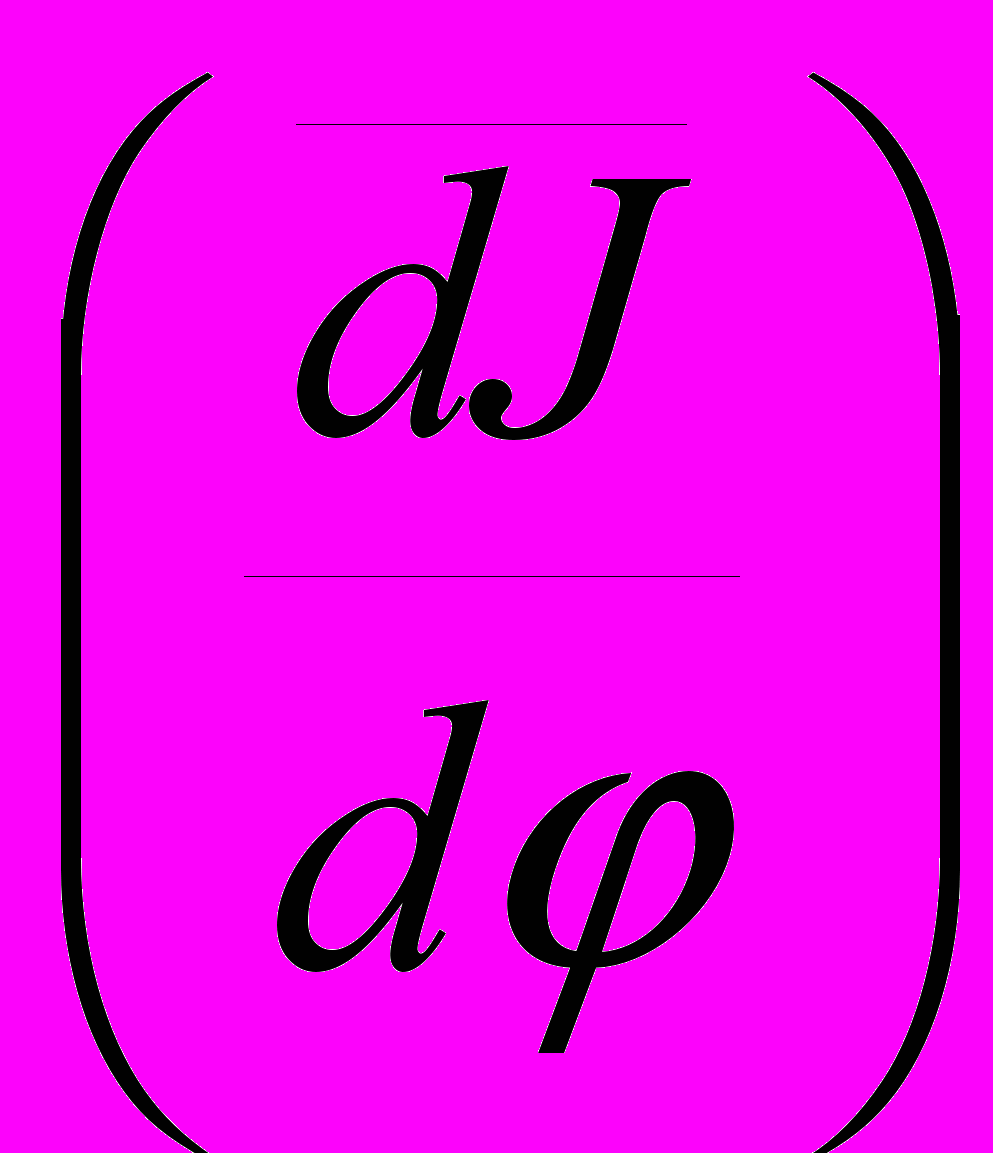– чертежное изображение искомой производной в расчетном положении, мм; h – полюсное расстояние, принятое в дифференцировании приведенного момента инерции, мм.

С учетом найденного углового ускорения начального звена  строят масштабный план ускорений.

Рассчитывают действующие на механизм внешние силы: силы тяжести звеньев G_i, силы инерции звеньев F_Иi, моменты сил инерции М_Иi , силы полезного сопротивления P_i..

В масштабе плана положений _S [м/мм] изображают схему силовой загрузки механизма в расчетном положении с сохранением обозначений кинематических пар, точек и номеров звеньев (см. кинематическое исследование механизма).

Кинетостатический расчет сил взаимодействия звеньев в кинематических парах выполняют в последовательности структурного анализа механизма, т.е. начинают с последней присоединенной структурной группы. Изображают группу в масштабе _S [м/мм] в рассматриваемом положении. Каждое звено группы загружают внешними силами, включая силы инерции и реакции от отбрасываемых звеньев. Рекомендуется буквенное обозначение реакций с нижними цифровыми индексами. Например, R₄₃ – реакция на звено 4 со стороны звена 3; R₃₄ – реакция на звено 3 со стороны звена 4.

В расчетах применяют кинетостатические уравнения равновесия моментов и сил по видам структурных групп, силами трения в кинематических парах при этом пренебрегают. Векторные уравнения равновесия сил решают графическим построением масштабных замкнутых планов сил. Для упрощения расчетов инерционные силу F_Иi и момент М_Иi каждого звена сложного движения заменяют одной силой инерции F_Иi, противоположной ускорению центра масс звена a_si и проходящей через центр качания коромысла или кулисы или через полюс инерции шатуна.

Положение центра качаний звена (точка К) рассчитывают по выражению


,


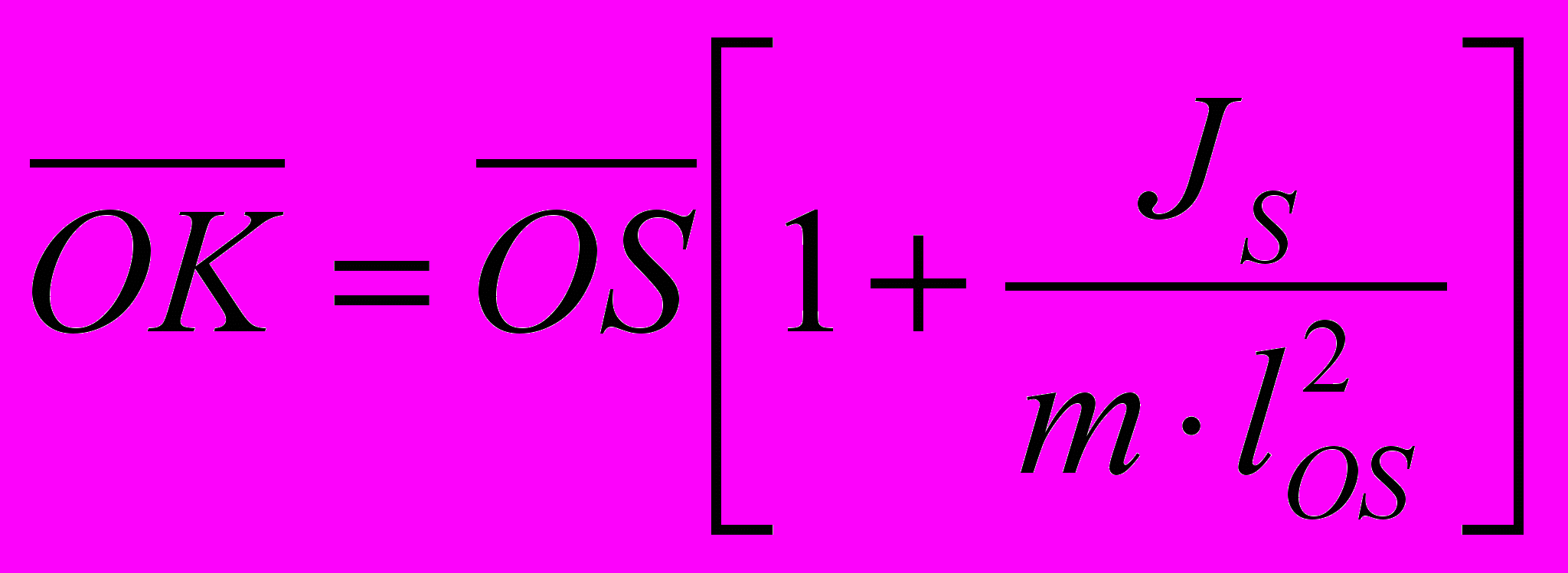где 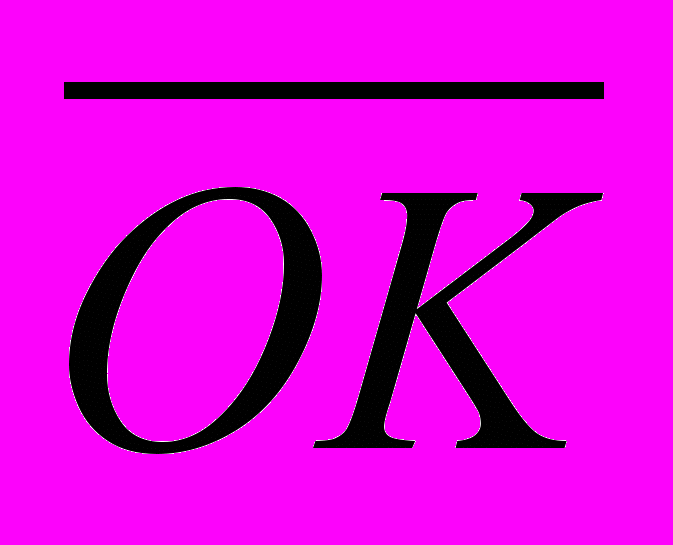и – соответственно изображения расстояний оси вращения до центра качаний и до центра масс звена, мм; J_S – момент инерции звена, кгм²; m – масса звена, кг; l_OS – истинное расстояние от оси вращения до центра масс звена, м.

Неизвестная реакция 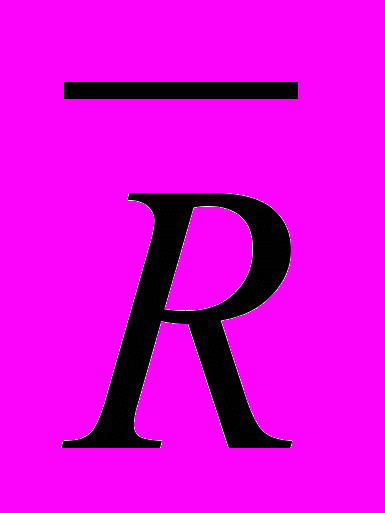во внешнем шарнире структурной группы равна


,


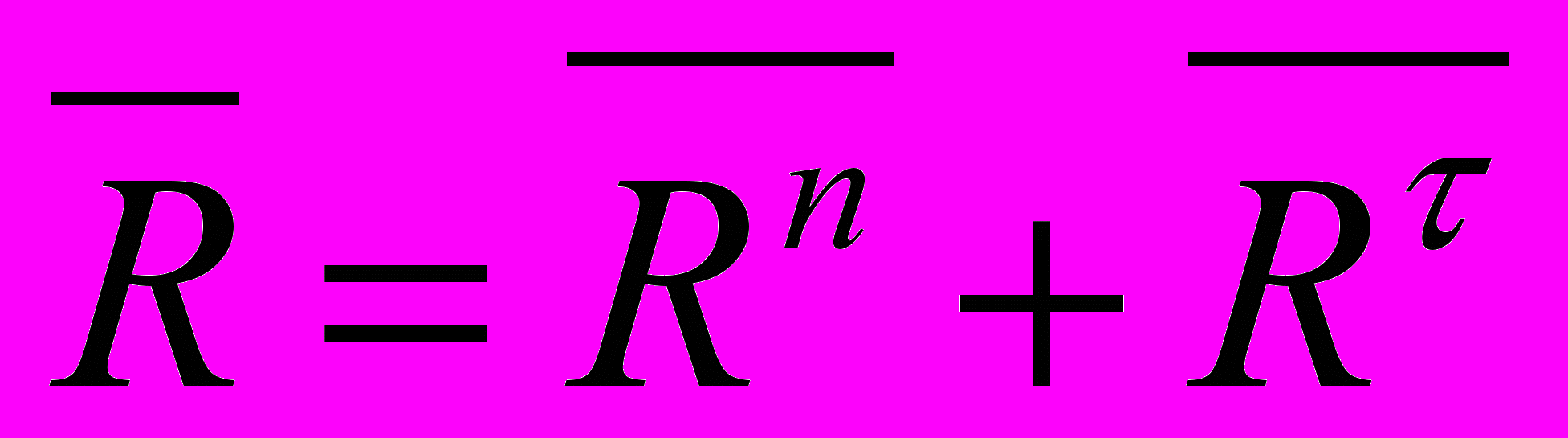где 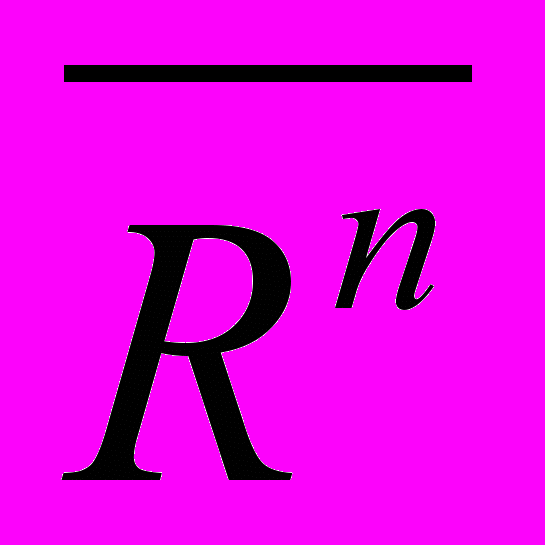– нормальная составляющая реакции, направленная вдоль прямой, соединяющей оси двух шарниров, Н; 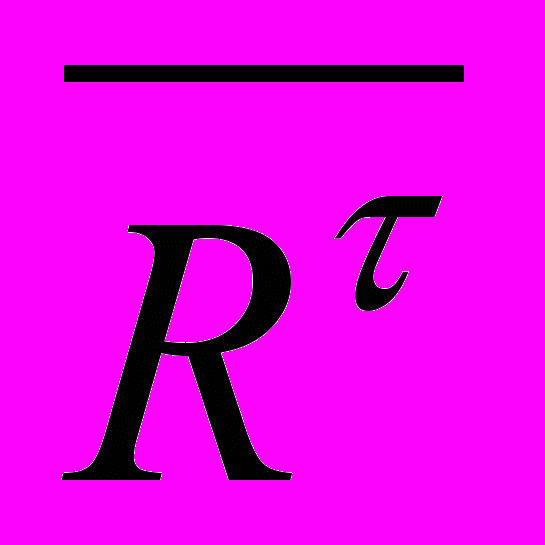– касательная составляющая реакции, перпендикулярная этой прямой, Н.

Каждую касательную составляющую реакции рассчитывают из уравнения равновесия моментов приложенных к звену сил относительно оси другого шарнира, при этом значения плеч сил h_i [мм] снимают с чертежа.

Нормальные составляющие реакций определяют по векторным уравнениям равновесия сил структурной группы и отдельного ее звена построением масштабного замкнутого плана сил. Масштабный коэффициент сил _F [Н/мм] определяют по модулю наибольшей силы. При этом план сил должен иметь однонаправленное течение векторов сил в замкнутом контуре.

В кинетостатическом расчете начального механизма из уравнения равновесия моментов сил относительно оси вращения начального звена определяют уравновешивающий момент М_у или уравновешивающую силу F_у на кривошипе – в зависимости от способа передачи механизму внешней энергии. Из условия равновесия сил, приложенных к кривошипу, рассчитывают реакцию на него со стороны стойки.

Заканчивают кинетостатический расчет механизма определением уравновешивающего силового фактора (М_у или F_у) более точным методом «жесткого рычага» проф. Н.Е. Жуковского. Роль «жесткого рычага» выполняет план скоростей механизма, повернутый на 90⁰ и загруженный всеми внешними силами в изображениях точек их приложения. Уравновешивающий силовой фактор рассчитывают из уравнения равновесия моментов сил относительно полюса плана (со значениями плеч сил, взятыми с чертежа в миллиметрах). С результатом этого расчета сравнивают вычисленный ранее уравновешивающий силовой фактор и оценивают расхождение в процентах. Точность решений в значительной мере определяется крупностью построений.


СПИСОК ЛИТЕРАТУРЫ


Основной:

1. Теория механизмов и механика машин. / Под ред. академика К.В. Фролова. – М.: Высшая школа, 2005. – 496 с.
   
2. Попов С.А. Курсовое проектирование по теории механизмов и механике машин. – М.: Высшая школа, 2004. – 458 с.
   
3. Ковалевский М.З. Динамика машин. – Л.: Машиностроение, 1989. – 287 с.
   

Дополнительный:

4. Артоболевский И.И., Эдельштейн Б.В. Сборник задач по теории механизмов и машин. – М.: Наука, 1975. – 256 с.
   
5. Курсовое проектирование по теории механизмов и машин. / Под ред. А.С. Кореняко. – М.-Л.: Машиностроение, 1980. – 324 с.
   
6. Теория механизмов и машин: Сборник контрольных работ и курсовых проектов. / Под ред. Н.В. Алехновича. – Минск.: Высшая школа, 1970. – 252 с.
   
7. Моргулис Ю.Б. Двигатели внутреннего сгорания. Теория, конструкция, расчет. – М.: Машиностроение, 1972. –336 с.
   

Основные принятые обозначения

№ п/п	Обозна-чение	Размер-ность	Наименование	Примечание
1.	1	c-1	Угловая скорость ведущего звена механизма
2.	дв	c-1	Угловая скорость двигателя
3.	mi	кг	Масса i-ого звена механизма
4.	JO1	кгм2	Момент инерции кривошипа относительно оси (О1), прохо-дящей через центр масс звена
5.	Jдв	кгм2	Момент инерции ротора двигателя
6.	JSi	кгм2	Момент инерции звена относи-тельно оси (Si), проходящей через центр масс звена
7.		–	Коэффициент неравномерности движения механизма
8.	d	мм	Диаметр поршня	Задается для механизмов двигателя
9.	mм	кг	Масса перемещаемого материала	Задается для механизмов перемещения желоба
10.	mш	кг	Масса штанги	Задается для механизмов станка-качалки
11.	mE	кг	Масса противовеса