Использование метода анализа иерархий при формировании инвестиционного портфеля

Вид материала

Содержание

Cn - число сочетаний из n
Рис.2. Варианты отображения иерархий:а) - декомпозиция; б) - синтез; в) - упорядочение
Степень значимости
Е1 доминирует над элементом Е
W положительной квадратной матрицы [E]
W(Bj) относительно элементов E
WEj - вектор приоритетов альтернатив относительно элемента E
Рис. 3. Иерархия для иллюстрации оценки однородности

Подобный материал:

Использование метода анализа иерархий при формировании инвестиционного портфеля

Центральной задачей при планировании инвестиционной деятельности инвестиционного фонда (банка) является задача оценки прибыльности и уровня риска портфеля инвестиционных проектов.

Предположим, что инвестиционный проект является моделью предприятия. предприятие рассматривается в качестве подсистемы экономической системы. Таким образом, внутренние параметры экономической системы являются внешними для проекта. Предположим, что существует модель, описывающая зависимость выходных параметров проекта от входных параметров. Следовательно, проблема оценки величины и степени неопределенности выходных параметров проекта определяется оценкой соответствующих показателей для внешних параметров проекта. В свою очередь внешние параметры проекта делятся на макро и микроэкономические. Эти параметры могут быть оценены следующими методами:

- статистическими;

- построения математических экономических моделей;

- экспертными;

- создания сценариев.

Использование статистических методов затрудняется отсутствием статистических данных или малым размером выборки по некоторым из параметров, что обусловлено уникальностью каждого инвестиционного проекта. Кроме того, с помощью этих методов нельзя предсказать изменение параметров, вызванное изменением внешних условий, так как предпосылкой использования статистических методов является неизменность внешних условий.

Математические экономические модели в настоящее время еще не могут обеспечить точность, существенно превышающую точность метода экспертных оценок, но их применение существенно дороже последнего.

Вышесказанное объясняет популярность методов экспертных оценок и анализа сценариев в инвестиционном проектировании, однако применение в рамках этих методов традиционных математических подходов существенно снижает результативность их использования.

Попробуем проанализировать различные математические аппараты оценки инвестиций. Выделяется пять критериев, по которым можно оценить пригодность использования того или иного математического аппарата к решению проблемы оценки инвестиций.

Во-первых, использование данного аппарата должно предполагать минимальное количество априорных предположений, жестко заложенных в данной модели и независящих от оценок эксперта. Во-вторых, аппарат должен позволять извлечь из эксперта максимум информации, которой тот обладает на сознательном и подсознательном уровне. В-третьих, процедура получения информации от эксперта должна быть максимально простой и понятной для опрашиваемого. В-четвертых, математический аппарат должен позволять легко производить быстрые компьютерные расчеты. В-пятых, он должен позволять учитывать как можно большее число сценариев развития ситуации.

Метод экспертных оценок обычно используется на основе традиционной теории вероятности, однако сама теория вероятности основана на системе аксиом, которые неадекватны решаемой задаче. Для этой теории характерна частотная интерпретация вероятности события: мы не знаем, каков будет исход данного конкретного эксперимента, но знаем, какова доля того или иного исхода во множестве всех возможных исходов эксперимента, многократно поставленного при неизменных начальных условиях. Понятно, что, если внешние условия постоянно изменяются, а эксперимент проводится однократно, данный подход сталкивается с существенными затруднениями. Поэтому просьба, чтобы эксперт оценил вероятность того или иного события, вообще говоря, некорректна. Другая проблема состоит в том, что в теории вероятности предполагается, что случайные величины распределены по некоторому "хорошему" распределению (обычно распределению Гаусса). В этом случае расчеты существенно упрощаются. Такое предположение не лишено оснований, скажем, при моделировании физических процессов (существует теорема о том, что среднее от независимых случайных величин, распределенных по произвольным законам, распределено по Гауссу), но совершенно необоснованно в экономике. Более того, даже на финансовых рынках, где играет множество игроков, и заключается огромное число сделок, случайные величины не подчиняются гауссову распределению. Поэтому, если, например, эксперту предъявляют требование оценить среднее значение и стандартное отклонение случайной величины, это некорректно по крайней мере по трем причинам: во-первых, делается совершенно необоснованно и в большинстве случаев совершенно неверное предположение о характере распределения случайной величины, во-вторых, эксперт ставится в положение, когда ему необходимо оценить труднопонятные с человеческой точки зрения параметры, в-третьих, иная информация, которая может иметься у эксперта по крайней мере на подсознательном уровне (например, об истинном характере распределения) начисто игнорируется. Следовательно, указанный подход не удовлетворяет по крайней мере трем критериям, принятым за основу оценки: минимума априорной информации, полного использования информации, имеющейся у эксперта, и простоты и понятности процедуры оценки.

Предпринимались неоднократные попытки приспособить традиционную теорию вероятности к выполнению этих условий, но они не дали ожидаемых результатов. Например, один из подходов выглядит следующим образом: пусть нам надо оценить вероятности конечного числа независимых взаимоисключающих исходов, относительно которых эксперт может дать заключение, что один из них более вероятен чем другой, но не может сказать, в какой мере. Согласно данному подходу эксперту предлагается сравнить исходы между собой попарно, затем для каждой пары исходов сравнить вероятность наступления объединения этих исходов с каждым из оставшихся простых исходов, затем провести подобное сравнение для троек исходов, и т.д. После того, как эксперт произведет все указанные сравнения, появляется возможность, используя предположение о том, что мы описали множество всех возможных исходов, рассчитать вероятности исходов. Несложно подсчитать, что в случае наличия n исходов, от эксперта требуется произвести

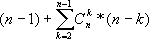
сравнений, где C^k_n - число сочетаний из n по k.

При этом число требующихся сравнений экспоненциально растет. Так, в случае наличия возможности 3 исходов потребуется 5 сравнений, 7 исходов - 405, 10 исходов - 5029, 20 исходов - более 10 миллионов. Очевидно, такая процедура не очень удобна для применения на практике. Кроме того, в том случае, если случайная величина распределена не по закону Гаусса, расчеты существенно усложняются.

Однако у теории вероятности имеется существенное преимущество: с помощью задания распределений вероятности можно учесть все возможные сценарии.

Таким образом, можно констатировать, что традиционная теория вероятности плохо приспособлена к решению задач методом экспертных оценок.

Альтернативным является подход на основе анализа чувствительности, согласно которому рассчитывается чувствительность проекта по всем внешним параметрам как частная производная дисконтированной прибыли по каждому из параметров. Затем параметры ранжируются экспертами по степени субъективной вероятности изменений. На параметры, вероятность изменения которых велика и велико их влияние на прибыль проекта, подлежат самому детальному анализу. Этот метод выгодно отличается простотой вычислений и понятностью задачи ранжирования; к его существенным недостаткам относятся априорное неправдоподобное предположение независимости изменения параметров. Этот недостаток устраняется в методе сценариев, когда эксперты предлагают различные сценарии совместного изменения нескольких показателей, и вычисляется дисконтированная прибыль для данного сценария. К недостаткам метода относятся произвольность выбора изменений в рамках сценария, отсутствие механизма оценки вероятности реализации каждого из сценариев, длительность обсчета всей совокупности сценариев, и, главное, возможность анализа только ограниченного числа сценариев. Этот метод наиболее часто используется в силу его простоты, что, однако, не может быть решающим аргументом в его пользу.

Метод анализа иерархий (МАИ) предполагает декомпозицию проблемы на все более простые составляющие части и обработку суждений лица, принимающего решение. В результате определяется относительная значимость исследуемых альтернатив для всех критериев, находящихся в иерархии. Относительная значимость выражается численно в виде векторов приоритетов. Полученные таким образом значения векторов являются оценками по шкале отношений и соответствуют так называемым жестким оценкам.

Можно выделить ряд модификаций МАИ, которые определяются характером связей между критериями и альтернативами, расположенными на самом нижнем уровне иерархии, а также методом сравнения альтернатив.

По характеру связей между критериями и альтернативами определяется два типа иерархий. К первому типу относятся такие, у которых каждый критерий, имеющий связь с альтернативами, связан со всеми рассматриваемыми альтернативами (тип иерархий с одинаковым числом и функциональным составом альтернатив под критериями). Ко второму типу иерархий принадлежат такие, у которых каждый критерий, имеющий связь с альтернативами, связан не со всеми рассматриваемыми альтернативами (тип иерархий с различными числом и функциональным составом альтернатив под критериями).

Построение иерархии начинается с очерчивания проблемы исследования. Далее строится собственно иерархия, включающая цель, расположенную в ее вершине, промежуточные уровни (например, критерии) и альтернативы, формирующие самый нижний иерархический уровень. На рис.1 приведен общий вид иерархии, где Eⁱ_j - элементы иерархии, А_i - альтернативы.

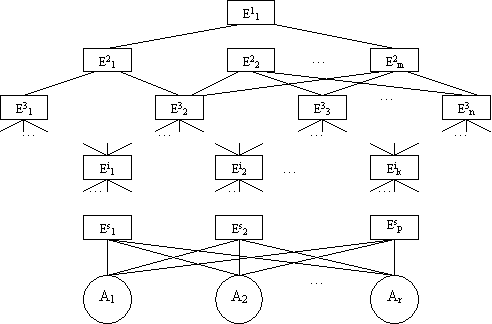
Рис.1

Верхний индекс у элементов указывает уровень иерархии, а нижний индекс - их порядковый номер. Существует несколько альтернативных способов графического отображения иерархии. На рис.2 приведены три варианта отображения одной иерархии

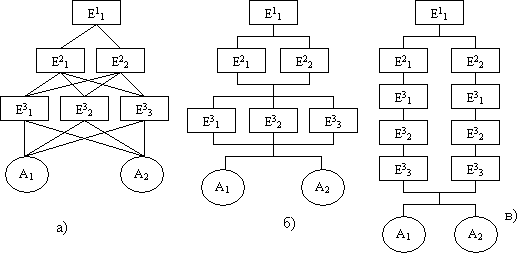
Рис.2. Варианты отображения иерархий:
а) - декомпозиция; б) - синтез; в) - упорядочение;

Первый вариант - конкретизация (декомпозиция) заданного множества элементов (в частности, критериев). Второй вариант противоположен первому и предполагает синтез более общих элементов из заданных частных. Третий вариант - упорядочение предварительно заданного множества элементов на основе их попарного сравнения.

Для установления относительной важности элементов иерархии используется шкала отношений (табл.1). Данная шкала позволяет лицу принимающему решение (ЛПР) ставить в соответствие степеням предпочтения одного сравниваемого объекта перед другим некоторые числа.

Таблица 1

Степень значимости	Определения	Объяснения
1	Одинаковая значимость	Два действия вносят одинаковый вклад в достижение цели
3	Некоторое преобладание значимости одного действия над другим (слабая значимость)	Существуют соображения в пользу предпочтения одного из действий, однако эти соображения недостаточно убедительны
5	Существенная или сильная значимость	Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность одного из действий
7	Очевидная или очень сильная значимость	Убедительное свидетельство в пользу одного действия перед другим
9	Абсолютная значимость	Свидетельства в пользу предпочтения одного действия другому в высшей степени убедительны
2, 4, 6, 8	Промежуточные значения между двумя соседними суждениями	Ситуация, когда необходимо компромиссное решение
Обратные величины приведенных выше ненулевых величин	Если действию i при сравнении с действием j приписывается одно из определенных выше ненулевых чисел, то действию j при сравнении с действием i приписывается обратное значение	Если согласованность была постулирована при получение N числовых значений для образования матрицы.

Правомочность этой шкалы доказана теоретически при сравнении со многими другими шкалами¹. При использовании указанной шкалы ЛПР, сравнивая два объекта в смысле достижения цели, расположенной на вышележащем уровне иерархии, должен поставить в соответствие этому сравнению число в интервале от 1 до 9 или обратное значение чисел. В тех случаях, когда трудно различить столько промежуточных градаций от абсолютного до слабого предпочтения или если этого не требуется в конкретной задаче, может использоваться шкала с меньшим числом градаций. В пределе шкала имеет две оценки: 1 - объекты равнозначны; 2 - предпочтение одного объекта над другим.

¹А.В. Андрейчиков, О.Н. Андрейчикова, "Анализ, синтез, планирование решений в экономике", Финансы и статистика, 2000 г.

После построения иерархии устанавливается метод сравнения ее элементов. Строится множество матриц парных сравнений. Для этого в иерархии выделяются элементы двух типов: элементы-"родители" и элементы-"потомки". Элементы-"потомки" воздействуют на соответствующие элементы вышестоящего уровня иерархии, являющиеся по отношению к первым элементами-"родителями". Матрицы парных сравнений строятся для всех элементов-"потомков", относящихся к соответствующему элементу-"родителю". Элементами-"родителями" могут являться элементы, принадлежащие любому иерархическому уровню, кроме последнего, на котором расположены, как правило альтернативы. Парные сравнения проводятся в терминах доминирования одного элемента над другим. полученные суждения выражаются в целых числах с учетом девятибалльной шкалы (см. табл.1).

Заполнение квадратных матриц парных сравнений осуществляется по следующему правилу. Если элемент Е₁ доминирует над элементом Е₂, то клетка матрицы, соответствующая строке Е₁ и столбцу Е₂, заполняется целым числом, а клетка, соответствующая строке Е₂ и столбцу Е₁, заполняется обратным к нему числом. Если элемент Е₂ доминирует над Е₁, то целое число ставиться в клетку, соответствующую строке Е₂ и столбцу Е₁, а дробь проставляется в клетку, соответствующую строке Е₁ и столбцу Е₂. Если элементы Е₁ и Е₂ равнопредпочтительны, то в обе позиции матрицы ставятся единицы.

Для получения каждой матрицы эксперт или ЛПР выносит n(n-1)/2 суждений (здесь n - порядок матрицы парных сравнений).

Рассмотрим в общем виде пример формирования матрицы парных сравнений.

Пусть Е₁, Е₂, ..., Е_n - множество из n элементов (альтернатив) и v₁, v₂, …, v_n - соответственно их веса, или интенсивности. Сравним попарно вес, или интенсивность, каждого элемента с весом, или интенсивностью, любого другого элемента множества по отношению к общему для них свойству или цели (по отношению к элементу-"родителю"). В этом случае матрица парных сравнений [E] имеет вид:

	Е₁	Е₂	...	Е_n
Е₁	v₁/v₁	v₁/v₂	...	v₁/v_n
Е₂	v₂/v₁	v₂/v₂	...	v₂/v_n
...	...	...	...
Е_n	v_n/v₁	v_n/v₂	...	v_n/v_n

Матрица парных сравнений обладает свойством обратной симметрии, т.е.

a_ij = 1/a_ji, где a_ij = v_i/v_j.

При проведении попарных сравнений следует отвечать на следующие вопросы: какой из двух сравниваемых элементов важнее или имеет большее воздействие, какой более вероятен и какой предпочтительнее.

При сравнении критериев обычно спрашивают, какой из критериев более важен; при сравнении альтернатив по отношению к критерию - какая из альтернатив более предпочтительна или более вероятна.

Ранжирование элементов, анализируемых с использованием матрицы парных сравнений [E], осуществляется на основании главных собственных векторов, получаемых в результате обработки матриц.

Вычисление главного собственного вектора W положительной квадратной матрицы [E] проводится на основании равенства

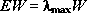(1)

где

- максимальное собственное значение матрицы [E].

Для положительной квадратной матрицы [E] правый собственный вектор W, соответствующий максимальному собственному значению

, с точностью до постоянного сомножителя С можно вычислить по формуле:

(2)

где e = {1,1,1,…,1}T - единичный вектор;
k = 1, 2, 3, … - показатель степени;
С - константа;
Т - знак транспонирования.

Вычисления собственного вектора W по выражению (1) производятся до достижения заданной точности:

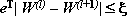(3)

где l - номер итерации, такой, что l = 1 соответствует k = 1; l = 2, k = 2; l = 3, k = 3 и т. д.;

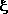- допустимая погрешность.

С достаточной для практики точностью можно принять

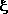= 0,01 независимо от порядка матрицы.

Максимальное собственное значение вычисляется по формуле:

= e^T [E] W.

В практических задачах количественная (кардинальная) и транзитивная (порядковая) однородность (согласованность) нарушается, поскольку человеческие ощущения нельзя выразить точной формулой. Для улучшения однородности в числовых суждениях, какая бы величина a_ij ни была бы взята для сравнения i-го элемента с j-м, a_ji приписывается значение обратной величины, т.е. a_ji = 1/a_ij. Отсюда следует, что если один элемент в "a" раз предпочтительнее другого, то последний только в "1/а" раз предпочтительнее первого.

При нарушении однородности ранг матрицы отличен от единицы и она будет иметь несколько собственных значений. Однако при небольших отклонениях суждений от однородности одно из собственных значений будет существенно больше остальных и приблизительно равно порядку матрицы. Таким образом, для оценки однородности суждений эксперта необходимо использовать отклонение величины максимального собственного значения

от порядка матрицы n.

Однородность суждений оценивается индексом однородности (ИО) или отношением однородности (ОО) в соответствии со следующими выражениями:

ИО = (

- n)/(n - 1);
OO = ИО/М(ИО),

где М(ИО) - среднее значение (математическое ожидание) индекса однородности случайным образом составленной матрицы парных сравнений [E], которое основано на экспериментальных данных (табл.2).

Таблица 2. Среднее значение индекса однородности в зависимости от порядка матрицы

Порядок матрицы (n)	М(ИО)	Порядок матрицы (n)	М(ИО)	Порядок матрицы (n)	М(ИО)
1	0,00	6	1,24	11	1,51
2	0,00	7	1,32	12	1,48
3	0,58	8	1,41	13	1,56
4	0,90	9	1,45	14	1,57
5	1,12	10	1,49	15	1,59

В качестве допустимого используется значение ОО

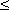0,10. Если для матрицы парных сравнений отношение однородности ОО > 0,10 то это свидетельствует о существенном нарушении логичности суждений, допущенном экспертом при заполнении матрицы, поэтому эксперту предлагается пересмотреть данные, использованные для построения матрицы, чтобы улучшить однородность.

Иерархический синтез используется для взвешивания собственных векторов матриц парных сравнений альтернатив весами критериев (элементов), имеющихся в иерархии, а также для вычисления суммы по всем соответствующим взвешенным компонентам собственных векторов нижележащего уровня иерархии. Ниже рассматривается алгоритм иерархического синтеза.

Ш а г 1. Определяются векторы приоритетов альтернатив W^A_(Bⁱ_j) относительно элементов Eⁱ_j предпоследнего уровня иерархии (i=S). Здесь через Eⁱ_j обозначены элементы иерархии, причем верхний i указывает уровень иерархии, а нижний индекс j - порядковый номер элемента на уровне. Вычисление множества векторов приоритетов альтернатив W^A_S относительно уровня иерархии S осуществляется по итерационному алгоритму, реализованному на основе отношений (2) и (3) по исходным данным, зафиксированным в матрицах попарных сравнений. В результате определяется множество векторов:

W^A_S = {W^A_E^S₁, W^A_E^S₂,..., W^A_E^S_p}

Ш а г 2. Аналогичным образом обрабатываются матрицы попарных сравнений собственно элементов Eⁱ_j. Данные матрицы построены таким образом, чтобы определить предпочтительность элементов определенного иерархического уровня относительно элементов вышележащего уровня, с которыми они непосредственно связаны. Например, для вычисления векторов приоритетов элементов третьего иерархического уровня (см. рис 1) обрабатываются следующие три матрицы попарных сравнений:

E₁²	E₁³	E₂³
E₁³	v₁/v₁	v₁/v₂
E₂³	v₂/v₁	v₂/v₂

E₂²	E₂³	E₃³	E_n³
E₂³	v₂/v₂	v₂/v₃	v₂/v_n
E₃³	v₃/v₂	v₃/v₃	v₃/v_n
E_n³	v_n/v₂	v_n/v₃	v_n/v_n

E_m²	E₂³	E₃³	E_n³
E₂³	v₂/v₂	v₂/v₃	v₂/v_n
E₃³	v₃/v₂	v₃/v₃	v₃/v_n
E_n³	v_n/v₂	v_n/v₃	v_n/v_n

В матрицах через v_j обозначен вес, или интенсивность, Е_j-го элемента.

В результате обработки матриц попарных сравнений определяется множество векторов приоритетов:

W^E = {W^E_(Eⁱ_j)}

Полученные значения векторов W^E_(Eⁱ_j) используются впоследствии при определении векторов приоритетов альтернатив относительно всех элементов иерархии.

Ш а г 3. Осуществляется собственно иерархический синтез, заключающийся в последовательном определении векторов приоритетов альтернатив относительно элементов Eⁱ_j, находящихся на всех иерархических уровнях, кроме последнего, содержащего элементы E^S_j. Вычисление векторов приоритетов проводится в направлении от нижних уровней к верхним с учетом конкретных связей между элементами, принадлежащими различным уровням. Вычисление проводится путем перемножения соответствующих векторов и матриц.

Общий вид выражения для вычисления векторов приоритетов альтернатив определяется следующим образом:

W^A_Eⁱ_j = [W^A_E1^i-1, W^A_E2^i-1,..., W^A_En^i-1] W^E_Ej^i-1

где W^A_Eⁱ_j - вектор приоритетов альтернатив относительно элемента E₁^i-1, определяющий j-й столбец матрицы;
W^E_Eⁱ_j - вектор приоритетов элементов E₁^i-1, E₂^i-1, …, E_n^i-1, связанных с элементом Eⁱ_j вышележащего уровня иерархии.

Ниже приведен конкретный пример по вычислению векторов приоритетов альтернатив относительно элементов третьего (Е³_j), второго (Е²_j) и первого (Е¹_j) уровней иерархии с учетом конкретных связей между элементами иерархии (см. рис. 1).

Определение векторов приоритетов альтернатив для элементов второго уровня осуществляется следующим образом:

W^A_E²₁ = [W^A_E³₁ W^A_E³₂] W^E_E²₁;
W^A_E²₂ = [W^A_E³₂ W^A_E³₃ ... W^A_E³_n] W^E_E²₂;
W^A_E²_m = [W^A_E³₂ W^A_E³₃ ... W^A_E³_n] W^E_E²_m.

Результирующий вектор приоритетов альтернатив относительно корневой вершины иерархии E¹₁ вычисляется следующим образом:

W^A_E¹₁ = [W^A_E²₁ W^A_E²₂ ... W^A_E²_m] W^E_E¹₁

После решения задачи иерархического синтеза оценивается однородность всей иерархии с помощью суммирования показателей однородности всех уровней, приведенных путем "взвешивания" к первому иерархическому уровню, где находится корневая вершина. Число шагов алгоритма по вычислению однородности определяется конкретной иерархией.

Рассмотрим принципы вычисления индекса ИО_и и отношения ОО_и однородности иерархии. Пусть задана иерархия критериев и альтернатив (рис. 3) и для каждого уровня определен индекс однородности и векторы приоритетов критериев следующим образом:

ИО₁ - индекс однородности 1-го уровня;
{ИО₂, ИО₃} - индексы однородности для 2-го уровня;
{ИО₄, ИО₅, ИО₆} - индексы однородности для 3-го уровня;
{W₁} - вектор приоритетов критериев К₂ и К₃ относительно критерия К₁;
{W₂}, {W₃} - векторы приоритетов критериев К₄, К₅, К₆ относительно критериев К₂ и К₃ второго уровня.

Рис. 3. Иерархия для иллюстрации оценки однородности

В этом случае индекс однородности рассматриваемой иерархии можно определить по формуле

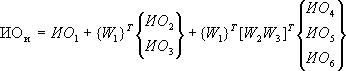(4)

где Т - знак транспонирования.

Определение отношения однородности ОО_и для всей иерархии осуществляется по формуле

ОО_и = ИО_и / М(ИО_и),

где М(ИО_и) - индекс однородности иерархии при случайном заполнении матриц попарных сравнений.

Расчет индекса однородности М(ИО_и) с учетом экспериментальных данных (см. табл. 2) выполняется по формуле, аналогичной (4):

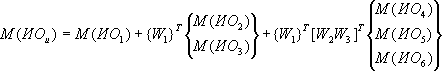
Однородность иерархии считается удовлетворительной при значениях ОО_и

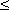0,10.

Описанный выше метод принятия решений, основанный на нечеткой математике позволяет удобно и достаточно объективно производить оценку альтернатив по отдельным критериям. В отличие от других методов, добавление новых альтернатив не изменяет порядок ранее ранжированных наборов. Представленная методика могла бы с успехом использоваться в инвестиционных фондах, а так же в кредитных отделах банков для оценки инвестиционных проектов, формирования инвестиционного портфеля и последующего анализа эффективности управления инвестиционным портфелем. С их помощью можно существенно оптимизировать бюджет капитальных вложений, а также повысить степень обоснованности принятия решений при оценке, анализе и отборе инвестиционных проектов.

Список литературы:

А.В. Андрейчиков, О.Н. Андрейчикова, "Анализ, синтез, планирование решений в экономике", Финансы и статистика, 2000 г.

П.В. Конюховский "Мат. Методы исследования операций в экономике", Питер Ком, 2000 г.

П.Л. Виленский, В.Н. Лившиц, "Оценка эффективности инвестиционных проектов", Дело, 1998 г.

А.Б. Идрисов, С.В. Картышев, А. В. Постников, "Стратегическое планирование и анализ эффективности инвестиций", ИД "Филинъ", 1997г.

Ковалев В.В. Методы оценки инвестиционных проектов.-М.: Финансы и статистика, 1998.

Бирман Г., Шмидт С. Экономический анализ инвестиционных проектов: Пер. с англ./Под. ред. Л.П. Белых.-М.: Банки и биржи, ЮНИТИ, 1997.

Саати Т. Принятие решений. Метод анализа иерархий: Пер. с англ. -М.: Радио и связь, 1989.

Борисов А.Н., Крумберг О.А., Федоров И.П. Принятие решений на основе нечетких моделей. - Рига: Зинатне, 1990.

Канторович Л.В., Горстко А.Б. Оптимальные решения в экономике. - М.: Наука, 1972.

Кофман А. Введение в теорию нечетких множеств: Пер. с англ. - М.: Радио и связь, 1982.

Емельянов С.В., Ларичев О.И. Многокритериальные методы принятия решений. - М.: Знание, 1985.

Blog

Использование метода анализа иерархий при формировании инвестиционного портфеля

Содержание