Анализ инвестиционных проектов методами нечетких экспертных систем

Вид материала

Анализ

Содержание Оценка инвестиционного риска. Алгоритм анализа инвестиционного риска. Совершенствование модели.

Подобный материал:

• Оценка инвестиционных проектов, 34.37kb.
• Оценка инвестиционных проектов, 42.7kb.
• Оценка инвестиционных проектов в нефтегазовой отрасли, 36.82kb.
• 6. Лекция: Методология построения экспертных систем, 291.07kb.
• В. А. Кулаков московский инженерно-физический институт (государственный университет), 28.6kb.
• Диссертации: «Оценка инвестиционных проектов в нефтегазовой отрасли», 37.59kb.
• Н. К. Пирогов Анализ эффективности инвестиционных проектов (на примере фармацевтической, 88.85kb.
• Применение экспертных систем на геотехнологическом предприятии атомной отросли, 94.06kb.
• Встатье рассмотрены вопросы применения экспертных систем в экономике и бизнесе, экспертные, 20kb.
• Контрольная работа по курсу: Инвестиции на тему: Оценка эффективности инвестиционных, 305.17kb.

Анализ инвестиционных проектов методами нечетких экспертных систем

Ryjenko I. N. Rychkova G. N.

Рассматривается возможность моделирования и анализа процесса формирования инвестиционного портфеля для минимизации инвестиционного риска страховой компании.

The possibility of modeling and analysis of the formation of an investment portfolio to minimize investment risk insurance company.

Введение. Страховые компании являются важным источником инвестиционных ресурсов в национальную экономику. Страховые компании, получая основную прибыль от страховых операций, дополнительную прибыль получают, от инвестиционного дохода размещая временно свободные средства в различные финансовые организации. Учитывая, что страховые компании предназначены для обеспечения исполнения своих обязательств по договорам страхования, страховщик должен минимизировать риск инвестиций при формировании инвестиционного портфеля, для обеспечения безусловных гарантий по выполнению своих обязательств. Для выполнения этой задачи страховщик должен выполнить анализ финансового состояния организаций выбранных, для размещения инвестиций. Определить количественную оценку степени риска размещения и оптимальный период размещения инвестиций.

Оценка инвестиционного риска. Традиционный анализ финансового состояния компании-заемщика в основном базируется на фундаментальном анализе и включает в себя детальное изучение операций компании-заемщика, динамику его денежных потоков, величины его будущих доходов. Основная цель при этом состоит в создании модели оценки инвестиционного риска. Принципы оценки инвестиционного риска разработаны в теории портфельного инвестирования Марковица–Шарпа. Согласно теории портфельного инвестирования, инвестору достаточно знать ожидаемую доходность и стандартное отклонение доходности при выборе объектов инвестирования. Также при формировании портфеля инвестиций инвестор должен учитывать [1]:

• вероятность дефолта для каждого инвестиционного инструмента в портфеле;
  
• вероятностное распределение убытков при условии наступления дефолта для каждого инструмента.
  

Для достоверного оценивания вероятностей дефолта, корреляций и других параметров модели требуются исторические данные за большое число лет. С некоторой периодичностью крупнейшие мировые рейтинговые агентства Standard&Poor's, Moody's Investors Service, Fitch Ratings, Thomson BankWatch и др. опубликовывают статистические исследования организаций-заемщиков. По каждой рейтинговой группе приводятся исторические данные частот дефолта, вариации частот дефолта и частоты переходов из одной рейтинговой категории в другую. Последние величины образуют так называемую матрицу переходных вероятностей рейтингов организаций-заёмщиков.

Известна модель эффективного портфеля для оценки инвестиционного риска, при размещении депозита в различные финансовые организации. Модель эффективного портфеля представлена следующей формулой[2]:

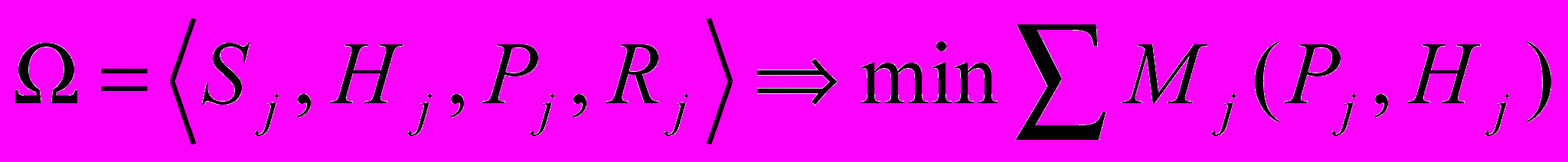, (1)

где 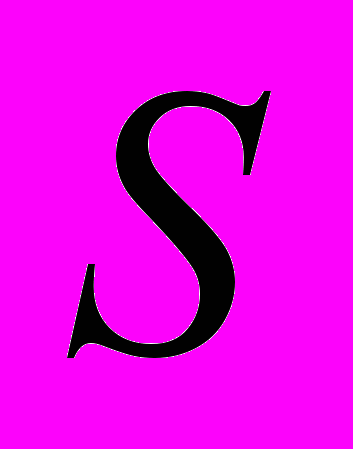– сумма инвестиции (депозит);

- срок размещения;

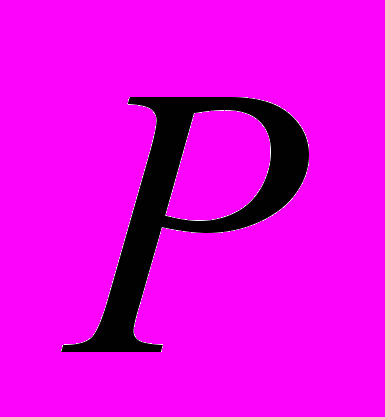- принятая вероятность дефолта заемщика;

M – математическое ожидание убытка;

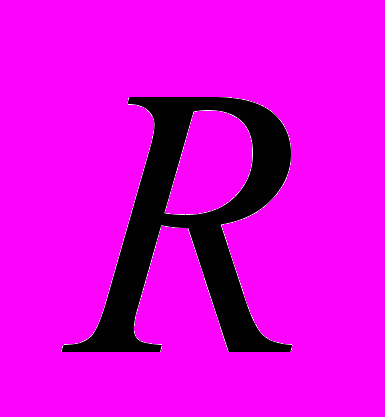- ставка процента;

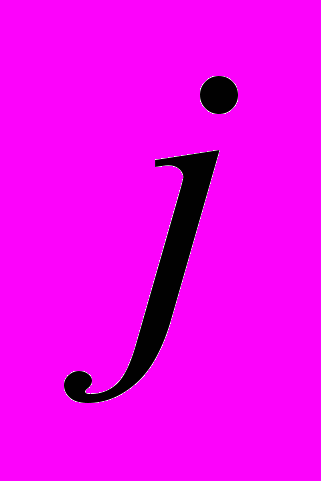- номер инвестиции в портфеле.

Алгоритм анализа инвестиционного риска. В формуле (1) известны сумма депозита, срок размещения, принятая вероятность дефолта для заемщика по результатам оценки рейтингового агентства, ставка процента.

1. Определяется относительный период размещения в единицу времени по формуле:

, (2)

где 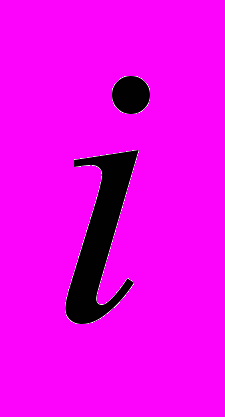- номер относительного периода.

2. Определяется относительная вероятность дефолта финансовой организации. При этом используется метод экспоненциальной зависимости вероятности дефолта от периода размещения по формуле:

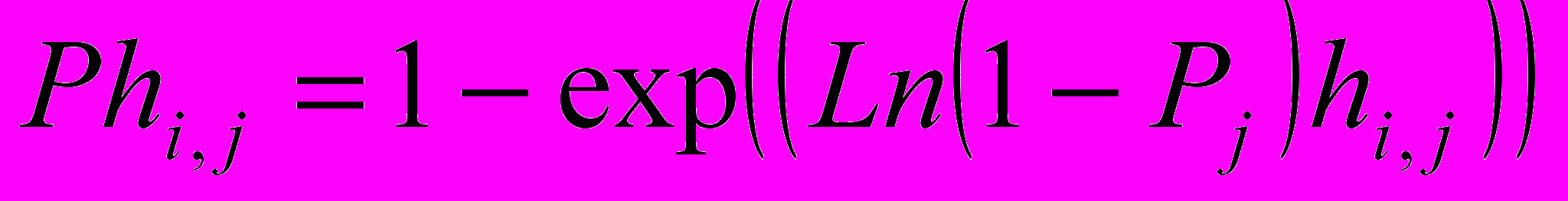(3)

3. В качестве оценки инвестиционного риска для каждого периода размещения инвестиции определяется математическое ожидание убытков в зависимости от относительной вероятности дефолта по формуле:

(4)

где 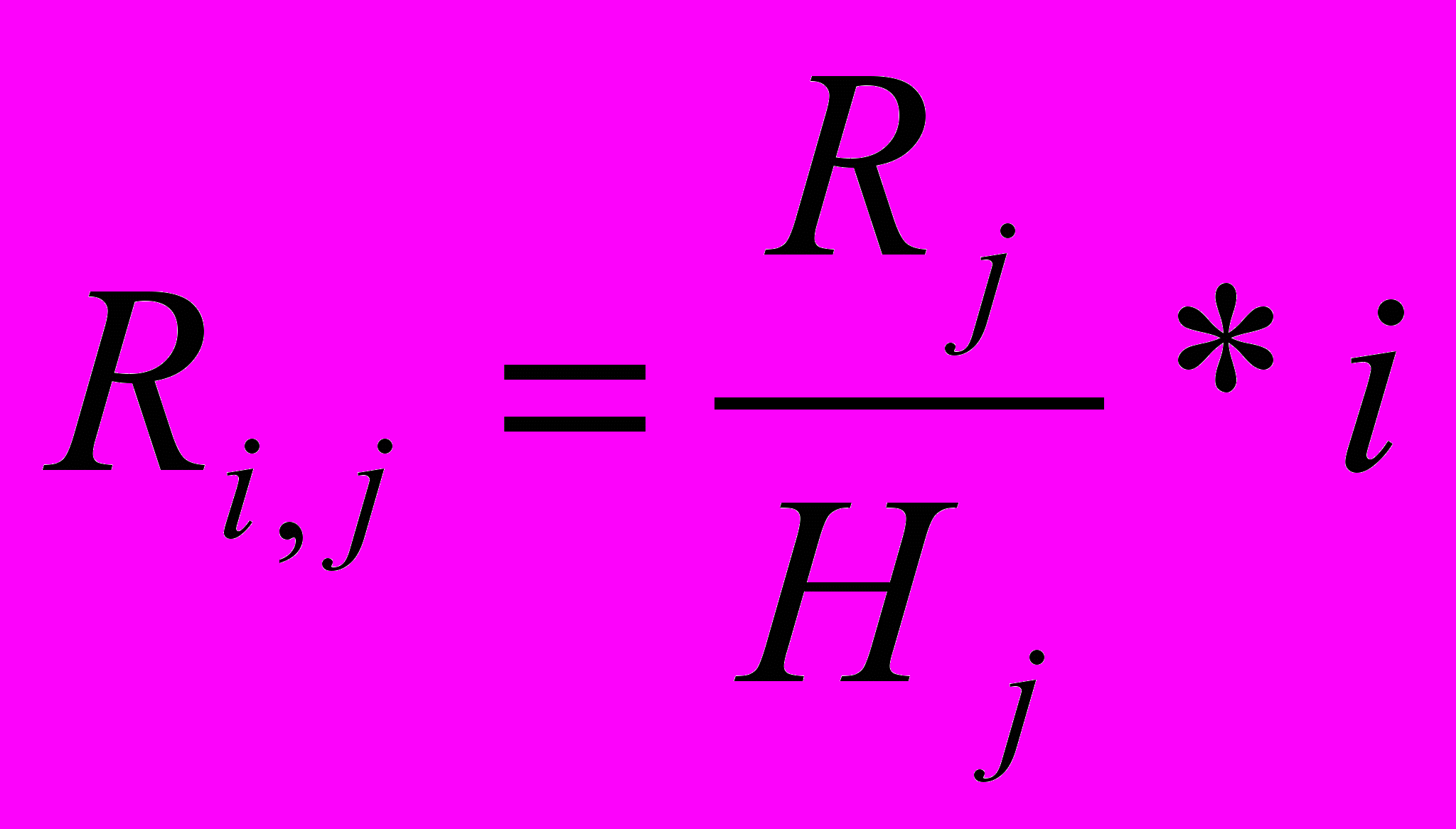- ставка процента за период.

Заметим, что в рассмотренной модели в пункте 2 относительная вероятность подчиняется экспоненциальному закону распределения, и значения вероятности дефолта увеличивается с увеличением периода размещения депозита. Реальная действительность такова, что вероятность дефолта распределена от значения минимума до значения максимума в любом из периодов размещения вклада.

Достоинством рассмотренной модели является её возможность реализации с помощью различных аналитических приложений.

Недостатком рассмотренной модели является: использование метода экспоненциальной зависимости вероятности дефолта в течение срока размещения вклада; не учитываются вариации частот дефолта и частоты переходов из одной рейтинговой категории в другую.

Совершенствование модели. С целью совершенствования модели, для уточнения оценки инвестиционного риска страховой компании введем в модель следующие параметры:

1. матрицу переходной вероятности рейтингов организаций-заемщиков;
   
2. определим, что вероятность дефолта в любом периоде размещения вклада распределена от min до значения принятой вероятности по данным рейтингового агентства и подчиняется нормальному закону распределения.
   

Таким образом, модель оценки инвестиционного риска будет представлена следующей формулой:

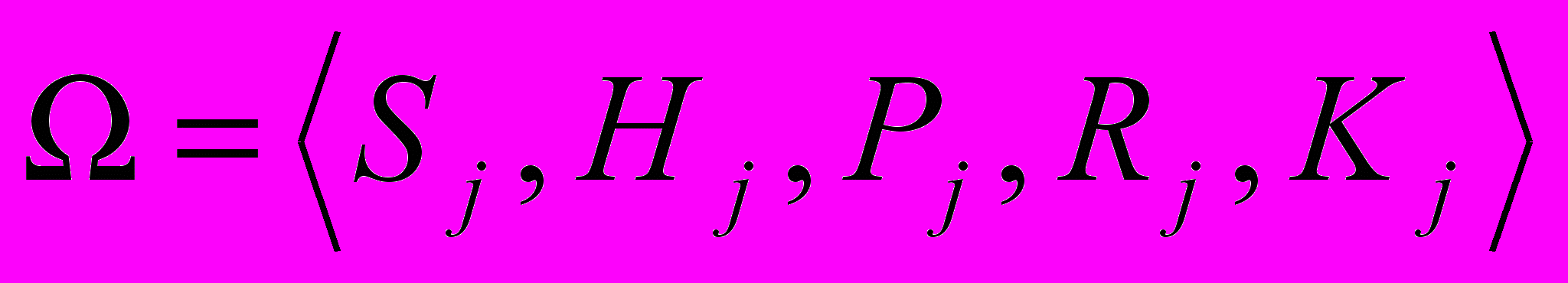, (5)

где K – матрица переходной вероятности.

Определим функцию принадлежности на основании матрицы переходных вероятностей:

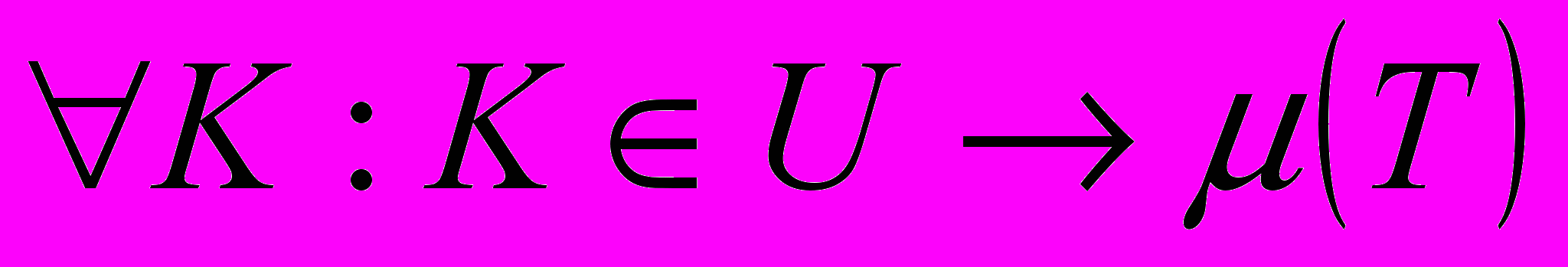, (6)

где 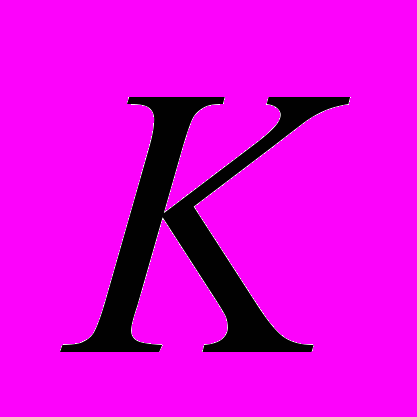- переходная вероятность;

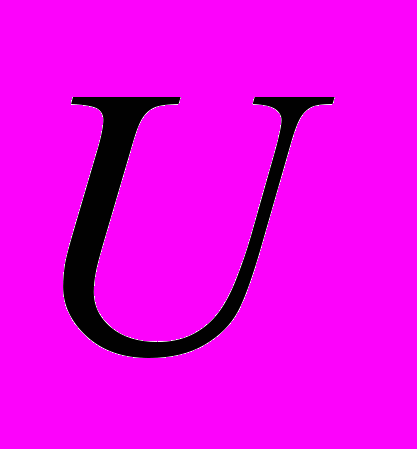- область определения вероятности дефолта;

- функция принадлежности;

- набор термов.

Соответственно анализ инвестиционного портфеля дополнен следующими пунктами.

4. Определим матрицу переходных вероятностей, корректирующих полученные расчетные относительные вероятности, в предположении, что вероятность дефолта в любом периоде распределена от min до значения принятой вероятности по данным рейтингового агентства и подчиняется нормальному закону распределения:

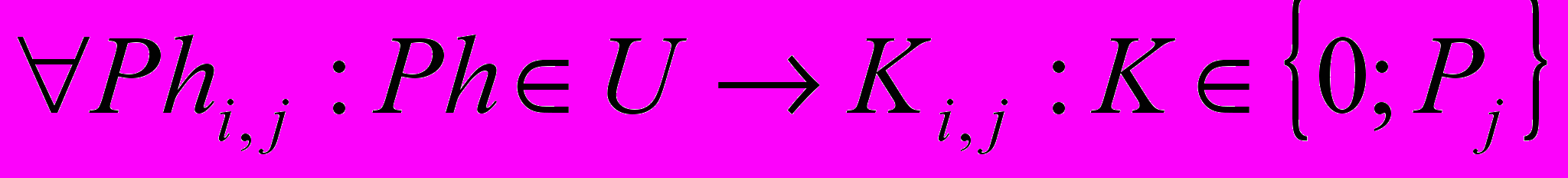(7)

5. Определим функции принадлежности, используя методы нечетких экспертных систем:

;

;

;

.

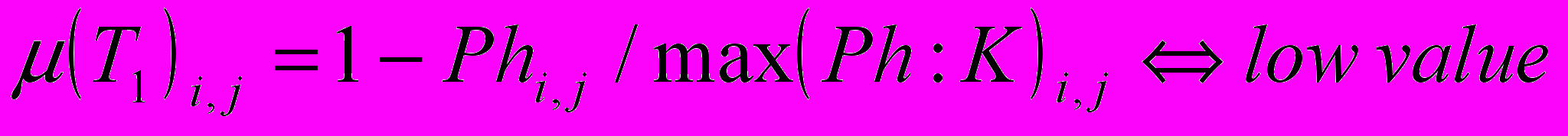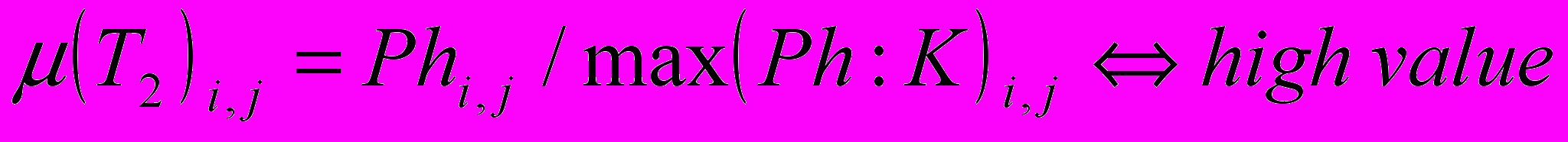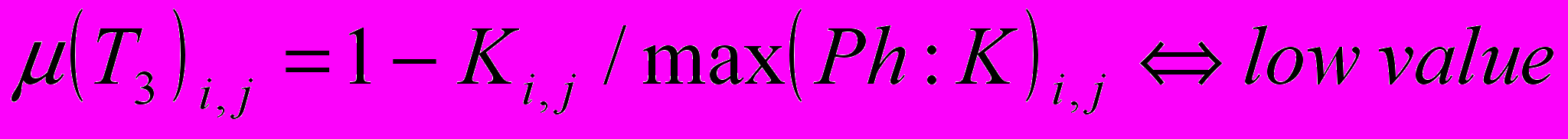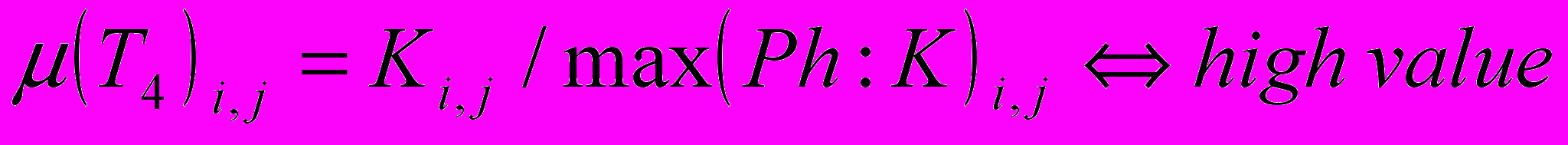6. Определим относительные вероятности, дефолта финансовой организации по предложенной модели, используя функцию вывода:

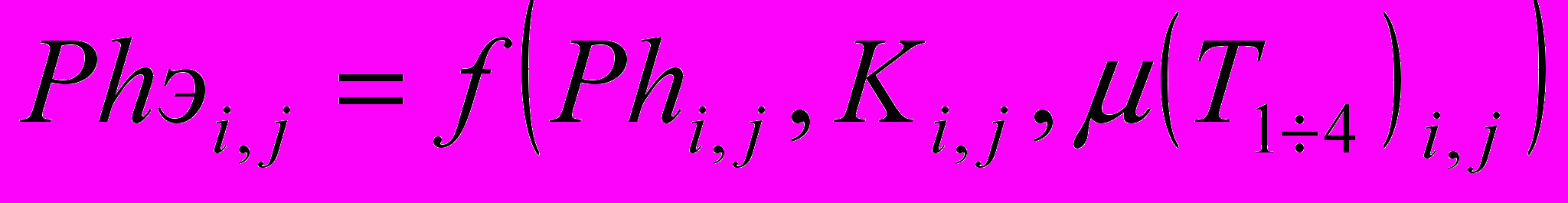(8)

7. Определим математическое ожидание убытков по предложенной модели по формуле:

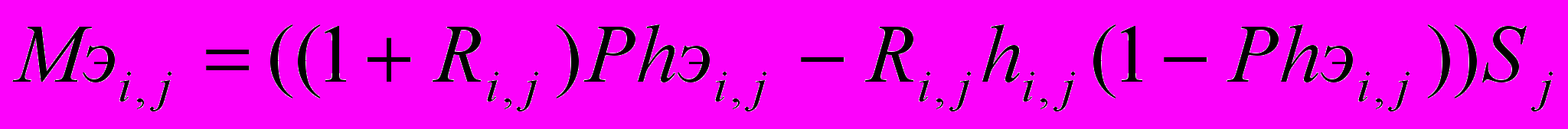(9)

8. Определим оптимальную границу размещения депозита, как операцию пересечения множеств оценок убытков, полученных по формулам (4) и (9):

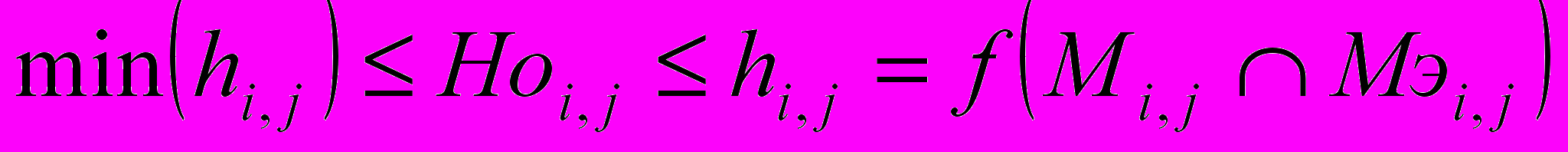, (10)

где Ho – оптимальная граница периода размещения вклада.

9. Проведем классификацию элементов инвестиционного портфеля страховой компании в зависимости от относительной вероятности дефолта финансовой организации и математического ожидания убытка. Введем следующие понятия:

;

;

.

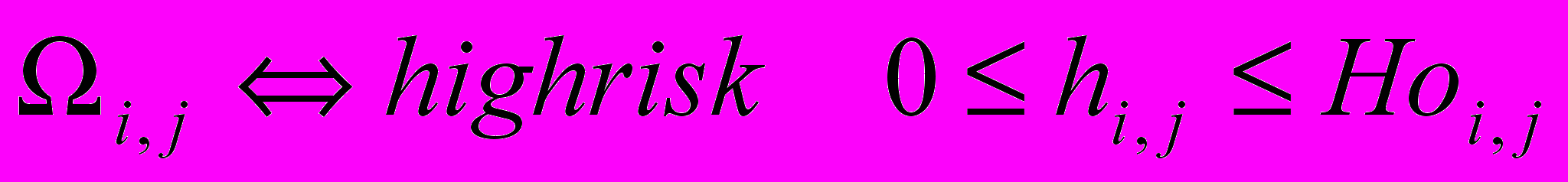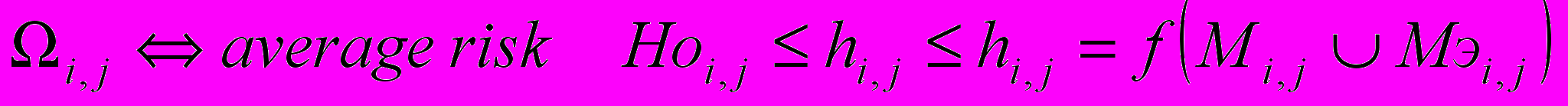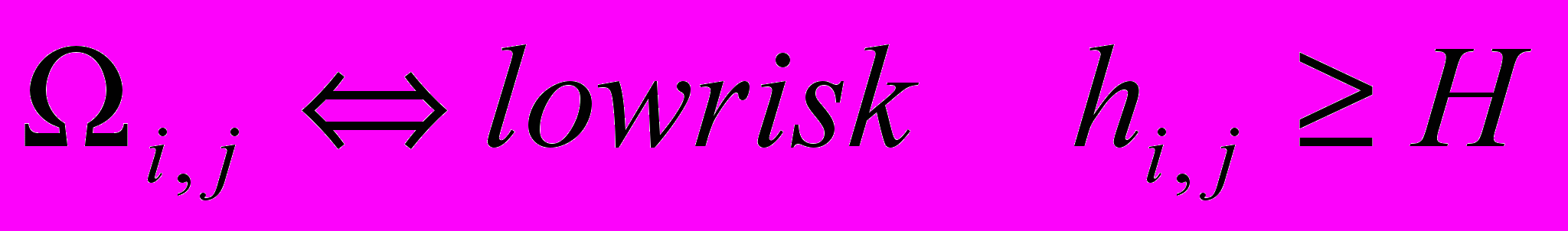Результат проведенного анализа инвестиционного портфеля страховой компании с целью выбора оптимального размещения депозита в 2008г. по историческим данным рейтинговых агентств приведен в табл. 1. В анализе участвовали три акционерных банка аттестованных рейтинговым агентством Fitch Ratings и Moody’s.

Таблица 1



По результатам анализа можно сделать заключение о целесообразности выбора для размещения депозита акционерный банк Альфа-Банк. В отношении АК Премьер известно что, 28.08.2008г. у банка была отозвана лицензия и объявлен банкротом [4].

Выводы. В предложенной модели инвестиционного риска страховой компании получены существенные отличия, заключающиеся в следующем:

1. определение вероятности дефолта организации-заёмщика в течение срока размещения вклада отражает возможность дефолта в любом из периодов размещения вклада;
   
2. учитываются вариации частот дефолта и частоты переходов из одной рейтинговой категории в другую при оценке возможных убытков;
   
3. обоснован выбор оптимального периода размещения инвестиции;
   
4. разработана классификация инвестиционного портфеля.
   

Литература:

1. Корянев А.В. Основы финансового анализа и портфельного инвестирования в рыночной экономике. – М.: МИФИ, 2002. – С. 35.
   
2. Инвестиции: учебное пособие. / Г.П. Подшиваленко, Н.И. Лахметкина, М.В. Макарова [и др.]. – М.: КНОРУС, 2006. – С. 165.
   
3. Мак Томас. Математика рискового страхования. - М.: Олимп-Бизнес, 2005. - 432 с.
   
4. .ru/banks/memory/?query=%CF%F0%E5%EC%FC%E5%F0&where=NAME