Конспект Лекций Лекция 1 Введение в компьютерную геометрию и графику Основные направления компьютерной графики
| Вид материала | Конспект |
СодержаниеАффинные преобразования Аффинные преобразования объектов на плоскости. Лекция 8 Геометрические модели плоских объектов |
- Учебной дисциплины «Компьютерная графика» для направления 010400 «Прикладная математика, 36.03kb.
- С. В. Шадрина Лекция 5 сентября, 15: 00-16: 30, Введение в геометрию пространства модулей, 5.97kb.
- Предлагаемый конспект опорных лекций отражает традиционный набор тем и проблем курса, 1047.31kb.
- Программа работа в графическом пакете corel draw г. Улан-Удэ 2009, 134.98kb.
- Положение о конкурсе компьютерной графики среди учащихся муниципального общеобразовательного, 44.56kb.
- Лекция №11 Сжатие изображений Курс лекций «Алгоритмические основы машинной графики», 54.41kb.
- Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.
- Конспект лекций н. О. Воскресенская Москва 2008 Оглавление: Лекция Введение в дисциплину, 567.5kb.
- Программа элективного курса «Графический дизайн» 9 класс, 84.59kb.
- Краткое содержание цикла лекций №1 «Проектирование и производство цифровых сбис нанометрового, 74.05kb.
Аффинные преобразования
Аффинным называется преобразование, обладающее следующими свойствами:
● любое аффинное преобразование может быть представлено как последовательность операций из числа простейших: сдвиг, растяжение/сжатие, поворот;
● сохраняются прямые линии, параллельность прямых, отношение длин отрезков, лежащих на одной прямой, и отношение площадей фигур.
Аффинные преобразования координат на плоскости:
(x, y) – двумерная система координат,
(X, Y) – координаты старой СК в новой системе координат.
О
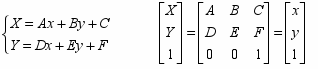
бщий вид аффинного преобразования:
A, B, C, D, E, F – константы.
Обратное преобразование также является аффинным:
Простейшие аффинные преобразования системы координат.
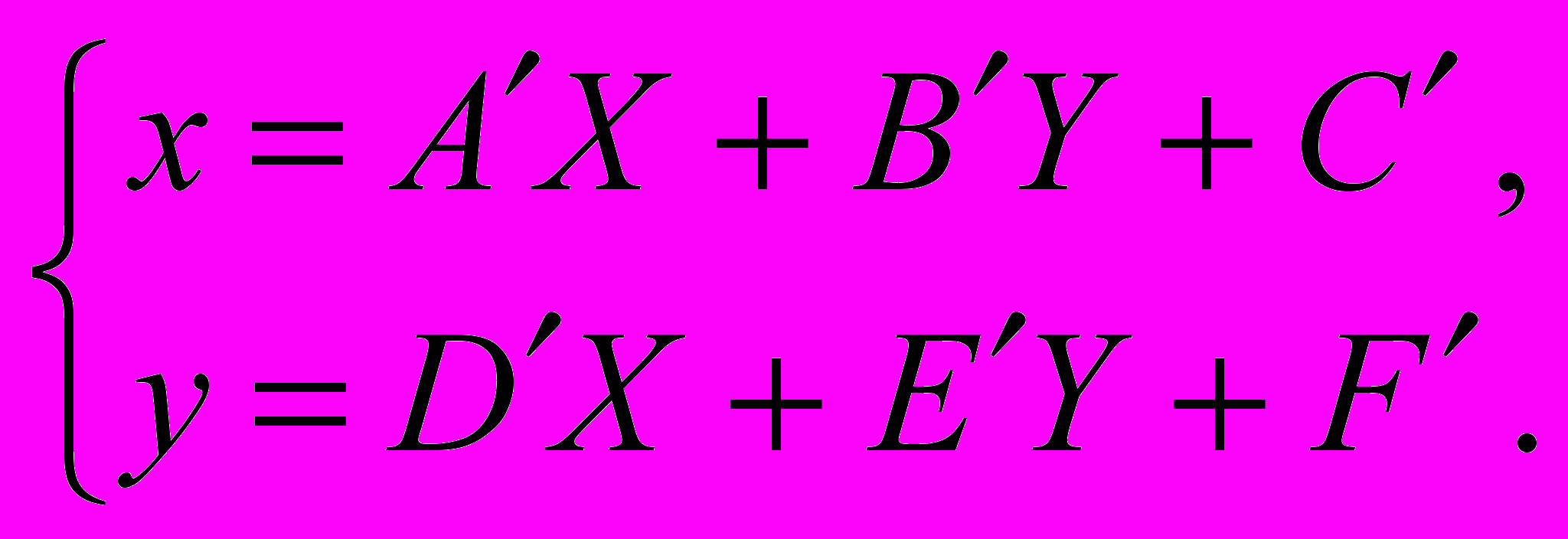
- П
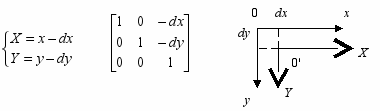
араллельный сдвиг координат:
О
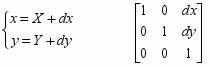
братное преобразование:
- Растяжение/сжатие осей:
Обратное преобразование:
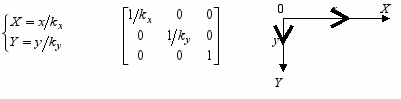
К
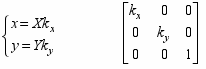
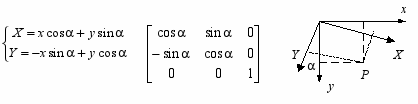
оэффициенты могут быть отрицательными. Например, при kx = -1 получаем зеркальное отображение относительно оси y.
- Поворот системы координат (x,y) на угол α:
О
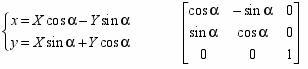
братное преобразование – поворот системы (X,Y) на угол (-α):
А
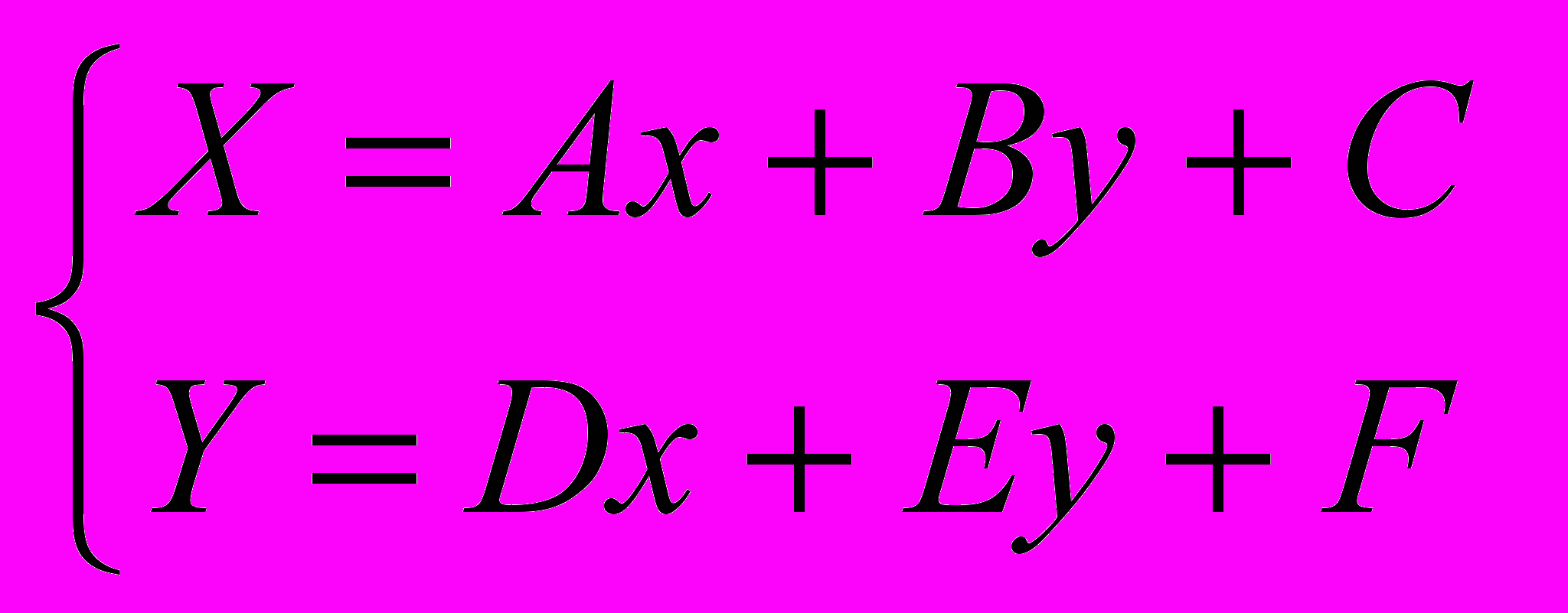
ффинные преобразования объектов на плоскости.
x, y – старые координаты точки, X, Y – новые координаты точки.
- С
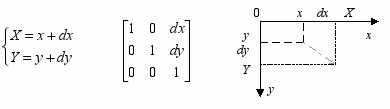
двиг:
О
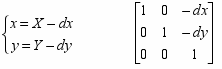
братное преобразование:
- М
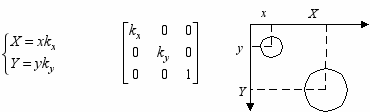
асштабирование объекта:
Обратное преобразование:
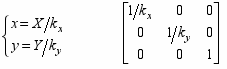
- Поворот вокруг центра координат:
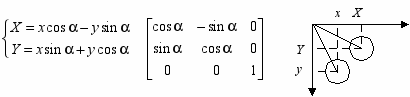
Обратное преобразование:
Л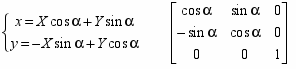
екция 8
Геометрические модели плоских объектов
Основные понятия
Положение точки в пространстве Rn (n-мерном пространстве) задается радиус-вектором p=[p1, p2, …, pn], имеющим n координат p1, p2, …, pn и разложение по n линейно-независимым базисным векторам e1, e2, …, en :
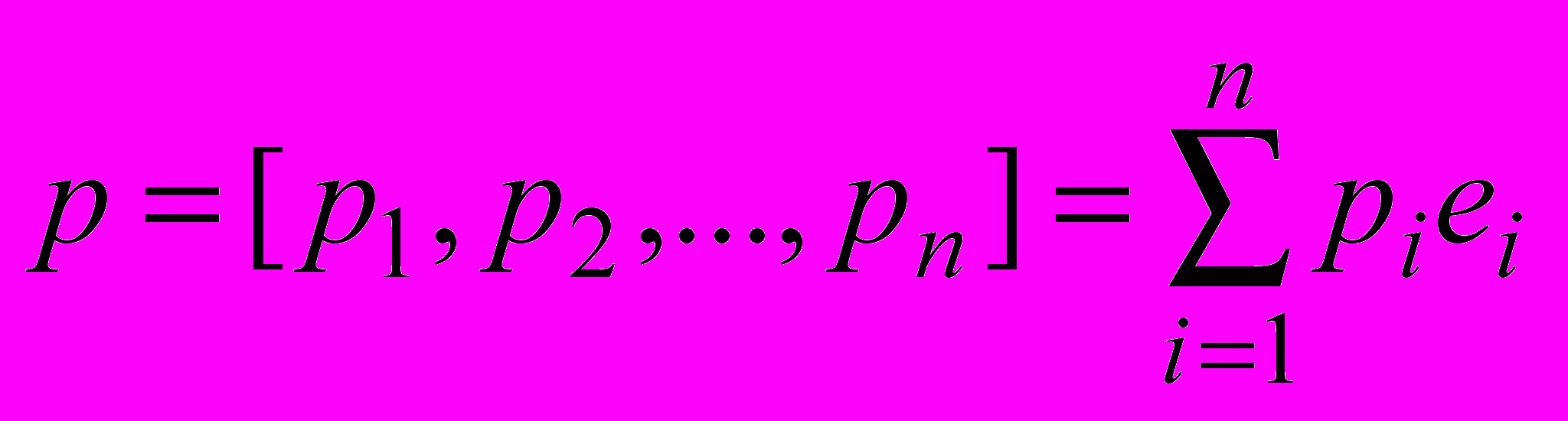 .
.Таким образом положение точки на плоскости определяется радиус-вектором точки p=[px, py]= pxex +pyey или p=[r, φ] в полярной системе координат.
Расстояние между двумя точками p1 и p2 равно:
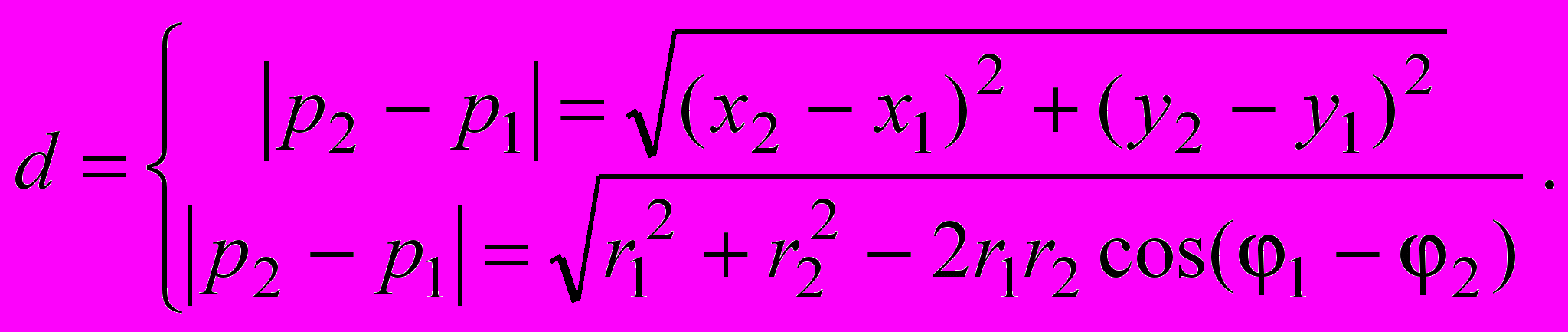
Линия на плоскости может быть задана с помощью уравнения в неявной форме:
(НФ) f(x,y)=0;
или в параметрической форме:
(ПФ) p(t)=[x(t), y(t)].
В любой регулярной (гладкой и некратной) точке на линии p0=[x0, y0]=p(t0) возможна линеаризация кривой, т.е. проведение к ней касательной прямой, уравнения которой имеют вид
(НФ) Nx(x - x0) + Ny(y - y0) = 0 или N ◦ (p - p0) = 0,
(ПФ) x(t) = x0 + Vx t, y(t)= y0 + Vy t или p(t) = p0 + Vt.
Вектор нормали N=[Nx, Ny] ортогонален линии и направлен в ту сторону, где f(p)> 0.
Направляющий вектор линии V=[Vx, Vy] начинается в точке p0 и направлен по касательной к p(t) в сторону увеличения t.
Векторы N и V ортогональны, т.е. N ◦ V = 0 или NxVx + NyVy = 0.
Связь вектора нормали и направляющего вектора:
N=[Vy, - Vx], V=[-Ny, Nx]
