Решение задача 1

Вид материала

Решение

Подобный материал:

• В. С. Алиев Решение и анализ оптимизационных задач Учебное пособие, 202.67kb.
• Домашнее задание по Теории информационных процессов и систем, 267.24kb.
• «Математическое моделирование» Общая трудоёмкость дисциплины составляет, 21.97kb.
• Пояснительная записка курсовой работы «Решение задачи о загрузке (задача о рюкзаке),, 608.78kb.
• Тема: «теория матриц» Основная задача линейной алгебры, 28.88kb.
• А. Ю. Горицкий 1 год, 3 курс, поток механиков  Задача, 39.92kb.
• Секция 7 А. Н. Васильев, Д. а тархов, 79.95kb.
• А. Л. Семенов мгу им. М. В. Ломоносова Экономический факультет Методология стратегического, 176.48kb.
• Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
• Т. М. Боровська кандидат технічних наук, доцент І. С. Колесник, 118.17kb.

ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ

СЕВЕРНОЕ ОКРУЖНОЕ УПРАВЛЕНИЕ ОБРАЗОВАНИЯ


СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ МАТЕМАТИКИ

№ 1384 ИМ.А.А.ЛЕМАНСКОГО


ЦЕНТР ПОДДЕРЖКИ ОДАРЕННЫХ ДЕТЕЙ «УСПЕХ»


ЗАОЧНАЯ ОЛИМПИАДА ПО ГЕОМЕТРИИ ИМ. А.А.ЛЕМАНСКОГО


5-6 КЛАСС

РЕШЕНИЕ


Задача 1

Листок тетради частично накрыт другим таким же листком. Какая его часть больше - открытая или закрытая?



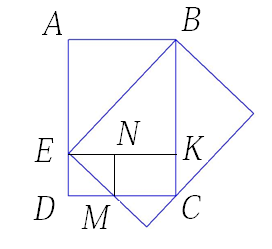
Решение:

1.Проведем отрезок ЕК, параллельный АВ. Получился прямоугольник ЕАВК, который делится диагональю ЕВ на два треугольника, площади которых равны:S_EAB = S_BKA

При этом треугольник ЕАВ открыт, а треугольник ВКЕ – закрыт

верхним листом бумаги.

2.Проведем отрезок МN, параллельный DЕ. Получился прямоугольник DЕNМ, который делится диагональю DM на два треугольника, площади которых равны: S_DEM = S_ENM

При этом треугольник DEM открыт, а треугольник ENM – закрыт

верхним листом бумаги.

3.Оставшаяся часть нижнего листа бумаги – прямоугольник MNКС полностью закрыт верхним листом бумаги.

4.Таким образом, суммарная площадь открытых частей меньше, чем суммарная площадь закрытой части на площадь прямоугольника NMKC:

S_EAB + S_DEM < S_BKA + S_ENM + S_NMCK


Задача 2

Прямоугольник размерами 20см и 30см разбит на клетки размерами 1 см и 1см. Можно ли провести прямую, пересекающую по внутренним точкам 50 клеток прямоугольника? Если можно, то сделайте рисунок. Если нет, то объясните.

Решение:

При переходе из клетки в соседнюю прямая пересекает либо вертикальную , либо горизонтальную линию сетки . (Дважды эти линии она пересечь не может.) Внутри прямоугольника 10+29=48 линий сетки. Значит, прямая не может пересечь более 49 клеток.

Задача 3

Зачеркните все 16 точек изображенных на рисунке шестью отрезками, не отрывая карандаша от бумаги и не проводя отрезков по линиям сетки

Решение:




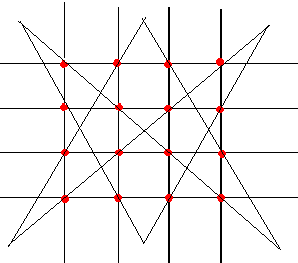
Задача 4

Разрежьте круг на 9 частей, среди которых есть 6 одинаковых треугольников.


Решение:

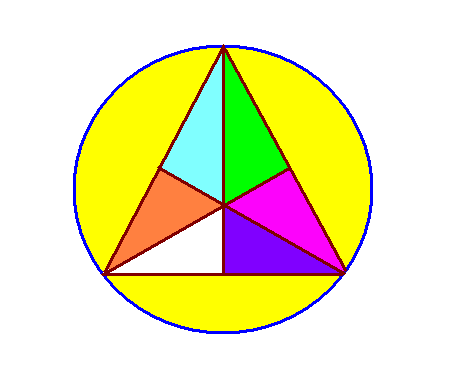Возможны другие решения


Задача 5

Квадратная шоколадка размером 5смХ5см разделена канавками на 25 одинаковых квадратных долек. Требуется несколькими разрезами, проходящими по канавкам , разделить шоколадку на 5 частей по 5 долек в каждой. Это легко сделать, проведя разрезы общей длиной 20 см (сделайте рисунок). А как это сделать, проведя разрезы общей длиной 16 см?


Решение: