Geum.ru

1. оценка деятельно техно природных систем

Вид материалаДокументы

Содержание


A были неразложимыми [Миркин Б.Г., 1974, - 256 с.]. Матрица A
Подобный материал:
1   2   3   4   5   6   7   8   9

Примечание. Список релевантных ПХП получен при уровне важности *= 0.01.


Методы определения весовых коэффициентов основаны на обработке экспертной информации для построения количественных шкал, позволяющих измерять относительную важность ПК. Они предусматривают организацию и проведение экспертиз для оценки различных свойств геообъектов. Здесь под экспертизой понимается процедура оценки важности некоторых ПК одним или несколькими экспертами.

Экспертные оценки степени важности ПК можно получить в порядковой шкале (в виде рангов), в промежуточных шкалах (в виде баллов), в шкале отношений (в виде точек на вещественной оси) и т.д.

Для повышения точности экспертного оценивания создают экспертную группу. Суждение группы специалистов считается более надежным, чем суждение одного эксперта. Однако при проведении групповой экспертизы возникает ряд проблем. Укажем три основных вопроса: 1) как на основе индивидуальных экспертных оценок построить групповую оценку, наилучшим образом отражающую мнение всех экспертов?; 2) как оценить величину расхождения между индивидуальными экспертными оценками? и 3) как обоснованно сблизить индивидуальные экспертные оценки, если они существенно различаются?

Пусть задача ранжирования геоданных состоит в определении весовых коэффициентов М показателей качества. В дальнейшем будем считать, что веса показателей bj удовлетворяют условию нормировки.

Для каждого типа экспертных оценок существуют различные методы определения весовых коэффициентов [Литвак Б.Г., 1984. - 184 с.; Миркин Б.Г., 1974. - 256 с.]. На практике удобными и надежными методами определения весовых коэффициентов являются методы, основанные на парных сравнениях всех ПК по степени важности
[Саати Т.Л., 1979. - №1. - с. 68-84.]. В результате анкетного опроса экспертов заполняются матрицы парных сравнений, после обработки которых определяют веса ПК. В данном методе исходная экспертная информация получается на основе M(M-1)/2 парных сравнений M ранжируемых ПК по степени важности и записывается в специальные таблицы (матрицы парных сравнений An). Элементами матриц An являются оценки аjkn предпочтительности j-го ПК по отношению к k-му ПК, данные n-м экспертом (j,k=1,2,...,M; n=1,2,...,L). Они могут задаваться в различных шкалах [Миркин Б.Г., 1974. - 256 с.]. Так, в порядковой шкале элементы матриц парных сравнений отражают только факт предпочтительности одного ПК по отношению к другому. При задании экспертной информации в шкале отношений используются различные градации степеней предпочтительности сравниваемых ПК. Отметим основные преимущества представления исходной экспертной информации о предпочтительности ПК в виде матриц парных сравнений: 1) эксперты концентрируют свое внимание не на всех ПК сразу, а только на двух. Это облегчает экспертизу и, следовательно, способствует повышению ее качества (надежности); 2) имеет место большое число сравнений каждого ПК с другими, благодаря чему повышается точность оценки; 3) каждая последующая оценка не связана с предыдущей; 4) экспертные оценки не обязаны быть транзитивными. Это значит, что если j-й ПК важнее k-го ПК, k-й важнее m-го и, то m-й может быть важнее
j-го; 5) имеется возможность применения аппарата статистических критериев для оценки степени согласованности экспертных суждений.

При задании экспертных оценок в шкале отношений для элементов матрицы парных сравнений должно выполняться соотношение: аjkn  akjn=1, ajjn=1. В качестве предварительного шага для получения экспертных оценок вводится градация важности ПК на основе задания точек шкалы отношений и их содержательной интерпретации. В этом случае целесообразно использовать табл.3.2, предложенную Т.Саати в работе [Саати Т.Л., 1979, - с. 68-84.].

В идеальном случае точных экспертных оценок аjkn имеет место соотношение: аjkn=bjn/bkn. Оно показывает, во сколько раз j-й ПК предпочтительнее k-го показателя. Тогда весовые коэффициенты bjn можно получить путем усреднения величин аjknbkn , т.е. используя формулу:

bjn=1/M 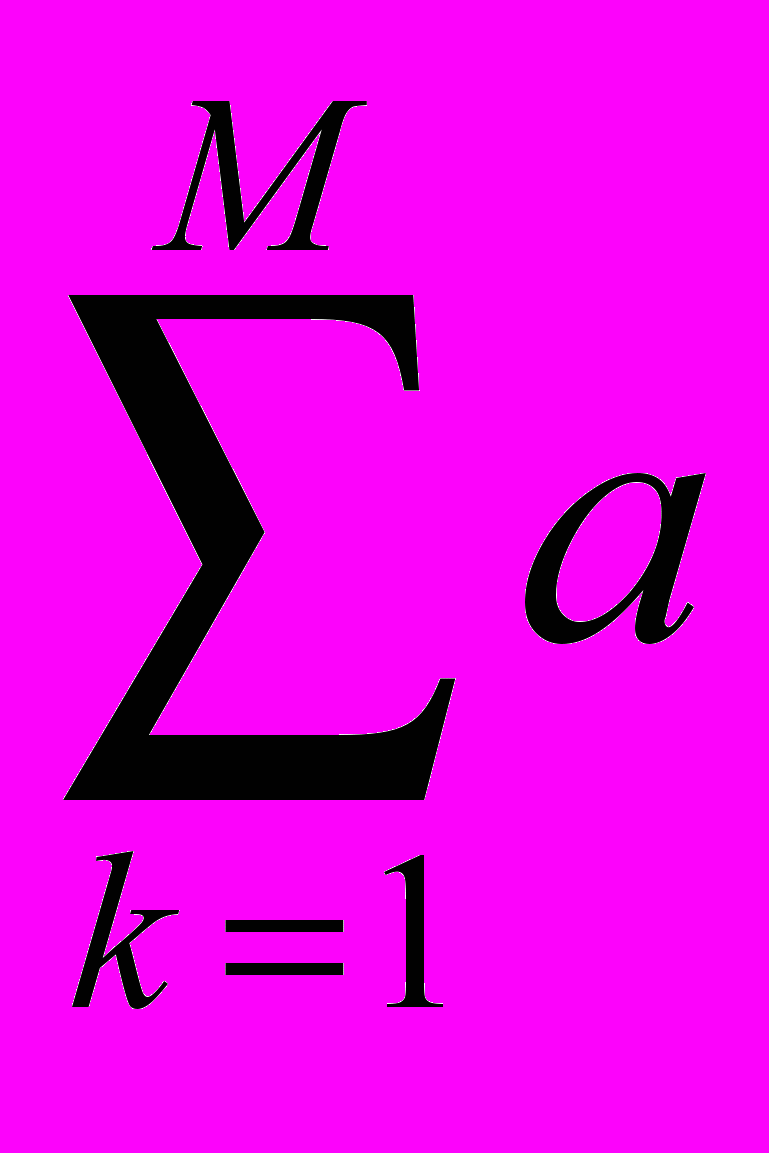jk nbkn или 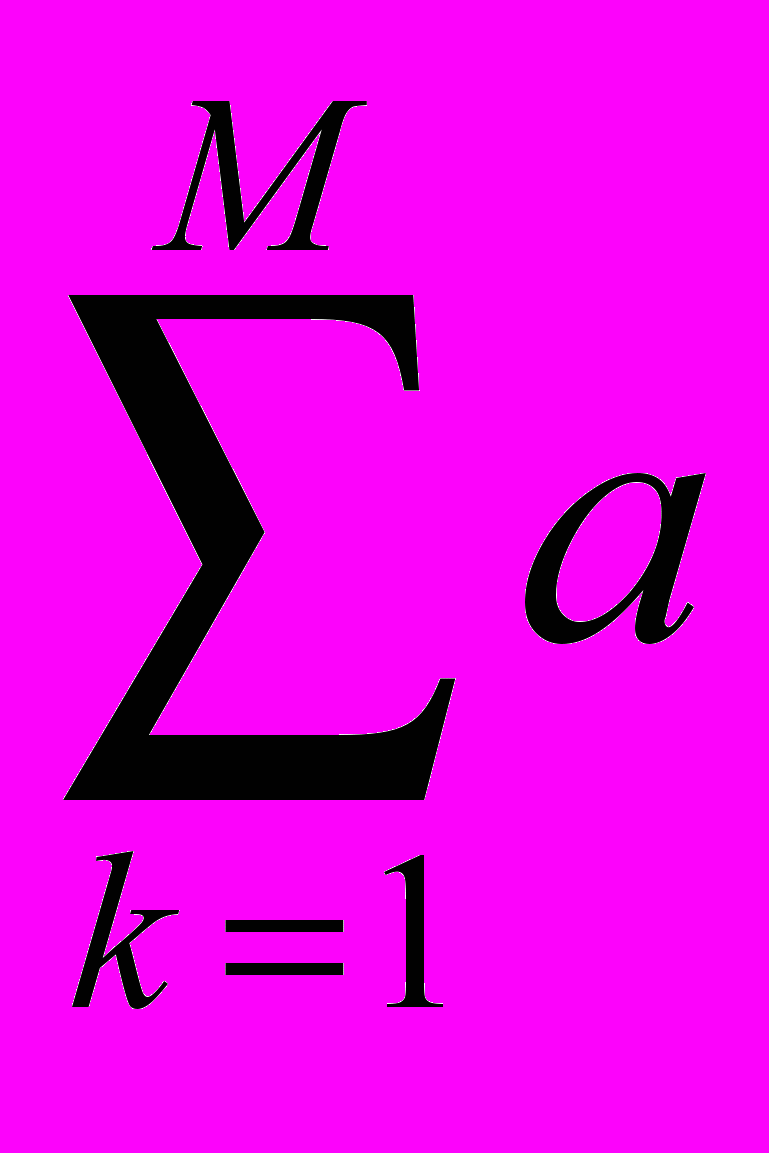jkn bkn=Mbjn.

В матричных обозначениях эта запись имеет вид: Anbn=Mbn, где An=||аjkn|| - "идеальная" матрица парных сравнений; n=(b1n,b2n,...,bMn)т - вектор-столбец весов, n=1,2,...,L. Отметим, что здесь вектор n может рассматриваться как собственный вектор матрицы An с собственным числом M [Миркин Б.Г., 1974. - 256 с.]. Очевидно, что "идеальная" матрица парных сравнений обладает свойством согласованности, т.е. оценки удовлетворяют условию:
аjkn  akmn=аjmn.

Однако в большинстве практических ситуаций требовать выполнения точных отношений типа аjkn=bjn/bkn нереально из-за возможных ошибок в экспертных оценках. При этом задача определения весов ПК заключается в нахождении нормированных собственных векторов n, которые соответствуют максимальным собственным числам max матриц парных сравнений An, т.е. удовлетворяет равенству Ann=maxn.

Аналогичным образом в методе парных сравнений определяются весовые коэффициенты при измерении экспертных оценок предпочтительности ранжируемых показателей в порядковой шкале.

Таблица 3.2



Задание экспертных оценок предпочтительности показателей качества
в шкале отношений

Степень

важности
Определение
Комментарий

1 (1)
Одинаковая значимость
Два показателя равнозначны (эквивалентны)

3 (1/3)
Слабая значимость
Существуют соображения в пользу предпочтения одного из показателей, однако, эти соображения недостаточно убедительны

5 (1/5)
Существенная значимость
Имеются надежные данные и логические соображения в пользу предпочтения одного из показателей

7 (1/7)
Очевидная значимость
Убедительное свидетельство в пользу предпочтения одного из показателей

9 (1/9)
Абсолютная значимость
В высшей степени убедительное свидетельство предпочтения одного из показателей

2,4,6,8

(1/2,1/4,

1/6,1/8)
Промежуточные значения между двумя соседними суждениями
Ситуации, когда необходимо компромиссное решение

Примечание. Если j-й показатель важнее k-го, то k-му показателю приписывается обратное значение числа, соответствующего степени важности j-го показателя.


В этом случае элементы матриц «А» должны удовлетворять условию: ajkn+akjn=2, аjjn=1. Ее заполнение осуществляется по правилам, аналогичным правилам формирования турнирных таблиц. На пересечении рассматриваемой строки и столбца матрицы парных сравнений ставится оценка "2", если оцениваемый ПК, соответствующий номеру строки, предпочтительнее ПК, соответствующего номеру столбца, и оценка "0" - в противном случае. При эквивалентности ПК на пересечении строки и столбца записывается оценка "1".

При задании экспертных оценок в порядковой шкале необходимо, чтобы матрицы парных сравнений An были неразложимыми [Миркин Б.Г., 1974, - 256 с.]. Матрица An называется разложимой, если множество индексов показателей I=1,2,...,M можно разбить на два подмножества I1 и I2 такие, что все ПК из I1 являются предпочтительнее всех ПК из I2. Разложимость матриц парных сравнений чаще всего говорит о непоследовательности экспертных суждений или об ошибках экспертов.

Если некоторые матрицы An являются разложимыми, то практическое применение рассмотренного метода парных сравнений может столкнуться с определенными затруднениями. Так, матрица парных сравнений может оказаться разложимой, а повторная экспертиза невозможной или нецелесообразной. При наличии разложимой матрицы An рекомендуется повторить экспертизу. Предполагается, что перед повторной экспертизой эксперт получит более подробное объяснение решаемой задачи ранжирования данных, либо будет использован другой эксперт. Однако даже разложимая матрица An может содержать достаточно информации для ранжирования ПК.

Можно показать [И.Б.Руссман, В.М.Умывакин, 1985. - 105 с.], что разложимость матрицы An устанавливается в результате упорядочения ее строк по убыванию сумм их элементов. Если матрица парных сравнений разложима, то перестройка в соответствии с новыми номерами строк и столбцов приводит ее к блочно - треугольному виду. В случае разложимости матриц An процедура определения весовых коэффициентов bjn базируется на нахождении собственных векторов, соответствующих максимальным собственным числам неразложимых диагональных подматриц матрицы An. После перестройки (диагонализации) матрицы An все ее элементы, лежащие левее диагональных подматриц будут нули, а правее - двойки.

Когда в процедуре парного сравнения участвуют несколько экспертов, на основе усреднения экспертной информации формируется групповая матрица предпочтений A'. Термин "усреднение" здесь понимается как способ получения групповой оценки при условии, что информация всех экспертов имеет одинаковую ценность. Введение коэффициентов компетентности экспертов не повлияет на дальнейшие рассуждения. Усреднять можно либо входную, либо выходную информацию. При усреднении входной информации элементами групповой матрицы предпочтений A' могут быть средние арифметические значения соответствующих матриц An , т.е.:

a'jk= 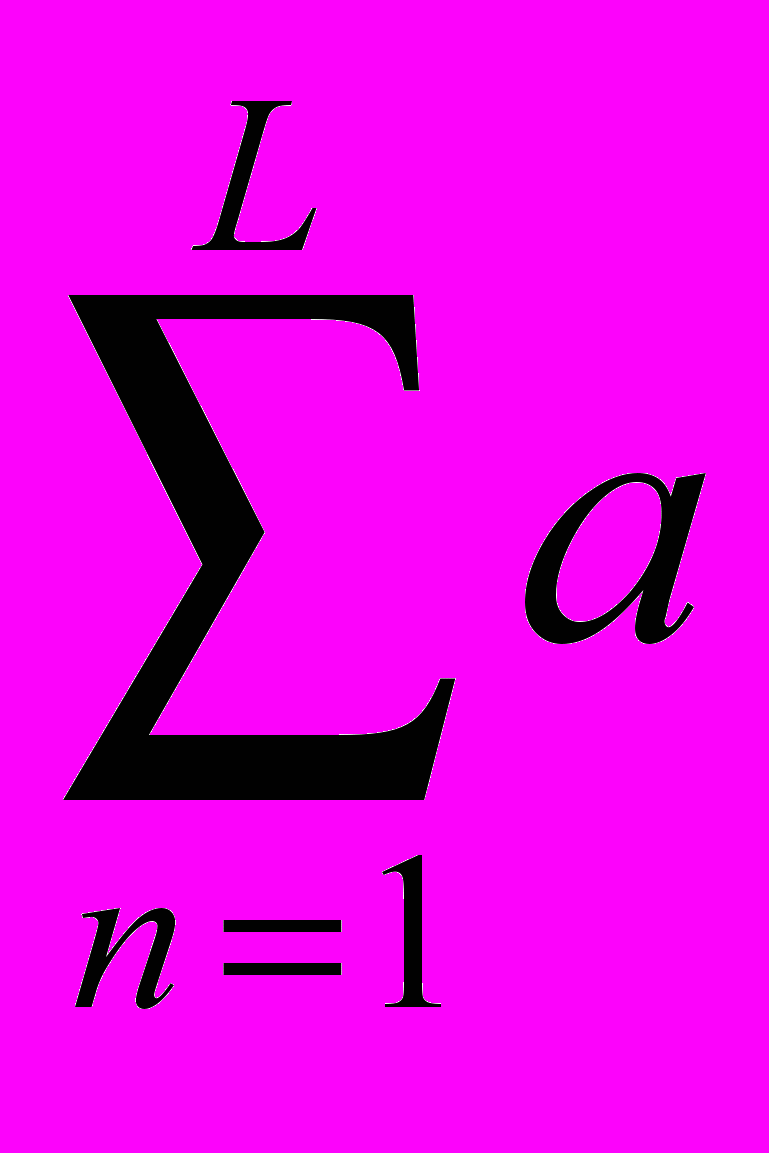jkn/2M

Затем отыскивается собственный вектор матрицы A', соответствующий её максимальному собственному значению. Усреднение входной информации, как правило, снимает проблему разложимости, так как из нескольких разложимых матриц An можно получить неразложимую матрицу A'. В тоже время при построении матрицы A' усредняется вся информация - и правильная и ошибочная. Кроме того, при данном способе усреднения нельзя судить о близости экспертных суждений.

Другой способ получения групповых весовых коэффициентов, основан на обработке выходной информации метода парных сравнений, и, следовательно, является инвариантным типу исходных экспертных оценок. На основе матриц An вычисляются индивидуальные весовые коэффициенты bjn, j=1,2,...,M. В качестве групповых оценок принимаются средние арифметические значения оценок отдельных экспертов. Данный способ усреднения выходной информации позволяет обоснованно сравнивать точки зрения различных экспертов, так как при вычислении компонент нормированного собственного вектора b'j учитываются не только прямые, но и косвенные связи между ПК [Миркин Б.Г., 1974. - 256 с.].

Групповые оценки a'jk предлагается определять следующим оригинальным способом:

a'jk= 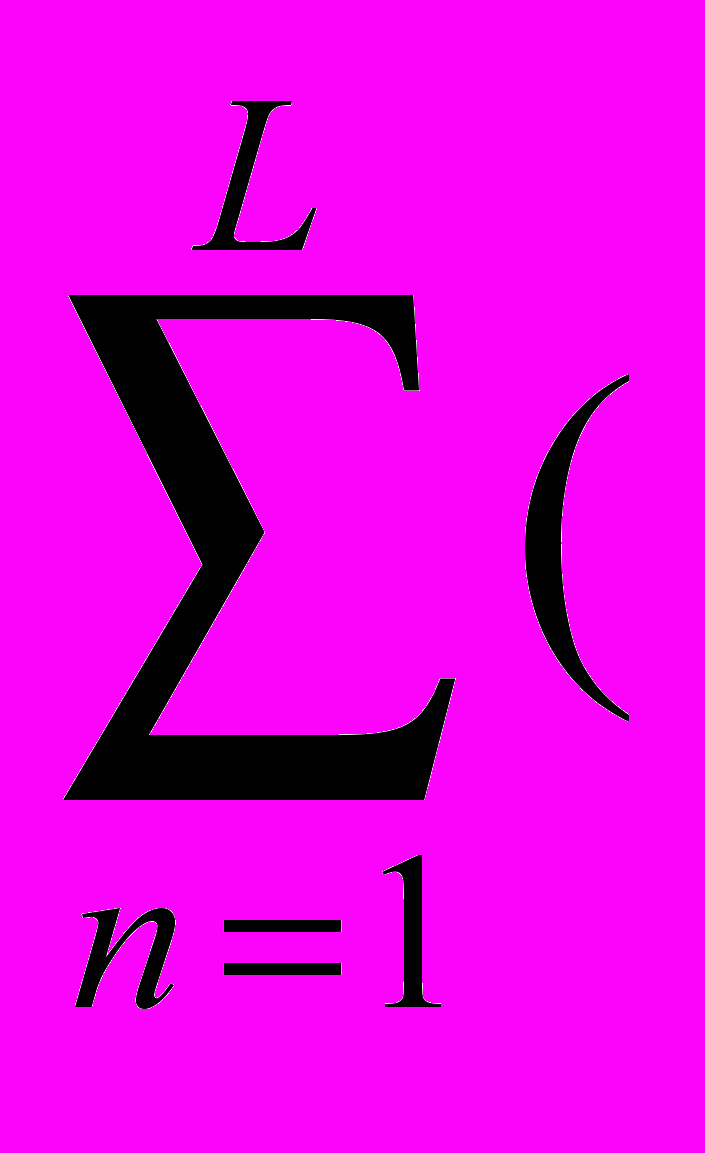b'jn - b'kn + 1)/2M ,

где b'jn = bjn / max bkn , k=1,2,...M.

Элементы а'jk групповой матрицы предпочтений А' характеризуют долю случаев, когда j-й ПК оказывается более значимым, чем k-й ПК в общем числе полученных экспертных оценок. Другими словами, они отражают частоту "общей" предпочтительности j-го ПК над k-м, т.е. удовлетворяют условию: a'jk+a'kj=1, a'jj=0.5.

Для получения групповых весов bj предлагается использовать вероятностные модели оценивания [Миркин Б.Г., 1974. - 256 с.]. Их применение основано на предположении, что существуют некоторые "истинные" оценки bj относительной важности ПК. При этом индивидуальные оценки bjn весовых коэффициентов, полученные на основе обработки экспертной информации, рассматриваются как реализации некоторой случайной величины b'j с математическим ожиданием b'j = bj. Считается, что случайная величина
b'j (экспертные оценки bjn) распределена по нормальному закону со средним bj и дисперсией j2.

После получения групповых оценок bj определяется степень согласованности экспертных суждений об относительной важности ранжируемых показателей. В качестве меры согласованности используется коэффициент конкордации (согласия) Кендэла [Кендэл М., 1975. - 216 с.]. Он изменяется в пределах от 0 до 1 и равен единице в случае полного совпадения мнений экспертов.

Таким образом, рассмотренный выше метод парных сравнений позволяет получать групповые оценки весовых коэффициентов ПК в тех случаях, когда некоторые из экспертных матриц парных сравнений Аn или групповая матрица предпочтений А' являются разложимыми и является инвариантным к типу исходных экспертных оценок.

Рассмотрим пример определения весов природно-хозяйственных показателей (ПХП) методов парных сравнений, перечень которых приведен в табл. 3.3. При этом исходные экспертные данные о степени предпочтительности одних ПХП над другими были получены в ранговой шкале. Подчеркнем, что экспертные оценки не являются транзитивными. Например, 1-й ПХП ("уклоны поверхности земли") "важнее", чем 8-й ПХП ("наличие коммуникаций, мешающих орошению"), который, в свою очередь, "важнее", чем 6-й ПХП ("коэффициент фильтрации грунтов"). В то же время, 6-й ПХП "предпочтительнее" 1-го ПХП. Общее число парных сравнений, произведенных экспертом, составляет М(М-1)/2=55, где М=11 – число ранжируемых ПХП. В результате использования программного комплекса, реализующего модифицированный метод парных сравнений, получены весовые коэффициенты ПХП (см. табл. 3.3).


3.2. Многоальтернативный анализ эколого-экономических решений по рациональному использованию и охране земель


Многокритериальные анализ и оценка качества компромиссных эколого - экономических решений по рациональному использованию и охране земель в регионе, предполагают наличие дискретного множества =1,2,...,N из N возможных вариантов природно-хозяйственной геосистемы (альтернативных вариантов реализации намечаемой хозяйственной и природоохранной деятельности). Каждый i-й возможный вариант ДТПС i=(xi,yi) характеризуется двумя наборам показателей: набором xi=(x1i,x2i,...,xLi) управляющих переменных (параметров) - воздействий на эколого-хозяйственное состояние территории и набором управляемых частных критериев качества yi=(y1i,y2i,...,yMi), отражающих экологические, социальные и экономические последствия реализации инженерных решений. Показатели ДТПС могут быть как нечисловыми, так и количественными (см. раздел 2.1.).