1. оценка деятельно техно природных систем

Вид материала

Документы

Содержание Коммутативность (равноценность). Ассоциативность (иерархическая одноуровненность).

Подобный материал:

• Кционировании техно-природных систем и другой антропогенной деятельности для последующего, 582.73kb.
• За курс 9 класса билет, 42.57kb.
• Организационный план 28 Оценка риска 32 Перечень рисков 34 Оценка рисков, 435kb.
• Проектирование логистических систем, 93.42kb.
• Виды природных ресурсов. Ресурсообеспеченность. Оценка ресурсообеспеченности страны, 42.68kb.
• Лекция № Методы количественного оценивания систем (продолжение) Оценка сложных систем, 156.28kb.
• Emergency Medicine Scott H. Plantz and J. N. Adler 1998. 780 p учебник, 44.15kb.
• План проспект новой книги, 114.81kb.
• Рабочей программы дисциплины «Основы цифровой схемотехники» по направлению подготовки, 23.13kb.
• Экономическая оценка природных ресурсов как фактор повышения инвестиционной привлекательности, 359.56kb.

<. В то же время, 0Р(АВ_j)1, гдеВ_j – событие противоположное В_j. Другими словами, P(AВ_j) – вероятность невыполнения требований к качеству ДТПС при необходимом (но может быть недостаточном в силу каких-либо обстоятельств) условии, что требования к качеству ДТПС выполнены по j-му КК. Эту вероятность и нужна определить. Отметим, что события АВ_j, и АВ_j, попарно несовместны и А=АВ_j+АВ_j. Учитывая, что Р(АВ_j)=1, из формулы полной вероятности следует

P(A)=Р(АВ_j)+Р(АВ_j)=Р(В_j)Р(А В_j)+Р(В_j) Р(АВ_j)=

=Р(В_j)+[1-Р(B_j)]Р(АВ_j).

Таким образом,

Р (АВ_j) = [Р(А) - Р (В_j)] / [1 - Р(В_j)] (2. 7)

Рассмотрим формулу умножения вероятностей
Р(АВ_j)=Р(А)Р(В_j А)=Р(В_j)Р(А В_j). Опять учитывая, что Р(А B_j)=1, получаем важное неравенство

0Р(А)=Р(В_j)/Р(В_j  А)1. (2.8)

Отсюда следует, что

Р(В_j)Р(В_j А). (2. 9)

Подставив выражение Р(А) из (2.8) в (2.7), получаем:

Р(АВ_j)=Р(В_j)[1-Р(В_j А)]/(Р(В_jА)[(1-Р(В_j)]. (2. 10)

Введем следующие обозначения: d_j=Р(АВ_j), _j=Р(B_j) – вероятность некачественности всех эколого-экономических решений по j-му КК, _j=Р(В_jА) – вероятность некачественности решений по j-му КК при условии, что требования к качеству ДТПС не выполнены. В результате получаем, что формула (2.10) совпадает с формулой (2.1) частных оценок качества ПХГС типа «трудность (риск)». В силу вероятностной природы величин d_j, _j, _j они принимают значения из интервала [0,1]. Причем, из неравенства (2.9) следует, что _j _j.

Подчеркнем, что событию АВ_j соответствует неопределенность информации (энтропия), равная – ln[Р(АВ_j)]=1n[1/Р(АВ_j)], а противоположному событию АВ_j – информационная оценка

I(d_j)= –1n[Р(АB_j)]=1n[1/ (1 – Р(АB_j)]=1n[1/ (1 – d_j)].

Укажем основные свойства оценок I(d_j): 1) I(d_j)=0 при d_j =0;
2) I(d_j)  при d_j 1.

Если величины d_j рассматривать как трудности достижения цели устойчивого экологически безопасного развития региональных ДТПС по j-му потребляемому ресурсу, то оценки I(d_j) отражают информацию о значимости (степени дефицитности) ресурсов в процессе получения требуемого качества результата социально–экономической деятельности [Каплинский А.И., Руссман И.Б., Умывакин В.М., 1989. - с.10-23; Каплинский А.И., Руссман И.Б., Умывакин В.М., 1991. - 168 с.]. Причем, чем больше I(d_j), тем больше чувствительность эколого-экономических решений к изменению качества и объема j-го ресурса для реализации общей цели развития ДТПС. Это позволяет рассматривать I(d_j) как своего рода универсальные стоимостные измерители единицы j-го ресурса и использовать их в роли коэффициентов информационной линейной целевой функции типа обобщенных затрат в оптимизационно-имитационных моделях ресурсного обеспечения допустимого развития региональных ДТПС [Каплинский А.И., Руссман И.Б., Умывакин В.М., 1991. - 168 с.]. Данная целевая функция стимулирует рациональное использование (экономию) дефицитных природных, материальных, энергетических, трудовых и других видов ресурсов.


2.2.2. Основные априорные требования к виду конструируемых интегральных оценок


Рассмотрим основные априорные требования, лежащие в основе аксиоматического (нормативного) подхода к построению интегральных оценок качества ДТПС. Предположим, что интегративное свойство (качество) ДТПС характеризуется фиксированным перечнем (набором) частных критериев y₁,y₂,...y_M, которые измерены в количественных шкалах. Увеличение или уменьшение значений частного КК означает улучшение качества ДТПС в целом (например, снижение интегральной экологической опасности земельных ресурсов). Все КК можно преобразовать (беря либо обратную величину, либо приписывая показателю противоположный знак) к одному виду: чем меньше значение КК, тем выше качество ДТПС. Поэтому, в дальнейшем предполагается, что уменьшению значений КК соответствует улучшение качества ДТПС.

Требуется построить интегральную оценку (критерий) качества ДТПС, которая обладает определенными содержательными свойствами и удовлетворяет определенным формальным априорным требованиям (аксиомам), и которая может быть использована для ранжирования и сравнения вариантов ДТПС при обосновании комплекса мероприятий по рациональному использованию и охране земель в регионе.

Наиболее часто на практике применяется две формы интегральных критериев (оценок) качества компромиссных эколого-экономических решений - линейная аддитивная и нелинейная мультипликативная свертки:

F₁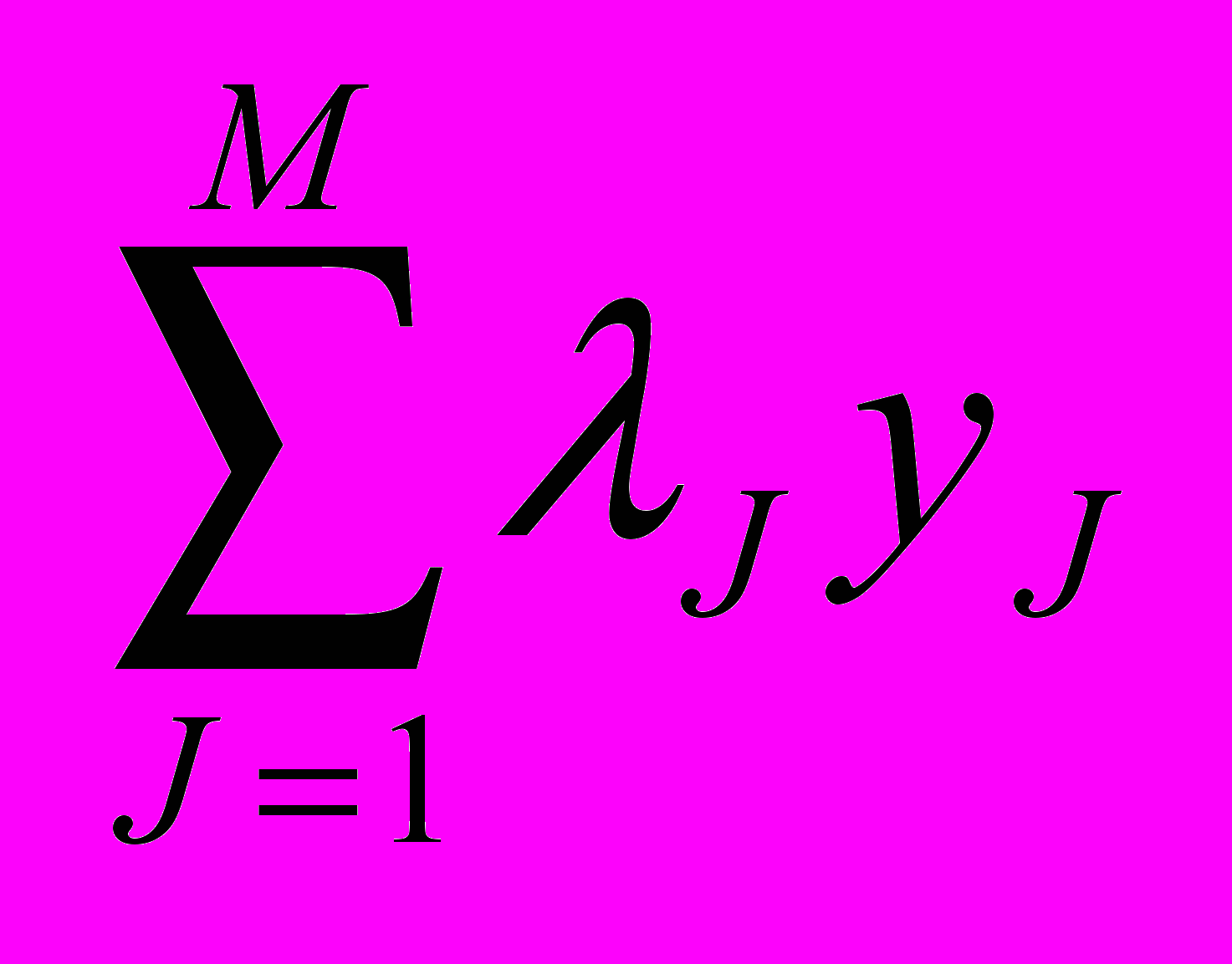₌ и F₂ =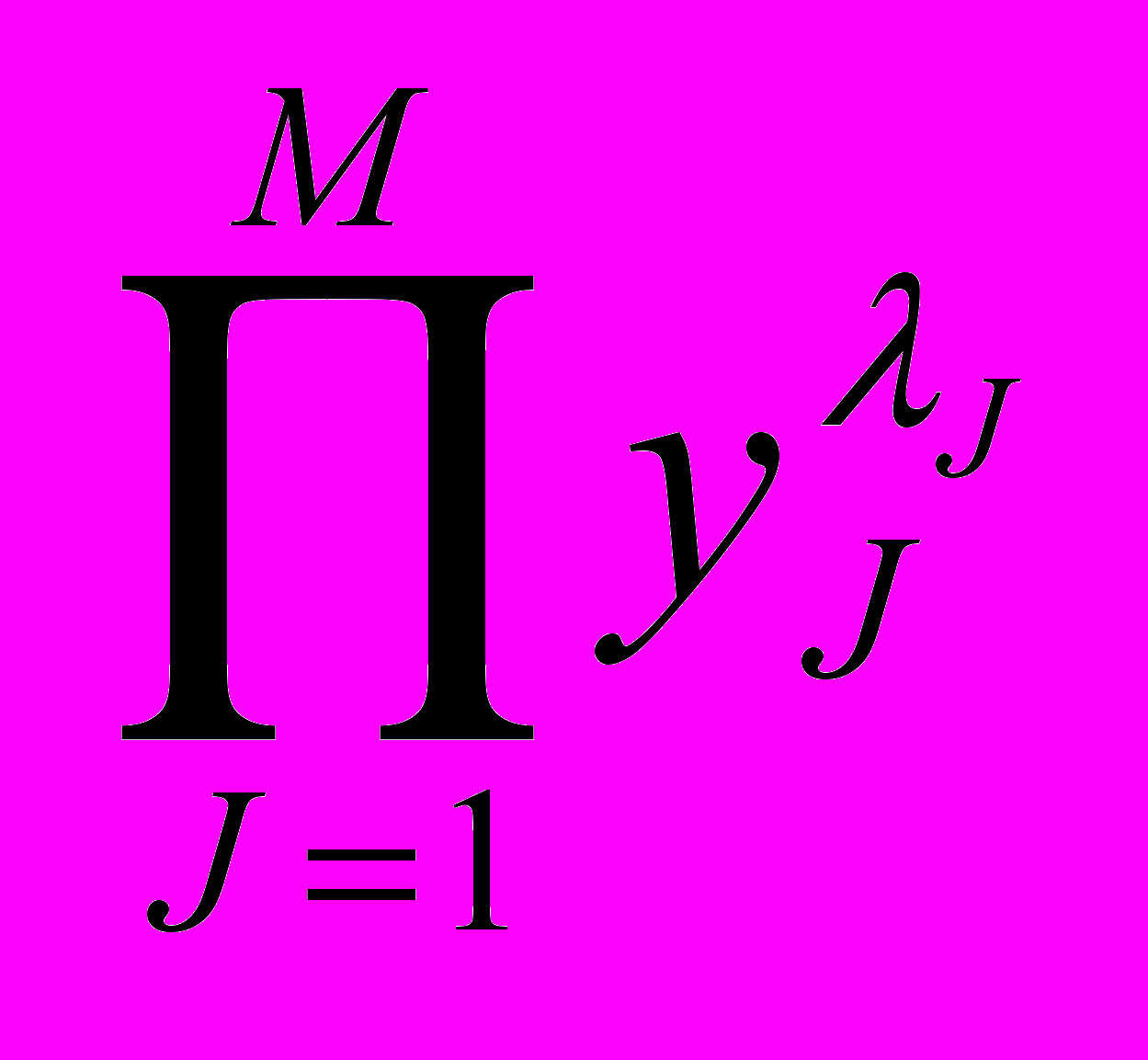. (2.2)

где j - весовые коэффициенты частных КК (оценок), которые выполняют выравнивающую и согласовывающую роль , j=1,2,...,M.

Если обозначить в первом случае y'_j=_jy_j, а во втором - _j y'_j=y_j , то после выравнивания частных оценок интегральные критерии качества принимают наиболее простой вид:

F'₁ = 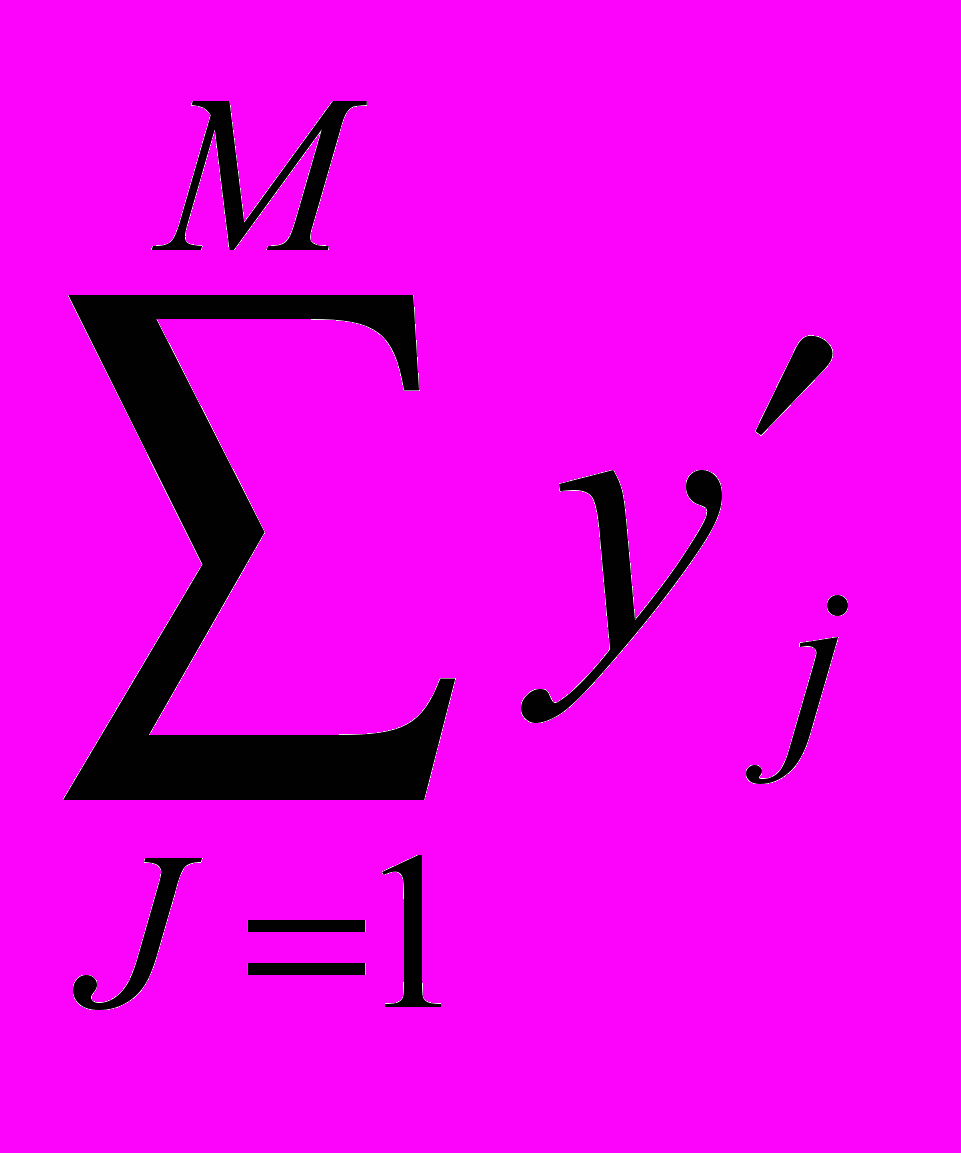и F'₂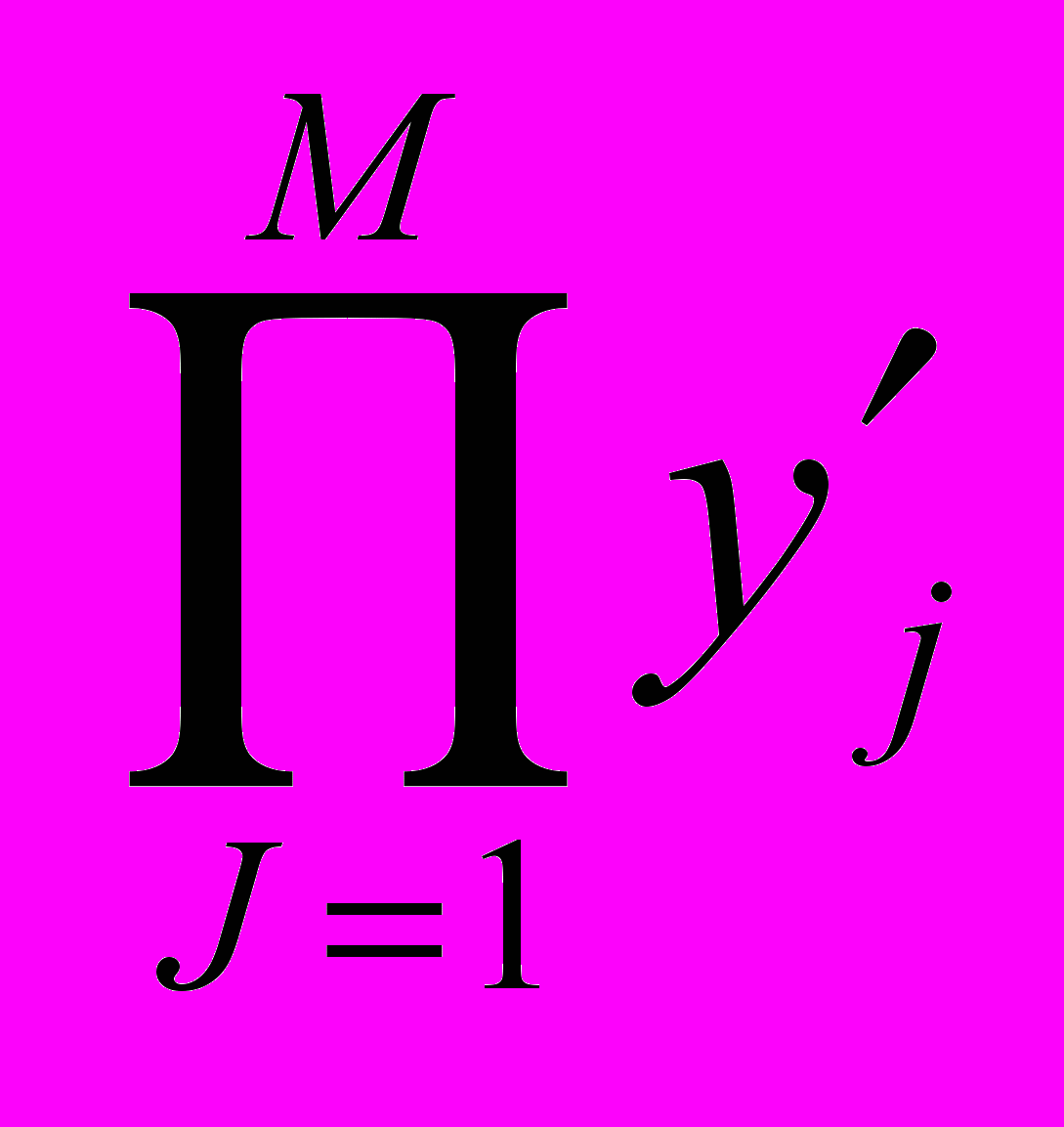₌. (2.3)

Здесь агрегированные критерии конструируются с помощью многократного последовательного применения бинарных (попарных) коммутативных операций (в первом случае - сложения, во втором - умножения). В связи с этим формирование интегральных оценок качества можно представить как процедуру последовательного попарного объединения КК с заменой их частных оценок качества на оценку пары как комплекса (агрегата). Можно предположить, что бинарные операции сложения и умножения не исчерпывают всей совокупности операций, допустимых для конструирования интегральных оценок качества ДТПС.

Предположим вначале, что качество ПХГС характеризуется только двумя критериями (абсолютными оценками) - y₁ и y₂. Пусть d₁ и d₂ - некоторые частные относительные оценки качества ДТПС по этим КК, а d(d₁,d₂) - интегральная оценка. Функция d(d₁,d₂) может рассматриваться как результат некоторой операции над частными оценками качества. В простейшем случае данная операция считается бинарной. Сформулируем набор основных априорных требований (аксиом) к виду функции d(d₁,d₂), зависящей от частных оценок качества [Каплинский А.И., Руссман И.Б., Умывакин В.М., 1989. - С.10-23; Каплинский А.И., Руссман И.Б., Умывакин В.М., 1991. - 168 с.; Руссман И.Б., 1978. - № 2. - С.201-204.]. Эту функцию естественно трактовать как оценку совместного действия (агрегата) нескольких частных критериев, объединенных в один комплексный (агрегированный) критерий. Причем, в многокритериальных задачах принятия эколого-экономических решений уровень агрегирования возрастает с ростом сложности и неопределенности априорной информации. Из всей совокупности различных (иногда очень частных) требований к виду интегральной оценки качества ДТПС выделим следующие.

Коммутативность (равноценность). От интегральной оценки d требуется выполнение условия:

d(d₁,d₂)=d(d₂,d₁) (2.2.8)

Здесь символ d определяет бинарную операцию, производимую над выравненными и согласованными частными оценками d₁ и d₂. Аксиома коммутативности является одной из наиболее часто встречающихся аксиом теории принятия решений [Подиновский В.В., 1975, – с. 330 – 344.] и требует равноценности или одинаковой важности частных однородных оценок d₁ и d₂. Отметим, что изменение одной из них на некоторую величину изменяет интегральную оценку точно также, как и изменение другой из них на ту же самую величину. Таким образом, аксиома кoммутативности интегрального критерия говорит о том, что комплексная оценка зависит от всего набора частных оценок, т.е. не зависит от порядка, в котором производится их свертка.

Ассоциативность (иерархическая одноуровненность). Это чрезвычайно важное свойство интегральных оценок, формулируется в виде:

d(d(d₁,d₂),d₃)=d(d₁,d(d₂,d₃)). (2.2.9)

Смысл ассоциативности состоит в том, что в интегральном критерии, удовлетворяющем этой аксиоме, агрегируются ("свертываются") лишь частные оценки одноуровневых КК. Другими словами, ассоциативность есть "антииерархическое" свойство интегральной оценки, означающее отсутствие иерархии среди агрегируемых частных оценок. Следовательно, если частные оценки принадлежат одному уровню иерархической структуры качества ДТПС и являются равноценными, то интегральная оценка с необходимостью удовлетворяет требованиям ассоциативности и коммутативности.

Гладкость. Естественным является предположение о непрерывной зависимости интегральной оценки от частных, т.к. в реальных ситуациях малым изменениям частных критериев качества должно соответствовать малое изменение комплексного критерия. К резкому снижению разнообразия форм интегральных оценок приводит условие, что свертка d(d₁,d₂) является многочленом. Кроме того, "многочленная" форма интегральной оценки наиболее проста для практических приложений.

Ограниченность. На практике задаются или предполагаются известными границы диапазоны изменения аргументов (частных оценок) и функции (интегральной оценки). Ниже будет показана роль этого требования на примере, когда аргументы и функция принимают значения из интервала [0,1]. Данное требование позволяет получить вероятностную интерпретацию конструируемых частных и интегральных оценок качества ДТПС.

Нейтральность. Данная аксиома названа так условно. Это просто требование к интегральной оценке d(d₁,d₂) типа d(d₁,d₂^min)=d₁, где d₂^min - минимальное значение частной оценки d₂. Она трактуется следующим образом: при рассмотрении взаимодействия двух частных оценок d₁ и d₂ общий эффект совпадает с действием лишь первой, когда вторая не действует вовсе (имеет минимальное значение). В обычном сложении при d₂^min=0 это аналог записи d₁+0=d₁. Именно таким образом полезно отличать действие сложения (агрегирования эффектов) от умножения с аннулирующим нулем: d₁0=0.

Из приведенных выше четырех априорных требований (коммутативности, гладкости, ограниченности и нейтральности) к свойствам интегральной оценки можно составить 16 различных наборов аксиом (условие ассоциативности выполняется везде). Исключение из рассмотрения неассоциативных интегральных оценок вызвано, в частности, следующими причинами. Во-первых, слишком широким является класс всех неассоциативных и коммутативных функций. Во-вторых, на практике обычно не сворачивают оценки, принадлежащие разным уровням иерархической структуры "качество ДТПС".

Ниже будут показаны преимущества приведенных аксиом:

1) разнообразие классов получаемых интегральных оценок качества;

2) возможность интерпретации аксиом на естественном для экспертов языке;

3) указание места часто применяемых на практике интегральных оценок качества в предлагаемой системе аксиом (в частности, аддитивных и мультипликативных сверток);

4) тесные связи получаемых интегральных оценок с вероятностными (риск, опасность) и иформационными (энтропия) характеристиками, что позволяет использовать их в оптимизационно-имитационном моделировании развития региональных ДТПС.


2.2.3. Нормативные модели интегральных оценок качества типа "минимальный обобщенный риск"


Приведем обоснование вида конструируемых интегральных оценок качества ДТПС. Предположим, что выполнены следующие требования, предъявляемые к форме интегрального критерия: 1) коммутативность частных оценок (2.2.8); 2) ассоциативность (2.2.9); 3) функция d(d₁,d₂) является многочленом.

В этом случае интегральная оценка качества ДТПС конструируется с помощью применения одной и той же бинарной ассоциативной и коммутативной операции к частным оценкам и является целой аналитической функцией от них. Общий вид таких оценок получается из следующей теоремы [Каплинский А.И., Руссман И.Б., Умывакин В.М., 1991. - 168 с.; Руссман И.Б., 1978, с.201-204].

Теорема 2.1. В классе многочленов от двух переменных существуют лишь три (с точностью до постоянных коэффициентов) функции:

1) d(d₁,d₂)=c=const; (2.2.10)

2) d(d₁,d₂)=d₁+d₂+c; (2.2.11)

3) d(d₁,d₂)=(d₁+d₂)+d₁d₂+(-1)/ (0). (2.2.12)

Доказательство теоремы основано на представлении функции d(d₁,d₂) в виде двойного степенного выражения, которое подставляется в условие (2.2.8). Сравнение коэффициентов в обеих частях равенства и учет условия (2.2.9) приводят к функциям (2.2.10)-(2.2.12).

Первая форма интегрального критерия (бинарной операции свертки) - тривиальна, т.к. в этом случае комплексная оценка не зависит от частных оценок. Вторая форма соответствует аддитивному интегральному критерию. Существенным недостатком данной комплексной оценки является невозможность описания с ее помощью взаимодействия отдельных частных оценок. Следует лишь отметить возможность сдвига интегральной оценки на постоянную, связанную, например, с выбором начала отсчета для каждой из частных оценок.

Наибольший теоретический и практический интерес представляет третья форма - наличие коэффициента  в знаменателе дроби не позволяет отнести полученную функцию d(d₁,d₂) к первой или второй бинарным операциям свертки. При =0 третья форма соответствует мультипликативному критерию, а при =1 принимает вид:

d=d₁+d₂-d₁d₂. (2.4)

В этом случае интегральная оценка формируется из суммы вкладов частных оценок и членов d₁d₂. Здесь коэффициент  определяет характер и результат взаимодействия пары отдельных оценок.

Перейдем к формированию нормативной модели интегральной оценки качества, которая характеризует риск недостижения требуемого качества ДТПС [Рекс Л.М., Ростопшин Ю.А., Русинов П.С., Руссман И.Б., Умывакин В.М., 1999. - 48 с.]. Введем дополнительные требования на значения частных оценок и интегральной оценки:

1) ограниченность 0d(d₁,d₂)1 при 0d₁,d₂1; (2.2.13)

2) нейтральность d(d₁,0)=d₁, d(0,d₂)=d₂; (2.2.14)

3) d(0,0)=0, d(1,1)=1. (2.2.15)

Можно показать, что указанным условиям отвечает лишь третья из приведенных выше форм интегрального критерия при =1, =-1. Действительно, условия (2.2.13)-(2.2.15) для функции d(d₁,d₂) вида (2.2.12) приводят к системе уравнений относительно неизвестных  и :

(-1)/=0, (2.2.16)

2++(-1)/=1. (2.2.17)

Система (2.2.16)-(2.2.17) имеет два решения: =0, =1 и =1, =-1. Первое решение приводит к обычной мультипликативной оценке d=d₁d₂, а второе - к бинарной операции вида

d=d₁+d₂-d₁d₂=1-(1-d₁)(1-d₂). (2.5)

Эта операция, в отличие от произведения частных оценок, обладает важным свойством (2.2.14) - интегральная оценка совпадает с одной из частных оценок, если вторая оценка равна нулю. Кроме того, формула (2.5) совпадает с формулой вероятности суммы двух независимых событий. Это позволяет использовать данную бинарную операцию для свертки частных оценок, имеющих смысл вероятности или субъективной вероятности. К таким частным оценкам относятся оценки типа надежность, риск, опасность и др.

Следовательно, интегральная оценка качества ДТПС вида (2.5) является единственным многочленом, удовлетворяющим требованиям коммутативности, ассоциативности, ограниченности и нейтральности. Она легко обобщается на случай M>2 частных оценок:

d=1-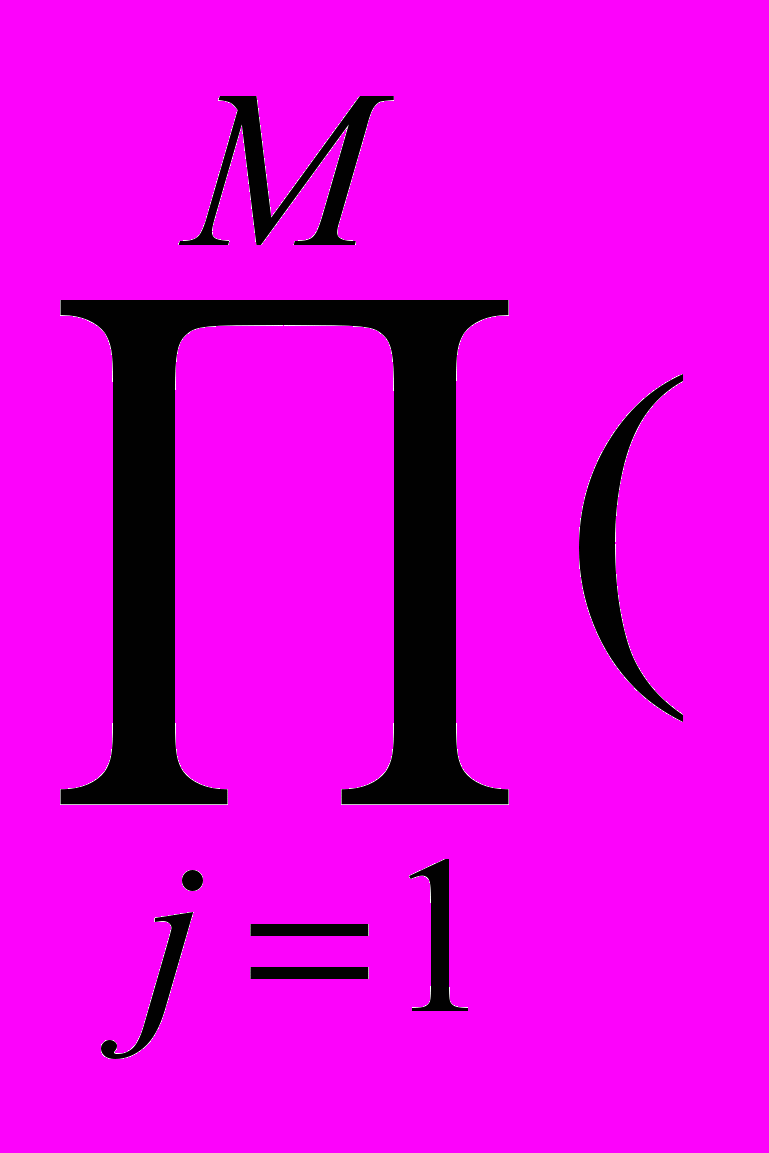1-d_j) (2.6)

Можно получить интерпретацию величины d (обобщенной трудности) как вероятности P(AB₁B₂...B_M) невыполнения требований к интегральному качеству (недостижения требуемого интегрального качества) ДТПС при условии выполнения требований ко всем частным свойствам (индивидуальным качествам).

Таким образом, получены оригинальные интегральные оценки d качества земельных ресурсов, имеющие содержательный смысл "риск невыполнения требований к эколого-хозяйственному состоянию земель, и которые имеют вероятностную интерпретацию, что позволяет измерять экологическую опасность природно-антропогенных ландшафтов. Они конструируются на основе сопоставления значений отдельных КК и соответствующих нормативных уровней. Для их практического применения необходимо преодолеть "разрыв" между реально измеряемыми натуральными частными КК (абсолютными оценками) и соответствующими им "искусственными" частными относительными оценками качества, которые позволяют использовать определенный комплекс операций для конструирования интегральных оценок качества ДТПС.


2.2.4. Выравнивание неравноцености частных оценок качества с помощью весовых коэффициентов


Операцию, задаваемую функцией вида (2.5), будем называть обобщенным сложением (квазисложением) и обозначать следующим образом:

d₁d₂=d₁+d₂-d₁d₂=1-(1-d₁)(1-d₂)=d. (2.11)

Эта операция обладает всеми свойствами обычной операции сложения. Можно показать, что операция обобщенного умножения на произвольное неотрицательное число , которую обозначим символом , может быть введена в форме

_jd_j=1-(1-d_j) ^j. (2.12)

Данная операция согласована с операцией квазисложения и удовлетворяет соотношениям вида: 1d_j=d_j, ₀(d₁d₂)=₀d₁₀d₂, (₁₂) d_j=₁d_j₂d_j,

Формула интегральной оценки качества (2.5) получена в предположении коммутативности (равноценности) и ассоциативности (иерархической одноуровненности) частных оценок качества ДТПС. Использование весовых коэффициентов для "выравнивания" значимости частных оценок d_j само по себе противоречиво. Дело в том, что аксиома коммутативности уже предполагает равноценность индивидуальных трудностей (частных оценок качества) d_j. Такого рода равноправность достигается единым способом измерения частных абсолютных оценок качества _j и нормативных уровней _j. Ранее уже отмечалось, что некоммутативная аддитивная линейная свертка оценок d₁ и d₂ вида ₁d₁+₂d₂ становится коммутативной для d'₁=₁d₁ и d'₂=₂d₂. Рассмотрим конкретные способы "выравнивания" индивидуальных трудностей d_j. Из формул (2.12) и (2.1) имеемd_{j =} _jd_j=1-(1-d_j)^j₌['_j(1-'_j)]/['_j(1-'_j)] (_j>0).

Тогда '_j=1-(1-_j), '_j=[1-(1-_j) ^j]/[1-(1-_j/_j) ]. Действительно,

d'_j=('_j/'_j-'_j)/(1-'_j)=[1-(1-_j/_j)^j-1+(1-_j)]/(1-_j)^j=1-[(1-_j/_j)/(1-_j)^j]=1-(1-d_j)^j.

Таким образом, в общем случае интегральные оценки качества типа «риск» принимают вид:

d=1-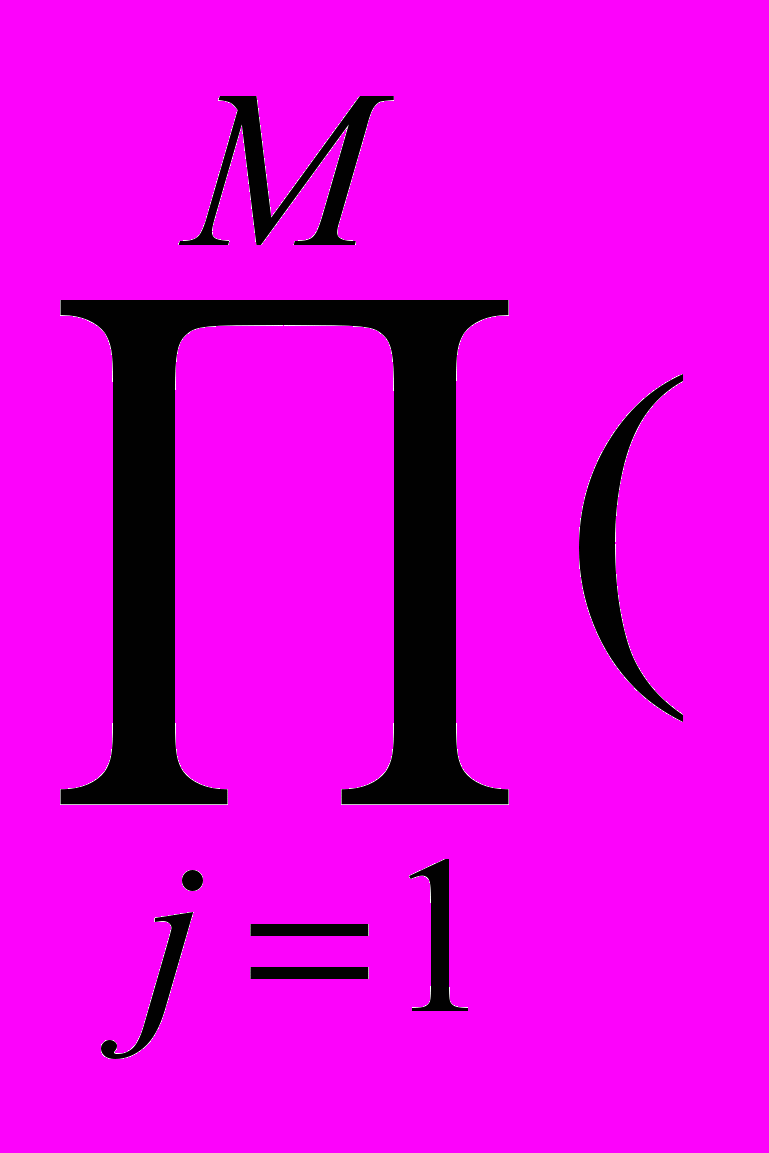1-d_j)^j (2.13)

где _j - весовые коэффициенты частных оценок d_j, удовлетворяющие условию нормировки: 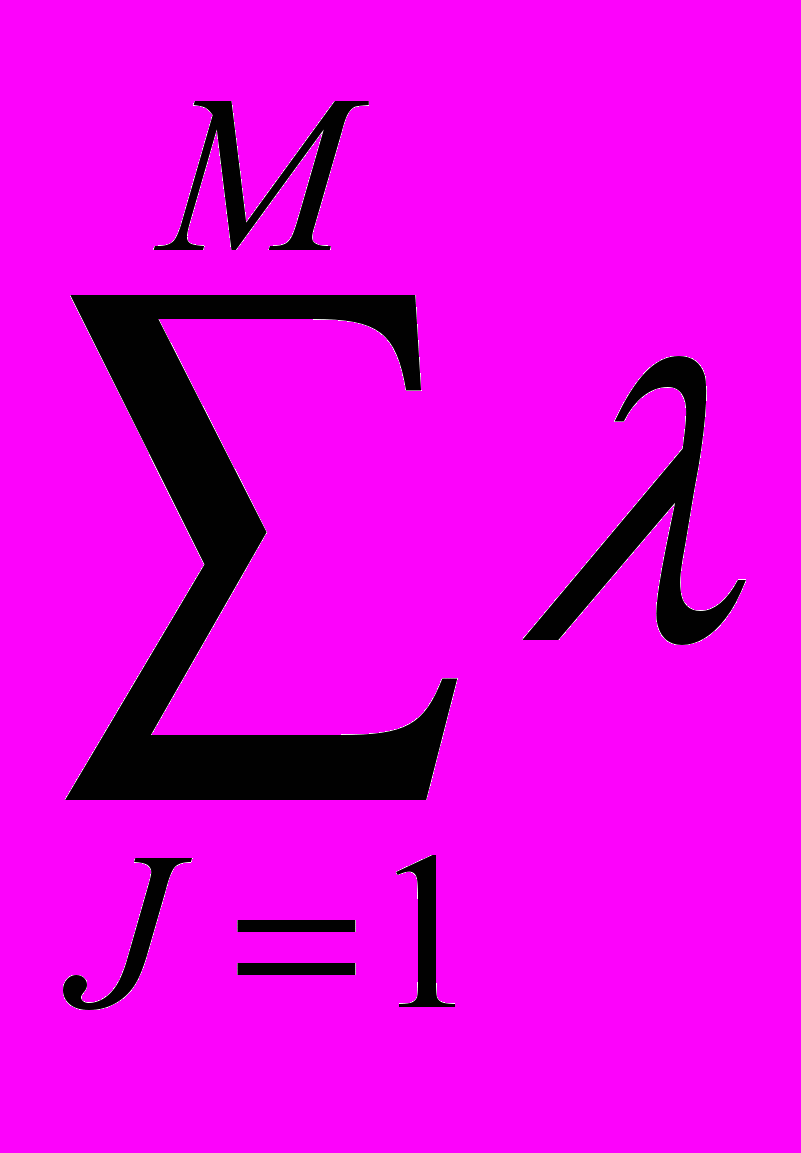_j =1, _j0, j=1,2,…,М.

В итоге может быть произведена оценка информации I(d_jⁱ), содержащейся в j-м критерии для i-го варианта ПХГС: I(d_jⁱ)=ln[1/(1-d_jⁱ)]. Тогда I(dⁱ)=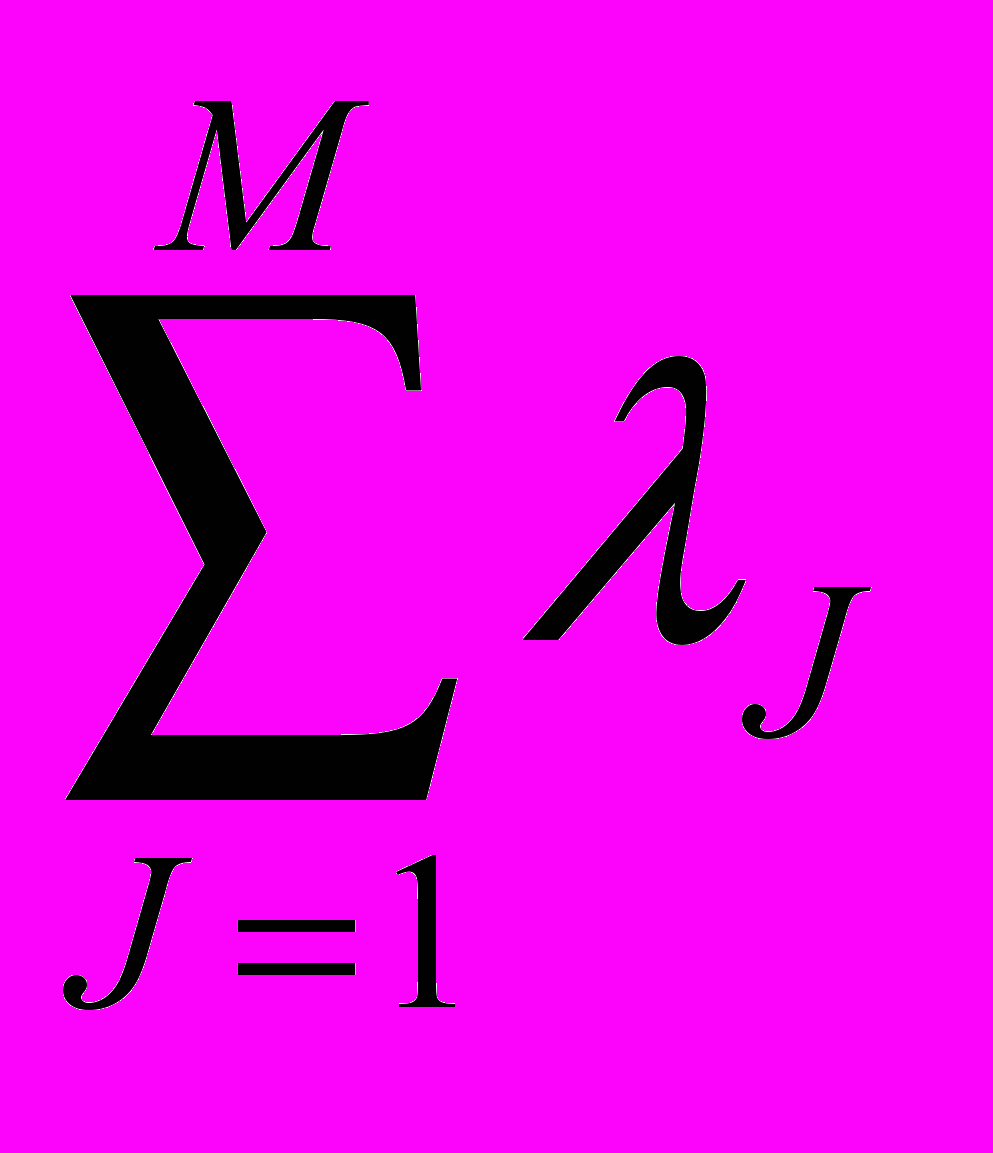I(d_jⁱ)=ln[1/(1-dⁱ)].


2.2.5. Дискретные интегральные оценки качества эколого-экономических решений


Приведем обобщение нормативной модели интегральной оценки качества ДТПС типа «минимальный риск» на случай частных критериев, измеримых в ранговой и балльной шкалах – будем считать, что все КК принимают значения из интервала [0,К], где К - некоторое целое число. Например, качество управленческих решений по использованию и охране земель может характеризоваться нечисловыми критериями типа "экологическая напряженность".

Вид агрегирования (свертки) дискретных оценок качества y_j^o для неаддитивных КК (в частности, для критерия "степень деградации земель") может быть получен из некоторых общих соображений [Руссман И.Б., Умывакин В.М., 1984. - с.67-70.]. Пусть Y₁^o и Y₂^o - частные оценки качества ДТПС, принимающие целые значения из интервала [0,К], а F(Y₁^o,Y₂^o) - агрегированная дискретная оценка качества, зависящая от частных. Потребуем выполнения следующих дополнительных условий, выделяющих класс допустимых сверток: 1) областью значений F(Y₁^o,Y₂^o) также являются целые числа в интервале [0,К]; 2) если частные оценки Y₁^o и Y₂^o принимают максимальные (минимальные) значения, то и агрегированная оценка F принимает соответственно максимальное (минимальное) значение, т.е. F(0,0)=0, F(К,К)=К; 3) частные оценки Y₁^o и Y₂^o являются равноценными. Это значит, что интегральная оценка не должна меняться при перестановке Y₁^o и Y₂^o, т.е. выполняется свойство коммутативности: F(Y₁^o,Y₂^o)=F(Y₂^o,Y₁^o); 4) частные оценки Y₁^o и Y₂^o, подлежащие свертке, соответствуют критериям, которые находятся на одном иерархическом уровне. Это свойство находит отражение в ассоциативности оценки: F(F(Y₁^o,Y₂^o),Y₃^o)=F(Y₁^o,F(Y₂^o ,Y₃^o));
5) если F - произвольная монотонная функция, ставящая в соответствие каждому числу из [0,К] некоторое число из этого же интервала, тогда из соотношения y^o=F(Y₁^o,Y₂^o) следует, что F(Y^o)=F[F(Y₁^o),F(Y₂^o)]. Это условие учитывает тот факт, что порядковые величины определены с точностью до произвольного монотонно вырастающего преобразования.

Может быть доказана следующая Теорема 2.2. [90]: Существуют только две функции F(Y₁^o,Y₂^o), удовлетворяющие условиям 1)-5):

min(Y₁^o,Y₂^o) и max(Y₁^o,Y₂^o).

Доказательство теоремы основано на представлении агрегированной дискретной оценки F(Y₁^o,Y₂^o) в виде функции (К+1)-значной логики [Яблонский С.В., 1986. - 384 с.] и проведении индукции по множеству возможных значений переменных и функций. Для К=1 существует 16 различных булевых функций, среди которых только две удовлетворяют сформулированным требованиям.

Теперь рассмотрим вопрос построения дискретной интегральной оценки качества ДТПС, которая зависит от локальных дискретных агрегированных оценок, принимающих значения из интервала [0,K]. Обозначим через M_j и E_j- соответственно частную оценку качества ДТПС по j-му КК и его нормативный уровень, измеренные в рангах или баллах. По аналогии с величиной d_j (см. формулу (2.1)) рассмотрим величину [Рекс Л.М., Умывакин В.М., 1982. - с. 86-90.]:

D_j=[E_j(K-M_j)]/[M_j(K-E_j)]. (2.14)

Очевидно, что D_J[0,K] при M_jE_j, где  - знак принадлежности.

Введем следующие требования:

1) D(D₁,D₂,...,D_M)[0,K] при D₁,D₂,...,D_M[0,K];

2) D(0,0,...,0)=0, D(K,K,...,K)=K_.

Если все частные оценки Dj удовлетворяют условиям коммутативности и ассоциативности, то в этом случае из теоремы 2.1 следует, что =1, =-1/K, а интегральная оценка качества принимает вид [34]:

D=K[1- 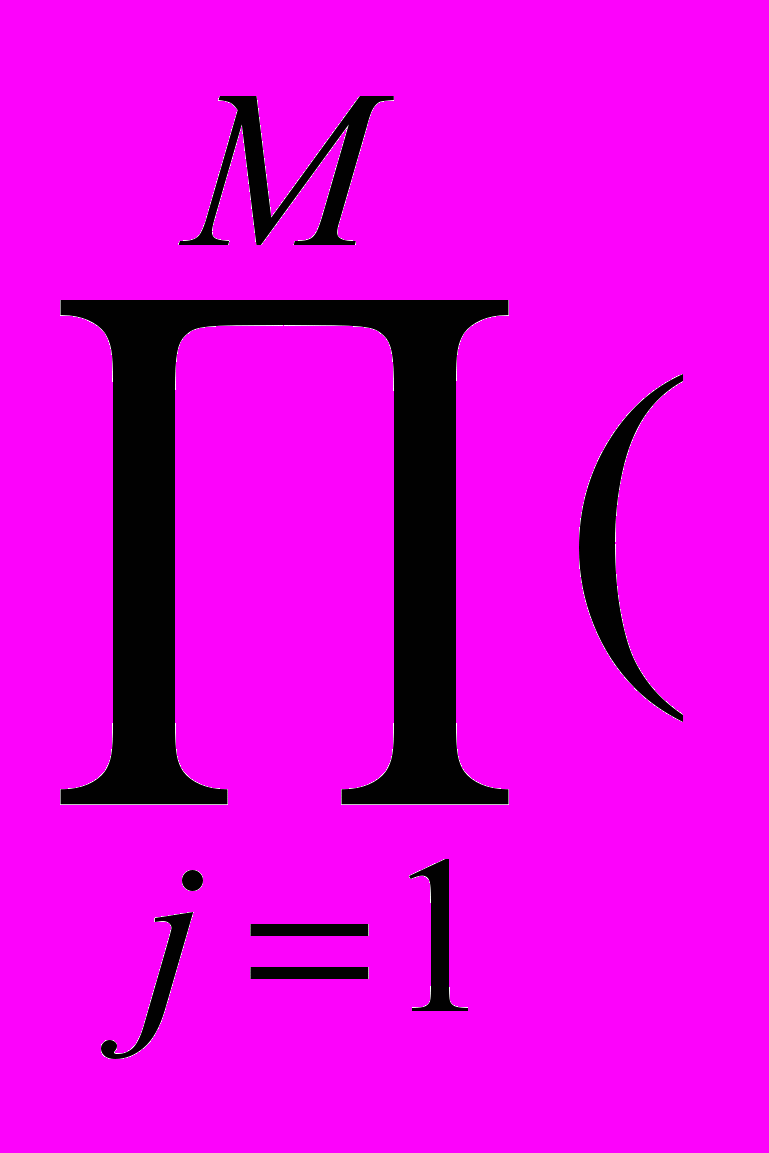1-D_j/K)]. (2.15)


2.3. Методическое обеспечение задач построения интегральных оценок качества ДТПС


Рассмотрим методику расчета нормативных интегральных оценок качества ДТПС типа "минимальный обобщенный риск" в соответствии со схемой на рис. 2.2. Пусть имеется некоторая совокупность (множество) из N ранжируемых вариантов ДТПС. Будем считать, что первичная информация о качестве ДТПС представлена в виде матрицы исходных природно-хозяйственных данных Y=||y_jⁱ|| с N строками и M столбцами. Элемент матрицы y_jⁱ является значением j-го частного КК i-го варианта ДТПС, j=1,2,...,M; i=1,2,...,N. Требуется:

1) перейти от натуральных значений y_jⁱ частных КК к соответствующим безразмерным относительным частным оценкам качества d_jⁱ по j-му КК i-го варианта ДТПС;

2) построить интегральную оценку качества dⁱ типа "обобщенная трудность" ("обобщенный риск") i-го варианта и использовать ее для ранжирования анализируемых вариантов ДТПС.

Обозначим через y_j^* - предельно-допустимый уровень критерия, который характеризует нормативное требование к качеству ДТПС по j-му частному КК. Будем считать, что нормативное требование к качеству i-го варианта по j-му КК (критериальное ограничение) выполняется, если y_jⁱ,y_j^* , j=1,2,...,M.

При наличии противоречивости и неопределенности (нечеткости) в требованиях к качеству эколого-экономических решений критериальные ограничения целесообразно задавать с некоторым "запасом" - допустимым отклонением (уступкой) _j^*>0 , т.е. в виде: y_jⁱy_j^*+_j^*, j=1,2,...,M.

1. Разработка семантической модели задачи оценки качества 1.1. Определение основной цели оценки качества 1.2. Формирование перечня ранжируемых вариантов ДТПС 1.3. Построение иерархической структуры качества ДТПС 1.4. Определение набора КК вариантов ДТПС 1.5. Обоснование и описание шкал измерений КК

2. Построение интегральной оценки типа "риск недостижения требуемого качества" вариантов ДТПС 2.1. Построение матрицы исходных данных 2.2. Преобразование КК в частные оценки качества типа "риск" 2.2.1. Определение диапазонов изменения КК 2.2.2. Определение нормативных уровней КК и допустимых отклонений 2.2.3. Расчет частных оценок качества вариантов ДТПС 2.3. Определение весовых коэффициентов частных оценок качества 2.4. Построение/пересчет интегральных оценок качества вариантов ДТПС 2.4.1. Выделение Парето-оптимальных вариантов ДТПС 2.4.2. Расчет интегральных оценок качества типа "риск" 2.4.3. Ранжирование вариантов ДТПС по интегральным оценкам качества 2.4.4. Анализ и ранжирование вариантов ДТПС, не удовлетворяющих требованиям по некоторым КК