1. оценка деятельно техно природных систем

Вид материала

Документы

Содержание 3. Математические модели анализа и синтеза дтпс Объем поливных вод

Подобный материал:

• Кционировании техно-природных систем и другой антропогенной деятельности для последующего, 582.73kb.
• За курс 9 класса билет, 42.57kb.
• Организационный план 28 Оценка риска 32 Перечень рисков 34 Оценка рисков, 435kb.
• Проектирование логистических систем, 93.42kb.
• Виды природных ресурсов. Ресурсообеспеченность. Оценка ресурсообеспеченности страны, 42.68kb.
• Лекция № Методы количественного оценивания систем (продолжение) Оценка сложных систем, 156.28kb.
• Emergency Medicine Scott H. Plantz and J. N. Adler 1998. 780 p учебник, 44.15kb.
• План проспект новой книги, 114.81kb.
• Рабочей программы дисциплины «Основы цифровой схемотехники» по направлению подготовки, 23.13kb.
• Экономическая оценка природных ресурсов как фактор повышения инвестиционной привлекательности, 359.56kb.

Рис. 2.3. Основные этапы автоматизированной технологии построения интегральных оценок качества вариантов ДТПС


Для расчета частных оценок d_jⁱ трудности достижения требуемого качества ДТПС по j-му ПК для i-го варианта по формуле (2.3) необходимо знать значения безразмерных величин _jⁱ и _j, являющихся соответственно абсолютной оценкой качества и нормативным требованием.

Пусть для каждого КК заданы: 1) a_j и b_j - соответственно нижняя и верхняя граница диапазона изменения; 2) y_j^* и _j^*>0 - соответственно нормативный уровень и допустимое отклонение. Причем, a_jy_j^*+_j^*b_j;
3) весовые коэффициенты _j частных оценок качества.

Тогда можно, принять:

_jⁱ=(y_jⁱ-a_j)/(b_j-a_j), _j=(y_j^*+_j-a_j)/(b_j-a_j) (2.16)

или _jⁱ=(exp(-(y_jⁱ-a_j))-exp(-(b_j-a_j))/(1-exp(-(b_j-a_j)),

_j=(exp(-(y_j*+_j-a_j))-exp(-(b_j-a_j))/(1-exp(-(b_j-a_j)),

где >0 - некоторый априорно установленный параметр.

Очевидно, что 0_jⁱ1 при всех i и j, а 0_j1 при a_jy_j^*+^*_jb_j. Кроме того, если выполняются нормативные требования, т.е. если y_jⁱy_j^*+^*_j, то _jⁱ_j. Отметим, что формуле (2.16) соответствует линейная замена переменных: _jⁱ=p_jy_jⁱ+q_j, _j=p_j(y_j^*+_j)+q_j. При этом коэффициенты p_j и q_j определяются из условия: _j^max=p_ja_j+q_j=1, _j^min=p_jb_j+q_j=0.

Чтобы определить диапазоны изменения и задать нормативные уровни для каждого критерия, перейдем от матрицы данных Y к матрице Y*, в которой значения j-го КК расположены в порядке возрастания (ухудшения качества) сверху вниз: y_jⁱ¹y_jⁱ²...y_j^iN, j=1,2,...,M, т.е. представлены в виде вариационных рядов. Тогда первая строка матрицы Y* будет описывать некоторый "идеальный" вариант ДТПС, имеющий наилучшие значения по всем КК. В ее последней строке будут расположены наихудшие значения частных КК. В результате анализа каждого столбца матрицы Y* (спектра значений каждого КК) устанавливаются диапазоны изменения [a_j,b_j] и нормативные уровни y_j*. При этом в качестве советующей информации для экспертов могут быть использованы описательные (дескриптивные) статистики, определенные на основе матрицы исходных данных Y. В частности, a_j=y_j^min, b_j=y_j^max, но может быть сделан и выбор a_jj^min, b_j>y_j^max. Здесь через y_j^min и y_j^max обозначены минимальное и максимальное значения j-го КК. Кроме того, для определения границ диапазонов изменения КК может быть использовано известное из математической статистики правило "трех сигм". Согласно этому правилу, для нормально распределенной случайной величины y_j с математическим ожиданиемy_j и стандартным (среднеквадратическим) отклонением _j в интервал с границамиa_j=y_j-3_j, b_j=y_j+3_j попадает около 99.7% значений j-го КК.

Рассмотрим методические вопросы построения интегральных критериев качества типа минимальный обобщенный риск" с учетом двух главных априорных требований к их виду - коммутативности (2.2.8) и ассоциативности (2.2.9). Требование коммутативности является довольно жестким и часто не выполняется на практике в силу неравнозначности частных КК с точки зрения экспертов. В результате, частные оценки качества также будут неравноценными. В этом случае для построения интегральных оценок качества ДТПС типа "риск" в соответствии с формулой (2.13) необходимо предварительно провести "выравнивание" частных оценок d_j, т.е. определить их веса _j. Причем, более важной считается оценка по частному КК, дающая при сравнении с оценкой по другому КК больший вклад в интегральную оценку качества ДТПС для одинаковых (при двух сравниваемых КК) значениях _j и _j. Для определения весовых коэффициентов _j рекомендуется использовать методы анализа иерархий и методы парных сравнений, описание которых приведено в разделе 3.1. настоящей работы.

Как отмечалось выше, требование ассоциативности частных оценок означает их принадлежность одному уровню иерархической структуры «Качество ДТПС», т.е. отсутствие иерархических связей среди КК, объединяемых в интегральный критерий качества с учетом их относительной важности. Если, например, в перечне КК есть критерии, характеризующие свойства ДТПС в целом, то аналогичные КК ее структурных компонентов в нем не должны содержаться. При наличии иерархии в совокупности частных КК, их агрегирование следует производить по иерархическим уровням, начиная с нижнего. На каждом уровне иерархии требуется осуществлять свое взвешивание частных оценок качества.

Следовательно, для построения интегральной оценки качества ДТПС типа "обобщенный риск" необходимо, чтобы частные оценки d_j были взвешены по относительной важности и принадлежали к одному уровню иерархии ее оцениваемых свойств. Другими словами, если частные оценки являются равноценными и одноуровневыми, то интегральная оценка с необходимостью удовлетворяет требованиям ассоциативности и коммутативности.

Подчеркнем, что вариантам ДТПС с минимальными значениями dⁱ соответствует наиболее высокая степень выполнения требований к их качеству. Данная интегральная оценка обладает простым и естественным свойством Парето - доминирования, т.е. если i и l – номера вариантов ДТПС таких, что y_jⁱ  y_j^l для всех j = 1, 2,..., M и хотя бы для одного k-го ПК y_kⁱ < y_k^l, то dⁱ < d^l, 1 kM.

Таким образом, предложенная нормативная модель агрегированного критерия качества ДТПС типа "минимальный обобщенный риск" позволяет упорядочить (ранжировать) сравниваемые варианты по значениям интегральных оценок качества.

В проблемах комплексного мониторинга и управления земельными ресурсами важное место принадлежит сравнению интегральных оценок текущих состояний (вариантов) ДТПС на фоне их предыдущих ранжирований для выявления изменений эколого-хозяйственного состояния земель, происходящих под влиянием интенсивного антропогенного воздействия. В связи с этим, рассмотрим метод "пересчета" интегральных оценок качества, инвариантный к получению дополнительной информации о "новых" вариантах ДТПС. Инвариантность по отношению к изменению множества вариантов ДТПС означает, что новые варианты получают свою оценку в шкале, выработанной для их первоначального множества. Тем самым исключается пересчет всех интегральных оценок при расширении множества ранжируемых вариантов ДТПС, что придает этой оценке свойство адаптивности.

Пусть к заданному множеству из N "первоначальных" вариантов ДТПС, состояние которых характеризуется M критериями качества, добавилось некоторое число L "новых" вариантов с тем же набором КК (по наименованиям и количеству). При этом, возможно, установлены новые нижняя a'_j и верхняя b'_j границы диапазона изменения j-го КК и новые нормативные уровни y'_j^*. Будем считать, что для всех j: a'_ja_j и b_j'b_j, т.е. диапазоны изменения КК не уменьшились. В дальнейшем также предполагается, что весовые коэффициенты _j частных оценок качества не изменились. Требуется проранжировать совокупность всех N+L вариантов ДТПС, учитывая первоначальное упорядочение N исходных вариантов на основе интегральной оценки качества dⁱ, определяемой по формуле (2.13).

Таким образом, необходимо откорректировать (пересчитать) все значения величин _jⁱ, _j, d_jⁱ для новых границ диапазона изменения и новых нормативных уровней по каждому КК, чтобы "включить" добавленные варианты в первоначальное ранжирование. При этом алгоритм пересчета должен обеспечивать переход от ранжирования вариантов, полученного в условиях изменившейся исходной информации, к первоначальному ранжированию вариантов.

Сформулируем согласно работе [Рекс Л.М., Ростопшин Ю.А., Русинов П.С., Руссман И.Б., Умывакин В.М., 1999. - 48 с.] правила пересчета: _jⁱ'_jⁱ, _je'_j, d_jⁱd'_jⁱ, где штрихованные величины рассчитываются для новых интервала [a'_j,b'_j] и требований y'_j^* к качеству j-го КК. Эти правила заключаются в следующем: если в первоначальном ранжировании i-й вариант лучше l-го варианта (или они эквивалентны), т.е. dⁱd^l, то добавление любого числа новых вариантов (лучших или худших, чем сравниваемые i и l) не должно изменить уже полученное отношение предпочтительности (эквивалентности), т.е. d'ⁱd'^l. При этом важнейшую роль играют величины y'_j^*. При пересчете оценок dⁱ возможны следующие случаи:

1) y'_j^*y_jⁱj^l; (2.3.1)

2) y_jⁱj^*y_j^l; (2.3.2)

3) y_jⁱj^lj^*. (2.3.3)

Случаи (2.3.1) и (2.3.2) практического интереса не представляют, т.к. здесь оба или один вариант из сравнения выпадают: они становятся неприемлемыми по j-му КК (можно считать, что ранжирование не меняется). Поэтому рассмотрим случай (2.3.3), когда добавились "худшие" варианты и величина y'_j^* такова, что выполняются нормативные требования к качеству по j-му КК для вариантов i и l.

Можно показать [[Рекс Л.М., Ростопшин Ю.А., Русинов П.С., Руссман И.Б., Умывакин В.М., 1999. - 48 с.], что в этом случае первоначальное ранжирование вариантов ДТПС сохраняется. Более того, т.к. это ранжирование основано на вычислениях оценок d_jⁱ, то в их пересчете нет необходимости. Вновь добавленные варианты со значениями КК, удовлетворяющими нормативным ограничениям a'_jy'_jⁱ y'_j*b'_j, ранжируются обычным образом, т.е. на основе вычисления значений величин m'_jⁱ, '_j,d'_jⁱ и d'ⁱ, где j=1,2,...,M; i=N+1, N+2,...,N+L. Наконец, по величине d'ⁱ - чем меньше ее значение, тем выше интегральное качество ПХГС, производится ранжирование вновь добавленных вариантов, т.е. они расставляются среди первоначальных вариантов ДТПС по значениям интегральной оценки dⁱ. Это объясняется тем, что пересчет выполняется так, что частные оценки качества d_jⁱ остаются неизменными для исходного множества вариантов, а, значит, не изменяется и их интегральная оценка dⁱ.

На основе проведенных теоретических исследований и методических разработок создана автоматизированная система экспертного оценивания (АСЭО), предназначенная для построения интегральных оценок качества ДТПС и эколого-экономических решений по рациональному использованию и охране земель в регионе. Ее "ядром" является автоматизированная технология построения интегральной оценки качества вариантов ДТПС
(см. рис.2.2).

Таким образом, предложена методология построения оригинальных агрегированных (интегральных) оценок качества вариантов ДТПС, позволяющая осуществить их ранжирование (упорядочение) по степени выполнения требований к совокупности взаимосвязанных, неравнозначных и разнородных критериев качества эколого-экономических решений. Конструируемые интегральные оценки имеют содержательный смысл "трудности выполнения требований к качеству эколого-экономических решений" и могут трактоваться с вероятностной точки зрения как обобщенная мера экологического риска (опасности) социально-экономической деятельности в ДТПС.

3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ АНАЛИЗА И СИНТЕЗА ДТПС

3.1. Иерархическая структуризация и ранжирование геоданных


3.1.1. Формирование перечня существенных показателей качества геообъектов на основе метода анализа иерархий


Определение перечня существенных (релевантных) показателей качества сложных геообъектов и расчет числовых оценок их приоритета имеет большое значение для решения различных слабоструктурированных эколого-географических задач: комплексного природно-хозяйственного районирования территории; многомерной классификации объектов земельного фонда; интегральной оценки экологической опасности природно-антропогенных ландшафтов; многокритериального выбора наилучших вариантов комплекса мероприятий по борьбе с негативными последствиями антропогенного воздействия на окружающую природную среду и др. Четкая содержательная постановка таких задач, прежде всего, предполагает наличие двух списков релевантных элементов семантической модели геоданных: перечня анализируемых геообъектов и набора характеризующих их частных показателей качества (ПК). Для иерархической структуризации и ранжирования природно-хояйственных данных целесообразно применялись методы системного анализа и экспертных оценок [Модели в географии, под ред. Р.Дж. Чорли и П.Хаггета, 1971. - 380 с.].

Выделение релевантных ПК геообъектов начинается с построения семантической модели анализируемых геоданных. Ее элементы связаны друг с другом по смыслу (содержанию). Для описания элементов семантической модели природно-хозяйственных данных и их взаимосвязей будем использовать понятийные иерархические структуры иерархии типа деревьев [Рекс Л.М., Русинов П.С., Умывакин В.М.,1999. - 21 с.]. Их построение базируется на методе анализа иерархий Т.Саати. [Симонов Ю.Г., Симонова Т.Ю., Шмыков В.И. и др., 2002, с. 5 – 8.].

Предлагаемая автоматизированная методика иерархической структуризации природно-хозяйственных геосистем (ДТПС) включает следующие основные этапы: 1) – построение понятийной иерархической структуры ДТПС;
2) расчет числовых оценок приоритета и ранжирование элементов нижнего уровня иерархии (ПК); 3) формирование перечня существенных ПК.

В основе разработки иерархической структуры «Качество ДТПС» лежат две взаимосвязанные технологические операции: 1) определение уровней и элементов иерархии; 2) установление связей между элементами смежных уровней. Обе эти операции выполняются "сверху-вниз" (рис.3.1.).


Сначала формулируется укрупненное понятие, связанное с системным свойством (качеством) ДТПС - единственный элемент первого уровня иерархии. Затем это понятие расчленяется на некоторое число основных понятий (основных свойств системы) - элементов второго уровня. Каждое основное понятие также расчленяется на ряд более конкретных понятий (свойств) - элементов третьего уровня иерархии, которые можно представить в виде совокупности еще меньших по размеру элементов иерархии. Например, природно-хозяйственных факторов, влияющих на экологическое состояние земель). При этом процесс детализации (декомпозиции) элементов иерархии продолжается до тех пор, пока не будут получены факторы, представляющие собой измеряемые характеристики ДТПС, дальнейшее расчленение которых не имеет смысла в рамках решаемой проблемы анализа геоданных. Элементы нижнего уровня иерархии будем называть подфакторами или ПК.

Процесс построения иерархической структуры направлен на выявление и оценку внутренних связей элементов рассматриваемой иерархии. Декомпозиция может выполнятся на основе различных принципов, что в итоге приведет к различным иерархическим структурам. Взаимосвязи между элементами каждой пары соседних уровней иерархии описываются с помощью специальных таблиц (матриц смежности), строки которых соответствуют элементам "нижнего", а столбцы - элементам "верхнего" уровня. На пересечении i-го столбца и j-й строки матрицы смежности ставится "1", если имеется связь i-го элемента верхнего уровня и j-го элемента нижнего уровня иерархии, и "0"-в противном случае.

Каждый элемент иерархии природно-хозяйственных условий территории характеризуется некоторым приоритетом по отношению к общему, системному свойству ДТПС. Как правило, числовые оценки приоритета отражают долю влияния ее элементов на эколого-хозяйственное состояние земель (см. рис. 3.1.). Исходной информацией для их определения являются понятийная иерархическая структура и весовые коэффициенты (веса) связей элементов смежных уровней иерархии. Отметим, что каждый элемент иерархии, не принадлежащий к нижнему уровню, можно представить в виде некоторой "геосистемы", имеющей определенную структуру и интегративное свойство (качество). Весовые коэффициенты используются для оценки степени связи элементов определенного уровня иерархии ("подсистем") с элементами вышележащего уровня ("системами"), а числовые оценки приоритета - для оценки доли вклада элементов иерархии в качество "макросистемы" - единственного элемента верхнего уровня иерархии.

Пусть построена иерархия, фрагмент которой приведен на рис.3.1. Здесь А - качество (системное свойство) ДТПС; В_i - i-е основное свойство, i=1,2,...,N; C_j - j-й фактор, j=1,2,...,M; D_k - k-й показатель, k=1,2,...,L; b_i, g_j и d_k - числовые оценки приоритета соответственно i-го элемента второго уровня, j-го элемента третьего уровня и k-го элемента четвертого уровня иерархии; s_ji и t_kj - соответственно веса связей j-го элемента третьего уровня с i-м элементом второго уровня и k-го элемента четвертого уровня с j-м элементом третьего уровня иерархии.

Числовые оценки приоритета и относительные веса связей элементов иерархии должны удовлетворять условиям нормировки:

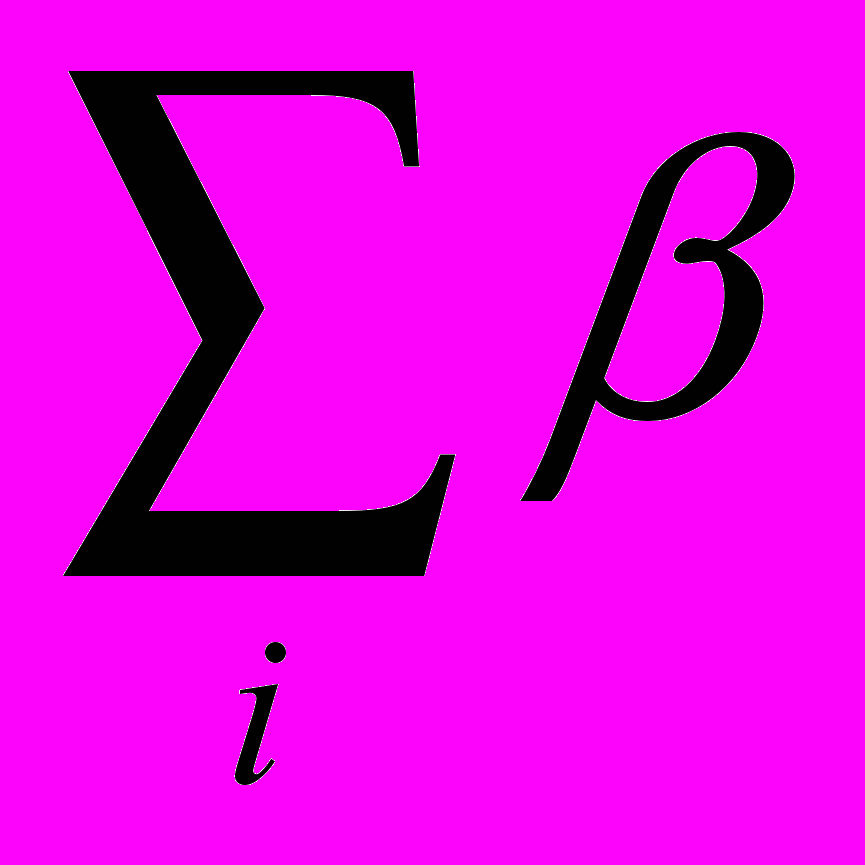_i=1, b_i0, i=1,2,...,N, 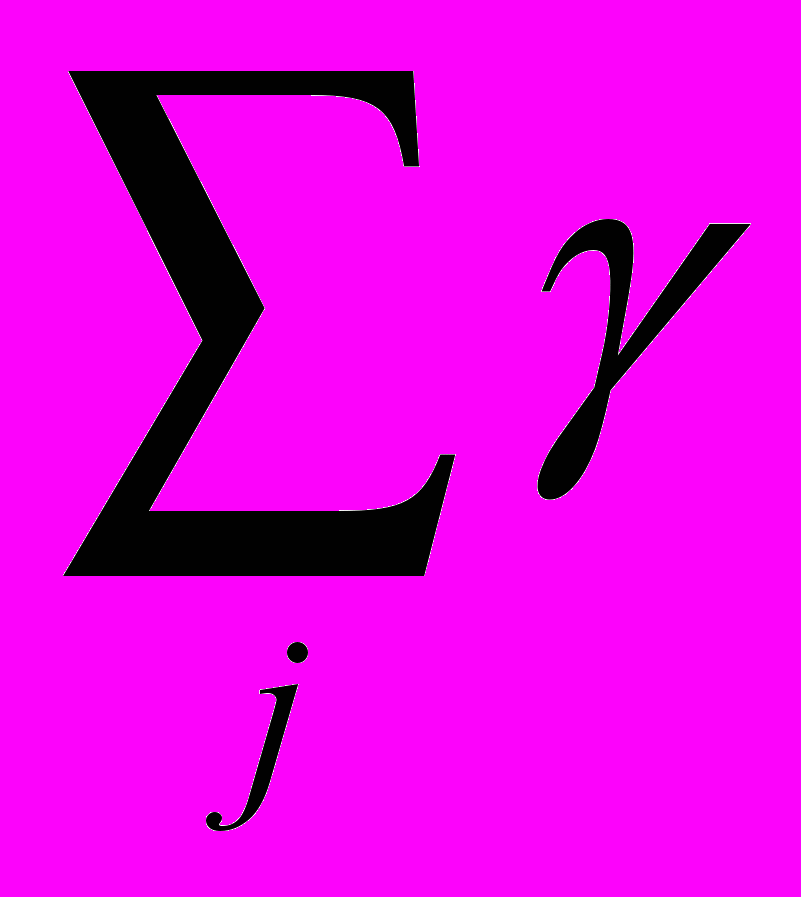_j=1, g_j0, j=1,2,...,M,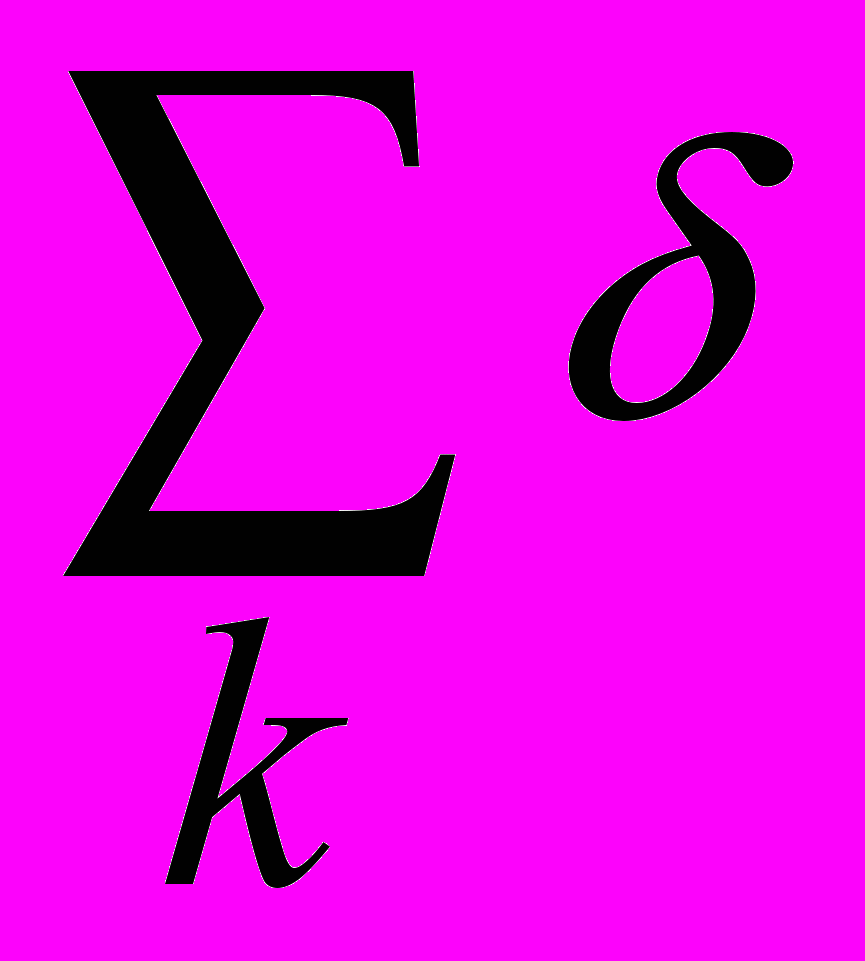_k=1, d_k0,k=1,2,...,L. (3.1)

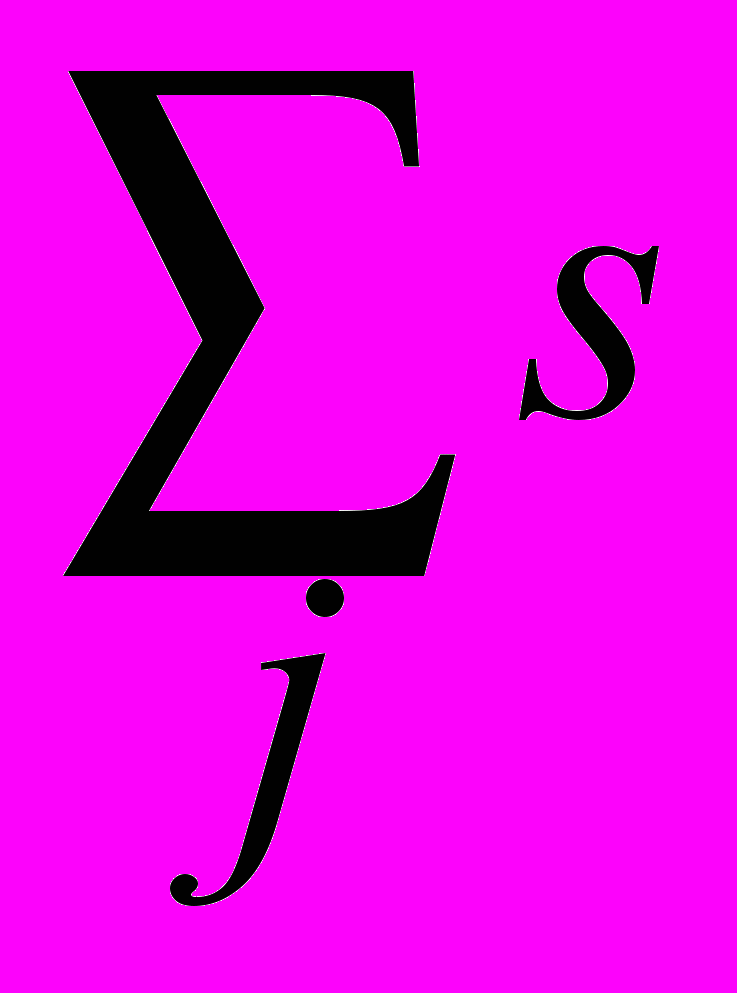_ji=1, s_ji0, j=1,2,...,M, i=1,2,...,N, 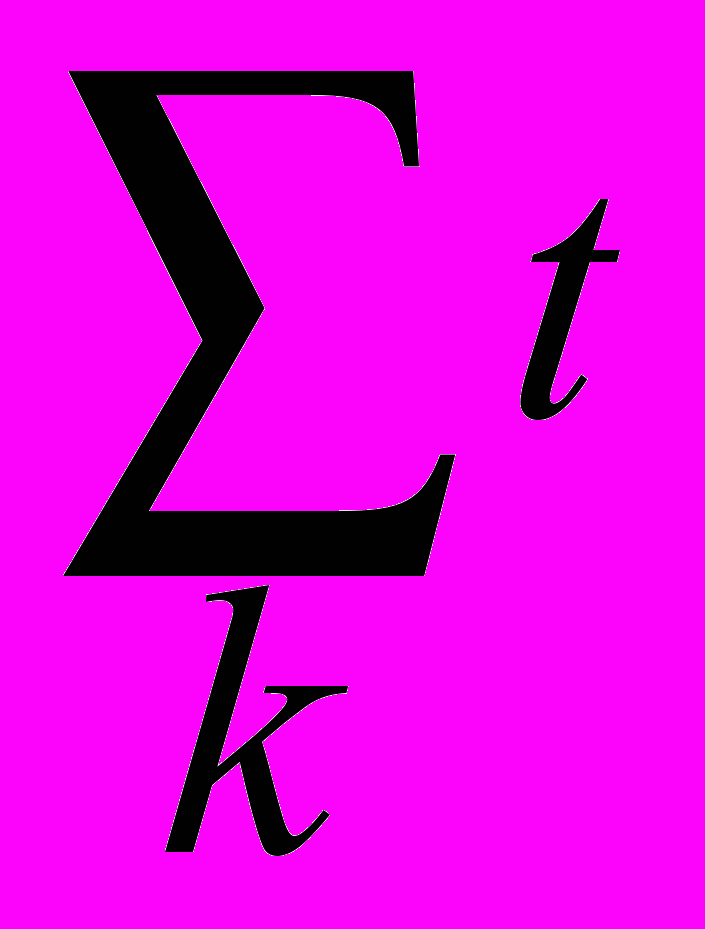_kj=1, t_kj0, k=1,2,...,L,j=1,2,...,M. (3.2)

Условия (3.1)-(3.2) следуют из того, что числовые оценки приоритета элементов каждого уровня иерархии характеризуют долю их вклада в оценку качества (в достижение цели "макросистемы"), а веса связей элементов смежных уровней - долю вклада подфакторов ("подсистем") в оценку факторов (достижение "целей системы"). Расчету числовых оценок приоритета предшествует технологическая операция определения весов связей элементов смежных уровней иерархии, которая выполняется "сверху-вниз". При наличии связей между элементами смежных уровней иерархии эти веса положительны, при их отсутствии - равны нулю. Рассмотрим два способа нахождения весовых связей на основе обработки экспертной информации. Если элементов иерархии (факторов, ПК) мало (3-5 штук), то эксперты могут указать их веса связей непосредственно в долях единицы на основе своего опыта и интуиции. Это значит, что указанные экспертом веса принимаются без их обоснования, т.е. от эксперта не требуют подкрепления своих оценок логическими рассуждениями или расчетами. При большом числе ранжируемых ПК непосредственные оценки экспертов весов связей элементов смежных уровней иерархии становятся недостаточно убедительными или их получение затруднительно. Поэтому определение весовых коэффициентов ПК предлагается осуществлять на основе специальных экспертных процедур - методов парных сравнений, удобного и надежного средства для решения задач ранжирования. Эти методы подробно рассмотрены в подразделе 3.1.2.

Расчет числовых оценок приоритета элементов иерархии ведется "сверху вниз". Приоритет элементов второго уровня b_j совпадает с относительными весами связей этих элементов с единственным элементом первого уровня иерархии и непосредственно характеризуют долю их вклада в понятие "качество" ДТПС. Приоритет элементов третьего и четвертого уровней иерархии вычисляются по формулам:

g_j = b_is_ji, d_k = g_jt_kj. (3.3)

При расчете числовых оценок приоритета по формуле (3.3) учитывается тот факт, что реальный эффект от влияния каждой подсистемы (подфактора) проявляется только в составе системы (фактора), в которую они включены. Отметим, что некоторые элементы иерархии, приведенной на рис.3.1., участвуют в формировании более чем одного элемента вышележащего уровня. Так, элемент D₂ характеризуется несколькими весами связей (а именно, t₂₁ и t₂₂), которые определяются независимо друг от друга. В данном случае числовые оценки приоритета показателей вычисляются по формуле:

d_k= 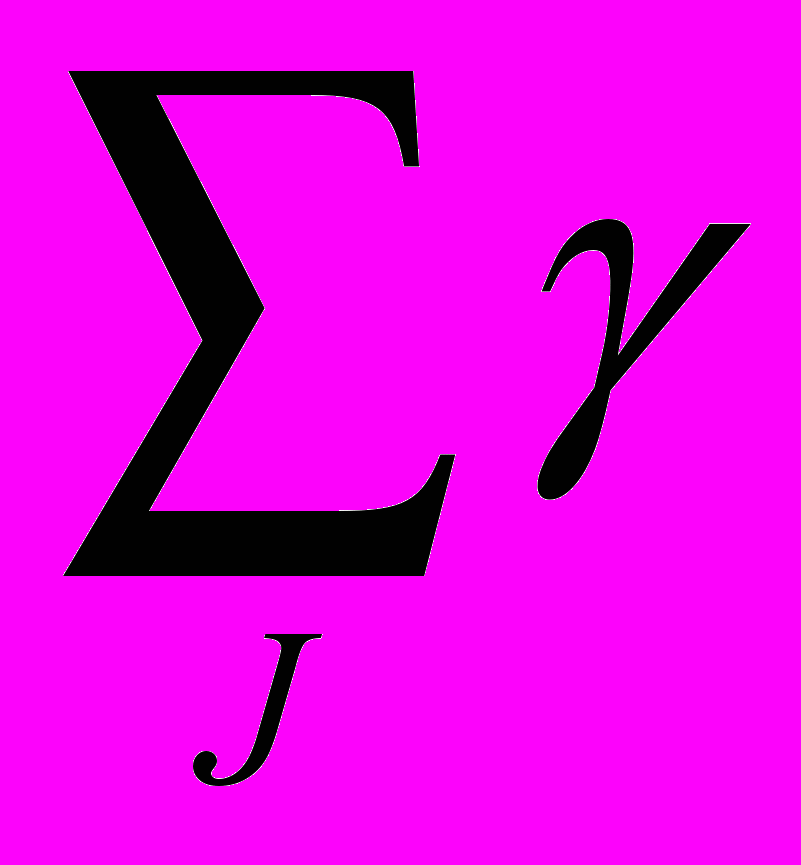_jt_kj, j=1,2,...,M, k=1,2,...,L (3.4)

После их расчета выделяются существенные ПК. При этом может быть использована следующая эвристическая процедура: 1) экспертами задается некоторый уровень важности d* из интервала [d^min,d^max]. Здесь d^min и d^max - соответственно минимальная и максимальная оценки приоритета ПК; 2) ПК включается в список существенных, если d_kd*; 3) осуществляется перенормировка числовых оценок приоритета

d^*_k=d_k/ 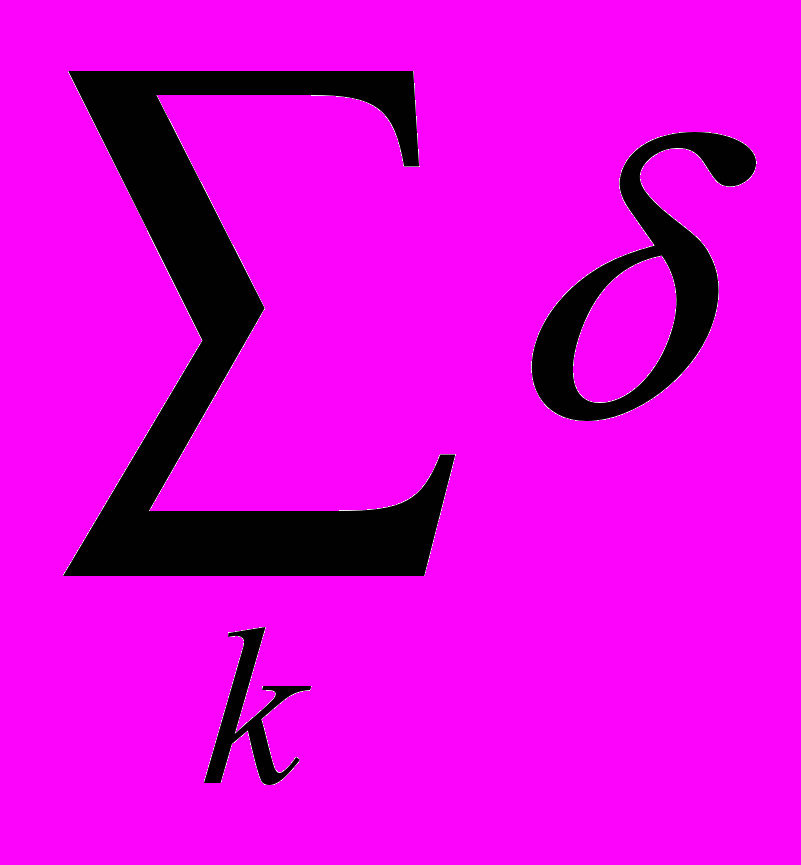_k, (3.5)

где суммирование ведется по индексам ПК, включенным в список существенных показателей.

На рис. 3.2. показана иерархическая структура эколого-мелиоративного состояния орошаемых земель, а в табл. 3.1. - список существенных природно-хозяйственных показателей (ПХП) и их оценки приоритета.


Рис. 3.2. Иерархическая структура водно-солевого баланса орошаемой территории.

Примечание: Указаны не все связи между элементами 4-го и 5-го уровне иерархии


3.1.2. Определение весовых коэффициентов показателей качества методами парных сравнений


В каждой конкретной ситуации анализа природно-хозяйственных данных показатели качества ДТПС имеют различную относительную важность (предпочтительность). В связи с этим возникает необходимость определения их весовых коэффициентов, которые позволяют осуществить ранжирование ПК – их упорядочение по мере убывания предпочтительности.


Таблица 3.1


Список существенных природно-хозяйственных показателей

Наименование ПХП (элемента последнего уровня иерархии)	Обозначение ПХП	Приоритет ПХП
Объем поливных вод	М	0.256
Уровень грунтовых вод	Н	0.188
Минерализация грунтовых вод	СГВ	0.078
Концентрация порового раствора	CWh	0.057
Минерализация поливных вод	CM	0.055
Начальная влажность почвы	Wh	0.051
Температура воздуха	T	0.050
Влагоемкость почвы	Вл	0.050
Относительная влажность воздуха	f	0.034
Глубина заложения дренажа	Нд	0.029
Атмосферные осадки	Х	0.028
Скорость ветра	V	0.022
КПД оросительной сети	КПД	0.020
Характеристика растительности	Р	0.020
Минерализация дренажного стока	СД	0.017
Абсолютная влажность воздуха	е	0.015
Радиационный баланс	R	0.015
Протяженность дренажной сети	Lд	0.014