1. оценка деятельно техно природных систем
| Вид материала | Документы |
- Кционировании техно-природных систем и другой антропогенной деятельности для последующего, 582.73kb.
- За курс 9 класса билет, 42.57kb.
- Организационный план 28 Оценка риска 32 Перечень рисков 34 Оценка рисков, 435kb.
- Проектирование логистических систем, 93.42kb.
- Виды природных ресурсов. Ресурсообеспеченность. Оценка ресурсообеспеченности страны, 42.68kb.
- Лекция № Методы количественного оценивания систем (продолжение) Оценка сложных систем, 156.28kb.
- Emergency Medicine Scott H. Plantz and J. N. Adler 1998. 780 p учебник, 44.15kb.
- План проспект новой книги, 114.81kb.
- Рабочей программы дисциплины «Основы цифровой схемотехники» по направлению подготовки, 23.13kb.
- Экономическая оценка природных ресурсов как фактор повышения инвестиционной привлекательности, 359.56kb.
Таблица 2.1
Виды допустимых преобразований показателей качества в различных шкалах измерений
| Тип шкалы | Вид допустимого преобразования | Основные свойства | ||
| Номинальная шкала | y'=f(y), где f – любая однозначная функция (преобразование) | Если y1 y2, то f(y1) f(y2) | ||
| Порядковая шкала. | y'=(y), где - любое монотонное преобразование | Если y1 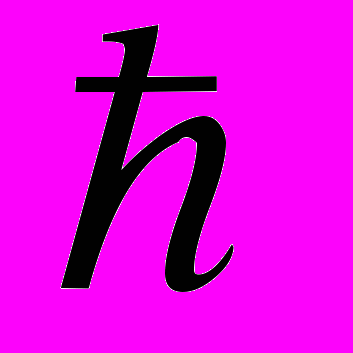 y2, то (y1)>(y2) y2, то (y1)>(y2) | ||
| Интервальная шкала | y'=by+a , где a,b=const; a>0,b-0 (линейное преобразование) | y'1 – y'2 | = | y1 – y'2 |
| y  '3 – y'4 '3 – y'4 | y  3 – y4 3 – y4 | |||
| Шкала разностей | y'=y+a, где a=const; a0 (преобразование сдвига) | y'1-y'2=y1-y2 | ||
| Шкала отношений | y'=by, где b=const; b0 (преобразование подобия) | y'1 y  '2 '2 | = | y1 y  2 2 |
Примечания: y и y' - соответственно исходный и преобразованный показатели; y1,y2,y3,y4 и y'1,y'2,y'3,y'4 - соответственно различные значения показателей y и y';
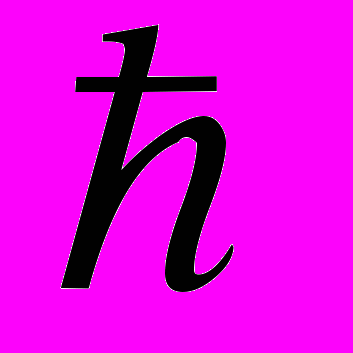 - знак отношения предпочтительности.
- знак отношения предпочтительности.Номинальные ПК, или признаки измеримые в номинальной шкале, (например, "морфогенетический тип почвы") позволяют классифицировать анализируемые геообъекты, т.е. разбивать их на однородные группы (районы, типы, классы, таксоны, кластеры). Их значениями являются имена определенных групп (например, "черноземы обыкновенные") из фиксированного списка, т.е. все объекты, отнесенные к одной группе, получают одинаковые наименования. Таким образом, номинальные шкалы по существу качественны. Произвести измерение ПК в данной шкале - это значит использовать число лишь для обозначения и выделения групп (классификации) геообъектов. Допустимым способом сопоставления и обработки результатов измерения в номинальной шкале является операция "отождествление - различение", а допустимым преобразованием - любая взаимно - однозначная функция (см. табл. 2.1).
Ранговые ПК, или признаки измеримые в ранговой шкале, (например, "степень засоления почв") дают возможность выделять группы геообъектов, упорядоченные по рангам - значениям ПК, описывающим степень проявления (выраженности) некоторого общего свойства геообъектов в различных группах. Обозначения групп должны соответствовать их рангу (например, ранг 1 - "незасоленные почвы", ранг 2 - "слабозасоленные почвы" и т.д.) Таким образом, ранговые оценки необязательно должны быть числами, хотя и могут иметь соответствующие числовые эквиваленты. Ранговые ПК значительно информативнее номинальных признаков, т.к. позволяют сравнивать геообъекты по отношению "лучше-хуже". В этом случае анализируемые объекты могут быть проранжированы (упорядочены), т.е. расположены в некотором порядке относительно одного общего свойства (например, "оврагоопасность почв"). Геообъекты, отображенные на ранговую шкалу, должны быть сравнимы между собой и транзитивны по общему свойству, т.е. ранговые оценки имеет смысл сравнивать между собой по принципу "больше-меньше". Следовательно, в порядковой шкале можно определить лишь отношение "предпочтительности" объектов по общему свойству, но нельзя ответить на вопросы "На сколько или во сколько один объект лучше другого?". При этом арифметические операции исключаются, т.к. объекты на ранговых шкалах (значения порядковых ПК) не обязательно расположены равномерно. Ранговые шкалы допускают те же статистические операции, что и номинальные шкалы, т.е. вычисление частот и мод, а также вычисление медианы. Кроме того, в порядковой шкале можно вычислять коэффициент ранговой корреляции [Кендэл М., 1975. - 216 с], который характеризует степень близости ранжирований (упорядочений) объектов (тесноту связи между порядковыми ПК). Допустимым преобразованием в шкале порядка является любая монотонно-возрастающая непрерывная функция (см. табл. 2.1.).
Таким образом, значения ПК геообъектов в номинальной и ранговой шкалах, вообще говоря, не являются числами. Они связаны либо с неупорядоченными (для номинальных ПК), либо с упорядоченными (для ранговых ПК) типологическими группировками (типилогизациями) геообъектов [Елисеева И.И., Рукавишников В.О., 1977.–144с]. При этом каждая группа (тип) содержит геообъекты с одинаковыми значениями ПК.
К количественным (метрическим) шкалам относятся интервальная шкала и шкала отношений (пропорциональная шкала). Количественные ПК позволяют численно измерить степень проявления анализируемого свойства геообъектов. Их значениям соответствуют действительные числа - точки на вещественной оси соответствующего ПК.
С помощью ПК, измеренных в шкале интервалов (например, показателя "температура почвы по Цельсию") появляется возможность не только классифицировать и ранжировать геообъекты, но и более точно описать отличие свойств одних геообъектов от других в результате определения разности (интервала) между соответствующими значениями этих ПК. Другими словами, ответить на вопрос: "На сколько сравниваемые значения ПК больше (меньше) друг друга?".
В шкалах интервалов нельзя применять ни одно из основных арифметических действий, т.к. вычитание, умножение и деление есть частные случаи сложения. В ряде случаев для интервальной шкалы устанавливают единицу измерения и произвольную (искусственную) точку отсчета (например, нуль для температуры по Цельсию), что позволяет рассматривать разности как абсолютные величины, обладающие свойством аддитивности. При этом оцениваемое свойство может не исчезать в результате измерения, равном нулю, а количественное выражение разности (интервала) между значениями ПК определяется масштабом измерения. В шкале интервалов нельзя корректно применять ни одно из основных арифметических действий. Здесь сохраняются все статистические операции, имеющие смысл в шкалах наименований и порядка. Дополнительно можно вычислять меры положения "центра" данных - математическое ожидание и модуль, а также другие статистические характеристики - стандартное отклонение, коэффициент асимметрии и смешанные моменты. Допустимыми преобразованиями в шкале интервалов являются положительные линейные преобразования - растяжения (см. табл.2.1.). В связи с этим, шкалу разностей (при b=1) можно рассматривать, как частный случай интервальной шкалы.
Признаки, измеримые в шкале отношений или пропорциональной шкале (например, показатель "уровень грунтовых вод") отличаются тем, что для них можно указать абсолютный нуль. Это позволяет определить во сколько раз одно значение ПК геообъектов больше (меньше) другого значения. Шкала отношений может рассматриваться как частный случай интервальной шкалы, при котором нулевая точка указывает на отсутствие измеряемого свойства - нуль шкалы отношений реален. Она обладает всем свойствами более слабых шкал (номинальной, ранговой и интервальной), а также важным свойством аддитивности. При этом изменение шкалы не изменяет отношения результатов одного измерения к другому, т.е. в качестве допустимого преобразования принимается преобразование подобия (см. табл.2.1.) - частный случай линейного преобразования при a=0. Таким образом, шкала отношений является дальнейшим развитием ранговой шкалы. Для шкал отношений разрешаются все арифметические операции над измерениями, включая извлечение корня, возведение в степень и логарифмирование. Для этих шкал допустимы любые статистические операции.
Промежуточное положение между ранговыми и количественными ПК занимают признаки, измеримые в балльных шкалах (например, показатель "бонитет почв"). Наибольшее распространение балльные оценки (баллы) получили в методах экспертных оценок [Литвак Б.Г., 1984. - 184 с.]. Баллы – ранговые оценки полезности (ценности) геообъектов, позволяют отобразить пропущенные ранговые позиции. Назначение баллов производится путем указания чисел (не обязательно целых) в некотором интервале, например, [1,10] или [0,100]. Балльные оценки всегда субъективны.
Балльные шкалы также используются в том случае, когда геоданные, измеренные в различных шкалах, необходимо привести к одному виду. Обработку балльных оценок можно производить двумя способами: либо представляя их в порядковой шкале, либо рассматривая как количественные. Ранговая шкала и балловые оценки играют существенную роль при построении эколого-хозяйственных оценок качества земельных ресурсов, т.к. позволяют произвести ранжирование различных состояний и/или вариантов развития ДТПС.
Среди методов измерения (определения значений) ПК можно выделить:
1) экспериментальные, предусматривающие непосредственное измерение (наблюдение) характеристик явлений или процессов, протекающих на геообъектах. Эти методы применяются в основном для определения значений ПК, имеющих определенную размерность;
2) расчетные, в которых искомые значения одних ПК (функций) вычисляются по определенным формулам (алгоритмам), где в качестве параметров (аргументов) выступают измеренные ранее другие характеристики геообъектов;
3) экспертных оценок, основанные на учете и обработке мнений компетентных специалистов (экспертов) о свойствах геообъектов. При серьезном и тщательном проведении экспертных процедур можно получить результаты, вполне удовлетворяющие потребностям практики.
Одна из основных проблем измерения качества геообъектов - это учет ошибок и оценка достоверности и валидности в количественных методах измерений. В ГОСТ Р ИСО 9000-2001 введен термин "валидация", который определяется как "подтверждение на основе представления объективных свидетельств (данных, подтверждающих наличие или истинность чего-либо) того, что требования (потребности или ожидания, которое установлено, обычно предполагается или является обязательным), предназначенные для конкретного использования или применения, выполнены".
Под ошибкой понимаются данные, не дающие точного представления об анализируемых геообъектах. Можно выделить несколько типичных факторов, способствующих появлению ошибок:
1) фактическая ошибка при измерении ПК - имеет место неисправность приборов наблюдения; плохо составлена анкета, неправильно записана информация и т.п.;
2) ошибка изменения - за время анализа и обработки информации произошло изменение состояния геообъекта или мнения экспертов;
3) ошибка при переходе от качественной (нечисловой) характеристики геообъекта к ее количественному выражению.
Это происходит тогда, когда сильно преувеличивают точность количественной информации, забывая, что приписывание количества нечисловой характеристике (операция квантификации) всегда лишь второй этап, существенно зависящий от первого - правильного выбора и интерпретации нечисловых характеристик. Если ошибки проанализированы и по возможности выявлены, то наступает очередь для анализа каждой процедуры измерения в отдельности. Прежде всего следует оценить ее достоверность. Под достоверностью понимается совпадение фактических данных различных наблюдателей в отношении одного и того же объекта. Наличие достоверности в определенном смысле гарантирует точность результата. Но одной достоверности измерения явно недостаточно. Можно достоверно измерять нечто, иметь инструмент (прибор, метод, эксперта) для этого измерения, но сам этот инструмент не пригоден для получения данных, необходимых для описания исследуемого понятия. Так, например, безукоризненно работающие весы не могут помочь нам при определении площади геообъекта.
Говорят, что инструмент (прибор, метод, эксперт) валиден, если он измеряет именно объект наблюдения. С эмпирической точки зрения валидность инструмента оценивается по точности предсказания поведения объекта в ситуациях, в которых участвует измеряемая характеристика. Валидность выявляется значительно сложнее (и труднее интерпретируется), чем достоверность. Она связывает полученные результаты и изучаемую действительность. Если достоверность подразумевает постоянство качеств инструмента, регулярность его использования и направлена на истинность в совпадении результатов, полученных разными исследователями, то валидность подразумевает точность результата относительно искомой цели, соответствие действительности. Оценка достоверности может быть получена с использованием методов математической статистики и анализа данных. Что касается валидности, то способность инструмента измерять объект измерения подразумевает наличие некоторого внешнего критерия и процедуры установления корреляции между непосредственным измерением и заданным критерием (эталоном). Точность и валидность неотделимы от целей мониторинга и управления земельными ресурсами и в каждом случае должны устанавливаться конкретно.
2.1.2. Основные принципы оценки качества геосистем в ранговой шкале
Нечисловые шкалы измерений ПК геообъектов называются также слабыми, а все количественные шкалы - сильными. Действительно, при движении по табл. 2.1 снизу вверх появляется все больше "свободы" в классе допустимых преобразований, отличие геообъектов друг от друга становится все менее определенным, результаты сравнения все более расплывчатыми (нечеткими). Вместе с тем ослабляются (и это самое существенное обстоятельство) требования к типу и точности исходных геоданных, позволяющих производить измерение в данной шкале. Например, для шкалы разностей допустим лишь произвольный выбор начала отсчета. Для номинальной шкалы неразличимыми будут любые объекты, попавшие в одну (произвольно сформированную по каким-либо соображениям) группу. В частности, те геообъекты, которые считаются экспертами похожими друг на друга или являются близкими к некоторому эталону (типичному представителю) группы.
Отметим, существенное для целей эколого-географических исследований усиление порядковой шкалы - шкалу баллов. Пусть три геообъекта сравниваются по качеству (ценности) от лучшего к худшему и ряд имеет вид: 1,2,3. Тогда геообъект 1 имеет высший ранг, 2 - следующий, а 3 - наименьший. Порядковая оценка качества геообъектов может быть получена различными способами. Например, так: для 1 - ранг 3, для 2- 2, для 3 - 1. Для этих же геообъектов можно в качестве рангов использовать значения какого-либо ПК в баллах и тогда геообъект 1 может иметь оценку 5, 2 - 3, а 3 - 2. Полученные баллы, как и в предыдущем случае, лишь порядковая оценка полезности (ценности) геообъектов, но с помощью баллов можно изображать пропущенные ранговые позиции. Это делает шкалу баллов (внутри типа порядковых шкал) более сильной, чем ранговая.
Характер геоданных и специфика анализируемых объектов чаще всего определяют тип шкалы измерения их ПК. Отметим лишь некоторые особенности таких геообъектов и способов измерения ПК:
1) сам геообъект часто бывает нечетко задан, размыты границы, отделяющие его от других. Отдельные составляющие принадлежат геообъекту в некоторой степени;
2) отсутствуют приборы (в физическом смысле), позволяющие производить необходимые измерения ПК геообъекта;
3) чаще всего используется заведомо неполный перечень ПК, описывающих качество геообъекта;
4) результаты измерений часто представляют собой экспертные суждения (оценки), что вносит субъективный фактор в процесс исследования;
5) если даже частные ПК измерены в сильной шкале, то вывод, общее суждение о качестве геообъекта, обычно должно носить лишь порядковый или номинальный (классификационный) характер.
Отметим, что регулярный способ перехода от количественных шкал к ранговой шкале связан с употреблением терминов нормативной оценки - большая, малая, средняя величина, соотносящих значение ПК с заранее определенной нормой.
Из всего вышесказанного можно сделать общий вывод: порядковая шкала (с разновидностями) обладает определенными преимуществами в эколого-географических исследованиях проблемы комплексного мониторинга, контроля и управления земельными ресурсами и, поэтому, процедуры формирования интегральных оценок качества геообъектов следует ориентировать на выработку ранговой шкалы ценности.
2.1.3. Нечеткие множества и проблема оценки качества земельных ресурсов
Как известно [Прангишвили И.В., Абрамова Н.А., Спиридонов В.Ф. и др., 1999. - 284 с.], системный анализ предназначен для решения слабоструктуризованных проблем, в которых доминируют качественная (нечисловая) информация, полнота исходных данных и наличие разного рода неопределенностей. Неопределенности могут быть результатом воздействия (обусловлены воздействием) большого числа природных и антропогенных факторов, детальный учет и анализ которых просто невозможен. Различают [Беллман Р., Заде Л., 1976. - С.172-215.] два основных вида неопределенностей, порожденные неточностью (imprecision) описания целей, ограничений и последствий возможных действий по управлению рациональным природопользованием и охраной окружающей среды: случайность (randomness), имеющая вероятностную природу, и нечеткость или расплывчатость (fuzziness). Например, рандомизация (случайность) может быть использована в задачах выбора наилучших вариантов социально-экономической деятельности при наличии неопределенности в выборе целей, противоречащих друг другу. Под расплывчатостью понимается тот вид неопределенности, который связан с теорией нечетких множеств [Беллман Р., Заде Л., 1976. - С.172-215; Орловский С.А., 1981. - 206 с.]. Ее основатель Л. Заде [Zadeh L.A., 1965. - P.338-353] нечеткими множествами называет классы (некоторые подмножества всего множества) элементов (геообъектов), "в которых нельзя указать резкую границу, отделяющую элементы, принадлежащие к данному классу, и элементы, не принадлежащие к нему" [Беллман Р., Заде Л., 1976., с.172-173]. Нечетким множеством является класс эродированных земель. В этой же работе подчеркивается различие между случайностью и нечеткостью: "случайность связана с неопределенностью, касающейся принадлежности или непринадлежности некоторого объекта к нерасплывчатому множеству. Понятие же расплывчатости относится к классам, в которых могут иметься различные градации степени принадлежности, промежуточные между полной принадлежностью и непринадлежностью объектов к данному классу" [Беллман Р., Заде Л., 1976., с.173]. Напомним, что под классическим ("четким") множеством понимается обычное множество с "четкой" характеристической фукцией, описывающей лишь принадлежность элементов множеству на бинарном (альтернативном) языке – языке "да" (1) и "нет" (0). В основе определения нечеткого множества лежит представление о том, что элементы произвольного класса, обладающие некоторым общим свойством (признаком), могут обладать им в различной мере, т.е. принадлежать этому классу в различной степени. Поэтому здесь используется "нечеткая" характеристическая функция (функции принадлежности), позволяющая измерить степень принадлежности элемента заданному "расплывчатому" множеству. Ее значениями являются числа из интервала [0,1]. По определению, F есть нечеткое множество в (исходном множестве объектов), если задана совокупность пар вида (,F()), где ,, а F() - функция принадлежности нечеткого множества F. (Здесь - знак принадлежности элемента множеству ). Для каждого элемента число F() называется степенью принадлежности этого элемента нечеткому множеству F. Таким образом, достигается возможность использования нечисловой информации в различных формальных процедурах (схемах) некоторым единообразным (универсальным) способом. Для нечетких множеств можно предложить естественные обобщения всех стандартных операций над обычными (классическими) множествами - объединение, пересечение, разность и т.д. Кроме них, вводятся некоторые специальные операции - концентрация, выпуклая комбинация и др. [Орловский С.А., 1981. - 206 с.].
Опишем проблему оценки качества ДТПС в ранговой шкале на языке теории нечетких множеств.
Приведем определение центрального для нашей работы понятия - "оценка качества" ДТПС (в частных случаях, "оценка эколого-хозяйственного состояния земельных ресурсов" и "оценка экологической опасности земель"). Рассмотрим две величины: 1) =F() - абсолютную оценку качества ДТПС, где - F() функция принадлежности состояния к нечеткому множеству F; 2) - характеристику нечеткости, с помощью которой можно оценить возможность достижения удовлетворительного состояния ДТПС, когда F() (01). Следовательно, можно однозначно выделить класс F() состояний, абсолютная оценка качества которых превышает заданный предельно-допустимый (нормативный) уровень качества . Аналогичным образом можно описать и процесс достижения цели рационального землепользования в ДТПС: цель считается достигнутой, если выполнены нормативные требования к качеству результата (варианту реализации ДТПС). Введенные в рассмотрение величины и для каждого частного ПК геосистемы в дальнейшем "объединяются" в частной относительной оценке. Затем эти оценки агрегируются в единую интегральную оценку качества, отражающую трудность достижения требуемого качества геосистемы или трудность достижения цели планируемой социально-экономической деятельности по оптимизации природно-антропогенных ландшафтов.
2.2. Нормативный подход к построению интегральных оценок качества ДТПС
2.2.1. Формирование частных эколого-хозяйственных оценок земельных ресурсов. Их геометрическая, вероятностная и информационная интерпретация
Чтобы сравнить между собой различные состояния (варианты развития) ПХГС, нужно иметь возможность оценки степени реализации их отдельных (частных) свойств, т.е. иметь оценки качества ДТПС по частным критериям (относительные частные оценки качества). Рассмотрим способ построения частной оценки dj трудности достижения (риска недостижения) требуемого качества ДТПС по j-му критерию качества (КК), которая может рассматриваться как относительная оценка некачественности отдельного свойства системы с учетом нормативных требований, предъявляемых к этому свойству (оценка несоответствия отдельного свойства системы определенным нормативным требованиям, предъявляемым к этому свойству).
Обозначим через yji - значение натурального j-го КК для i-го состояния (варианта), а через yj* - заданный нормативный уровень качества j-го КК для всех анализируемых вариантов ДТПС. Поставим им в соответствие две величины: ji=j(yji) - некоторую безразмерную характеристику достигнутого качества по j-му КК для i-го варианта, и j=j(y*j) - соответствующий безразмерный норматив качества. Будем считать, что 0ji, j1, j=1,2,...,M; i=1,2,...N. При этом нормативное требование к качеству ДТПС по j-му КК для i-го варианта выполнено, если jj.
Разнообразие ("спектр") значений КК может быть представлено как нечеткое множество с заданной функцией принадлежности j=j(yj). Обозначим через j - порог принадлежности множеству наилучших вариантов по j-му КК. Таким образом, функция принадлежности j фактически характеризует достигнутый уровень качества, а величина j - определяет пороговые (предельно-допустимые, нормативные) требования к наилучшим по качеству вариантам ПХГС с точки зрения j-го КК. Причем, значению j=1 соответствует "идеальное" качество, а значению j=0 - предельно низкое качество ДТПС по j-му КК. Поэтому величину ji будем называть абсолютной оценкой качества i-го варианта ДТПС по j-му КК.
Для сопоставления безразмерных характеристик j и j в относительной частной оценке качества введем и формализуем понятие "трудность достижения" ("риск недостижения") требуемого качества ДТПС по j-му КК. Очевидно, что частная оценка качества dji i-го варианта ДТПС по j-му КК, как функция величин j и ji, должна удовлетворять следующим условиям:
1) 0dji1 при jij; (2.2.1)
2) dji=0 при j=0, ji>0 (2.2.2)
(риск минимален, если нет никаких требований к качеству вариантов);
3) dji=0 при ji=1 и ji>j (2.2.3)
(риск минимален при предельно возможном качестве независимо от требований);
4) dji=1 при ji=j0 (2.2.4)
(трудность, риск максимальны при предельно низком допустимом качестве).
Таким образом, частная трудность (риск) dji является относительной оценкой некачественности i-го варианта ДТПС по j-му КК и может быть интерпретирована как мера несоответствия достигнутого качества вариантов ji и предъявляемого к их качеству требования - нормативного уровня j.
Покажем, что при j ij этим условиям удовлетворяет единственная функция "трудности" вида:
dji=[j(1-ji)]/[ji(1-j)]. (2.1)
Рассмотрим "геометрическое" обоснование формулы (2.1). Рассмотрим на прямой отрезок AD с двумя внутренними точками В и С (рис. 2.2).
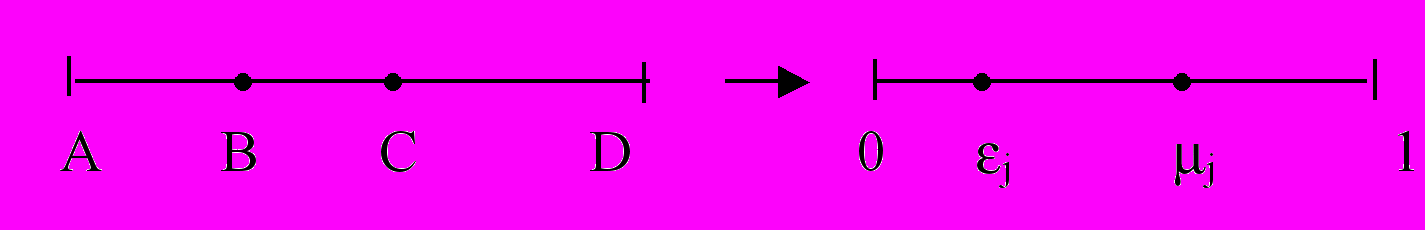
Рис. 2.2. Геометрическая интерпретация частных оценок качества типа "трудность"
Для четырех точек A, B, C, D определяется величина: =[АВ/BD]/[CD/AC]. Из проективной геометрии известно, что это есть так называемое двойное или ангармоническое отношение (отношение отношений) четырех точек на прямой. Если перейти к внутренней координате отрезка: А0, Bj, Cjj, D1, то получим формулу для расчета частной оценки качества dj, т.к.:
=[j/(1-j)]/[(1-j)/j]=[j(1-j)]/[j(1-j]=dj.
Важнейшее свойство двойного отношения состоит в том, что оно является инвариантом проективного преобразования. В проективной геометрии построены аналоги двойного отношения для прямых, плоскостей, углов и т. д. Все это позволяет сделать вывод о том, что частная оценка качества типа "риск" dj является выделенным, в некотором смысле, критерием. Доопределим оценку dj следующим образом:
1) dj=1 при j=j=1; (2.2.5)
2) dj=0 при j=j=0; (2.2.6)
3) dj=1 для всех j<j. (2.2.7)
Отметим, что оценка dj является убывающей функцией по j и возрастающей по j.
Приведем вероятностную интерпретацию величин dj [Каплинский А.И., Руссман И.Б., Умывакин В.М., 1991. - 168 с.]. Покажем, что их можно рассматривать как меру «некачественности» j-го свойства или как субъективную вероятность недостижения требуемого качества ДТПС по j-му КК. Обозначим через - интегральное качество (качество в целом) ДТПС, а через - требование к этому качеству. Будем считать, что требование к интегральному качеству ДТПС выполнено, если . Причем, если качество j эколого-экономических решений хотя бы по одному КК ниже соответствующего нормативного уровня j , то удовлетворить требование к интегральному качеству ДТПС невозможно. Пусть А — событие, состоящее в том, что не выполнено требование к интегральному качеству, а Bj – событие, состоящее в том, что не выполнено требование к качеству ДТПС по j-му КК. Тогда условная вероятность Р(АВj)=1, т.к. если <j,то
