Розповсюдження та тиражування без офіційного дозволу хінем заборонено!

Вид материала

Документы

Содержание 5 Приклади розв'язку типових завдань

Подобный материал:

• Міністерство освіти І науки України Дніпродзержинський технологічний коледж, 631.81kb.
• Облік І аудит", 050. 104 „Фінанси І кредит", 050. 100 „Економічна кібернетика" Вінниця, 803.77kb.
• Всеукраїнської науково-практичної конференції (30 жовтня 2009 р.) Київ 2009 ббк 74., 6863.63kb.
• Розповсюдження та тиражування без офіційного, 331.87kb.
• Розповсюдження та тиражування без офіційного, 462.04kb.
• Право власності на цей документ належить державі. Відтворювати, тиражувати І розповсюджувати, 161.25kb.
• Вступ, 594.31kb.
• Слухай Н. В. Художественный образ в аспекте лингвистики текста, 142.47kb.
• На суму 154,5 мільйона доларів США, 1816.97kb.
• С. И. Гиндин считает, что годом появления советской лт является 1948г., хотя предыстория, 173.59kb.

Завдання 4

Дослідити гру на наявність сідлової точки.

Варіант 1.	Варіант 2.	Варіант 3.
4 6 5 -1 8 3 6 0 2	4,5 3,6 1,8 2,9 1,7 0,8 3,7 3,6 2,7	-0,5 0,12 1,8 1,9 0,07 -0,8 0,7 0,13 0,26
Варіант 4.	Варіант 5.	Варіант 6.
11 11 13 10 9 22 11 11 12	3 -3 2 0 -1 -1 4 -2 0	32 44 21 23 35 21 -95 10 -39
Варіант 7.	Варіант 8.	Варіант 9.
2,8 1,6 2,8 3,9 4,7 3,8 1,7 0,6 1,6	4 6 5 3 5 2 9 7 8	-44 5 13 4 -10 -7 11 9 23
Варіант 10.	Варіант 11.	Варіант 12.
-0,3 0,6 -0,8 -0,2 0,1 -0,2 -0,7 0,6 -0,6	0,5 1,6 2,8 2,9 3,7 6,8 8,1 7,6 7,1	-10 1,3 3,7 0,2 -9,7 -4,8 8,7 6,6 5,9
Варіант 13.	Варіант 14.	Варіант 15.
1,5 0,45 1,81 2,9 0,35 0,82 3,7 -4,2 4,63	0,4 0,6 0,1 0,3 0,7 0,2 0,5 0,6 0,5	0,5 0,6 6,8 7,5 9,7 7,5 0,2 7,5 1,7
Варіант 16.	Варіант 17.	Варіант 18.
2 -3 -5 0 -7 10 -1 -2 12	15 4 9 17 22 18 7 14 32	8,5 -9,6 -21 -0,6 7,7 -6,8 7,7 8,6 8,6
Варіант 19.	Варіант 20.
5 6 3 7 4 3 8 6 6	1,5 2,61 1,8 -0,9 3,73 0,8 0,77 -0,6 2,6

5 ПРИКЛАДИ РОЗВ'ЯЗКУ ТИПОВИХ ЗАВДАНЬ

Нижче наведені зразки розв'язання типових контрольних завдань. У задачі 5.1 даний короткий запис математичної моделі ЗЛП, знайдений оптимальний план прямої задачі. Тут же розібраний графічний метод, розв'язання завдання. Уважно розберіться в розв'язанні задачі 5.1. Це допоможе виконати Вам завдання 1 і 2. Розібравши розв'язання задач 5.2, 5.3, Вам простіше буде впоратися із завданнями 3 і 4.

Задача 5.1

Для виготовлення двох видів продукції Р₁ і Р₂ використовують 4 виду ресурсів: S₁, S₂, S₃, S₄. Запаси ресурсів, число одиниць ресурсів, що витрачені на виготовлення одиниці продукції, наведені в таблиці 5.1:

Таблиця 5.1 – Вихідні дані

Вид ресурсу	Запас ресурсу	Число одиниць ресурсу, витрачених на виготовлення одиниці продукції
P1	P2
S1	18	1	3
S2	16	2	1
S3	5	-	1
S4	21	1	-
Прибуток, одержувана від одиниці продукції, грн		2	3

Необхідно скласти такий план виробництва продукції, при якому прибуток від її реалізації була б максимальною. Необхідно.

1. Записати математичну модель прямої задачі.
   
2. Розв'язати задачу симплекс-методом
   
3. Розв'язати задачу графічно.
   

Розв'язок

1. Математична модель прямої задачі:
   

x1 і x2 – число одиниць продукції видів Р1 и Р2 відповідно, запланованих до випуску

а) z=2x1+3x2 →max

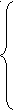б) х1+3х2≤18 2х1+х2≤16 x2≤5 3х1≤21

в) x1 ≥0, x2 ≥0

2) Розв'язок прямої задачі симплекс- методом.

Канонічна форма запису системи обмежень:

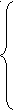
х₁+3х₂+х₃=18

2х₁+х₂+х₄=16

х₂+х₅=5

3х₁+х₆=21

Складемо симплекс- таблицю для розв'язку прямоі задачі.

Базис	Сбаз.	План	2	3	0	0	0	0	Σ	Θ	Хбаз.
х1	х2	х3	х4	х5	х6
х3 х4 х5 х6	0 0 0 0	18 16 5 21	1 2 0 3	3 1 1 0	1 0 0 0	0 1 0 0	0 0 1 0	0 0 0 1	23 20 7 25	6 16 5 -	x1={18;16;5;21;0;0}
Δj ≥0	-	0	-2	-3	0	0	0	0	-	-
х3 х4 х2 х6	0 0 3 0	3 11 5 21	1 2 0 3	0 0 1 0	1 0 0 0	0 1 0 0	-3 -1 1 0	0 0 0 1	2 13 7 25	3 5,5 5 7	x2={0;5;3;11;0;21}
Δj ≥0	-	15	-2	0	0	0	3	0	-	-
х1 х4 х2 х6	2 0 3 0	3 5 5 12	1 0 0 0	0 0 1 0	1 -2 0 -3	0 1 0 0	-3 5 1 9	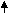0 0 0 1	2 9 7 19	- 1 5 4/3	x3={3;5;0;5;0;12}
Δj ≥0	-	21	0	0	2	0	-3	0	-	-
х1 х5 х2 х6	2 0 3 0	6 1 4 3	1 0 0 0	0 0 1 0	-1/5 -2/5 2/5 3/5	3/5 1/5 -1/5 -9/5	0 1 0 0	0 0 0 1	37/5 9/5 26/5 14/5	- - - -	x4={6;4;0;0;1;3}
Δj ≥0	-	24	0	0	4/5	3/5	0	0	-	-

X^*={6; 4; 0; 0; 1; 3} – оптимальний план прямоі задачі.

max z = 24, дійсно, z_max = 26+34=24.


Оптимальний план прямоі задачі передбачає виробництво обох видів продукції Р₁ и Р₂ у кількості відповідно 6 од. и 4 од.

Додаткові змінні х₃, х₄, х₅, х₆ характеризують залишок (невикористану частину) ресурсів відповідно S₁, S₂, S₃, S₄.

Оскільки х₅=1, х₆=3, те третій ресурс S₃ і четвертий ресурс S₄ використовуються в процесі виробництва продукції не повністю, а ресурси S₁ и S₂ – повністю (х₃=х₄=0). При такому оптимальному плані виробництва продукції та використанні ресурсів виробництво дістане найбільший прибуток у розмірі 24 у.о.

3) ЗЛП зводиться до розв'язку задачі, у якому кожній лінійній нерівності відповідає якась півплощина. Перетинання цих півплощин є опуклий багатокутник. Область припустимих розв'язків визначимо, побудувавши граничні прямі:

х₁ + 3х₂ = 18 (I); 2х₁ + х₂ =16 (II); х₂ = 5 (III); 3х₁ = 21 (IV); х₁ = 0 (V); х₂ = 0 (VI). Потім будуємо лінію нульового рівня 2х₁ + 3х₂ = 0 і градієнт N={2; 3}. Направлення градієнта вказує на направлення зростання цільової функції.

x<sub>2


A B</sub>

^C

D

O ¹ _E

0 1 x₁


Z_max = Z(C), де С –точка перетинання прямих I и II.

Координати точки С знайдемо, розв'язавши систему двох рівнянь:

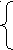х₁+ 3х₂ = 18

2х₁ + х₂ = 16; С (6; 8)

Z(C) =26 +34 = 24; Z_max = 24.

Z_min = Z(O), где О – початок системи координат.

Z(O) =20 +30 =0; Z_min = 0.

Отже, при оптимальному розв'язанні х₁ = 6, х₂ = 4, Z_max = 24, а при оптимальном решении х₁ = 0, х₂= 0, Z_min = 0.

Задача 5.2

На три бази надійшов однорідний вантаж у кількості 300 т – на базу А₁, 150 т – на базу А₂, 250т – на базу А₃. Отриманий вантаж потрібно перевезти в п'ять пунктів: 170 т – у пункт В₁; 110 т – у пункт В₂; 100 т – у пункт В₃, 120 т – у пункт В₄, 200 т – у пункт В₅. Відстані між пунктами відправлення (базами) і пунктами призначення визначені в таблиці (матриця відстаней):

Таблиця 5.3 – Матриця відстаней

Пункти відправлення	Пункти призначення
В1	В2	В3	В4	В5
А1	70	50	15	80	70
А2	80	90	40	60	85
А3	50	10	90	11	25

Вартість перевезень пропорційна кількості вантажу та відстані. Спланувати перевезення так, щоб загальна вартість перевезень була мінімальна.

Розв'язок

У випадку пропорційності витрат, кількості вантажу та відстані для розв'язання задачі достатньо мінімізувати загальний обсяг плану перевезень, виражений у тонно-кілометрах. Число баз m = 3, а число пунктів призначення n = 5. Число базисних змінних 3+5-1=7. Знайдемо перший опорний план діагональним методом (методом північно-західного кута).

Заповнення таблиці починається з її північно-західного кута, тобто клітки з невідомим х₁₁. Перша база А₁ може цілком задовольнити потребу першого замовника В₁ (a₁ = 300, b₁ = 170, a₁ > b₁). Припустимо, х₁₁ = 170, уписуємо це значення в клітинку х₁₁ і виключає з розгляду перший стовпець. На базі А₁ залишається змінений запас a₁' = 130. У новій таблиці із трьома рядками А₁, А₂, А₃ і чотирма стовпцями В₂, В₃, В₄, В₅ північно-західним кутом буде клітинка для невідомого х₁₂. Перша база а₁ може задовольнити цілком потребу другого замовника В₂ (a₁' = 130, b₂ = 110, a₁' > b₂). Нехай х₁₂ = 110, уписуємо це значення в клітинку х₁₂ і виключаємо з розгляду другий рядок. На базі А₁ новий залишок (запас) а₁'' = 20. У новій таблиці із трьома рядками А₁, А₂, А₃ і трьома стовпцями В₃, В₄, В₅ північно-західним кутом буде клітинка для невідомого х₁₃. Тепер третій замовник В₃ може прийняти весь запас із бази А₁ (а₁'' = 20, b₂ = 100, а₁''< b₃). Нехай х₁₃ = 20, уписуємо це значення в клітинку х₁₃ і виключаємо з розгляду перший рядок. У замовника В₃ залишилася ще незадоволеною потреба b₃'=80. Тепер переходимо до заповнення клітинки для х₂₃ и т.д. Через шість кроків залишиться одна база А₃ с запасом вантажу (залишком від попереднього кроку) а₃' = 200 і один пункт В₅ с потребою b₅ = 200. Заповнюємо клітинку, яка залишиться. План складений.

Таблиця 5.4

Пункти відправлення	Пункти призначення	Запас
В1	В2	В3	В4	В5
А1		70		50		15		80		70	300
170	110	20
А1		80		90		40		60		85	150
		80	70
А1		50		10		90		11		25	250
			50	200
Потреби	170	110	100	120	200	700

Базис утворений невідомими х₁₁, х₁₂, х₁₃, х₂₃, х₂₄, х₃₄, х₃₅.

Правильність складеного плану легко перевірити, підрахувавши суму чисел, що стоять у заповнених клітинках по рядках і стовпцям. Загальний обсяг перевезень у тонно-кілометрах для даного плану складе:

S=70170+50110+1520+4080+6070+1150+25200=30650.

Для оцінки та поліпшення плану скористаємося методом потенціалів. Встановлюємо, що непрямі тарифи перевищують дійсні для клітинок з невідомими х₂₁ і х_32. А перерахувавши по циклу, який відповідає вільному невідомому х₂₁, був отриманий новий базисний план перевезень. Оцінимо цей другий крок. Складемо систему рівнянь і розв'яжемо її.

α₁ + β₁ = 70,

α₁ + β₂ = 50, β₁ = 70,

α₁ + β₃ = 15, α₁ = 0, β₂ = 50,

α₂ + β₁ = 80, => α₂ = 10, β₃ = 15,

α₂ + β₄ = 60, α₃ = -39, β₄ = 50,

α₃ + β₄ = 11, β₅ =65.

α₃ + β₅ = 25,

Знайдемо непрямі тарифи та порівняємо їх з дійсними:

с₁₄' = α₁ + β₄ = 50 < с₁₄,

с₁₅' = α₁ + β₅ = 64 < с₁₅,

с₂₅' = α₂ + β₅ = 74 < с₂₅,

с₂₂' = α₂ + β₂ = 60 < с₂₂,

с₃₁' = α₃ + β₁ = 31 < с₃₁,

с₂₃' = α₂ + β₃ = 25 < с₂₃,

с₃₂' = α₃ + β₂ = 11 > с₃₂,

с₃₃' = α₃ + β₃ = -24 < с₃₃.

Непрямий тариф більше дійсного тільки для однієї клітинки з невідомим х₃₂. Складемо для нього цикл х₃₂⁺; х₃₄^-; х₂₄⁺; х₂₁^-; х₁₁⁺; х₁₂^-;х₃₂⁺.

Уведемо в базис невідому х₃₂, зробивши перерахунок по циклу із числом

х = min{х₃₄; х₂₁; х₁₂}= min{50; 80; 110}=50, отримаємо нові значення у вершинах циклу.

х₃₂'=0+50=50; х₃₄'=50-50=0; х₂₄'=70+50=120; х₂₁'=80-50=30; х₁₁'=90+50=140; х₁₂'=110-50=60.

Вільна змінна х₃₂ стала базисною, а базисна змінна х₃₄ – вільної. Таким чином, новий план має вигляд:

Таблиця 5.5

Пункти відправлення	Пункти призначення	Запас
В1	В2	В3	В4	В5
А1		70		50		15		80		70	300
140	60	100
А1		80		90		40		60		85	150
30			120
А1		50		10		90		11		25	250
	50			200
Потребности	170	110	100	120	200	700

Для оцінки цього плану складемо систему рівнянь потенціалів для заповнених клі­тинок і розв'яжемо її.

α₁ + β₁ = 70,

α₁ + β₂ = 50, β₁ = 70,

α₁ + β₃ = 45, α₁ = 0, β₂ = 50,

α₂ + β₁ = 80, => α₂ = 10, β₃ = 15,

α₂ + β₄ = 60, α₃ = -40, β₄ = 50,

α₃ + β₄ = 10, β₅ =65.

α₃ + β₅ = 25,

Запишемо непрямі тарифи для вільних клітинок і порівняємо їх з дійсними.

с₁₄' = α₁ + β₄ = 50 < с₁₄,

с₁₅' = α₁ + β₅ = 65 < с₁₅,

с₂₂' = α₂ + β₂ = 60 < с₂₂,

с₂₃' = α₂ + β₃ = 25 < с₂₃,

с₂₅' = α₂ + β₅ = 75 < с₂₅,

с₃₁' = α₃ + β₁ = 30 < с₃₁,

с₃₃' = α₃ + β₃ = -25 < с₃₃,

с₃₄' = α₃ + β₄ = 10

Усі непрямі тарифи менше дійсних, значить отриманий оптимальний план.


Задача 5. 3

Визначити нижню та верхню ціну гри, заданою платіжною матрицею

0,5 0,6 0,8

С= 0,9 0,7 0,8

0,7 0,6 0,6 .

Дослідити гру на наявність сідлової точки.

Розв'язок

Усі розрахунки зручно здійснювати в таблиці 5.6, у якій, крім матриці С, уведені стовпець α_i і рядок β_j.

Таблиця 5.6

Aj	Bi	αi
В1	В2	В3
А1	0,5	0,6	0,8	0,5
А2	0,9	0,7	0,8	0,7
А3	0,7	0,6	0,6	0,6
βj	0,9	0,7	0,8	α = β=0,7

Аналізуючи рядки матриці (стратегія гравця А), заповнюємо стовпець α_i: α₁=0,5; α₂=0,7; α₃=0,6 – мінімальні числа в рядках 1, 2, 3. Аналогічно β₁ = 0,9; β₂ = 0,7;
β₃ = 0,8 – максимальні числа в стовпцях 1, 2, 3 відповідно.

Нижня ціна гри: α = max{0,5; 0,7; 0,6} = 0,7 (найбільше число в стовпці α_i),

Верхня ціна гри: β = min{0,9; 0,7; 0,8} = 0,7 (найменше число в рядку β_j).

Ці значення рівні, т.е. α = β і досягаються на одній і тій же парі стратегій (А₂; В₂). Отже, гра має сідлову точку (А₂; В₂) і ціна гри ν = 0,7.