Geum.ru

Розповсюдження та тиражування без офіційного дозволу хінем заборонено!

Вид материалаДокументы

Содержание


4.2 Практичні завдання
Подобный материал:
1   2   3   4   5

4.2 Практичні завдання


Завдання 1

Підприємство виготовляє 4 (або 3) виду продукції А; В; С; D. (А; В; С), використовуючи для цього три види ресурсів:1, 2, 3. Норми витрат ресурсів на одиницю продукції кожного виду (в умовних одиницях) приведені в таблиці 4.1.

Таблиця 4.1 – Норми витрат ресурсів на одиницю продукції

Ресурс
Норми витрат ресурсів на од. продукції по видах продукції
Запас ресурсу

A
B
C
D

1












F1

2












F2

3












F3


Відома ціна одиниці продукції кожного виду: для А – ЦА; для В – ЦВ; для С –ЦС; для D – ЦD. (у.о.).

Визначити оптимальний план виробництва продукції в умовах обмеженості ресурсів, який дасть виробництву найбільший прибуток. Завдання розв'язати симплексним методом. Дані для розв'язання цього завдання дано в таблиці 4.2.

Таблиця 4.2 – Вихідні дані

№ варіанту
Ресурс
А
В
С
D
ЦА
ЦВ
ЦС
ЦD
F1
F2
F3

1
1
18
15
12
-
9
10
16
-
360
192
180

2
6
4
8
-

3
5
3
3
-

2
1
4
2
1
-
10
14
12
-
180
210
244

2
3
1
3
-

3
1
2
5
-

3
1
2
1
1
1
4
3
6
7
280
80
250

2
1
-
1
1

3
1
5
1
-

4
1
6
1
2
4
4
2
3
4
300
200
90

2
5
2
2
4

3
2
3
1
1

5
1
3
2
1
2
27
10
15
28
200
500
400

2
3
1
3
4

3
1
1
1
3

6
1
2
1
1
3
8
3
2
1
300
70
340

2
1
-
2
1

3
1
2
1
-

7
1
1
-
2
1
9
6
4
7
180
250
800

2
-
1
3
2

3
4
2
-
4

8
1
1
2
2
1
3
2
5
4
300
600
200

2
3
-
2
2

3
1
4
-
1

9
1
2
1
2
-
2
3
4
-
120
200
120

2
3
1
2
-

3
2
2
1
-

Продовження таблиці 4.2

№ варіанту
Ресурс
А
В
С
D
ЦА
ЦВ
ЦС
ЦD
F1
F2
F3

10
1
3
1
3
4
27
10
15
28
200
500
400

2
3
2
1
2

3
1
1
1
3

11
1
6
4
8
-
9
10
16
-
360
192
180

2
18
15
12
-

3
5
3
3
-

12
1
12
15
18
-
16
10
9
-
180
192
360

2
8
4
6
-

3
3
3
5
-

13
1
1
2
4
-
12
14
10
-
244
210
180

2
3
1
3
-

3
5
2
1
-

14
1
1
1
1
2
7
6
3
4
250
80
280

2
1
1
-
1

3
-
1
5
1

15
1
4
2
1
6
4
3
2
4
90
300
200

2
4
2
2
5

3
1
1
3
2

16
1
2
5
2
4
2
4
3
4
250
280
80

2
1
6
2
4

3
3
2
1
1

17
1
3
1
1
2
1
2
3
8
340
70
300

2
1
2
-
1

3
-
1
2
1

18
1
2
1
2
-
4
3
2
-
120
200
120

2
2
1
3
-

3
1
2
2
-

19
1
6
4
8
-
9
10
16
-
360
192
180

2
5
3
3
-

3
18
15
12
-

20
1
5
2
1
-
12
14
10
-
244
210
180

2
1
2
4
-

3
3
1
3
-


Завдання 2

Побудувати на площині область припустимих рішень системи нерівностей. Геометрично знайти найбільше та найменше значення цільової функції в цій області.
У всіх варіантах х1 ≥ 0 , х2 ≥ 0.



Варіант 1.
Варіант 2.
Варіант 3.

2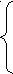х1 + 3х2 ≤ 50

3х1 - х2 ≥ 9

-х1 + 4х2 ≥ 19

z = х1 + 5х2;
2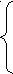х1 - 3х2 ≤ 6

5х1 + 6х2 ≤ 30

2х1 + х2 ≥ 2

z = 2х1 + х2;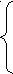
-2х1 + 7х2 ≥ 15

11х1 - 3х2 ≥ 24

9х1 + 4х2 ≤ 110

z = 9х1 + 2х2;

Варіант 4.
Варіант 5.
Варіант 6.

3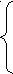х1 - х2 ≤ 14

-4х1 + 5х2 ≤ 29

5х1 + 2х2 ≥ 38

z = 3х1 + 2х2;
х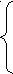1 - х2 ≥ 3

7х1 -3х2 ≥ 71

х1 + 4х2 ≤ 53

z = 9х1 + 2х2;
х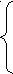1 + 7х2 ≥ 77

-х1 + х2 ≤ 3

5х1 + 3х2 ≤ 97

z = 3х1 + 4х2;

Варіант 7.
Варіант 8.
Варіант 9.

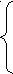-4х1 + 9х2 ≥ 20

х1 + 3х2 ≤ 37

2х1 - х2 ≥ 4

z = 4х1 + 3х2;
9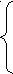х1 + 8х2 ≤ 157

4х1 - х2 ≥ 6

-3х1 + 11х2 ≥ 16

z = 8х1 + 5х2;
1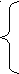5х1 + 8х2 ≤ 120

2х1 + 5х2 ≤ 30

7х1 + 10х2 ≤ 70

z = х1 + 4х2;

Варіант 10.
Варіант 11.
Варіант 12.

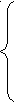-х1 + х2 ≤ 1

х1 + х2 ≥ 1

6х1 + 7х2 ≤ 42

3х1 ≤ 15

z = 5х1 + х2;
2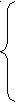х1 - 3х2 ≥ 6

5х1 + 6х2 ≤ 30

2х1 + х2 ≤ 2

-х1 + 4х2 ≤ 19

z = 2х1 + х2;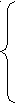
-4х1 + 2х2 ≤ 4

х1 + 3х2 ≥ 6

х1 ≤ 4

х2 ≤ 3

z = 2х1 + х2;

Варіант 13.
Варіант 14.
Варіант 15.

6х1 - 7х2 ≤ 15

2х1 +3х2 ≤ 53

10х1 -х2 ≥ 57

z = 2х1 + 3х2;
-х1 +х2 ≤ 5

4х1 + 5х2 ≤ 40

2х1 + 3х2 ≥ 6

z = 2х1 + 5х2;
2х1 + 3х2 ≤ 53

10х1 - х2 ≥ 57

6х1 - 7х2 ≤ 15

z = 5х1 + х2;

Варіант 16.
Варіант 17.
Варіант 18.

5х1 + х2 ≥ 10

х1 + 7х2 ≥ 7

-5х1 + 3х2 ≤ 30

z = 3х1 + 3х2;
-4х1 +9х2 ≥ 20

2х1 - х2 ≥ 4

х1 + 3х2 ≤ 37

z = х1 + 3х2;
3х1 - 7х2 ≤ 21

-8х1 +5х2 ≤ 40

2х1 + 3х2 ≥ 18

х1 ≤ 15

х2 ≤ 10

z = 7х1 + 3х2;




Варіант 19.
Варіант 20.



10х1 - 3х2 ≤ 30

2х1 + 2х2 ≤ 12

х1 + 5х2 ≥ 5

х1 + х2 ≥ 2

z = 3х1 + 2х2;
-4х1 + х2 ≤ 4

х1 + х2 ≥ 4

4х1 - х2 ≤ 4

3х2 ≤ 21

z = х1 + 5х2.



Завдання 3

Розв'язати транспортне завдання: скласти оптимальний план перевезень однорідного вантажу від постачальників до споживачів, при якому сумарні транспортні витрати були б мінімальними. Вартість перевезення одиниці вантажу, потреби та наявність вантажу задана таблицею 4.3.

Таблиця 4.3 – Вартість перевезення одиниці вантажу, потреби та наявність вантажу

Постачальники (Аi)
Споживачі (Bj)
Запаси вантажу

B1
B2
B3
B4
B5

А1
с11=
с12=
с13=
с14=
с15=
а1=

А2
с21=
с22=
с23=
с24=
с25=
а2=

А3
с31=
с32=
с33=
с34=
с35=
а3=

Потреба у вантажі
b1
b2
b3
b4
b5



Числові значення витрат за перевезення одиниці продукції від і- го постачальника до j-го споживачеві, потреб, запасів вантажу знаходяться у таблиці 4.4.

Таблиця 4.4 – Вихідні дані

№ варіанту
i
j
аi

1
2
3
4
5

1
1
1
2
1
3
-
30

2
1
2
2
1
-
50

3
2
2
1
2
-
70

bj
25
25
4
60
-



2
1
3
1
2
1
-
40

2
1
4
1
3
-
55

3
2
2
2
3
-
60

bj
20
65
20
50
-



3
1
2
2
3
1
-
40

2
1
2
1
3
-
50

3
3
2
3
3
-
60

bj
20
20
55
50
-



4
1
1
2
1
3
-
50

2
1
2
2
1
-
30

3
2
2
1
2
-
70

bj
25
40
25
60
-






5
1
8
7
1
2
-
10

2
6
12
3
5
-
60

3
11
4
9
10
-
30

bj
40
20
10
30
-



6
1
10
6
1
2
-
10

2
7
8
3
5
-
60

3
4
9
12
11
-
30

bj
40
20
10
30
-



7
1
12
18
8
16
-
90

2
17
11
9
12
-
115

3
10
15
14
7
-
205

bj
95
150
15
80
-



8
1
9
12
1
2
-
10

2
8
6
3
5
-
60

3
4
10
11
7
-
30

bj
40
20
10
30
-



9
1
3
1
2
1
-
55

2
1
4
1
3
-
40

3
1
2
2
3
-
60

bj
65
20
50
20
-



10
1
3
3
2
2
-
40

2
3
4
2
4
-
50

3
2
4
3
4
-
60

bj
45
40
30
35
-



11
1
27
36
35
31
29
250

2
22
23
26
32
35
250

3
36
42
38
32
39
200

bj
120
130
100
160
140



12
1
19
17
15
5
-
115

2
11
9
10
12
-
90

3
13
18
14
14
-
205

bj
95
150
85
85
-



13
1
4
5
6
4
-
20

2
3
2
3
4
-
40

3
2
2
3
2
-
90

bj
60
50
20
20
-



14
1
11
8
1
2
-
10

2
7
6
3
5
-
60

3
10
4
12
9
-
30

bj
40
20
10
30
-



15
1
3
1
2
4
-
45

2
2
2
3
3
-
35

3
2
1
3
4
-
70

bj
25
35
45
45
-



16
1
4
1
2
5
-
40

2
3
2
3
7
-
60

3
4
4
5
2
-
90

bj
45
35
55
65
-






17
1
9
6
1
2
-
10

2
10
4
3
5
-
60

3
8
7
12
11
-
30

bj
40
20
10
30
-



18
1
4
10
1
2
-
10

2
6
9
3
5
-
60

3
7
8
11
12
-
30

bj
40
20
30
30
-



19
1
1
3
-
-
-
15

2
2
5
-
-
-
15

3
-
-
-
-
-



bj
10
20
-
-
-



20
1
6
10
4
-
-
150

2
12
2
8
-
-
90

3
-
-
-
-
-



bj
60
70
110
-
-