Омской области истоки творчества сборник материалов лауреатов региональной научно-практической конференции школьников Калачинск 2008
| Вид материала | Документы |
- Рецензент: Румынина Г. И. кандидат педагогических наук, доцент, 1701.37kb.
- Федеральное государственное образовательное учреждение высшего профессионального образования, 4063.78kb.
- Доклады и тезисы представлены в авторской редакции. Сподробными материалами конференции, 2528.5kb.
- Положение о Конференции (приложение 1); состав оргкомитета Конференции (приложение, 259.96kb.
- Томск, Россия Информационные технологии: к истокам некоторых заблуждений Сборник материалов, 293.71kb.
- Ственный институт наука и студенты: новые идеи и решения Сборник материалов viii-й, 5467.94kb.
- Взаимодействия структур, 65.6kb.
- Итоги IV областной научно-практической конференции школьников Сахалинской области, 38.81kb.
- Сборник материалов научно практической конференции, 2793.85kb.
- Вторая региональная научно-практическая студенческая конференция городу, 4253.28kb.
§2. Происхождение частушки. Одни ученые считают, что частушка родилась очень давно, что песенки, похожие на частушки, распевали и плясали под них бродячие артисты - скоморохи - еще в XVII-XVIII вв. Другие убеждены: частушка как особая песенная форма появилась не раньше середины XIX века.
§3. Частушка в наши дни. Главное назначение частушки не в том, чтобы подробно рассказать о тех или иных фактах, а в том, чтобы дать этим фактам и событиям определенную идейно-эмоциональную оценку, выразить те или иные мысли или чувства.
§4. Тематика частушек. Тематический диапазон частушек безграничен. В ней находят яркое выражение и острая публицистическая мысль, и любовное чувство, и едкая, убийственная сатира, и мягкий дружеский юмор. Частушки предназначены для публичного исполнения в кругу молодежи. В них говорится решительно обо всем, что как-то взволновало или просто было замечено в жизни.
§5. Композиция частушек. Подавляющее число частушек имеет форму монолога. И это вполне объяснимо, так как монолог является самой естественной и самой простой формой выражения мыслей и чувств. Монологическую форму имеют также частушки-повествования и частушки-описания.
В огороде я косила
Зеленую травушку,
За реку платком махала
Дорогому Санюшке.
Монологи-размышления – самая распространённая композиционная форма частушек.
Описательные частушки можно разделить на две группы: а) частушки, рисующие картины быта и природы, и б) частушки — портретные характеристики.
Как у милого домок,
Семь окошек во рядок;
Супротив зеленый сад,
Растет малина, виноград.
Диалогическая форма менее распространена в частушках, чем монологическая. Но тем не менее и она в частушках встречается довольно часто.
— Дорогой, мой родненькой,
Купи конфетку с барынькой!
— Все лавочки обошел —
Такой конфетки не нашел.
По своей внутренней композиционной структуре они делятся на одночастные и двучастные.
Одночастными мы называем частушки, все строки которых представляют собою единое, нераздельное художественное целое. Такая одночастная частушка нередко представляет собой одно законченное предложение. Например:
Через поле яровое,
Через десять деревень,
Через сорок три дорожки
Ходит милый каждый день.
Значительно большее распространение в частушках получил принцип их двучастного построения. При этом первая и вторая пары строк имеют синтаксическую законченность и относительную смысловую самостоятельность, как, например:
Ты играй, играй, тальяночка,
Играть бы тебе век;
Не тальянка завлекает,
Завлекает человек.
Глава 2. §1. Эпитеты в частушках. Частушкам присущи все основные качества и признаки фольклорных произведений. Как и в традиционных лирических песнях, в них в их конкретном содержании мы видим сочетание элементов коллективного и индивидуального.
Выйду, выйду в чисто поле,
Посмотрю в такую даль.
Ветры буйные сказали:
«Дролечку не ожидай».
«Чистое поле» и «буйные ветры» — символом тоски и печали.
Живая разговорная речь:
Полюбила тракториста,
Грязного, немытого.
Что я, дура, не купила
Мыла духовитого.
Устойчивые выражения:
Не брани, тятя, за волю,
За веселую гульбу,
Пройдут годы молодые —
Посылай, так не пойду.
В частушку перешло большое количество эмоционально-выразительных эпитетов традиционных лирических песен. Назовем лишь некоторые из них: «родимая сторона, «милые родители», «чужая сторона», «горючие слезы».
Эпитеты:
Извини, моя милая,
Что вчерася не пришел:
Только вышел на крылечко —
Частый дождичек пошел.
В частушках встречаются также эпитеты, которые служат средством портретных характеристик. О «красной девушке» говорится, что она «лицебела» и «черноброва», у нее «румяное лицо», «русая коса», а в этой косе «лента алая». Примерно таким же в частушках рисуется и портрет молодца. Он «чернобровый», у него «лицо бело, румяно», «кудрявые волосы».
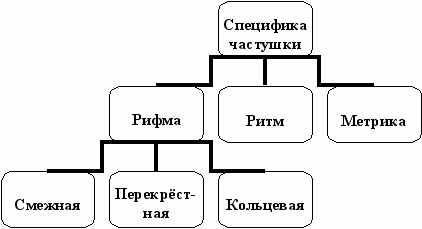 §2. Стих частушки.
§2. Стих частушки. Частушечная рифма продолжает народные песенные и пословичные традиции. Рифмы частушек довольно разнообразны. Рифмоваться могут все части речи, но преимущественно слова, относящиеся к одной части речи.
Я сидела на диване,
Вышивала платок Ване —
Петухами, курами,
Всякими фигурами.
Основным метрическим размером частушек является хорей.
Бабы хают — я бродяга,
Девки хвалят — работяга,
Бабы хают — я подлец,
Девки хвалят — молодец.
Иногда встречаются и ямбические частушки.
§3. Частушка в произведениях литературы. Частушка используется авторами для создания достоверных образов, раскрытия характеров героев. Василий Белов – автора повести «Привычное дело». Василий Макарович Шукшин также использует частушки в своём рассказе «Алёша Бесконвойный. В повести «Живая вода» Владимира Крупина – соревнование в исполнении частушек Ларисы и Дуси.
Председатель на трубе,
Бригадир на крыше.
Председатель говорит:
Я тебя повыше.
§4. Школьные частушки. Ее импровизированный характер, необычайная широта тематики, эмоциональное разнообразие, метко выраженная сатира и дружеский юмор.
Как-то раз учитель Свете
Объяснил, что знанье-свет.
Света спать легла при свете,
Утром встала – знаний нет.
Герои частушки - мальчишки и девчонки.
§5. Всемирно известна Мария Николаевна Мордасова - знаменитая исполнительница русских песен и частушек.
Мария Мордасова прославила не только частушку, но и свою Родину. Частушек знала "великое" множество, да и сама сложила более трехсот. Далеко за пределами России известны ее
Топится, топится в огороде баня
Женится, женится мой дружочек Ваня.
В начале 80-х годов прошлого века в Калачинске образовался хор ветеранов «Сударушки».
В 1999 году ему было присвоено почётное звание «народный коллектив». В 2005 году коллектив принял участие в I областном празднике «Певческое поле».
С большим удовольствием «Сударушки» выезжают с концертными программами в сёла Калачинского района, на предприятия города.
Пойду, выйду на высокий
Я на берег Иртыша.
Эх, ты, русская гармошка,
До чего ж ты хороша!
Воспитывать любовь к народному творчеству нужно с детства. Поэтому в 1984 году в г. Калачинске был образован фольклорный ансамбль «Росинка», руководителем которого является Ярыгина Тамара Васильевна.
В 1994 году коллективу было присвоено звание «образцовый». Ансамбль активно участвует в культурной жизни района и области.
В октябре 2007 года Министерством труда и социального развития Омской области был объявлен конкурс на лучшую предновогоднюю частушку. Более двадцати пенсионеров, проживающих в Калачинском районе, приняли участие в этом нелёгком состязании. Победительницей же областного конкурса стала жительница Калачинска Мария Григорьевна Ранцен. Среди частушек, участвующих в этом конкурсе были:
Говорила деду бабка:
«Завяжи потуже шапку!»
Не послушал деда бабку,
И стащили детки шапку.
Ёлки-палки, лес густой,
Ходит с лысой головой!
Заключение. С частушкой народное искусство обрело свободу речевого жеста, и образ лирического героя стал раскрываться через социальную и психологическую характерность высказывания человека, через прямое соответствие слова и интонации персонажа его облику и душевному состоянию.

Ильченко Мария, 10 класс МОУ «Гимназия №1»
Руководитель: Ткаченко О.Ф., учитель русского языка и литературы
Особенности словообразования профессионализмов
в телевизионной журналистике
Предмет исследовательской работы: слова- профессионализмы, используемые в тележурналистике
Цель исследования:
Выявить особенности словообразования профессиональных жаргонизмов в тележурналистике.
Гипотеза:
Если в тележурналистике имеются профессиональные жаргонизмы, то есть особенности их образования и продуктивности их словообразования.
Для начала определены понятия, которые будут использованы в работе. Что такое профессионализмы, словообразование (или деривация) и понятия, связанные с ним?
По мнению Муруговой Елены Валерьевны, язык как саморегулирующаяся система ищет разные способы компенсации недостающих в языке слов для отображения тех или иных сторон объективной действительности. В этой связи на помощь приходит человеку, который в своей лингвокреативной деятельности старается номинировать предметы окружающего его внешнего и ментального мира при помощи имеющихся в его арсенале языковых средств. Тот факт, что большинство слов в языке – это производные слова, расширяет возможности выбора языковых средств, реализует речевую свободу говорящего, создает условия для более простого доступа к структурам сознания. А это, в свою очередь, обеспечивает выполнение важнейших функций языка – репрезентативной, когнитивной и коммуникативной.
Далее мы определяем средства и способы словообразования, принятые в современной лингвистике.
Основополагающие из них определены по Виноградову:
- Морфологическое словообразование
- Морфолого-синтаксическое словообразование
- Фонетико-морфологическим
- Словосложение
- Лексико-семантический способ словообразования
Классификация профессиональных жаргонизмов
Определившись с основополагающими для цели исследования понятиями, мы можем перейти к практической, собственно исследовательской его части.
Для составления словаря профессиональных жаргонизмов и сленга телевизионной журналистики использовались, как уже уточнялось, различные источники:
1. Фиксирование лексики непосредственно на производственных студиях: ГТРК «Иртыш», телестудии «Омь» г. Калачинск,
2. В издательских источниках: журнал «Журналист», исследования Олеси Кольцовой «Производство новостей: типы «влияний» на работу журналистов».
3. Интернет-источники.
| Паркет | Сюжет об официальном мероприятии | От «паркет» | Пол из деревянных дощечек. Такой пол был в официальных, строгих, представительных зданиях и кабинетах. | Метафорический перенос значения |
| Джинса | Рекламный сюжет | От Америк. «Джинсы» | Первая реклама про джинсы | Ассоциативный перенос значения |
| Стэндап | Монолог корреспондента, где он сам присутствует в кадре | От англ. «Stend up» | Вставать, встать | Заимствование из другого языка |
| Бэзэшка | Видеоряд без звука | От «без звука»+ суф. –к- | | Сокращение слова + суф. |
| Загон | Передача файла (видео, звук,…) с одного носителя на другой | От «загонять» | Войти куда-нибудь, поместиться где-нибудь | Метафорический перенос значения |
Выводы
Итак, из всего вышеизложенного можно сделать следующие выводы:
Всего собрано в мини-словарь профессионализмов телевизионной журналистики 31 лексическая единица; из них - 23 слова и 8 идиоматических выражений.
- В соответствии со словообразовательным критерием, делаем следующие выводы.
Образование новых слов:
- по способу ассоциативного переноса определено в 8 случаях,
- образование по способу метафорического переноса + аффикс – 6 случаев,
- образование по способу каламбурного переосмысления – 3 случая,
Образование идиом – по способу метафорического переноса – 8 случаев.
Таким образом, мы имеем возможность определить самые продуктивные модели словообразования исследуемых лексических единиц – жаргонных профессионализмов из сферы телевизионной журналистики:
Самым продуктивным, причем со значительным перевесом, можно признать:
- метафорический способ (25 случая);
Затем идет позиция использования аффиксов (10 случаев);
И менее продуктивными можно считать способы:
- сокращение + суффикс (3 случая);
- заимствование(2 случая);
- префиксация (1 случай).
Лексико-семантический способ исследуемых лексических единиц(26 случаев из 30) можно отнести к главному, самому продуктивному способу словообразования в исследуемой лексической сфере.
Стремление к экономии языковых средств выражения смыкается с другим внутренним стимулом словарного обогащения языка тенденцией к регулярности (однотипности) внутриязыковых отношений. Говорящий стремится к сокращению сложных, составных наименований.
Таким образом, выявленные особенности словообразования профессиональных жаргонизмов телевизионной журналистики позволяют говорить о последовательном соответствии словообразовательных процессов законам функционирования языка, и в частности, закономерностям, присущим функционированию жаргонизмов. Отсутствие достаточной изученности на сегодня в языкознании данной лексики и ее словообразовательных процессов, оставляет большое поле деятельности по формированию собственно словаря профессионализмов телевизионной журналистики и дальнейшего исследования их словообразовательного аспекта.

Бабкова Мария, 6 класс МОУ «Сорочинская СОШ»
Руководитель: Заморовская Т.И. , учитель русского языка и литературы
УТРО
… Спят деревья в сугробах усталых,
С веток сыплется иней крупой.
И на снежных узорных порогах
Вьюга кружит с метелью одной.
Кружат в вальсе подружки-снежинки!
И ни звука неслышно в ночи.
Иней ветви покрыл паутинкой,
Спрятал месяц от утра ключи.
Звёзды тихо мерцают на небе.
Долгой ночи не видно конца.
И бесшумно сметает ветер
Паутинки с земли – лица.
… Но забрезжил рассвет на востоке,
И молочными звёздочки стали,
И в последнем ночном потоке
На прощание бледно мерцали.
Месяц медленно в тучах скрывался,
В облаках, будто он умывался.
И с последним лучиком солнца
Скрылся месяц в волшебном оконце.
И морозная свежесть повеяла,
Красным, огненным стал рассвет.
И опять небо снегом посеяло,
Край родной серебром одет!
ДЕНЬ РОЖДЕНИЯ
Вот настал мой день Рожденья
День подарков и веселья!
Полон дом народу: ни выходу,
ни входу!
Тут и Маши, и Наташи, доедают торт две Даши!
Без конца трезвонит дверь:
«Открывай же гостю дверь!»
Вдруг тук-тук, звенит звонок…
Выбегаю на порог, открываю гостю дверь,
Но удивляюсь я теперь…
Нет гостей и нет подарков
Не видать открыток ярких…
На пороге лишь одно чёрно-белое
пятно!
Пригляделась поскорей, но…
Что за чудо! Уж поверь!
Белый, в пятнышко щенок,
Рвётся прямо на порог.
Я от счастья завизжала,
В дом его скорей позвала…
«Вот такой мой День Рожденья-
День подарков и веселья!
БАБОЧКА
Возле речки на мосточке
Дружно сели на цветочки
Все жучки и паучки!
Только бабочка порхала
И садиться не желала,
Все кричат ей в дружном хоре:
«Что за горе? Что за горе?
Почему ты не садишься?
Только вертишься, кружишься?»
Но как бабочка сказала,
Изумленье пробежало
По жучкам и паучкам,
Потому что был ответ:
«У меня же денег нет!»
ОМСК
Омск - родные просторы!
Как люблю я тебя городок!
Я люблю твоё небо и звёзды,
Милый сердцу, родной уголок.
Я люблю твой первый луч солнца,
Зимний холод, весенний закат.
Яркий взгляд ночного оконца,
Новых зданий прекрасных фасад.
Как люблю я твои просторы,
Золотые твои купола!
Как люблю я тебя, Прииртышье!
Ты - родная моя земля!
ГОД
На улице зимняя сказка,
И солнышко смотрит в окно.
Сугробы серебряной маской
Легли предо мной, как стекло.
И кружат снежинки под солнцем,
И ясное небо вокруг.
Сижу и гляжу я в оконце
На птиц, улетающих круг.
Но вот прошёл месяц ледащий.
На смену пришла весна,
Она подвенечное платье
Черёмухе принесла
Неделя идёт за неделей,
Весенние сутки прошли
И птицы уж все прилетели,
И в гнездах поют птенцы.
И высохли лужи цветущие,
И травка пробилась совсем,
И дни полетели грядущие,
И радостно было всем - всем!
И лето вступило в права свои,
И в клумбах цветы зацвели.
И птицы трелью чудесною,
От скуки нас берегли!
И дети, и взрослые люди
Купались в прозрачной реке.
И скуки в сердцах их нет места
Там только веселье и смех!
Но лето ушло ненадолго,
И листья с деревьев ушли.
И три жёлтых месяца грустных
Пристанище где - то нашли…


Дорошева Дарья, 11 класс МОУ «Гимназия №1»
Руководитель: Аникина Л.А. , учитель английского языка
Тезисы к работе по английскому языку «Концепт «свои-чужие»
в дискурсе американской языковой личности
на примере рассказа Д. Сэлинджера «The Laughing Man»
Наша работа посвящена исследованию концепта «свои-чужие» в дискурсе американской языковой личности.
Цель данной исследовательской работы – выявить степень реализации концепта «свои-чужие» в дискурсе американской языковой личности, на примере рассказа Д. Сэлинджера “The Laughing Man” .
Задачи:
- выявить структуру концепта «свои-чужие» и его значимость в современной культуре;
- проанализировать проявление концепта «свои-чужие» на лексическом, грамматическом и семантическом уровнях, на примере рассказа Д. Сэлинджера «Человек, который смеется».
- проанализировать личность главного героя с точки зрения психологии поведения в конфликтной ситуации.
Методы исследования: анализ теоретической литературы, анализ словарных дефиниций, анализ контекста
Мы предполагаем, что в рассказе Д. Сэлинджера «Человек, который смеется», концепт «свои-чужие» проявляется на различных уровнях и представляет модель мира, свойственную этому сюжету.
В I главе мы рассматриваем понятие концепта, в современной науке, как он проявляется в культуре этноса и каким образом под его влиянием формируется «картина мира». Теоретической основой нашего анализа являются работы Ю.С. Степанова, А.П. Бабушкина, З.Д.Поповой, и других ученых.
Во II главе мы анализируем концепт «свои-чужие» на материале рассказа Д.Сэлинджера «Человек, который смеется».
Мы делаем вывод, что концепт «свои-чужие», образует представление этноса о мире и проявляется в зависимости от ценностей, на которых построена модель мира. Таким образом концепт – одно из основных понятий современного мира.
Наша работа актуальна, так как концепт является элементом вхождения человека в культуру. Понятие появилось в отечественной лингвистике сравнительно недавно и определяется учеными по-разному. Единого и точного определения концепта пока не существует, так как это явление иррационального порядка, но наиболее четко явление концепта определено Ю.С. Степановым. Он определил концепт как элемент, сгусток культуры, элемент вхождения человека в культуру. Совокупность концептов образует некую область знания в сознании этноса – концептосферу.
Модель мира представляет собой определенным образом организованные знания о мире, свойственные когнитивной системе или модели. «Свои-чужие» - это противопоставление, которое в разных видах пронизывает всю культуру и является одним из главных концептов всякого коллективного, массового, народного, национального мироощущения.
Ни один человек не существует вне этноса, поэтому логично признать этнический признак первичным, доминирующим.
Правила воплощения в литературном произведении внушаемого эффекта гнева требуют целого ряда специфических изобразительных средств, которые употребляет автор: усложненной композиции, использования напыщенного, временами витиеватого стиля, доминирования красного цвета. Витиеватость рассказа обязывает к употреблению сложных прилагательных.. Для того чтобы детально проанализировать концепт «свои-чужие» в рассказе, следует проследить его реализацию на трех базовых уровнях:
- лексическом;
- грамматическом;
- семантическом.
- психологическом.
Основными концептами этой категории являются противопоставленные единицы «свой» - «чужой». В этой системе координаты устанавливаются отношениями между «я» говорящего, собеседника и третьими лицами. Так как модель мира является базовым концептом оппозиции «свои-чужие», разграничение часто происходит на основе Добра и Зла, соответственно модели мира. Из дефиниций следует, что Вождь был не только «своим» в группе индейцев, но и являлся непосредственно их «Вождем», признанным всеми лидером, образцом и примером, отожествляющим положительное, позитивное начало.
описание на негативных характеристиках, акцентируется внимание на факте, что герой не принадлежит к «своему кругу» окружающих в силу своего внешнего уродства, вызывающего у людей эмоции отвращения и страха, ему лишь позволяют присутствовать среди окружающих, когда лицо его скрывает маска.
Концепт «свои-чужие» организован по правилам «отклонения от нормы». круг «своих» Человека, который смеется образован по общим свойствам входящих в нее членов.
Наряду с вышеупомянутыми лексическими конструкциями концепт «свои-чужие» реализуется в рассказе за счет стилистических средств. Метафора в описании главного героя – Человек, который смеется, придает повествованию особое настроение и тональность, характерное для литературной сказки.
Наряду с лексическими и синтаксическими проявлениями концепта «свои-чужие», необходимо обратить внимание на построение содержания текста. Содержание художественного текста ни в коем случае не является автоматическим отображением жизненных фактов – оно имеет сложные, исторически изменчивые, до конца еще не изученные законы построения.
Итак, концепт «свои-чужие» реализуется в рассказе Сэлинджера «The Laughing Man» на трех уровнях: лексическом, грамматическом, семантическом и психологическом причем соотношение отдельных концептов «свой» и «чужой» является равнозначным, что и предоставляет возможность наблюдать концептуальную оппозицию «свои-чужие».
«Свои-чужие» - это несомненно эмоциональный концепт, ведь принципы разграничения на «своих» и «чужих» организуется по принципу общих свойств, которые способны вызывать различные эмоции. Эмоции ужаса, страха, гнева, которые доминируют в рассказе, служат одной из категорий, на основе которой происходит разграничение: вызывая отрицательные суждения, обуславливают принадлежность личности к кругу «своих» или же исключение из него.
Проведя исследование концепта «свои-чужие» на основе рассказа Д.Сэлинджера «Человек, который смеется» мы сделали следующие выводы.
Концепт – это явление иррационального порядка. Находясь на уровне выше, чем понятие, концепт является неотъемлемой частью культуры этноса. Проявляясь и взаимодействуя по-разному, концепты образуют представление этноса о мире. Концепт взаимосвязи образуют базу для модели мира в сознании нации, функционируют и проявляются в зависимости от ценностей, на основе которых построена модель мира.
Модель мира представлена определенными характеристиками, выраженными вербально или семантически, которые и являются основой концептуальной оппозиции. Проявление концепта «свои-чужие» во многом зависит от идейного построения художественного текста, тесно связано с его тематикой, тональностью, сюжетом, идеей, особенностями личности автора, взаимодействует с авторскими представлениями об устройстве общества и нравственными критериями.

Козлов Вадим, 11 класс МОУ «Гимназия №1»
Руководитель: Аникина Л.А. , учитель английского языка
Атрибутивные подчинительные словосочетания
в английской спортивной лексике
Наше исследование посвящено изучению подчинительных атрибутивных словосочетаний в английской спортивной лексике.
Цель работы – выявить существующие закономерности в морфологической сочетаемости семантических и структурных отношений атрибутивных подчинительных конструкций на примере английских словосочетаний, взятых из спортивной лексики.
Для достижения цели решаются следующие конкретные задачи:
- Определение морфологического состава подчинительных структур
- Исследование комбинаторики и автокомбинаторики внутри сочетаний
- Выявление структурно-семантических отношений между главным и зависимыми членами атрибутивных конструкций.
Мы предполагаем, что:
- словосочетание является единицей языка;
- между элементами словосочетания существуют любые синтаксические связи, которые подразделяются на определенные типы.
В работе используются следующие методы:
- метод анализа теоретической литературы;
- метод толкований определений по словарю;
- метод анализа контекста;
- метод математических подсчетов и классификации.
В первой главе исследуются теоретические источники: работы отечественных и зарубежных лингвистов Ф. Фортунатова, А. Шахманова, Л. Блумфилда, Л. Бархударова. Например, Л. Блумфилд понимает словосочетание очень широко и не считает нужным ограничивать сферу словосочетания. Американский лингвист делил словосочетания на эндоцентрические и экзоцентрические. Л. Блумфилд относит к эндоцентрическим все те словосочетания, в которых одна или любая составляющая может функционировать в большей структуре так же, как и вся группа. Например, poor player – эндоцентрическое словосочетание, т. к. составляющая player может заменить сочетание poor player в более развернутом построении: poor player ran away. Экзоцентрические структуры характерны тем, что ни одна из составляющих не может заменить всю группу в большей структуре: John ran или beside John.
Традиционно в синтаксисе различают сочинение и подчинение как основные типы связей: the game began, new powerful short. Различают и другой ряд, состоящий из четырех членов, обозначающих отношения, называемые предикативными, объектными, обстоятельственными и атрибутивными. В предикативных словосочетаниях составляющие классифицируются как подлежащее и сказуемое: Football is popular, become champions. Атрибутивная связь наблюдается в словосочетаниях, которые содержат второстепенный член, именуемый как определение: the desperate late flitting, world title fight, old famous referee.
Анализ отобранных словосочетаний показал, что их структура представлена различными комбинациями, в зависимости от компонента, выполняющего функцию определения. Удалось выделить четыре комбинации: А + N, N1+N, Pl + N, Pll + N. Примеры соответственно: the far corner, team manager, winning point, hurried pass.
На основании проведенного исследования можно сделать следующие выводы. Словосочетание – это единица языка. Между элементами словосочетания могут существовать любые из возможных синтаксических отношений.
При изучении комбинаторики слов для получения более точного описания существующих закономерностей необходимо учитывать морфологические классы. Подчинительные структуры могут быть образованы не только комбинациями слов разных морфологических классов, но и группами, состоящими из одних и тех же частей речи. Этот вид сочетаемости удобно называть автокомбинаторикой.
Компоненты подчинительных словосочетаний с атрибутивным типом отношений между элементами структуры представлены в данной работе цепочками от двух до шести элементов, но теоретическое количество зависимых компонентов, выраженных определениями к ядру словосочетания, не ограничено. В атрибутивных построениях в качестве определения могут выступать различные части речи, а морфологические комбинации нескольких определений при одном субстантивном ядре достаточно многообразны.
Семантические отношения между компонентами словосочетаний могут обозначать: отношения части и целого, местоположение, время, сравнение, назначение, принадлежность, характеристику, причину. Составляющие многокомпонентных словосочетаний, как правило, последовательную регрессивную зависимость.
Наличие дополнительного определения в атрибутивной группе в словосочетаниях более двух компонентов в некоторых случаях обязательно, а в некоторых может опускаться.
Гипотеза, выдвинутая нами в начале исследования, нашла свое подтверждение. Тема исследования актуальна, так как результаты исследования помогут обеспечить всем, кто стремиться изучить английский язык в совершенстве, дать возможность понять, что словосочетание является единицей синтаксиса и от семантических компонентов и синтаксических отношений в словосочетании зависит толкование того или иного текста, той или иной статьи.
Работа над темой помогла развить мне мои личностные качества, такие как: трудолюбие, усидчивость и сила воли. А главное, мои знания английского языка намного расширились, особенно по грамматике и лексике на спортивную тему.


Мецлер Наталья, 9 класс МОУ «СОШ №3»
Руководитель: Воробьёв В.В. , учитель математики
Нахождение значений неизвестных параметров,
при которых выполняются равенства специального вида
Глава 1. Нахождение неизвестных значений параметров для
равенства, содержащего двойной модуль:
x - a = n x + m x - a + k x + a + d
Пример 1.
Дано:
x - a = n x + m x - a + k x + a + d
Найти: n, m, k, d при а = 1
Решение:
Во-первых, заменим в выражении коэффициент а на 1. Оно будет иметь следующий вид:
x - 1 = n x + m x - 1 + k x + 1 + d
Далее приступим к раскрытию модулей в выражении с помощью числовой прямой, отметив на ней числа -1, 0 и 1.

-1 0 1


 -x-1=-nx-mx+m+kx+k+d x-1= nx+mx-m+kx+k+d -x - 1 =-nx-mx+m–kx-k +d x-1= nx-mx+m+kx+k+d
-x-1=-nx-mx+m+kx+k+d x-1= nx+mx-m+kx+k+d -x - 1 =-nx-mx+m–kx-k +d x-1= nx-mx+m+kx+k+d 



-x - 1 =-nx-mx+m–kx-k +d x +1 =-nx-mx+m+kx+k +d -x +1 =nx-mx+m+kx+k +d x -1 =nx+mx-m+kx+k +d

В каждом из четырех полученных равенств сгруппируем подобные :
1) -x - 1 = (-n- m- k) x + (m-k +d)
2) x+1 = (-n-m+k) x + (m + k +d)
3) -x +1 = (n-m+k) x + (m + k +d)
4) x-1 = (n+ m +k) x + (-m + k +d)
Так как в равенствах левая часть равняется правой, можно из наших выражений получить системы уравнений:
1
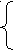
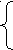
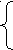
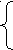 ) -n – m - k = -1 2) -n – m +k = 1 3) n – m + k =-1 4) n + m +k =1
) -n – m - k = -1 2) -n – m +k = 1 3) n – m + k =-1 4) n + m +k =1m - k + d = -1 m + k + d = 1 m +k + d = 1 -m+k +d =-1
Теперь согласно методу последовательного исключения неизвестных в каждой системе складываем II и I уравнения. Получаем несколько выражений, которые имеют следующий вид:
1) - n -2k + d =-2 2) - n +2k + d =2 3) n +2k + d =0 4) n +2k + d =0
Составим новую систему, но так как выражения (3) и (4) одинаковые, она будет содержать три уравнения:
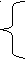 -n-2k + d =-2
-n-2k + d =-2-n+2k + d = 2
n +2k + d = 0
Воспользуемся еще раз методом последовательного исключения чисел и к I уравнению прибавим II. Из данного сложения получается:
-2n + 2d = 0 -2n = -2d n = d
Подставляем значение n = d в I уравнение системы:
-n – 2k +d = -2
-d -2k +d = -2
k=1
подставляем в III уравнение системы известные нам значения: n=d, k=1
n + 2k + d =0 d + 2 + d = 0 d = -1
Учитывая, что n = d, n = -1. Для того чтобы найти последний неизвестный коэффициент m подставим известные нам значения в следующее уравнение:
-n – m – k = - 1
1 - m -1 = -1
m = 1
Ответ: k=1, n = -1, d = -1, m = 1
Пример 2.
Дано:
x - a = n x + m x - a + k x + a + d
Найти: n, m, k, d при a = 2
Решение:
Во-первых, заменим в выражении коэффициент a на 2. Оно будет иметь следующий вид:
x - 2 = n x + m x - 2 + k x + 2 + d
Далее приступим к раскрытию модулей с помощью числовой прямой, отметив на ней числа -2, 0 и 2.



 -2 0 2
-2 0 2-x-2=-nx-mx+2m+kx+2k+d x-2= nx+mx-2m+kx+2k+d -x-2=-nx-mx+2m–kx-2k+d x-2= nx-mx+2m+kx+2k+d




-x -2=-nx-mx+2m–kx-2k +d x +2 =-nx-mx+2m+kx+2k +d -x +2=nx-mx+2m+kx+2k +d x-2 =nx+mx-2m+kx+2k +d

В каждом из четырех полученных равенств сгруппируем подобные:
1) -x-2 = (-n-m-k)x + (2m-2k+d)
2) x+2= (-n-m+k)x + (2m+2k+d)
3) -x+2 =(n-m+k)x + (2m+2k+d)
4) x-2 =(n+m+k)x + (-2m+2k+d)
Так как в равенствах левая часть равняется правой, можно из наших выражений получить системы уравнений:
1
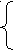
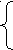
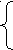
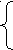 ) -n – m - k = -1 2) -n – m +k = 1 3) n – m + k =-1 4) n + m +k =1
) -n – m - k = -1 2) -n – m +k = 1 3) n – m + k =-1 4) n + m +k =12m - 2k + d = -2 2m + 2k + d =2 2m +2k + d =2 -2m+2k +d =-2
(Аналогично решению первого примера)
Будем решать методом последовательного исключения неизвестных,
а именно, ко II уравнению прибавляем I. Получаем несколько выражений, которые имеют следующий вид:
1) –n+m–3k+d = -3 2) –n+m+3k+d = 3 3) n+m+3k+d = 1 4) n–m+3k+d = -1
Составим новую систему, которая будет содержать четыре уравнения.
-
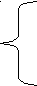 n+m–3k+d = -3
n+m–3k+d = -3–n+m+3k+d = 3
n+m+3k+d = 1
n–m+3k+d = -1
Воспользуемся еще раз методом последовательного исключения чисел и из I уравнения вычтем II. Из этого следует:
-6k = -6 -k =-1 k =1
Теперь из III уравнения вычтем IV.
2m = 2 m = 1
Подставим известные значения k и m в следующую систему уравнений:
-
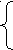 n – m - k = -1
n – m - k = -12m - 2k + d = -2
Так как k =1 и m = 1:
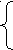
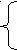 -n – 1 - 1 = -1 n =-1
-n – 1 - 1 = -1 n =-1 2 - 2 + d = -2 d = -2
Ответ: n = -1, m = 1, k = 1, d = -2
Из примеров 1, 2, 3 можно заметить, что m, n, k, d – постоянные параметры равенства x - a = n x + m x - a + k x + a + d , где m, n, k при любом a остаются неизменны, а d всегда равен –a.
Глава 2. Нахождение неизвестных значений
параметров для равенства, содержащего тройной модуль:
x - a -a= n x + m x - a + k x + a + b x - 2a + c x + 2a +d
Пример 1.
Дано:
x - a -a= n x + m x - a + k x + a + b x - 2a + c x + 2a +d
Найти: n, m, k, b, c, d при а = 1
Решение:
Во-первых, заменим в выражении коэффициент а на 1. Оно будет иметь следующий вид: x -1 -1= n x + m x - 1 + k x + 1 + b x - 2 + c x + 2 +d
Далее приступим к раскрытию модулей в выражении с помощью числовой прямой, отметив на ней числа -2,-1, 0, 1 и 2.

-2 -1 0 1 2




 -
- x-1-1= -nx – -
x-1-1= -nx – - x-1-1= -nx– -x-1-1= -nx - -x -1-1=nx - -x-1-1=nx + -x-1-1=nx+
x-1-1= -nx– -x-1-1= -nx - -x -1-1=nx - -x-1-1=nx + -x-1-1=nx+ - mx +m –kx –k – -mx +m–kx–k – -mx +m +kx +k– -mx +m +kx +k – +mx -m +kx +k – +mx- m+kx+k+
- bx+2b-cx- 2c+d bx +2b+cx+2c+d -bx+2b+cx+2c+d -bx+2b+cx+2c+d -bx+2b+cx+2c+d +bx-2b+cx+2x+d








 -
- x-1-1= -nx – -x-2= -nx– x+1-1= -nx - -x +1-1=nx - x -1-1=nx + x – 1 -1=nx+
x-1-1= -nx – -x-2= -nx– x+1-1= -nx - -x +1-1=nx - x -1-1=nx + x – 1 -1=nx+ - mx +m –kx –k – -mx +m–kx–k – -mx +m +kx +k– -mx +m +kx +k – +mx -m +kx +k – +mx- m+kx+k+
- bx+2b-cx- 2c+d bx +2b+cx+2c+d -bx+2b+cx+2c+d -bx+2b+cx+2c+d -bx+2b+cx+2c+d +bx-2b+cx+2x+d






-x-2= -nx – x + 2= -nx– -x - 0= -nx - x +0 = nx - -x +2 =nx + x – 2 =nx+
- mx +m –kx –k – -mx +m–kx–k – -mx +m +kx +k– -mx +m +kx +k – +mx -m +kx +k – +mx- m+kx+k+
- bx+2b-cx- 2c+d bx +2b+cx+2c+d -bx+2b+cx+2c+d -bx+2b+cx+2c+d -bx+2b+cx+2c+d +bx-2b+cx+2c+d
В каждом из полученных равенств сгруппируем подобные:
1) -x - 2 = (-n- m- k-b-c) x + (m-k +2b-2c +d)
2) x + 2 = (-n- m- k-b+c) x + (m-k +2b+2c+d)
3) -x - 0 = (-n- m+ k-b+c) x + (m+k +2b+2c +d)
4) x + 0 = (n- m-+k-b+c) x + (m+k +2b+2c +d)
5) -x +2 = (n+ m+ k-b+c) x + (-m+k +2b+2c +d)
6) x - 2 = (n+ m+ k-+b+c) x + (-m+k -2b+2c +d)
Т
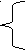 ак как в равенствах левая часть равняется правой, можно из наших выражений получить системы уравнений:
ак как в равенствах левая часть равняется правой, можно из наших выражений получить системы уравнений:- -
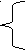
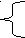 n- m- k-b-c= -1 2) -n- m- k-b+c =1 3) -n- m+ k-b+c =-1
n- m- k-b-c= -1 2) -n- m- k-b+c =1 3) -n- m+ k-b+c =-1
m-k +2b-2c +d =-2 m-k +2b+2c+d=2 m+k +2b+2c +d=0
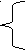
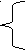
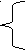 4) n- m-+k-b+c =1 5) n+ m+ k-b+c = -1 6) n+ m+ k-+b+c = 1
4) n- m-+k-b+c =1 5) n+ m+ k-b+c = -1 6) n+ m+ k-+b+c = 1m+k +2b+2c +d = 0 -m+k +2b+2c +d= 2 -m+k -2b+2c +d= -2
Теперь согласно методу последовательного исключения неизвестных в каждой системе складываем II и I уравнения. Получаем несколько выражений, которые имеют следующий вид:
1) - n -2k + b – 3c + d =-3 2) - n -2k + b + 3c + d =3 3) - n +2k + b + 3c + d =-1
4) n +2k + b +3c + d = 1 5) n + 2k + b + 3c + d =1 6) n + 2k - b + 3c + d =-1
Составим новую систему, которая будет содержать шесть уравнений с пятью неизвестными:
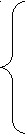
- n -2k + b – 3c + d =-3
- n -2k + b + 3c + d =3
- n +2k + b + 3c + d =-1
n +2k + b +3c + d = 1
n + 2k + b + 3c + d =1
n + 2k - b + 3c + d =-1
Воспользуемся еще раз методом последовательного исключения чисел и из I уравнения вычтем II, из II – III и т.д.
 .
. Из данного вычитания получается:
1)-6c = -6
c = 1
2)-4k = 4
k = -1
3)-2n = -2
n=1
4) 2b=2
b= 1
Теперь подставим известные значения в уравнение, чтобы найти d
- 1 + 2 + 1 – 3 + d =-3
d = -2
Есть еще одно неизвестное, чтобы найти его подставим известные значения в первое уравнение:
-1- m+1-1-1= -1
m= -1
Ответ: В уравнении x - a -a= n x + m x - a + k x + a + b x - 2a + c x + 2a +d
c = 1, k = -1 , n=1, b= 1, m= -1, d = -2 при а=1
Пример 2.
Дано:
x - a -a= n x + m x - a + k x + a + b x - 2a + c x + 2a +d
Найти: n, m, k, b, c, d при а = 2
Решение:
Во-первых, заменим в выражении коэффициент а на 2. Оно будет иметь следующий вид: x -2 -2 = n x + m x - 2 + k x + 2 + b x - 4 + c x + 4 +d
Далее приступим к раскрытию модулей в выражении с помощью числовой прямой, отметив на ней числа -4,-2, 0, 2 и 4.
 -4 -2 0 2 4
-4 -2 0 2 4




 -
- x-2-2= -nx – -
x-2-2= -nx – - x-2-2= -nx– -x-2-2= -nx - x -2-2=nx - x-2-2=nx + x-2-2=nx+
x-2-2= -nx– -x-2-2= -nx - x -2-2=nx - x-2-2=nx + x-2-2=nx+ - mx +2m –kx –2k – -mx +2m–kx–2k – -mx +2m +kx +2k– -mx +2m-kx-2k– +mx +2m+kx -2k– +mx- 2m+kx+2k+ - bx+4b-cx- 4c+d bx +4b+cx+4c+d -bx+4b+cx+4c+d -bx+4b+cx+4c+d -bx+4b+cx+4c+d +bx-4b+cx+4x+d








 -
- x-2-2= -nx – -x-2-2= -nx– x+2-2= -nx - -x +2-2=nx - x -2-2=nx + x – 2 -2=nx+
x-2-2= -nx – -x-2-2= -nx– x+2-2= -nx - -x +2-2=nx - x -2-2=nx + x – 2 -2=nx+ - mx +2m –kx –2k – -mx +2m–kx–2k – -mx +2m +kx +2k–-mx +2m +kx +2k– +mx -2m +kx +2k– +mx- 2m+kx+2k+
- bx+4b-cx- 4c+d bx +4b+cx+4c+d -bx+4b+cx+4c+d -bx+4b+cx+4c+d -bx+4b+cx+4c+d +bx-4b+cx+4с+d






-x-4= -nx – x + 4= -nx– -x - 0= -nx - x +0 = nx - -x +4 =nx + x – 4 =nx+
- mx +2m –kx –2k – -mx +2m–kx–2k – -mx +2m +kx +2k– -mx +2m +kx +2k– +mx -2m +kx +2k– +mx- 2m+kx+2k+
- bx+4b-cx- 4c+d bx +4b+cx+4c+d -bx+4b+cx+4c+d -bx+4b+cx+4c+d -bx+4b+cx+4c+d +bx-4b+cx+4c+d
В каждом из четырех полученных равенств сгруппируем подобные :
1) -x - 4 = (-n- m- k-b-c) x + (2m-2k +4b-4c +d)
2) x + 4 = (-n- m- k-b+c) x + (2m-2k +4b+4c+d)
3) -x - 0 = (-n- m+ k-b+c) x + (2m+2k +4b+4c +d)
4) x + 0 = (n- m-+k-b+c) x + (2m+2k +4b+4c +d)
5) -x +4 = (n+ m+ k-b+c) x + (-2m+2k +4b+4c +d)
6) x - 4 = (n+ m+ k-+b+c) x + (-2m+2k -2b+22c +d)
Так как в равенствах левая часть равняется правой, можно из наших выражений получить системы уравнений:
- -
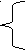
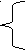
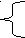 n- m- k-b-c= -1 2) -n- m- k-b+c =1 3) -n- m+ k-b+c =-1
n- m- k-b-c= -1 2) -n- m- k-b+c =1 3) -n- m+ k-b+c =-1
2m-2k +4b-4c +d =-4 2m-2k +4b+4c+d=4 2m+2k +4b+4c +d=0
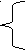
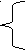
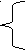 4) n- m-+k-b+c =1 5) n+ m+ k-b+c = -1 6) n+ m+ k-+b+c = 1
4) n- m-+k-b+c =1 5) n+ m+ k-b+c = -1 6) n+ m+ k-+b+c = 12m+2k +4b+4c +d = 0 -2m+2k +2b+2c +d= 4 -2m+2k -4b+4c +d= -4
Теперь согласно методу последовательного исключения неизвестных в каждой системе складываем II и I уравнения. Получаем несколько выражений, которые имеют следующий вид:
1) - n +m-3k + 3b – 5c + d =-5 2) - n +m-3k + 3b + 5c + d =5
3) - n+m+3k+3b+5c+d =-1 4) n +m+3k + 3b +5c + d = 1
5) n - m+3k + 3b +5c + d =3 6) n -m+3k-3b + 5c + d =-3
Составим новую систему, которая будет содержать шесть уравнений с пятью неизвестными:
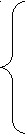
- n +m-3k + 3b – 5c + d =-5
- n +m-3k + 3b + 5c + d =5
- n+m+3k+3b+5c+d =-1
n +m+3k + 3b +5c + d = 1
n - m+3k + 3b +5c + d =3
n -m+3k-3b + 5c + d =-3
Воспользуемся еще раз методом последовательного исключения чисел и из I уравнения вычтем II, из II – III и т.д.

Из данного вычитания получается
1)-10c = -10 c = 1
2)-6k = 6 k = -1
3)-2n = -2 n=1
4) 2m=-2 m=-1
5) 6b=6 b= 1
Теперь подставим известные значения в уравнение, чтобы найти d
- 1-1 + 3 + 3 -5 + d =-5
d = -4
Ответ: В уравнении x - a -a= n x + m x - a + k x + a + b x - 2a + c x + 2a +d
c = 1, k = -1 , n=1, b= 1, m= -1, d = -4 при а = 2
В ходе работы я заметила, что в равенстве x - a -a= n x + m x - a + k x + a + b x - 2a + c x + 2a +d всегда c = 1, k = -1 , n=1, b= 1, m= -1, а вот d всегда равен -2а.
Вывод:
В результате проделанной работы мы выполнили поставленную в начале задачу, то есть нашли все значения неизвестных параметров при различном значении коэффициента а. Было доказано, что равенство
x - a = n x + m x - a + k x + a + d выполняется при любом а.
После решения третьего примера стало очевидным, что значения параметров n, m, k не изменяются ни при каком а, то есть всегда n = -1, m =1, k =1. А вот на d значение коэффициента а оказывает влияние, так как при решении примеров было установлено, что d = -а.
Предположенная гипотеза подтвердилась, так как равенство
x - a = n x + m x - a + k x + a + d действительно выполняется при любом а и n, m, k, d имеют постоянные значения (n = -1, m =1, k =1, d = -а.).
Во второй части работы мы усложнили первый вариант равенства, добавив в него еще один модуль.
Выяснили, что равенство x - a -a= n x + m x - -a + k x + a + b x - 2a + c x + 2a +d выполняется также при любом значении а, а вот значения некоторых параметров не совпадают со значениями первого варианта работы, теперь они равны: c = 1, k = -1 , n=1, b= 1, m= -1 - на коэффициент d значение а также оказывает влияние d=-2a.
Очевидно
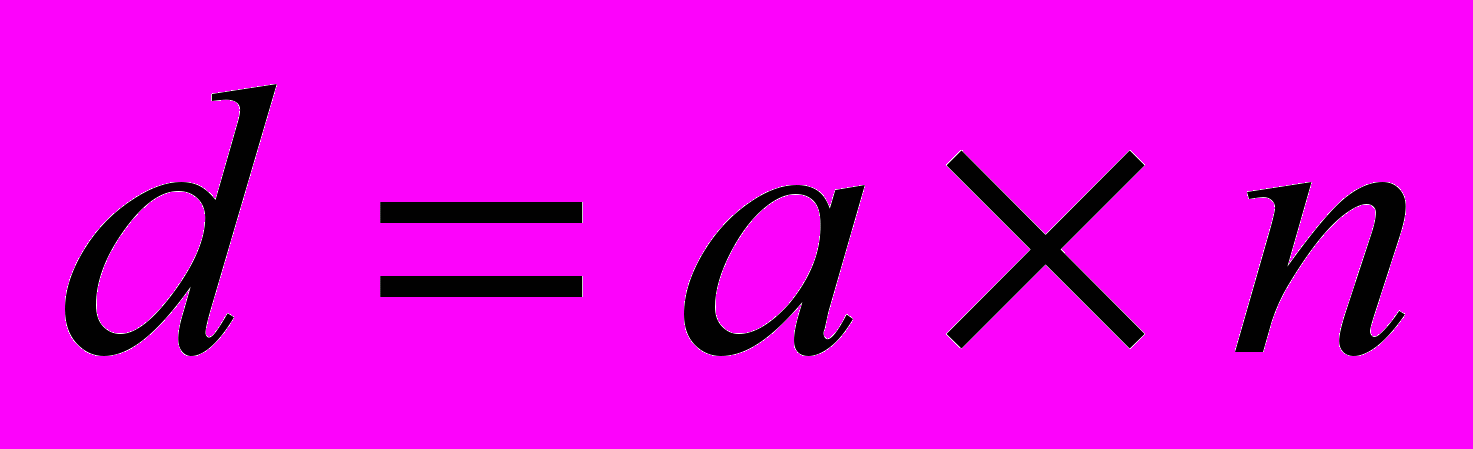 , где n - количество коэффициентов а под модулями в левой части равенства
, где n - количество коэффициентов а под модулями в левой части равенстваЯ думаю, что мое исследование поможет мне в дальнейших работах, связанных с вычислениями, а именно при встрече с уравнением вида: x - 1 = b - я смогу заменить его на следующее:- x + x - a + x + a-d= b – так как считаю его решение более рациональным. Мы уже доказали равенство двух представленных выражений, поэтому замена одного на другое возможна. Также можно заменить x - a -a= k на x - a -a= n x + m x - a + k x + a + b x - 2a + c x + 2a +d = k.
Также при встрече с подобным уравнением, где коэффициент d будет не известен, я смогу найти его по представленной выше формуле.

Петрова Екатерина, 7 класс МОУ «Орловская СОШ» Руководитель: Страздина Е.А., учитель математики
«Зрительные иллюзии и геометрия»
Иллюзии – обман чувств, нечто кажущиеся. Ошибочное восприятие предметов, явлений. Представителей естественных наук, в частности физиков и астрономов всегда волновала надежность визуальных наблюдений.
Стоит ли доверять всему, что мы видим? Можно ли увидеть то, что никто не видел? Правда ли, что неподвижные предметы могут двигаться? Почему дети и взрослые видят один и тот же предмет по-разному? Всегда ли можно доверять своему зрению?
Ответы на эти и другие «почему» я постаралась найти в своей работе с помощью геометрии, строгие законы, которой объясняют некоторые особенности зрительного восприятия.
Объектом исследования являются зрительные иллюзии, а предметом - изучение причин иллюзий.
Цель работы: Объяснить зрительные иллюзии с точки зрения геометрии.
Гипотеза: Зрительные иллюзии можно объяснить с помощью законов геометрии.
Задачи исследования:
Подобрать и изучить литературу по теме исследования.
Провести опыты, связанные со зрительными иллюзиями, и доказать их с точки зрения геометрии.
Найти примеры использования оптических иллюзий.
Разработать рекомендации по использованию иллюзий в современной жизни.
Сделать выводы, заключение
Я использовала следующие методы исследования:
1. Изучение литературы.
2. Сопоставление существенных признаков.
3. Доказательство, анализ, сравнение, обобщение.
В результате изучения литературы я узнала, что иллюзии делятся на:
1. Двойственные.
2. Зрительные искажения.
3. Иллюзии цвета и контраста.
4. Восприятие размера.
5. Кажущиеся фигуры.
6. Невозможные фигуры.
7. Перевернутые фигуры.
8. Распознавание образа.
9. Соотношение фигур и фона. (подобранны примеры, иллюстрации)
Наиболее часто картины с иллюзиями писал Сальвадор Дали, которого можно смело назвать величайшим гением сюрреализма 20-го века. (Приведена краткая биография)
Далее в работе приведено описание практической работы по выявлению иллюзий и их доказательство. Я решила провести опрос. Предложила некоторые картины Сальвадора Дали учителям и учащимся нашей школы с вопросом: Что изображено на картине? Предлагалось 6 картин. Например, Иисус в Иерусалиме Таинственный рыцарь и другие.


Мною было опрошено 10 учителей и 10 учащихся.
Результаты опроса представлены на диаграмме.
Вывод: 50% опрошенных учителей, 40% опрошенных учащихся обладают развитым стереометрическим зрением. 100% опрошенных сказали, что ранее не знали, что такое сюрреализм.
Так же для доказательства связи зрительных иллюзий и геометрии мной были проведены опыты:
Опыт №1.
Сравним относительные размеры находящихся в поле зрения предметов.
Если предметы удалены от глаз на одно и то же расстояние и расположены достаточно близко друг к другу, их сравнить легко. В этом случае мы редко ошибаемся в своей оценке: более высокий предмет виден под большим углом, поэтому и кажется выше.
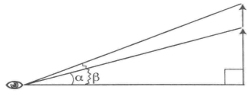 Рис.1
Рис.1Усложним задачу: расположим предметы на разном расстоянии от глаза, в том числе предметы разного размера. Тогда их видимые размеры кажутся одинаковыми.
Выстроим, друг за другом по росту несколько матрешек, посмотрим на них со стороны с самой маленькой фигурки, а затем начнем медленно отходить назад, не изменяя при этом направления взгляда, то можно наблюдать, как матрешки будут постепенно «сливаться», загораживая друг друга. Наконец, на некотором расстоянии будет видна только одна из них – та, что расположена ближе остальных.
Вывод: Независимо от формы предметов, наблюдаемое явление должно описываться «на языке математики» одним и тем же законом, в котором ключевую роль играют, вероятно, такие параметры, как линейный размер и расстояние до предмета.
Опыт №2.
Рассмотрим фрагменты висящей на стене картины. Почему, чем ближе мы подходим к ней, тем больше начинаем различать такие подробности, которые не замечали раньше?
Доказательство. Чем больше угол зрения, тем крупнее изображение каждой детали на сетчатке глаза, оно «захватывает» все больше нервных окончаний, благодаря чему мы начинаем различать в предмете такие подробности, которые не замечали раньше.
Вывод: хотите разглядеть фрагмент висящей на стене картины или мелкий шрифт на странице книги – попробуйте увеличить угол зрения, подойдя к холсту поближе (приблизив текст к глазам). А если объект наблюдения слишком мал или его детали плохо различимы невооруженным глазом, следует воспользоваться лупой или другим оптическим прибором, который позволяет увидеть объект под большим углом.
Опыт№3
Рассмотрим две «убегающие» от нас параллельные линии (трамвайные или железнодорожные).
Они кажутся сходящимися в некоторой точке горизонта. При этом сама точка представляется нам бесконечной удаленной и недосягаемой. Зрение словно пытается убедить нас в том, что вопреки законам геометрии параллельные прямые пересекаются.
Доказательство: Эта иллюзия объясняется рассмотренной нами выше особенностью зрительного восприятия. Объект (шпала), находящийся на различных расстояниях от наблюдателя, виден под разными углами зрения и по мере удаления вдоль параллельных прямых (рельсов), его угловой размер уменьшается, что приводит к видимому уменьшению расстояния между линиями (в данном случае оно определяется величиной шпалы). Очевидно, когда угол зрения достигает некоторой «критической» величины, глаз перестает различать удаляющийся объект как тело, имеющее размеры, и прямые «сливаются» для него в одну точку.
Вывод: существует предельное значение угла зрения – наименьшее значение, при котором глаз способен видеть раздельно две точки.
