Назаров а. А. Элементарное доказательство Великой теоремы Ферма
| Вид материала | Документы |
СодержаниеОбобщенное утверждение |
- Ferma-pifagor- 2m © Н. М. Козий, 2007 Украина, А. С. №22108, №27312, №28607 доказательство, 61.13kb.
- «Загадка песчаных гор», 62.53kb.
- А. Н. Рудаков 1-2 курс Кватернионы, октавы и теорема Гурвица Литература, 8.27kb.
- Ема урока. Свойство медианы равнобедренного треугольника, 39.45kb.
- Доклад По философии на тему: Биография Пифагора Самосского, 106.58kb.
- Программа междисциплинарного государственного экзамена по специальности 090102 Компьютерная, 116.53kb.
- Карен Бликсен. Прощай, Африка!, 4654.85kb.
- Содержание: Введение, 134.15kb.
- Программа вступительного экзамена в магистратуру математического факультета, 107.92kb.
- Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора, 42.5kb.
или z5 = x5 + y5.
Следовательно, утверждение справедливости x6 + y6 = z6 привело к x5 + y5 = z5, что, как известно, противоречит единственности решения для тройки чисел x, y и z относительно n.
В общем виде прямоугольника Паскаля можно записать, что
| a0 | a1 | … | a i | … | an-1 | an | | |
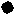 |  | … |  | … |  | 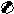 | ~ | xn |
| … | … | … | … | … | … | … | … | … |
| 1 | k + 1 | … | Ck+ii | … | Ck+n-1n-1 | Ck+nn | ~ | yn = (x + k)n |
| … | … | … | … | … | … | … | … | … |
| 1 | m + 1 | … | Cm+ii | … | Cm+n-1n-1 | Cm+nn | ~ | zn = (x + m)n |
| 1 + 1 | k + 2 | … | Ck+ii + 1 | … | Ck+n-1n-1 + 1 | Ck+nn + 1 | ~ | zn = yn + xn |
| 0 | m – k –1 | … | Cm+ii – – Ck+ii – 1 | … | Cm+n-1n-1 – – Ck+n-1n-1 – 1 | Cm+nn – – Ck+nn – 1 | ~ | 1a0 |
влечет
| a0 | a1 | … | a i | … | an-1 | | | |
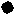 |  | … |  | … |  | | ~ | xn-1 |
| … | … | … | … | … | … | | … | … |
| 1 | k + 1 | … | Ck+ii | … | Ck+n-1n-1 | | ~ | yn-1 = (x + k)n-1 |
| … | … | … | … | … | … | | … | … |
| 1 | m + 1 | … | Cm+ii | … | Cm+n-1n-1 | | ~ | zn-1 = (x + m)n-1 |
| 1 + 1 | k + 2 | … | Ck+ii + 1 | … | Ck+n-1n-1 + 1 | | ~ | zn-1 = yn-1 + xn-1 |
| 0 | m – k –1 | … | Cm+ii – – Ck+ii – 1 | … | Cm+n-1n-1 – – Ck+n-1n-1 – 1 | | ~ | 1a0 |
или xn + yn = zn влечет xn-1 + yn-1 = zn-1, что является противоречием.
Обратное не верно.
Известное существование решения x2 + y2 = z2 в целых положительных ограничивает применение рассмотренного доказательства по степени n > 2. Хотя этому имеются и иные, комбинаторные, основания.
Кроме того, можно предположить, если Ферма рассуждал, как мы рассмотрели, что лишь работа с целыми предметами (камешками или шарами) могла помешать автору Великой теоремы снять ограничение целостности x.
Естественно, Ферма не раскладывал камешки или шары по ящичкам или ячейкам. Это всего лишь образ. Он и его современники более увлекались играми в кости и в карты. Опыт этих игр со временем позволил Ферма и Паскалю сформулировать основы комбинаторики и теории вероятностей – новых направлений в математике.
Но что бесспорно, так это то, что Ферма в совершенстве владел приемами исчисления приращений и методом спуска. На нашем примере это могло выглядеть так
| (x – 5) = 8 | (x – 4) = 9 | (x – 3) = 10 | (x – 2) = 11 | (x – 1) = 12 | x = 13 |
| (x – 5)4 = 4096 | (x – 4)4 = 6561 | (x – 3)4 = 10000 | (x – 2)4 = 14641 | (x – 1)4 = 20736 | x4 = 28561 |
| | 2465 | 3439 | 4641 | 6095 | 7825 |
| | | 974 | 1202 | 1454 | 1730 |
| | | | 228 | 252 | 276 |
| | | | | 24 | 24 |
| | | | | 0 | 0 |
для степени n = 4,
где в первой строке проставлен ряд натуральных чисел,
во второй – значения 4–х степей этих чисел,
в третьей – первые приращения, например, 2465 = 6561 – 4096,
в четвертой – вторые приращения, например, 974 = 3439 – 2465, и так далее.
Достаточно было установить, что ряд (спуск) приращений всегда обрывается на n–м шаге, и что на этом последнем шаге для всех чисел появляется всегда одинаковое число (n!). Сразу же становится ясно, что n–я степень x всегда равна сумме приращений для n–й степени числа x – 1, включая самою эту степень (x – 1)n.
Так, в примере, x4 = 28561 = 24 + 252 + 1454 + 6095 + 20736, где 20736 = (x – 1)n.
Всё это Ферма проделывал великое множество раз, доведя, в конце концов, исчисление приращений степенных последовательностей до исчисления бесконечно малых и методов дифференцирования степенных функций.
Делая обобщения в исчислении приращений степенных последовательностей, вполне вероятно, Ферма пришел к пониманию того, что во втором параграфе названо биноминальным базисом для числа x n.
Для нашего примера это обобщение выглядит следующим образом
| x – 5 | x – 4 | x – 3 | x – 2 | x – 1 | x |
| | | | | | |
| (x – 5)4 | (x – 4)4 | (x – 3)4 | (x – 2)4 | (x – 1)4 | x4 |
| | | | | | |
| | (x – 4)4 – (x – 5)4 | (x – 3)4 – (x – 4)4 | (x – 2)4 – (x – 3)4 | (x – 1)4 – (x – 2)4 | x4 – (x – 1)4 |
| | | (x – 3)4 – (x – 4)4 – ((x – 4)4 – (x – 5)4) | (x – 2)4 – (x – 3)4 – ((x – 3)4 – (x – 4)4) | (x – 1)4 – (x – 2)4 – ((x – 2)4 – (x – 3)4) | x4 – (x – 1)4 – ((x – 1)4 – (x – 2)4) |
| | | | (x – 2)4 – (x – 3)4 – ((x – 3)4 – (x – 4)4) – ((x – 3)4 – (x – 4)4 – ((x – 4)4 – (x – 5)4)) | (x – 1)4 – (x – 2)4 – ((x – 2)4 – (x – 3)4) – ((x – 2)4 – (x – 3)4 – ((x – 3)4 – (x – 4)4)) | x4 – (x – 1)4 – ((x – 1)4 – (x – 2)4) – ((x – 1)4 – (x – 2)4 – ((x – 2)4 – (x – 3)4)) |
| | | | | (x – 1)4 – (x – 2)4 – ((x – 2)4 – (x – 3)4) – ((x – 2)4 – (x – 3)4 – ((x – 3)4 – (x – 4)4)) – ((x – 2)4 – (x – 3)4 – ((x – 3)4 – (x – 4)4) – ((x – 3)4 – (x – 4)4 – ((x – 4)4 – (x – 5)4))) = 24 | x4 – (x – 1)4 – ((x – 1)4 – (x – 2)4) – ((x – 1)4 – (x – 2)4 – ((x – 2)4 – (x – 3)4)) – ((x – 1)4 – (x – 2)4 – ((x – 2)4 – (x – 3)4) – ((x – 2)4 – (x – 3)4 – ((x – 3)4 – (x – 4)4))) = 24 |
| | | | | | x4 – (x – 1)4 – ((x – 1)4 – (x – 2)4) – ((x – 1)4 – (x – 2)4 – ((x – 2)4 – (x – 3)4)) – ((x – 1)4 – (x – 2)4 – ((x – 2)4 – (x – 3)4) – ((x – 2)4 – (x – 3)4 – ((x – 3)4 – (x – 4)4))) – ((x – 1)4 – (x – 2)4 – ((x – 2)4 – (x – 3)4) – ((x – 2)4 – (x – 3)4 – ((x – 3)4 – (x – 4)4)) – ((x – 2)4 – (x – 3)4 – ((x – 3)4 – (x – 4)4) – ((x – 3)4 – (x – 4)4 – ((x – 4)4 – (x – 5)4)))) = 0 |
и можно непосредственно убедиться в общем виде приращений для x4 по уровням, начиная с 0–го, то есть с (x – 1)4,
0. (x – 1)4
1. (x – 1)4 – (x – 2)4
2. (x – 1)4 – 2(x – 2)4 + (x – 3)4
3. (x – 1)4 – 3(x – 2)4 + 3(x – 3)4 – (x – 4)4
4. (x – 1)4 – 4(x – 2)4 + 6(x – 3)4 – 4(x – 4)4 + (x – 5)4.
Очевидно, что коэффициенты слагаемых в этих выражениях составляют арифметический треугольник или треугольник Б. Паскаля. С последним Ферма состоял в переписке. Вид этого треугольника приведен ранее в первом параграфе.
Далее доказательство утверждения Ферма формировалось, вероятно, так, как изложено в настоящем обсуждении. Доказательство или, по крайней мере, основное в идее доказательства вполне могло состояться в 1637 году.
Однако, спустя некоторое время, из-под пера Ферма появляется частное доказательство утверждения при n = 4. И … ни слова о существовании «удивительного доказательства». Что и послужило впоследствии поводом для мнения, что «удивительного доказательства» не было.
Полагаю, что для такого изменения позиции у Ферма имелись некоторые причины.
Многие математики того времени, делая свои открытия, сначала нарабатывали фактуру: достаточное, на взгляд математика, количество решенных задач на интересующую тему. А затем интуитивно находилось обобщение, которое еще не раз проверялось на примерах. В случае положительного исхода всех доступных расчетов объявлялся результат. Этот результат содержал, как правило, формулы, позволяющие вычислить те или иные величины, которые бы удовлетворяли объявленному результату – утверждению. Как нам представляется, в случае «удивительного доказательства», Ферма вдруг обнаружил, что расчетные формулы решения, позволяющие подтвердить его результат для целых положительных чисел, в равной мере дают решение и для некоторых нецелых чисел x, y и z. Но такие решения очевидны и тривиальны по форме. Видимо, Ферма, обнаружив такие числа, не стал анализировать причины их появления, а просто постарался «забыть» о своем доказательстве, как ошибочном.
Судить историкам.
Но ошибкой оказалось как раз признание «удивительного доказательства» ошибочным, о чем свидетельствует утверждение, доказываемое в следующем разделе.
- Обобщенное утверждение
