Доклад По философии на тему: Биография Пифагора Самосского

Вид материала

Доклад

Содержание Был ли Пифагор «выдающимся математиком» своего времени?

Подобный материал:

• Теорема пифагора, 105.05kb.
• Тема. Теорема Пифагора, 72.28kb.
• История теорема Пифагора, 154kb.
• Доклад на 1й сессии Института Человекознания, 50.4kb.
• Интегрированный урок, 88.71kb.
• Доклад на тему: «Взаимодействие философии и частных наук (метафизическая, натурфилософская, 152.34kb.
• С. В. Гиппиус тренинг развития креативности, 5128.29kb.
• Интересна история теоремы Пифагора. Хотя эта теорема и связана с именем Пифагора, она, 97.78kb.
• Тайное Слово Учения мир охранит, Жемчуг волшебный, для душ человечьих Магнит! Золото, 1748.57kb.
• Портреты Владимира Соловьева крупных русских художников Бердяев Н. А. Трагедия философа, 3509.32kb.

Доклад

По философии на тему:


Биография Пифагора Самосского




Биография Пифагора


      Пифагор Самосский (6-й век до н.э.), древнегреческий мыслитель, религиозный и политический деятель,основатель пифагореизма, математик. Пифагору приписывается изучение свойств целых чисел и пропорций, доказательство теоремы Пифагора и другое.

"ЧИСЛО ЕСТЬ СУЩНОСТЬ ВСЕХ ВЕЩЕЙ"
Этого крепкого юношу с упрямой шеей и коротким носом, настоящего драчуна, судьи одной из первых в истории олимпиад не хотели допускать к соревнованиям, укоряли маленьким ростом. Он пробился и победил всех противников. Случись такое каких-нибудь 2530 лет спустя, и газеты всего мира вышли бы с аншлагами: "Никому не известный Пифагор (Греция) завоевал золотую медаль в кулачных боях". Впрочем, в нынешних олимпийских программах нет кулачного боя. А тогда не было газет и медалей. А если бы и были - они не дожили бы до наших дней. Газеты и медали не живут тысячелетия. Только легенды выживают...
Вся жизнь его - легенда. Даже не легенда, а наслоения многих легенд. Наверное, среди самых удивительных и противоречивых домыслов есть самородки истины, но огромная тяжесть ушедшего времени вдавила, растворила их в этом фантастическом окружении, сделала невидимым и для нас. Очень мало мы знаем о жизни Пифагора. Он родился на острове Самос. Меньше пяти километров голубой воды залива Кушада отделяло остров от берегов Малой Азии. Он видел в теплой дымке ясных дней желтые дороги, бегущие по большой земле в большой мир. Они звали его, и он пошел к ним. Совсем юным покинул родину молодой сын Мнезарха Пифагор. Он прошел по дорогам Египта и 12 лет жил в Вавилоне, жадно впитывая речи халдейских жрецов, передававших как эстафету неизвестно кому и когда открывшиеся истины астрономии и бредни астрологии. Может быть, именно астрология породила в нем то бессильное оцепенение мистика, которое так мешало его гению и выросло затем в философию пифагорейской школы. После возвращения домой он переселяется в Италию, затем в Сицилию, и здесь, в Кротоне, рождается эта школа, процветающая под покровительством тирана Поликрата.
Они были трудолюбивы и аскетичны- Пифагор и его ученики. Вот их заповеди:
- Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться.
- Не делай никогда того, чего не знаешь. Но научись всему, что следует знать...
- Не пренебрегай здоровьем своего тела...
- Приучайся жить просто и без роскоши.
- Не закрывай глаз, когда хочется спать, не разобравши всех своих поступков в прошлый день.
Трудно сказать, какие научные идеи принадлежали Пифагору, какие - его воспитанникам. И еще неизвестно, он ли вывел прутиком на песке чертеж Пифагоровой теоремы, известной сегодня каждому школьнику. Они часто гуляли и на прогулках занимались наукой, так что очень вероятно, что теорема родилась на песке. Так же как и доказательство того, что сумма внутренних углов любого треугольника равна двум прямым. Так же, как геометрические решения квадратных уравнений. И может быть, в радостном удивлении склонились они однажды над зыбким чертежом своим, боясь, что ветер унесет первое в истории доказательство несоизмеримости диагонали квадрата и его стороны.
Рассказывают - это опять лишь легенда, - что, когда Пифагор доказал свою знаменитую теорему, он отблагодарил богов, принеся им в жертву 100 быков. Немецкий поэт Шамиссо много веков спустя написал об этом стихи. Он говорил в них, что со времен Пифагоровой жертвы все скоты на земле дрожат от страха, когда открывают что-нибудь новее.
Пифагор не записал своего учения. Оно известно лишь в пересказах Аристотеля и Платона. Гераклит утверждал, что Пифагор ученее всех современников, хотя и считал, что в гении его есть "худое искусство - магия", противная богам. "Они признали математические начала за начала всего существующего", - пояснял Аристотель. Четные числа, например, допускавшие раздвоение, казались пифагорейцам более разумными, олицетворяли некое положительное явление. Так число получало характер, теряло вечное абстрактное начало, как теряют абстракцию числа 2 или 5 для школьника, выводящего мелом "пифагоровы штаны". Число 4, например, олицетворяло у пифагорейцев здоровье, гармонию, разумность. Мистика цифр оказалась очень живучей и дожила до наших дней. Много веков спустя после смерти Пифагора церковники "изобрели" "чертову дюжину", объявили 12 знаком счастья и нарекли 666 "числом зверя". Но в преклонении перед гармонией цифр, перед незыблемостью математической логики было и великое откровение, которое Гегель называл смелостью, о которой писал Энгельс: "Подобно тому как число подчинено определенным законам, так подчинена им и вселенная; этим впервые высказывается мысль о закономерности вселенной".
Пифагор изучал акустику. Он нашел, что все музыкальные интервалы подчинены простейшим рациональным числовым отношениям. Он изучал астрономию, считал Землю шаром, первым вывел наклон эклиптики и планетных орбит и построил свою систему мира, опять-таки отражающую, по его мнению, великую гармонию чисел. Он даже душу математизировал, утверждая, что "душа - солнечные пылинки". В. И..Ленин помечает в скобках в своих "Философских тетрадях": "(=пылинка, атом)" - и рядом пишет на полях: "Пифагорейцы: догадки, фантазии о сходстве макрокосма и микрокосма".
Итак, при всех издержках у знаменитогo философа из Кротона - кстати, первого философа, который назвал себя философом, - немало великих догадок и фантазий. Вот почему люди помнят его уже две с половиной тысячи лет. Вот почему среди знаменитых олимпийских чемпионов он, мне кажется, долго останется самым знаменитым, потому что ему выпало счастье не только победить соперника, но и победить время.

Был ли Пифагор «выдающимся математиком» своего времени?

Теорема почти всюду носит имя Пифагора, но в настоящее время все согласны с тем, что она была открыта не Пифагором. Однако одни полагают, что он первым дал её полноценное доказательство, другие же отказывают ему и в этой заслуге.
Если судить по объему математических знаний своего времени, то может быть и был   выдающимся математиком. Но чтобы стать «выдающимся математиком», как мне кажется, необходимо внести свой вклад в развитие математики – сделать что-то такое, что до тебя сделать никому не удавалось. А именно этот вклад Пифагора в математику достаточно скромный.

Пифагор Самосский  жил около 2,5 тысяч лет тому назад. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко не достоверны. С его именем связано много легенд. Достоверно известно, что Пифагор много путешествовал по странам Востока, посещал Египет и Вавилон. В одной из греческих колоний Южной Италии им была основана знаменитая «Пифагорова школа», сыгравшая важную роль в научной и политической жизни древней Греции. Именно Пифагору приписывают доказательство известной геометрической теоремы. На основе преданий, распространенных известными математиками (Прокл, Плутарх и др.), длительное время считали, что до Пифагора эта теорема не была известна, отсюда и название – теорема Пифагора.

Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Ещё раз напомним, что и  до Пифагора древние египтяне знали о том, что    треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т. е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий.

Да и поныне сельские строители, и плотники, закладывая фундамент избы, изготовляя ее детали,

вычерчивают этот треугольник, чтобы получить прямой угол. Это же самое проделывалось тысячи лет назад при строительстве великолепных храмов в Египте, Вавилоне, Китае, вероятно, и в Мексике.Таким образом, Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым из области практики в область науки. Мы не знаем, как он это сделал.

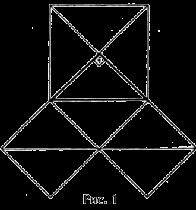
Некоторыми историками математики предполагается, что все же доказательство Пифагора было не принципиальным, а лишь подтверждением, проверкой этого свойства на ряде частных видов треугольников, начиная с равнобедренного прямоугольного треугольника, для которого оно, очевидно, следует из рис. 1.

С глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые замыслы ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более пяти сотен, но стремление к преумножению их числа сохранилось.


Источники:

1. ссылка скрыта (биография)

2. ссылка скрыта (был ли Пифагор «выдающимся математиком» своего времени?)