Интересна история теоремы Пифагора. Хотя эта теорема и связана с именем Пифагора, она была известна задолго до него

Вид материала

Содержание

Сторона треугольника равна корню квадратному из суммы квадратов двух других ее сторон минус удвоенное произведение этих сторон н
1. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
3. Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.
2) Доказательство ан-Найризия
3) Одно из возможных доказательств Пифагора
3) Доказательство Гарфилда
4) Доказательство основанное на теории подобия.

Подобный материал:

ТЕОРЕМА ПИФАГОРА

И

нтересна история теоремы Пифагора. Хотя эта теорема и связана с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора, а в Египте это соотношение использовалось для построения прямого угла еще пять тысяч лет назад. Возможно, что тогда еще не знали ее доказательства, а само соотношение между гипотенузой и катетами было установлено опытным путем на основе измерений. Пифагор, по-видимому, нашел доказательство этого соотношения. Сохранилось древнее предание, что в честь своего открытия Пифагор принес в жертву богам быка, по другим свидетельствам - даже сто быков. На протяжении последующих веков были найдены различные другие доказательства теоремы Пифагора. В настоящее время их насчитывается более пятиста, в том числе: геометрических, алгебраических, механических и прочих. Благодаря такому количеству доказательств, теорема Пифагора попала в Книгу рекордов Гиннеса, как теорема с наибольшим количеством доказательств. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора послужила источником для множества обобщений и плодородных идей. Глубина этой древней истины, по-видимому, далеко не исчерпана.

Существует так называемое дерево Пифагора - гипотетическое дерево, которое составлено из соединенных между собой прямоугольных треугольников, с построенными на катетах и гипотенузе квадратами.

У теоремы Пифагора есть следствие для произвольного треугольника:
Сторона треугольника равна корню квадратному из суммы квадратов двух других ее сторон минус удвоенное произведение этих сторон на косинус угла между ними.
В виде формулы это записывается так:

a² = b² + c² - 2bc*cos α

Это следствие принято называть теоремой косинусов, но по сути - это теорема Пифагора для произвольного треугольника.

Существует три формулировки теоремы Пифагора:

1. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

2. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.

3. Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.

ДОКОЗАТЕЛЬСТВА:

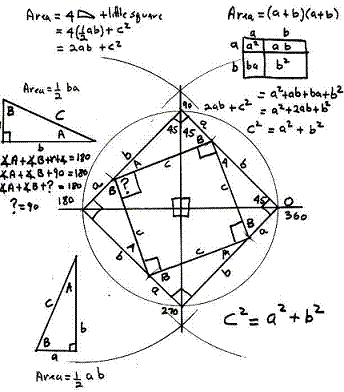
На рисунке изображено два равных квадрата. Длина сторон каждого квадрата равна a + b. Каждый из квадратов разбит на части, состоящие из квадратов и прямоугольных треугольников. Ясно, что если от площади квадрата отнять учетверенную площадь прямоугольного треугольника с катетами a, b, то останутся равные площади, т. е. c² = a² + b². Впрочем, древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали чертеж лишь одним словом: «смотри!» Вполне возможно, что такое же доказательство предложил и Пифагор.

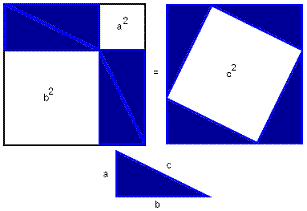
2) Доказательство ан-Найризия*

Доказательство ан-Найризия тоже довольно легкое. Оно примечательно тем, что все фигуры совпадают с равными им исключительно при параллельном переносе.
Д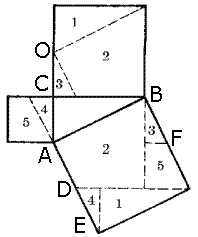ано: при разделении на фигуры надо учитывать, что DE=BF.
Доказательство:
По чертежу ясно видно, что фигруы. отмеченные одинаковыми цифрами, равны. Треугольники 1 и 1, 3 и 3, 4 и 4 равны между собой. Четырехугольники 2 и 2, 5 и 5 также равны. Следовательно, теорема доказана.

* - Латинизированное имя - Аннариций.

3) Одно из возможных доказательств Пифагора

Среди доказательств теоремы Пифагора алгебраическим методом первое место (возможно, самое древнее) занимает доказательство, использующее подобие. Приведем в современном изложении одно из таких доказательств, возможно принадлежащих Пифагору.
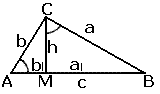
Дано: ΔАВС - прямоугольный с прямым углом С; СМ - высота; b₁ - проекция катета b на гипотенузу, а₁ - проекция катета а на гипотенузу.
Доказательство: Из того, что ΔABC подобен ΔACM следует:

b² = cb₁; (1)

из того, что ΔABC подобен ΔBCM следует:

a² = ca₁. (2)

Складывая почленно равенства (1) и (2), получим a² + b² = cb₁ + ca₁ = c(b₁ + a₁) = c².Теорема доказана.
Если Пифагор действительно предложил такое доказательство, то он был знаком и с целым рядом важных геометрических теорем, которые современные историки м

атематики обычно приписывают Евклиду.

3) Доказательство Гарфилда

Дано: Три пря моугольных треугольника.
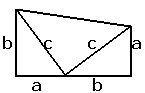
Доказательство: На иллюстрации три прямоугольных треугольника составляют трапецию. Поэтому площадь этой фигуры можно находить по формуле площади прямоугольной трапеции, либо как сумму площадей трех треугольников. В первом случае эта площадь равна

S = (a + b)²,

а во втором случае

ab/2 + ab/2 + c²/2.

Приравнивая эти выражения, получаем теорему Пифагора.

4) Доказательство основанное на теории подобия.

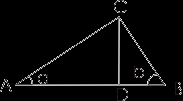
В прямоугольном треугольника АВС проведем из вершины прямого угла высоту CD; тогда треугольник разобьется на два треугольника, также являющихся прямоугольными. Полученные треугольники будут подобны друг другу и исходному треугольнику. Это легко доказать, пользуясь первым признаком подобия треугольников (по двум углам). В самом деле, сразу видно что, кроме прямого угла, треугольники АВС и ACD имеют общий угол a, треугольники CBD и АВС - общий угол b. То, что малые треугольники также подобны друг другу, следует из того, что каждый из них подобен большому треугольнику. Впрочем, это можно установить и непосредственно.
Т.к. катеты прямоугольного треугольника являются средним геометрическим между гипотенузой и проекцией катета на гипотенузу, имеем:

a² = a₁c и b² = b₁c.

Складывая почленно эти равенства, получаем:

a² + b² = c².

Теорема опять доказана.