Применима ли теорема Пифагора к сферическому треугольнику?

Вид материала

Реферат

Содержание Глава 1. Теорема Пифагора в евклидовой геометрии Формулировки и доказательства теоремы Пифагора. Доказательства теоремы Пифагора ABC есть прямоугольный треугольник с прямым углом C Ещё одно доказательство теоремы Пифагора Глава 2. Сферический треугольник и его свойства Прямоугольный сферический треугольник. Глава 3. Сферический аналог теоремы Пифагора

Подобный материал:

• История теорема Пифагора, 154kb.
• Тема. Теорема Пифагора, 72.28kb.
• Интересна история теоремы Пифагора. Хотя эта теорема и связана с именем Пифагора, она, 97.78kb.
• Теорема пифагора, 105.05kb.
• План лекций по физике на 1 семестр 2009/10 уч г. для 1 курса маш факультета, 60.13kb.
• Знаете ли вы, что многие известные люди были инвалидами?, 113.51kb.
• «Теорема Пифагора», 146.81kb.
• Гипотеза: Теорема Пифагора – одна из главных теорем геометрии, 89.67kb.
• Интегрированный урок, 88.71kb.
• Програма н/к "Основи мсс" курс- 3, семестр-1, 54год лекц, 28.91kb.

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа №6»


Тема реферата: «Применима ли теорема Пифагора к сферическому треугольнику?»


выполнил учащийся

8Б класса:

Коен Антон

Руководитель:

Шубина Ирина Николаевна


Муром 2011


Оглавление


Введение………………………………………………………………………3

Глава 1. Теорема Пифагора в евклидовой геометрии……………………4

1. История теоремы Пифагора……………………………………….. –
   
2. Формулировки и доказательства теоремы Пифагора……………5
   

Глава 2. Сферический треугольник и его свойства……………………….10

2.1 Прямоугольный сферический треугольник……………………….12

Глава 3. Сферический аналог теоремы Пифагора………………………..14

Заключение…………………………………………………………………...15

Список литературы………………………………………………………….16


Введение

На протяжении многих веков человечество не переставало пополнять свои научные знания в той или иной области науки. Например, всем известную теорему Пифагора знали задолго до нашей эры, ведь теорема Пифагора – одна из важнейших теорем геометрии. В Древнем Египте она была очень нужна землемерам, чтобы восстанавливать границы участков после разлива Нила. Да и в наши дни она очень важна – на ней основываются доказательства многих теорем, например, теоремы о высоте, проведённой из прямого угла, или основного тригонометрического тождества.

В нашей жизни огромную роль играет такой раздел геометрии, как стереометрия – наука о фигурах в пространстве. Множество учёных геометров, да и простых людей, интересовались такой фигурой как шар и его «оболочкой», носящей название сфера. Удивительно, но шар является единственным телом, обладающим меньшей площадью поверхности при объёме, равном объёму других сравниваемых тел, таких как куб, призма или прочие всевозможные многогранники. С шарами мы имеем дело ежедневно. К примеру, почти каждый человек пользуется шариковый ручкой в конец стержня которой вмонтирован металлический шар, вращающийся под действием сил трения между ним и бумагой и в процессе поворота на своей поверхности шар «выносит» очередную порцию чернил. В автомобильной промышленности изготавливаются шаровые опоры, являющиеся очень важной деталью в автомобиле и обеспечивающей правильный поворот колёс и устойчивость машины на дороге. Элементы машин, самолётов, ракет, мотоциклов, снарядов, плавательных судов, подвергающиеся постоянным воздействиям воды или воздуха, преимущественно имеют какие либо сферические поверхности, называемые обтекателями.

Другой раздел геометрии – сферическая геометрия – наука о фигурах на сфере. И из всех «сферических» фигур наибольший интерес представляет сферический треугольник. В какой-то степени он похож на плоский треугольник, в какой-то – нет. И в своей работе я постараюсь совместить эти два важнейших понятия – теорема Пифагора и сферический треугольник.

Цель работы – узнать о сферическом аналоге теоремы Пифагора.


Глава 1. Теорема Пифагора в евклидовой геометрии

История теоремы Пифагора

Сначала познакомимся с историей теоремы Пифагора.

В Древнем Китае особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:

"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".

Кантор (крупнейший немецкий историк математики) считает, что равенство

3 ² + 4 ² = 5² было известно уже египтянам ещё около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).

По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Очень легко можно воспроизвести способ построения. Возьмём верёвку длиною в 12 м и привяжем к ней по цветной полоске на расстоянии 3 и 4 м от одного конца. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. В самом древнем индийском геометрическом сборнике «Сульвасутра» («Правила верёвки», 600 год до н.э.), представляющем собой своеобразную инструкцию по сооружению алтарей в храмах, даются правила построения прямых углов при помощи верёвки с узлами, расстояния между которыми равны 15, 36 и 39 падас (мера длины). В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифагор первым дал её полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал".

Насчитывается более пятисот доказательств теоремы. Благодаря такому количеству доказательств теорема Пифагора попала в Книгу рекордов Гиннеса как теорема с наибольшим количеством доказательств. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора послужила источником для множества обобщений и плодородных идей. Глубина этой древней истины, по-видимому, далеко не исчерпана.

Ван-дер-Варден (голландский математик) сделал следующий вывод:

"Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но её систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку."


Формулировки и доказательства теоремы Пифагора.

Существует три формулировки теоремы Пифагора:

1. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

2. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.

3. Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.

Обратная теорема Пифагора:

Для всякой тройки положительных чисел a, b и c, такой, что a² + b² = c², существует прямоугольный треугольник с катетами a и b и гипотенузой c.


На данный момент в научной литературе зафиксировано более трёхсот доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.

Данный факт даже нашёл отражение в художественной литературе: в повести «Приключения Электроника» Евгения Велтистова главный герой на школьном уроке математики приводит у доски 25 различных доказательств теоремы Пифагора, повергнув в изумление учителя и всех одноклассников.

Доказательства теоремы Пифагора

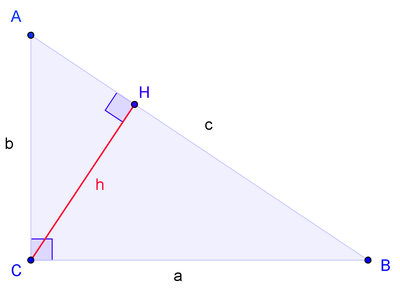
Доказательство через подобные треугольники

Это доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.

Пусть  ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения




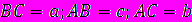
получаем:



Что эквивалентно




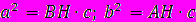
Сложив, получаем



или




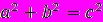
Ещё одно доказательство теоремы Пифагора



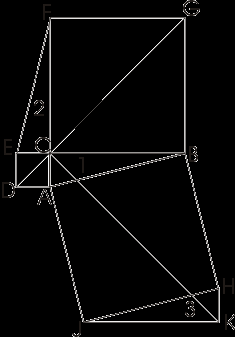
Прямая DG обязательно пройдет через C. Заметим теперь, что шестиугольники DABGFE и CAJKHB равновелики. Если мы от первого из них отнимем треугольники 1 и 2, то останутся квадраты, построенные на катетах, а если от второго шестиугольника отнимем равные треугольники 1 и 3, то останется квадрат, построенный на гипотенузе. Отсюда вытекает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах.


Глава 2. Сферический треугольник и его свойства

Сферическая геометрия - раздел математики, в котором изучаются фигуры, расположенные на сфере. Она представляет собой своеобразный мост между планиметрией и стереометрией, так как сферические многоугольники получаются в пересечении сферы с многогранными углами с вершинами в центре сферы, сферические окружности – в пересечении сферы с коническими поверхностями и т.д. Сферическая геометрия возникла в связи с потребностями астрономии. По-видимому, первым обращением человечества к тому, что потом получит название сферической геометрии, была планетарная теория греческого математика Евдокса (ок. 408–355гг. до н.э.), объяснявшая вращение планет с помощью четырёх концентрических сфер.

Значительный вклад в сферическую геометрию внес Менелай из Александрии жившего в 1 веке. Его труд Сферика стал вершиной достижений греков в этой области. В Сферике рассматриваются сферические треугольники – предмет, которого нет у Евклида.


Сферический треугольник представляет среди всех сферических многоугольников наибольший интерес. Три больших окружности, пересекаясь попарно в двух точках, образуют на сфере восемь сферических треугольников. Зная элементы (стороны и углы) одного из них, можно определить элементы всех остальных, поэтому рассматривают соотношения между элементами одного из них, того, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла ОАВС, углы треугольника – двугранными углами того же трехгранного угла


На поверхности шара кратчайшее расстояние между двумя точками измеряется вдоль окружности большого круга, т. е. окружности, плоскость которой проходит через центр шара. Вершины сферического треугольника являются точками пересечения трех лучей, выходящих из центра шара и сферической поверхности. Сторонами a, b, c сферического треугольника называют те углы между лучами, которые меньше (если один из этих углов равен , то сферический треугольник вырождается в полуокружность большого круга). Каждой стороне треугольника соответствует дуга большого круга на поверхности шара (см. рисунок).





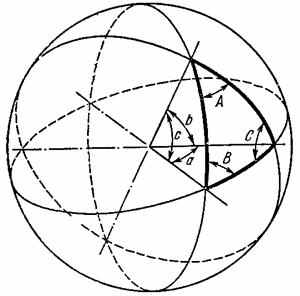
Углы A, B, C сферического треугольника, противолежащие сторонам a, b, c соответственно, представляют собой, по определению, меньшие, чем , углы между дугами больших кругов, соответствующими сторонам треугольника, или углы между плоскостями, определяемыми данными лучами.

Сферическая тригонометрия занимается изучением соотношений между сторонами и углами сферических треугольников (например, на поверхности Земли и на небесной сфере).

Свойства сферических треугольников. Каждая сторона и угол сферического треугольника по определению меньше .

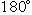В каждом сферическом треугольнике сумма углов заключена между 180^о и 540^о . В каждом сферическом треугольнике против большей стороны лежит больший угол. Сумма любых двух сторон больше третьей стороны, сумма любых двух углов меньше, чем плюс третий угол.

Сферический треугольник единственным образом определяется (с точностью до преобразования симметрии):

1) тремя сторонами,

2) тремя углами,

3) двумя сторонами и заключенным между ними углом,

4) стороной и двумя прилежащими к ней углами.

Замечание. Для каждого сферического треугольника можно определить большие круги, играющие роль перпендикуляров, проведенных через середины сторон, биссектрис, медиан и высот. Плоскости трех больших кругов каждого типа пересекаются по прямой.

В полной аналогии с описанной окружностью плоского треугольника существует описанный прямой круговой конус, содержащий три прямые линии, определяющие треугольник; ось этого конуса есть прямая, по которой пересекаются плоскости перпендикуляров, проведенных через середины сторон. Существует также вписанный прямой круговой конус, касающийся трех плоскостей, соответствующих сферическому треугольнику; ось этого конуса есть прямая, по которой пересекаются плоскости биссектрис. "Радиус" описанной окружности и "радиус" вписанной окружности представляют собой углы, равные соответственно половинам углов при вершинах первого и второго конусов. Если R - радиус шара, то площадь S_R сферического треугольника выражается формулой

S_R=R² ε

где ε - сферический эксцесс (избыток):

ε=(α+ β+γ)-180^о, измеряемый в радианах.

Прямоугольный сферический треугольник.

В прямоугольном сферическом треугольнике по меньшей мере один угол, например C, равен 90^о; противоположная сторона c называется гипотенузой. Соотношения между сторонами и углами прямоугольного сферического треугольника могут быть извлечены из следующих двух мнемонических правил Непера:


В диаграмме на рисунке синус любого из указанных в ней углов равен

1) произведению тангенсов двух углов, прилежащих к нему на диаграмме,

2) произведению косинусов двух углов, противолежащих ему на диаграмме.



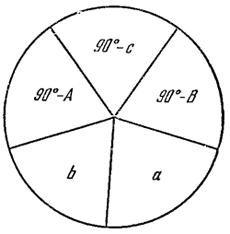
Пример. Найти стороны и углы прямоугольного сферического треугольника, зная гипотенузу c и сторону a.

Эта задача имеет решение только при условии sin a≤sin c, тогда



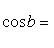
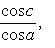
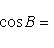
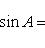
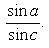
Замечание. Если a меньше, равно или больше 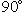, то и A соответственно меньше, равно или больше 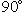, и наоборот.

Если даны a и A, то задача имеет решение только в том случае, когда предыдущее условие выполнено и, кроме того, sin a≤sin A; если 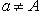, то решений два.

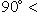
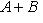
Если даны A и B, задача имеет решение только при выполнении услови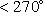й и .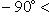

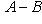
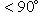Сферический треугольник со стороной, равной 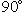, называется квадрантным треугольником и может рассматриваться как полярный треугольник прямоугольного сферического треугольника.

Ко всем задачам, включающим решение сферических треугольников (прямоугольных и косоугольных), настоятельно рекомендуется делать эскиз, ясно показывающий, будут ли различные углы и стороны меньше, равны или больше.


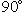Глава 3. Сферический аналог теоремы Пифагора

Выведем аналог теоремы Пифагора на сфере, т.е. выражение гипотенузы

прямоугольного сферического треугольника через его катеты.

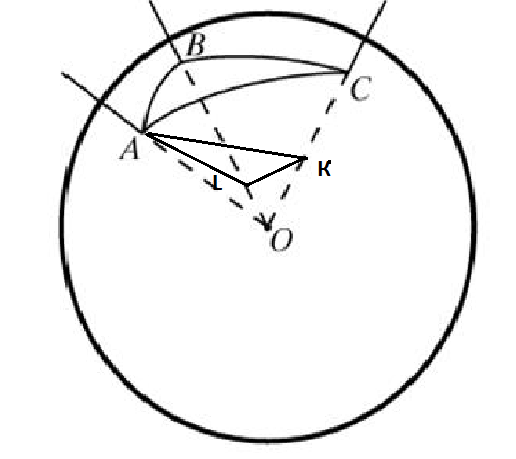
Возьмём треугольник ABC (С - вершина прямого угла) на сфере с центром в точке О. Положим BC=a, CA=b, AB=c (длины соответствующих дуг больших кругов сферы). Проведем теперь некоторые построения в евклидовом пространстве, в котором находится наша сфера. Опустим из точки A перпендикуляр AK на радиус OC. Поскольку плоскости AOC и BOC перпендикулярны, отрезок AK будет перпендикулярен плоскости

BOC. Опустим из точки K перпендикуляр KL на радиус OB. По теореме о трех перпендикулярах отрезок AL будет также перпендикулярен радиусу OB. Имеем

a = угол BOC, b = угол COA, c = угол AOB.

Из прямоугольных треугольников AOK, AOL и KOL находим:

OK = cos b, OL = cos c = OK* cos a,

откуда

cos c = cos a cos b.

Это и есть теорема Пифагора в сферической геометрии.




Заключение

Теорема Пифагора для сферического треугольника нужна не только астрономам, штурманам морских кораблей, самолетов, космических кораблей, которые по звездам определяют свои координаты, но и строителям шахт, метрополитенов, тоннелей, а также геодезических съемках больших поверхностях земли, когда становится необходимым учитывать ее шарообразность.

Подводя итоги проделанной работе, необходимо отметить, что в ней я

показал важность и необходимость теоремы Пифагора и сферической геометрии, и это доказывает актуальность сферического аналога этой теоремы и в наши дни.




Литература

1. dia.org/wiki/Сферическая_геометрия

2. .ru/sferich.php

3. АбрамовА.М, Виленкин Н.Я, ДорофеевГ.В, и др Избранные вопросы математики 10 кл.: Факультативный курс./Под ред. ФирсоваВ.В/-М. : Просвещение 1992.

4. В. Литцман. Теорема Пифагора, ОНТИ, 1962.

5. П. С. Александров Что такое неевклидова геометрия, АПН РСФСР, 1950