Домашнее задание Два шарика одинакового радиуса и массы, подвешенные на нитях одинаковой длины, опускаются в жидкий диэлектрик, плот­ность которого  1 и диэлектрическая проницаемость. Како­ва должна быть плотность

Вид материала

Документы

Содержание R = 5 см окру­жен сферическим слоем диэлектрика толщиной d R = 2 см несет заряд, равномерно распределенный по объему с объемной плотно­стью  = Домашнее задание Е = 60 кВ/м. Расстояние между пластинами конденсатора d А радиусом 2 см приводится в соприкос­новение с незаряженным шаром В С = 10 пФ за­ряжена до потенциала  R равномерно заряжен электри­чеством с объемной плотностью . Сфера какого радиуса R S = 400 cм, заполнен двумя слоями диэлектрика. Граница между ними параллельна обкладкам. Первый слой - прессшпан ( = 2) толщины R = 10 см заряжен равномерно по объему с объемной плотностью  = 10 нКл/м. Определить энергию W Тема 3: Законы постоянного тока U = 6,6 кВ. Потребитель находится на расстоянии l = I = 10 А. Какую наибольшую силу тока может измерить этот амперметр без шунта, если сопротивление амперметра R N одинаковых элементов с э.д.с. и внутренним сопротивлением r Домашнее задание R = 100 Ом равномерно нарастает от I R = 3 Ом течёт равномерно нарастающий ток. Количество теплоты, выделившееся в проводнике за время t = R = 15 Ом равномерно возрастает от I Домашнее задание R. (рис.7). Найти индукции магнитного поля в точке О. Задача 11. Тонкая лента шириной l = 2d параллельно её поверхности. Найти индукцию магнитного поля этого тока как функцию расстояния X ... Полное содержание

Подобный материал:

• Контрольная работа №2 №3-1 Два одинаковых шарика подвешены на нитях одинаковой длины, 195.88kb.
• Домашнее задание по дисциплине «Стратегический менеджмент» Домашнее задание может быть, 41.07kb.
• Лекция магнитооптические явления, Гиротропия, 119.87kb.
• Программа вступительного экзамена подготовки магистров, 187.59kb.
• Личность Ивана Грозного. Начало правления. $ Беседа. Домашнее задание $ Внешняя политика, 28.5kb.
• Домашнее задание 3 по дисциплине "Программирование на языке высокого уровня, 25.78kb.
• Домашнее задание ответа на зачете Алгоритм формирования оценки таков: вес посещаемости, 76.53kb.
• Т. А.. учитель русского языка и литературы цо №1943 Цели, 120.64kb.
• Его причины и особенности, силовые связи между частицами среды, перенос энергии без, 14.74kb.
• Домашнее задание по дисциплине «Стратегический менеджмент», 41.68kb.

Пояснение: в контрольной работе предлагаются задачи по семи темам. Из каждой темы на выбор нужно решить по две задачи, в соответствии со своим вариантом. Вариант определяется по последним двум цифрам зачётной книжки.


Электростатика


Тема 1: Закон Кулона. Методы расчета электростатических полей


Домашнее задание


1. Два шарика одинакового радиуса и массы, подвешенные на нитях одинаковой длины, опускаются в жидкий диэлектрик, плот­ность которого ₁ и диэлектрическая проницаемость . Како­ва должна быть плотность  материала шариков, чтобы углы расхождения нитей в воздухе и в диэлектрике были одинаковыми?

2. Два точечных заряда 6,7 нКл и 13,2 нКл находятся на рассто­янии 6 см друг от друга. Найти напряженность электрического поля в точке, расположенной на расстоянии 3 см от первого за­ряда и 4 см от второго.

3. В трех вершинах квадрата со стороной 40 см находятся положительные одинаковые заряды по 5 нКл каждый. Найти напря­женность поля в четвертой вершине.

4. Полуокружность радиуса R = 2 м равномерно заряжена зарядом q = 10^-9 Кл. Определить напряженность электрическо­го поля, созданного этим зарядом в геометрическом центре по­луокружности .

5. В вершинах квадрата расположены точечные заряды 10,33; -0,66; 0,99; -1,32 нКл. Определить потенциал поля в центре квадрата, если его диагональ равна 20 см.

6. Шарик, имеющий массу 0,4 г и заряд 4,9 нКл, подвешен на нити в поле плоского конденсатора, заряд которого 4,43 нКл и площадь пластин 50 см². На какой угол от вертикали отклонится при этом нить с шариком?

7. Тонкое кольцо радиуса R = 8 см несет заряд, равномерно распределенный с линейной плотностью  = 10 нКл/см. Какова напряженность электрического поля в точке, равноудаленной от всех точек кольца на расстояние r = 10 см?

8. В центр квадрата, в вершинах которого находится по заря­ду в 20 нКл, помещен отрицательный заряд. Найти величину этого заряда, если результирующая сила, действующая на каждый заряд, равна нулю.

9. Тонкий стержень длиной l = 12 см заряжен с линейной плотностью  = 200 нКл/м. Найти напряженность электрическо­го поля в точке, находящейся на расстоянии r = 5 см от стер­жня, против его середины.

1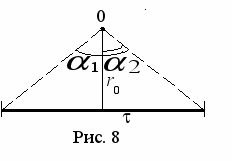0. Определить напряженность поля отрезка, равномерно заря­женного с линейной плотностью , в точке O, удаленной от отрезка на расстояние r₀. Углы ₁ и ₂, заданы (см. рис.8).

11. Тонкий стержень длиной 20 см равномерно заряжен с линейной плотностью 1 нКл/см. Определить напряженность поля, созданного стержнем в точке А на продолжении его оси, на рас­стоянии 10 см от ближнего конца, и силу взаимодействия стержня и заряда 10^-8 Кл, если его поместить в точку А.

12. На отрезке тонкого прямого проводника длиной l = 10 см равномерно распределен заряд с линейной плотностью  = 3 мкКл/м. Вычислить напряженность, создаваемую этим зарядом в точке, расположенной на оси проводника и удаленной от бли­жайшего конца отрезка на расстояние, равное длине этого от­резка. Диэлектрик - воздух.

13. Прямая бесконечная нить, равномерно заряженная электричеством с линейной плотностью ₁ = 3  10^-7 Кл/м, и отрезок длины l = 20 см, равномерно заряженный электричеством с линейной плотностью ₂ = 2  10^-7 Кл/м, расположены в одной пло­скости перпендикулярно друг к другу на расстоянии r₀ = 10 см. Определить силу взаимодействия между ними.

14. Прямая тонкая бесконечная нить несет равномерно распределенный по длине заряд (₁ = 1 мкКл/м). В плоскости, со­держащей нить, перпендикулярно к нити находится тонкий стер­жень длиной l. Ближайший к нити конец стержня находится на расстоянии l от нее. Определить силу, действующую на стер­жень, если он заряжен с линейной плотностью ₂ = 0,1 мкКл/м.

15. Сто одинаковых капель ртути, заряженных до потенциала  =20 В, сливаются в одну большую каплю. Каков потенциал образовавшейся капли?

16. Электрическое поле создано бесконечной, прямой, равно­мерно заряженной нитью ( = 0,3 мкКл/м). Определить поток N_E вектора напряженности через прямоугольную площадку, две большие стороны которой параллельны заряженной нити и одина­ково удалены от нее на расстояние r = 20 см. Стороны пло­щадки имеют размеры a = 20 см, в = 40 см.

17. Имеются две металлические концентрические сферы, ради­усы которых 5 и 10 см и заряды 2  10^-8 и –10^-8 Кл. Определить напряженность поля, созданного этими сферами, в точках, от­стоящих от центров сфер на расстояния 3, 8 и 14 см. Построить график зависимости напряженности поля от расстояния точки от центра сфер.

18. Металлический заряженный шар радиусом R = 5 см окру­жен сферическим слоем диэлектрика толщиной d = 5 см. Диэ­лектрическая проницаемость слоя  = 3. Заряд шара q = 3,6 нКл. Найти напряженность поля в точках, лежащих на рассто­яниях r₁ = 6 см и r₂ = 12 см от центра шара.

19. Два бесконечных тонкостенных коаксиальных цилиндра ра­диусами R₁ = 5 см и R₂ = 10 см равномерно заряжены электри­чеством с поверхностными плотностями ₁=10 нКл/м² и ₂=-3 нКл/м². Пространство между цилиндрами заполнено парафином (= 2). Определить напряженность поля в точках, находя­щихся на расстояниях r₁ = 2 см, r₂ = 6 см и r₃ = 15 см от оси цилиндров.

20. Большая плоская пластина толщиной  = 1 см несет за­ряд, равномерно распределенный с объемной плотностью  = 100 нКл/м³. Найти напряженность электрического поля вблизи центральной части пластины, вне нее, на малом расстоянии от ее поверхности.

21. Длинный парафиновый цилиндр радиусом R = 2 см несет заряд, равномерно распределенный по объему с объемной плотно­стью  = 10 нКл/м³. Определить напряженность электрического поля в точках, находящихся от оси цилиндра на расстояниях: 1) r₁ = 1 см, 2) r₂ = 3 см. Обе точки равноудалены от концов цилиндра. Построить график зависимости Е(r).

22. Бесконечно длинная тонкая прямая нить несет равномерно распределенный по длине нити заряд с линейной плотностью  = 0,01 мкКл/м. Определить разность потенциалов двух точек поля, удаленных от нити на r₁ = 2 см и r₂ = 4 см.

23. Сплошной шар из диэлектрика ( = 3) радиусом R = 10 см заряжен с объемной плотностью  = 50 нКл/м³. Напряженность электрического поля внутри и на поверхности такого шара выражается формулой Е = r / 3₀, где r - расстояние от центра шара до точки, в которой вычисляется напряженность поля. Вычислить разность потенциалов между центром шара и точками, лежащими на его поверхности.

24. Эбонитовый толстостенный шар ( = 3) несет равномер­но распределенный по объему заряд с объемной плотностью  = 2 мкКл/м³. Внутренний радиус шара R₁ = 3 см, наружный R₂ = 5 см. Определить потенциал шара в следующих точках: 1) на наружной поверхности шара, 2) на внутренней поверхности шара, 3) в центре шара.

25. Две металлические концентрические сферы имеют радиусы R₁ и R₂. На внутренней сфере находится заряд q₁, на внешней - заряд q₂. Найти напряженность E и потенциал  поля вне сфер, а также внутри малой и большой сфер.


Тема 2: Работа сил электростатического поля. Емкость проводников и конденсаторов. Энергия электростатического поля