Общие указания к решению задач

Вид материала

Задача

Содержание Критерии оценивания индивидуальных заданий 22 - 25 баллов 18 - 21 баллов 14 - 17 баллов 10 - 13 баллов 7 - 9 баллов

Подобный материал:

• Рабочей программы учебной дисциплины методика обучения решению задач уровень основной, 104.55kb.
• Элективный курс по математике, 168.73kb.
• Методические указания по выполнению контрольных работ для студентов заочной формы обучения, 140.67kb.
• Налоговое планирование методические указания по выполнению контрольных работ для студентов, 194.91kb.
• Литература И. Л. Акулич. Математическое программирование в примерах и задачах, 63.8kb.
• Стандарт основного общего образования, 198.78kb.
• Заседание Совета безопасности. Д. Медведев, 562.99kb.
• Планирование работы учителя по обучению учащихся решению текстовых задач арифметическим, 495.12kb.
• Рекомендации абитуриентам Экзамен по физике проводится в письменной форме. На выполнение, 87.67kb.
• Методика использования компьютерных моделей в обучении школьников 10-11 классов решению, 40.67kb.

ОБЩИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ

1. Указать основные законы и формулы, на которых базируется решение, разъяснить буквенные обозначения формул. Если при решении задач применяется формула, полученная для частного случая, не выражающая какой-нибудь физический закон, или не являющаяся определением какой-нибудь физической величины, то ее следует вывести.
   
2. Дать чертеж, поясняющий содержание задачи (в тех случаях, когда это возможно).
   
3. Сопровождать решение задачи краткими, но исчерпывающими пояснениями.
   
4. Получить решение задачи в общем виде.
   
5. Подставить в правую часть полученной рабочей формулы вместо символов величин обозначения единиц, произвести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине.
   
6. Подставить в рабочую формулу числовые значения величин, выраженные в единицах одной системы.
   
7. Произвести вычисление величин, подставленных в формулу, руководствуясь правилами приближенных вычислений, записать в ответе числовое значение и сокращенное наименование единицы искомой величины.
   
8. Оценить, где это целесообразно, правдоподобность численного ответа.
   

КРИТЕРИИ ОЦЕНИВАНИЯ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ

В каждом модуле студент должен защитить 4 задачи. Одна задача оценивается в 25 баллов.

22 - 25 баллов	Задача решена верно. В оформлении присутствует дано, найти, чертеж. Указаны основные законы и формулы, на которых базируется решение, разъяснены буквенные обозначения в формулах, получена расчетная формула. Проведена проверка единиц измерения. Студент отвечает на вопросы по решению задачи.
18 - 21 баллов	В решении отсутствуют разъяснения обозначений, нет проверки единиц измерения, при вычислении допущены арифметические ошибки, которые ставят под сомнение правдоподобность численного ответа. Студент не всегда поясняет ход решения.
14 - 17 баллов	В решении имеются недочеты, нет чертежа, нарушена логика решения задачи. Студент затрудняется отвечать на отдельные вопросы. Верно решенная задача, сданная повторно (в первый раз решение было не верно).
10 - 13 баллов	В решении присутствуют элементы верного решения, но при выводе расчетной формулы допущены ошибки. При решении используется "готовая" формула.
7 - 9 баллов	Задача решена правильно, но студент не может пояснить ход решения задачи – очевидно, что решение задачи – плод чужого труда. Правильно решенная задача без «защиты».

Т Е М Ы З А Д А Ч

ЭЛЕКТРИЧЕСТВО

I. Закон Кулона

II. Напряженность и потенциал точечного заряда

III. Напряженность и потенциал поля объемного заряда. Принцип суперпозиции полей.

IV. Напряженность и потенциал поля объемного заряда. Теорема Остроградского- Гаусса

V. Заряженная частица в электрическом поле

VI. Законы Ома. Правила Кирхгофа

VII. Энергия электрического поля. Закон Джоуля Ленца.

ЭЛЕКТРОМАГНЕТИЗМ

VIII. Сила Ампера

IX. Закон Био- Савара- Лапласа. Принцип суперпозиции магнитных полей

X. Сила Лоренца

XII. Энергия магнитного поля

XII. Индукция. Самоиндукция


ЭЛЕКТРИЧЕСТВО


I. Закон Кулона

1. Сила гравитационного притяжения двух водяных одинаково заряженных капель радиусом 0,1 мм уравновешивается кулоновской силой отталкивания. Определить заряд капель. Плотность воды равна 1 г/см³.
   
2. Два заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин плотностью 0,8 г/см³. Какова должна быть плотность материала шариков, чтобы угол расхождения нитей в воздухе и керосине был один и тот же? Диэлектрическая проницаемость керосина =2.
   
3. В вершинах равностороннего треугольника находятся одинаковые положительные заряды Q=2 нКл. Найти силу, действующую на заряд со стороны двух других.
   
4. В центр квадрата, в каждой вершине которого находится заряд q=2 нКл, помешен отрицательный заряд q₀. Найти этот заряд, если на каждый заряд q действует результирующая сила F=0.
   
5. Два шарика одинакового радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. После сообщения шарикам заряда q=0,4 мкКл они оттолкнулись друг от друга и разошлись на угол 2=60. Найти массу каждого шарика, если расстояние от центра шарика до точки подвеса L=20 см.
   
6. Два шарика одинакового радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. Какой заряд q нужно сообщить шарикам, чтобы после расхождения шариков на некоторый угол  сила натяжения нитей стала равной Т=89 мН? Расстояние от центра шарика до точки подвеса L=10 см, масса каждого шарика m=5 г.
   
7. Два шарика массой m=0,1 г каждый подвешены в одной точке на нитях длиной 20 см каждая. Получив одинаковый заряд, шарики разошлись так, что нити образовали между собой угол =60. Найти заряд каждого шарика.
   
8. Два одинаковых шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол . Шарики погружаются в масло плотностью ₀=8·10² кг/м³. Определить диэлектрическую проницаемость  масла, если угол расхождения нитей при погружении шариков в масло остается неизменным. Плотность материала шариков =1,6·10³ кг/м³.
   
9. Даны два шарика массой m=1 г каждый. Какой заряд Q надо сообщить каждому шарику, чтобы сила взаимного отталкивания зарядов уравновесила силу взаимного притяжения шариков по закону тяготения Ньютона? Рассматривать шарики как материальные точки.
   
10. Расстояние между двумя точечными зарядами Q₁=1 мкКл и Q₂=-Q₁ равно 10 см. Определить силу F, действующую на точечный заряд Q=1 мкКл, удаленный на r₁=6 см от первого и на r₂=8 см от второго зарядов.
    
11. В вершинах правильного шестиугольника со стороной а=10 см расположены точечные заряды Q, 2Q, 3Q, 4Q, 5Q, 6Q (Q=0,1 мкКл). Найти силу F, действующую на точечный заряд Q, лежащий в плоскости шестиугольника и равноудаленный от его вершин.
    
12. Два одинаковых заряженных шарика находятся на расстоянии 60 см. Сила отталкивания шаров равна 70 мкН. После того, как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной 160 мкН. Вычислить заряды Q₁ и Q₂ , которые были на шарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними.
    
13. Два положительных точечных заряда Q и 4Q закреплены на расстоянии 60 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд Q₁ так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения заряда возможны только вдоль прямой, проходящей через закрепленные заряды.
    
14. Два алюминиевых шарика радиусами 2 см и 1 см соединены легкой непроводящей нитью длиной 1 м. Шарики находятся на гладкой горизонтальной непроводящей поверхности. У каждых z=10⁹ атомов большего шарика взято по одному электрону и все они перенесены на меньший шарик. Какую минимальную силу нужно приложить к меньшему шарику, чтобы нить натянулась? Плотность и молярная масса алюминия равны соответственно =2,7·10³ кг/м³ и =2,7·10^-2 кг/моль, заряд электрона е=1,6·10^-19 Кл.
    
15. С какой силой будут притягиваться два одинаковых свинцовых шарика диаметром 1 см, расположенные на расстоянии 1 м друг от друга, если у каждого атома первого шарика отнять по одному электрону и все эти электроны перенести на второй шарик?
    
16. На двух одинаковых каплях масла радиусом 8,22·10^-3 см находятся одинаковые одноименные заряды. Определите их модуль, если сила кулоновского отталкивания уравновешивает силу гравитационного притяжения капель. Расстояние между каплями гораздо больше их линейных размеров.
    
17. Два маленьких заряженных шарика, одинаковые по размеру, притягиваются друг к другу с некоторой силой. После того как шарики были приведены в соприкосновение и раздвинуты на расстояние в n раз большее, чем прежде, сила взаимодействия между ними уменьшилась в m раз. Каков был заряд первого шарика до соприкосновения, если второй шарик имел заряд q.
    
18. Три одинаковых заряда, каждый из которых равен q, расположены в вершинах равностороннего треугольника. Где и какой заряд надо поместить, чтобы система находилась в равновесии.
    
19. Заряженные шарики, находящиеся на расстоянии 2 м друг от друга, отталкиваются с силой 1 Н. Общий заряд шариков 5·10^-5Кл. Как распределен этот заряд между шариками?
    
20. На двух одинаковых капельках находится по одному лишнему электрону, причем сила электрического отталкивания капелек уравновешивает силу их взаимного тяготения. Каковы радиусы капелек.
    
21. Четыре маленьких шарика соединены тонкими непроводящими нитями, так что в растянутом состоянии нити образуют ромб. Чему равен угол между нитями, если шарики, находящегося в противоположных вершинах ромба, имеют заряды Q₁=Q₂=Q, q₁=q₂=q.
    
22. Три маленьких шарика массой по 10 г каждый подвешены на шелковых нитях длиной по 1 м, сходящихся наверху в одном узле. Шарики одинаково заряжены и висят в вершинах равностороннего треугольника со стороной 0,1м. Каков заряд каждого шарика?
    
23. Два одинаковых проводящих заряженных шарика находятся на расстоянии 30 см. Сила притяжения шаров равна 90 мкН. После того, как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, они стали отталкиваться друг от друга с силой 160 мкН. Вычислить заряды Q₁ и Q₂, которые были на шарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними.
    
24. Три одинаковых точечных заряда Q₁=Q₂=Q₃=2 нКл находятся в вершинах равностороннего треугольника со стороной а=10 см. Определить модуль и направление силы F, действующей на один из зарядов со стороны двух других.
    
25. На расстоянии d=20 см находятся два точечных заряда Q₁=50 нКл и Q₂=100 нКл. Определить силу F, действующую на заряд Q₃=10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.
    

II. Напряженность и потенциал точечного заряда

1. В вершинах квадрата со стороной 5 см находятся одинаковые положительные заряды Q=2 нКл. Определить напряженность электростатического поля: 1) в центре квадрата; 2) в середине одной из сторон.
   
2. Расстояние L между зарядами Q=±2 нКл равно 20 см. Определить напряженность Е поля, созданного этими зарядами в точке, находящейся на расстоянии r₁=15 см от первого и r₂=10 см от второго заряда.
   
3. Определить напряженность поля, создаваемого диполем с электрическим моментом р=10^-9 Кл·м на расстоянии r=25 см от центра диполя в направлении, перпендикулярном оси диполя.
   
4. Два точечных заряда Q₁=4 нКл и Q₂=-2 нКл находятся на расстоянии 60 см друг от друга. Определить напряженность Е поля в точке, лежащей посередине между зарядами. Чему равна напряженность, если второй заряд положительный?
   
5. Свинцовый шарик (=11,3 г/см³) диаметром 0,5 см помещен в глицерин (=1,26 г/см³). Определить заряд шарика, если в однородном электростатическом поле шарик оказался взвешенным в глицерине. Электростатическое поле направлено вертикально вверх, и его напряженность Е=4 кВ/см.
   
6. Расстояние d между двумя точечными зарядами Q₁ =8 нКл и Q₂=-5,3 нКл равно 40 см. Вычислить напряженность Е поля в точке, лежащей посередине между зарядами. Чему равна напряженность, если второй заряд будет положительным?
   
7. Электрическое поле создано двумя точечными зарядами Q₁=10 нКл и Q₂=-20 нКл, находящимися на расстоянии 20 см друг от друга. Определить напряженность Е поля в точке, удаленной от первого заряда на 30 см и от второго на 50 см.
   
8. Расстояние d между двумя точечными положительными зарядами Q₁ =9Q и Q₂=Q равно 8 см. На каком расстоянии r от первого заряда находится точка, в которой напряженность Е поля зарядов равна нулю? Где находилась бы эта точка, если бы второй заряд был отрицательным?
   
9. Расстояние между двумя точечными зарядами Q₁ =2Q и Q₂=-Q равно d. Найти положение точки на прямой, проходящей через эти заряды, напряженность Е поля в которой равна нулю.
   
10. Электрическое поле создано двумя точечными зарядами Q₁=40 нКл и Q₂=-10 нКл, находящимися на расстоянии 10 см друг от друга. Определить напряженность Е поля в точке, удаленной от первого заряда на 12 см и от второго на 6 см.
    
11. Три одинаковых заряда, q=10^-9Кл каждый, расположены в вершинах прямоугольного треугольника с катетами а=40 см и b=30 см. Найти напряженность электрического поля, создаваемого всеми зарядами в точке пересечения гипотенузы с перпендикуляром, опущенным на не из вершины прямого угла.
    
12. Определить напряженность Е электрического поля, создаваемого точечным зарядом Q=10 нКл на расстоянии 10 см от него. Диэлектрик - масло.
    
13. Электрическое поле создано двумя точечными зарядами Q₁=30 нКл и Q₂=-10 нКл, находящимися на расстоянии 20 см друг от друга. Определить напряженность Е поля в точке, удаленной от первого заряда на 15 см и от второго на 10 см.
    
14. Электрическое поле создано двумя точечными зарядами Q₁=2 нКл и Q₂=-3 нКл, находящимися на расстоянии 20 см друг от друга. Определить 1) напряженность Е; 2) потенциал  поля в точке, удаленной от первого заряда на 15 см и от второго на 10 см.
    
15. В вершинах квадрата со стороной 15 см находятся одинаковые положительные заряды Q=3 нКл. Определить напряженность электростатического поля: 1) в центре квадрата; 2) в середине одной из сторон.
    
16. Расстояние L между зарядами Q=±4 нКл равно 10 см. Определить напряженность Е поля, созданного этими зарядами в точке, находящейся на расстоянии r₁=10 см от первого и r₂=15 см от второго заряда.
    
17. Определить напряженность поля, создаваемого диполем с электрическим моментом р=10^-9 Кл·м на расстоянии r=15 см от центра диполя в направлении, перпендикулярном оси диполя.
    
18. Два точечных заряда Q₁=6 нКл и Q₂=-4 нКл находятся на расстоянии 30 см друг от друга. Определить напряженность Е поля в точке, лежащей посередине между зарядами. Чему равна напряженность, если второй заряд положительный?
    
19. Какой угол с вертикалью составит нить, на которой висит шарик массы 25 мг, если поместить шарик в горизонтальное однородное электрическое поле с напряженностью 35 В/м, сообщив ему заряд 7 мкКл?
    
20. В однородном электрическом поле с напряженностью 1МВ/м, направленной под углом 30 к вертикали, висит шарик массы 2 г, несущий заряд 10 нКл. Найти силу натяжения нити Т.
    
21. Шарик массы 1 г подвешен на нити длины 36 см. Как изменится период колебаний шарика, если, сообщив ему положительный или отрицательный заряд |q|=20 нКл, поместить шарик в однородное электрическое поле с напряженностью 100 кВ/м, направленной вниз?
    
22. Одинаковые по модулю, но разные по знаку заряды |q|=18 нКл расположены в вершинах равностороннего треугольника со стороной а=2 см. Найти напряженность Е в третьей вершине треугольника.
    
23. В вершинах при острых углах ромба, составленного из двух равносторонних треугольников со стороной а, помещены одинаковые положительные заряды q₁=q₂=q. В вершине при одном из тупых углов ромба помещен положительный заряд Q. Найти напряженность Е в четвертой вершине ромба.
    
24. В вершинах при острых углах ромба, составленного из двух равносторонних треугольников со стороной а, помещены одинаковые положительные заряды q₁=q₂=q. В вершине при одном из тупых углов ромба помещен отрицательный заряд Q. Найти напряженность Е в четвертой вершине ромба, в случае, когда |Q|>q.
    
25. В вершинах при острых углах ромба, составленного из двух равносторонних треугольников со стороной а, помещены одинаковые положительные заряды q₁=q₂=q. В вершине при одном из тупых углов ромба помещен отрицательный заряд Q. Найти напряженность Е в четвертой вершине ромба, в случае, когда |Q|

III. Напряженность и потенциал поля объемного заряда. Принцип суперпозиции полей.

1. Тонкий стержень длиной 20 см несет равномерно распределенный заряд =0,1 мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а=20см от его середины.
   
2. По тонкому полукольцу радиуса R=10см равномерно распределен заряд с линейной плотностью =1мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
   
3. Тонкое кольцо несет распределенный заряд Q=0,2мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, равноудаленной от всех точек кольца на расстояние r=20см. Радиус кольца R=10см.
   
4. Треть тонкого кольца радиуса R=5 см несет равномерно распределенный заряд Q=50нКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
   
5. Бесконечный тонкий стержень, ограниченный с одной стороны, несет равномерно распределенный заряд с линейной плотностью =0,5мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а=20см от его начала.
   
6. По тонкому кольцу радиусом R=20см равномерно распределен заряд с линейной плотностью =0,2мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, находящейся на оси кольца на расстоянии h=2R от его центра.
   
7. По тонкому полукольцу равномерно распределен заряд Q=20мкКл с линейной плотностью =0,1мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
   
8. Четверть тонкого кольца радиусом R=10см несет равномерно распределенный заряд Q=0,05мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
   
9. По тонкому кольцу равномерно распределен заряд Q=10нКл с линейной плотностью =0,01мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное радиусу кольца.
   
10. Две трети тонкого кольца радиусом R=10см несут равномерно распределенный заряд с линейной плотностью =0,2мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
    
11. Тонкий стержень равномерно заряжен зарядом Q=60 мкКл. Определить напряженность в точке, отстоящей от конца стержня на расстоянии R=20 см, а от середины стержня на расстоянии R₀=15 см.
    
12. Кольцо радиусом R=5 см из тонкой проволоки равномерно заряжено зарядом Q=50 мкКл. Определить потенциал в центре кольца и в точке, лежащей на перпендикуляре, восстановленном из центра кольца, на расстоянии h=10 см от него.
    
13. Определить потенциалы точек, находящихся на расстояниях 3 и 5 см от центра шара радиусом 2см. На шаре находится заряд 210^-8 Кл. Шар окружен сферической металлической оболочкой радиусом 4 см, концентрической с шаром. На оболочке находится заряд -410^-8 Кл.
    
14. Кольцо радиусом R=10 см из тонкой проволоки равномерно заряжено зарядом 0,5нКл. Определить напряженность поля в центре кольца и в точке, находящейся на перпендикуляре к плоскости кольца, восстановленном из центра кольца, и отстоящей от него на расстоянии h= 15 см.
    
15. Две плоские пластинки площадью 200 см² , заряженные равными зарядами, притягиваются, находясь в керосине, с силой 2,510^-2 Н. Расстояние между пластинками столь мало, что напряженность поля можно рассчитывать по формуле для бесконечных плоскостей. Определить находящиеся на них заряды.
    
16. Половина тонкого кольца радиуса R=5 см несет равномерно распределенный заряд Q=50нКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
    
17. Тонкий стержень длиной 20 см несет равномерно распределенный заряд =0,1 мкКл. Определить потенциал электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а=20см от его середины.
    
18. Шарик (R=2 см), сделанный из диэлектрика, заряжен электричеством с объемной плотностью 0,7нКл/м³. Какова напряженность поля на расстоянии 3 см от центра шара.
    
19. Две пластинки (S=2 дм²) находятся в керосине на расстоянии d=4 мм друг от друга. С какой силой они взаимодействуют, если они заряжены до разности потенциалов U=150 В.
    
20. Тонкий стержень длиной 20 см несет равномерно распределенный заряд =1 мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на перпендикуляре к середине стержня на расстоянии а=20 см от него.
    
21. По тонкому кольцу радиуса R=10 см равномерно распределен заряд с линейной плотностью =1мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
    
22. Тонкое кольцо несет распределенный заряд Q=1 мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, равноудаленной от всех точек кольца на расстояние r=20 см. Радиус кольца R=10 см.
    
23. По тонкому кольцу радиусом R=10 см равномерно распределен заряд с линейной плотностью =2 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, находящейся на оси кольца на расстоянии R от его центра.
    
24. По тонкому полукольцу равномерно распределен заряд 10 мкКл с линейной плотностью =0,5 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в центре кольца.
    
25. Четверть тонкого кольца радиусом R=10 см несет равномерно распределенный заряд Q=5мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в центре кольца.
    

IV. Напряженность и потенциал поля объемного заряда. Теорема Остроградского- Гаусса

1. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1) используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=4, ₂=; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =30нКл/м², r=1,5R; 3) построить график Е(r).
   

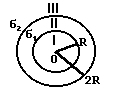
2. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=, ₂=-; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =0,1мкКл/м², r=3R; 3)построить график Е(r).
   

3. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-4, ₂=; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =50нКл/м², r=1,5R; 3)построить график Е(r).
   

4. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-2, ₂=; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =0,1мкКл/м², r=3R; 3)построить график Е(r).
   

5. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=2, ₂=; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =40нКл/м², r=2R; 3)построить график Е(r).
   

6. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-, ₂=; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =10нКл/м², r=3R; 3)построить график Е(r).
   

7. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=3, ₂=-6; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =0,2мкКл/м², r=4R; 3)построить график Е(r).
   

8. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-3, ₂=6; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =0,3мкКл/м², r=3R; 3)построить график Е(r).
   

9. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=6, ₂=; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =0,3мкКл/м², r=1,5R; 3)построить график Е(r).
   

10. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=2, ₂=; 2)вычислить напряженность Е в точке, расположенной слева от плоскостей , и указать направление вектора Е. Принять =0,1мкКл/м²; 3)построить график Е(x).
    

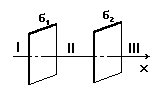
11. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-4, ₂=2; 2)вычислить напряженность Е в точке, расположенной между плоскостями, и указать направление вектора Е. Принять =40нКл/м²; 3)построить график Е(x).
    

12. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=4, ₂=-2; 2)вычислить напряженность Е в точке, расположенной справа от плоскостей , и указать направление вектора Е. Принять =20нКл/м²; 3)построить график Е(x).
    

13. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-4, ₂=; 2)вычислить напряженность Е в точке, расположенной слева от плоскостей , и указать направление вектора Е. Принять =0,1мкКл/м²; 3)построить график Е(x).
    

14. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=4, ₂=; 2)вычислить напряженность Е в точке, расположенной между плоскостями, и указать направление вектора Е. Принять =40нКл/м²; 3)построить график Е(x).
    

15. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-, ₂=; 2)вычислить напряженность Е в точке, расположенной справа от плоскостей , и указать направление вектора Е. Принять =10нКл/м²; 3)построить график Е(x).
    

16. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=3, ₂=-6; 2)вычислить напряженность Е в точке, расположенной слева от плоскостей, и указать направление вектора Е. Принять =0,2 мкКл/м²; 3)построить график Е(x).
    

17. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-3, ₂=6; 2)вычислить напряженность Е в точке, расположенной между плоскостями, и указать направление вектора Е. Принять =0,3 мкКл/м²; 3)построить график Е(x).
    

18. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-2, ₂=; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =50нКл/м², r=1,5R; 3)построить график Е(r).
    

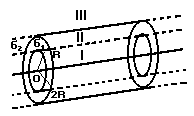
19. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=, ₂=-; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =60нКл/м², r=3R; 3) построить график Е(r).
    

20. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-, ₂=4; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =30нКл/м², r=4R; 3)построить график Е(r).
    

21. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-2, ₂=4; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =10нКл/м², r=3R; 3)построить график Е(r).
    

22. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=, ₂=-3; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =15нКл/м², r=2R; 3)построить график Е(r).
    

23. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=4, ₂=3; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =30нКл/м², r=5R; 3)построить график Е(r).
    

24. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=3, ₂=; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =10нКл/м², r=2R; 3)построить график Е(r).
    

25. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=6, ₂=-4; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =20нКл/м², r=3R; 3)построить график Е(r).
    

V. Заряженная частица в электрическом поле

1. Расстояние между пластинами плоского конденсатора d=4 см. Электрон начинает двигаться от отрицательной пластины к положительной в тот момент, когда от положительной пластины начинает двигаться протон. На каком расстоянии L от положительной пластины встретятся электрон и протон?
   
2. Расстояние между пластинами плоского конденсатора d=1 см. От одной из пластин начинают двигаться одновременно протон и -частица. Какое расстояние L пройдет -частица за то время, в течение которого протон пройдет весь путь от одной пластины до другой?
   
3. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобретает скорость v=10⁶ м/с. Расстояние между пластинами d=5,3мм. Найти разность потенциалов U между пластинами, напряженность Е электрического поля внутри конденсатора и поверхностную плотность заряда  на пластинах.
   
4. Электрическое поле образовано двумя параллельными пластинами, находящимися на расстоянии 2 см друг от друга. К пластинам приложена разность потенциалов U=120 В. Какую скорость получит электрон под действием поля, пройдя по линии напряженности расстояние r=3 мм.
   
5. Электрон в однородном электрическом поле получает ускорение а=10¹² м/с². Найти напряженность Е электрического поля, скорость v, которую получит электрон за время t=1мкс своего движения, работу сил электрического поля за это время и разность потенциалов U, пройденную при этом электроном. Начальная скорость электрона v₀=0.
   
6. Протон и -частица, двигаясь с одинаковой скоростью, влетают в плоский конденсатор параллельно пластинам. Во сколько раз отклонение протона полем конденсатора будет больше отклонения -частицы?
   
7. Протон и -частица, ускоренные одной и той же разностью потенциалов, влетают в плоский конденсатор параллельно пластинам. Во сколько раз отклонение протона полем конденсатора будет больше отклонения -частицы?
   
8. Электрон, пролетая в электрическом поле путь от точки а до точки b, увеличил свою скорость с v_a =1000 км/с до v_b =3000 км/с. Найти разность потенциалов между точками а и b электрического поля.
   
9. В плоский конденсатор влетает электрон со скоростью 2·10⁷ м/с, направленной параллельно пластинам конденсатора. На какое расстояние h от своего первоначального направления сместится электрон за время пролета конденсатора? Расстояние между пластинами 2 см, длина конденсатора 5 см, разность потенциалов между пластинами 200 В.
   
10. Положительно заряженная пылинка массы 10^-8 г находится в равновесии внутри плоского конденсатора, пластины которого расположены горизонтально. Между пластинами создана разность потенциалов U₁=6000 В. Расстояние между пластинами 5 см. На какую величину необходимо изменить разность потенциалов, чтобы пылинка осталась в равновесии, если ее заряд уменьшится на q₀=1000e? (е=1,6·10^-19 Кл)
    
11. В электрическое поле плоского конденсатора, пластины которого расположены горизонтально, помещена капелька масла, имеющая заряд q=1e. Напряженность электрического поля подобрана так, что капелька покоится. Разность потенциалов между пластинами конденсатора 500 В, расстояние между пластинами 0,5 см. Плотность масла 0,9·10³ кг/м³. Найти радиус капельки масла. (е=1,6·10^-19 Кл)
    
12. Электрон, двигавшийся со скоростью 5·10⁶м/с, влетает в параллельное его движению электрическое поле напряженностью 10³ В/м. Какое расстояние пройдет электрон в этом поле до момента остановки и сколько времени ему для этого потребуется?
    
13. Электрон, двигавшийся со скоростью 5·10⁶м/с, влетает в параллельное его движению электрическое поле напряженностью 10³ В/м. Какую долю своей первоначальной энергии потеряет электрон, двигаясь в этом поле, если поле обрывается на расстоянии 0,8 см пути электрона?
    
14. В плоском конденсаторе, помещенном в вакууме, взвешена заряженная капелька ртути. Расстояние между пластинами конденсатора 1 см, приложенная разность потенциалов 1000 В. Внезапно разность потенциалов падает до 995 В. Через какое время капелька достигнет нижней пластины, если первоначально она находилась посередине конденсатора?
    
15. Между вертикальными пластинами плоского конденсатора, находящегося в воздухе, подвешен на нити шарик, несущий заряд 3,3·10^-9 Кл. Какой величины заряд надо сообщить пластинам конденсатора, чтобы нить с шариком отклонилась на угол =45 от вертикали? Масса шарика 0,04 г, площадь пластин конденсатора 314 см². Массой нити пренебречь.
    
16. Между вертикальными пластинами плоского конденсатора, находящегося на расстоянии 2 см друг от друга, подвешен на нити шарик массой 0,1 г. После того, как на пластины была подана разность потенциалов 1000 В, нить с шариком отклонилась на угол =5 от вертикали. Найти заряд шарика.
    
17. Электрон вылетает из точки, потенциал которой 600 В, со скоростью 12·10⁶ м/с в направлении силовых линий поля. Определить потенциал точки, дойдя до которой электрон остановится.
    
18. В плоский конденсатор длиной 5 см влетает электрон под углом =15 к пластинам. Энергия электрона 1500 эВ. Расстояние между пластинами конденсатора 1 см. Определить величину напряжения в конденсаторе, при котором электрон при выходе из пластин будет двигаться параллельно им.
    
19. В плоский конденсатор длиной 5 см влетает электрон со скоростью 10⁷ м/с параллельно пластинам. Энергия электрона 1500 эВ. Напряженность поля в конденсаторе 100 В/см. Найти величину и направление скорости электрона перед вылетом из конденсатора.
    
20. Электрон влетает параллельно пластинам в плоский конденсатор, поле в котором Е=60 В/см. Найти изменение модуля скорости электрона к моменту вылета его из конденсатора, если начальная скорость 2·10⁷ м/с, длина пластины конденсатора 6 см.
    
21. Пылинка массой m=200 мкг, несущая на себе заряд Q=40 нКл, влетела в электрическое поле в направления силовых линий. После прохождения разности потенциалов U=200 В пылинка имела скорость v₀=10 м/с. Определить скорость v пылинки до того, как она влетела в поле.
    
22. Электрон, обладавший кинетической энергией Т=10 эВ, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя b этом поле разность потенциалов U=8 В?
    
23. Электрон с энергией T=400 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R=10 см. Определить минимальное расстояние a, на которое приблизится электрон к поверхности сферы, если заряд ее Q=10 нКл.
    
24. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрел скорость v=10⁵ м/c. Расстояние между пластинами d=8 мм. Найти: 1) разность потенциалов U между пластинами; 2) поверхностную плотность заряда  на пластинах.
    
25. Пылинка массой m=5 нг, несущая да себе N=10 электронов, прошла в вакууме ускоряющую разность потенциалов U=1 мВ. Какова кинетическая энергия Т пылинки? Какую скорость v приобрела пылинка?
    

VI. Законы Ома. Правила Кирхгофа

1. Напряжение U на шинах электростанции равно 6,6 кВ. Потребитель находится на расстоянии l=10 км. Определить площадь S сечения медного провода, который следует взять для устройства двухпроводной линии передачи, если сила тока I в линии равна 20 А и потери напряжения в проводах не должны превышать 3%.
   
2. К источнику тока с ЭДС 1,5 В присоединили катушку с сопротивлением R=0,1 Ом. Амперметр показал силу тока, равную I₁=0,5 А. Когда к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, сила тока I в той же катушке оказалась равной 0,4 А. Определить внутренние сопротивления r₁ и r₂ первого и второго источников тока.
   
3. Две группы из трех последовательно соединенных элементов соединены параллельно. ЭДС каждого элемента равна 1,2 В, внутреннее сопротивление r=0,2 Ом. Полученная батарея замкнута на внешнее сопротивление R=1,5 Ом. Найти силу тока I во внешней цепи.
   
4. Два элемента (Е=1,2 В, r₁=0,1 Ом; Е=0,9 В, r₂=0,3 Ом) соединены одноименными полюсами. Сопротивление R соединительных проводов равно 0,2 Ом. Определить силу тока I в цепи.
   
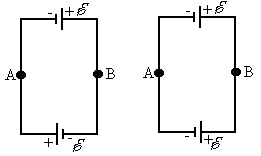
5. Два одинаковых источника тока с ЭДС 1,2 В и внутренним сопротивлением r= 0,4 Ом соединены, как показано на рис. а, б. Определить силу тока I в цепи и разность потенциалов U между точками А и В в первом и втором случаях.
   

6. Катушка и амперметр соединены последовательно и присоединены к источнику тока. К зажимам катушки присоединен вольтметр сопротивлением R_V =1 кОм. Показания амперметра I=0,5 А, вольтметра U= 100 В. Определить сопротивление R катушки. Сколько процентов от точного значения сопротивления катушки составит погрешность, если не учитывать сопротивления вольтметра?
   
7. Зашунтированный амперметр измеряет токи силой до I=10 А. Какую наибольшую силу тока может измерить этот амперметр без шунта, если сопротивление R_A амперметра равно 0,02 Ом и сопротивление R_ш шунта равно 5 мОм?
   
8. Вольтметр, включенный в сеть последовательно с сопротивлением R₁, показал напряжение U₁=198 В, а при включении последовательно с сопротивлением R₂=2R₁ - U₂=180 В. Определить сопротивление R₁ и напряжение в сети, если сопротивление вольтметра R_V=900 Ом.
   
9. В цепь, состоящую из батареи и резистора сопротивлением R=8 Ом, включают вольтметр, сопротивление которого R_V=800 Ом, один раз последовательно резистору, другой раз - параллельно. Определить внутреннее сопротивление батареи, если показания вольтметра в обоих случаях одинаковы.
   
10. Элемент с ЭДС Е = 2 В имеет внутреннее сопротивление r=0,5 Ом. Найти падение потенциала U_r внутри элемента при токе в цепи I=0,25 А. Каково внешнее сопротивление R цепи при этих условиях?
    
11. Имеется предназначенный для измерения токов до I=15 мА амперметр с сопротивлением R_А=5 Ом. Какое сопротивление R надо взять и как его включить, чтобы этим прибором можно было измерять:а) ток I₀=150 мА; б) разность потенциалов до U₀=150 В?
    
12. В сеть с напряжением U=100 В подключили катушку с сопротивлением R₁=2 кОм и вольтметр, соединенные последовательно. Показания вольтметра U₁= 80 В. Когда катушку заменили другой, вольтметр показал U₂= 60 В. Определить сопротивление R₂ другой катушки.
    
13. Сопротивление R измеряется вольтметром и амперметром по схеме, показанной на рисунке. Амперметр показывает I=0,32 А, вольтметр- U=9,6 В. Сопротивление амперметра R_А=0,03 Ом. Определить относительную ошибку, которую делают, вычисляя сопротивление без учета сопротивления амперметра. Произвести тот же расчет при I=7 А и U=2,1 В.
    

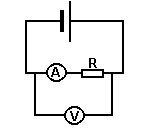
14. Сопротивление R измеряется вольтметром и амперметром по схеме, показанной на рисунке. Амперметр показывает I=2,4 А, вольтметр - U=7,2 В. Сопротивление вольтметра R_V=1000 Ом. Определить относительную ошибку, которую делают, вычисляя сопротивление без учета тока, идущего в вольтметр. Произвести тот же расчет при I=24 мА и U=7,2 В.
    

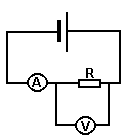
15. Генератор постоянного тока дает ЭДС 12 В. Его внутреннее сопротивление 0,2 Ом. Он заряжает батарею аккумуляторов с ЭДС 10 В и внутренним сопротивлением 0,6 Ом. Параллельно батарее включена лампочка с сопротивлением 3 Ом. Определить ток в батарее аккумуляторов и в лампочке.
    
16. Три гальванических элемента с ЭДС 1,3 В; 1,4 В и 1,5 В и с внутренними сопротивлениями по 0,3 Ом каждый включены параллельно друг другу на внешнее сопротивление 0,6 Ом. Определить ток в каждом элементе.
    
17. Каковы внутренние сопротивления гальванических элементов с ЭДС 1,6 В; 1,4 В; 1,1 В, если, будучи соединены параллельно при внешнем сопротивлении 1 Ом, они дают токи 0,8 А; 0,6 А и 0,2 А?
    
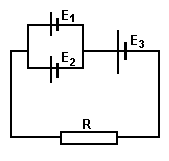
18. Три гальванических элемента с ЭДС 1,3 В; 1,5 В; 2 В и внутренними сопротивлениями по 0,2 Ом каждый включены, как это показано на рисунке. Сопротивление R=0,55 Ом. Определить токи в элементах.
    

19. Присоединение к вольтметру некоторого добавочного сопротивления увеличивает предел измерения напряжения в n раз. Другое добавочное сопротивление увеличивает предел измерения в m раз. Во сколько раз увеличится предельно измеримое вольтметром напряжение, если включить последовательно с вольтметром эти два сопротивления, соединенные между собой параллельно?
    
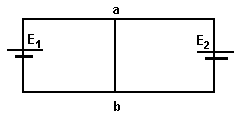
20. Два аккумулятора с ЭДС Е₁=57 В и Е₂=32 В соединены, как показано на рисунке. Какова разность потенциалов между точками a и b, если отношение внутренних сопротивлений аккумуляторов r₁ / r₂= 1,5?
    

21. ЭДС батареи Е=80 В, внутреннее сопротивление R=5 Ом. Внешняя цепь потребляет мощность Р=100 Вт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее сопротивление R.
    
22. При внешнем сопротивлении R₁=8 Ом сила тока в цепи I₁=0,8 А, при сопротивлении R₂=15 Ом сила тока I₂=0,5 А. Определить силу тока I_к.з. короткого замыкания источника ЭДС.
    
23. В сеть с напряжением U=100 В подключили катушку с сопротивлением R₁=2 кОм и вольтметр, соединенные последовательно. Показание вольтметра U₁=80 В. Когда катушку заменили другой, вольтметр показал U₂=60 В. Определить сопротивление R₂ другой катушки.
    
24. ЭДС батареи 12 В. При силе тока I=4 А к.п.д. батареи =0,6. Определить внутреннее сопротивление r батареи.
    
25. Резистор сопротивлением R=6 Ом подключен к двум параллельно соединенным источникам тока с ЭДС E₁=2,2 В и E₂=2,4 В и внутренними сопротивлениями R₁=0,8 Ом и R₂=0,2 Ом. Определить силу тока I в этом резисторе и напряжение U на зажимах второго источника тока.
    

VII. Энергия электрического поля. Закон Джоуля Ленца.

1. Сила тока в проводнике равномерно увеличивается от I₀=0 до некоторого максимального значения в течение времени =10 с. За это время в проводнике выделилось количество теплоты Q=1 кДж. Определить скорость нарастания тока в проводнике, если сопротивление R его равно 3 Ом.
   
2. Сила тока в проводнике сопротивлением R=15 Ом равномерно возрастает от I₀=0 до некоторого максимального значения в течение времени =5 с. За это время в проводнике выделилось количество теплоты Q=10 кДж. Найти среднюю силу тока в проводнике за этот промежуток времени.
   
3. По проводнику сопротивлением R=3 Ом течет ток, сила которого возрастает. Количество теплоты Q, выделившееся в проводнике за время =8 с, равно 200 Дж. Определить количество электричества q, протекшее за это время по проводнику. В момент времени, принятый за начальный, сила тока в проводнике равна нулю.
   
4. Сила тока в проводнике сопротивлением R=12 Ом равномерно убывает от I₀=5 А до I=0 в течение времени t=10 с. Какое количество теплоты Q выделяется в этом проводнике за указанный промежуток времени?
   
5. ЭДС батареи равна 20 В. Сопротивление внешней цепи равно 2 Ом, сила тока I=4 А. Найти КПД батареи. При каком значении внешнего сопротивления R КПД будет равен 99%?
   
6. Сила тока в проводнике сопротивлением R=100 Ом равномерно нарастает от I₀=0 до I_max=10 А в течение времени =30 с. Определить количество теплоты Q, выделившееся за это время в проводнике.
   
7. К зажимам батареи аккумуляторов присоединен нагреватель. ЭДС батареи равна 24 В, внутреннее сопротивление r=1 Ом. Нагреватель, включенный в цепь, потребляет мощность P=80 Вт. Вычислить силу тока I в цепи и КПД  нагревателя.
   
8. При силе тока I₁=3 А во внешней цепи батареи аккумуляторов выделяется мощность P₁=18 Вт, при силе тока I₂ = 1 А - соответственно P₂=10 Вт. Определить ЭДС и внутреннее сопротивление r батареи.
   
9. Обмотка электрического кипятильника имеет две секции. Если включена только первая секция, то вода закипает через t₁ = 15 мин., если только вторая, то вода закипает через t₂=30 мин. Через сколько минут закипит вода, если обе секции включить последовательно? Параллельно?
   
10. Сила тока в проводнике сопротивлением R=120 Ом равномерно возрастает от I₀=0 до I_max=5 А за время =15 с. Определить выделившееся за это время в проводнике количество теплоты.
    
11. Сила тока в проводнике сопротивлением R=100 Ом равномерно убывает от I₀=10 А до I =0 за время =30 с. Определить выделившееся за это время в проводнике количество теплоты.
    
12. Определить напряженность электрического поля в алюминиевом проводнике объемом V=10 см³, если при прохождении по нему постоянного тока за время t=5 мин выделилось количество теплоты Q=2,3 кДж. Удельное сопротивление алюминия =26 нОм·м.
    
13. Два цилиндрических проводника одинаковой длины и одинакового сечения, один из меди, а другой из железа, соединены параллельно. Определить отношение мощностей токов для этих проводников. Удельные сопротивления меди и железа равны соответственно 17 и 98 нОм·м.
    
14. Какую наибольшую мощность может отдать во внешнюю цепь элемент с электродвижущей силой 2 В и внутренним сопротивлением 0,1 Ом?
    
15. Светотепловая ванна, имеющая 12 параллельно соединенных ламп накаливания сопротивлением по 360 Ом каждая, включена в сеть напряжением 120 В. Какое количество теплоты выделится в такой ванне в течение 15 мин?
    
16. Через сколько времени в стерилизаторе с обмоткой из проволоки сопротивлением 18 Ом закипит 0,5 кг воды, если начальная температура воды 10⁰ С и средний КПД при нагреве стерилизатора 50%? Стерилизатор включен в сеть постоянного тока напряжением 110 В.
    
17. К источнику тока с ЭДС 12 В присоединена нагрузка. Напряжение U на клеммах источника стало при этом 8 В. Определить КПД источника тока.
    
18. Внешняя цепь источника тока потребляет мощность P=0,75 Вт. Определить силу тока в цепи, если ЭДС источника тока 2 В и внутреннее сопротивление R=1 Ом.
    
19. Какая наибольшая полезная мощность P_max может быть получена от источника тока с ЭДС 12 В и внутренним сопротивлением R=1 Ом?
    
20. Сила тока в проводнике сопротивлением R=10 Ом за время t=50 с равномерно нарастает от I₁=5 А до I₂=10 А. Определить количество теплоты Q, выделившееся за это время в проводнике
    
21. Сила тока в проводнике изменяется со временем по закону I=I₀sint. Найти заряд Q, протекающий через поперечное сечение проводника за время t, равное половине периода t, если начальная сила тока I₀=10 А, циклическая частота =50 с^-1.
    
22. За время t=8 с при равномерно возраставшей силе тока в проводнике сопротивлением R=8 Ом выделилось количество теплоты Q=500 Дж. Определить заряд q, протекший в проводнике, если сила тока в момент времени t=0 равна нулю.
    
23. За время t=20 с при равномерно возраставшей силе тока от нуля до некоторого максимума в проводнике выделилось количество теплоты Q=4 кДж. Определить скорость нарастания силы тока, если сопротивление проводника R=5 Ом.
    
24. В проводнике за время t=10 с при равномерном возрастании силы тока от I₁=5 А до I₂=2 А выделилось количество теплоты Q=5 кДж. Найти сопротивление R проводника.
    
25. Определить количество теплоты Q, выделившееся за время t=10 с в проводнике сопротивлением R=10 Ом, если сила тока в нем, равномерно уменьшаясь, изменилась от I₁= 10 А до I₂=0.