Литература И. Л. Акулич. Математическое программирование в примерах и задачах
| Вид материала | Литература |
СодержаниеГрафическое решение задач линейного программирования Прямая называется опорной Исследование устойчивости (дополнительный материал) |
- Литература, 154.39kb.
- Учебной дисциплины «Выпуклый анализ и математическое программирование» для направления, 34.33kb.
- Аттестационное тестирование в сфере профессионального образования, 72.49kb.
- Программа дисциплины Математическое программирование Семестры, 10.84kb.
- И математическое моделирование, 1392.77kb.
- Учебно-методический комплекс курса по выбору "задачи егэ по информатике" (физико-математический, 704.64kb.
- Программа вступительного экзамена по специальности 05. 13. 18 Математическое моделирование,, 115.33kb.
- Рабочая программа по курсу "Функциональное программирование" Специальность, 144.38kb.
- Программа вступительных экзаменов по специальности 08. 00. 13 «Математические и инструментальные, 40.42kb.
- В примерах и задачах, 3217.34kb.
Линейное программирование
Литература
- И. Л. Акулич. Математическое программирование в примерах и задачах
- Е. С. Вентцель. Исследование операций: задачи, принципы, методология
- Методические указания по графическому решению задач линейного программирования. Составитель Г. А. Кузнецова. – Иваново, 1989.
Примеры (задача о диете, составление плана производства, см. например ссылка скрыта )
Многие задачи сводятся к следующей математической модели:
F(x) extr, (1)
xG. (2)
Такие задачи называются задачами математического программирования. Неизвестный вектор x называется вектором управляемых переменных. Функция F(x) называется целевой функцией, множество G называется допустимым множеством, а вектор x, удовлетворяющий условию (2), называется допустимым вектором. Допустимый вектор, доставляющий минимум (или максимум) целевой функции называется оптимальным решением задачи (1)–(2), а соответствующее значение целевой функции называется оптимумом.
Если F(x) и функции, задающие множество G, – линейные, то задача (1) (2) называется задачей линейного программирования. В общем виде ЗЛП может быть сформулирована так:
Найти набор (x1, x2, …, xn), такой, что
целевая функция (линейная) должна достигнуть своего минимума (максимума)

при ограничениях в виде линейных равенств и неравенств
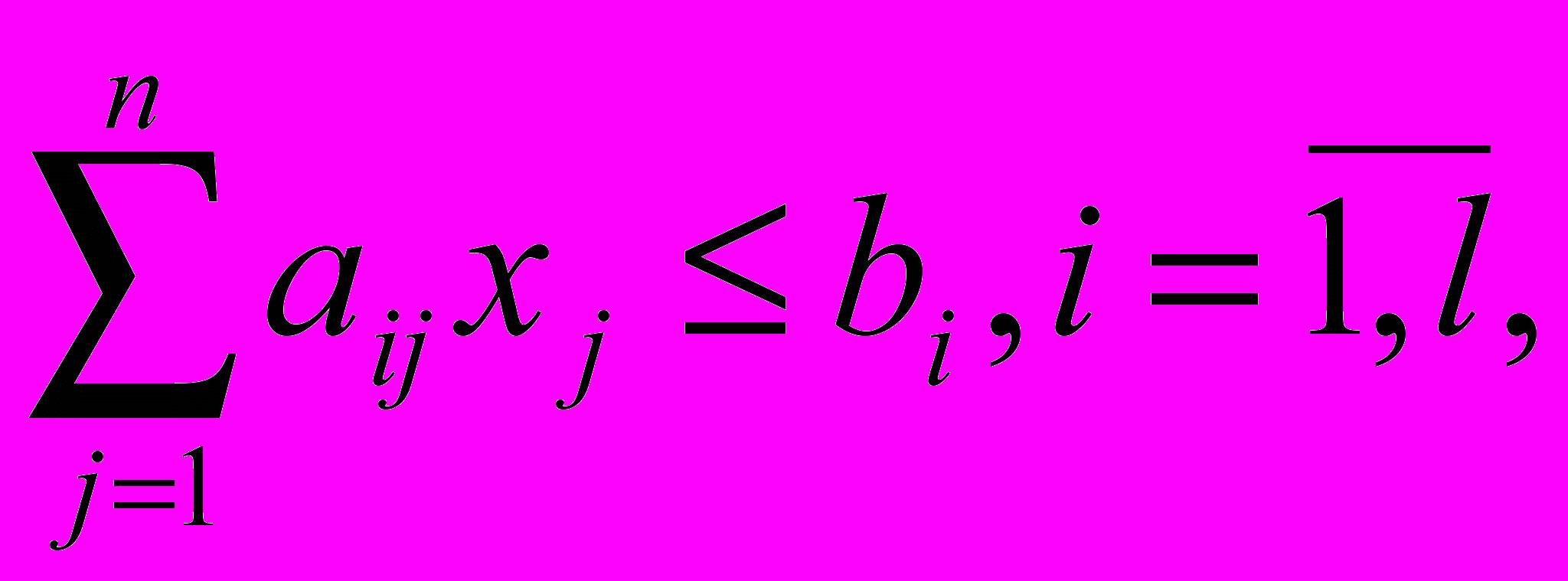

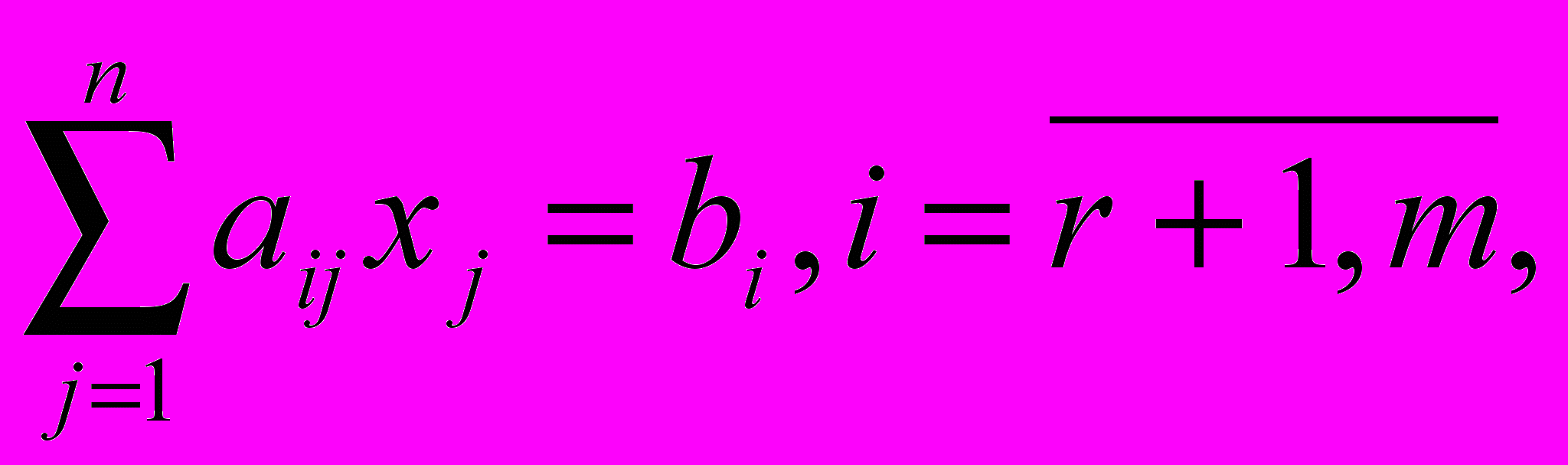
на некоторые переменные накладывается условие неотрицательности
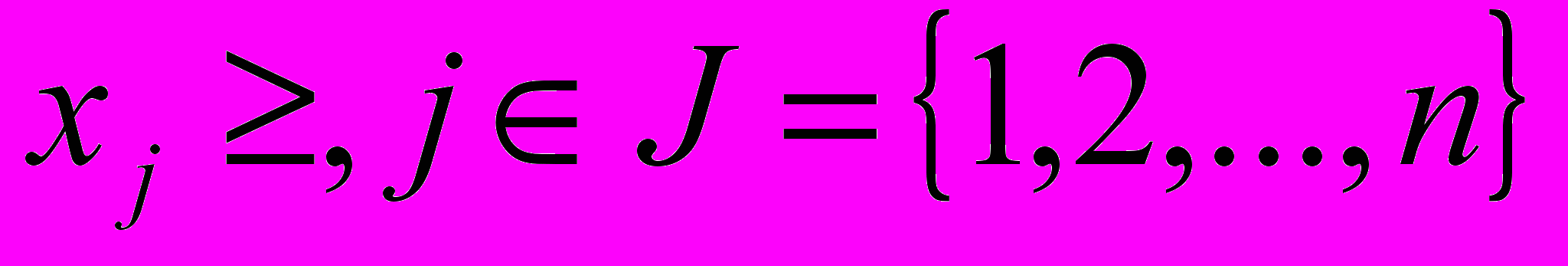 .
.В 1947 году Данциг предложил симплекс-метод для решения ЗЛП. Мы его не рассматриваем (познакомитесь в курсе исследования операций). Мы же рассмотрим графический метод решения ЗЛП.
Графическое решение задач линейного программирования
Задача.
Имеются две линии по выпуску приемников.
| | Мощность линии (изд./сут.) | Схем на один приемник (шт.) | Прибыль (долл.) |
| I линия | 60 | 10 | 30 |
| II линия | 75 | 8 | 20 |
Запас схем на сутки составляет 800 шт. Определить оптимальные суточные объемы производства так, чтобы прибыль была максимальна.
Решение.
Пусть xi – количество приемников, выпускаемых на i-той линии. Тогда математическая модель данной задачи имеет вид:
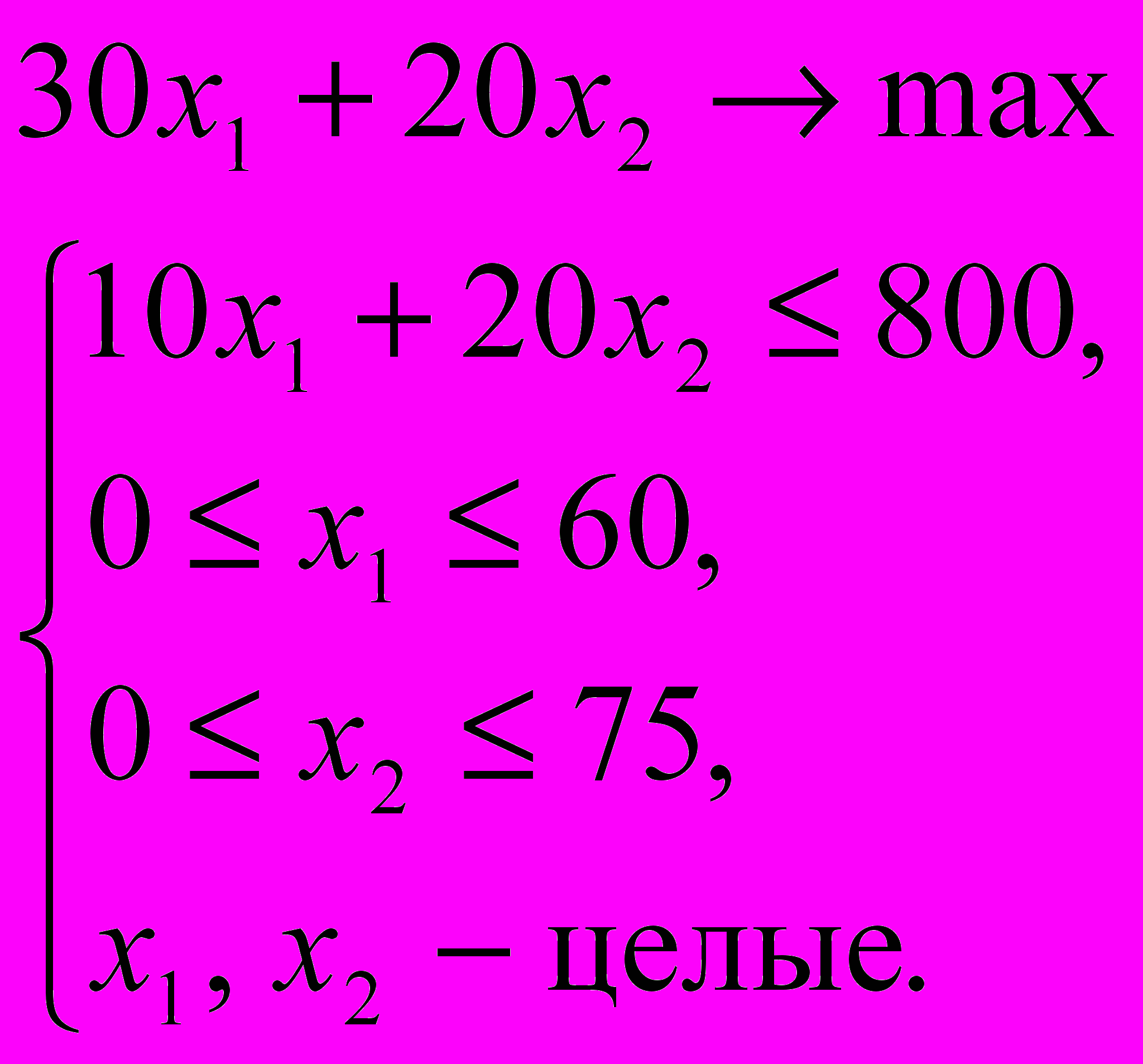
Изобразим сначала допустимое множество.
Напомним, что линейное неравенство с двумя переменными ax1 + bx2 c задаёт на плоскости полуплоскость. Чтобы изобразить эту полуплоскость, сначала проводим прямую, заданную уравнением ax1 + bx2 = c. Чтобы определить, какую именно из двух полуплоскостей определяет заданное неравенство, достаточно подставить в него координаты какой-нибудь одной точки, не лежащей на граничной прямой. Если неравенство удовлетворяется, то искомая полуплоскость – та, в которой лежит выбранная точка, а если не удовлетворяется, – то искомая полуплоскость – та, которой не принадлежит выбранная точка.
Допустимое множество является пересечением всех полуплоскостей, соответствующих неравенствам-ограничениям, то есть состоит из всех точек, которые принадлежат одновременно всем полуплоскостям, определяемым отдельными ограничениями.

Рис. 1
На рис. 1 изображено допустимое множество нашей задачи, которое представляет собой многоугольник OABCD. Нетрудно уточнить координаты вершин допустимого множества: O(0, 0), A(0, 75), B(20, 75), C(60, 25), D(60, 0).
Рассмотрим теперь целевую функцию F(x1, x2) = d1x1 + d2x2. Линией уровня этой функции называется множество всех точек (x1, x2) плоскости x1Ox2, в которых функция принимает одно и то же заданное значение. Зафиксировав некоторое значение d, получаем, что линии уровня соответствует уравнение d1x1 + d2x2 = d, которое задает на плоскости прямую. При этом, взяв прямые, соответствующие разным значениям d, получим семейство параллельных прямых. Вектор-нормаль к любой прямой этого семейства имеет координаты (d1, d2). Можно показать, что при перемещении прямой семейства в направлении, указанном вектором-нормалью, мы получим линию уровня с большим значением целевой функции, а движение в направлении, противоположном вектору-нормали, уменьшает значение целевой функции.
Прямая называется опорной для множества G, если она имеет хотя бы одну общую точку с множеством G, а множество G лежит целиком по одну сторону относительной этой прямой. Чтобы найти графически решение ЗЛП, нужно найти опорную прямую (линию уровня) с соответствующим (максимальным или минимальным) значением функции.
Проведём произвольную линию уровня целевой функции так, чтобы она пересекала допустимое множество (см. на рис. 1 красные пунктирные линии). В нашей задаче нужно максимизировать значение целевой функции, поэтому будем сдвигать линию уровня в направлении вектора-нормали до тех пор, пока прямая не станет опорной для многоугольника OABCD. Линия уровня, соответствующая оптимальному решению проходит через точку C(60, 25). Значит, оптимальным решением нашей задачи являются x1 = 60, x2 = 25, а максимальное значение целевой функции F(x1, x2) = 3060 + 2025 = 2300.
Ответ: следует производить 60 приемников на линии I и 25 приемников на линии II, прибыль при этом равна 2300 долл.
Исследование устойчивости (дополнительный материал)
Как можно изменять коэффициенты целевой функции и ограничений, чтобы оптимальное решение оставалось неизменным?
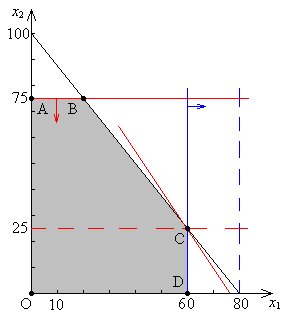
Рис. 2

Рис. 3
- Мощность линий (рис. 2).
Мощность II линии можно уменьшить до 25 изд./сут. (т. е. в 3 раза) и не потерять в прибыли. Мощность I линии можно увеличить до 80 изд./сут., при этом прибыль увеличится.
- Запас схем на сутки (рис. 3).
a = 10 · 60 + 8 · 75 = 1200, b = 10 · 60 + 8 · 0 = 600.
Увеличив запас схем на сутки до 1200 шт., получим увеличение прибыли до максимально возможного значения. Уменьшить запас схем можно до 600 шт., чтобы использовать мощность линии (I-ой или II-ой) полностью.
- Прибыль за один приемник (рис. 4 и 5).
Оптимум останется в точке C, если прямая l расположена в угле BCD'.
CD':
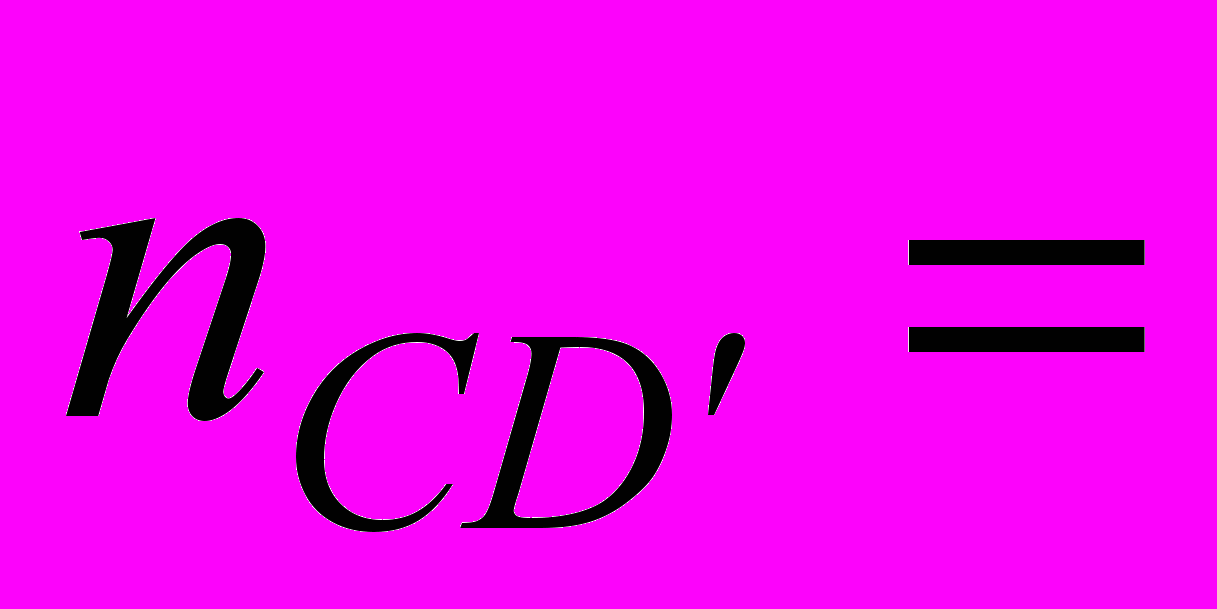 (30, 0), BC:
(30, 0), BC:  (10, 8).
(10, 8).
Рис. 4
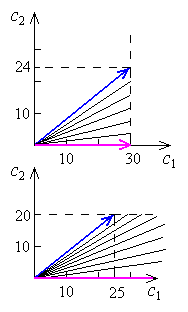
Рис. 5

Рис. 6
При фиксированном c1 = 30: (c1, c2) изменяется от (30, 0) до (10, 8) = (30, 24), т. е. c2 изменяется от 0 до 24. При фиксированном c2 = 20: (c1, c2) изменяется от (10, 8) = (25, 20) до (, 20), т. е. c1 изменяется от 25 до . Итак, прибыль для второго приемника может колебаться от 0 до 24 долл., для первого – неограниченно увеличиваться от 25 долл.
4*. Прибыль за оба приемника (см. рис. 6).
Предположим, что мы хотим изменить прибыль на оба приемника: за первый приемник – на 1 долл., за второй – на 2 долл. (i > 0, а знак показывает, что прибыль может увеличиться или уменьшиться).
Если известно, что прибыль от первого приемника может измениться на 1, то рассмотрим изменение прибыли второго при фиксированном c1 = 30 1. Вектор (c1, c2) может изменяться от (30 1, 0) до
(10, 8) = (30 1, 0,8·(30 1)) =
= (30 1, 24 0,8 1),
т. е. c2 изменяется от 0 до 24 ,8 1.
Если известно, что прибыль от второго приемника может измениться на 2, то рассмотрим изменение прибыли второго при фиксированном c2 = 20 2. (c1, c2) может изменяться от
(10, 8) = (
 ·(20 2), 20 2) =
·(20 2), 20 2) == (25 1,25 2, 20 2)
до (, 20 2), т. е. c1 изменяется от (25 1,25 2) до .
Итак, если прибыль за первый приемник возрастает на 1, то прибыль за второй может увеличиваться не более чем на (4 + 0,8 1). Если прибыль на первый приемник уменьшается на 1, то прибыль второго не может превышать (24 0,81). Но поскольку изначально прибыль второго составляла 20 долл., то 24 – 0,81 < 20 при 1 > 5, т. е. если прибыль за первый приемник падает более, чем на 5 долл., то и цену за второй приемник придется снижать. Если же снижение цены на первый приемник менее 5 долл., то на второй приемник есть возможность немного цену поднять (до значения 24 0,81).
Если прибыль за второй приемник изменяется на 2, то прибыль за первый можно неограниченно увеличивать, т. е. изменение прибыли на второй приемник не влияет на прибыль первого.
