Отделение Прикладной Математики и Информатики программа дисциплины
| Вид материала | Программа дисциплины |
- Правительство Российской Федерации Государственный университет Высшая школа экономики, 91.67kb.
- Отделение Прикладной Математики и Информатики программа дисциплины, 257.84kb.
- Программа дисциплины основные методологические проблемы прикладной математики и информатики, 67.07kb.
- Аннотация примерной программы учебной дисциплины б 9 «История и методология прикладной, 2416.02kb.
- Программа курса по выбору для учащихся учреждений, обеспечивающих получение, 84.43kb.
- Отделение Прикладной Математики и Информатики программа дисциплины, 225.44kb.
- Задачи на графах программа, 81.89kb.
- Рабочая программа учебной дисциплины история и методология прикладной математики, 537.44kb.
- М. К. Аммосова Институт математики и информатики Кафедра прикладной математики рабочая, 219.2kb.
- М. К. Аммосова Институт математики и информатики Кафедра прикладной математики рабочая, 460.29kb.
Правительство Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего профессионального образования
"Национальный исследовательский университет
"Высшая школа экономики"
Факультет бизнес-информатики
Отделение Прикладной Математики и Информатики
Программа дисциплины
«Избранные модели теории полезности»
для направления 010400.68 «Прикладная математика и информатика»
подготовки магистра
Авторы:
Ф.Т.Алескеров, И.А. Зутлер, М. Грабиш
Рекомендована секцией УМС Одобрена на заседании кафедры
Прикладная математика и информатика высшей математики
на факультете экономики
Председатель Зав. кафедрой
________________ С.О.Кузнецов _____________ Ф.Т.Алескеров
Утверждена УС факультета
бизнес-информатики
Ученый секретарь
_________________________________
« ____» ___________________20__ г.
Москва
1. Область применения и нормативные ссылки
Настоящая программа учебной дисциплины «Избранные модели теории полезности» устанавливает минимальные требования к знаниям и умениям студента и определяет содержание и виды учебных занятий и отчетности.
Программа предназначена для преподавателей, ведущих данную дисциплину, учебных ассистентов и студентов направления 010400.68 «Прикладная математика и информатика», обучающихся по магистерской программе «Математическое моделирование», изучающих дисциплину «Избранные модели теории полезности».
Программа разработана в соответствии с:
- Рабочим учебным планом университета по направлению 010400.68 «Прикладная математика и информатика» подготовки магистра, утвержденным 5 августа 2011г.
2. Цели освоения дисциплины
Целью дисциплины «Избранные модели теории полезности» является освоения студентами некоторых глав теории полезности. В первой части курса рассматриваются классические модели теории полезности и пороговые модели максимизации полезности. В рамках курса будут описаны основные виды бинарных отношений, модели выбора с учетом предпочтений, также будут описаны неклассические модели максимизации полезности, основанные на пороговых функциях. Кроме того, в данном курсе вводятся и изучаются новые классы бинарных отношений.
Классическая теория ожидаемой полезности в аксиоматике Дж. Неймана и О, Моргенштерна наиболее часто используется для анализа действий индивидуумов и моделирования социально-экономических процессов. Вместе с тем существует достаточное количество примеров (парадоксов выбора) в которых данная модель перестает работать. На фоне наиболее известных парадоксов нарушения классической модели полезностей будет сделан краткий экскурс в модели субъективной ожидаемой полезности1, модели сравнительной полезности и интенсивности предпочтений, кумулятивной теории проспектов, теорию вероятностных предпочтений и Марковский процесса выбора перебором. Вторая часть курса посвящена играм с ограниченной кооперацией и читается профессором М. Грабишем из Университета Париж-I Пантеон Сорбонна.
В результате курса студенты смогут более глубоко самостоятельно анализировать и выявлять психологические аспекты выбора, необходимые для моделирования экономических процессов.
3. Компетенции обучающегося, формируемые в результате освоения дисциплины
В результате освоения дисциплины студент должен:
Знать: классические модели теории полезности и пороговые модели максимизации полезности, виды бинарных отношений, модели сравнительной полезности и теории кумулятивных проспектов, теоретические основы современных моделей в указанной области, ограничения классической теории полезностей.
Уметь: использовать типовые методы оценки полезности для принятия решений, строить модели выбора с учетом предпочтений, пользоваться моделями выбора наилучших вариантов для формализации и решения различных задач в области социальных и политических процессов, анализировать психологию выбора с целью построения адекватной модели.
Владеть: терминологией и методами классической теории полезности, теории ожидаемой полезности, теории сравнительной полезности, теории игр с ограниченной кооперацией..
В результате освоения дисциплины студент осваивает следующие компетенции:
| Компетенция | Код по ФГОС/ НИУ | Дескрипторы – основные признаки освоения (показатели достижения результата) | Формы и методы обучения, способствующие формированию и развитию компетенции |
| владение культурой мышления, способность к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения | ОК-1 | умеет дать формально- логическое описание и построить математическую модель ситуации выбора, умеет применить различные критерии для оценки моделируемой реальности | использование формально-логических доказательств, практика анализа реальных ситуаций с помощью построения их математических моделей |
| способность анализировать социально-значимые проблемы и процессы, происходящие в обществе, и прогнозировать возможное их развитие в будущем | ОК-4 | умеет дать формально- логическое описание и построить математическую модель ситуации выбора, умеет применить различные критерии для оценки моделируемой реальности | использование формально-логических доказательств, практика анализа реальных ситуаций с помощью построения их математических моделей |
| способность логически верно, аргументировано и ясно строить устную и письменную речь | ОК-6 | умеет дать формально- логическое описание и построить математическую модель ситуации выбора, умеет применить различные критерии для оценки моделируемой реальност | использование формально-логических доказательств |
| владение одним из иностранных языков на уровне не ниже разговорного | ОК-14 | знает английскую терминологию, умеет прочесть английский текст научной статьи по данной предметной области | чтение специальной литература на английском языке, знакомство с международной (английской) терминологией данной предметной области |
4. Место дисциплины в структуре образовательной программы
Настоящая дисциплина относится к циклу специальных дисциплин и блоку дисциплин, обеспечивающих подготовку магистров по направлению 010400.68 «Прикладная математика и информатика».
Изучение данной дисциплины базируется на следующих дисциплинах:
- Теория вероятностей
- Математический анализ
- Дискретная математика
- Теория игр
Для освоения учебной дисциплины, студенты должны владеть следующими знаниями и компетенциями:
- необходимо знать основы теории вероятностей, теории множеств и теории игр
- владеть базовой терминологией и методами указанных дисциплин.
5. Тематический план учебной дисциплины
| № | Название раздела | Всего часов | Аудиторные часы | Самостоятельная работа | |
| Лекции | Сем. и практ. занятия | ||||
| 1 модуль | |||||
| 1 | Предпочтения и полезность – Классические модели. Максимизация полезности с постоянным порогом или с порогом, зависящим от одной альтернативы | 18 | 4 | 4 | 10 |
| 2 | Максимизация полезности с порогом, зависящим от обеих альтернатив. Максимизация полезности с порогом, зависящим от множества альтернатив | 18 | 4 | 4 | 10 |
| 3 | Теория ожидаемой полезности. | 9 | 2 | 2 | 5 |
| 4 | Теория сравнительной полезности. | 9 | 2 | 2 | 5 |
| 5 | Выбор последовательными сравнениями. | 9 | 2 | 2 | 5 |
| 6 | Кумулятивная теория проспектов. | 9 | 2 | 2 | 5 |
| | Всего | 72 | 16 | 16 | 40 |
| 2 модуль | |||||
| 1 | Basic notions of cooperative game theory and mathematical prerequisites | 9 | 2 | 2 | 5 |
| 2 | The core of games with restricted cooperation | 9 | 2 | 2 | 5 |
| 3 | The Shapley value for games on regular set systems. How to make the core bounded for games with restricted cooperation | 9 | 2 | 2 | 5 |
| 4 | The Choquet integral for capacities defined on set systems | 9 | 2 | 2 | 5 |
| | Всего | 36 | 8 | 8 | 20 |
| | Итого: | 108 | 24 | 24 | 60 |
6. Формы контроля знаний студентов
| Тип контроля | Форма контроля | 1 год | Кафедра | Параметры ** | |||
| 1 | 2 | 3 | 4 | ||||
| Текущий (неделя) | Контрольная работа | * | | | | | Письменная работа, 80 минут |
| Домашнее задание | | * | | | | | |
| Промежуточный | Зачет | * | | | | | Письменная работа, 80 минут |
| Итоговый | Зачет | | * | | | | Письменная работа, 80 минут |
7. Содержание дисциплины
1 модуль
Лекция 1. Предпочтения и полезность – Классические модели
Бинарные отношения и предпочтения. Бинарные отношения и функции полезности. Важнейшие классы бинарных отношений: линейные порядки, слабые порядки, частичные порядки.
Теорема представления для конечного множества альтернатив. Теорема представления для бесконечного множества альтернатив. Теорема Кантора.
Неотрицательные пороговые функции: случай интервального выбора. Интервальные порядки и полупорядки. Свойства интервальных порядков и полупорядков. Максимальные антицепи в интервальных порядках.
Произвольные пороговые функции и бипорядки. Теорема о представлении интервальных порядков, полупорядков и бипорядков.
Практическое применение этих моделей.
Лекция 2. Максимизация полезности с порогом, зависящим от обеих альтернатив
Теорема о представлении. Пороговые функции, удовлетворяющие свойству полуметрики. Случай аддитивных пороговых функций. Мультипликативные пороговые функции и их свойства.
Мультипликативные пороговые функции – два специальных случая. Теоремы о представлении. Полупорядки и интервальные порядки, представимые через максимизацию полезности с порогами обоих специальных типов.
Четыре типа пороговых функций. Эквивалентные модели для максимизации полезности для этих типов пороговых функций. Свойства соответствующих функций выбора. Связь модели максимизации полезности с порогом, зависящим от множества альтернатив, с теоремой Самуэльсона.
Вложение отношений и проблема максимизации полезности с порогом, зависящим от множества альтернатив. Слабые бипорядки и их представление. Аддитивные пороги, зависящие от множества альтернатив. Простые и простейшие полупорядки. Слабое условие Чипмана и описание простых полупорядков.
Практическое применение этих моделей.
Лекция 3. Теория ожидаемой полезности. Санкт-Петербургский парадокс. Аксиоматика Неймана-Моргенштерна. Субъективная теория полезностей. Аксиоматика Сэвиджа и Энскомбе-Ауманна. Коэффициент неприятия риска Арроу-Пратта. Нарушения принципов ожидаемой полезности: парадоксы Мэя, Алле, Эллсберга. Обратимость предпочтений.
Лекция 43. Теория сравнительной полезности. Аксиоматика Фишберна SSB интенсивности предпочтений. Теорема существования. Единственность максимального элемента. Обоснование парадоксов Мэя, порога чувствительности и Алле. Модель сравнительной полезности. Вероятностные предпочтения.
Лекция 5. Выбор последовательными сравнениями. Аксиоматика марковского процесса выбора. Свойства выбора - “наследования” (Heredity), “согласия” (Concordance) и “отбрасывания” (Outcast). Вводные элементы бескоалиционной теории игр, теории массового обслуживания.
Лекция 6. Кумулятивная теория проспектов. Аксиоматика кумулятивной теории проспектов. Интеграл Шоке, сведение к интегралу Римана. Вероятностное расширение. Разрешение парадокса Алле,
2 модуль
Лекция 1. Basic notions of cooperative game theory and mathematical prerequisites
- cooperative games: basic definitions; convex games
- the core of a game; classical results on the structure of the core; the Weber set; balanced games
- The Shapley value
- basic notions on partially ordered sets (posets); main families of posets: lattices, regular set systems, weakly union-closed systems; relations between these families
Лекция 2. The core of games with restricted cooperation
- basic notions on convex polyhedra
- general results for arbitrary set systems: balancedness, vertices and rays of the core
- the case of distributive lattices
- the case of regular set systems
- the case of weakly union-closed set systems: the positive core and Monge extensions
Лекция 3. The Shapley value for games on regular set systems. How to make the core bounded for games with restricted cooperation
- the general idea: add e_ciency constraints (notion of restricted core)
- the case of distributive lattices; the Weber set
- the general case
Лекция 4. The Choquet integral for capacities de_ned on set systems
- prerequisites on the Choquet integral: definition, characterization results, Möbius transform, belief functions
- upper integrals
- the Monge algorithm
- the case of weakly union-closed systems
- supermodularity and super additivity
8. Образовательные технологии
8.1. Методические рекомендации преподавателю
Практические занятия по теме «Выбор последовательными сравнениями» целесообразно частично проводить в компьютерном классе.
8.2. Методические указания студентам
Для успешного изучения дисциплины рекомендуется перед каждым семинарским занятием повторить теоретический материал по конспекту лекций, а после активной работы на занятии – выполнять полученные задания (решать предложенные задачи, изучать рекомендованную литературу).
9. Оценочные средства для текущего контроля и аттестации студента
9.1. Примеры заданий промежуточного /итогового контроля
1. Найти функцию полезности, если А
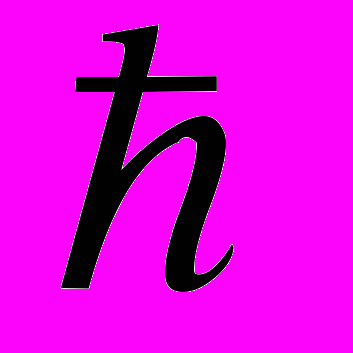 B
B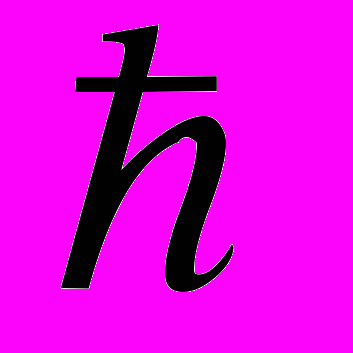 C
C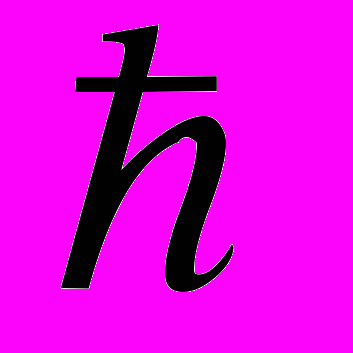 D и
D и B~1/3А+2/3D,
В~1/4A+3/4C.
2. Пусть функция полезности ЛПР есть и(х) = 1п(1 + х), уровень его капитала w. Ему предлагают лотерею, в которой выигрыш х и проигрыш х имеют вероятность соответственно р и 1 - р. Найдите х, при котором такая лотерея ему безразлична. Каков ответ при p = 0,5?
3. Интенсивность обслуживания заявки прибором μ. То есть обслуживание заявки завершится за время Δt с вероятностью μΔt.
Какова вероятность того, что за время Δt завершится обслуживание на одном приборе из пяти?
4. В магазине имеется три консультанта. Интенсивность прихода клиентов - 10 клиентов в час, среднее время консультирования 15 минут. Если все консультанты заняты, клиент уходит.
- Написать систему дифференциальных уравнений, описывающих систему (при t=0 система пуста).
- Найти стационарное состояние системы.
- Найти вероятность того, что пришедший клиент будет потерян (в стационарном состоянии).
10. Порядок формирования оценок по дисциплине
Итоговая оценка K формируется как взвешенная сумма:
K = 0,2 Текущий контроль + 0,8 Итоговый контроль.
10-балльная итоговая оценка округляются до целого числа баллов. При округлении учитывается работа студента на семинарах. Перевод в 5-балльную шкалу осуществляется по правилу:
- 0 ≤ К ≤ 3 - неудовлетворительно,
- 4 ≤ К ≤ 5 - удовлетворительно,
- 6 ≤ К ≤ 7 - хорошо,
- 8 ≤ К ≤10 -отлично.
Таблица соответствия оценок по десятибалльной и пятибалльной системам
| По десятибалльной шкале | По пятибалльной шкале |
| неудовлетворительно – 2 |
| удовлетворительно – 3 |
| Хорошо – 4 |
| отлично – 5 |
11. Учебно-методическое и информационное обеспечение дисциплины
Базовый учебник
- Aizerman M. and F.Aleskerov (1995) 'Theory of choice', Elsevier, Amsterdam
- Aleskerov F., Bouyssou D., Monjardet B. (2007) "Utility Maximization, Choice and Preference", Springer, Berlin
- Льюс Р. Д., Райфа Х. (1961), Игры и решения. Москва, «Иностранная литература».
- m/book/Igri_i_resheniya__Vvedenie_i_kriticheskij_obzor#1
- M. Grabisch. Ensuring the boundedness of the core of games with restricted cooperation. Annals of Operations Research.
- M. Grabisch. The core of games on ordered structures and graphs. 4OR, 7:207-238, 2009. DOI: 10.1007/s10288-009-0109-9.
Основная литература
- Плаус С. (1998) Психология оценки и принятия решений / М.: “Филинъ”.
- Нейман фон Дж., Моргенштерн О.(1970). Теория игр и экономическое поведение.
- F. J. Anscombe; R. J. Aumann . (1963), A Definition of Subjective Probability The Annals of Mathematical Statistics, Vol. 34, No. 1pp. 199-205.
- Fishburn P.C. (1982) Nontransitive Measurable Utility // J. of Mathematical Psychology. 1982. No. 26, p. 3l–67.
- Fishburn P.C. (1984) Dominance in SSB Utility Theory // J. of economic theory. No. 34, p. 130–148.
- Зутлер И.А. (2011), Выбор последовательными сравнениями как непрерывное марковское блуждание, Автоматика и Телемеханика
- Вентцель Е.С. Теория вероятностей. -М.: Высшая школа, 1999.
- Kahneman D., Tversky А. (1979), Prospect Theory: An Analysis of Decision under Risk, Econometrica 47, 263-291.
- Tversky A, Kahneman D, (1992) “Advances in Prospect Theory: Cumulative Representation of Uncertainty,” Journal of Risk and Uncertainty 5, 297–323.
- M. Grabisch and L. J. Xie. The restricted core of games on distributive lattices: how to share benefits in a hierarchy. Mathematical Methods of Operations Research, 73:189-208, 2011.
- G. Owen. Game Theory. Academic Press, 3d edition, 1995.
- U. Faigle and M. Grabisch. A discrete Choquet integral for ordered systems. Fuzzy Sets and Systems, 168:3-17, 2011. DOI 10.1016/j.fss.2010.10.003.
Дополнительная литература
- Fishburn, P. (1970) Utility Theory for Decision Making. John Wiley, New York
- Halmos, P. (1974) Naïve Set Theory. Springer Verlag, Berlin
- Harary, F. (1962) Graph Theory. Addison Wesley, Mass.
- Kreps D. (1988) Notes on the Theory of Choice, Vestview Press, Boulder and London
- Riguet, J. (1948) Relations binares, fermetures, correspondences de Galois. Bull. Soc.Math.France, v.76
- Savage L,. J. (1954). The Foundations of Statistics. Wiley, New York.
- Alain CHATEAUNEUF, Michèle COHEN, Jean-Marc TALLON (2008)
- Decision under risk : The classical Expected Utility Model
- ссылка скрыта
- Edi Karni (2005) Savages’ Subjective Expected Utility Model
- ссылка скрыта
- Tsogbadral Galaabaatar, Edi Karni (2011)
- Objective and Subjective Expected Utility with Incomplete Preferences ссылка скрыта
- Кирута А.Я., Рубинов А.М., Яновская Е.Б. (1980), Оптимальный выбор распределений в сложных социально-экономических задачах. - Л.: Наука. Ленингр. отд-ие.
- Данилов В.И. (2006) Лекции о неподвижной точке.
- Ивченко Г. И., Каштанов В. А., Коваленко И. Н. Теория массового обслуживания.-М.: Высшая школа, 1982.
- Печерский С.Л., Беляева А.А., Теория игр для экономистов, 2002.
- Weibull J.W. (2002), What have we learned from evolutionary game theory so far? Resarch Institute of Industrial Economics, ссылка скрыта №487.
- Wakker P., Tversky A. (1993), An Axiomatization of Cumulative Prospect Theory, Journal of Risk and Uncertainty, 7:7:147-176
- Wakker P. (2010), Prospect Theory for risk and ambiguity. Cambridge university press.
- Blavatskyy P. (2011), Probabilistic Subjective Expected Utility.
- https://editorialexpress.com/cgi-bin/conference/download.cgi?db_name=NASM2011&paper_id=68
- B. Peleg and P. Sudhöolter. Introduction to the theory of cooperative games. Kluwer Academic Publisher, 2003.
- H. Peters. Game Theory: A Multilevel Approach. Springer, 2008.
Разработчики:
кафедра высшей математики
на факультете экономики ГУ-ВШЭ, профессор, д.т.н., Ф.Т. Алескеров
кафедра высшей математики
на факультете экономики ГУ-ВШЭ, доцент, к.ф.-м.н., И.А. Зутлер
Université Paris 1 Panthéon-Sorbonne
Associate researcher Michel Grabisch
1 Subjective expected utility – некоторые понятия не имеют устойчивого русского перевода, потому в процессе курса будут использованы обозначения на языке оригинала.
