Отделение Прикладной Математики и Информатики программа дисциплины
| Вид материала | Программа дисциплины |
- Правительство Российской Федерации Государственный университет Высшая школа экономики, 91.67kb.
- Отделение Прикладной Математики и Информатики программа дисциплины, 219.98kb.
- Программа дисциплины основные методологические проблемы прикладной математики и информатики, 67.07kb.
- Аннотация примерной программы учебной дисциплины б 9 «История и методология прикладной, 2416.02kb.
- Программа курса по выбору для учащихся учреждений, обеспечивающих получение, 84.43kb.
- Отделение Прикладной Математики и Информатики программа дисциплины, 225.44kb.
- Задачи на графах программа, 81.89kb.
- Рабочая программа учебной дисциплины история и методология прикладной математики, 537.44kb.
- М. К. Аммосова Институт математики и информатики Кафедра прикладной математики рабочая, 219.2kb.
- М. К. Аммосова Институт математики и информатики Кафедра прикладной математики рабочая, 460.29kb.
Правительство Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего профессионального образования
"Национальный исследовательский университет
"Высшая школа экономики"
Факультет бизнес-информатики
Отделение Прикладной Математики и Информатики
Программа дисциплины
«Избранные модели теории полезности»
для направления 010100.68 подготовки магистра
«Прикладная математика и информатика»
Авторы:
д.т.н., проф. Ф.Т.Алескеров, к.т.н., доцент Зутлер И.А. и проф. Грабиш М.
Рекомендована секцией УМС Одобрена на заседании кафедры
_____________________________ ________________________________
Председатель Зав. кафедрой
_____________________________ ________________________________
«_____» __________________ 20__ г. «____»__________________ 20__ г
Утверждена УС факультета
_________________________________
Ученый секретарь
_________________________________
« ____» ___________________20__ г.
Москва
1. Цели и задачи дисциплины.
В первой части курса рассматриваются классические модели теории полезности и пороговые модели максимизации полезности. В рамках курса будут описаны основные виды бинарных отношений, модели выбора с учетом предпочтений, также будут описаны неклассические модели максимизации полезности, основанные на пороговых функциях. Кроме того, в данном курсе вводятся и изучаются новые классы бинарных отношений.
Классическая теория ожидаемой полезности в аксиоматике Дж. Неймана и О, Моргенштерна наиболее часто используется для анализа действий индивидуумов и моделирования социально-экономических процессов. Вместе с тем существует достаточное количество примеров (парадоксов выбора) в которых данная модель перестает работать.
На фоне наиболее известных парадоксов нарушения классической модели полезностей будет сделан краткий экскурс в модели субъективной ожидаемой полезности1, модели сравнительной полезности и интенсивности предпочтений, кумулятивной теории проспектов, теорию вероятностных предпочтений и Марковский процесса выбора перебором.
В результате курса студенты смогут более глубоко самостоятельно анализировать и выявлять психологические аспекты выбора, необходимые для моделирования экономических процессов.
Вторая часть курса посвящена играм с ограниченной кооперацией и читается профессором М.Грабишем из Университета Париж-I Пантеон Сорбонна.
A classical cooperative game is a pair (N; v), where N is a finite set of players, and v : 2N→R with the convention v(
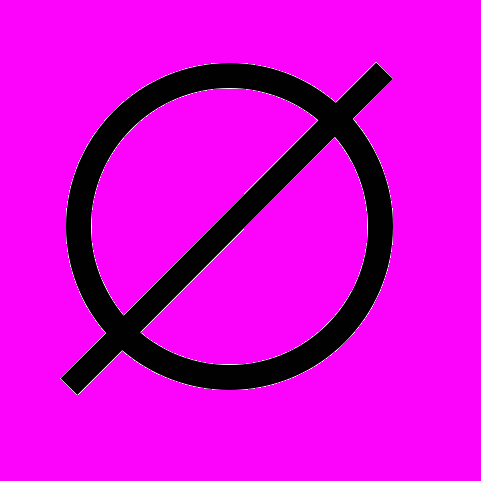 ) = 0. For any
) = 0. For any 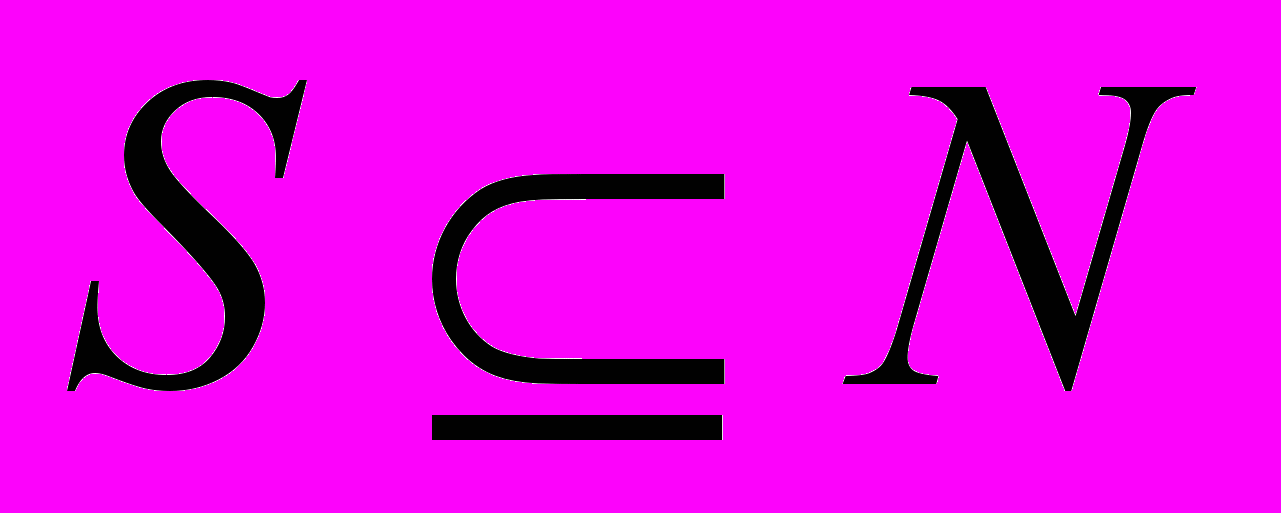 , the quantity v(S) represents the best amount of money the coalition S can achieve by itself without the help of the other players (worth of S). Cooperative game theory primarily aims at defining rational ways (called solution concepts) of sharing the worth of the grand coalition N among the players in N, when it is supposed that eventually all players cooperate to form the coalition N. Most classical solution concepts are the core, the Shapley value and the nucleolus (see, e.g., the following textbooks: [5, 6, 7]).
, the quantity v(S) represents the best amount of money the coalition S can achieve by itself without the help of the other players (worth of S). Cooperative game theory primarily aims at defining rational ways (called solution concepts) of sharing the worth of the grand coalition N among the players in N, when it is supposed that eventually all players cooperate to form the coalition N. Most classical solution concepts are the core, the Shapley value and the nucleolus (see, e.g., the following textbooks: [5, 6, 7]).The classical framework of cooperative game theory tacitly assumes that every coalition
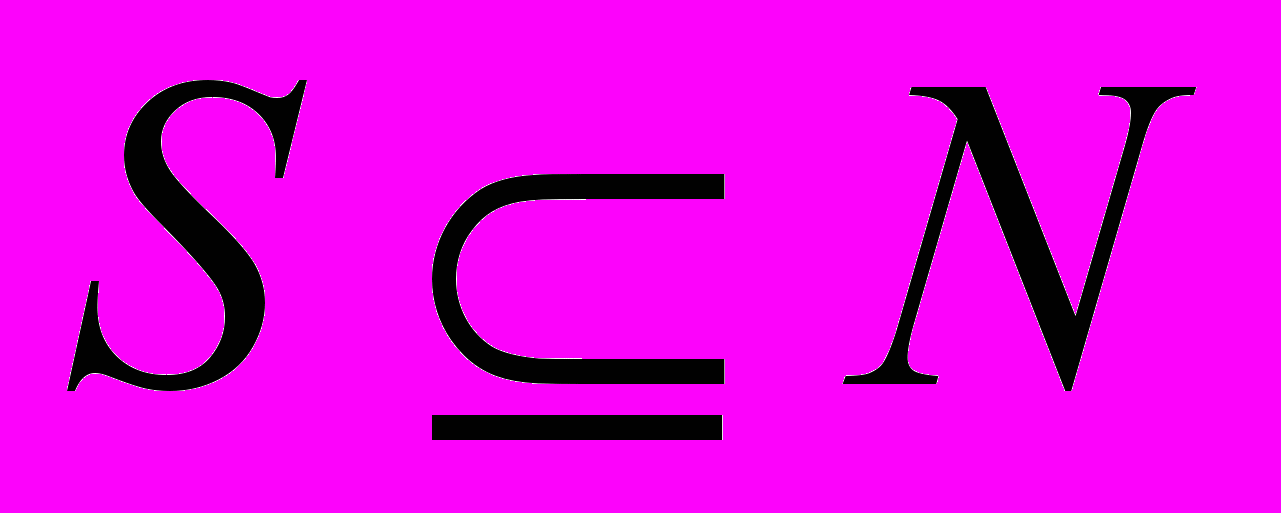 can form. In most real situation however, this is too strong an assumption. The formation of coalition may be constrained by hierarchy relations, affinity and compatibility (e.g., of political nature) between players, size restrictions, etc. It is therefore of interest to generalize the de_nition of a cooperative game as follows: it is a triple (N,F ,v), where F is a nonempty collection of subsets (coalitions) of N, and v : F→R. Such games are called games with restricted cooperation. Once this is done, it remains the difficult task to redefine and study the properties of the main solution concepts, like the core and the Shapley value. Many researchers have worked on this topic, and this course will present a synthesis of the work done, with an emphasis on the core (see especially the survey [3] where many references can be found, and [4, 2] for further studies).
can form. In most real situation however, this is too strong an assumption. The formation of coalition may be constrained by hierarchy relations, affinity and compatibility (e.g., of political nature) between players, size restrictions, etc. It is therefore of interest to generalize the de_nition of a cooperative game as follows: it is a triple (N,F ,v), where F is a nonempty collection of subsets (coalitions) of N, and v : F→R. Such games are called games with restricted cooperation. Once this is done, it remains the difficult task to redefine and study the properties of the main solution concepts, like the core and the Shapley value. Many researchers have worked on this topic, and this course will present a synthesis of the work done, with an emphasis on the core (see especially the survey [3] where many references can be found, and [4, 2] for further studies).In decision making, capacities introduced by Choquet can be seen as particular cooperative games: they are mappings
 : 2N→R,
: 2N→R,  (
(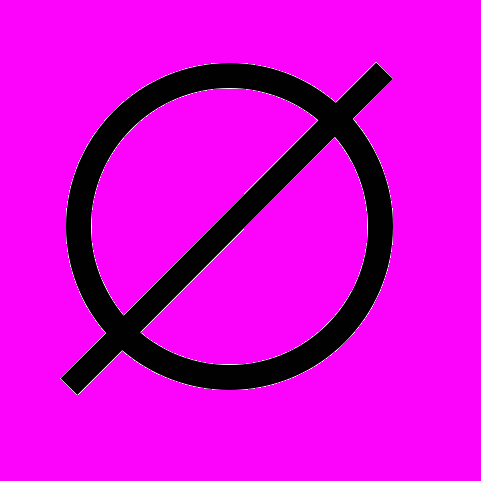 ) = 0, with the additional requirement that they are monotone w.r.t. inclusion:
) = 0, with the additional requirement that they are monotone w.r.t. inclusion: 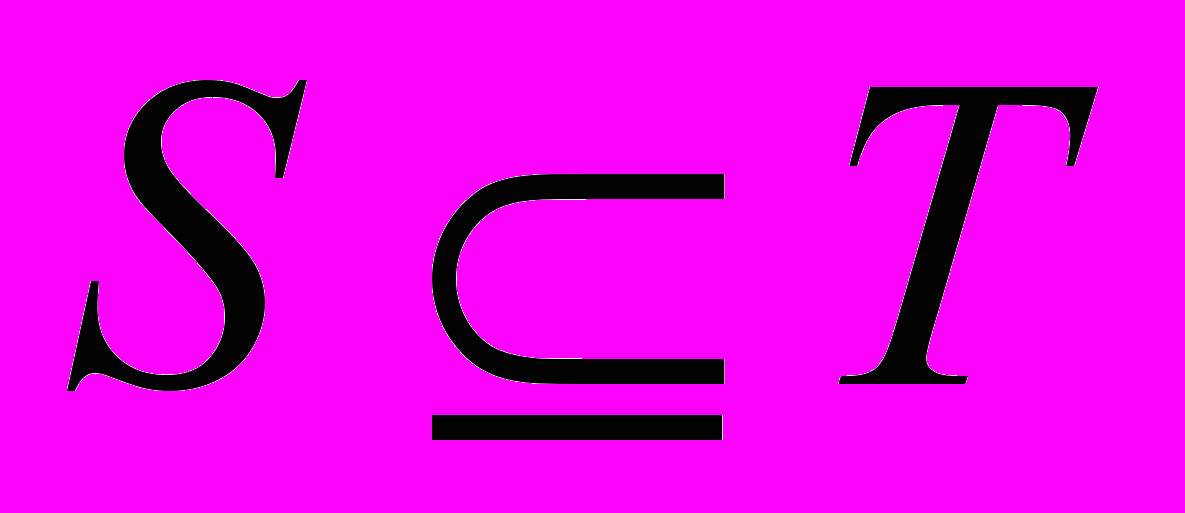 implies
implies 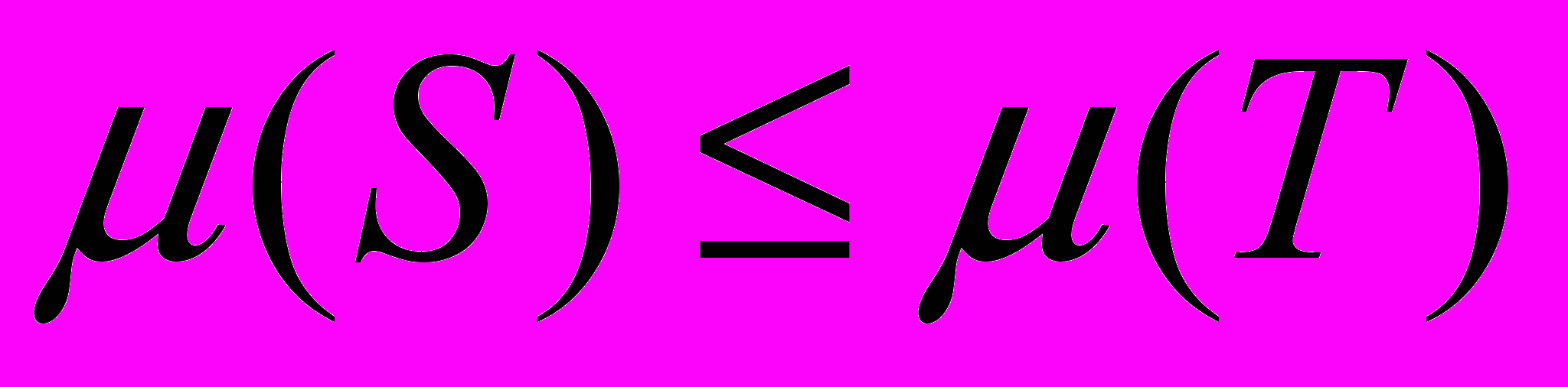 . In decision making, capacities often play the role of a generalized probability, and therefore the question of how to compute an expected value w.r.t. a capacity arises. This is usually achieved by the Choquet integral, a generalization of the Lebesgue integral.
. In decision making, capacities often play the role of a generalized probability, and therefore the question of how to compute an expected value w.r.t. a capacity arises. This is usually achieved by the Choquet integral, a generalization of the Lebesgue integral.Going back to restricted cooperation, one can imagine as well capacities defined on a subcollection F of
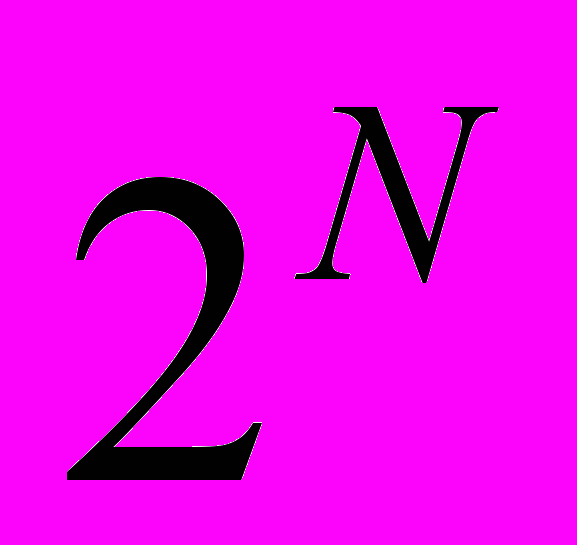 . Then arises the problem of a proper definition of the Choquet integral. We propose here a general de_nition, which can be reached by several ways (see [1] for details).
. Then arises the problem of a proper definition of the Choquet integral. We propose here a general de_nition, which can be reached by several ways (see [1] for details).Задачи дисциплины
В результате изучения курса студенты должны:
- уметь пользоваться моделями выбора наилучших вариантов для формализации и решения различных задач в области социальных и политических процессов.
- иметь представление о теоретических основах современных моделей в указанной области.
- понимать ограничения классической теории полезностей.
- знать модели сравнительной полезности и теории кумулятивных проспектов
- анализировать психологию выбора с целью построения адекватной модели
- уметь использовать типовые методы оценки полезности для принятия решений.
2. Место дисциплины в структуре ООП.
Программа учебной дисциплины «Избранные модели теории полезностей» предназначена для подготовки студентов, обучающихся по направлению «Прикладная математика и информатика». Программа составлена в соответствии с Федеральным государственным образовательным стандартом высшего профессионального образования.
Изучение курса «Избранные модели теории полезностей» требует предварительных знаний теории вероятностей, математического анализа и дискретной математики в объёме, доступном магистрам математических специальностей университетов. Желательно знакомство слушателей с классической теорией ожидаемой полезности, основами бескоалиционной теории игр.
Основными формами изучения дисциплины являются:
- лекции
- семинары
- самостоятельная работа слушателей.
Формы контроля
- текущий контроль: работа на семинарах,
- итоговый контроль: домашняя работа или письменный экзамен.
Итоговая оценка K формируется как взвешенная сумма:
K = 0,1 Текущий контроль + 0,9 Итоговый контроль.
10-балльная итоговая оценка округляются до целого числа баллов. При округлении учитывается работа студента на семинарах. Перевод в 5-балльную шкалу осуществляется по правилу:
- 0 ≤ К ≤ 3 - неудовлетворительно,
- 4 ≤ К ≤ 5 - удовлетворительно,
- 6 ≤ К ≤ 7 - хорошо,
- 8 ≤ К ≤10 -отлично.
Таблица соответствия оценок по десятибалльной и пятибалльной системам
| По десятибалльной шкале | По пятибалльной шкале |
| неудовлетворительно – 2 |
| удовлетворительно – 3 |
| Хорошо – 4 |
| отлично – 5 |
Тематический план учебной дисциплины
| № | Название темы | Всего часов по дисциплине | Аудиторные часы | Самостоятельная работа | |
| Лекции | Сем. и практ. занятия | ||||
| 1 модуль | |||||
| 1 | Предпочтения и полезность – Классические модели. Максимизация полезности с постоянным порогом или с порогом, зависящим от одной альтернативы | 18 | 4 | 4 | 10 |
| 2 | Максимизация полезности с порогом, зависящим от обеих альтернатив. Максимизация полезности с порогом, зависящим от множества альтернатив | 18 | 4 | 4 | 10 |
| 3 | Теория ожидаемой полезности. | 9 | 2 | 2 | 5 |
| 4 | Теория сравнительной полезности. | 9 | 2 | 2 | 5 |
| 5 | Выбор последовательными сравнениями. | 9 | 2 | 2 | 5 |
| 6 | Кумулятивная теория проспектов. | 9 | 2 | 2 | 5 |
| | Всего | 72 | 16 | 16 | 40 |
| 2 модуль | |||||
| 1 | Basic notions of cooperative game theory and mathematical prerequisites | 9 | 2 | 2 | 5 |
| 2 | The core of games with restricted cooperation | 9 | 2 | 2 | 5 |
| 3 | The Shapley value for games on regular set systems. How to make the core bounded for games with restricted cooperation | 9 | 2 | 2 | 5 |
| 4 | The Choquet integral for capacities defined on set systems | 9 | 2 | 2 | 5 |
| | Всего | 36 | 8 | 8 | 20 |
| | Итого: | 108 | 24 | 24 | 60 |
Содержание программы
1 модуль
Лекция 1. Предпочтения и полезность – Классические модели
Бинарные отношения и предпочтения. Бинарные отношения и функции полезности. Важнейшие классы бинарных отношений: линейные порядки, слабые порядки, частичные порядки.
Теорема представления для конечного множества альтернатив. Теорема представления для бесконечного множества альтернатив. Теорема Кантора.
Неотрицательные пороговые функции: случай интервального выбора. Интервальные порядки и полупорядки. Свойства интервальных порядков и полупорядков. Максимальные антицепи в интервальных порядках.
Произвольные пороговые функции и бипорядки. Теорема о представлении интервальных порядков, полупорядков и бипорядков.
Практическое применение этих моделей.
Базовые учебники:
- Aizerman M. and F.Aleskerov (1995) 'Theory of choice', Elsevier, Amsterdam
- Aleskerov F., Bouyssou D., Monjardet B. (2007) "Utility Maximization, Choice and Preference", Springer, Berlin
Дополнительная литература:
- Fishburn, P. (1970) Utility Theory for Decision Making. John Wiley, New York
- Halmos, P. (1974) Naïve Set Theory. Springer Verlag, Berlin
- Harary, F. (1962) Graph Theory. Addison Wesley, Mass.
- Kreps D. (1988) Notes on the Theory of Choice, Vestview Press, Boulder and London
- Riguet, J. (1948) Relations binares, fermetures, correspondences de Galois. Bull. Soc.Math.France, v.76
Лекция 2. Максимизация полезности с порогом, зависящим от обеих альтернатив
Теорема о представлении. Пороговые функции, удовлетворяющие свойству полуметрики. Случай аддитивных пороговых функций. Мультипликативные пороговые функции и их свойства.
Мультипликативные пороговые функции – два специальных случая. Теоремы о представлении. Полупорядки и интервальные порядки, представимые через максимизацию полезности с порогами обоих специальных типов.
Четыре типа пороговых функций. Эквивалентные модели для максимизации полезности для этих типов пороговых функций. Свойства соответствующих функций выбора. Связь модели максимизации полезности с порогом, зависящим от множества альтернатив, с теоремой Самуэльсона.
Вложение отношений и проблема максимизации полезности с порогом, зависящим от множества альтернатив. Слабые бипорядки и их представление. Аддитивные пороги, зависящие от множества альтернатив. Простые и простейшие полупорядки. Слабое условие Чипмана и описание простых полупорядков.
Практическое применение этих моделей.
Базовые учебники:
- Aizerman M. and F.Aleskerov (1995) 'Theory of choice', Elsevier, Amsterdam
- Aleskerov F., Bouyssou D., Monjardet B. (2007) "Utility Maximization, Choice and Preference", Springer, Berlin
Дополнительная литература:
- Fishburn, P. (1970) Utility Theory for Decision Making. John Wiley, New York
- Halmos, P. (1974) Naïve Set Theory. Springer Verlag, Berlin
- Harary, F. (1962) Graph Theory. Addison Wesley, Mass.
- Kreps D. (1988) Notes on the Theory of Choice, Vestview Press, Boulder and London
- Riguet, J. (1948) Relations binares, fermetures, correspondences de Galois. Bull. Soc.Math.France, v.76
Лекция 3. Теория ожидаемой полезности. Санкт-Петербургский парадокс. Аксиоматика Неймана-Моргенштерна. Субъективная теория полезностей. Аксиоматика Сэвиджа и Энскомбе-Ауманна. Коэффициент неприятия риска Арроу-Пратта. Нарушения принципов ожидаемой полезности: парадоксы Мэя, Алле, Эллсберга. Обратимость предпочтений.
Базовые учебники:
- Льюс Р. Д., Райфа Х. (1961), Игры и решения. Москва, «Иностранная литература».
m/book/Igri_i_resheniya__Vvedenie_i_kriticheskij_obzor#1
- Плаус С. (1998) Психология оценки и принятия решений / М.: “Филинъ”.
- Нейман фон Дж., Моргенштерн О.(1970). Теория игр и экономическое поведение.
- F. J. Anscombe; R. J. Aumann . (1963), A Definition of Subjective Probability The Annals of Mathematical Statistics, Vol. 34, No. 1pp. 199-205.
Дополнительная литература:
- Savage L,. J. (1954). The Foundations of Statistics. Wiley, New York.
- Alain CHATEAUNEUF, Michèle COHEN, Jean-Marc TALLON (2008)
Decision under risk : The classical Expected Utility Model
ссылка скрыта
- Edi Karni (2005) Savages’ Subjective Expected Utility Model
ссылка скрыта
- Tsogbadral Galaabaatar, Edi Karni (2011)
Objective and Subjective Expected Utility with Incomplete Preferences ссылка скрыта
Лекция 3. Теория сравнительной полезности. Аксиоматика Фишберна SSB интенсивности предпочтений. Теорема существования. Единственность максимального элемента. Обоснование парадоксов Мэя, порога чувствительности и Алле. Модель сравнительной полезности. Вероятностные предпочтения.
Лит-ра: [9]-[12].
Базовые учебники:
- Fishburn P.C. (1982) Nontransitive Measurable Utility // J. of Mathematical Psychology. 1982. No. 26, p. 3l–67.
- Fishburn P.C. (1984) Dominance in SSB Utility Theory // J. of economic theory. No. 34, p. 130–148.
Дополнительная литература:
- Кирута А.Я., Рубинов А.М., Яновская Е.Б. (1980), Оптимальный выбор распределений в сложных социально-экономических задачах. - Л.: Наука. Ленингр. отд-ие.
- Данилов В.И. (2006) Лекции о неподвижной точке.
Лекция 4. Выбор последовательными сравнениями. Аксиоматика марковского процесса выбора. Свойства выбора - “наследования” (Heredity), “согласия” (Concordance) и “отбрасывания” (Outcast). Вводные элементы бескоалиционной теории игр, теории массового обслуживания.
Лит-ра: [13]-[19].
Базовые учебники:
- Зутлер И.А. (2011), Выбор последовательными сравнениями как непрерывное марковское блуждание, Автоматика и Телемеханика
- Айзерман М. А., Алескеров Ф. Т. Выбор вариантов: основы теории. М.: Наука, 1990.
- Вентцель Е.С. Теория вероятностей. -М.: Высшая школа, 1999.
Дополнительная литература:
- Ивченко Г. И., Каштанов В. А., Коваленко И. Н. Теория массового обслуживания.-М.: Высшая школа, 1982.
- Печерский С.Л., Беляева А.А., Теория игр для экономистов, 2002.
- Weibull J.W. (2002), What have we learned from evolutionary game theory so far? Resarch Institute of Industrial Economics, ссылка скрыта №487.
- Kahneman D., Tversky А. (1979), Prospect Theory: An Analysis of Decision under Risk, Econometrica 47, 263-291.
Лекция 5. Кумулятивная теория проспектов. Аксиоматика кумулятивной теории проспектов. Интеграл Шоке, сведение к интегралу Римана. Вероятностное расширение. Разрешение парадокса Алле,
Лит-ра: [19]-[23].
Базовые учебники:
- Kahneman D., Tversky А. (1979), Prospect Theory: An Analysis of Decision under Risk, Econometrica 47, 263-291.
- Tversky A, Kahneman D, (1992) “Advances in Prospect Theory: Cumulative Representation of Uncertainty,” Journal of Risk and Uncertainty 5, 297–323.
Дополнительная литература:
- Wakker P., Tversky A. (1993), An Axiomatization of Cumulative Prospect Theory, Journal of Risk and Uncertainty, 7:7:147-176
- Wakker P. (2010), Prospect Theory for risk and ambiguity. Cambridge university press.
- Blavatskyy P. (2011), Probabilistic Subjective Expected Utility.
https://editorialexpress.com/cgi-bin/conference/download.cgi?db_name=NASM2011&paper_id=68
2 модуль
Лекция 1. Basic notions of cooperative game theory and mathematical prerequisites
- cooperative games: basic definitions; convex games
- the core of a game; classical results on the structure of the core; the Weber set; balanced games
- The Shapley value
- basic notions on partially ordered sets (posets); main families of posets: lattices, regular set systems, weakly union-closed systems; relations between these families
Лекция 2. The core of games with restricted cooperation
- basic notions on convex polyhedra
- general results for arbitrary set systems: balancedness, vertices and rays of the core
- the case of distributive lattices
- the case of regular set systems
- the case of weakly union-closed set systems: the positive core and Monge extensions
Лекция 3. The Shapley value for games on regular set systems. How to make the core bounded for games with restricted cooperation
- the general idea: add e_ciency constraints (notion of restricted core)
- the case of distributive lattices; the Weber set
- the general case
Лекция 4. The Choquet integral for capacities de_ned on set systems
- prerequisites on the Choquet integral: definition, characterization results, Möbius transform, belief functions
- upper integrals
- the Monge algorithm
- the case of weakly union-closed systems
- supermodularity and super additivity
Базовые учебники:
- U. Faigle and M. Grabisch. A discrete Choquet integral for ordered systems. Fuzzy Sets and Systems, 168:3-17, 2011. DOI 10.1016/j.fss.2010.10.003.
- M. Grabisch. Ensuring the boundedness of the core of games with restricted cooperation. Annals of Operations Research.
- M. Grabisch. The core of games on ordered structures and graphs. 4OR, 7:207-238, 2009. DOI: 10.1007/s10288-009-0109-9.
- M. Grabisch and L. J. Xie. The restricted core of games on distributive lattices: how to share benefits in a hierarchy. Mathematical Methods of Operations Research, 73:189-208, 2011.
- G. Owen. Game Theory. Academic Press, 3d edition, 1995.
Дополнительная литература:
- B. Peleg and P. Sudhöolter. Introduction to the theory of cooperative games. Kluwer Academic Publisher, 2003.
- H. Peters. Game Theory: A Multilevel Approach. Springer, 2008.
Вариант билета зачётной работы.
1. Найти функцию полезности, если А
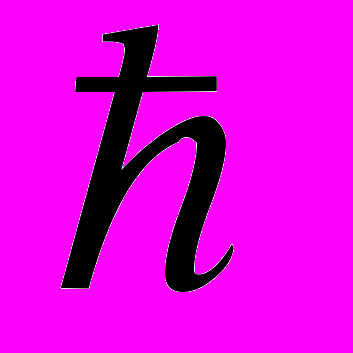 B
B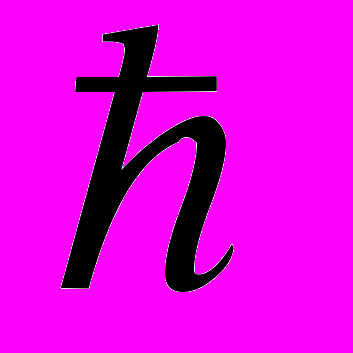 C
C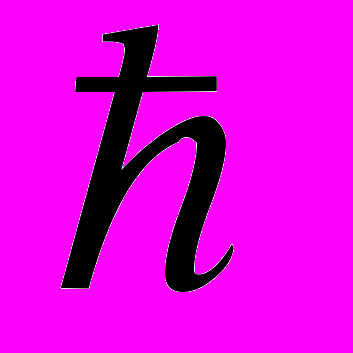 D и
D и B~1/3А+2/3D,
В~1/4A+3/4C.
2. Пусть функция полезности ЛПР есть и(х) = 1п(1 + х), уровень его капитала w. Ему предлагают лотерею, в которой выигрыш х и проигрыш х имеют вероятность соответственно р и 1 - р. Найдите х, при котором такая лотерея ему безразлична. Каков ответ при p = 0,5?
3. Интенсивность обслуживания заявки прибором μ. То есть обслуживание заявки завершится за время Δt с вероятностью μΔt.
Какова вероятность того, что за время Δt завершится обслуживание на одном приборе из пяти?
4. В магазине имеется три консультанта. Интенсивность прихода клиентов - 10 клиентов в час, среднее время консультирования 15 минут. Если все консультанты заняты клиент уходит.
Написать систему дифференциальных уравнений, описывающих систему (при t=0 система пуста).
Найти стационарное состояние системы.
Найти вероятность того, что пришедший клиент будет потерян (в стационарном состоянии).
---------------------------------------------------------------------------------------------------------------------------------------------------------
Автор программы: _____________________________Алескеров Ф.Т.
Зутлер И.А.
Грабиш М.
1 Subjective expected utility – некоторые понятия не имеют устойчивого русского перевода, потому в процессе курса будут использованы обозначения на языке оригинала.
