Отделение Прикладной Математики и Информатики программа дисциплины
| Вид материала | Программа дисциплины |
- Правительство Российской Федерации Государственный университет Высшая школа экономики, 91.67kb.
- Отделение Прикладной Математики и Информатики программа дисциплины, 257.84kb.
- Отделение Прикладной Математики и Информатики программа дисциплины, 219.98kb.
- Программа дисциплины основные методологические проблемы прикладной математики и информатики, 67.07kb.
- Аннотация примерной программы учебной дисциплины б 9 «История и методология прикладной, 2416.02kb.
- Программа курса по выбору для учащихся учреждений, обеспечивающих получение, 84.43kb.
- Задачи на графах программа, 81.89kb.
- Рабочая программа учебной дисциплины история и методология прикладной математики, 537.44kb.
- М. К. Аммосова Институт математики и информатики Кафедра прикладной математики рабочая, 219.2kb.
- М. К. Аммосова Институт математики и информатики Кафедра прикладной математики рабочая, 460.29kb.
Правительство Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего профессионального образования
"Национальный исследовательский университет
"Высшая школа экономики"
Факультет бизнес-информатики
Отделение Прикладной Математики и Информатики
Программа дисциплины
«Принятие индивидуальных и коллективных решений»
для направления 010400.68 «Прикладная математика и информатика»
подготовки магистра
Авторы:
Ф.Т.Алескеров, А.А Рубчинский
Рекомендована секцией УМС Одобрена на заседании кафедры
Прикладная математика и информатика высшей математики
на факультете экономики
Председатель Зав. кафедрой
________________ С.О.Кузнецов _____________ Ф.Т.Алескеров
Утверждена УС факультета
бизнес-информатики
Ученый секретарь
_________________________________
« ____» ___________________20__ г.
Москва
1. Область применения и нормативные ссылки
Настоящая программа учебной дисциплины «Принятие индивидуальных и коллективных решений» устанавливает минимальные требования к знаниям и умениям студента и определяет содержание и виды учебных занятий и отчетности.
Программа предназначена для преподавателей, ведущих данную дисциплину, учебных ассистентов и студентов направления 010400.68 «Прикладная математика и информатика», обучающихся по магистерской программе «Математическое моделирование», специализация "Анализ и принятие решений", изучающих дисциплину «Принятие индивидуальных и коллективных решений».
Программа разработана в соответствии с:
- Рабочим учебным планом университета по направлению 010400.68 «Прикладная математика и информатика» подготовки магистра, утвержденным 5 августа 2011г.
2. Цели освоения дисциплины
Целью дисциплины «Принятие индивидуальных и коллективных решений» является освоения студентами некоторых глав теории выбора. В рамках курса будут описаны основные виды бинарных отношений, модели выбора с учетом предпочтений, также будут описаны неклассические модели максимизации полезности, основанные на пороговых функциях, а также ряд основных разделов теории выбора, таких как теория локальных процедур агрегирования, теория решений, основанных на правиле большинства.
Классическая теория ожидаемой полезности в аксиоматике Дж. Неймана и О, Моргенштерна наиболее часто используется для анализа действий индивидуумов и моделирования социально-экономических процессов. Вместе с тем существует достаточное количество примеров (парадоксов выбора) в которых данная модель перестает работать. На фоне наиболее известных парадоксов нарушения классической модели полезностей будет сделан краткий экскурс в модели субъективной ожидаемой полезности1, модели сравнительной полезности и интенсивности предпочтений, кумулятивной теории проспектов, теорию вероятностных предпочтений и Марковский процесса выбора перебором.
3. Компетенции обучающегося, формируемые в результате освоения дисциплины
В результате освоения дисциплины студент должен:
Знать: классические модели теории полезности и пороговые модели максимизации полезности, виды бинарных отношений, модели сравнительной полезности и теории кумулятивных проспектов, теоретические основы современных моделей в указанной области, основные факты теории локальных процедур агрегирования, теории решений, основанных на правиле большинства.
Уметь: использовать типовые методы оценки полезности для принятия решений, строить модели выбора с учетом предпочтений, пользоваться моделями выбора наилучших вариантов для формализации и решения различных задач в области социальных и политических процессов, анализировать психологию выбора с целью построения адекватной модели, строго доказывать все утверждения, сделанные при изложении материала курса.
Владеть: терминологией и методами классической теории полезности, теории ожидаемой полезности, теории сравнительной полезности, теории игр локальных процедур агрегирования и теории решений, основанных на правиле большинства.
В результате освоения дисциплины студент осваивает следующие компетенции:
| Компетенция | Код по ФГОС/ НИУ | Дескрипторы – основные признаки освоения (показатели достижения результата) | Формы и методы обучения, способствующие формированию и развитию компетенции |
| владение культурой мышления, способность к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения | ОК-1 | умеет дать формально- логическое описание и построить математическую модель ситуации выбора, умеет применить различные критерии для оценки моделируемой реальности | использование формально-логических доказательств, практика анализа реальных ситуаций с помощью построения их математических моделей |
| способность анализировать социально-значимые проблемы и процессы, происходящие в обществе, и прогнозировать возможное их развитие в будущем | ОК-4 | умеет дать формально- логическое описание и построить математическую модель ситуации выбора, умеет применить различные критерии для оценки моделируемой реальности | использование формально-логических доказательств, практика анализа реальных ситуаций с помощью построения их математических моделей |
| способность логически верно, аргументировано и ясно строить устную и письменную речь | ОК-6 | умеет дать формально- логическое описание и построить математическую модель ситуации выбора, умеет применить различные критерии для оценки моделируемой реальност | использование формально-логических доказательств |
| владение одним из иностранных языков на уровне не ниже разговорног | ОК-14 | знает английскую терминологию, умеет прочесть английский текст научной статьи по данной предметной области | чтение специальной литература на английском языке, знакомство с международной (английской) терминологией данной предметной области |
4. Место дисциплины в структуре образовательной программы
Настоящая дисциплина относится к циклу специальных дисциплин и блоку дисциплин, обеспечивающих подготовку магистров по направлению 010400.68 «Прикладная математика и информатика».
Изучение данной дисциплины базируется на следующих дисциплинах:
- Дискретная математика
- Геометрия и алгебра
- Теория вероятностей и математическая статистика
- Теория игр
Для освоения учебной дисциплины, студенты должны владеть следующими знаниями и компетенциями:
- необходимо знать основы теории вероятностей, теории множеств, теории графов и теории игр
- владеть базовой терминологией этих дисциплин, уметь строить и анализировать логически строгие доказательства математических утверждений.
- владеть базовой терминологией и методами указанных дисциплин.
5. Тематический план учебной дисциплины
| № | Название раздела | Всего часов | Аудиторные часы | Самостоятельная работа | |
| Лекции | Сем. И практ. Занятия | ||||
| 1 модуль | |||||
| 1 | Предпочтения и полезность – Классические модели. | 12 | 4 | 2 | 6 |
| 2 | Максимизация полезности с постоянным порогом или с порогом, зависящим от одной альтернативы | 20 | 6 | 4 | 10 |
| 3 | Максимизация полезности с порогом, зависящим от обеих альтернатив. | 16 | 4 | 4 | 8 |
| 4 | Максимизация полезности с порогом, зависящим от множества альтернатив | 16 | 4 | 4 | 8 |
| 5 | Теория ожидаемой полезности. | 12 | 4 | 2 | 6 |
| 6 | Теория сравнительной полезности. | 12 | 4 | 2 | 6 |
| 7 | Кумулятивная теория проспектов. | 12 | 4 | 2 | 6 |
| | Всего | 100 | 30 | 20 | 50 |
| 2 модуль | |||||
| 1 | Постановка задачи выбора. Парадокс Кондорсе. | 6 | 2 | - | 4 |
| 2 | Локальное агрегирование вида P→P | 12 | 2 | 4 | 6 |
| 3 | Локальное агрегирование вида С→С | 8 | 2 | 2 | 4 |
| 4 | Локальное агрегирование вида P→С | 8 | 2 | 2 | 4 |
| 5 | Нелокальное агрегирование | 18 | 2 | 6 | 10 |
| 6 | Конструирование коллективных предпочтений. Решения на мажоритарном графе. | 14 | 2 | 4 | 8 |
| 7 | Нелокальные правила. Аксиоматика Мэя. Решения, основанные на принципе устойчивости. Правило Коупленда. Матрично-векторное представление решений. Рейтинги. | 22 | 4 | 6 | 12 |
| | Всего | 88 | 16 | 24 | 48 |
| | Итого: | 188 | 46 | 44 | 98 |
6. Формы контроля знаний студентов
| Тип контроля | Форма контроля | 1 год | Кафедра | Параметры ** | |||
| 1 | 2 | 3 | 4 | ||||
| Текущий (неделя) | Контрольная работа | | | | 1 | | Письменная работа, 80 минут |
| Домашнее задание | | | 1 | 1 | | | |
| Промежуточный | Зачет | | | * | | | Письменная работа, 80 минут |
| Итоговый | Зачет | | | | * | | Письменная работа, 80 минут |
7. Содержание дисциплины
3 модуль
Лекция 1. Предпочтения и полезность – Классические модели
Бинарные отношения и предпочтения. Бинарные отношения и функции полезности. Важнейшие классы бинарных отношений: линейные порядки, слабые порядки, частичные порядки.
Теорема представления для конечного множества альтернатив. Теорема представления для бесконечного множества альтернатив. Теорема Кантора.
Практическое применение этих моделей.
Лекция 2. Максимизация полезности с постоянным порогом или с порогом, зависящим от одной альтернативы
Неотрицательные пороговые функции: случай интервального выбора. Интервальные порядки и полупорядки. Свойства интервальных порядков и полупорядков. Максимальные антицепи в интервальных порядках.
Произвольные пороговые функции и бипорядки. Теорема о представлении интервальных порядков, полупорядков и бипорядков.
Практическое применение этих моделей.
Лекция 3. Максимизация полезности с порогом, зависящим от обеих альтернатив
Теорема о представлении. Пороговые функции, удовлетворяющие свойству полуметрики. Случай аддитивных пороговых функций. Мультипликативные пороговые функции и их свойства.
Мультипликативные пороговые функции – два специальных случая. Теоремы о представлении. Полупорядки и интервальные порядки, представимые через максимизацию полезности с порогами обоих специальных типов.
Практическое применение этих моделей.
Лекция 4. Максимизация полезности с порогом, зависящим от множества альтернатив
Четыре типа пороговых функций. Эквивалентные модели для максимизации полезности для этих типов пороговых функций. Свойства соответствующих функций выбора. Связь модели максимизации полезности с порогом, зависящим от множества альтернатив, с теоремой Самуэльсона.
Вложение отношений и проблема максимизации полезности с порогом, зависящим от множества альтернатив. Слабые бипорядки и их представление. Аддитивные пороги, зависящие от множества альтернатив. Простые и простейшие полупорядки. Слабое условие Чипмана и описание простых полупорядков.
Практическое применение этих моделей.
Лекция 5. Теория ожидаемой полезности. Санкт-Петербургский парадокс. Аксиоматика Неймана-Моргенштерна. Субъективная теория полезностей. Аксиоматика Сэвиджа и Энскомбе-Ауманна. Коэффициент неприятия риска Арроу-Пратта. Нарушения принципов ожидаемой полезности: парадоксы Мэя, Алле, Эллсберга. Обратимость предпочтений.
Лекция 6. Теория сравнительной полезности. Аксиоматика Фишберна SSB интенсивности предпочтений. Теорема существования. Единственность максимального элемента. Обоснование парадоксов Мэя, порога чувствительности и Алле. Модель сравнительной полезности. Вероятностные предпочтения.
Лекция 7. Выбор последовательными сравнениями. Аксиоматика марковского процесса выбора. Свойства выбора - “наследования” (Heredity), “согласия” (Concordance) и “отбрасывания” (Outcast). Вводные элементы бескоалиционной теории игр, теории массового обслуживания.
Лекция 8. Кумулятивная теория проспектов. Аксиоматика кумулятивной теории проспектов. Интеграл Шоке, сведение к интегралу Римана. Вероятностное расширение. Разрешение парадокса Алле,
4 модуль
Лекция 1. Постановка задачи выбора. Парадокс Кондорсе.
Общий взгляд на проблему выбора. Описание возможных задач, связанных с рациональным выбором. Парадоксы голосования. История теории индивидуального и коллективного выбора. Турниры. Победитель Кондорсе. Парадокс Кондорсе.
Лекция 2. Локальное агрегирование вида P→P
Локальное агрегирование вида P→P (и индивидуальные мнения, и коллективное решение выражаются в виде бинарных отношений). Рациональность индивидуального поведения. Типы бинарных отношений. Аксиома независимости от посторонних альтернатив. Списочное представление процедур. Нормативные свойства процедур коллективного выбора. Ограничения рациональности. Федерационные правила и их частные случаи - диктатор, олигархия, коллегия.
Лекция 3. Локальное агрегирование вида С→С
Локальное агрегирование вида С→С (и индивидуальные мнения, и коллективное решение выражаются в виде функций выбора). Свойства функций выбора. Нормативные свойства функциональных правил.
Лекция 4. Локальное агрегирование вида P→С
Локальное агрегирование вида P→С (индивидуальные мнения выражаются в виде бинарных отношений, а коллективное решение в виде функции выбора). Нормативные свойства соответствий коллективного выбора. Ограничения рациональности. Q-федерационные правила и их частные случаи: q-диктатор, q-олигархия, q-Паретовское правило и др. Механизмы коллективного выбора.
Лекция 5. Нелокальное агрегирование
Нелокальное агрегирование. Позиционные правила. Пороговое агрегирование. Аксиоматика порогового агрегирования. Применение этих правил.
Лекция 6. Конструирование коллективных предпочтений. Решения на мажоритарном графе.
Условия репрезентации предпочтений субьекта выбора множеством бинарных отношений. Оптимальный выбор как выбор максимальных элементов множества бинарных отношений, репрезентирующих предпочтения. Связь наличия максимальных элементов отношения с отсутствием циклов в ориентированном графе, представляющем это отношение. Отношение мажоритарного доминирования µ и отношение равенства голосов τ как система предпочтений коллектива, принимающего решения. Понятие решения в задаче оптимального коллективного выбора.
Лекция 7. Нелокальные правила. Аксиоматика Мэя. Решения, основанные на принципе устойчивости. Правило Коупленда. Матрично-векторное представление решений. Рейтинги.
Максимальный цикл TC, непокрытое множество UC, незахваченное множество UCp, минимальное слабоустойчивое множество MWS. Связь этих решений с путями и циклами в орграфе, репрезентирующем отношение µ. Теоретико-множественные соотношения этих решений. Понятие k-устойчивой альтернативы и k-устойчивого множества. Ранжирование по степени устойчивости. Ранжирование по Коупленду. Матрично-векторное представление решений. Рейтинги.
8. Образовательные технологии
Курс "Принятие индивидуальных и коллективных решений" является более глубоким изучением материала, излагающегося в курсе "Методы оптимальных решений", поэтому рекомендуется читать один курс после того, как прочитан другой.
Занятия по курсу проходят в форме лекций и семинаров, с элементами живого обсуждения, что требует хорошей самостоятельной подготовки студентов, которую следует мотивировать домашними заданиями. Студенты должны быть строго ориентированы на самостоятельное овладение вопросами дисциплины и самостоятельное выполнение заданий, предусмотренных данным курсом. Самостоятельная работа студентов является важнейшей частью их занятий по данному курсу. Для усвоения материала курса и подготовке к контрольным работам студенты обязаны дома решать задачи, которые им высылает преподаватель. Для выполнения домашних заданий студентов можно разделить на мини-группы по три человека.
Перед зачетом необходимо проводить установочную консультацию в часы и дни, согласованные с деканатом. Время проведения установочной консультации доводится до студентов учебной частью деканата.
9. Оценочные средства для текущего контроля и аттестации студента
9.1. Примеры заданий промежуточного /итогового контроля
- Найти функцию полезности, если А
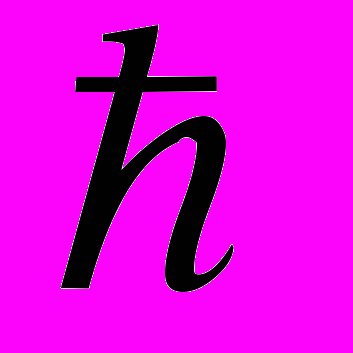 B
B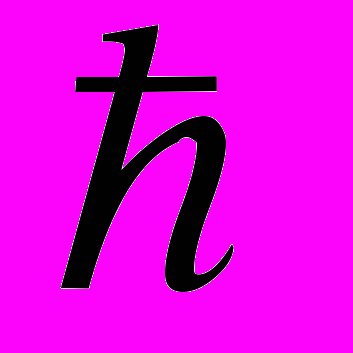 C
C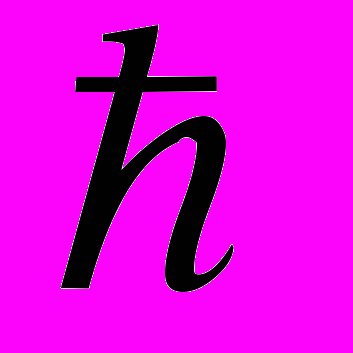 D и
D и
B~1/3А+2/3D,
В~1/4A+3/4C.
- Пусть функция полезности ЛПР есть и(х) = 1п(1 + х), уровень его капитала w. Ему предлагают лотерею, в которой выигрыш х и проигрыш х имеют вероятность соответственно р и 1 - р. Найдите х, при котором такая лотерея ему безразлична. Каков ответ при p = 0,5?
- Интенсивность обслуживания заявки прибором μ. То есть обслуживание заявки завершится за время Δt с вероятностью μΔt.
- Какова вероятность того, что за время Δt завершится обслуживание на одном приборе из пяти?
- Какова вероятность того, что за время Δt завершится обслуживание на двух приборах из пяти?
- Какова вероятность того, что за время Δt завершится обслуживание на одном приборе из пяти?
- В магазине имеется три консультанта. Интенсивность прихода клиентов - 10 клиентов в час, среднее время консультирования 15 минут. Если все консультанты заняты, клиент уходит.
- Написать систему дифференциальных уравнений, описывающих систему (при t=0 система пуста).
- Найти стационарное состояние системы.
- Найти вероятность того, что пришедший клиент будет потерян (в стационарном состоянии).
- Написать систему дифференциальных уравнений, описывающих систему (при t=0 система пуста).
- Prove that Borda aggregation rule can't produce relations, which may be regarded as collective preferences.
- Prove that for any two dominant sets it always holds true that one of them includes the other.
- Prove that any dominant set is a direct sum of top cycles of all degrees no greater than some natural number i.
- Prove that the set of all generally stable alternatives coincides with the top cycle.
- Prove that the uncovered set coincides with the set of 2-stable alternatives.
- Prove that Copeland set is always a subset of the uncovered set.
- Prove that Banks set is always a subset of the uncovered set.
- Prove alternative x covers alternative y in tournament T iff strategy x dominates strategy y in corresponding 2-player tournament game G(T).
- For a tournament on A, |A|=7, calculate
- uncovered set UC;
- union of minimal weakly stable sets MWS;
- uncaptured set UCp;
- top cycle TC;
- all dominant sets;
- ranking based on stability (k-stable alternative and sets);
- Copeland ranking and Copeland set C;
- Banks set B;
- Long path ranking and Long path solution LP;
- Markov ranking and Markov solution MK;
- Minimal covering set MC;
- Bipartisan set BP
10. Порядок формирования оценок по дисциплине
Задания контрольной работы, зачета и экзамена состоят из задач, эквивалентных или аналогичных тем, которые были даны студентам в домашних заданиях для самостоятельной работы. На написание зачетной и экзаменационной контрольных работ и контрольной работы дается 80 мин. Любой факт списывания, отмеченный преподавателем, приведет к получению оценки «1» (единица) за данную работу.
Преподаватель также оценивает самостоятельную работу и работу студентов на семинарских занятиях. На лекциях и семинарских занятиях студентам даются домашние задания для самостоятельной работы, которые нужно выполнить до следующего семинарского занятия.
Результирующая оценка за промежуточный контроль в форме зачета выставляется по
следующей формуле, где Озачет – оценка за зачетную письменную работу, а N3 – число баллов за работу на семинарах в течение 3 модуля:
Опромежуточный = 0,8·Озачет + 0,2·N3
Способ округления накопленной оценки промежуточного (итогового) контроля в форме
зачета: арифметический.
Результирующая оценка за итоговый контроль в форме экзамена выставляется по следующей формуле, где Оэкзамен - оценка за экзаменационную письменную работу, а N4 – число баллов, набранных на семинарах в течение 4 модуля.
Оитоговый = 0,8·Озачет + 0,2·N4
Способ округления накопленной оценки итогового контроля в форме зачета: арифметический. На пересдаче студенту не предоставляется возможность получить дополнительный балл для компенсации оценки за текущий контроль.
В диплом выставляет результирующая оценка по учебной дисциплине, которая формируется по следующей формуле:
Одисциплина = 0,6·Опромежуточный + 0,4·Оитоговый
Способ округления результирующей оценки по учебной дисциплине: арифметический
10-балльная итоговая оценка округляются до целого числа баллов. При округлении учитывается работа студента на семинарах. Перевод в 5-балльную шкалу осуществляется по правилу:
- 0 ≤ К ≤ 3 - неудовлетворительно,
- 4 ≤ К ≤ 5 - удовлетворительно,
- 6 ≤ К ≤ 7 - хорошо,
- 8 ≤ К ≤10 -отлично.
Таблица соответствия оценок по десятибалльной и пятибалльной системам
| По десятибалльной шкале | По пятибалльной шкале |
| неудовлетворительно – 2 |
| удовлетворительно – 3 |
| Хорошо – 4 |
| отлично – 5 |
11. Учебно-методическое и информационное обеспечение дисциплины
Базовый учебник
- Aizerman M. and F.Aleskerov (1995) 'Theory of choice', Elsevier, Amsterdam
- Aleskerov F., Bouyssou D., Monjardet B. (2007) "Utility Maximization, Choice and Preference", Springer, Berlin
- Алескеров Ф.Т., Хабина Э.Л., Шварц Д.А. Бинарные отношения, графы и коллективные решения. М.: Издательский дом ГУ-ВШЭ, 2006.
- Льюс Р. Д., Райфа Х. (1961), Игры и решения. Москва, «Иностранная литература».
- m/book/Igri_i_resheniya__Vvedenie_i_kriticheskij_obzor#1
Основная литература
- Плаус С. (1998) Психология оценки и принятия решений / М.: “Филинъ”.
- Нейман фон Дж., Моргенштерн О.(1970). Теория игр и экономическое поведение.
- F. J. Anscombe; R. J. Aumann . (1963), A Definition of Subjective Probability The Annals of Mathematical Statistics, Vol. 34, No. 1pp. 199-205.
- Fishburn P.C. (1982) Nontransitive Measurable Utility // J. of Mathematical Psychology. 1982. No. 26, p. 3l–67.
- Fishburn P.C. (1984) Dominance in SSB Utility Theory // J. of economic theory. No. 34, p. 130–148.
- Вентцель Е.С. Теория вероятностей. -М.: Высшая школа, 1999.
- Kahneman D., Tversky А. (1979), Prospect Theory: An Analysis of Decision under Risk, Econometrica 47, 263-291.
- Tversky A, Kahneman D, (1992) “Advances in Prospect Theory: Cumulative Representation of Uncertainty,” Journal of Risk and Uncertainty 5, 297–323.
- Алескеров Ф.Т., Субочев А.Н. Об устойчивых решениях в ординальной задаче выбора// Доклады Академии Наук. 2009. Т. 426. №3. С. 318-320.
- 2. Айзерман М.А., Алескеров Ф.Т. Задача Эрроу в теории группового выбора (анализ проблемы) // Автоматика и телемеханика. 1983. № 9. С. 127-151.
- 3. Субочев А.Н. Доминирующие, слабоустойчивые и непокрытые множества: свойства и обобщения // Автоматика и Телемеханика. 2010. №1. C. 130-143.
- 4. Мюллер Д. Общественный выбор III. М.: Изд. дом ГУ-ВШЭ, 2007.
- 5. Aleskerov F., Kurbanov E. A Degree of Manipulability of Known Social Choice Procedures // Current Trends in Economics: Theory and Applications / Eds. Alkan A., Aliprantis Ch., Yannelis N. N.Y.: Springer-Verlag, 1999. P. 13-27.
- 6. Aleskerov F., Subochev A. Matrix-vector representation of various solution concepts. Working paper WP7/2009/03. M.: State University - Higher School of Economics, 2009.
Дополнительная литература
- Fishburn, P. (1970) Utility Theory for Decision Making. John Wiley, New York
- Halmos, P. (1974) Naïve Set Theory. Springer Verlag, Berlin
- Harary, F. (1962) Graph Theory. Addison Wesley, Mass.
- Kreps D. (1988) Notes on the Theory of Choice, Vestview Press, Boulder and London
- Riguet, J. (1948) Relations binares, fermetures, correspondences de Galois. Bull. Soc.Math.France, v.76
- Savage L,. J. (1954). The Foundations of Statistics. Wiley, New York.
- Alain CHATEAUNEUF, Michèle COHEN, Jean-Marc TALLON (2008)
- Decision under risk : The classical Expected Utility Model
- ссылка скрыта
- Edi Karni (2005) Savages’ Subjective Expected Utility Model
- ссылка скрыта
- Tsogbadral Galaabaatar, Edi Karni (2011)
- Objective and Subjective Expected Utility with Incomplete Preferences ссылка скрыта
- Кирута А.Я., Рубинов А.М., Яновская Е.Б. (1980), Оптимальный выбор распределений в сложных социально-экономических задачах. - Л.: Наука. Ленингр. отд-ие.
- Данилов В.И. (2006) Лекции о неподвижной точке.
- Ивченко Г. И., Каштанов В. А., Коваленко И. Н. Теория массового обслуживания.-М.: Высшая школа, 1982.
- Печерский С.Л., Беляева А.А., Теория игр для экономистов, 2002.
- Weibull J.W. (2002), What have we learned from evolutionary game theory so far? Resarch Institute of Industrial Economics, ссылка скрыта №487.
- Wakker P., Tversky A. (1993), An Axiomatization of Cumulative Prospect Theory, Journal of Risk and Uncertainty, 7:7:147-176
- Wakker P. (2010), Prospect Theory for risk and ambiguity. Cambridge university press.
- Blavatskyy P. (2011), Probabilistic Subjective Expected Utility.
- https://editorialexpress.com/cgi-bin/conference/download.cgi?db_name=NASM2011&paper_id=68
- Adams J., Merrill S. III. Voter turnout and candidate strategies in American elections // The Journal of Politics. 2003. V. 65. P. 161-189.
- Aizerman M., Aleskerov F. Voting operators in the space of choice functions // Mathematical Social Sciences. 1986. V. 11. N. 3. P. 201-242.
- Aleskerov F. Arrovian Aggregation Models. Dordercht: Kluwer Academic Publishers, 1999.
- Ansolabehere S., de Figueiredo J., Snyder J. Why is there so little money in US politics? // Journal of Economic Perspectives. V. 17. P. 105-130.
- Duggan J. 2007. A systematic approach to the construction of non-empty choice sets // Social Choice and Welfare. 2007. V. 28. P. 491-506.
- Laslier J.F. Tournament Solutions and Majority Voting. Berlin: Springer, 1997.
- Laver M. Policy and the dynamics of political competition // The American Political Science Review. 2005. V. 99. N. 2.
- Lin T., Enelow J., Dorussen H. Equilibrium in multicandidate probabilistic spatial model
- Myerson R., Weber R. A theory of voting equilibria // American Political Science Review. 1993. V. 87. N. 1.
- Patty J., Snyder J., Ting M. Two’s Company, Three’s an Equilibrium: Strategic Voting and Multicandidate Elections // Quarterly Journal of Political Science. V. 4. N. 3. P. 251-278.
- Polischuk L., Savvateev A. Spontaneous (non) emergence of property rights // Economics of Transition. 2004. V. 12. P. 103-127.
- Subochev A. Dominant, Weakly Stable, Uncovered Sets: Properties and Extensions. Working paper WP7/2008/03. Moscow: State University - Higher School of Economics, 2008.
Разработчики:
кафедра высшей математики
на факультете экономики ГУ-ВШЭ, профессор, д.т.н., Ф.Т. Алескеров
кафедра высшей математики
на факультете экономики ГУ-ВШЭ, доцент, к.ф.-м.н., А.А. Рубчинский
1 Subjective expected utility – некоторые понятия не имеют устойчивого русского перевода, потому в процессе курса будут использованы обозначения на языке оригинала.
