Geum.ru

Правительство Российской Федерации Государственный университет Высшая школа экономики Факультет Бизнес-информатики Отделение Прикладной математики и информатики программа дисциплины

Вид материалаПрограмма дисциплины

Содержание


Тематический план учебной дисциплины
Поршнев С.В.
Мэтьюз Дж. Г., Финк К.Д.
Мэтьюз Дж. Г., Финк К.Д.
Поршнев С.В.
Боглаев Ю.П.
Основы вычислительной математики
Годунов С.К., Рябенький. В.С.
Типовой вариант зачетной работы
Подобный материал:

Правительство Российской Федерации

Государственный университет - Высшая школа экономики
Факультет Бизнес-информатики
Отделение Прикладной математики и информатики



Программа дисциплины


Численные методы

для IV курса отделения Прикладной математики и информатики


Автор программы: И.Л. Кривцун

Рекомендована секцией УМС Одобрена на заседании кафедры


Математические и статистические высшей математики методы в экономике на факультете экономики

Председатель Зав. кафедрой

__________________А.С. Шведов Ф.Т. Алескеров ________________________________

«_____» __________________ 20 г. «____»_____________________ 20 г


Москва


Тематический план учебной дисциплины

№
Название темы
Всего
часов
Аудиторные часы
Самост.
работа

лекции
семинары

1
Элементы теории погрешностей
8
2
2
4

2
Приближенные методы поиска корней алгебраических многочленов
16
2
2
12

3
Общая задача интерполирования и аппроксимация функций
22
6
4
12

4
Вычислительные основы линейной алгебры
34
6
8
20

6
Разностные схемы
28
6
6
16




Итого
108
22
22
64



Формы контроля знаний студентов:
  • текущий контроль: контрольная работа в компьютерном классе во 2-м модуле:
  • итоговый контроль: зачет в конце 3-го модуля.


Итоговая оценка по учебной дисциплине определяется на основе оценок за следующие виды работ:
  • контрольная работа в компьютерном классе,
  • зачет.


Оценки за контрольную работу 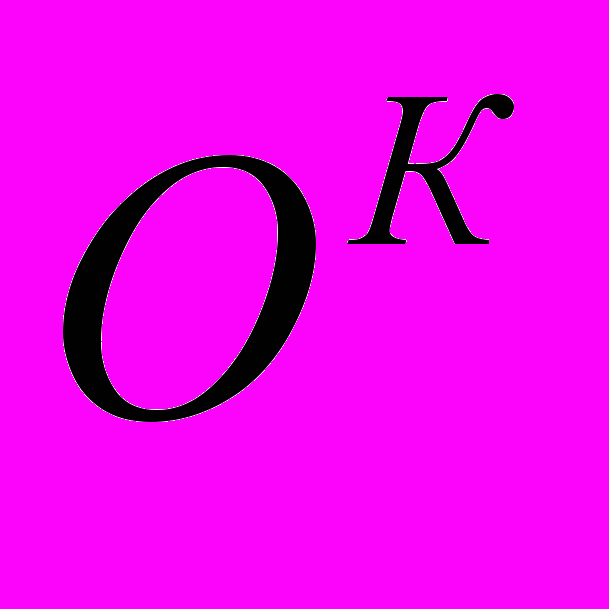, и зачетную работу 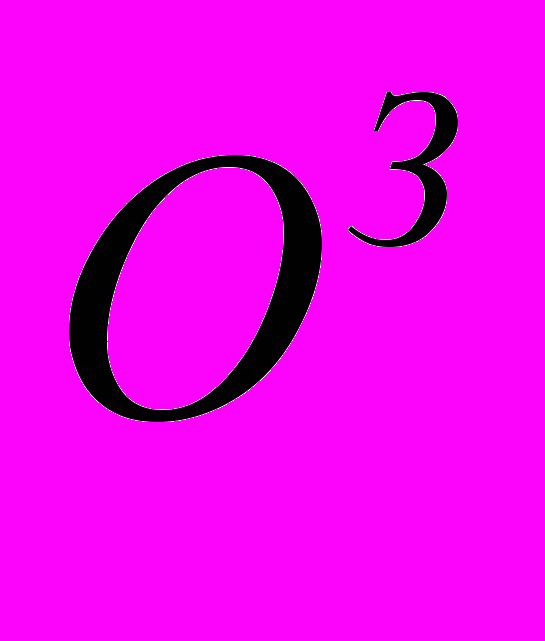ставятся в десятибалльной шкале. Итоговая десятибалльная оценка успеваемости студента по дисциплине в целом 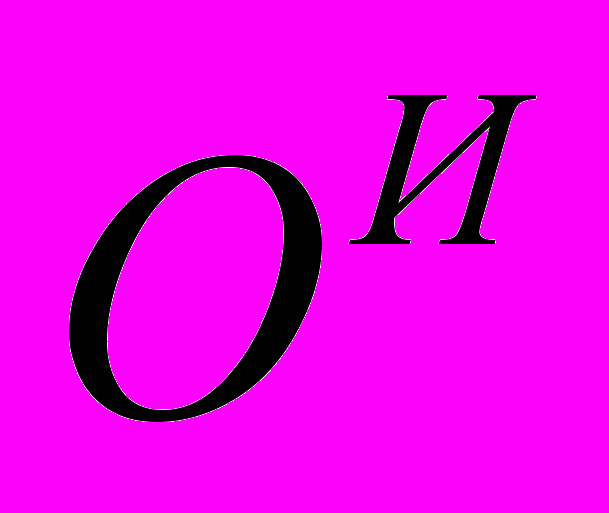определяется на основе всех этих оценок по формуле

.

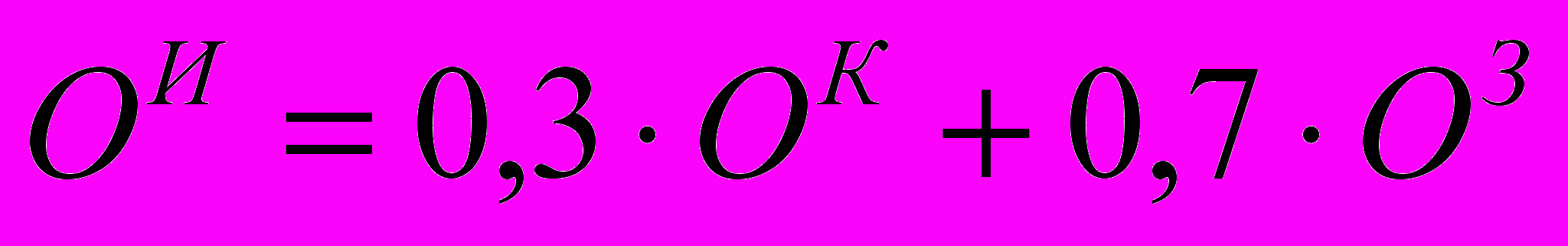Оценки за все виды работ и итоговая оценка округляются до целого числа баллов; при этом учитываются выполнения домашних работ и активность студента на практических занятиях.

Перевод итоговой десятибалльной оценки в пятибалльную осуществляется по правилу:

0  ОИ  3 – неудовлетворительно, 4  ОИ  5 – удовлетворительно,

6  ОИ  7– хорошо, 8  ОИ  10 – отлично.


Содержание программы

Тема 1. Элементы теории погрешностей.

Общие сведения об источниках погрешностей, их классификация. Абсолютная и относительная погрешности. Формы записи данных. Вычислительная погрешность. Понятие о погрешности машинных вычислений. Значащая цифра, число верных знаков. Связь относительной погрешности приближенного числа с количеством верных знаков этого числа. Погрешности суммы, разности, произведения и частного. Число верных знаков произведения и частного. Общая формула для погрешности. Обратная задача теории погрешностей.




Базовые учебники



Поршнев С.В. Вычислительная математика. Курс лекций (с использованием MATLAB). СПб.: «БХВ-Петербург», 2004 (лекция 1).

Деминович Б.П., Марон И.А. Основы вычислительной математики. - М.: «Наука», любое изд., начиная с 1968 г. (гл. I).

Дополнительная литература



Мэтьюз Дж. Г., Финк К.Д. Численные методы. Использование MATLAB. - М.: изд. дом «Вильямс», 2001 (гл. 1).


Тема 2. Приближенные методы поиска корней алгебраических многочленов

Отделение корней при решении уравнений с одной неизвестной. Общая формула оценки погрешностей приближенного корня. Простейшие способы решения уравнений: метод половинного деления, пропорциональных частей, Ньютона-Рафсона, комбинированный; скорость сходимости, оценки возникающих погрешностей. Метод Ньютона для случая комплексных корней. Метод итераций как пример применения принципа сжимающих отображений в метрическом пространстве. Преобразование уравнения к итерационному виду. Оценки погрешностей метода итераций. Границы действительных корней алгебраических уравнений; теорема Лагранжа; метод знакопеременных сумм. Число действительных корней полинома.





Базовые учебники



Мэтьюз Дж. Г., Финк К.Д. Численные методы. Использование MATLAB. - М.: изд. дом «Вильямс», 2001 (гл. 2).

Деминович Б.П., Марон И.А. Основы вычислительной математики. - М.: «Наука», любое изд., начиная с 1968 г. (гл. IV-V).

Дополнительная литература



Поршнев С.В. Вычислительная математика. Курс лекций (с использованием MATLAB). СПб.: «БХВ-Петер­бург», 2004 (лекция 2).


Тема 3. Общая задача интерполирования и аппроксимация функций.


Постановка общей задачи интерполирования. Частный случай базисной системы степенных функций с целым неотрицательным показателем. Полином Эрмита для заданной функции; его существование и единственность. Явный вид полинома Эрмита в частном случае задания значений функции и ее производной в узлах интерполяции. Интерполяционная формула Эрмита и ее остаточный член. Полиномы Чебышева и их основные свойства. Узлы Чебышева. Феномен Рунге. Теорема Файера о равномерной сходимости полиномов Эрмита в случае, когда узлами интерполяции являются корни многочлена Чебышева. Использование полиномов Эрмита для оценки погрешности квадратурных формул Ньютона-Котеса. Рациональное приближение функций. Метод Паде.

Базовые учебники



Боглаев Ю.П. Вычислительная математика и программирование. - М., «Высшая школа», 1990.

Самарский А.А., Гулин А.В. Численные методы. - М.: Наука, 1989.

Дополнительная литература



Мэтьюз Дж. Г., Финк К.Д. Численные методы. Использование MATLAB. - М.: изд. дом «Вильямс», 2001 (гл. 4).


Тема 4. Вычислительные основы линейной алгебры.


Метод простых итераций решения системы линейных уравнений крамеровского типа как пример применения принципа сжимающих отображений в метрическом пространстве. Нормы линейных операторов в конечномерном пространстве. Приведение системы к виду удобному для итераций. Метод Зейделя. Достаточные условия сходимости метода Зейделя для трех простейших норм конечномерного линейного пространства. Оценки погрешности приближений процесса Зейделя по 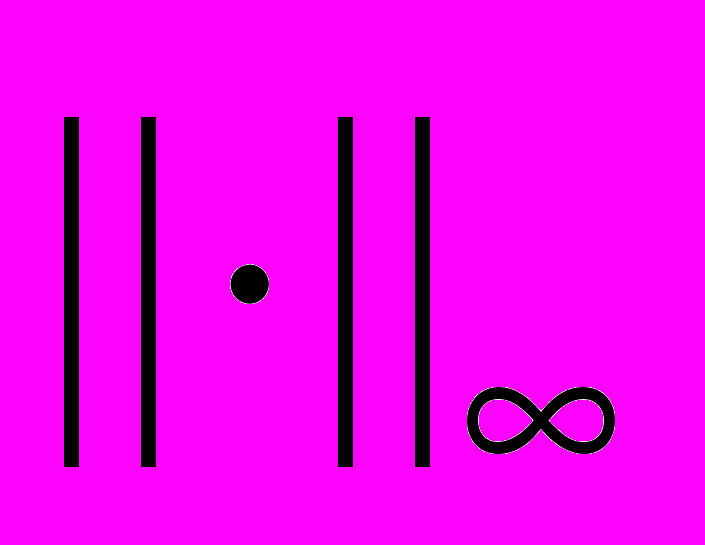-норме. Нормальные системы линейных уравнений. Приведение системы к нормальному виду. Метод релаксаций. Треугольные матрицы. Представление квадратной матрицы в виде произведения треугольных матриц различных структур. Обращение матрицы, разложенной в произведение треугольных матриц. Метод квадратных корней. Схема Халецкого. Метод прогонки для трехдиагональной системы.

Вращение плоскости. Подобные и ортогональные преобразования. Метод Якоби нахождения собственных пар симметричной матрицы. Отражение Хаусхольдера. Преобразование Хаусхольдера. Метод Хаусхольдера. QR-метод.

Базовые учебники



Мэтьюз Дж. Г., Финк К.Д. Численные методы. Использование MATLAB. - М.: изд. дом «Вильямс», 2001 (гл. 3, 11).

Деминович Б.П., Марон И.А. Основы вычислительной математики. - М.: «Наука», любое изд., начиная с 1968 г. (гл. VIII-IX).

Дополнительная литература



Воеводин В.В. Вычислительные основы линейной алгебры. М.: «Наука», любое изд., начиная с 1977 г. (гл. IV-VI).


Тема 5. Разностные схемы.


Постановка задачи численного решения краевой задачи для уравнения с частными производными. Устойчивость численного решения. Построение разностной схемы простейшей задачи для уравнения гиперболического типа; явная и неявная схемы. Необходимое условие устойчивости явной схемы. Решение Даламбера. Построение явной разностной схемы простейшей задачи для уравнения параболического типа. Необходимое и достаточное условие устойчивости явной схемы. Метод Кранка-Николсона. Дискретный вид оператора Лапласа. Сборка разностных схем простейших краевых задач для уравнений Лапласа, Пуассона, Гельмгольца. Итеративные методы.

Базовые учебники



Годунов С.К., Рябенький. В.С. Разностные схемы. - М.: «Наука», 1973 (гл. 7).

Дополнительная литература



Мэтьюз Дж. Г., Финк К.Д. Численные методы. Использование MATLAB. - М.: изд. дом «Вильямс», 2001 (гл. 10).


Типовой вариант контрольной работы

(в компьютерном классе)


Задание 1. Определите границы действительных корней уравнения

.


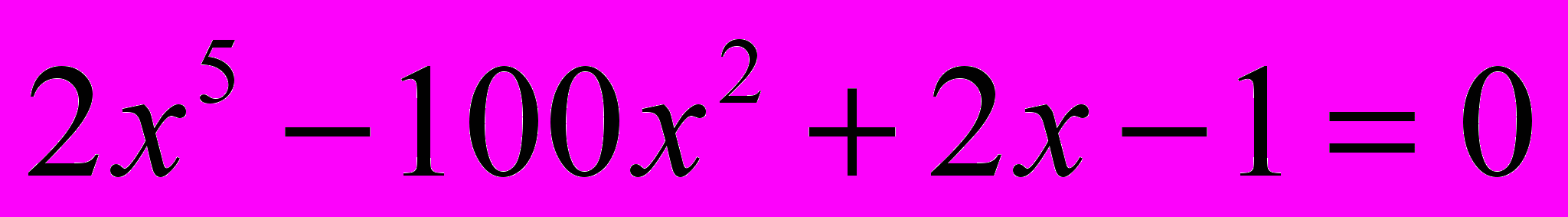Задание 2. Определите количество положительных корней уравнения 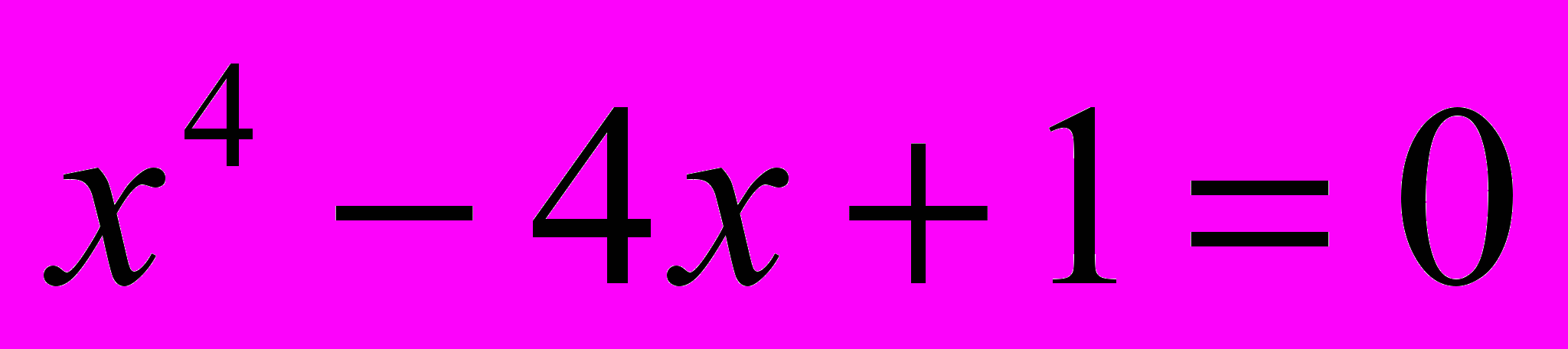и, отделив их, найдите с точностью до 10-6, предварительно приведя уравнение к виду, удобному для итераций. Сравните решения, полученные по методу итераций и комбинированному методу. Все вычисления необходимо реализовать в среде MATLAB, написав для этого соответствующие программы.


Задание 3. Найдите максимальное и минимальное значения полинома Чебышева .


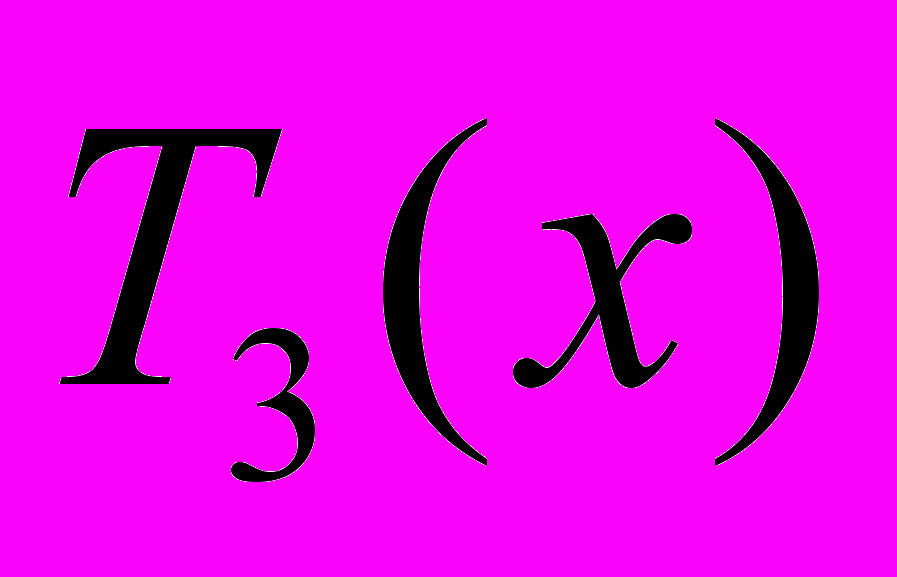Задание 4. Постройте полином Эрмита, который в точках 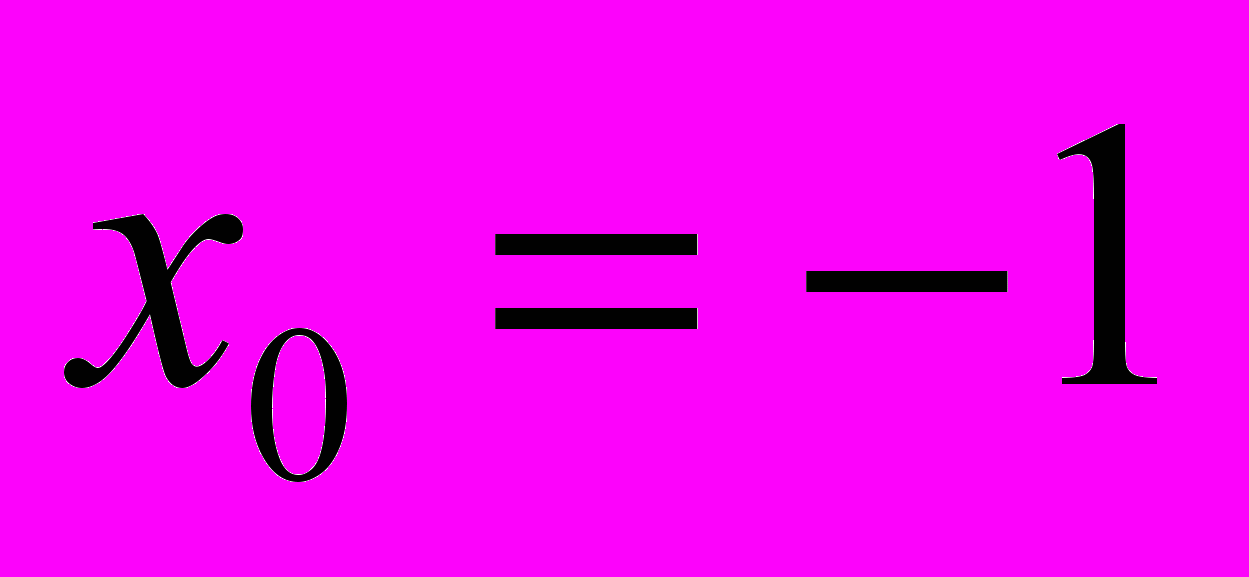,,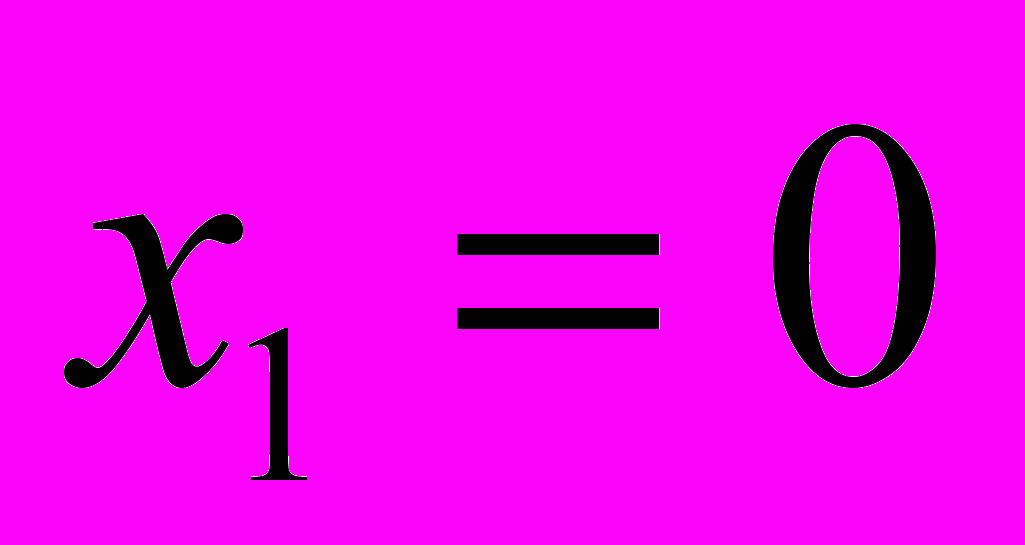 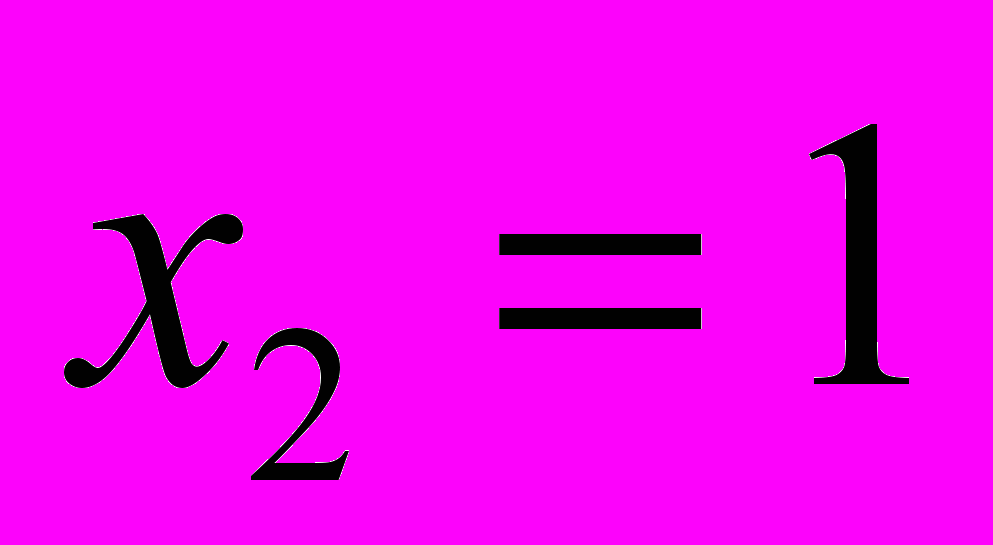принимает значения 2; -1; 0, соответственно, а его производная в точках 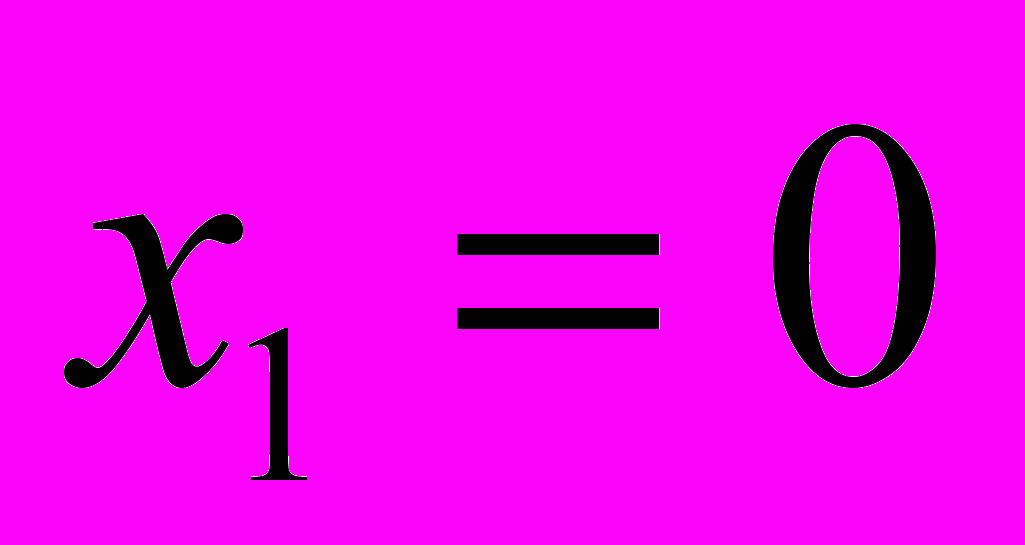, 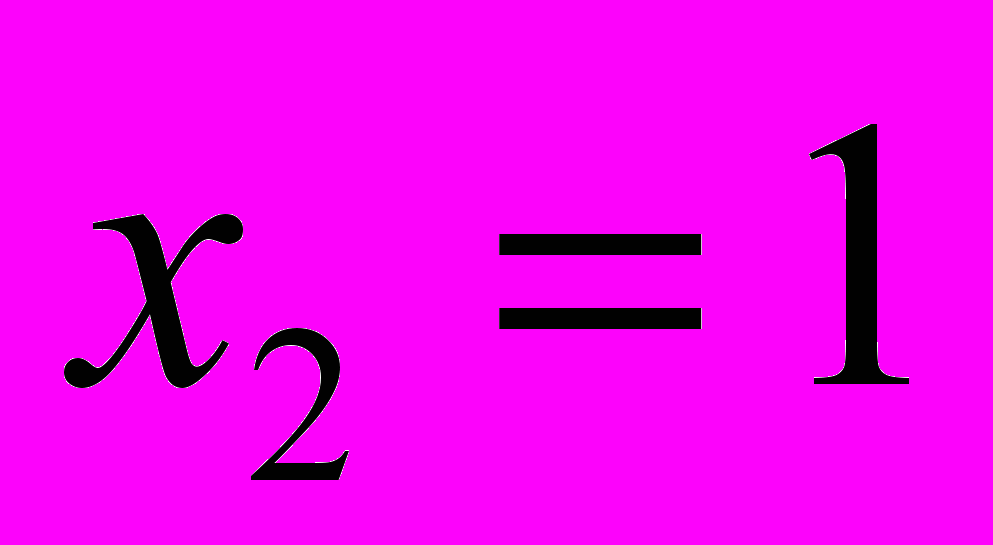– значения 0; 1, соответственно.


Типовой вариант зачетной работы

(в компьютерном классе)


Задание 1. Пусть 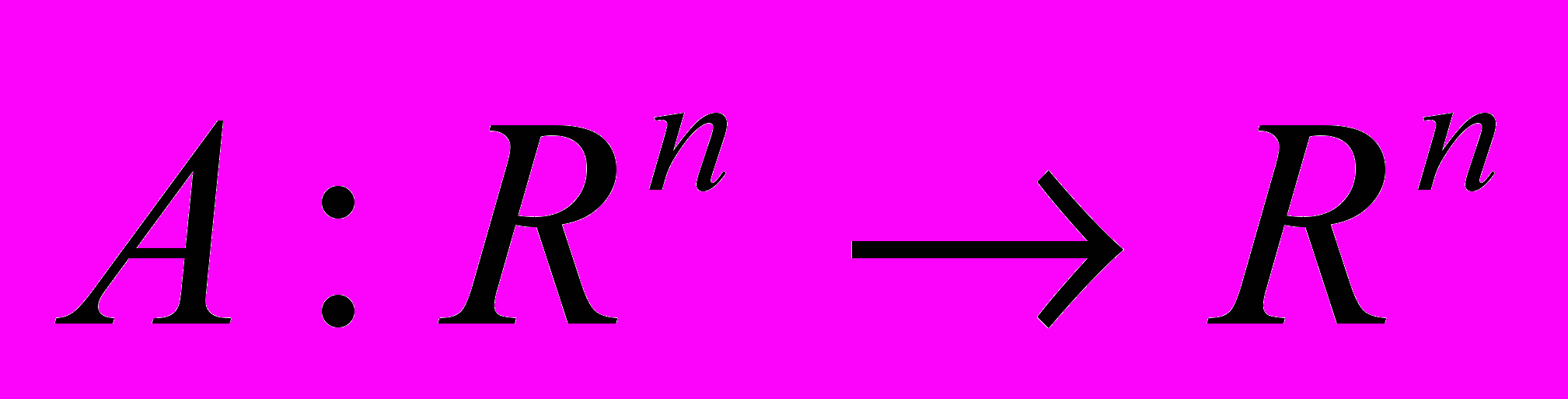- невырожденный линейный оператор. Выразите 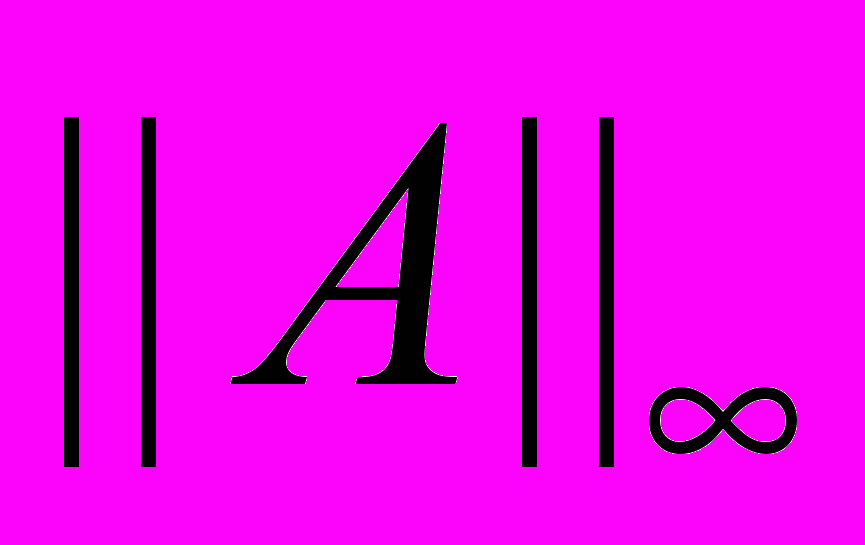через элементы матрицы оператора в стандартном базисе. Докажите, что достаточным условием сходимости по норме 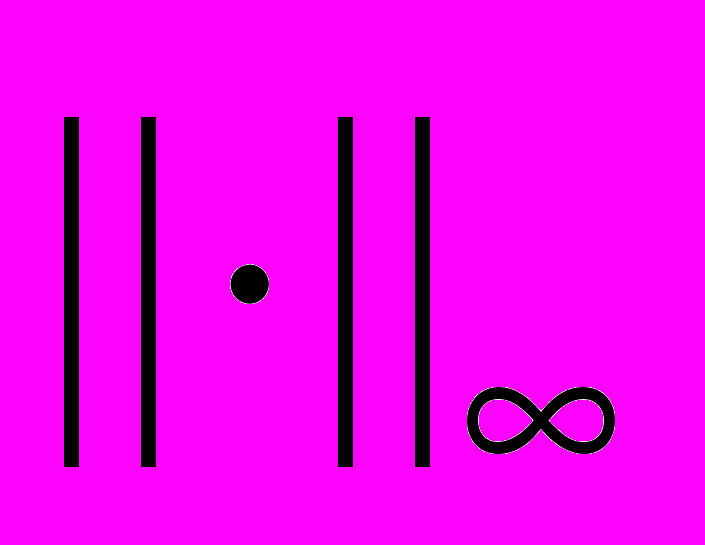последовательности приближений к точному решению системы 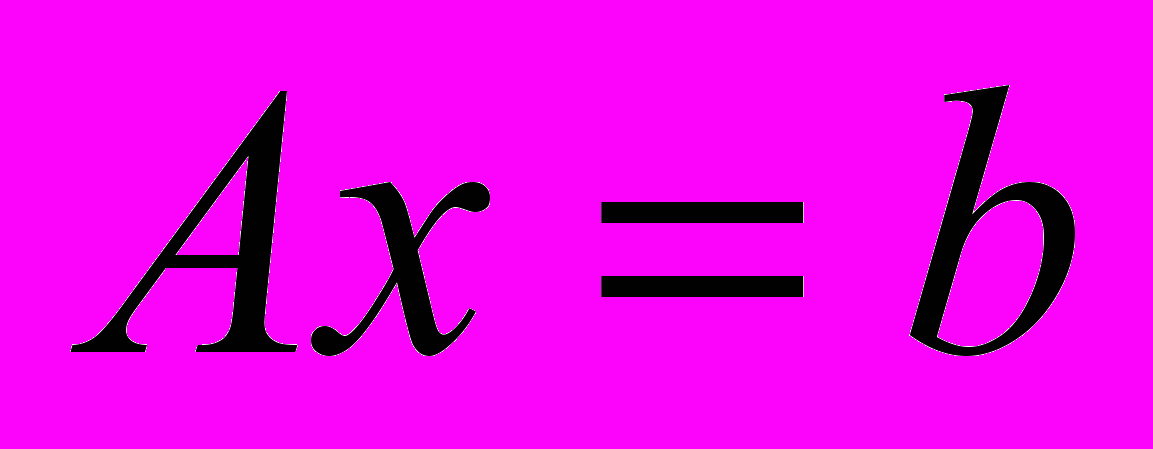в процессе Зейделя является выполнение неравенства .


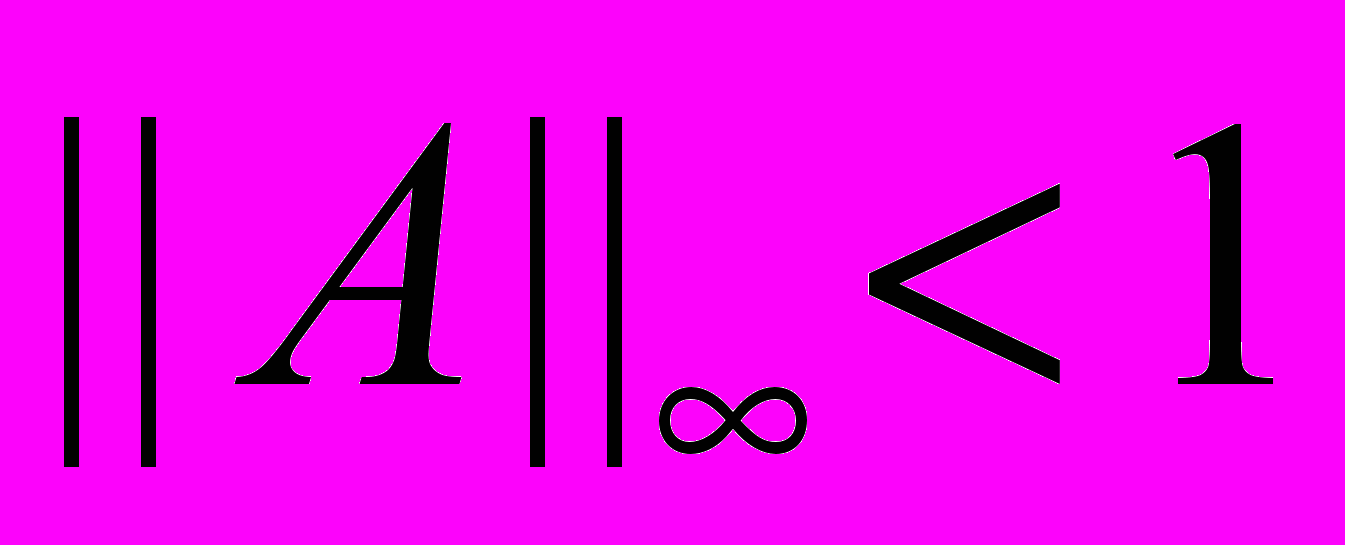Задание 2. Напишите в среде MATLAB программу обращения матрицы методом разбиения ее на произведение двух треугольных матриц. Проверьте работу программы на примере матрицы

.


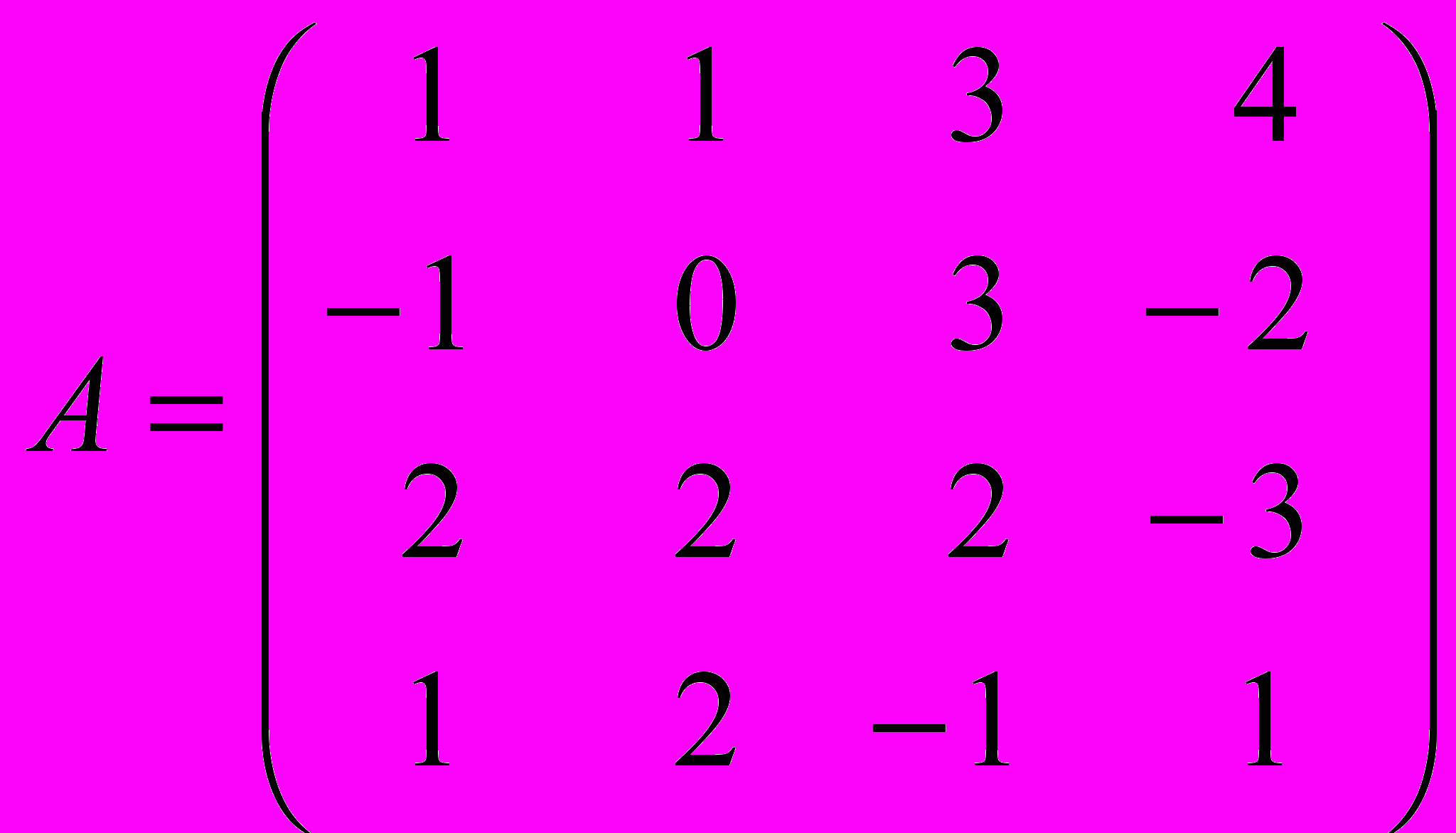Задание 3. Напишите в среде MATLAB программу решения с помощью схемы Халецкого системы линейных уравнений крамеровского типа. Проверьте работу программы на примере решения системы

.


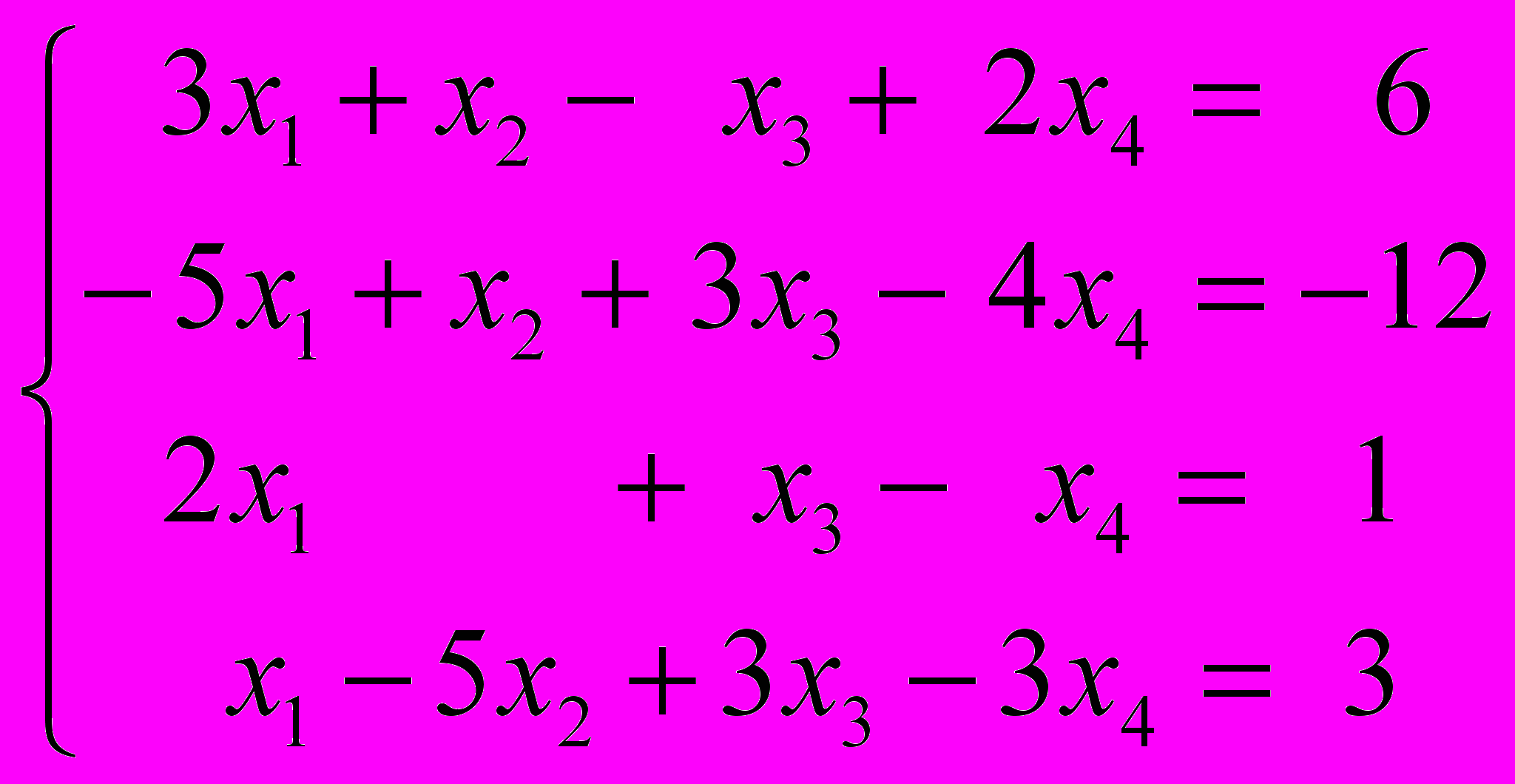Задание 4. Напишите в среде MATLAB программы приведения симметричной матрицы к трехдиагональному виду с использованием преобразований Хаусхольдера и и приближенного вычисления собственных значений симметричной трехдиагональной матрицы с использованием QR-метода. Проверьте работу программы на примере матрицы

.


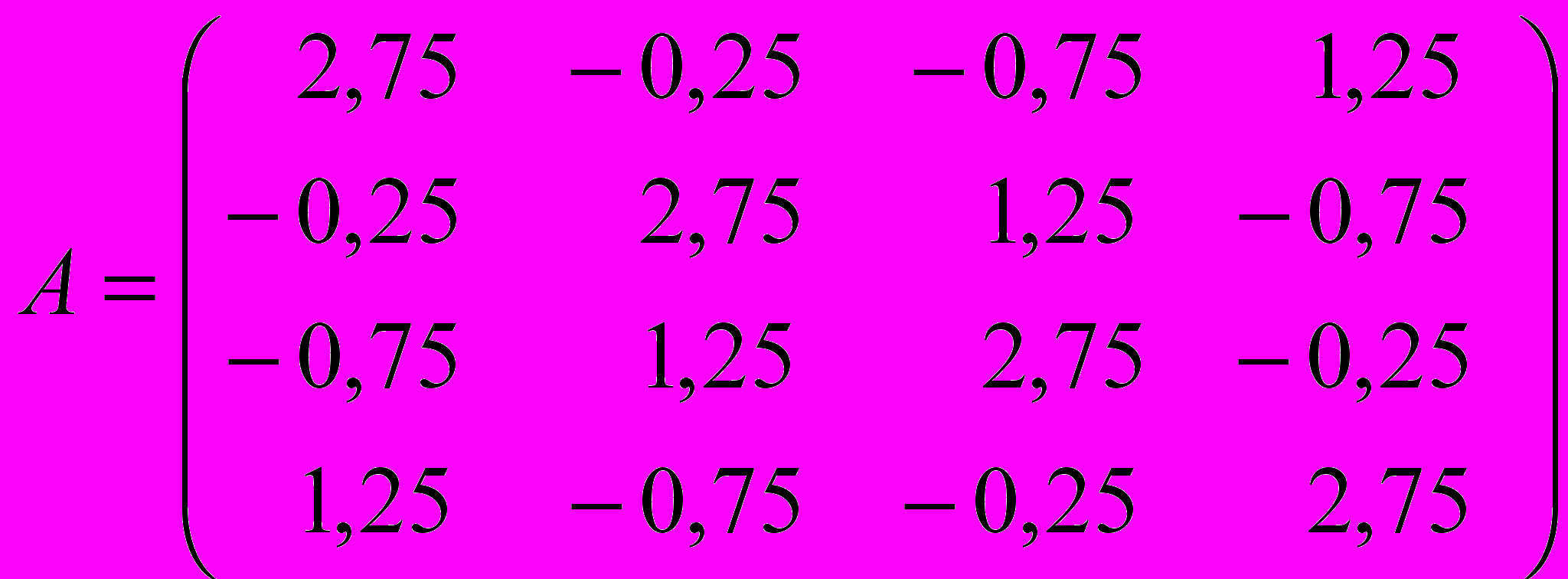Задание 5. С помощью явной схемы решите следующую краевую задачу

,

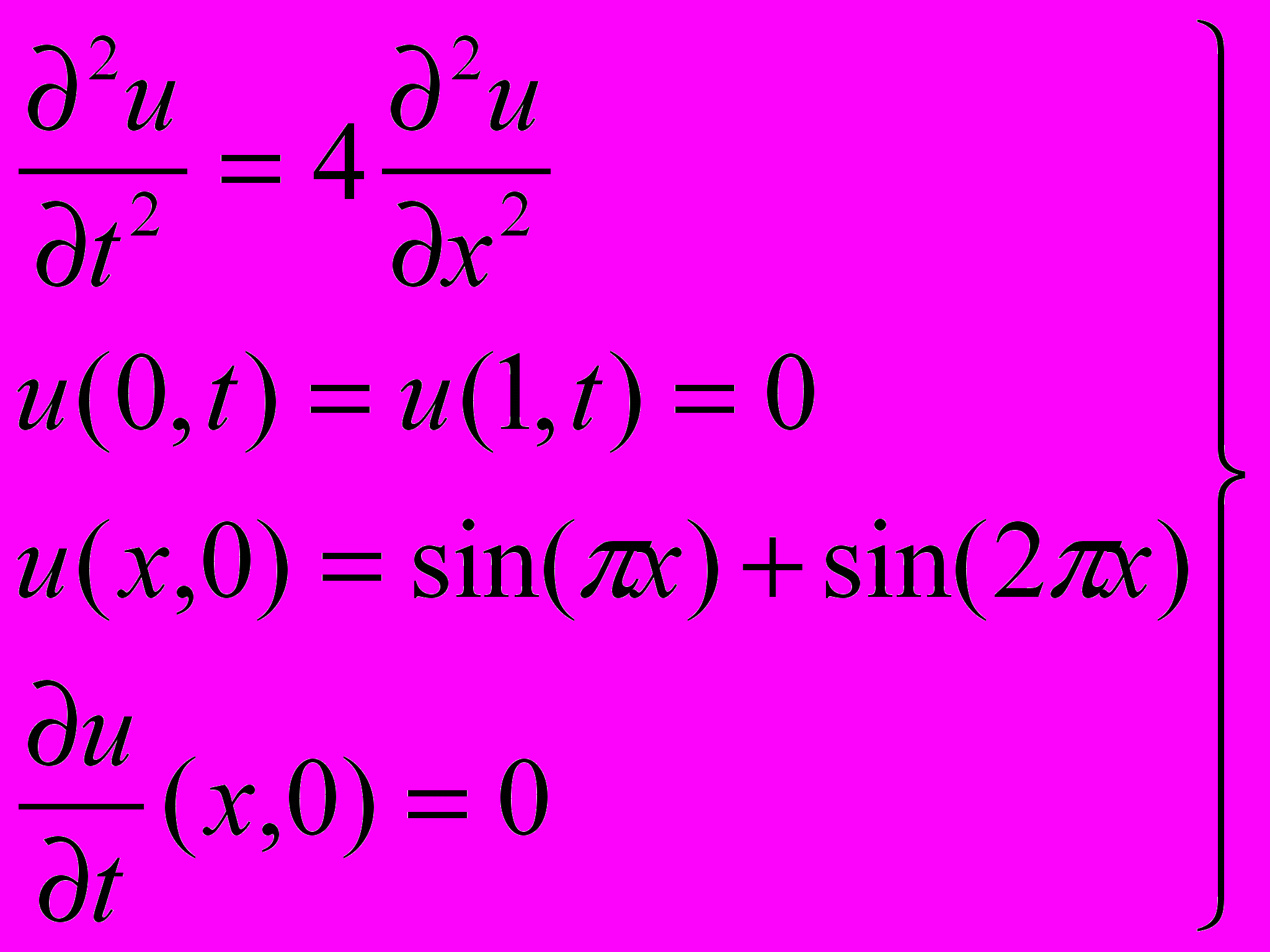
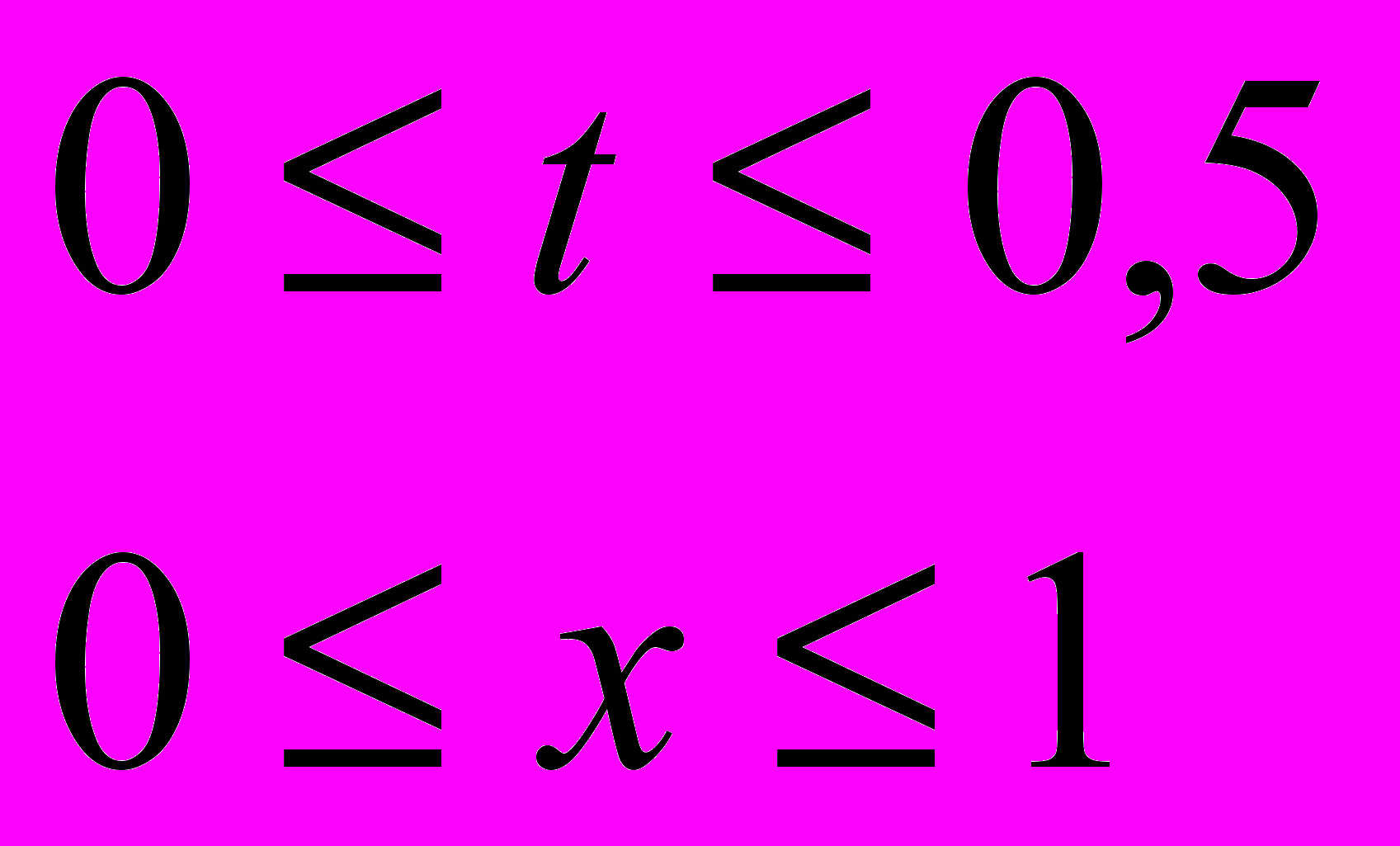выбрав шаги по x и t, равные h = 0,1 и k = 0,05, соответственно.