Карпова Н. В., учитель математики и информатики
| Вид материала | Документы |
- Урок геометрии и информатики. Тема урока по учебному плану: Построение правильных многоугольников, 131.04kb.
- Карпова Маргарита Петровна г. Буинск 2008 г Тип урок, 62.19kb.
- Никогда не спрашивай, по ком звонит колокол… Руководители проекта, 84.79kb.
- Конспект бинарного урока по изобразительному искусству и информатике (5 класс), 96.06kb.
- Организационно-педагогические условия функционирования педагогической технологии исследования, 304.79kb.
- Магнитогорский Государственный Университет, квалификация учитель математики и информатики, 36.23kb.
- Учебно-методический комплекс по дисциплине "компьютерное моделирование" (факультет, 384.08kb.
- Оводова Елена Геннадьевна, учитель математики и информатики основной школы при Посольстве, 84.3kb.
- Меркушкиной Светланы Адольфовны, 89.24kb.
- Правительство Российской Федерации Государственный университет Высшая школа экономики, 91.67kb.
| |
Михеев Никита
Пантелеев Сергей
Учащиеся 9 класса
Системы счисления и
их практическое применение
Руководитель:
Карпова Н.В., учитель математики и информатики
Оглавление
| Введение………………………………………………………………………………………………. | 3 |
| Теоретическая часть………………………………………………………………………………….. | 4 |
| Практическая часть………………………………………………………………………………….. | 10 |
| Заключение……………………………………………………………………………………………. | 13 |
| Список литературы. …………………………………………………………………………………. | 14 |
| Приложение 1..……………….………………………………………………………………………. | 15 |
Введение
В средней школе предмет «Информатика» – сравнительно молодой. Как обязательная дисциплина информатика в программу школы была введена в 1985 г. Все недолгие годы своего существования этот предмет оставался, наверное, самым спорным в школьной программе. Менялось название предмета, его место в учебном плане, содержательная концепция, техническое обеспечение. В настоящее время в школе введен предмет «Информатика и информационно-коммуникационные технологии», направленный на обеспечение всеобщей компьютерной грамотности. Многие учащиеся считают, что изучение этого предмета направлено лишь на овладение школьниками пользовательскими навыками (работа в текстовых, графических, числовых редакторах и т. п.).
С целью привлечения внимания к теоретической части курса, в частности, к изучению систем счисления в школе, как неотъемлемой части информационных технологий, создан данный проект. Актуальность расширенного знакомства с теоретическими разделами курса «Информатика и информационно-коммуникационные технологии» и совершенствование навыков решения задач обусловлена введением ЕГЭ по предмету.
Тема проекта: «Системы счисления и их практическое применение».
Тема «Системы счисления» имеет прямое отношение к математической теории чисел. Однако в школьном курсе математике она, как правила, не изучается. Необходимость изучения этой темы в курсе информатики связана с тем фактом, что числа в памяти компьютера представлены в двоичной системе счисления, а для внешнего представления содержимого памяти, адресов памяти используют шестнадцатеричную или восьмеричную систему счисления. Являясь смежной с математикой, данная тема вносит вклад в фундаментальной математическое школьное образование.
Вид проекта: групповой.
Задачи проекта:
- выяснить какие системы счисления существуют, возможен ли переход из одной системы счисления в другую;
- выяснить какие системы счисления используются в компьютере;
- рассмотреть практические задания по теме.
Форма представления проекта: реферат, мультимедийная презентация.
Теоретическая часть
Понятие систем счисления.
Числа не управляют миром,
но показывают, как управляется мир.
И.-В. Гете
Система счисления – это определенный способ записи чисел и соответствующие правила действия над числами.
Знаки, используемые при записи чисел, называются цифрами.
Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные.
Непозиционные системы счисления.
Непозиционной называется такая система счисления, в которой от положения цифры в записи числа не зависит величина, которую она обозначает.
Непозиционные системы счисления возникли раньше позиционных.
В этих системах счисления значение (величина) числа определяется как сумма или разность цифр в числе.
Непозиционные системы счисления имеют ряд недостатков:
1. Для записи больших чисел приходиться вводить новые цифры.
2. Невозможно записывать дробные и отрицательные числа.
3. Сложно выполнять арифметические операции.
Примеры непозиционных систем счисления:
1. У многих народов использовалась система, алфавит которой состоял из одного символа – палочки. Для изображения какого-то числа в этой системе нужно записать определенное множество палочек, равное данному числу: ||||| – число пять.
2. Египтяне применяли для записи чисел иероглифы. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. Если штрихов нужно изобразить несколько, то их объединяли в группы из трех или четырех черт и изображали в несколько рядов, причем в нижнем должно быть столько же штрихов сколько и в верхнем, или на одну больше.
Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку.
Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам.
Множество из десяти подковообразных символов, т.е. число 100, они заменили другим новым символом, напоминающим силки; десять силков, т.е. число 1 000, египтяне обозначили стилизованным изображением лотоса. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем, десять согнутых пальцев – волнистой линией и десять волнистых линий – фигуркой удивленного человека. В итоге древние египтяне могли представлять числа до миллиона.
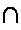 | 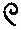 | 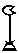 | 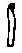 | 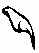 | 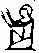 | 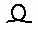 |
| 10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 | 10 000 000 |
3. Самой распространенной непозиционной системой счисления является римская, в которой в качестве цифр используются латинские буквы.
I – 1; V – 5; X – 10; L – 50; C – 100; D – 500; M – 1 000
Величина числа определяется как сумма или разность цифр в числе (например, II – два, III – три, XXX – тридцать, CC – двести). Если большая цифра стоит перед меньшей цифрой, то они складываются (VII – семь), если наоборот – вычитаются (IX – девять).
Позиционные системы счисления.
Позиционной называется такая система счисления, в которой величина, обозначаемая цифрой в записи числа, зависит от ее позиции.
Французский математик Пьер Симон Лаплас (1749— 1827) такими словами оценил "открытие" позиционной системы счисления: "Мысль выражать все числа немногими знаками, придавая им, кроме значения но форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна".
Первая известная нам система, основанная на позиционном принципе – шестидесятeричная вавилонская. Для малых чисел вавилонская система счисления в основных чертах напоминала египетскую. Одна вертикальная клинообразная черта означала единицу; повторенный нужное число раз, этот знак служил для записи чисел меньше десяти; для обозначения числа 10 вавилоняне ввели новый коллективный символ – более широкий клиновидный знак с острием, направленным влево, напоминающий по форме угловую скобку:
 - 1
- 1 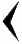 - 10
- 10Повторенный соответствующее число раз, этот знак служил для обозначения чисел 20, 30, 40 и 50. Принцип повторного использования знаков позволял, например, записать число 59 в виде
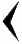
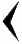
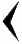
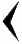
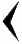








 , т.е. 59 = 5 · 10 + 9.
, т.е. 59 = 5 · 10 + 9.Но для записи чисел больше 59 древние вавилоняне впервые использовали новый принцип позиционности, т.е. зависимости значения символа от его местоположения в записи числа. Вавилоняне заметили, что в качестве коллективных символов более высокого порядка можно применять уже ранее использованные символы, если они будут занимать в записи числа новое положение левее предыдущих символов. При обозначении чисел больше 60 знаки, выступающие в новом качестве, отличались от старых тем, что символы разбивались на «места», или «позиции», и единицы более высокого порядка располагались слева, с небольшими пробелами между ними. При таком способе записи для обозначения сколь угодно больших чисел уже не нужно было других символов, кроме уже известных. Так, например, число 302 будет иметь вид:






 , то есть 302 = 5 · 60 + 2. А число 3725:
, то есть 302 = 5 · 60 + 2. А число 3725:






 , то есть 3725 = 1· 60· 60 + 2· 60 + 5
, то есть 3725 = 1· 60· 60 + 2· 60 + 5 В Древнем Вавилоне система счисления оставалась лишь относительно позиционной, поскольку не существовало эквивалента современной десятичной запятой, равно как и символа для обозначения отсутствующей позиции. Однако эта неоднозначность была устранена введением специального символа в виде двух небольших клиньев, помещаемого на пустующее место. При отсутствии разряда вставлялся значок 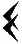 , игравший роль нуля.
, игравший роль нуля.

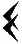
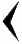

 , то есть 3632 = 1 · 60 · 60 + 0 · 60 + 3·10 + 2
, то есть 3632 = 1 · 60 · 60 + 0 · 60 + 3·10 + 2Однако отсутствие низшего разряда не обозначалось, и поэтому число 180 = 3 · 60 записывалось так


 , а обозначать эта запись могла и 3, и 180, и 10800 (3 · 60 · 60), и т. д. Различать эти числа можно было только по смыслу текста. Именно поэтому вавилонскую систему мы считаем лишь относительно позиционной, ибо самый правый знак мог означать либо единицы, либо кратные какой-нибудь степени числа 60.
, а обозначать эта запись могла и 3, и 180, и 10800 (3 · 60 · 60), и т. д. Различать эти числа можно было только по смыслу текста. Именно поэтому вавилонскую систему мы считаем лишь относительно позиционной, ибо самый правый знак мог означать либо единицы, либо кратные какой-нибудь степени числа 60. Запись чисел в позиционных системах счисления осуществляется следующим образом:
Множество цифр, используемых для записи чисел в позиционных системах счисления, образует алфавит. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе – позиция. Сущность позиционного представления чисел отражается в развернутой форме записи числа.
| Основание (n) | Название | Алфавит |
| n=2 | двоичная | 0, 1 |
| n=3 | троичная | 0, 1, 2 |
| n=5 | пятеричная | 0, 1, 2, 3, 4 |
| n=8 | восьмеричная | 0, 1, 2, 3, 4, 5, 6, 7 |
| n=10 | десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| n=16 | шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Основные достоинства любой позиционной системы счисления – простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любого числа.
Каким же способом переводятся числа из одной позиционной системы в другую? Основная идея заключается в следующем: перевод чисел неизбежно связан с выполнением вычислений. Поскольку нам хорошо знакома лишь десятичная арифметика, то любой перевод следует свести к выполнению вычислений над десятичными числами.
Перевод из произвольной позиционной системы счисления в десятичную систему.
Метод развернутой формы записи числа также используется для перевода чисел из любой позиционной системы счисления в десятичную:
Aq = an-1·qn-1 + an-2·qn-2 + ... + a0·q0 + a-1·q-1 + a-2q-2+ ... +a-m·q-m , где
q – основание системы счисления, n – число разрядов целой части числа, m – число разрядов дробной части числа, ai – цифра числа, Aq – само число.
Алгоритм перевода:
Пронумеруем цифры в изначальной записи числа справа налево, начиная с нуля.
Умножим каждое число на соответствующую степень основания.
Складываем получившиеся произведения.
Примеры:
1) 11012 =1·23 + 1·22 + 0·21+ 1·20= 8+4+0+1=1310
3 2 1 0
2) 423,31210 = 4·102 + 2·101+ 3·100+ 3·10-1+1·10-2 +2·10-3
3) 423,3125 = 4·52 + 2·51+ 3·50+ 3·5-1+1·5-2 +2·5-3
4) 423,3128 = 4·82 + 2·81+ 3·80+ 3·8-1+1·8-2 +2·8-3
5) 1204205= 1·55+2·54+0·53+4·52+2·51+0·50= 3125+1250+0+100+10+0=448510
Перевод десятичных чисел в другие системы счисления.
Перевод целых чисел.
Алгоритм перевода:
1. Основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной системе.
2. Последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя.
3. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
4. Составить число в новой системе счисления, записывая его, начиная с последнего частного.
Примеры:
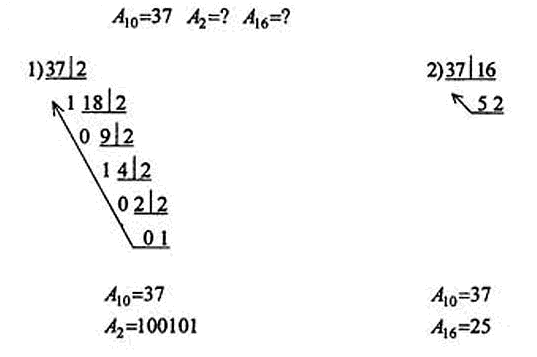
Перевод дробных чисел.
Алгоритм перевода:
1. Основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной системе.
2. Последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления чисел в новой системе счисления.
3. Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
4. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Примеры:

Перевод смешанных чисел.
Алгоритм перевода:
1. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам.
2. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой.
Пример:
11,187510= 1110 + 0,187510 = 1011,00112
«Машинные» системы счисления.
Системы счисления, используемые в компьютерах.
Перед математиками и конструкторами 50-х годов встала проблема отыскания таких систем счисления, которые отвечали бы требованиям, как разработчиков ЭВМ, так и создателей программного обеспечении. Одним из итогов этих исследований стало значительное изменение представлений о системах счисления и о методах вычислений. Оказалось, что арифметический счет, которым человечество пользуется с древнейших времен, может совершенствоваться, подчас весьма неожиданно и на удивление эффективно.
Специалисты выделили так называемую «машинную» группу систем счисления и разработали способы преобразования чисел этой группы. К «машинной» группе систем счисления относятся: двоичная, восьмеричная, шестнадцатеричная.
Этих систем счисления обычно хватает для полноценной работы как человека, так и вычислительной машины, однако иногда в силу различных обстоятельств все-таки приходится обращаться к другим системам счисления, например к троичной, семеричной или системе счисления по основанию 32.
Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
- для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
- представление информации посредством только двух состояний надежно и помехоустойчиво;
- возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
- двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
Двоичная система счисления в компьютерах рассматривается в двух аспектах: двоичная нумерация и двоичная арифметика.
Представление информации, хранящейся в компьютерной памяти, в ее истинном двоичном виде весьма громоздко из-за большого количества цифр. Имеется в виду запись такой информации на бумаге или вывод ее на экран. Для этого принято использовать восьмеричную и шестнадцатеричную системы счисления.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2). А перевод чисел из «16» или «8» в «2» и обратно производится путем формальной перекодировки, что будет рассмотрено ниже.
Почему же не используются другие системы счисления? В основном, потому, что в повседневной жизни люди привыкли пользоваться десятичной системой счисления, и не требуется никакая другая. В вычислительных же машинах используется двоичная система счисления, так как оперировать числами, записанными в двоичном виде, довольно просто. Часто в информатике используют шестнадцатеричную систему, так как запись чисел в ней значительно короче записи чисел в двоичной системе. Может возникнуть вопрос: почему бы не использовать для записи очень больших чисел систему счисления, например по основанию 50? Для такой системы счисления необходимы 10 обычных цифр плюс 40 знаков, которые соответствовали бы числам от 10 до 49 и вряд ли кому-нибудь понравится работать с этими сорока знаками. Поэтому в реальной жизни системы счисления по основанию, большему 16, практически не используются.
Перевод чисел в «машинной группе».
Для записи целого двоичного числа в системе счисления с основанием q=2n используется следующий алгоритм перевода:
- Данное двоичное число разбить справа налево на группы по n чисел.
- Если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов.
- Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n.
Для удобства переводов можно использовать таблицы переводов:
-
Двоично-восьмеричная таблица
8
2
0
000
1
001
2
010
3
011
4
100
5
101
6
110
7
111
-
Двоично-шестнадцатеричная таблица
16
2
0
0000
1
0001
2
0010
3
0011
4
0100
5
0101
6
0110
7
0111
8
1000
9
1001
A
1010
B
1011
C
1100
D
1101
E
1110
F
1111
Пример:
Перевести 1011,100112 в восьмеричную и шестнадцатеричную системы счисления:
Практическая часть
Практические задания по теме «Системы счисления».
1. Какие числа записаны римскими цифрами:
а) MCMXCIX; б) CMLXXXVIII; в) MCXLVII?
2. Запишите год, месяц и число своего рождения c помощью римских цифр.
3. Некоторые римские цифры легко изобразить, используя палочки или спички. Ниже написано несколько неверных равенств. Как можно получить из них верные равенства, если разрешается переложить с одного места на другое только одну спичку (палочку)?
VII - V=XI IX-V=VI
VI - IX=III VIII - III=X
4. Заполните следующую таблицу:
| Система счисления | Основание | Цифры |
| шестнадцатеричная | 16 | |
| десятичная | | 0,1,2,3,4,5,6,7,8,9 |
| | 8 | 0,1,2,3,4,5,6,7 |
| | 2 | |
5. Заполните следующую таблицу:
| Система счисления | Основание | Разряды (степени) | ||||
| десятичная | 10 | 10000 | 1000 | 100 | 10 | 1 |
| восьмеричная | 8 | | | | | |
| двоичная | 2 | | | | | |
6. Запишите в развернутом виде числа:
-
а) А8=143511;
г) А10=143,511;
б) А2=100111;
в) А16=143511;
д) А8=0,143511;
е) А16=1A3,5C1.
7. Запишите в свернутой форме следующие числа:
-
а) А10= 9·101+1·100+5·10-1+3·10-2;
б) А16=А·161+1·160+7·16-1+5·16-2.
8. Правильно ли записаны числа в соответствующих системах счисления:
-
а) А10=А,234;
б) А8=-5678;
в) А16=456,46;
г) А2=22,2;
9. Какое минимальное основание имеет система счисления, если в ней записаны числа 127, 222, 111? Определите десятичный эквивалент данных чисел в найденной системе счисления.
10. Чему равен десятичный эквивалент чисел 101012, 101018 1010116?
11. Какое из чисел 1100112, 1114, 358 и 1В16 является: а) наибольшим; б) наименьшим.
12. Существует ли треугольник, длины сторон которого выражаются числами 128, 1116 и 110112?
13. Выпишите целые десятичные числа, принадлежащие следующим числовым промежуткам:
-
а) [1011012; 1100002]; б) [148; 208];
в) [2816; 3016].
14. В классе 11112 девочек и 11002 мальчиков. Сколько учеников в классе?
15. У меня 100 братьев. Младшему 1000 лет, а старшему 1111 лет. Старший учится в 1001 классе. Может ли такое быть?




