Дружининская Ирина Михайловна Хованская Ирина Аскольдовна Матвеев Виктор Федорович Мышкис Петр Анатольевич Банк задач по теории вероятностей для студентов экономических специальностей Выпуск 1 учебное пособие

Вид материала

Подобный материал:

1 2 3

Образец варианта
экзаменационной контрольной работы

Первая часть

(каждый вопрос требует ответа: «ДА» или «НЕТ»)

Вероятность события, которое не может произойти, не существует.
Медиана всякой случайной величины обязательно совпадает с ее математическим ожиданием.
. Если Х и Y- любые независимые случайные величины, a и b любые числа, то D(aХ +bY)=aD(Х)+bD(Y).
Случайная величина, распределенная по закону Пуассона, не может принять значение, равное трем.

Вторая часть

(в этой части «вес» каждой задачи равен 1 баллу)

Производится серия независимых испытаний. В каждом испытании вероятность появления события А одинакова и равна 0.3. Найти вероятность того, что в семи испытаниях событие А возникнет четыре раза.
Случайная величина имеет нормальное распределение с математическим ожиданием (-1) и средним квадратическим отклонением 3. Какова вероятность попадания такой случайной величины в интервал (-2; 1)? Показать математическое ожидание и вычисленную вероятность на графике плотности нормального распределения.
Случайная величина подчинена закону распределения Пуассона, причем интенсивность потока событий равна 2 события за единицу времени. Найти вероятность того, что за единицу времени произойдет ровно 4 события.
Имеется простейший поток событий, в котором время между двумя соседними событиями подчиняется экспоненциальному закону распределения. Найти вероятность того, что между двумя последовательными событиями пройдет более 0.8 единиц времени, если интенсивность потока событий такая же, как в предыдущей задаче.

Третья часть

(в этой части «вес» каждой задачи указан в квадратных скобках)

9. [0.5] Вероятность получить высокие дивиденды по акциям на первом предприятии - 0.1, на втором - 0.2, на третьем – 0.25. Определить вероятность того, что акционер, имеющий акции всех предприятий, получит высокие дивиденды: а) на всех предприятиях; б) только на одном предприятии; в) хотя бы на одном предприятии.

10. [1] Ежедневная прибыль фирмы «Ой-ой-ой» является случайной величиной с плотностью вероятностей вида

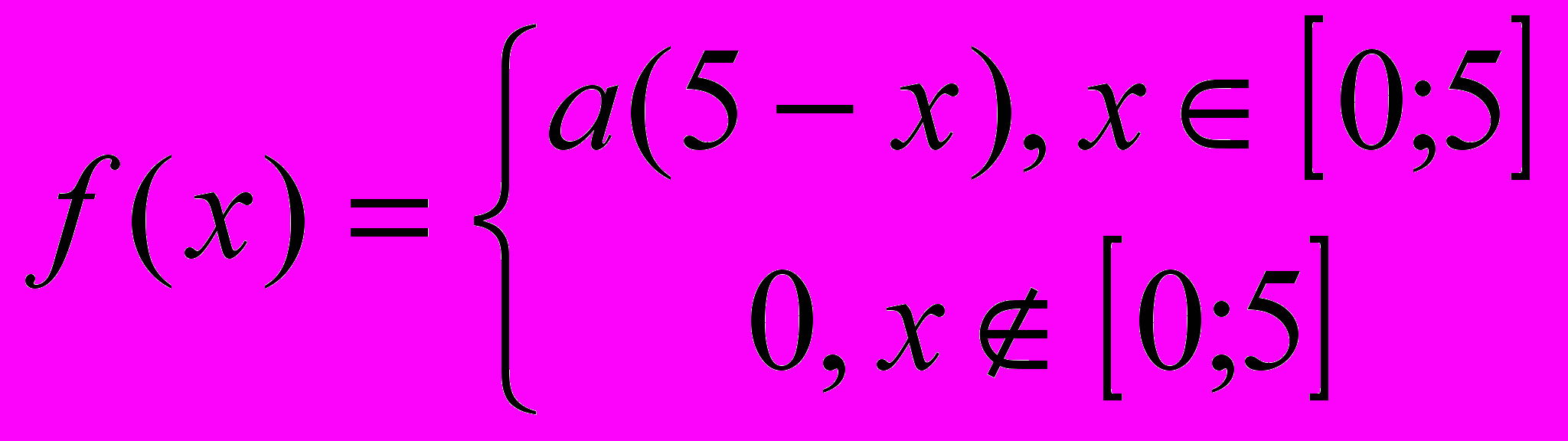. Найти параметр

, математическое ожидание и среднее квадратическое отклонение прибыли. Вычислить вероятность того, что случайная величина попадает в промежуток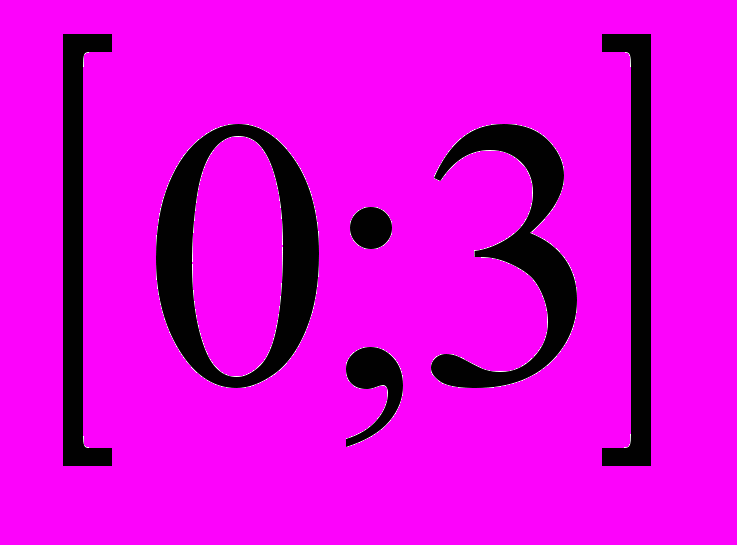

. Построить график

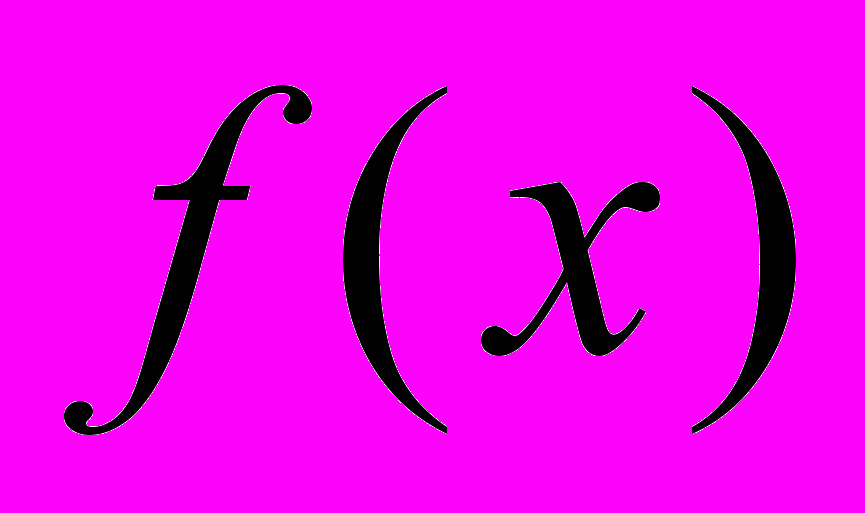, показать на нем

.

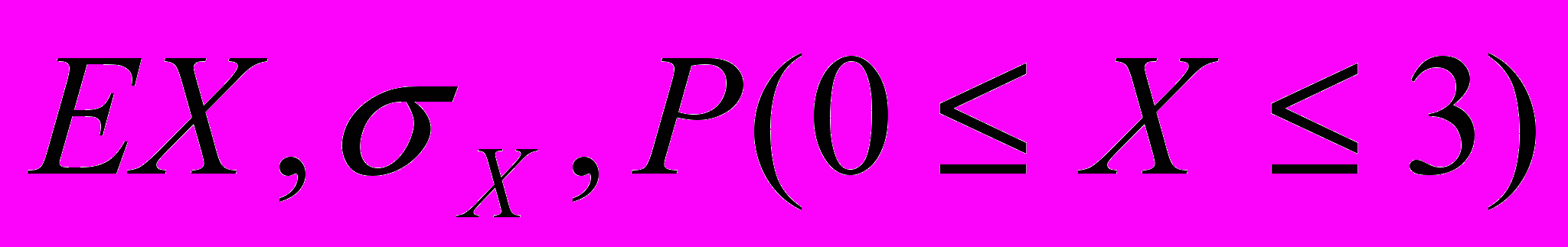11. [0.5] Для типичного посетителя данной торговой точки вероятность покупки бензина составляет 0.23, вероятность покупки бакалейных товаров равна 0.23, а вероятность покупки бакалейных товаров при условии покупки бензина равна 0.85. а) Являются ли независимыми события покупки бензина и покупки бакалейных товаров? б) Какова вероятность того, что посетитель купит и бензин и бакалейные товары?

12. [1] В гипермаркете «Большая Калоша» на понедельник объявлена рекламная акция: в среднем каждый третий покупатель получит в подарок сумку в виде калоши. В понедельник в магазине побывали 2500 покупателей. а) Какова вероятность, что сумки в подарок получат более 800 человек? б) Найти наивероятнейшее число покупателей, получивших подарок, и вероятность того, что подарки получат наивероятнейшее число покупателей.

13. [1] В банке оператор тратит на обслуживание одного клиента в среднем 15 минут. Какова вероятность того, что: а) за один час оператор обслужит менее двух клиентов; б) за два часа он обслужит 8 клиентов?

14. [1] Автомат заполняет банки кофе. Масса кофе и масса банки являются независимыми случайными величинами, имеющими нормальное распределение со средними значениями, соответственно, 250 г и 40 г и средними квадратическими отклонениями 8 г и 6 г. Какова вероятность того, что вес готовой к продаже продукции будет менее 280 г?

Четвертая часть

Последние две задачи решаются студентом по собственному выбору - либо 15 , либо 16; каждая из них имеет «вес» 1 балл

15. Студент Усердный идёт пешком от станции метро к институту. Институт удален от станции на 2 км. Этот путь занимает у студента 20 минут (2км со скоростью 6 км/ч; время = 2км / 6км за час = 20минут). Если его обгоняет маршрутка, студент садится в неё. Будем считать, что маршрутка едет в 5 раз быстрее, чем идёт студент (т.е. со скоростью 30 км/час). Время появления маршрутки на пути студента равномерно распределено по всему пути. Найти математическое ожидание времени, которое займёт у студента путь от станции метро до института.

16. Экспериментатор подбрасывает игральную кость и монетку. Если выпадает орел, то количество очков, выпавших на кубике, увеличивается на 1, если решка – уменьшается на 1. Найти математическое ожидание количества полученных очков.

Список литературы

Шведов А.С. Теория вероятностей и математическая статистика: учебное пособие для вызов – 2-е издание, переработанное и дополненное – М: Изд. дом ГУ ВШЭ, 2005. – 254 с.
Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами по теории вероятностей в задачах с решениями. Учебное пособие. – Москва-Ростов-на-Дону: Март,2005.
Белько И.В., Свирид Г.П. Теория вероятностей и математическая статистика: Примеры и задачи. Учебное пособие. – Минск: Новое знание, 2004.
Прохоров Ю.В., Пономаренко Л.С. Лекции по теории вероятностей и математической статистике: Учебное пособие. – М: Изд. ВМиК МГУ, 2004. – 196 с.
Ватутин В.А. и др. Теория вероятностей и математическая статистика в задачах. – М.: Агар, 2003.
Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. Учебник, второе издание. – М.: ЮНИТИ, 2003.
Вентцель Е.С., Овчаров Л.А. «Задачи и упражнения по теории вероятностей. – М.: Высшая школа, 2002.
Горелова Г.В., Кацко И.А. Теория вероятностей и математическая статистика в примерах и задачах с применением EXEL. Учебное пособие для ВУЗов. – Ростов-на-Дону: Феникс, 2002.
Сигел Э. Практическая бизнес-статистика. Четвертое издание.- Москва-Санкт-Петербург-Киев: Вильямс, 2002.
Кремер Н.Ш. Теория вероятностей и математическая статистика. Учебник для ВУЗов. – М.: ЮНИТИ-ДАНА, 2001.
Ниворожкина Л.И., Морозова З.А. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач. – Ростов-на-Дону, Феникс,1999.
Бородин А.Н. Элементарный курс теории вероятностей и математической статистики. – Санкт-Петербург, 1999.
Сборник задач по теории вероятностей, математической статистике и теории случайных функций. Под ред. Свешникова А.А. – Москва: Наука, 1970.
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебное пособие для ВУЗов. – М.: Высшая школа,1999.
Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для ВУЗов. – М.: Высшая школа, 1999.

Blog