Пояснительная записка Вариант 12. 1 Выполнил студент гр. Асу-03-1 Кладов А. А. Проверил доцент кафедры итас
| Вид материала | Пояснительная записка |
СодержаниеЗадание на курсовую работу Построение моделей. Решение построенных моделей. Список литературы |
- Шустова Наталья Евгеньевна канд социологических наук, доцент кафедры общей и социальной, 607.93kb.
- Пояснительная записка, 132.41kb.
- Пояснительная записка, 146.94kb.
- Пояснительная записка, 131.41kb.
- Петровская Ольга Владимировна, старший преподаватель кафедры оо «Искусство» и«Технология», 169.39kb.
- Рюмшина Любовь Ивановна, доктор психологических наук, доцент кафедры социальная психология, 400.08kb.
- Пояснительная записка Эндокринология область медицины, изучающая процессы биосинтеза, 134.86kb.
- Пояснительная записка Эндокринология область медицины, изучающая процессы биосинтеза, 138.66kb.
- Попов Владимир Петрович доцент кафедры национальной и региональной экономики Санкт-Петербург, 234.71kb.
- Пояснительная записка Составитель: доцент кафедры гражданского права и процесса Москаль, 276.89kb.
Пермский государственный технический университет
Кафедра
Информационных Технологий и Автоматизированных Систем
КУРСОВАЯ РАБОТА
ПО ИССЛЕДОВАНИЮ ОПЕРАЦИЙ
Пояснительная записка
Вариант 12.1
Выполнил студент гр. АСУ-03-1
Кладов А.А.
Проверил доцент кафедры ИТАС
Гольдштейн А. Л.
Пермь 2006 г
Содержание
- Задание на курсовую работу…………………………….2
- Построение моделей…………………………………......3
- Решение построенных моделей........................................7
- Заключение.........................................................................7
- Список литературы............................................................8
- Приложения........................................................................9
Задание на курсовую работу
Условия. Пункт техобслуживания машин работает с 8 до 20 часов. Один работник пункта может обслужить две машины. Продолжительность рабочего дня 8 часов, включая 1 час перерыва на обед. Начало рабочего дня и время перерыва устанавливается для каждого работника индивидуально, согласно графику расстановки рабочей силы, который составляется с учетом колебания нагрузки по часам. При этом соблюдаются следующие условия:
- Начавшись, рабочий день не прерывается, за исключением перерыва на обед.
- До и после перерава продолжительность работы должна быть не меньше трех часов.
Велечина нагрузки на пункт Qi по часам известна:
-
Время
работы
Qi
Время
работы
Qi
8-9
20
13-14
80
9-10
40
14-15
80
10-11
40
15-16
40
11-12
60
16-17
40
12-13
40
17-18
60
Известно так же количество работников на пункте W=30.
Требуется определить оптимальный график расстановки работников по 2-3 критериям, один из которых должен характеризовать равномерность недообслуживания в течение всего времени работы пункта.
Показать как изменяется решение по одному из критериев, если одновременно увеличивать Q2 до 2 Q2 и Q9 до 1,5 Q9.
Построение моделей.
Определим возможные графики работы
| | 8-9 | 9-10 | 10-11 | 11-12 | 12-13 | 13-14 | 14-15 | 15-16 | 16-17 | 17-18 |
| 1 | | | | Обед | | | | | | |
| 2 | | | | | Обед | | | | | |
| 3 | | | | | Обед | | | | | |
| 4 | | | | | | Обед | | | | |
| 5 | | | | | | Обед | | | | |
| 6 | | | | | | | Обед | | | |
Введем переменные
x1-колличество работников, работающих по 1 графику
x2-колличество работников, работающих по 2 графику
x3-колличество работников, работающих по 3 графику
x4-колличество работников, работающих по 4 графику
x5-колличество работников, работающих по 5 графику
x6-колличество работников, работающих по 6 графику
n1-недоработка (количество не обслуженных машин) с 8 до 9
n2-недоработка (количество не обслуженных машин) с 9 до 10
n3-недоработка (количество не обслуженных машин) с 10 до 11
n4-недоработка (количество не обслуженных машин) с 11 до 12
n5-недоработка (количество не обслуженных машин) с 12 до 13
n6-недоработка (количество не обслуженных машин) с 13 до 14
n7-недоработка (количество не обслуженных машин) с 14 до 15
n8-недоработка (количество не обслуженных машин) с 15 до 16
n9-недоработка (количество не обслуженных машин) с 16 до 17
n10-недоработка (количество не обслуженных машин) с 17 до 18
Количество обслуженных машин в час и недоработка в сумме не должны быть меньше притока машин Qi.
Целесообразно уменьшить недоработку на пункте, следовательно, критерий будет выглядеть как минимизация суммированной по часам недоработки.
Модель 1:
L= n1+n2+n3+n4+n5+n6+n7+n8+n9+n10 -> min
2*x1+2*x2+n1 20
2*x1+2*x2+2*x3+2*x4+n2 40
2*x1+2*x2+2*x3+2*x4+2*x5+2*x6+n3 40
2*x2+2*x3+2*x4+2*x5+2*x6+n4 60
2*x1+2*x4+2*x5+2*x6+n5 40
2*x1+2*x2+2*x3+2*x6+n6 80
2*x1+2*x2+2*x3+2*x4+2*x5+n7 80
2*x1+2*x2+2*x3+2*x4+2*x5+2*x6+n8 40
2*x3+2*x4+2*x5+2*x6+n9 40
2*x5+2*x6+n10 60
x1+x2+x3+x4+x5+x6 30
xi,ni 0
Увеличить Q2 до 2 Q2 и Q9 до 1,5 Q9.
Модель 2:
L= n1+n2+n3+n4+n5+n6+n7+n8+n9+n10 -> min
2*x1+2*x2+n1 20
2*x1+2*x2+2*x3+2*x4+n2 80
2*x1+2*x2+2*x3+2*x4+2*x5+2*x6+n3 40
2*x2+2*x3+2*x4+2*x5+2*x6+n4 60
2*x1+2*x4+2*x5+2*x6+n5 40
2*x1+2*x2+2*x3+2*x6+n6 80
2*x1+2*x2+2*x3+2*x4+2*x5+n7 80
2*x1+2*x2+2*x3+2*x4+2*x5+2*x6+n8 40
2*x3+2*x4+2*x5+2*x6+n9 60
2*x5+2*x6+n10 60
x1+x2+x3+x4+x5+x6 30
xi,ni 0
Один из критериев должен характеризовать равномерность недообслуживания.
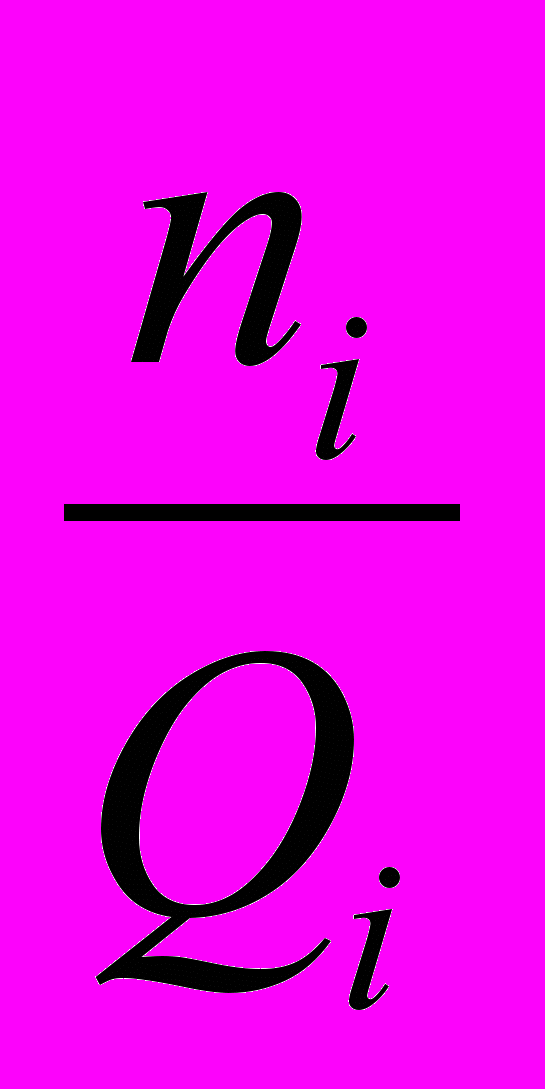- соотношение недообслуживания и общего потока машин, т.е. невыполненная часть заявок.Чем равномернее недообслуживание, тем меньше разность между максимальным
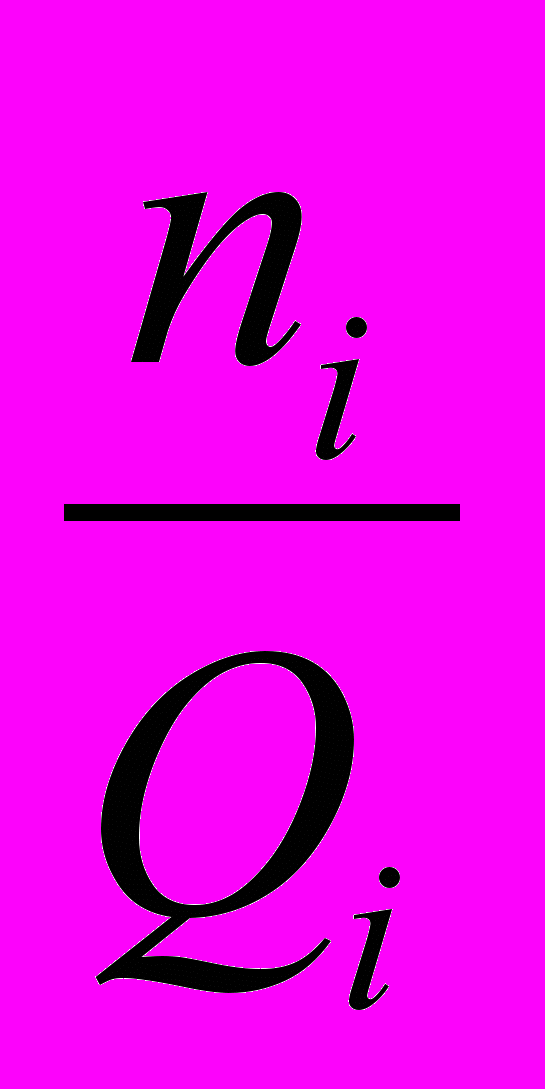и любым другим. Критерий будет выглядеть так:(max
-
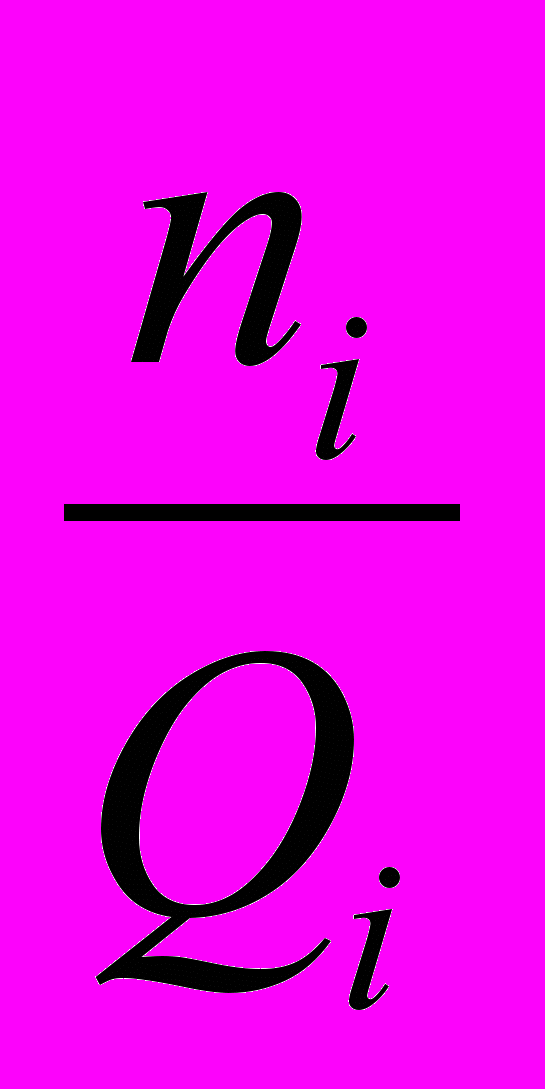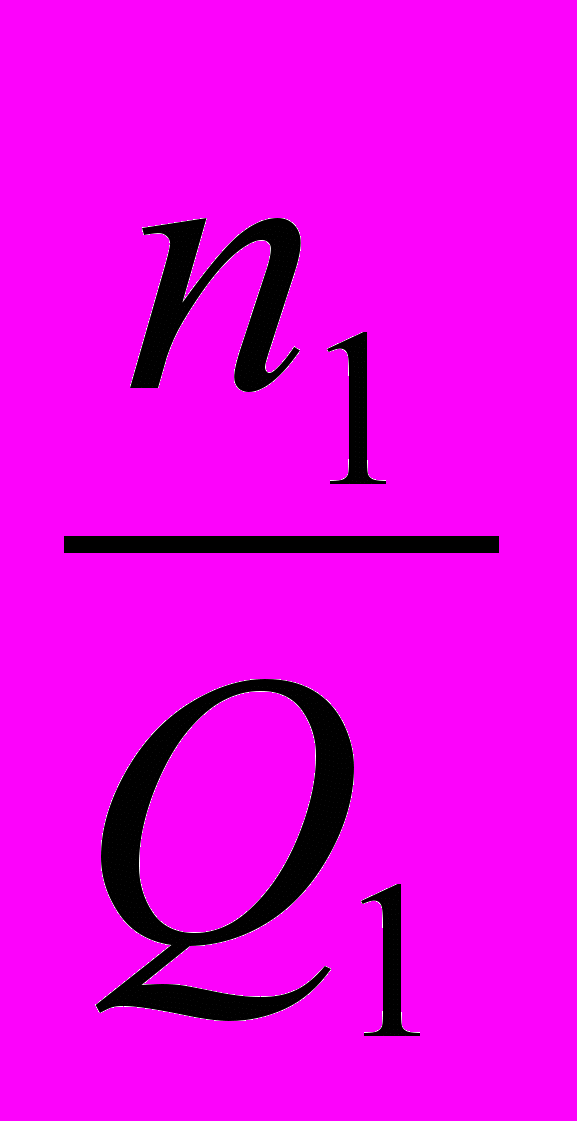)+(max-
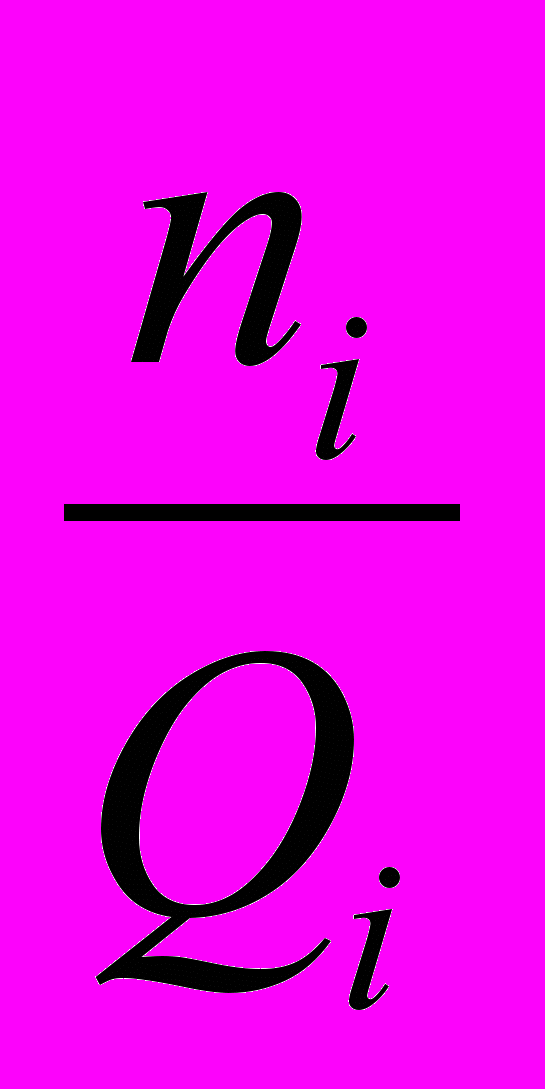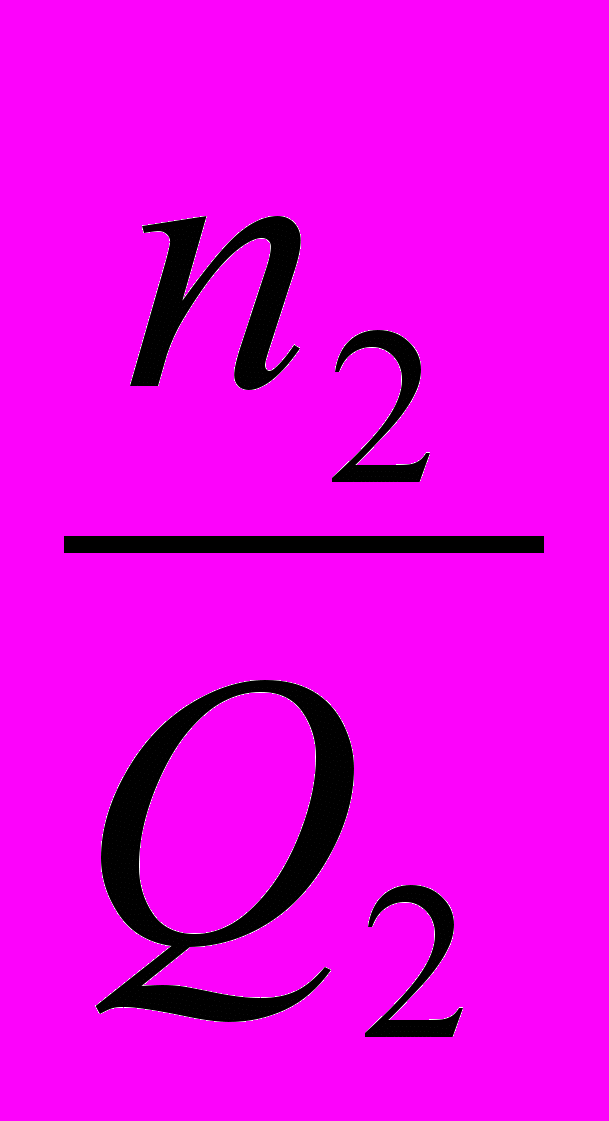)+…+(max-
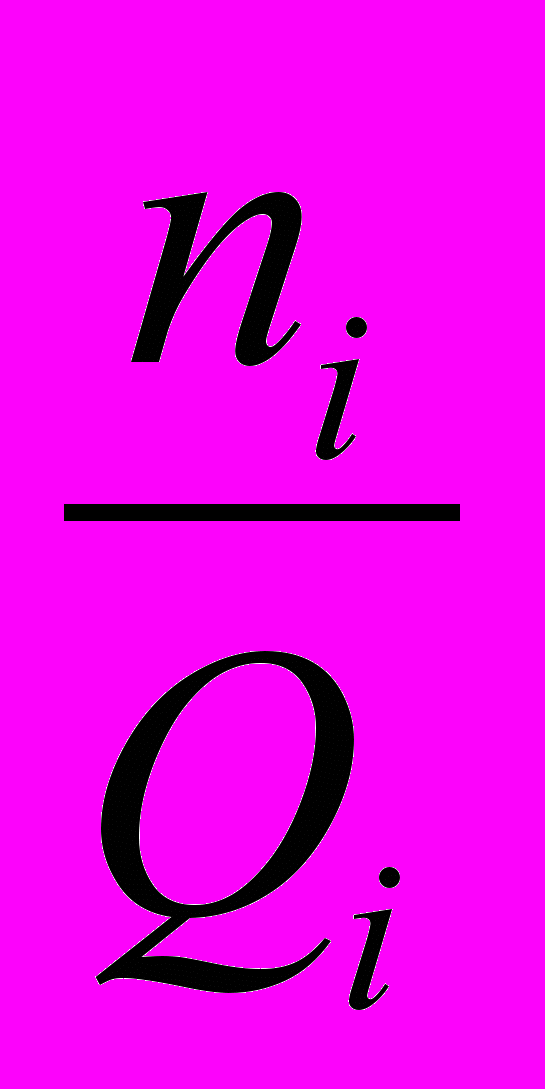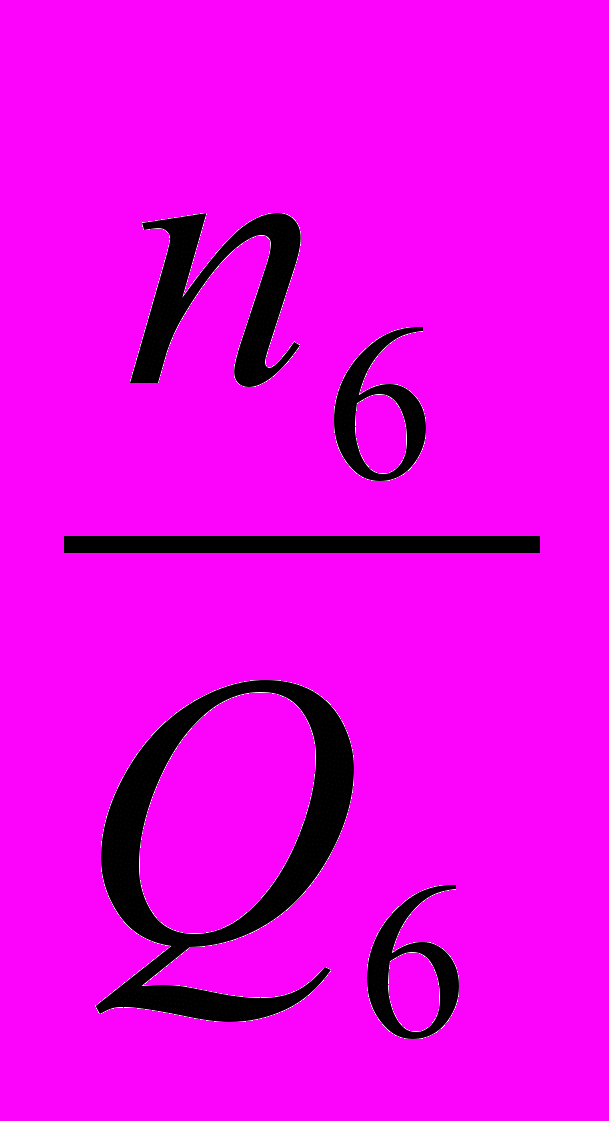) -> minМодель 3:
L= 10- 1/20*n1 - 1/40*n2 - 1/40*n3 - 1/60*n4 - 1/40*n5 - 1/80*n6 - 1/80*n7 - 1/40*n8 - 1/40*n9 - 1/60*n10 -> min
2*x1+2*x2+n1 20
2*x1+2*x2+2*x3+2*x4+n2 40
2*x1+2*x2+2*x3+2*x4+2*x5+2*x6+n3 40
2*x2+2*x3+2*x4+2*x5+2*x6+n4 60
2*x1+2*x4+2*x5+2*x6+n5 40
2*x1+2*x2+2*x3+2*x6+n6 80
2*x1+2*x2+2*x3+2*x4+2*x5+n7 80
2*x1+2*x2+2*x3+2*x4+2*x5+2*x6+n8 40
2*x3+2*x4+2*x5+2*x6+n9 40
2*x5+2*x6+n10 60
x1+x2+x3+x4+x5+x6 30
1/20*n1- 0
1/40*n2- 0
1/40*n3- 0
1/60*n4- 0
1/40*n5- 0
1/80*n6- 0
1/80*n7- 0
1/40*n8- 0
1/40*n9- 0
1/60*n10- 0
xi,ni 0
Для решения данной модели в LINDO ее необходимо масштабировать, чтобы избавиться от дробных коэффициентов:
L= 2400- 12*n1 - 6*n2 - 6*n3 - 4*n4 - 6*n5 - 3*n6 - 3*n7 - 6*n8 - 6*n9 - 4*n10 -> min
2*x1+2*x2+n1 20
2*x1+2*x2+2*x3+2*x4+n2 40
2*x1+2*x2+2*x3+2*x4+2*x5+2*x6+n3 40
2*x2+2*x3+2*x4+2*x5+2*x6+n4 60
2*x1+2*x4+2*x5+2*x6+n5 40
2*x1+2*x2+2*x3+2*x6+n6 80
2*x1+2*x2+2*x3+2*x4+2*x5+n7 80
2*x1+2*x2+2*x3+2*x4+2*x5+2*x6+n8 40
2*x3+2*x4+2*x5+2*x6+n9 40
2*x5+2*x6+n10 60
x1+x2+x3+x4+x5+x6 30
12*n1- 0
6*n2- 0
6*n3- 0
4*n4- 0
6*n5- 0
3*n6- 0
3*n7- 0
6*n8- 0
6*n9- 0
4*n10- 0
xi,ni 0
- это max
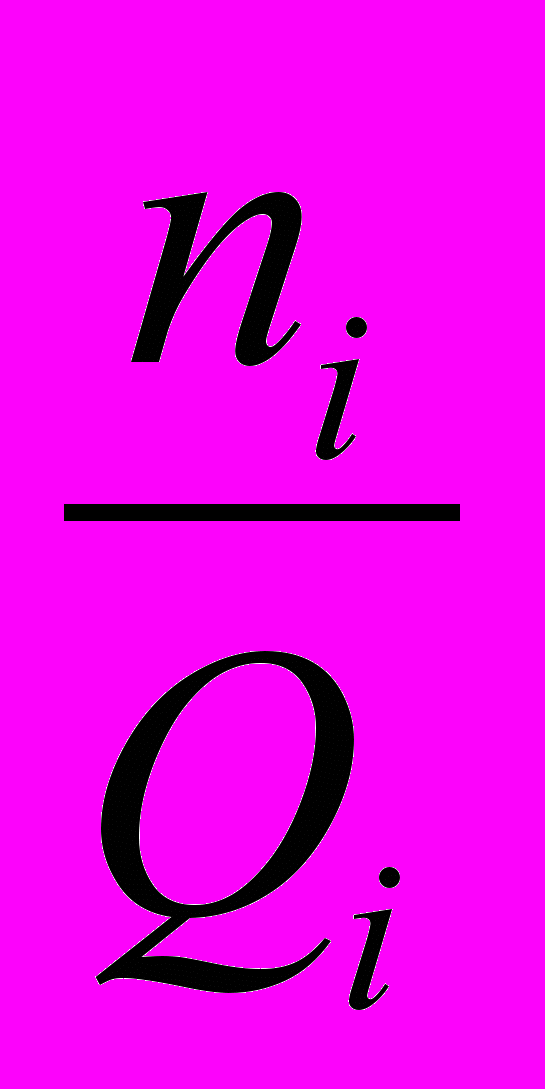
Решение построенных моделей.
Решение модели 1:
Общее недообслуживание за весь рабочий день составило 120 машин (L=120).
Работники должны выйти по следующему графику:
- 10 человек с 8 часов, обед в 11 часов (x1=10)
- 10 человек с 9 часов, обед в 12 часов (x3=10)
- 10 человек с 10 часов, обед в 14 часов (x6=10)
Решение модели 2:
Общее недообслуживание за весь рабочий день составило 160 машин (L=160).
Работники должны выйти по следующему графику:
- 10 человек с 8 часов, обед в 11 часов (x1=10)
- 10 человек с 9 часов, обед в 12 часов (x3=10)
- 10 человек с 10 часов, обед в 14 часов (x6=10)
Решение модели 1:
Общее недообслуживание за весь рабочий день составило 120 машин (L=120).
Работники должны выйти по следующему графику:
- 10 человек с 8 часов, обед в 11 часов (x1=10)
- 10 человек с 9 часов, обед в 12 часов (x3=10)
- 10 человек с 10 часов, обед в 14 часов (x6=10)
Решение модели 3:
Достигнута абсолютная равномерность недообслуживания (L=0).
Работники должны выйти по следующему графику:
- 18 человек с 8 часов, обед в 11 часов (x1=18)
- 12 человек с 10 часов, обед в 14 часов (x6=12)
Сумма необслуженных машин равна 300.
=0,6 , т.е. пунктом обслуживается только 40% приезжающих автомобилей.
Заключение.
В ходе выполнения данной курсовой работы была произведена формализация исходной задачи, построены модели, и получены оптимальные решения по критериям минимального и равномерного недообслуживания при помощи программы LINDO.
Список литературы
- Вентцель Е.С. Исследование операций. М.: Сов. радио, 1972 – 552 с.
- Волков И.К., Загоруйко Е.А. Исследование операций: Учеб. для вузов. 2-е изд./ Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. – 436 с.
- Гольдштейн А.Л. Оптимизация в LINDO: Учеб. пособие / Перм. гос. техн. ун-т. Пермь, 2000. 88 с.
Приложение.
Модели и решения в LINDO.
Модель 1:
MIN n1+n2+n3+n4+n5+n6+n7+n8+n9+n10
ST
2x1+2x2+n1 >=20
2x1+2x2+2x3+2x4+n2 >= 40
2x1+2x2+2x3+2x4+2x5+2x6+n3 >= 40
2x2+2x3+2x4+2x5+2x6+n4 >= 60
2x1+2x4+2x5+2x6+n5 >= 40
2x1+2x2+2x3+2x6+n6 >= 80
2x1+2x2+2x3+2x4+2x5+n7 >= 80
2x3+2x4+2x5+2x6+n8 >= 40
2x1+2x2+2x3+2x4+2x5+2x6+n9 >= 40
2x5+2x6+n10 >= 60
x1+x2+x3+x4+x5+x6 <=30
END
GIN 16
Решение:
LP OPTIMUM FOUND AT STEP 12
OBJECTIVE VALUE = 120.000000
FIX ALL VARS.( 2) WITH RC > 1.00000
NEW INTEGER SOLUTION OF 120.000000 AT BRANCH 0 PIVOT 14
BOUND ON OPTIMUM: 120.0000
ENUMERATION COMPLETE. BRANCHES= 0 PIVOTS= 14
LAST INTEGER SOLUTION IS THE BEST FOUND
RE-INSTALLING BEST SOLUTION...
OBJECTIVE FUNCTION VALUE
1) 120.0000
VARIABLE VALUE REDUCED COST
X1 10.000000 0.000000
X2 0.000000 0.000000
X3 10.000000 0.000000
X4 0.000000 0.000000
X5 0.000000 0.000000
X6 10.000000 0.000000
N1 0.000000 1.000000
N2 0.000000 1.000000
N3 0.000000 1.000000
N4 20.000000 1.000000
N5 0.000000 1.000000
N6 20.000000 1.000000
N7 40.000000 1.000000
N8 0.000000 1.000000
N9 0.000000 1.000000
N10 40.000000 1.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 0.000000 0.000000
3) 0.000000 0.000000
4) 20.000000 0.000000
5) 0.000000 0.000000
6) 0.000000 0.000000
7) 0.000000 0.000000
8) 0.000000 0.000000
9) 0.000000 0.000000
10) 20.000000 0.000000
11) 0.000000 0.000000
12) 0.000000 0.000000
NO. ITERATIONS= 14
BRANCHES= 0 DETERM.= 1.000E 0
Модель 2:
MIN n1+n2+n3+n4+n5+n6+n7+n8+n9+n10
ST
2x1+2x2+n1 >=20
2x1+2x2+2x3+2x4+n2 >= 80 ! Q2=2*Q2
2x1+2x2+2x3+2x4+2x5+2x6+n3 >= 40
2x2+2x3+2x4+2x5+2x6+n4 >= 60
2x1+2x4+2x5+2x6+n5 >= 40
2x1+2x2+2x3+2x6+n6 >= 80
2x1+2x2+2x3+2x4+2x5+n7 >= 80
2x3+2x4+2x5+2x6+n8 >= 40
2x1+2x2+2x3+2x4+2x5+2x6+n9 >= 60 ! Q9=1.5*Q9
2x5+2x6+n10 >= 60
x1+x2+x3+x4+x5+x6 <=30
END
GIN 16
Решение:
LP OPTIMUM FOUND AT STEP 10
OBJECTIVE VALUE = 160.000000
FIX ALL VARS.( 4) WITH RC > 1.00000
NEW INTEGER SOLUTION OF 160.000000 AT BRANCH 0 PIVOT 10
BOUND ON OPTIMUM: 160.0000
ENUMERATION COMPLETE. BRANCHES= 0 PIVOTS= 10
LAST INTEGER SOLUTION IS THE BEST FOUND
RE-INSTALLING BEST SOLUTION...
OBJECTIVE FUNCTION VALUE
1) 160.0000
VARIABLE VALUE REDUCED COST
X1 10.000000 0.000000
X2 0.000000 0.000000
X3 10.000000 0.000000
X4 0.000000 0.000000
X5 0.000000 0.000000
X6 10.000000 0.000000
N1 0.000000 1.000000
N2 40.000000 1.000000
N3 0.000000 1.000000
N4 20.000000 1.000000
N5 0.000000 1.000000
N6 20.000000 1.000000
N7 40.000000 1.000000
N8 0.000000 1.000000
N9 0.000000 1.000000
N10 40.000000 1.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 0.000000 0.000000
3) 0.000000 0.000000
4) 20.000000 0.000000
5) 0.000000 0.000000
6) 0.000000 0.000000
7) 0.000000 0.000000
8) 0.000000 0.000000
9) 0.000000 0.000000
10) 0.000000 0.000000
11) 0.000000 0.000000
12) 0.000000 0.000000
NO. ITERATIONS= 10
BRANCHES= 0 DETERM.= 1.000E 0
Модель 3:
MIN 2400v-12n1-6n2-6n3-4n4-6n5-3n6-3n7-6n8-6n9-4n10
ST
2x1+2x2+n1 >=20
2x1+2x2+2x3+2x4+n2 >= 40
2x1+2x2+2x3+2x4+2x5+2x6+n3 >= 40
2x2+2x3+2x4+2x5+2x6+n4 >= 60
2x1+2x4+2x5+2x6+n5 >= 40
2x1+2x2+2x3+2x6+n6 >= 80
2x1+2x2+2x3+2x4+2x5+n7 >= 80
2x3+2x4+2x5+2x6+n8 >= 40
2x1+2x2+2x3+2x4+2x5+2x6+n9 >= 40
2x5+2x6+n10 >= 60
x1+x2+x3+x4+x5+x6 =30
12 n1-240v<=0
6 n2-240v<=0
6 n3-240v<=0
4 n4-240v<=0
6 n5-240v<=0
3 n6-240v<=0
3 n7-240v<=0
6 n8-240v<=0
6 n9-240v<=0
4 n10-240v<=0
END
GIN 16
Решение:
LP OPTIMUM FOUND AT STEP 124
OBJECTIVE VALUE = -0.241584530E-12
SET N6 TO >= 46 AT 1, BND= 0.0000E+00 TWIN= 0.0000E+00 134
SET N1 TO >= 12 AT 2, BND= 0.0000E+00 TWIN= -6.000 138
NEW INTEGER SOLUTION OF 0.000000000E+00 AT BRANCH 2 PIVOT 138
BOUND ON OPTIMUM: 0.0000000E+00
DELETE N1 AT LEVEL 2
DELETE N6 AT LEVEL 1
ENUMERATION COMPLETE. BRANCHES= 2 PIVOTS= 138
LAST INTEGER SOLUTION IS THE BEST FOUND
RE-INSTALLING BEST SOLUTION...
OBJECTIVE FUNCTION VALUE
1) 0.0000000E+00
VARIABLE VALUE REDUCED COST
X1 18.000000 0.000000
X2 0.000000 0.000000
X3 0.000000 0.000000
X4 0.000000 0.000000
X5 0.000000 0.000000
X6 12.000000 0.000000
N1 12.000000 -12.000000
N2 24.000000 -6.000000
N3 24.000000 -6.000000
N4 36.000000 -4.000000
N5 24.000000 -6.000000
N6 48.000000 27.000000
N7 48.000000 -3.000000
N8 24.000000 -6.000000
N9 24.000000 -6.000000
N10 36.000000 -4.000000
V 0.600000 0.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 28.000000 0.000000
3) 20.000000 0.000000
4) 44.000000 0.000000
5) 0.000000 0.000000
6) 44.000000 0.000000
7) 28.000000 0.000000
8) 4.000000 0.000000
9) 8.000000 0.000000
10) 44.000000 0.000000
11) 0.000000 0.000000
12) 0.000000 0.000000
13) 0.000000 0.000000
14) 0.000000 0.000000
15) 0.000000 0.000000
16) 0.000000 0.000000
17) 0.000000 0.000000
18) 0.000000 10.000000
19) 0.000000 0.000000
20) 0.000000 0.000000
21) 0.000000 0.000000
22) 0.000000 0.000000
NO. ITERATIONS= 140
BRANCHES= 2 DETERM.= 1.000E 0