Образовательная программа Клуба «Юный математик» 2007/2008 2008/2009 учебный год Классы 2007-2008 5 класс 2008-2009 6 класс

1   2   3   4   5

Внеклассное мероприятие.

ИГРА « Счастливый случай» 9 класс.

Вступительное слово ведущего.

Добрый день дорогие друзья!

Сегодня мы проводим игру «Счастливый случай» в математике.


Чтобы спорилось нужное дело,

Чтобы в жизни не знать неудач,

Мы в поход отправляемся смело –

В мир загадок и сложных задач.

Не беда, что идти далеко,

НЕ боимся, что путь будет труден.

Достижения крупные людям

Никогда не давались легко.


Но наши команды уже приготовились идти по этому нелегкому пути к победе. И сегодня они будут бороться не только за победу, но и за «счастливый случай». И сейчас я передаю слово нашим командам.

( Приветствия жюри, соперникам, название команды и девиз).

ПЛАН ИГРЫ.

1 гейм. Гонка за лидером.( Заходит первая команда и отвечает на вопросы 1 гейма, затем заходит вторая команда и отвечает на те же вопросы. Кто больше наберет очков, тот первым начинает 2 гейм).

2 гейм. Дальше, дальше… ( Учитель задает вопросы в течении 2 минут, команда отвечает.

Если команда не знает ответа, то она говорит: « Дальше, дальше..»

3 гейм. Лото – счастливый случай. ( Вытягивают бочонки с номерами заданий и отвечают на вопрос. Время для подготовки, не более 1минуты. Кому попадет бочонок с №13, та команда получает 5 очков.)

4 гейм. Ты мне – я тебе. ( Домашнее задание командам. По 6 вопросов каждой команде. Вопросы задают по очереди.)

5 гейм. Темная лошадка. ( Отгадать о ком идет речь в тексте, который читает ведущий).


ГЕЙМ №1. ГОНКА ЗА ЛИДЕРОМ.

( Вопросы по определению лидера).

1. Почему в поездах стоп-краны всегда красные, а в самолетах – голубые?( В самолетах их нет)
   
2. Соперник нолика? ( крестик)
   
3. Говорят, что математика – царица всех наук, а царица математики?( арифметика)
   
4. На какой вопрос невозможно ответить « ДА»?( ты спишь?)
   
5. В комнате немного теплее, чем в коридоре. В комнате немного холоднее, чем на кухне. Где холоднее всего? ( в коридоре)
   
6. Когда часы бьют 13 раз? ( Когда их пора нести в ремонт)
   
7. Название 13 книг Евклида по геометрии.(Начала)
   

8. Известно, что бумеранг можно бросить так, чтобы он вернулся обратно. Можно ли бросить мяч так, чтобы он вернулся обратно?( вверх)


2 ГЕЙМ. ДАЛЬШЕ, ДАЛЬШЕ…

Вопросы 1 команде.

1. Высший балл в школах России.
   
2. Четырехугольник, у которого 2 стороны параллельны, а 2 другие нет.
   
3. Направленный отрезок.
   
4. Город, состоящий из 101 имени.
   
5. Геометрия, в которой изучаются фигуры на плоскости.
   
6. Сумма одночленов.
   
7. Геометрическая фигура в любовных делах.
   
8. Название натурального числа, которое делится на данное без остатка.
   
9. На что похожа половина яблока?
   
10. Кто был автором первого учебника геометрии?
    
11. Какое название имеет сотая часть числа?
    
12. Цифровой знак, обозначающий отсутствие величины.
    
13. Отношение противолежащего катета к прилежащему.
    
14. Фигура, состоящая из точек и последовательно соединяющих их отрезков.
    
15. Параллелограмм с равными сторонами.
    
16. Масса кубического литра воды.
    
17. Какой вал изображен на картине Айвазовского?
    
18. Центральный угол равен…
    
19. Отрезок, соединяющий две соседние вершины многоугольника.
    
20. Фигура, состоящая из всех точек плоскости, равноудаленных от данной точки этой плоскости?
    

2 ГЕЙМ. ДАЛЬШЕ, ДАЛЬШЕ…

Вопросы 2 команде.

1. Простейшая линия в геометрии.
   
2. Уравнения, имеющие одни и те же корни.
   
3. Утверждение, не требующее доказательства.
   
4. Сколько лет спал Илья Муромец?
   
5. Треугольник со сторонами 3,4,5.
   
6. Кому принадлежит восклицание: « А все-таки она вертится!»
   
7. Сколько точек нужно определить, чтобы построить график прямой пропорциональности?
   
8. На какое наибольшее целое число делится без остатка любое целое число?
   
9. Кто ввел прямоугольную систему координат?
   
10. Вписанный угол равен…
    
11. К однозначному числу приписали такую же цифру. Во сколько раз увеличилось это число?
    
12. Назовите древнегреческого математика, философа, спортсмена.
    
13. Продолжите: Если накрест лежащие углы равны, то…
    
14. Чему равно отношение противолежащего катета к прилежащему?
    
15. Вектора, лежащие на параллельных прямых.
    
16. Два числа, произведение которых равно 1.
    
17. Равнобедренный треугольник, основание которого равно боковой стороне.
    
18. Равенство двух отношений.
    
19. Замкнутая ломаная, звенья которой не лежат на одной прямой.
    
20. Чему равно отношение площадей подобных фигур?
    

Гейм №3

ЛОТО ( заморочки из бочки).

1. С борта теплохода спущен трап. Три его нижних ступеньки погружены в воду. Расстояние между двумя ступеньками 20см. Начался прилив, который поднимается со скоростью 30см/ч. Подсчитайте сколько ступенек трапа окажутся под водой через 1ч30мин. ( Три)

2. Вычислите устно:  42² + 56² (70).

3. В Дано: В АВК АВ = ВК, КАС

КАС А = С + 30

Найти: КВС


Ответ: 30

А К С

4. Почему крышки уличных люков делают круглыми, а не квадратными?

5. Найдите не менее 5 терминов,

В характеризующих ВD








А К

6. Может ли число диагоналей многоугольника равняться числу его сторон?

7. Какое самое большое число можно написать 4 единицами? ( 11¹¹)

8. Отгадайте ребус: К ( Полка)

2

9. Как из числа 12 получить семь, не проводя никаких арифметических

действий?( XII перегнуть пополам)

10. Чье изречение: Вдохновение нужно в геометрии не меньше, чем в

поэзии. ( А.С.Пушкин)

11. Разделите фигуру на 4 равные части.



12. Может ли быть справедливым неравенство: х >10х.( если х<0)

13. СЧАСТЛИВЫЙ СЛУЧАЙ.

14. Прочитайте запись: MДССХСIX и вы прочтете в каком году

родился А.С.Пушкин. (1799)

15. 60 листов книги имеют толщину 1см. Какова толщина всех листо

книги, если в ней 240 страниц? ( 2см)

16. Как из трех спичек сделать четыре? (IV)


ГЕЙМ №5. ТЕМНАЯ ЛОШАДКА.


В начале 18 века по указу Петра 1, хорошо понимавшего необходимость математических наук для караблестроения, для строительства и торговли, для развития экономики в Москве была создана школа математических и навигационных наук. Человек, которого вы должны назвать был преподавателем в этой школе и подготовил первый учебник математики на русском языке. По «Арифметике» напечатанной в Москве в 1703г училось несколько поколений. Михаил ломоносов называл эту книгу « вратами своей учености». Создатель этой книги был очень образованным человеком, он самостоятельно изучил математические науки, немецкий, латинский, итальянский и голландский языки. Петр 1 был восхищен его глубокими познаниями, и прозвал его « магнитом». Кто этот человек, который до самой смерти руководил школой, из которой вышли тысячи образованных людей?

( Леонтий Филиппович Магницкий).


Вот несколько задач из арифметики Магницкого.

1. Хозяин нанял работника на год, обещая уплатить ему 12 рублей и тулуп. Работник прослужил только 7 месяцев; хозяин уплатил ему 5 рублей и тулуп. Определите цену тулупа.( 4р80к)
   
2. Муж и жена выпивают бочонок питья за 10 дней, муж один выпивает такой же бочонок за 14 дней. За сколько дней выпьет такой же бочонок жена? (35дней)
   
3. Некто взял кошелек и пошел покупать игрушки. За первую игрушку он уплатил 1/5 своих денег, за вторую – 3/7 остатка, за третью- 3/5 нового остатка, после чего у него остался 1 р. 90к. Сколько денег было в кошельке и сколько стоила каждая игрушка? (10р50к; 1игрушка -2,1р., 2 игрушка- 3,6р., 3игрушка – 2,88р.)
   

Великолепная семерка

(игра для учащихся 10-11 классов)

Правила игры:

• в игре участвует 7 старшеклассников;
  
• игра состоит из 6 туров;
  
• из каждого тура выбывает один участник, тот, который наберет наименьшее количество баллов в данном туре;
  
• участник, победивший в последнем туре, объявляется победителем игры и получает звание «великолепнейший математик».
  

Цель игры:

• развивать логическое мышление, умение быстро принимать решение в экстремальной ситуации;
  

Оборудование: 7 наборов карточек с цифрами 1, 2, 3, 4, 5, 6.

Игра сопровождается презентацией.

Время игры: 40 минут.

Ход игры:


1). Вступительное слово ведущего.


Ведущий приветствует участников и болельщиков игры, представляет великолепную семерку, членов жюри, сообщает правила игры.


2) Первый тур.


Ведущий: «Сейчас игрокам надо упростить фразы, употребляя математические термины. Например: прямая, проходящая через любые две точки графика функции – это секущая». Я буду читать предложения, тот, кто знает ответ – поднимает руку, сообщает его нам и, если он правильный, проходит в следующий тур. Остальные участники продолжают игру. Последний – выбывает из игры.».

Задания:

- число, к которому стремится отношение приращения функции к приращению аргумента, если приращение аргумента стремится к нулю (производная);

- раздел геометрии, в котором изучаются свойства фигур в пространстве (стереометрия)

- операция нахождения производной (дифференцирование);

- абсцисса точки числовой единичной окружности (косинус);

- две прямые в пространстве, которые не лежат в одной плоскости (скрещивающиеся);

- ненулевые векторы, которые лежат на параллельных прямых или на одной прямой (сонаправленные);

- последовательность чисел, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом (арифметическая прогрессия);

Дополнительные вопросы (используются в спорных ситуациях):

- отношение противолежащего катета к гипотенузе (синус);

- выпуклый многоугольник, у которого все стороны и углы равны (правильный);

- отрезок, для которого указано, какой из его концов является началом, а какой – концом (вектор).

Подведение итогов тура. Прощание с выбывающим игроком.


3). Второй тур.


Ведущий: «Сейчас нашим участникам за одну минуту надо будет решить анаграммы и исключить лишнее слово. За каждое слово – 1 балл. Игрок, набравший наименьшее количество баллов, к сожалению, покинет нашу игру. Итак, продолжаем!»

Демонстрируется слайд:

МУЕТНАРГ АДЬЛИГОАН НАГЬР ЕТДАРТЭР

(Ответы: аргумент, диагональ, грань, тетраэдр. Лишнее слово – аргумент.)

Замечание: если возникнет спорная ситуация в случае, когда какие – то участники наберут одинаковое минимальное количество баллов, можно попросить их объяснить данные математические понятия. Самый некомпетентный из них – выбывает из игры.

Ведущий подводит итоги тура, прощается с выбывающим игроком.


4). Третий тур.


Ведущий: «Сейчас, вам, уважаемые игроки, будут предлагаться вопросы и несколько вариантов ответов. Ваша задача – выбрать правильный. На обдумывание каждого ответа вам будет даваться некоторое время. По моей команде вы поднимаете карточку с номером правильного, на ваш взгляд, ответа. За каждый правильный ответ вы получаете один балл. Напоминаю, игрок, набравший наименьшее количество баллов, покинет нашу игру. Итак, удачи вам! Продолжаем игру!»

Задания:

1. График какой функции изображен на рисунке (демонстрируется слайд):
   

1) у=сos2x; 2) y=cos; 3) y=sin2x; 4) y=sin

(Ответ: 2)

2. Ведущий: «В последнее время во всем мире широкое распространение получил конкурс по решению математических задач «Кенгуру». Поль выиграл футболку, на которой написано «КЕНГУРУ». Он надел её и подошел к зеркалу. Какую надпись он увидел?»
   

Демонстрируется слайд:



(Ответ: 2).

3). Демонстрируется слайд:


Выберите нужную фигуру из шести пронумерованных.





Ответ: 1.


Ведущий подводит итоги тура и благодарит за участие в игре выбывающего старшеклассника.


5). Четвертый тур.


Ведущий: «Сейчас нашим игрокам предстоит продолжить числовые ряды, дописав ещё по два числа. За каждый правильный ответ – 1 балл. Время на выполнение задания – 2 минуты. Как всегда, желаем вам удачи!»

Демонстрируется слайд:

2, 3, 4, 9, 8, 27, 16, 81,… 174, 171, 57, 54, 18, 15,… 31, 24, 18, 13, 9, 6,… 111, 213, 141, 516, 171, 819, 202,…

Ответы: 1) 32, 243; 2) 5, 2; 3) 4, 3; 4) 122, 232.

Ведущий подводит итоги тура и благодарит за участие проигравшего игрока.


6). Пятый тур.


Ведущий: «Далее вам, игроки, будут предлагаться задания, но уже без вариантов ответов. Вы обдумываете ответ в течение некоторого времени. По моей команде записываете его на листочке. За каждое правильное решение – 1 балл. Вы готовы? Продолжаем!»

Задания (демонстрируются на слайдах):

1) (30 секунд)

Передвиньте одну цифру так, чтобы равенство стало верным:

101-102=1

(Ответ: 101-10²=1)

2) Какой цифрой оканчивается число 4²¹? (1 минута)

(Ответ: 4).

3) Сколько треугольников на рисунке? (1 минута)



(Ответ: 14 треугольников)

Ведущий проводит разбор заданий, подводит итоги тура, благодарит выбывающего игрока.


7) Шестой тур (заключительный).


Ведущий: «Я приветствую наших финалистов. Последний тур – аукцион. Сейчас участникам надо будет записать как можно больше предложений о функции, график которой изображен на слайде. Ровно через две минуты по моей команде игроки по очереди будут называть свойства данной функций. Тот, за кем будет последнее слово, и станет победителем нашей игры. Итак, время пошло».


Демонстрируется слайд:




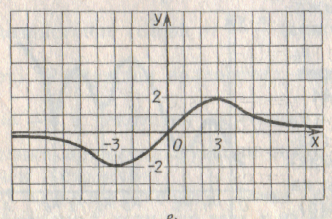
Возможные варианты ответов:

- область определения функции – вся числовая прямая;

- множество значений функции - отрезок [-2;2];

- у функции один нуль х=0;

- функция убывает при х≤-3 и при х≥3;

- функция возрастает при -3≤х≤3;

- наибольшее значение функции равно 2;

- наименьшее значение функции равно -2;

- функция положительна при х>0;

- функция отрицательна при х<0;

- точка минимума х=-3;

- точка максимума х=3;

- максимум функции у=2;

- минимум функции у=-2;

- производная функции равна нулю в точках х=3 и х=-3;

- функция нечетная;

- производная функции положительна при -3<х<3;

- производная функции отрицательна при -33;

- касательная к графику функции параллельна оси абсцисс в точках х=-3 и х=3.

8). Подведение итогов игры.

Ведущий подводит итоги игры, поздравляет победителя, вручает ему памятную ленту с надписью «Великолепный математик». Все участники игры еще раз приглашаются на сцену, им вручаются сувениры.

Звучит заключительная песня.

КВН 6 класс.

Алиса в Стране математики.

В этом КВНе вместо жюри — почтенный суд: Король, Ко­ролева, Мартовский Заяц, Болванщик (герои сказки «Алиса в Стране чудес»). Команды — это помощники Алисы. Можно завести пластинку с песнями из мультфильма, пока команды занимают свои места.

В этот КВН входят все традиционные конкурсы.

1 • Приветствие (3б)

2 • Разминка болельщиков (3б)

1)Что больше:102102102 • 103103 или 103103103 • 102102?

Ответ: Одинаково.

2) Проведя один разрез, получим две части, два разреза — 4 части, три разреза — 6 частей и т. д. «Хорошо, — сказала Алиса, — я разрежу торт на 8 частей тремя прямолинейными разрезами». Как она это может сделать? (Ребятам дают рисунки тортов, на которых они должны изобразить ответ.)

Ответ:




3) На трех банках с вареньем рассеянная хозяйка сделала надписи, как показано на рисунке. Алиса хочет клуб­ничное варенье. В какой оно банке, если известно, что все надписи перепутаны?



Ответ: № 1 — клубника, № 2 — вишня, № 3 — малина.

3 • Разминка команд (3б)

1)Первой задачей обмениваются команды (домашняя заго­товка).

2) У Алисы двое часов: одни стоят, другие спешат. Какие часы лучше? (С точки зрения математики) Ответ: Которые стоят, т. к. они показывают правиль­ное время 2 раза в сутки.

3)У щенят и утят 42 ноги и 12 голов. Сколько утят и сколько щенят?



Ответ: 9 щенят, 3 утенка.

4 • Ребус (2 б)

1)Отгадывать ребус выходят по 2 участника от команды.

МЕЙБЛ + АДА = АЛИСА

(Ребус написан на доске для каждой команды.)

Ответ: 79350

+ 868

80218 Л=0, Е=9, М + 1 = А и т.д.


5 • Конкурс художников (3 б)

Нарисовать план Страны математики, по которой путешествует Алиса (используя геометрические фигуры, знаки, математические символы).

6 • Задание для капитанов.

1)Алиса: «4 • 5= 12,4 • 6 = 13,4 • 7 = 14,4 • 8 = 15,4 • 9=16, так я не дойду до 20» . (Для выполнения этого задания ребята должны знать различные системы счисления). Возможны ли такие равенства и почему Алиса не дой­дет до 20?

Ответ: Нет такой системы, в которой выполняются любые два из этих равенств.

2)Если от задуманного числа отнять 11, результат разде­лить на 11, то останется 4. Если отнять 8 и разделить на 8, то останется 4. Если отнять 7 и разделить на 7, то получится 4. Найдите задуманное число.

Ответ: 620.


Решение: х— 11 = 11k+4

х— 8 = 8n+ 4

х— 7 = 7m+4  число х при делении на 11; 8; 7 дает остаток 4  11 • 8 • 7 + 4 = 620.

7 • Домашнее задание: «Путешествие Алисы по Стране мате­матики» (4б)

Небольшая математическая сказка, которую команда со­чиняет к КВНу. На выступление дается 5 мин (время об­говаривается заранее). В этой сказке Алиса должна встре­тить как можно больше математических понятий, изучаемых в этом году. (Можно дать задание всем ребятам на­писать сказку и выбрать из них лучшую для КВНа.)

8 • Конкурс счетчиков (3б)

Расставьте скобки так, чтобы получилось верное равенство.

Задание 1 участнику: 240 : 40 +20 · 2 = 52

Ответ: (240:40+20)·2=52

Задание 2 участнику: 90 – 30 : 3 · 5 = 100

Ответ: (90-30):3·5=100

9 • Встреча Алисы с математиками (26)

Написать как можно больше имен известных матема­тиков и об одном из них рассказать подробнее ( на подготовку конкурса дается 10 мин.)

К неделе математики на дверях всех кабинетов в школе были развеша­ны таблички и плакаты с высказываниями известных математиков. При выполнении этого задания нужно было их использовать.

10 • Лабиринт (2 б)

Участвуют 2 человека от команды.

Может ли Алиса прогуляться по замку так, чтобы пройти через каждую дверь ровно один раз?

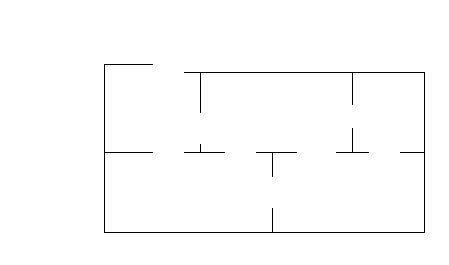Ответ: Нет.

Чтобы совершить требуемую прогулку, залов с нечетным количеством дверей должно быть не больше двух. В этом замке таких залов – три.

11 • Конкурс смекалистых (2б)

Расшифруйте анаграммы и исключите лишнее слово:

ЛИЧОС ЧАТОК ГУРК ШААК РЬБОД

Ответ: число, точка, круг, каша, дробь. (Лишнее слово: каша)

12 • Итоговый конкурс(3б).

Конкурс проводится у доски, на которую записываются ответы.

Ведущий. Но вот впереди забрезжил свет. Команды у выхода из туннеля, а поможет им выбраться ключ. Запи­шите первые буквы следующих названий и сложите из них слово-ключ.

1)Название натурального числа, которое делится на дан­ное без остатка. (Делимое.)

2) Знак, который содержит пропорции. (Равно.)

3) Равенство, содержащее переменную. (Уравнение.)

4)Третий цвет радуги. (Желтый.)

5) Положительное у составляет 3/7 от х — знак сравнения

между х и у. (Больше.)

6) Царица математики. (Арифметика.)

Слово-ключ: Дружба.

13 • Подведение итогов.

Пока жюри подводит итоги, команды показывают номера художественной самодеятельности (стихи о математике, смешные сценки с уроков математики).






Игры со спичками.





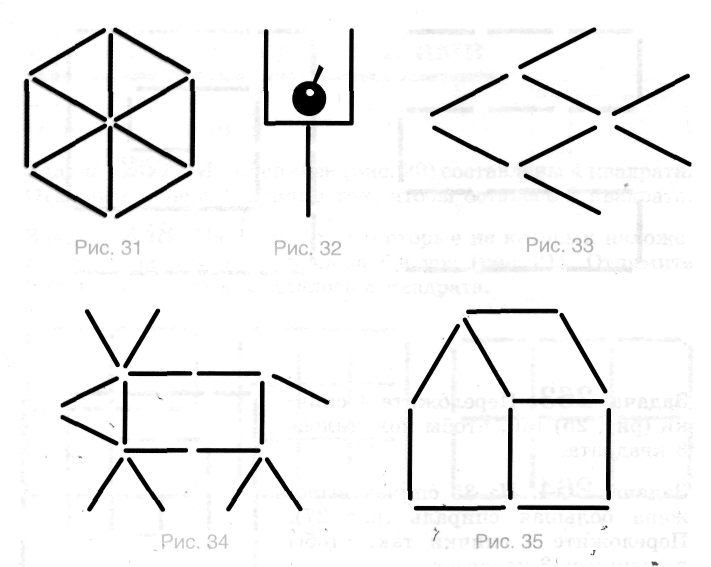
Задача 1 Переложите 3 спички .(рис. 1) так, чтобы получилось 6 равных четырехугольников.

Задача 2. 4 спички образуют рюмку, в которой, лежит вишенка (рис. 2). Как, переложив только 2 спички, вы­нуть вишенку из рюмки?

Задача3. Переложите 3 спички так, чтобы рыбка (рис. 3) поплыла в противоположную сторону.

Задачу 4. Из спичек составлена корова (рис. 4). Пе­реложите 2 спички так, чтобы корова посмотрела в другую сторону.

Задача 5. Из 10 спичек построен дом (рис. 5). Перело­жите 2 спички так, чтобы он повернулся другой стороной.

Задача 6. Модель фасада греческого храма построена из 11 спичек (рис. 6). Переложите 4 спички так, чтобы получилось 15 квадратов





Задача 7. Переложите 6 спичек так, чтобы из двух рюмок (рис. 7) получился дом.

Задача 8. Переложите 2 спички (рис. 8) так, чтобы из подсвечника получилась шляпа.

Задача 9. Переложив только одну спичку, сделайте неверное равенство (рис. 9) верным.