И. Г. Петровского рабочая программа
| Вид материала | Рабочая программа |
СодержаниеВиленкин Н. Я., Балк М.Б., Петров В.А. Математический анализ. Мощность. Метрика. Интеграл. – М.: Просвещение, 1980. |
- И. Г. Петровского рабочая программа, 441.14kb.
- И. Г. Петровского утверждаю заведующий кафедрой С. Ф. Блуменау 200 Рабочая программа, 130.77kb.
- И. Г. Петровского рабочая программа, 84.24kb.
- И. Г. Петровского рабочая программа, 82.24kb.
- И. Г. Петровского рабочая программа, 88.57kb.
- И. Г. Петровского Утвержда ю: зав кафедрой рабочая программа, 52.3kb.
- Рабочая программа педагога борисовой Татьяны Валентиновны, 1 квалификационной категории, 666.85kb.
- И. Г. Петровского Утверждаю: Зав кафедрой 10. 09. 2009 г. Рабочая программа, 120.64kb.
- И. Г. Петровского утверждаю заведующий кафедрой С. Ф. Блуменау 200 Рабочая программа, 116.12kb.
- И. Г. Петровского Факультет технологии, экономики и психологии Кафедра технологии, 590.14kb.
Брянский государственный университет имени академика И.Г.Петровского
РАБОЧАЯ ПРОГРАММА
по курсу (дисциплине) математический анализ для студентов физико-математического факультета
3 курса, специальность прикладная математика, 5 семестр, 2009-2010 учебный год.
Общий объём учебного курса 84 часа, из них лекций 50 часов, практических 34 часа.
Программу разработала Ярославцева О.В.
Утверждаю:
Зав. кафедрой
______________________
«_____»_______________200__г.
| Тема (раздел) курса | Количество часов | Деление темы (раздела) на | |||
| Лекции | Количест-во часов | Практические занятия | Количест-во часов | ||
| 1. Элементы теории мно-жеств и метри-ческих прост-ранств 2. Элементы теории меры и интеграла Лебе-га 3. Ряды Фурье | 14+16 22+8 14+10 |
| 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 |
| 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 |
Литература
-
Виленкин Н. Я., Балк М.Б., Петров В.А. Математический анализ. Мощность. Метрика. Интеграл. – М.: Просвещение, 1980.
- Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М.: Наука, 1972.
- Вайнберг М.М. Функциональный анализ. – М.: Просвещение, 1979.
- Натансон И.П. Теория функций вещественной переменной. – М.: Наука, 1974.
- Кудрявцев Л.Д. Курс математического анализа. Т.3. – М.: Высшая школа, 1988.
- Очан Ю.С. Сборник задач и теорем по теории функций действительного переменного. – М.: Просвещение, 1965.
- Петров В.А., Виленкин Н.Я., Граев М.И. Элементы функционального анализа в задачах. – М.: Просвещение, 1978.
- Треногин В.А. Функциональный анализ. – М.: Физматлит, 2002.
- Фихтенгольц Г.Л. Основы математического анализа. Т.3. – СПб.: Лань, 1997.
- Соболев В.И. Лекции по дополнительным главам математического анализа. – М.: Наука, 1968.
- Вулих Б.З. Введение в функциональный анализ. – М.: Наука, 1967.
- Макаров И.П. Дополнительные главы математического анализа. – М.: Наука, 1968.

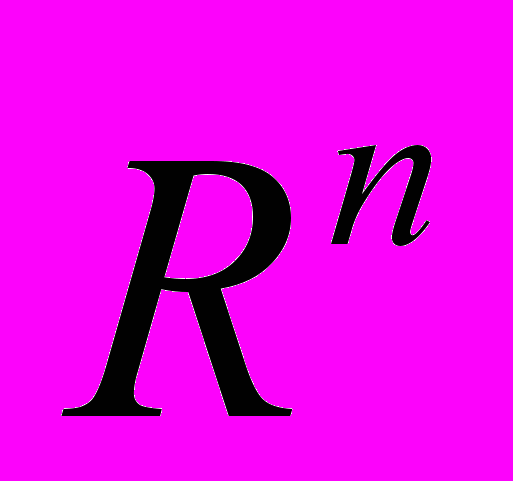 и
и 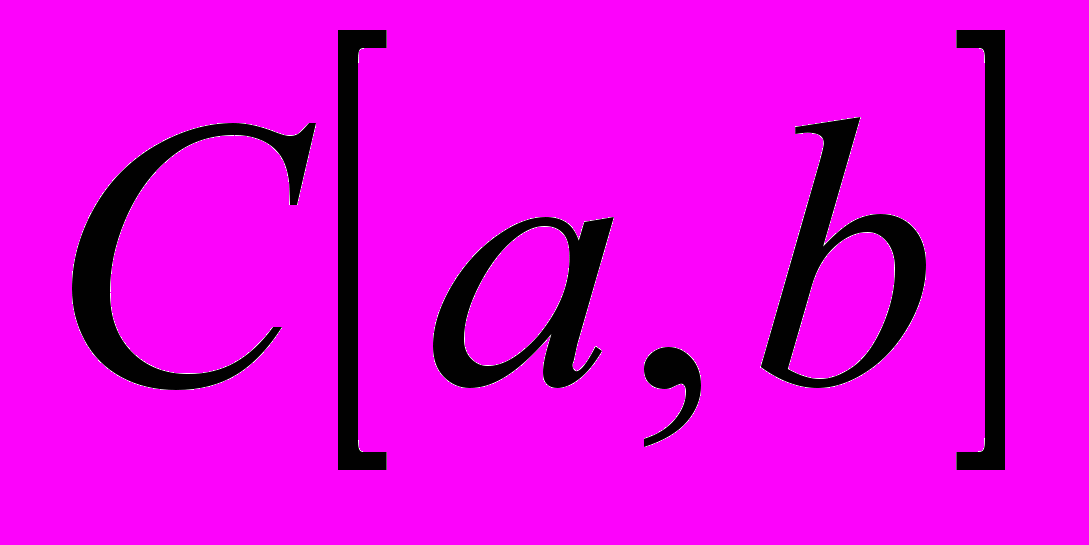 . Фундаментальные по-следовательности. Полные метрические пространства.
. Фундаментальные по-следовательности. Полные метрические пространства.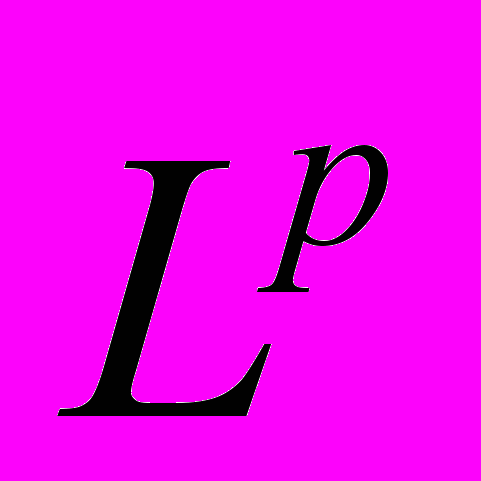 .
.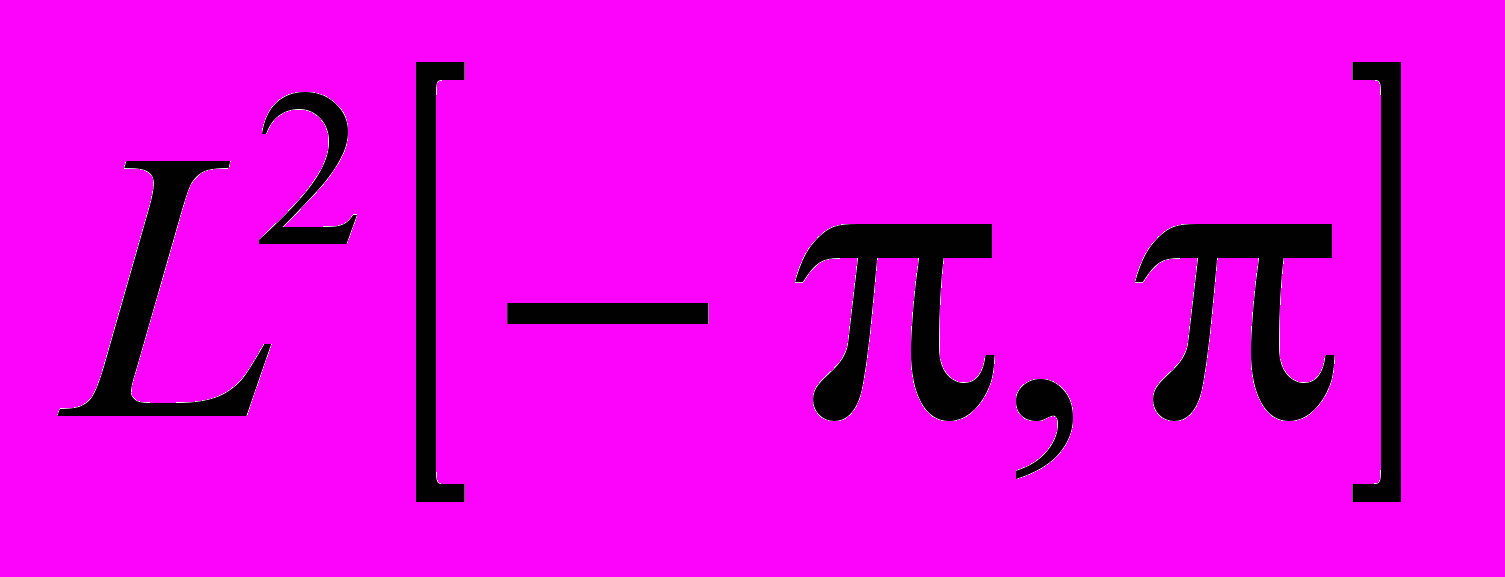 .
.