Функциональный анализ

Вид материала

Программа

Содержание Перечень дисциплин, усвоение которых необходимо для изучения курса Содержание курса Тема 2. Метрические пространства Тема 3. Полные метрические пространства Тема 4. Компактность в метрических пространствах Более подробно Тема 5. Линейные нормированные пространства Тема 6. Линейные функционалы Тема 7. Слабая сходимость в сопряжённом пространстве Тема 8. Гильбертово пространство Тема 9. Ортонормальные системы в гильбертовых пространствах Тема 10. Задачи вариационного исчисления Тема 11. Задача со свободными концами Тема 12. Свойства выпуклых и поглощающих множеств векторных пространств

Подобный материал:

• Программа кандидатского экзамена по специальности 01. 01. 01 Вещественный, комплексный, 118.98kb.
• Программа дисциплины Функциональный анализ для направления 010100. 62 «Математика», 242.48kb.
• Функциональный анализ направление подготовки, 15.46kb.
• Функциональный подход, 291.02kb.
• Утверждаю, 105.37kb.
• Функциональный анализ. Лекции читает Шаповаленко Василий Всеволодович, 30.76kb.
• I функциональный анализ морфемы, лексемы, фраземы, 91.7kb.
• Программа по курсу «Функциональный анализ», 36.73kb.
• Программа-минимум кандидатского экзамена по специальности, 37.75kb.
• I общие основы грамматической стилистики современного испанского языка I. Функциональный, 658.42kb.

УЧЕБНАЯ ПРОГРАММА ПО ДИСЦИПЛИНЕ

ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ

Крюковский А.С., Келлин Н.С.


Для очной формы обучения ВСЕГО 72

лекции 26

семинары 8

Всего аудиторных занятий 34

самостоятельная работа 38


Требования ГОС к обязательному минимуму содержания основной

образовательной программы:

Линейные, топологические и нормированные пространства; пространства непрерывных и суммируемых функций; гильбертово пространство; категорный метод; теория двойственности.


Целью изучения дисциплины является знакомство с основными понятиями, положениями и методами функционального анализа, получение навыков построения математических доказательств путем логически непротиворечивых рассуждений, с широким использованием идей двойственности и выпуклости, уже рассматривавшихся в рамках курсов алгебры и геометрии и топологии за первый-третий семестры, навыков решения прикладных задач.

Перечень дисциплин, усвоение которых необходимо для изучения курса: в объёме программы «Математика» за первый-третий семестры.

В результате изучения дисциплины каждый студент должен:

• иметь представление о:
  

• месте и огромной роли функционального анализа в современном мире, мировой культуре и истории развития самой математики;
  
• функциональном мышлении, о развитии идей двойственности и выпуклости и принципе неподвижной точки и основанных на нем математических доказательствах;
  
• структуре современного анализа; об основных проблемах современного его развития (обобщённые функции, гиперфункции).
  

• знать:
  

• базовые понятия и свойства функциональных пространств: гильбертова, банаховых, лебеговых, пространств обобщённых функций;
  
• теории положительных на конусе полугрупп.
  

• уметь:
  

• линейной алгебры и классического математического анализа (неравенства, полнота и замкнутость систем функций, метод наименьших квадратов);
  
• дифференциального и интегрального исчислений функций многих переменных (описание экстремумов и более общо – критических точек);
  
• теории обыкновенных дифференциальных уравнений, уметь находить условия существования решения основных типов дифференциальных уравнений и систем, включая в рассмотрение первую и вторую вариации;
  
• в теории линейных операторов в линейных и, в частности, в евклидовых пространствах (решения уравнений как неподвижные точки).
  

Основные виды занятий: лекции и практические занятия.

Основные виды текущего контроля занятий: коллоквиумы.

Основной вид рубежного контроля знаний: зачет.


СОДЕРЖАНИЕ КУРСА

Введение.

Тема 1. Множества

Множества (операции над множествами; мощность; счётные и континуальные множества). Более подробно: множества, их объединение, пересечение, дополнение, разность и симметрическая разность; мощности: конечные счётная континуальная – кардиналы; порядковые типы – ординалы – конечные, א(алеф)-0, אּ(алеф)-1, … принципы индукции: полной математической и трансфинитной.

Тема 2. Метрические пространства

Метрические пространства (основные понятия, примеры; открытые и замкнутые множества; сепарабельность). Более подробно: Определение, примеры и построение новых м.п. из уже имеющихся. Критерий полноты.

Тема 3. Полные метрические пространства

Полные метрические пространства. Принцип сжатых отображений. Более подробно: Пополнение м.п. Применение полных м.п., основанное на принципе Банаха о неподвижной точке. Предкомпактные множества в м.п., их связь с ограниченными и конечными множествами.

Тема 4. Компактность в метрических пространствах

Компактность в метрических пространствах (критерий Хаусдорфа, непрерывные функции на компактах; теорема Арцела). Более подробно: Критерий Хаусдорфа, использующий понятие - сети. Свойства непрерывных функционалов на компакте. Теорема Арцела и критерий предкомпактности в 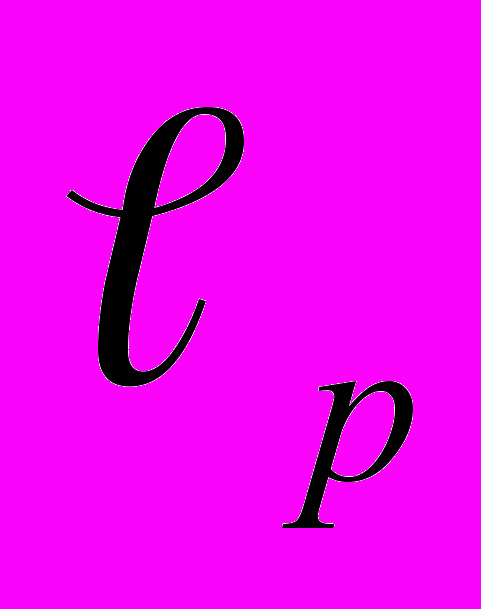- пространствах. Сепарабельность м.п. и подпространств. Теоремы Тихонова и Чеха-Стоуна.

Тема 5. Линейные нормированные пространства

Линейные нормированные пространства. Изоморфизм и изометрия. Задача о наилучшем приближении. Более подробно: Определение, примеры ЛНП, банаховы пространства. Норма линейного оператора, процедура ее поиска. Пространство линейных непрерывных (ограниченных) операторов, случай его полноты. Теорема о ближайшем элементе, разложение в прямую сумму подпростантсв; поиск сопряженного пространства.

Тема 6. Линейные функционалы

Линейные функционалы (основные понятия, примеры; сопряжённое пространство; теорема о продолжении). Более подробно: Основные теоремы функционального анализа: Хана – Банаха, Банаха – Штейнгауза и теорема Банаха об изоморфизме. Случай некоторых конкретных ЛНП, общий вид линейных непрерывных функционалов в них. Теория Рисса для линейных уравнений с компактным оператором.

Тема 7. Слабая сходимость в сопряжённом пространстве

Слабая сходимость в сопряжённом пространстве. Более подробно: Полнота сопряженного пространства. Общие свойства сопряженных пространств. Теорема отождествления и теорема замкнутости подпространств. Определения, примеры и признаки слабой сходимости последовательности элементов в ЛНП. Критерий Банаха – Штейнгауза. Признаки конечномерности ЛНП и компактности линейного оператора. Понятие, свойства и применение сопряженного оператора в проблеме разрешимости линейных уравнений.

Тема 8. Гильбертово пространство

Гильбертово пространство (основные понятия; задача о наилучшем приближении и теорема об ортогональном дополнении; общий вид линейного функционала). Более подробно: Признаки обратимости и понятие спектра компактного оператора. Определение, примеры и свойства самосопряженного оператора на Гильбертовом пространстве; свойства его спектра. Теорема Гильберта – Шмидта, применение.

Тема 9. Ортонормальные системы в гильбертовых пространствах

Ортонормальные системы в гильбертовых пространствах. Процесс ортогонализации. Полнота и замкнутость. Теорема о разложении в ряд Фурье. Изоморфизм гильбертовых пространств. Более подробно: Гильбертовы пространства, аксиоматика, примеры, ряды Фурье по ортонормальным системам (ОНС). Полные ОНС, их роль в получении классификации сепарабельных гильбертовых пространств. Биортогональные системы Чебышева, альтернатива Фредгольма.

Тема 10. Задачи вариационного исчисления

Постановка и примеры задач вариационного исчисления. Дифференцируемые функционалы. Необходимое условие экстремума. Простейшая задача вариационного исчисления.

Тема 11. Задача со свободными концами

Задача со свободными концами. Функционалы от вектор-функций. Принцип Гамильтона. Вариационный вывод уравнения колебаний. Исследование квадратичного функционала. Вторая вариация и условие экстремума.

Тема 12. Свойства выпуклых и поглощающих множеств векторных пространств

Свойства выпуклых и поглощающих множеств векторных пространств. Функционал Минковского и его свойства. Дальнейшие свойства линейных функционалов. Гиперплоскости и нестрогое отделение выпуклых множеств гиперплоскостями. Свойства компактов, являющихся выпуклыми множествами. Теорема строгой отделимости; частный случай конечномерных пространств.


Темы семинарских занятий.

1. Счётные и континуальные множества.
   
2. Метрические пространства. Свойства метрик.
   
3. Компактность.
   
4. Нормированные пространства. Линейные функционалы.
   
5. Гильбертово пространство.
   
6. Простейшая вариационная задача.
   
7. Заключительное занятие.
   

ЛИТЕРАТУРА

Основная:

1. А.Н.Колмогоров, С.В.Фомин. Элементы теории функций и функционального анализа. М: «Наука», любое издание.
   
2. Л.А.Люстерник, В.И.Соболев. Элементы функционального анализа. М: «Наука», 1965, 520с.
   
3. В.А.Треногин, Б.М.Писаревский, Т.С.Соболева. Задачи и упражнения по функциональному анализу. М: «Наука», 1984, 256с.
   

Дополнительная:

1. В.А.Садовничий. Теория операторов. М: изд.МГУ, 1979, 296с.
   
2. Л.В.Канторович, Г.П.Акилов. Функциональный анализ. М: «Наука», 1977, 744с.
   
3. К.Иосида. Функциональный анализ. М.: «Мир», 1967, 624с.
   
4. П.Халмош. Гильбертово пространство в задачах. М: «Мир», 1970, 352с.
   
5. А.А.Кириллов, А.Д.Гвишиани. Теоремы и задачи функционального анализа. М: «Наука», 1977, 384с.
   
6. СМБ – Функциональный анализ. – Под общей редакцией С.Г.Крейна, М: «Наука», 1977, 744с.
   
7. Н.Данфорд, Дж.Т.Шварц. Линейные операторы. Общая теория. М.: ИЛ, 1962
   
8. М.А.Красносельский и др. Интегральные операторы в пространствах суммируемых функций. М.: «Наука», 1966.
   
9. В.С.Владимиров. Математические задачи односкоростной теории переноса частиц. Труды МИАН СССР им.В.А.Стеклова, 1961, т.61.
   
10. М.А.Красносельский. Положительные решения операторных уравнений. М.: Физматлит, 1962.
    
11. Э.Хилле, Р.Филлипс. Функциональный анализ и полугруппы. М: «Мир», 1972, 744с.
    
12. Т.Като. Теория возмущений линейных операторов. М: «Мир», 1972, 552с.
    
13. Ю.С.Очан. Сборник задач и теорем по ТФДП. М.: «Просвещение», 1965.
    
14. Л.Д.Фадеев. О модели Фридрихса в теории возмущений непрерывного спектра.– Труды МИАН СССР им.В.А.Стеклова, 1964, т.73, сс.292-313.