Geum.ru

И. Г. Петровского рабочая программа

Вид материалаРабочая программа
Подобный материал:


Брянский государственный университет имени академика И.Г. Петровского




РАБОЧАЯ ПРОГРАММА




по курсу (дисциплине) математический анализ для студентов


физико - математического факультета 2 курса, специальности информационные технологии

3 семестр, 2009-2010 учебный год.


Общий объём учебного курса:3-ий семестр: лекций 52 часа, практических 52 часа.

Программу разработала Беднаж В.А.


Утверждаю:

Зав. кафедрой


______________________


«_____»_______________200__г.


Тема (раздел)

курса (кол-во

часов)

Лекции (кол-во часов)

Практические (кол-во часов)
Межпред-метные связи
Вынесено на самостоят.

работу
Формы контроля

за усвоением

темы

I. Функциональные последовательности и ряды

(11/13)


II. Ряды Фурье (6/8)


I I I.

Интегральное исчисление функций нескольких переменных

Кратные интегралы (11/12)


Криволинейные интегралы

(11/10)


Интегралы, зависящие от параметра

(13/9)
1. Функциональная последовательность, функциональный ряд, его область сходимости и сумма. Равномерная сходимость функциональных последовательностей и рядов. Достаточный признак равномерной и абсолютной сходимости функционального ряда (признак Вейерштрасса) (2 ч.)

2. Свойства равномерно сходящихся функциональных последовательностей и рядов. (3 ч.)

3. Степенной ряд. Теорема Абеля. Радиус и область сходимости степенного ряда. Свойства суммы степенного ряда. (3 ч.)

4. Ряд Тейлора. Разложение функции в степенной ряд. Необходимое и достаточное условие разложение функции в ряд Тейлора, достаточные условия разложения. Разложение в ряд Тейлора некоторых элементарных функций. (3 ч.)


5. Понятие ряда Фурье 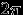-периодической функции и задача о разложении периодической функции в ряд Фурье. Ряд Фурье функции с произвольным периодом. Разложение в ряд Фурье четных и нечетных функций. ( 2 ч.)

6. Лемма Римана - Лебега Ядро Дирихле Теорема о представимости функции в точке своим рядом Фурье. (2 ч.)

7. Равномерная сходимость ряда Фурье.


8. Задача об объеме цилиндрического бруса. Определение и свойства двойного интеграла. Необходимое условие интегрируемости. Интегрируемость непрерывной функции. ( 4 ч.)

9. Вычисление двойного интеграла повторным интегрированием. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах. (3 ч.)

10. Задача о массе тела. Тройной интеграл: определение, условия существования, вычисление. ( 2ч.)

11. Геометрические и физические приложения кратных интегралов.


12. Задача о работе плоского силового поля. Определение, свойства и вычисление криволинейного интеграла второго рода. ( 3ч.)

13. Формула Грина-Остроградского. Вычисление площадей с помощью криволинейного интеграла. ( 3ч.)

14. Криволинейные интегралы, не зависящие от пути интегрирования. Нахождение функции по её полному дифференциалу. ( 3ч.)

15. Криволинейные интегралы первого рода: определение, вычисление, геометрические и физические приложения. ( 2ч.)


16. Собственные интегралы, зависящие от параметра, их интегрирование и дифференцирование. ( 3ч.)

17. Несобственные интегралы, зависящие от параметра. Равномерная сходимость, критерии Коши, Дирихле, Абеля. (3ч.)

18. Свойства, несобственных интегралов, зависящих от параметра. ( 2ч.)

19.Вычисление некоторых несобственных интегралов. (2ч.)

20. Эйлеровы интегралы. (3ч.)
1. Функциональные ряды. Область сходимости. (3 ч.)

2. Равномерная сходимость функциональных рядов. Признак Вейерштрасса. (2 ч.)

3.Степенные ряды: радиус, интервал и область сходимости. (3 ч.)

4. Интегрирование и дифференцирование рядов. Вычисление суммы ряда. (3 ч.)

5.Ряд Тейлора. Разложение функций в степенной ряд. Применение степенных рядов к приближенным вычислениям. (2 ч.)


6. Разложение функций в ряд Фурье. (3 ч.)

7. Разложение в ряд Фурье четных и нечетных функций. (3 ч.)


8 . Контрольная работа №1. (2 ч.)


9. Вычисление двойного интеграла по прямоугольным и произвольным областям. Двойной интеграл в полярных координатах. ( 4ч.)

10. Вычисление тройных интегралов. (3 ч.)

11. Геометрические приложения кратных интегралов. (3 ч.)

12. Лабораторная работа “Кратные интегралы”. (2 ч.)


13. Вычисление криволинейных интегралов второго рода. Формула Грина.(2ч.)

14. Интегралы, не зависящие от пути интегрирования.(2ч.)

15. Восстановление функции по ее полному дифференциалу. (2ч.)

16. Вычисление криволинейного интеграла 1-го рода.(2 ч.)

17.Контрольная работа №2. (2ч.)


18.Собственные интегралы, зависящие от параметра. Предельных переход под знаком интеграла, дифференцирование и интегрирование под знаком интеграла. (2ч.)

19. Несобственные интегралы, зависящие от параметра. Равномерная сходимость. (2ч.)

20. Несобственные интегралы, зависящие от параметра. Предельных переход под знаком интеграла, непрерывность несобственного интеграла. (2ч.)

21. Дифференцирование и интегрирование по параметру. (2ч.)

22. Эйлеровы интегралы. (1ч.)
Геометрическая прогрессия и ее сумма


Численные методы


Интеграль-ное исчисление функций одной пе-ременной

Геометрия: объемы и площади геометрических фигур

Физика: статика

Физика: работа силового поля


Д-во свойств двойного интеграла


Вычисление площади поверхности


Физические приложения кратных интегралов


“



Литература
  1. Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу. – М.: Высшая школа, 1999
  2. Фихтенгольц Г.М. Основы математического анализа. М.: Наука. Т.2-3. 1967.
  3. Кудрявцев Л.Д. Курс математического анализа. М.: Высшая школа. Т.1-2.1981.
  4. Берман Г.Н. Сборник задач по курсу математического анализа. - М.: Наука, 1980.
  5. Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). - М.: Высшая школа, 1983.
  6. Виленкин Н.Я и др. Задачник по курсу математического анализа. Ч. 2. - М.: Наука, 1971
  7. Виноградова И.А. и др. Задачи и упражнения по математическому анализу. – М.: МГУ, 1988.
  8. Демидович Б.П. Сборник задач и упражнений по математическому анализу. - М.: Наука, 1977
  9. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч.1-2. - М.: Наука, 1983.
  10. Зорич В.А. Математический анализ. Ч.1-2. – М.: Наука, 1981.
  11. Кудрявцев Л.Д. и др. Сборник задач по математическому анализу. Функции нескольких переменных. - СПб. 1994.
  12. Кудрявцев Л.Д. и др. Сборник задач по математическому анализу. Интегралы. Ряды. – М.: Наука , 1986.