О хозяйства материалы студенческой научной конференции (18 февраля 3 марта 2008г.) Махачкала 2008
| Вид материала | Документы |
- Работа студентов материалы 58-й научной студенческой конференции, 3780.58kb.
- Научно-исследовательская работа студентов: Материалы юбилейной 60-й научной студенческой, 4190.87kb.
- Материалы студенческой научной конференции 23 апреля 2008 г г. Екатеринбург, Россия, 1681.38kb.
- Программа XXX v III студенческой научной конференции Краснодар 2011, 5443.59kb.
- Актуальные социально-экономические и правовые аспекты устойчивого развития региона., 3483.41kb.
- Знание есть сила материалы 65 итоговой межвузовской научной студенческой конференции, 2615.55kb.
- Министерство культуры рсо–Алания, 724.4kb.
- Программа студенческой научной конференции за 2011 год воронеж, 696.04kb.
- Программа XXX v II студенческой научной конференции Краснодар 2010, 5432.78kb.
- Материалы международной научной конференции 11-12 ноября 2008 г. Тамбов 2009, 4576.13kb.
Список использованной литературы
- Информатика: Учебник.-3-е перераб. изд./ Под ред. Н.В.: Финансы и статистика, 2006.- 768с.
- Информатика для юристов и экономистов/Симонович С.В. и др. – СПб.: Питер, 2002.-688с.
Системы счисления
Шахманова З.М.,
студентка 1 курса 1 группы
факультета иностранных языков
Системой счисления называется совокупность правил для обозначения действительных чисел с помощью цифровых знаков. Для записи чисел в конкретных системах счисления используется некоторый конечный алфавит, состоящий из цифр а1, а2, а3, . . . ,аn. При этом каждой аi в записи числа ставится в соответствие определенный количественный эквивалент. Различают непозиционные и позиционные системы счисления.
Непозиционные системы счисления
В ней количественный эквивалент каждой цифры, входящей в запись данного числа, не зависит от места этой цифры в ряду других цифр. Пример: римская система счисления. Общим недостатком непозиционных систем является сложность представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр. В ЭВМ применяют только позиционные системы счисления, в которых количественный эквивалент каждой цифры алфавита зависит не только от вида этой цифры, но и от ее местоположения в записи числа.
Позиционные системы счисления
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число. Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления - это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание можно принять любое натуральное число- 2, 3, 4, 16 и т.д. Следовательно, возможно бесконечное множество позиционных систем.
В позиционной системе счисления любое вещественное число в развернутой форме может быть представлено в следующей форме:
Аq=a
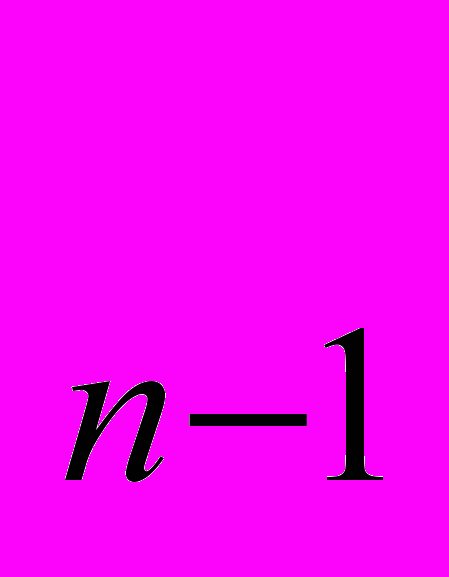 q
q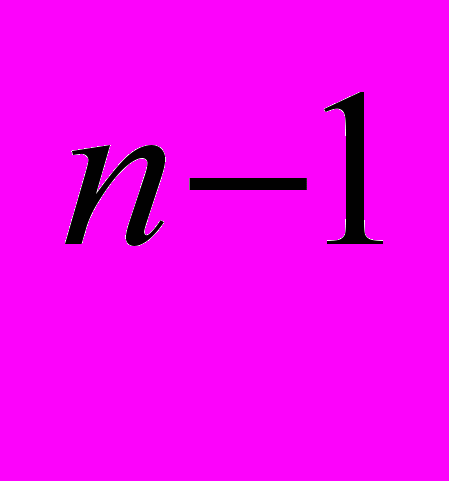 +a
+a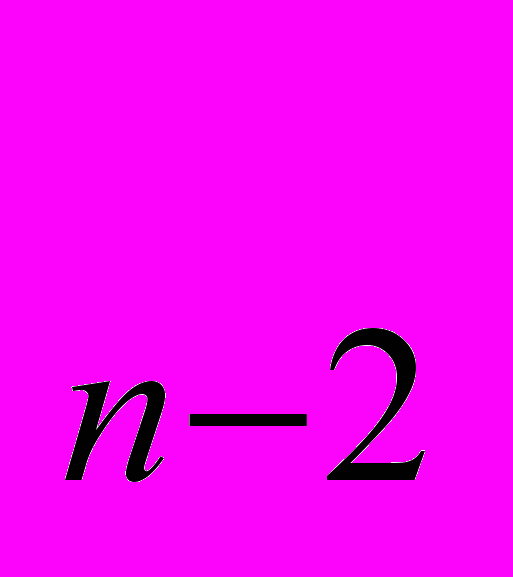 q
q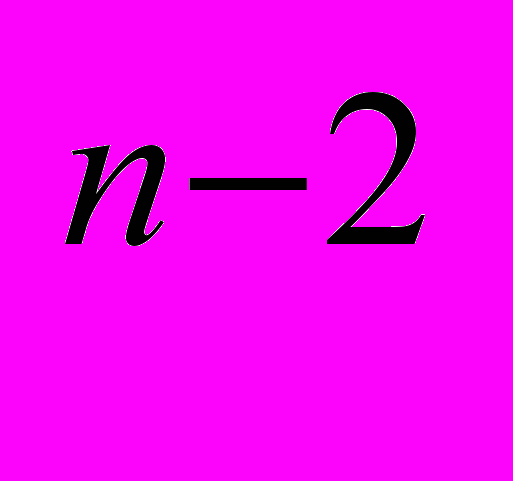 +…+a
+…+a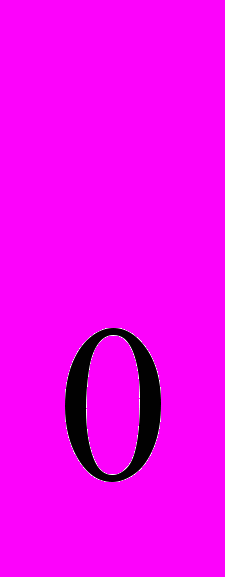 q
q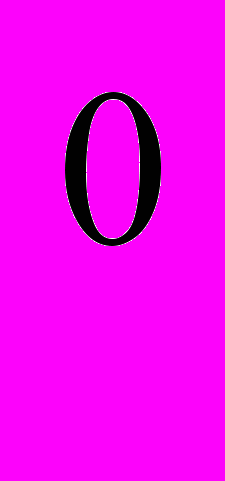 +a
+a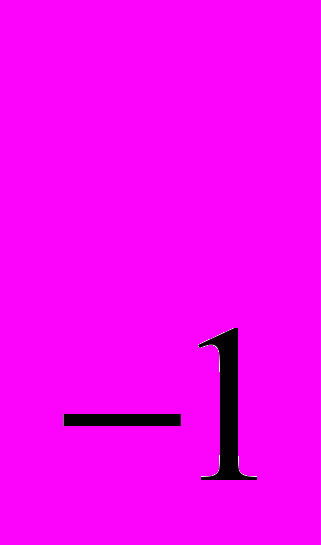 q
q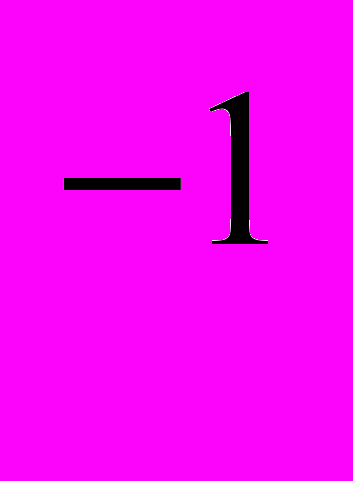 +…+a
+…+a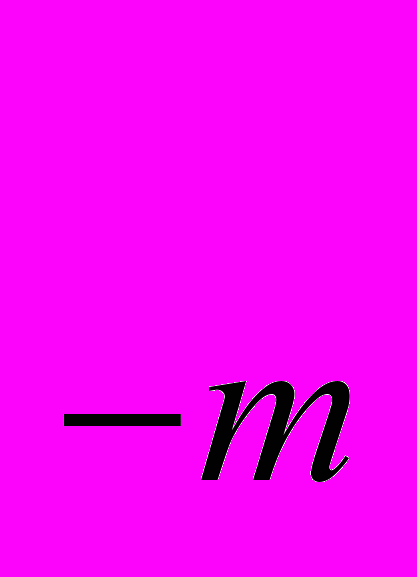 q
q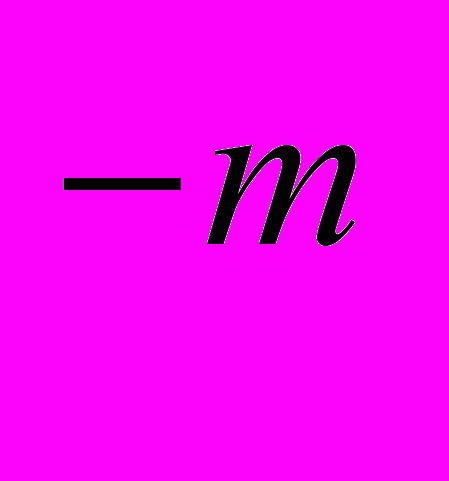 , где a само число, q основание системы счисления; a
, где a само число, q основание системы счисления; a - это цифры принадлежащие алфавиту данной системы счисления; n – число целых разрядов; m – число дробных разрядов числа.
- это цифры принадлежащие алфавиту данной системы счисления; n – число целых разрядов; m – число дробных разрядов числа.Пример 1: Десятеричная система счисления
А
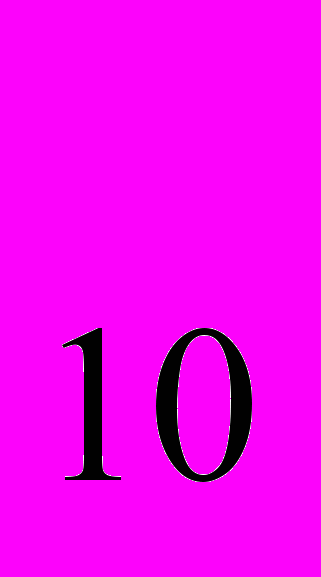 = 583; А
= 583; А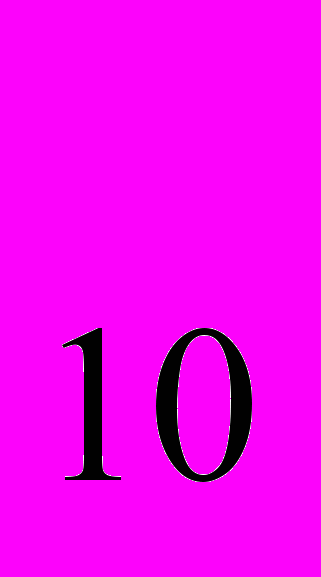 =5*10
=5*10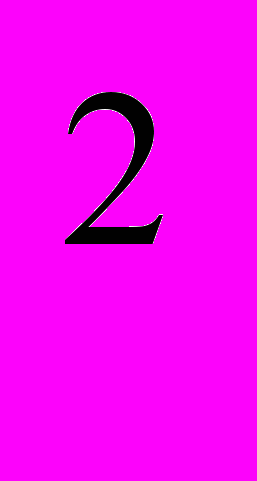 +8*10
+8*10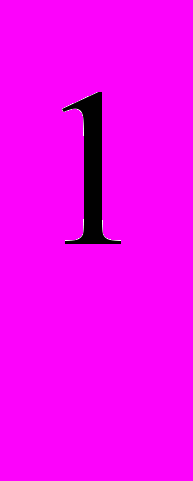 +3*10
+3*10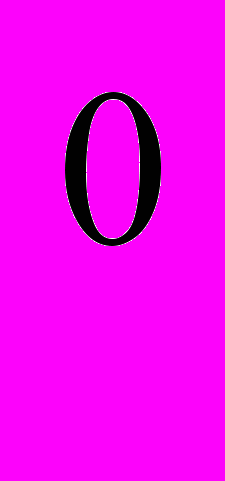 =5*100+8*10+3*1=500+80+3=583
=5*100+8*10+3*1=500+80+3=583А
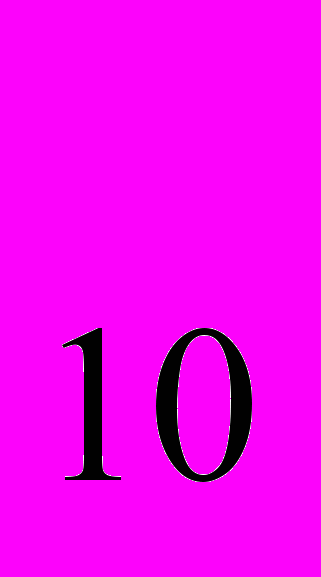 = 871; А
= 871; А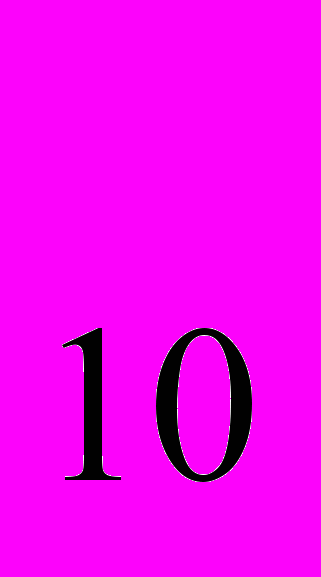 = 8*10
= 8*10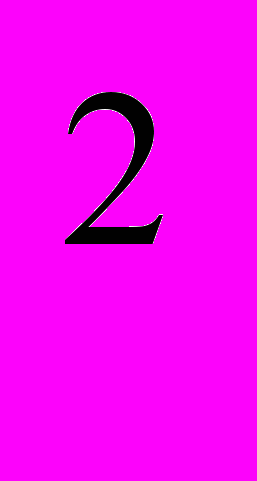 +7*10
+7*10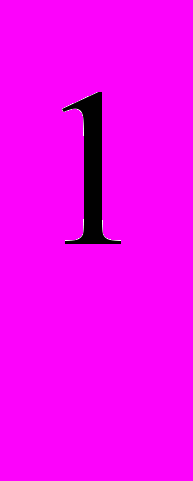 +1*10
+1*10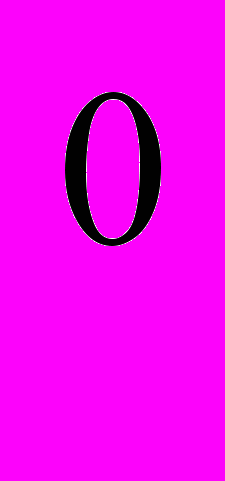 =8*100+7*10+1*1=800+70+1=871
=8*100+7*10+1*1=800+70+1=871Пример 2: Восьмеричная система счисления
С основанием q=8, алфавит составляют цифры от 0до 7.
А
 =7543.7; А
=7543.7; А =7*8
=7*8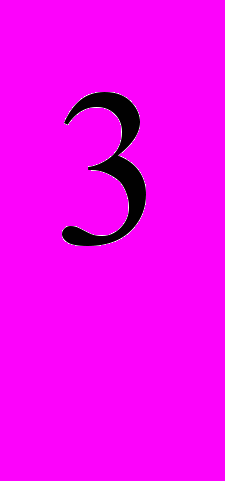 +5*8
+5*8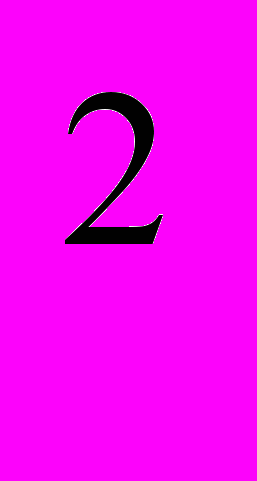 +4*8
+4*8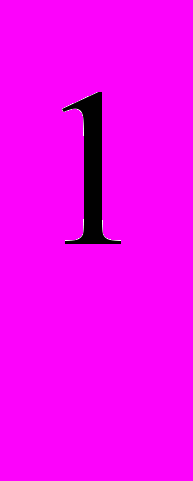 +3*8
+3*8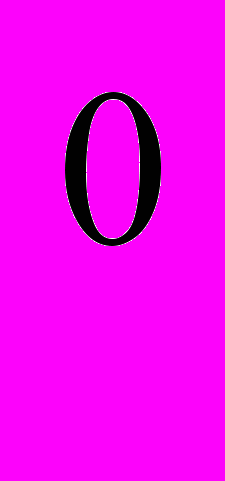 +7*8
+7*8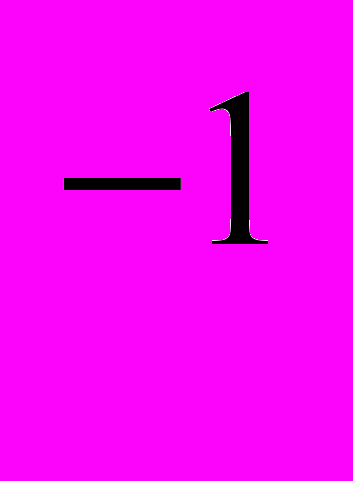 =7*512+5*64+4*8+3*1+7*1/8=3584+320+32+3+0.875=
=7*512+5*64+4*8+3*1+7*1/8=3584+320+32+3+0.875==3939.875
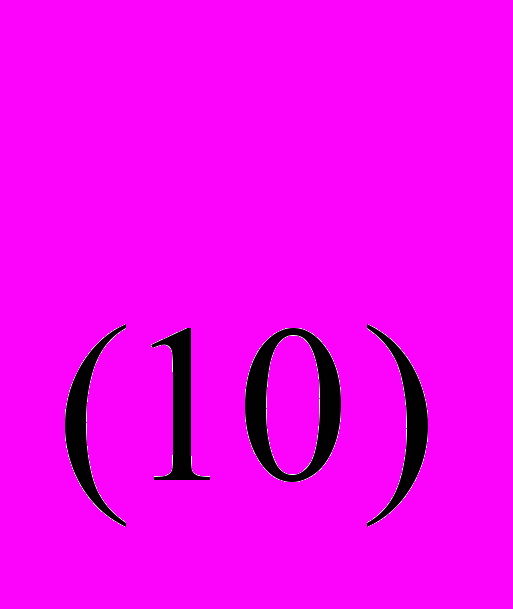
Пример 3: Двоичная система счисления
Двоичное число с основанием q=2, представляет собой цыпочку из 0и 1.
А
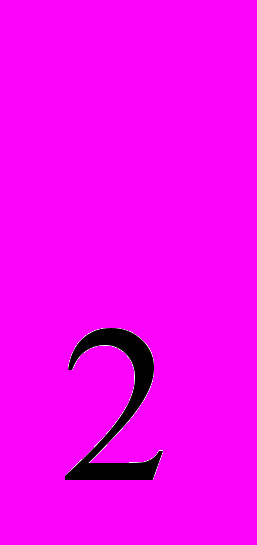 = 1101; А
= 1101; А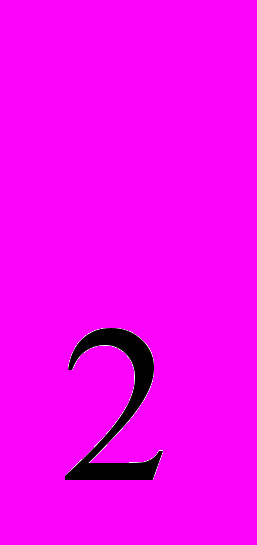 = 1*2
= 1*2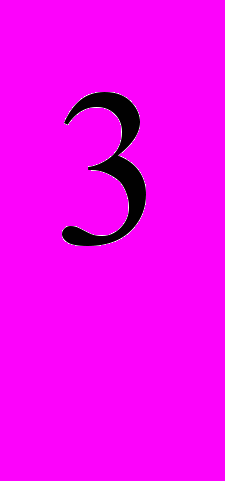 +1*2
+1*2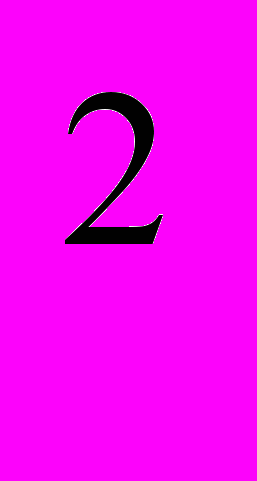 +0*2
+0*2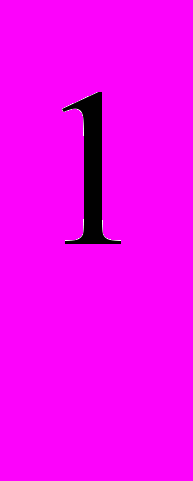 +1*2
+1*2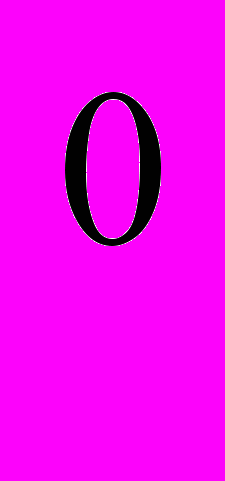 = 8+4+0+1=13
= 8+4+0+1=13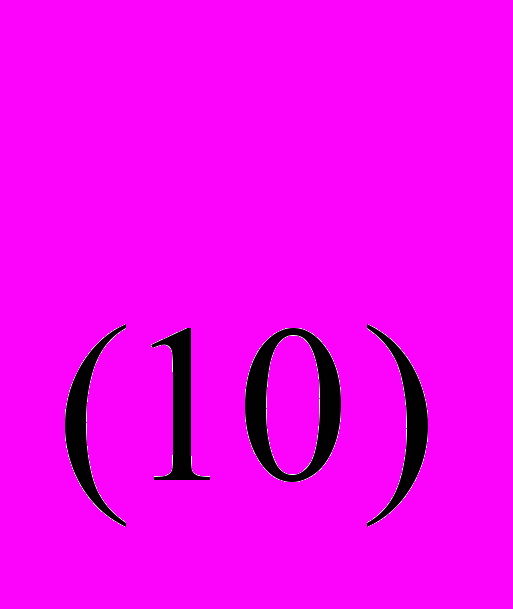 ;
;А
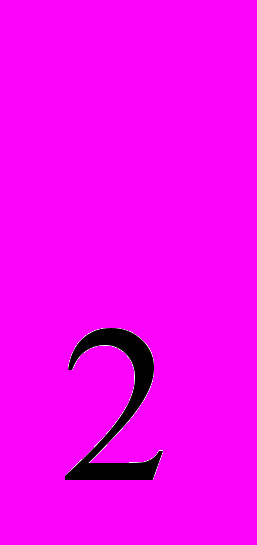 = 1001.1; А
= 1001.1; А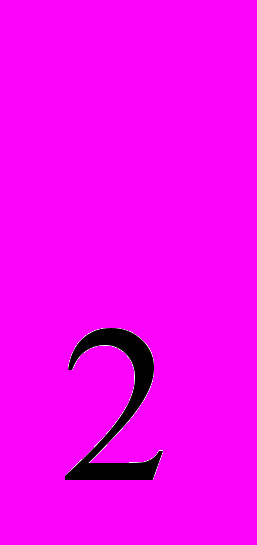 = 1*2
= 1*2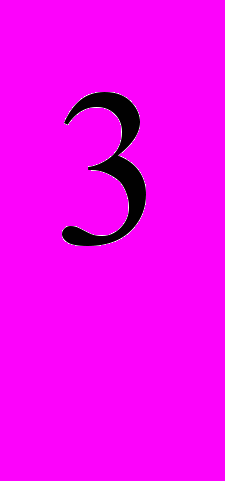 +0*2
+0*2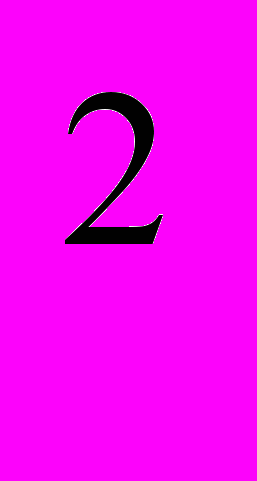 +0*2
+0*2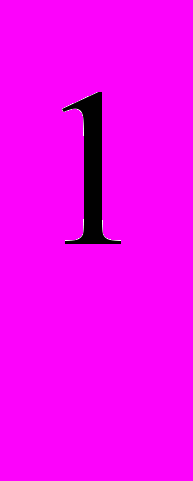 +1*2
+1*2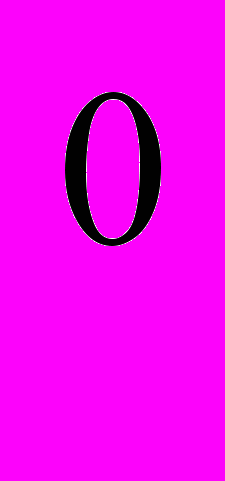 +1*2
+1*2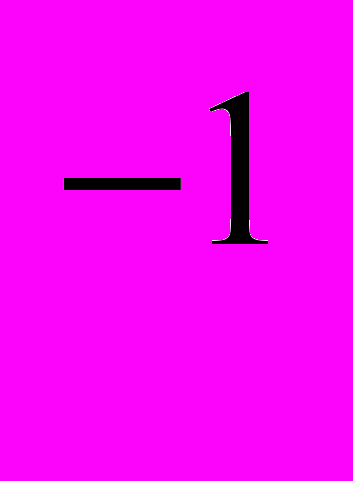 = 8+0+0+1+1/2=9.5
= 8+0+0+1+1/2=9.5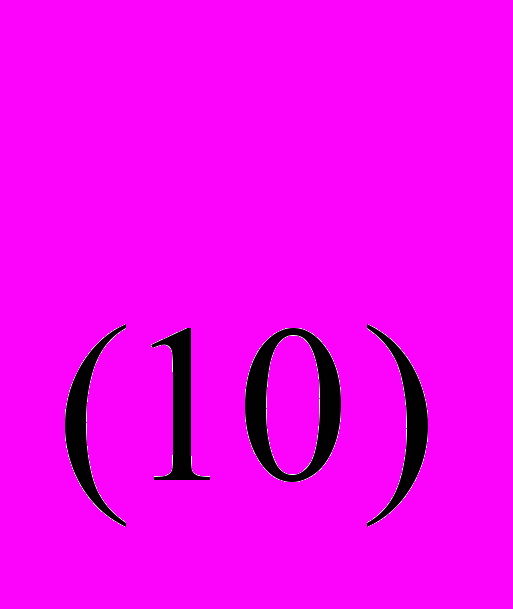
Десятичная система счисления
Пришла в Европу из Индии, где она появилась не позднее 6 века н.э. В этой системе 10 цифр: 0, 1, 2, 3,4, 5, 6, 7, 8, 9, но информацию несет не только цифры, но и место, на котором цифра стоит. В десятичной системе счисления особую роль играют число 10 и его степени: 10, 100, 1000 и т.д. Самая правая цифра числа показывает число единиц, вторая справа-число десятков, следующая-число сотен и т.д. Позиции цифр в записи числа называют его разрядами. В десятичной системе счисления вес каждого разряда в 10 раз больше веса предыдущего. Всякое число в десятичной системе счисления можно представить в виде суммы различных целых степеней десяти с соответствующими коэффициентами ai (0-9), взятыми из алфавита данной системы счисления.
Двоичная система счисления
В этой системе всего две цифры – 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т. д. Самая правая цифра числа показывает число единиц, следующая цифра – число двоек , следующая- число четверок и т.д. Двоичная система счисления позволяет закодировать любое натуральное число – представить его в виде последовательности нулей и единиц. В двоичном виде можно представить не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически. Наиболее простыми с точки зрения технической реализации являются двухпозиционные элементы, например, электромагнитное реле, транзисторный ключ.
Восьмеричная система счисления
В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. цифра 1, указанная в самом младшем разряде, означает - как и в десятичном числе – просто единицу. Та же цифра 1 в следующем разряде означает 8 , в следующем 64 и т. д. Число 100(восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему , например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться , что для перевода многозначного двоичного числа в восьмеричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.
Шестнадцатеричная система счисления
Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означает просто единицу. Та же цифра 1 в следующем -16 (десятичное), в следующем – 256 (десятичное) и т. д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.
С основанием q=16, алфавит составляет цифры от0до 9 и буквы из латинского алфавита.
0 1 2 3 4 5 6 7 8 9 A B C D E F
10 11 12 13 14 15
Переведем число из шестнадцатеричной системы счисления в десятеричную систему.
А
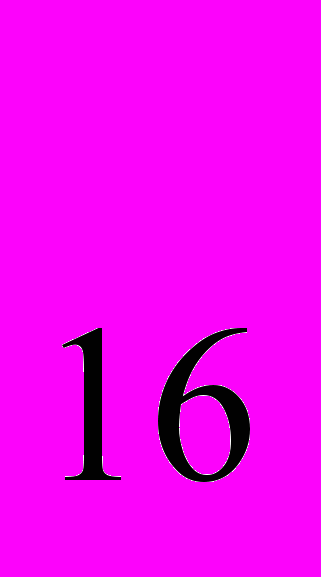 = 1А; А
= 1А; А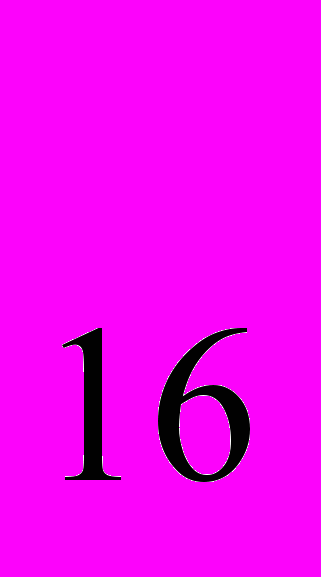 =1*16
=1*16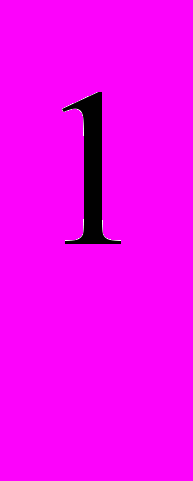 +А*16
+А*16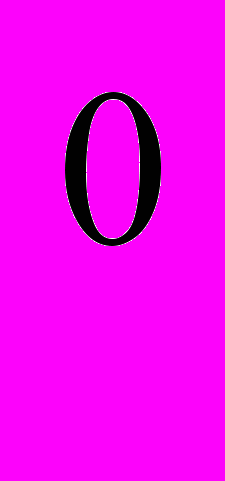 = 1*16+10*1=26
= 1*16+10*1=26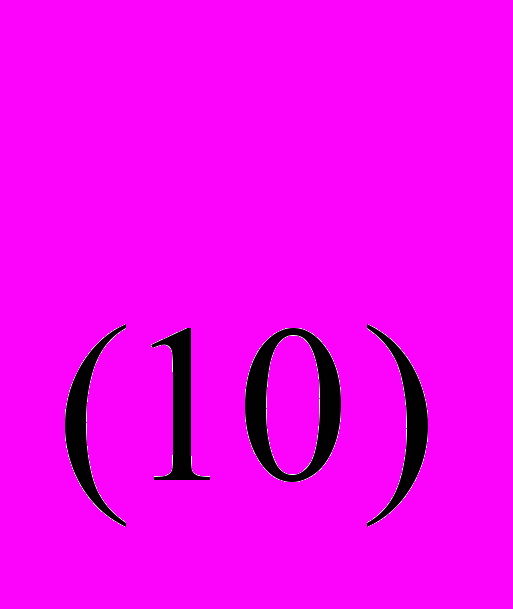 ;
;Перевод целых чисел
Для перевода целых чисел из одной системы счисления с основанием S в другую с основанием S1 надо это число последовательно делить на основание S1 новой системы счисления до тех пор, пока не получится частное меньше S1. Число в новой системе запишется в виде остатков деления, начиная с последнего. Это последнее частное дает цифру старшего разряда в новой системе счисления. Деление выполняют в исходной системе счисления.
Пример 1: Переведем число из десятеричной системы в восьмеричную систему счисления.
138
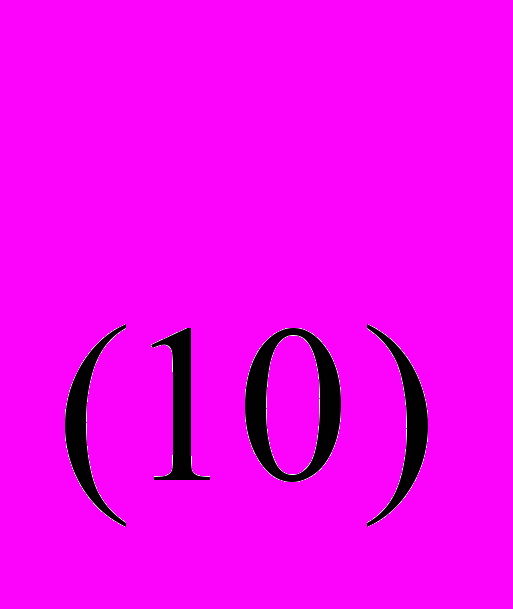 =Х
=Х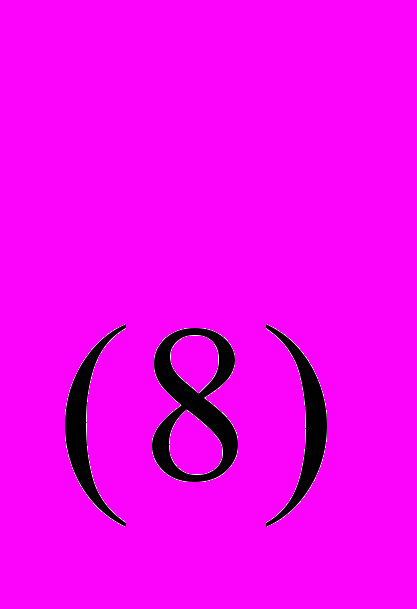
138├
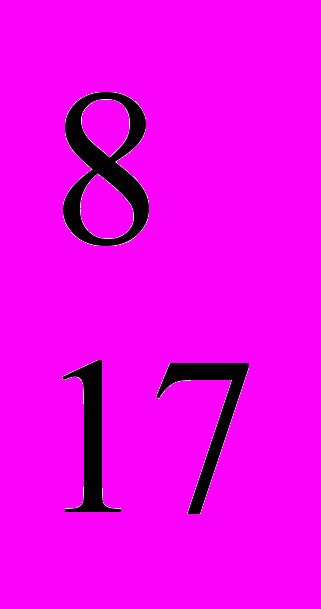
1
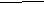 36
362 17├
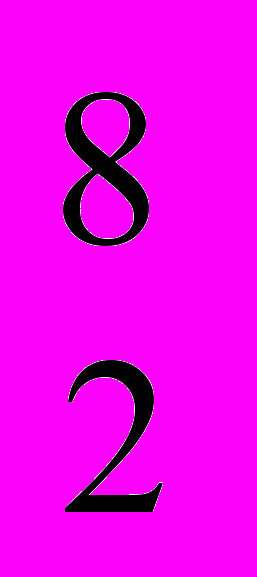
 16 Х=212
16 Х=2121
Пример 2: переведем число из десятичной системы в шестнадцатеричную систему счисления.
173
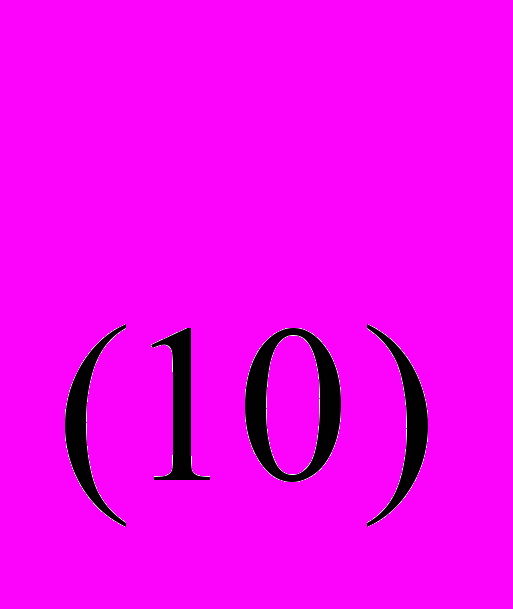 =Х
=Х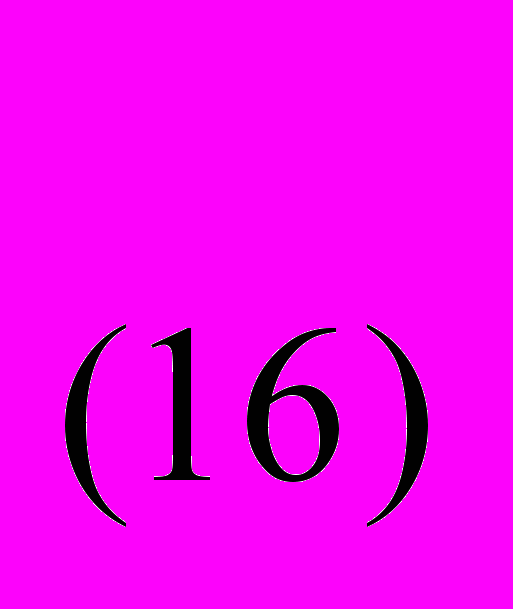
173├
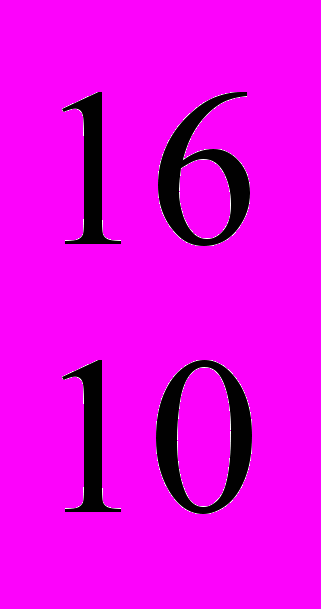
1
 60 10-A, 13-D → Х=AD
60 10-A, 13-D → Х=AD13
Список использованной литературы
1. Информатика: Учебник.-3-е перераб.изд./ Под ред. Н.В. Макаровой.-И74 М.: Финансы и статистика, 2006.-768 с.
2. Информатика для юристов и экономистов/Симонович С.В.и др.- СПб.:Питер,2002.- 688 с.
3. Атагишиева Г.С., Абдеева А.Т. Лабораторный практикум по информатике. Махачкала.: Изд-во “Деловой мир”,2006. - 180 с.
Кафедра «Теория и практика перевода»
ОБЩАЯ ХАРАКТЕРИСТИКА ГРАММАТИЧЕСКОГО СТРОЯ
АНГЛИЙСКОГО ЯЗЫКА
Акагаджиев Т.М.
студент 3 курса 2 группы
факультета иностранных языков
О понятии строя языка
Каждый язык представляет собой систему, т.е. функционально обусловленную, структурно организованную совокупность элементов двух планов: выражения (фонетические для устной разновидности языка, графические для письменной), и содержания (лексические и грамматические). Соответственно в единой системе языка взаимодействуют 3 подсистемы: фонетическая, лексическая и грамматическая.
Элементами языковых систем служат не сами звуки, предметы, явления, а формированные на их субстантной базе языковые единицы.
Система и строй каждого языка специфичны, они присущи только ему и формируются в ходе его исторической эволюции. Случаи совпадения системы и строя у 2 языков имеют место лишь тогда, когда в силу социально-исторических причин складываются 2 этнических общества провозгласивших самостоятельность своих языковых систем, несмотря на отсутствие или слабость собственной языковой дивергенции.
Грамматический строй
В грамматической подсистеме языка следует различать 2 области: грамматику слова и грамматику предложения. Первую нередко отождествляют с морфологией, вторую – с синтаксисом. Но морфология есть лингвистическая дисциплина, в центре которой стоят взаимоотношения морфемы и слова, а отношения эти принадлежат не только грамматической подсистеме, включающей в себя словоизменительную морфологию, но и лексической, куда входят морфология словообразования. Таким образом, к грамматике слова относится лишь одно из ветвей морфологии. Не тождественна синтаксису и грамматика предложения.
В современной лингвистике утвердилось расщепленное понятие предложения в традиционном грамматическом смысле на два понятия: предложения как высшей грамматической единицы, обеспечивающий стандартное представление любого события и высказывания как мельчайшей, элементарной единицы коммуникации.
В языкознании нередко приходится встречаться с утверждением, что существо различия между лексическим и грамматическим является особенным, специальным, ограниченным, а грамматическое общим, продуктивным, «живым».
Таким образом, получается как будто, что склонение местоимений «я», «ты» и др., а может быть и склонения существительных вроде, «лев» («льва»), день (дня), сосед (соседи), а не соседы и пр., относится не к грамматике, а к лексике. Это уже само по себе представляется странным, т.к. и здесь мы имеем дело с таким же по существу явлением как и при склонении существительных вроде «тигр», «вол», «стол» и пр: в общих случаях мы находим те же самые дополнительные значения (падежные и числовые) сопровождающие различия между отдельными образованиями и выступают и там и здесь как различия между формами в пределах того или другого слова. Кроме того, например, в таком языке как русский, очень трудно отделить «более или менее живые» способы образования форм от способов иного характера: ср. «Вода-воду-водой» и т.п. является ли изменение ударения здесь «более или менее живым?».
Как известно в грамматике мы имеем дело с отвлечением от какой бы то ни было конкретности слова на первый взгляд может показаться, что эта особенность грамматики действительно исключает возможность отношения к грамматической сфере таких частных случаев склонения, как склонение ряда местоимений в русском языке и т.п. Положение относительно отвлеченного и обобщающего характера грамматики нельзя понимать в плане простого механического отделения общих (general), «более или менее живых» фактов специальных (special) частных «неживых». Даже в таком крайне специальном частном совершенно исключительном факте, как соотношение «я» - «меня», есть нечто грамматически общее. Соотношение двух грамматических форм одного и того же слова.
И даже конкретизация этих форм как форм Именительного падежа единственного числа и Родительного падежа того же числа сама по себе еще позволяет видеть в данном слове лишь «слова вообще» поскольку рассматривается внутренние взаимоотношения и различия между этими формами, а не то, как они характеризуют данное слово в целом. Но коль те же формы скоро выступают уже как характерное данное слово в качестве слова субстантивного, они уже выполняют и лексическую функцию, и мы имеем дело с фактом лексико-грамматическим.
Лексико-грамматическим является конечно, и само специфическое образование данных форм: суффиксы «-(-)» и «-а» («-я») и использование супплетивной пары корней – «я» - «меня», но поскольку мы отвлекаемся от конкретности данных суффиксов и данной супплетивной пары и от того, что с их помощью образованны формы именно местоимения 1-го лица ед.ч., т.е. определенного конкретного слова, поскольку мы и в этом совершенно особом случае вскрываем некоторый способ образования грамматических форм, т.е. вскрываем собственно грамматический момент. Именно в таком смысле следует понимать отвлеченность грамматики в области формообразования, т.е. изменения слов от всякой конкретности.
Принципы выделения грамматических категорий
Прежде всего, необходимо обратить внимание на то, что всякая грамматическая форма слова входит в какую-нибудь грамматическую категорию или, иначе говоря, представляет собой какую-либо грамматическую категорию. Такие величины, как «первое лицо» или «настоящее время» - и т.п. которые в чистом виде т.е. в отвлечении от других категорий, представляют собой отдельные грамматические категории в тех или других грамматических формах, а следовательно и в определенных конкретных словоформах могут быть названы категориальными формами.
Следует отметить что:
- Всякая грамматическая категория обязательно должно быть представлена по меньшей мере двумя категориальными формами: иначе она не может существовать так как она есть общее в отдельным.
- Никакая категориальная форма не может охватывать слово в целом, т.е. быть представленной словоформами данного слова.
- В одной и той же словоформе могут соединяться различные грамматические категории (напр. лицо, число и пр.).
Сравним, например, английское (he) takes «берет» совмещающее в себе (3-е) лицо (ед.) число, (настоящее) время (действительный) залог, (общий) вид, (изъявительное) наклонение и пр.
Ни в какой словоформе не могут соединяться одновременно 2 категориальные формы 1 и той же категории, т.е. не может быть одновременно формы 2 падежей, 2 чисел и пр.
Каждая словесная грамматическая форма представляет собой обязательно, по крайней мере, хотя бы одну категориальную форму, а следовательно принадлежат к какой-нибудь грамматической категории: словесных грамматических форм, стоящих вне грамматической категории не бывает. Так, если «reading» (читающий) не выделяется в качестве самостоятельной части речи, а стоит на положении формы слова-глагола read – читать, то должна обязательно существовать какая-либо категория, которая конструируется на основе противопоставления этой формы глагола read всем прочим его формам.
Отличительные особенности грамматического строя английского языка сравнительно с русским
Основное отличие грамматического строя английского языка от строя русского языка лежит в способах выражения связи слов в предложении. Например, в русском предложении «мой брат подождет вас» функция слова «брат» в форме именительного падежа; связь слова «подождет» как сказуемого с подлежащим «брат» выражена формой лица и числа (3-е лицо; ед. ч.); слово «мой» оформлено как определение при слове «брат» тем, что согласуется с ним вроде, числе и падеже; наконец слово «вас» оформлено как прямое дополнение при глаголе тем, что стоит в форме В.п. Такого рода грамматический строй, при котором связи слов в предложении выражаются главным образом формами слов, т.е. при помощи изменения самих слов называется синтетическим строем.
В соответствующем английском предложении «My brother will wait for you», напротив ни одно из входящих в предложение слов не указывает своей собственной формой, с какими словами оно связано в строе данного предложения. Связь слова «my» со словом brother выражена тем, что оно стоит на фиксированном месте – перед определяемым существительным; связь между словами brother как подлежащим и will wait как сказуемым выражена их взаимным местоположением: подлежащее непосредственно предшествует сказуемому: наконец, зависимость слова you как дополнения от глагола will wait выражена, во-первых, его постановкой после данного глагола и во-вторых наличии перед ним служебного слова – предлога for. Такого рода грамматический строй, при котором связи слов в предложении выражаются, главным образом, не формами слов, а при помощи порядка слов и служебных слов, называется аналитическим строем.
Следует иметь в виду, что сказуемое относится именно к способам выражения связи слов в предложении. Те синтетические формы, которые сами по себе не выражают связей в предложении (например, число у существительных), прочно удерживаются (например) в английском языке.
Список использованной литературы
1. Бархударов Л.С., Штеллинг Д.А. Грамматический строй английского языка. – М., 2002.
2. Смирницкий А.И. Морфология английского языка. – М., 2001.
3. Плоткин В.А. Грамматика английского языка. – М., 1998.
