Непрерывность справа, слева

Вид материала

Лекция

Содержание Опр. Если существуют конечные пределы Доказательство критерия Х. Обратное неверно. Теорема ( Кантор). Всякая непрерывная на [a,b] функция f равномерно непрерывна на [a,b].

Подобный материал:

• Константин Стешик, 261.91kb.
• E-mails: lunik8@mail, 263.71kb.
• Календарный план учебных занятий по дисциплине математический анализ Индекс специальности, 165.93kb.
• В. С. Высоцкого. Сопоставительный анализ стихотворений «Бесы» А. С. Пушкина и «Слева, 69.07kb.
• Декорация: Слева лес, избушка, около избы бочка, лопата, ведра, справа домик Красной, 61.69kb.
• Декорация: Слева лес, избушка, около избы бочка, лопата, ведра, справа домик Красной, 51kb.
• Моу : сош д. Шапша, 2007уч год, 44.2kb.
• Декорация: слева лес, избушка, около избы бочка, лопата, ведра, справа домик Красной, 101.89kb.
• Тема 3 Непрерывные функции. Точки разрыва функции. Теоретические вопросы, 130.27kb.
• Если верить в чудеса, то сбываются мечты Имена на небесах слева я а справа ты… Парижские, 559.1kb.

Лекция 11

§5 Непрерывные функции

1. Непрерывность в точке и на множестве
   

f определена на XU(x₀). Эта функция называется непрерывной в точке, если

f(x)=f(x₀)

Определение непрерывности в точке по Коши

>0>0x X,|x-x₀|<: |f(x)-f(x₀)|<.

Определение непрерывности в точке по Гейне

x_n,{x_n}x₀, {x_n} из области определения: f(x_n)=f(x₀)

Непрерывность справа, слева.

Непрерывность на [a,b]

Непрерывность на множестве.

2. Простейшие свойства непрерывных функций
   
   1. Сумма, разность и произведение двух непрерывных функций в точке. Следствие: Тоже на множестве.
      
   2. Сохранение знака непрерывной функции: f(x₀)>0U(x₀):f(x)>f(x₀)/2.
      
   3. f непрерывна в точке x₀, g в x₀, g(x₀)0f/g непрерывна в x₀.
      
   4. |f| непрерывна, если непрерывна f.
      
   5. Суперпозиция непрерывных функций есть непрерывная функция
      

f определена в окрестности x₀ и непрерывна x₀,

g определена в окрестности t₀ и непрерывна t₀, g(t₀)=x₀. Тогда в некоторой окрестности тоски t₀ определена суперпозиция F(t)=f(g(t)) и непрерывна в т. t_0.

Классификация точек разрыва

Если f не является непрерывной в точке x₀, то x₀ – точка разрыва. В дальнейшем будет предлагать, что f определена в некоторой окрестности x₀ ( быть может односторонней).

Опр. Если существуют конечные пределы

f(x₀-0)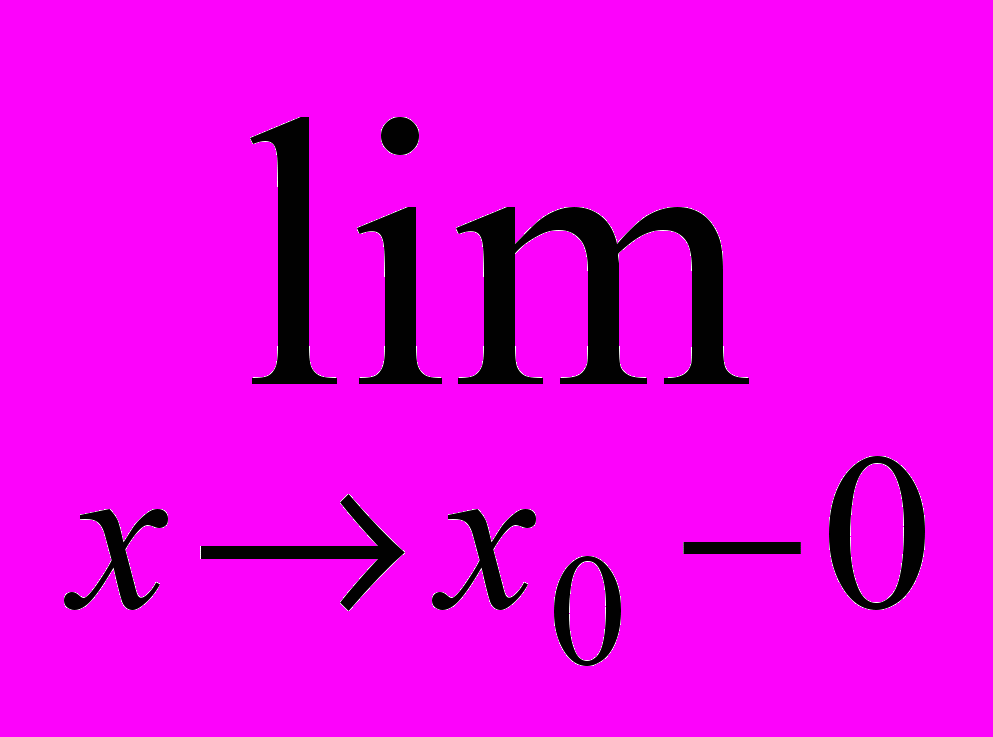f(x) и f(x₀+0)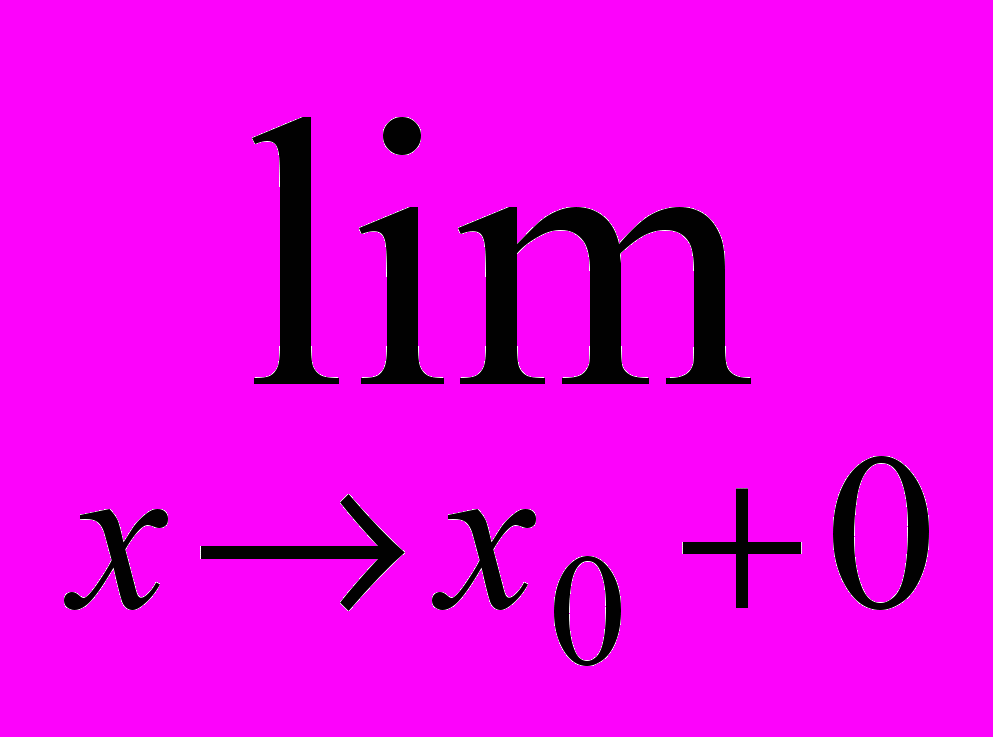f(x)

и f разрывна в точке x₀, то такой разрыв называется разрывом первого рода. Если при этом f(x₀-0)=f(x₀+0), То разрыв называется устранимым.

Разрыв не первого рода называется разрывом второго года.

Аналогично классифицируются разрывы для функции, определенной в полуокрестности точки.

Например, функция определена на [a,b]. Дать определение в точке a.

3. Ограниченность непрерывной функции. Теоремы Вейерштрасса.
   

Лемма. Если {x_n}[a,b] и 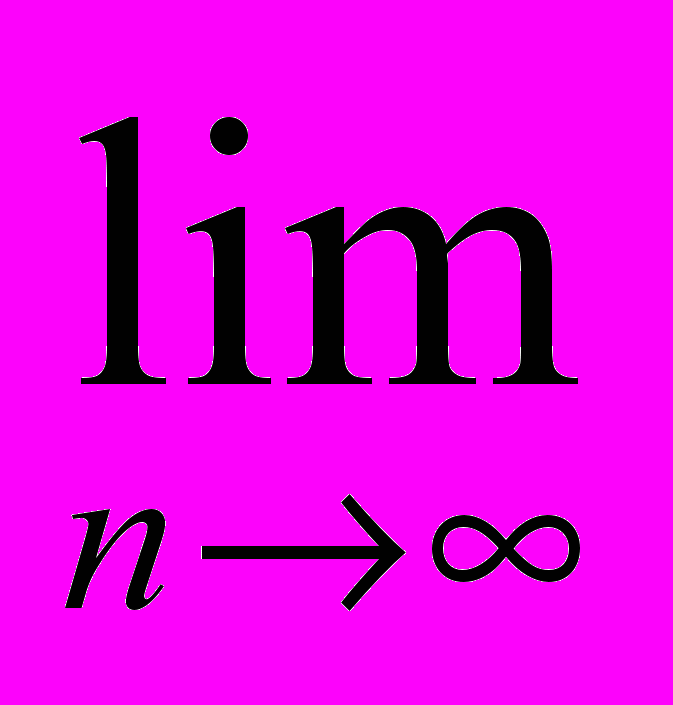x_n=x₀, то x₀[a,b].

Доказательство. Теорема о переходе к пределу в неравенствах.

Теорема 1(Первая теорема Вейерштрасса). Непрерывная на [a,b] функция f ограничена на [a,b].

Доказательство. Ограниченность: Mx[a,b]:|f(x)|M. Отрицание Mx[a,b]:|f(x)|>M. В частности, nx_n[a,b]:|f(x_n)|>n. Пусть {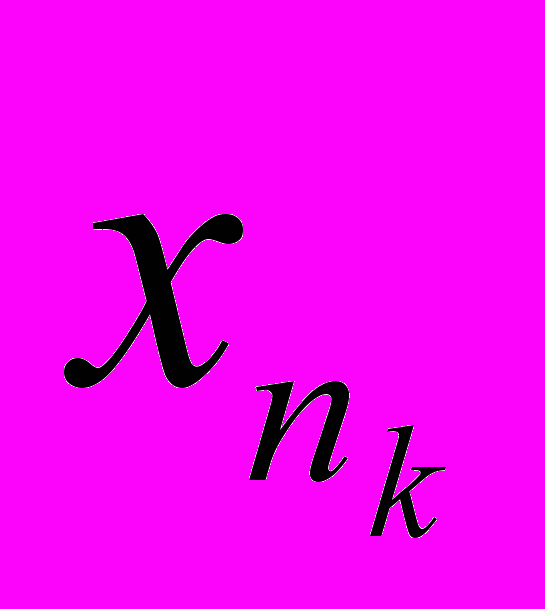}x₀, x₀[a,b]. Тогда, с одной стороны |f(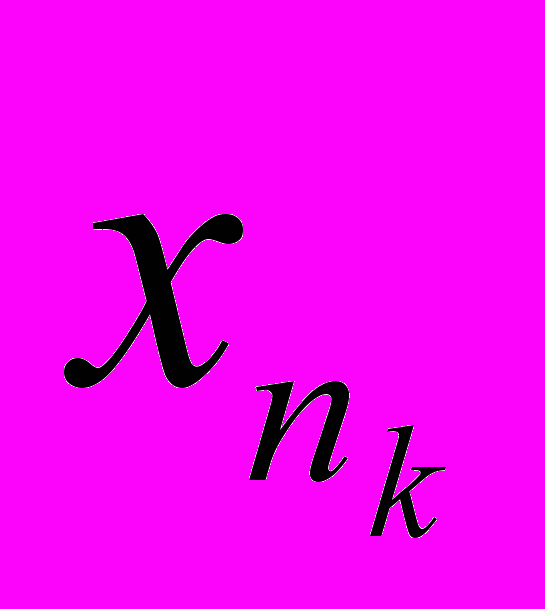)|>n_k, с другой стороны f(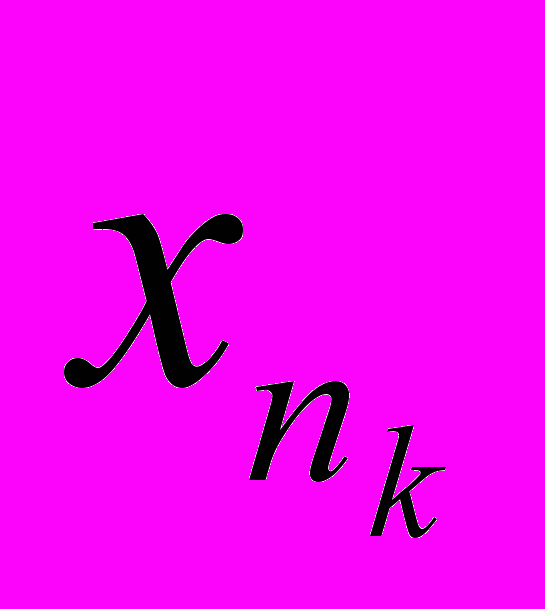)f(x₀).

Теорема 2. Непрерывная на [a,b] функция f(x) достигает своих точных верхней и точной нижней граней.

Доказательство. M= 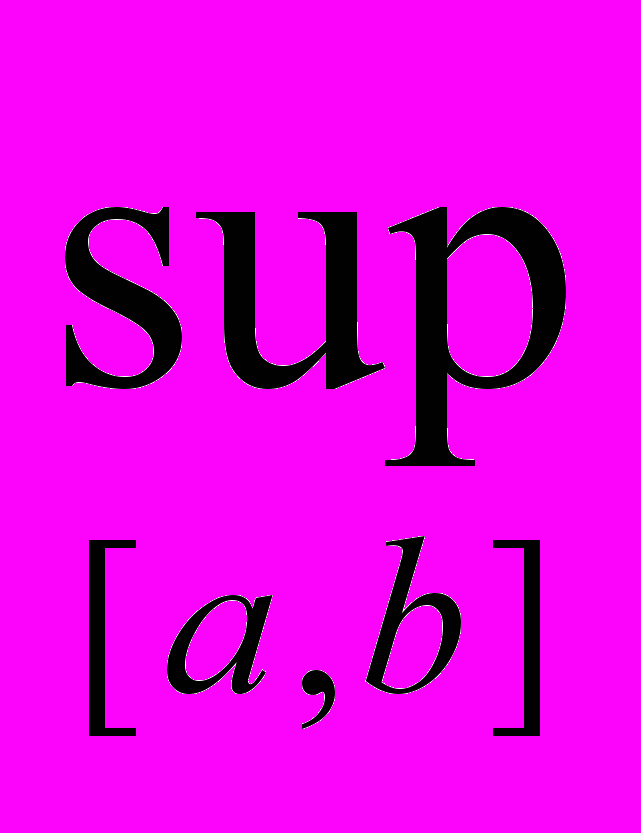f(x), nx_n:M-1/n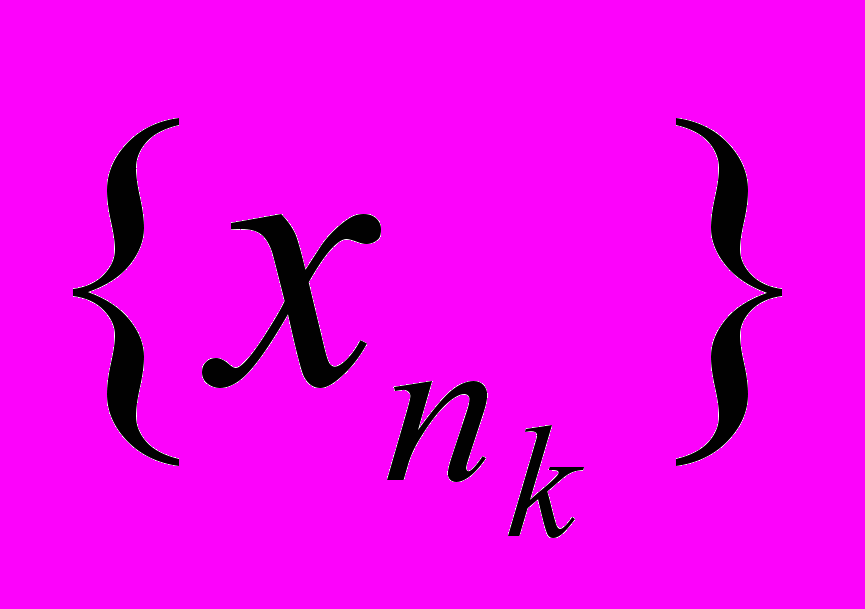_n)M. Пусть x₀, x₀[a,b], M-1/n)Mf(x₀)=M.

4. Теорема о промежуточных значениях непрерывной функции.
   

Теорема. Если непрерывная на [a,b] функция f(x) принимает на концах промежутка значения разных знаков, то c(a,b):f(c)=0.

Доказательство. Пусть A=f(a)0, B=f(b)0. Последовательное деление отрезка пополам так, что f(a_n)0f(b_n). Тогда

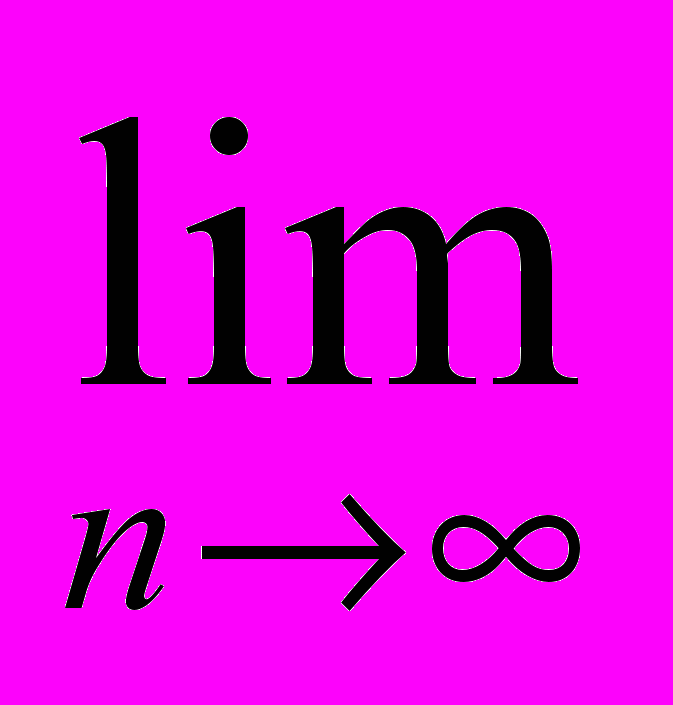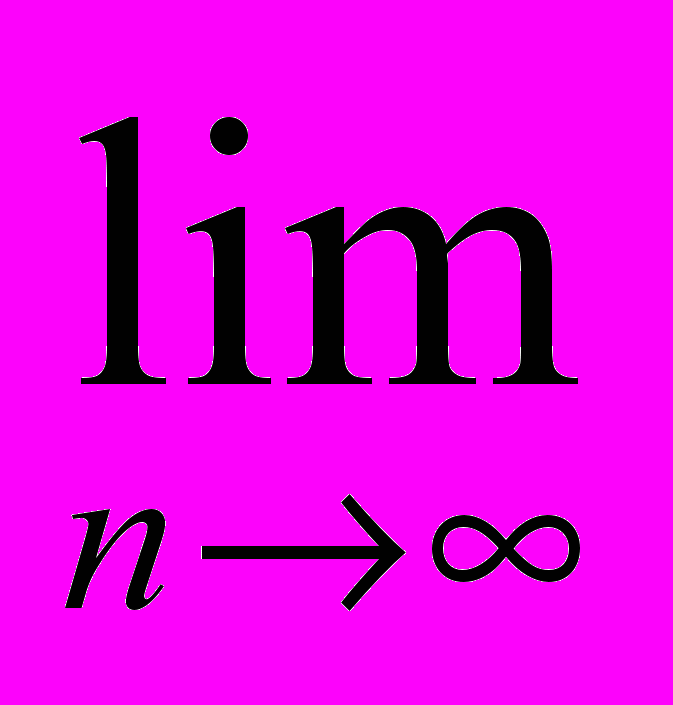a_ncb_n, b_n-a_n0a_n=c=b_n,

f(a_n)0f(b_n)f(c)0f(c)

Следствие 1. f непрерывна на [a,b], f(a)f(b). Тогда для M из промежутка f(a),f(b) c[a,b]:f(c)=M

Доказательство: A=f(a)

Следствие 2. f непрерывна на [a,b], m=inf f(x), M = sup f(x), тогда множеством значений этой функции будет отрезок [m,M].

5. Критерий непрерывности монотонной функции.
   

Теорема. Для того, чтобы монотонная функция f определенная на [a,b] была непрерывна на [a,b] необходимо и достаточно, чтобы множество значений f заполняло целиком отрезок с концами f(a),f(b).

Доказательство.

Лемма. Для монотонно возрастающей на данном отрезке функции существуют: 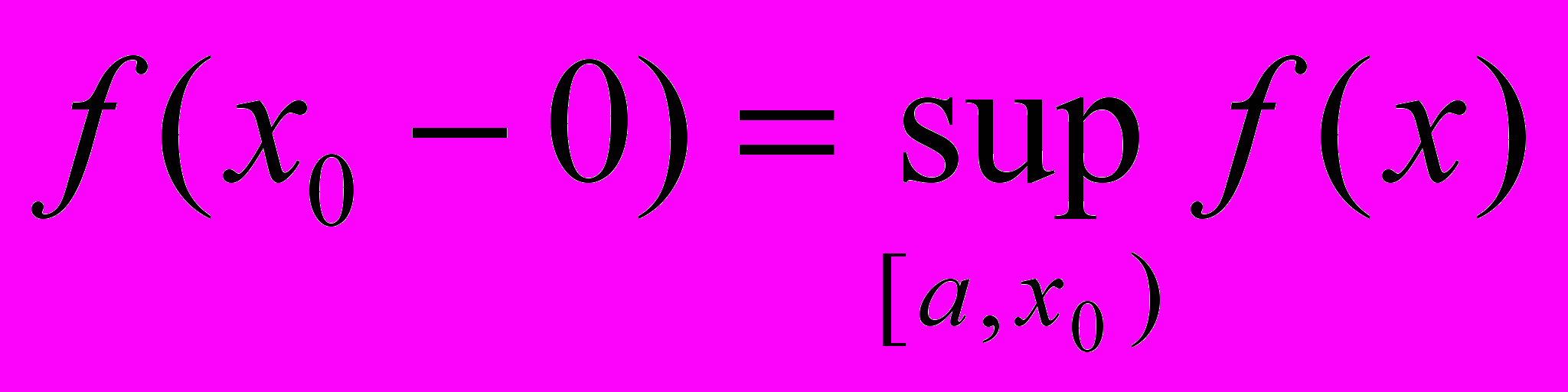для x₀(a,b], и

для x₀[a,b).

Доказательство леммы. Положим для некоторого x₀(a,b], A=, тогда для x[a,x₀):f(x)A и для >0x[a,x₀):A-Следовательно, для x(x,x₀):A-. Таким образом, первое равенство доказано.

Аналогично для предела справа. Для монотонно убывающей функции справедливо похожее утверждение.

Следствие 1. Монотонно убывающая на [a,b] функция имеет конечные односторонние пределы.

Следствие 2. Монотонно убывающая (возрастающая) на [a,b] функция может иметь там лишь разрывы первого рода.

Доказательство критерия. Необходимость уже была доказана ранее ( пункт 4, следствие 2).

Достаточность. Предположим противное. В точке x₀ имеется разрыв. Например, f(x₀)₀+0). По лемме f(x₀+0)=. Имеем f(x)f(x₀) при xx₀, f(x₀) < f(x₀+0)  f(x) при x>x₀. Таким образом, значения между f(x₀), f(x₀+0) не достигаются.

Аналогично проводится доказательство в случае существования разрыва слева.

Замечание. Для монотонно убывающей функции доказательство проводится заменой f на –f.

6. Непрерывность обратной функции.
   

Определение. Пусть f(x) определена на X, Y – множество ее значений. Предположим, что различным значениям x₁ и x₂ соответствуют различные значения y₁ =f(x₁), y₂=f(x₂). Тогда для любого y Y !xX:y=f(x), такое соответствие yx называется обратной функцией и обозначается x=f^-1(y).

Теорема ( существование обратной функции у монотонной )

Если y=f(x) строго монотонно возрастает на [a,b] и непрерывна там, то на Y=[f(a),f(b)] существует обратная функция и является непрерывной на этом множестве.

Доказательство. Существование обратной функции следует из монотонности. Кроме того обратная функция также будет монотонной с областью значений [a,b]. Из критерия непрерывности монотонной функции следует ее непрерывность.

7. Непрерывность элементарных функций.
   
   1. Непрерывность функции a^x, a>0.
      

a) a>1, 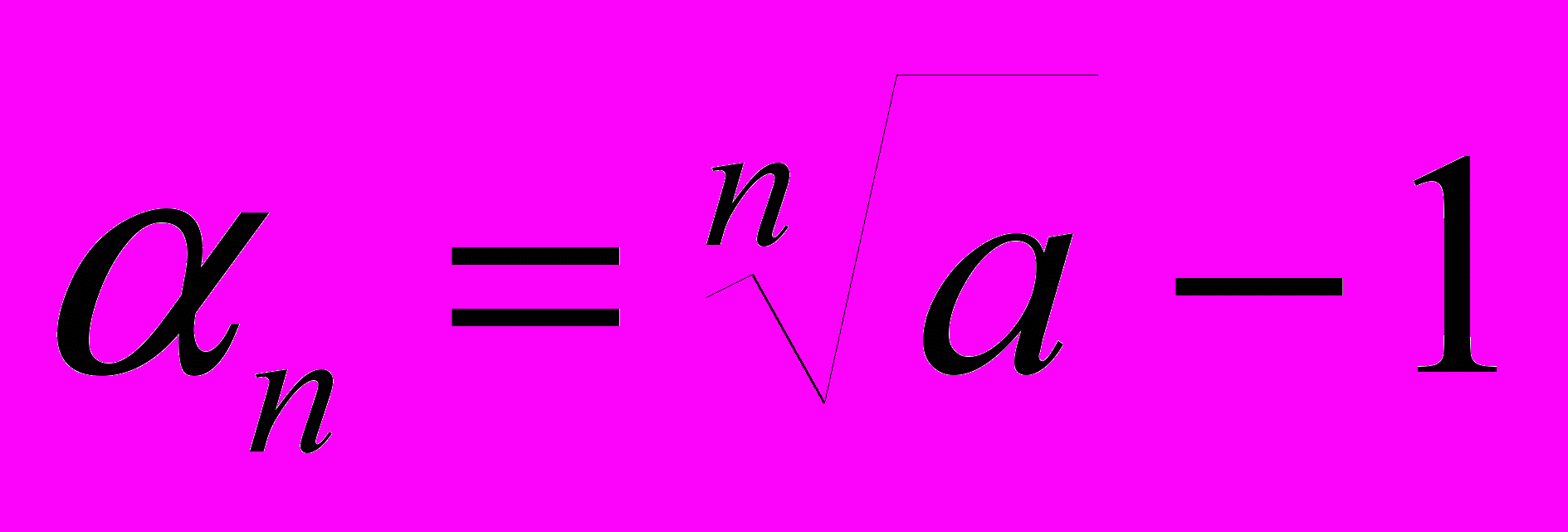,a=(_n+1)ⁿ > n_n, _n

b) a<1,

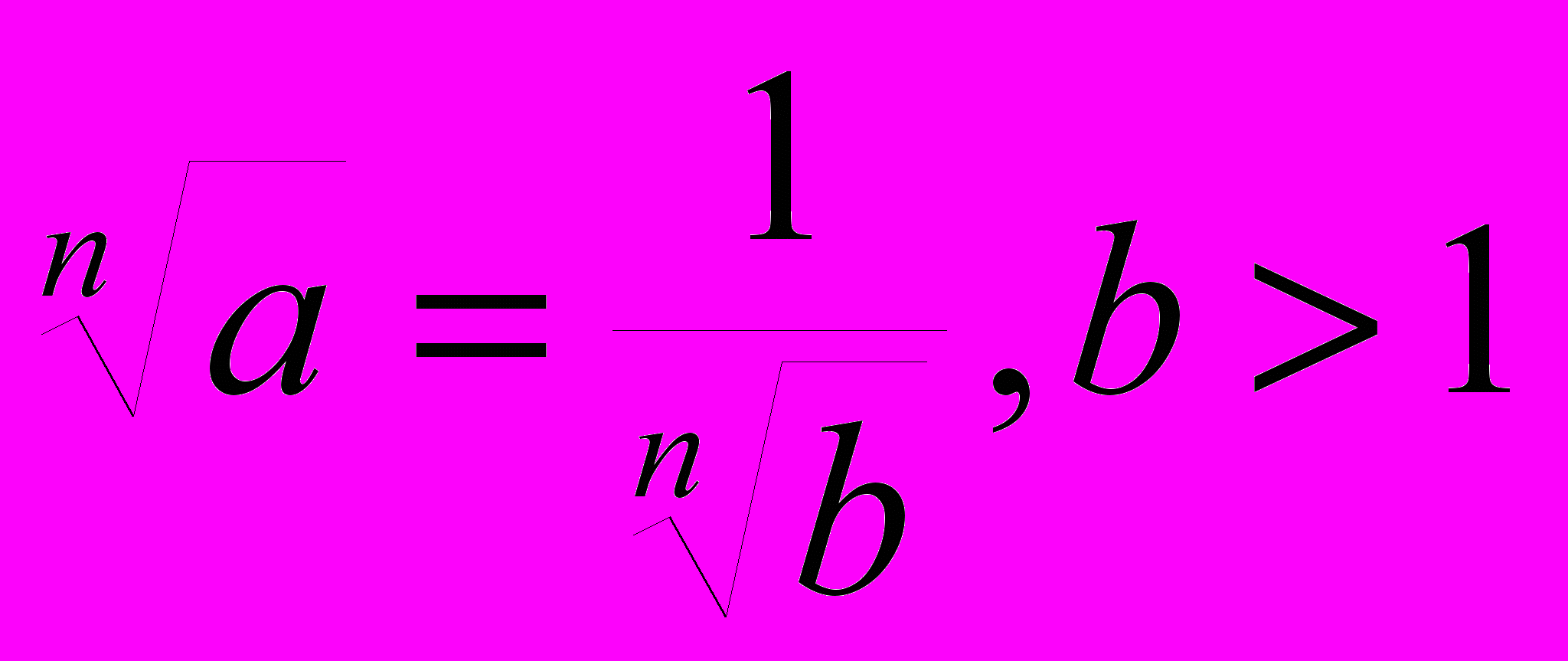
Докажем, что (непрерывность в 0)

1 a> 1

Пусть {x_k} типа Гейне для 0+0

1. x_k0
   
2. x_k>0
   

 n_k+ и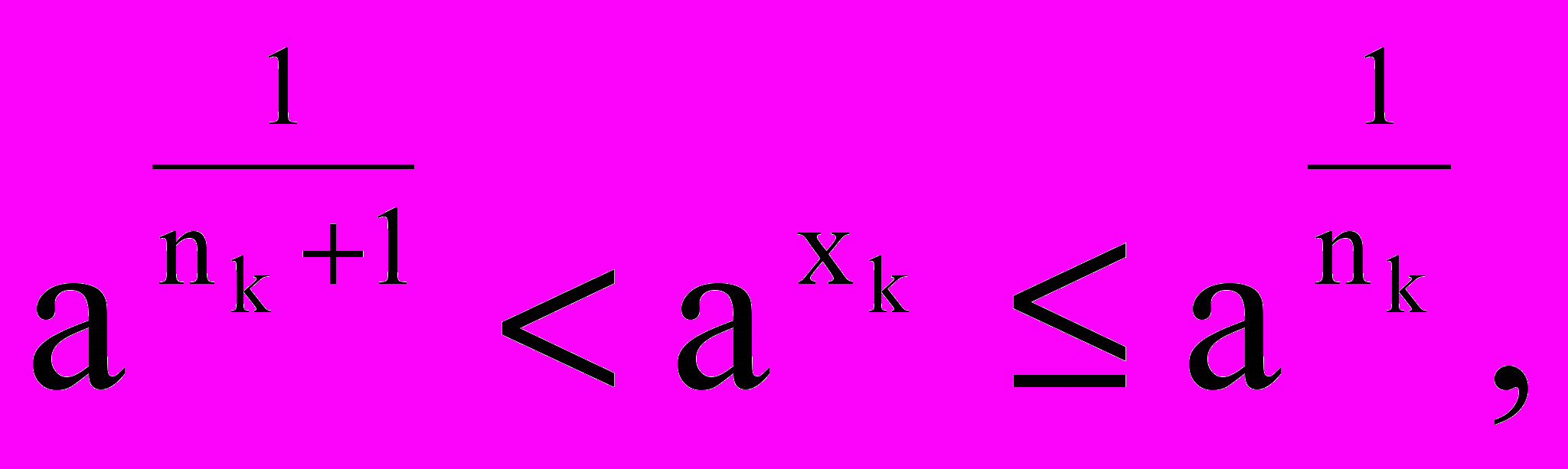

далее k.

Аналогично рассматривается случай x0-0. Откуда получаем утверждение для x0.

2 a<1, b^x=1/a^x, b=1/a>1

2) a^x непрерывна .

3). log_ax непрерывна, как обратная к непрерывной строго монотонной функции.

4). Степенная функция y=x^. Докажем непрерывность при x>0. Имеем x^=e^{ ln x}, далее теорема о непрерывности суперпозиции.

5).

суперпозиция непрерывной и имеющей предел функции. Аналогично доказывается, что



6)

a^x -1=y, x=log_a(1+y)

x0  y0



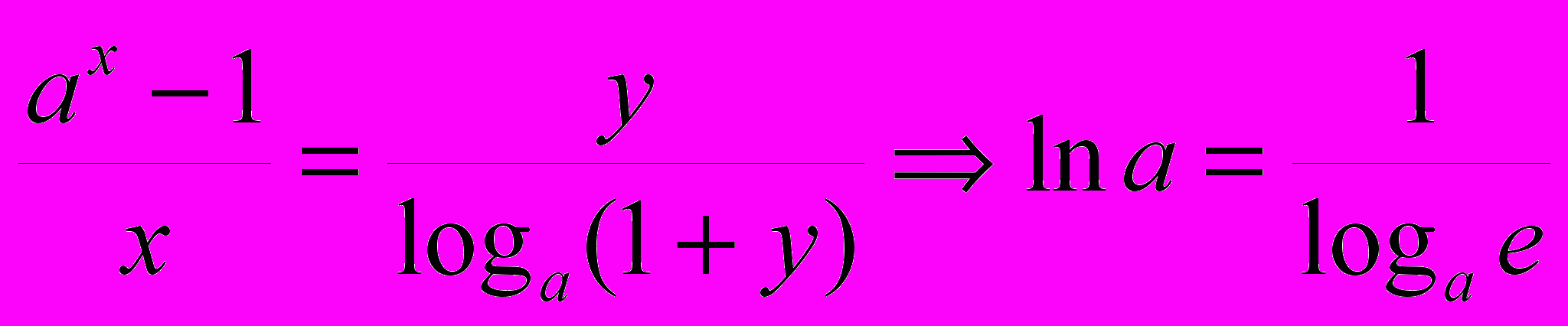
7)

(1+x)^ - 1=y,  ln(1+x) = ln(1+y)



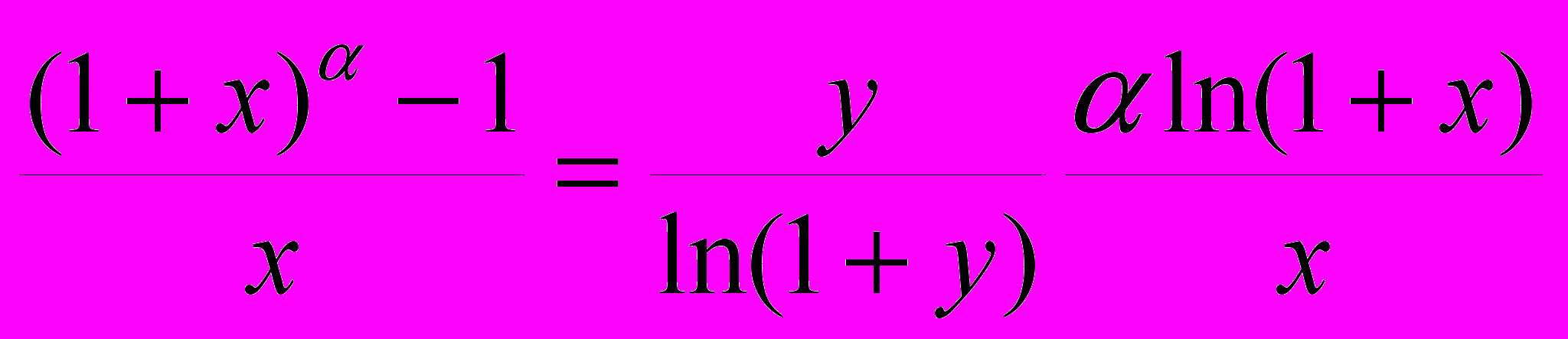
8) sin x

|sin x –sin x₀|=2|sin(x-x₀)/2 cos(x+x₀)/2||x-x₀|

cos x = sin(x+/2)

tg x, ctg x, arcsin, arcos, arctg, arcctg

9) f=const, x, P_n, R_n.


§6 Равномерная непрерывность


Функция f, определенная на Х называется равномерно непрерывной на Х, если

x,xX,|x-x|<:|f(x)-f(x)|<

Всякая равномерно непрерывная функция на Х непрерывна на Х.

Обратное неверно.

Теорема ( Кантор). Всякая непрерывная на [a,b] функция f равномерно непрерывна на [a,b].

Доказательство. От противного.

₀>0>0u,v [a,b],|u-v|<:|f(u)-f(u)|₀

=1/n u_n,v_n,| u_n-v_n|<1/n: |f(u_n)-f(v_n)|₀ (1)

По Т. Б-В тогда и 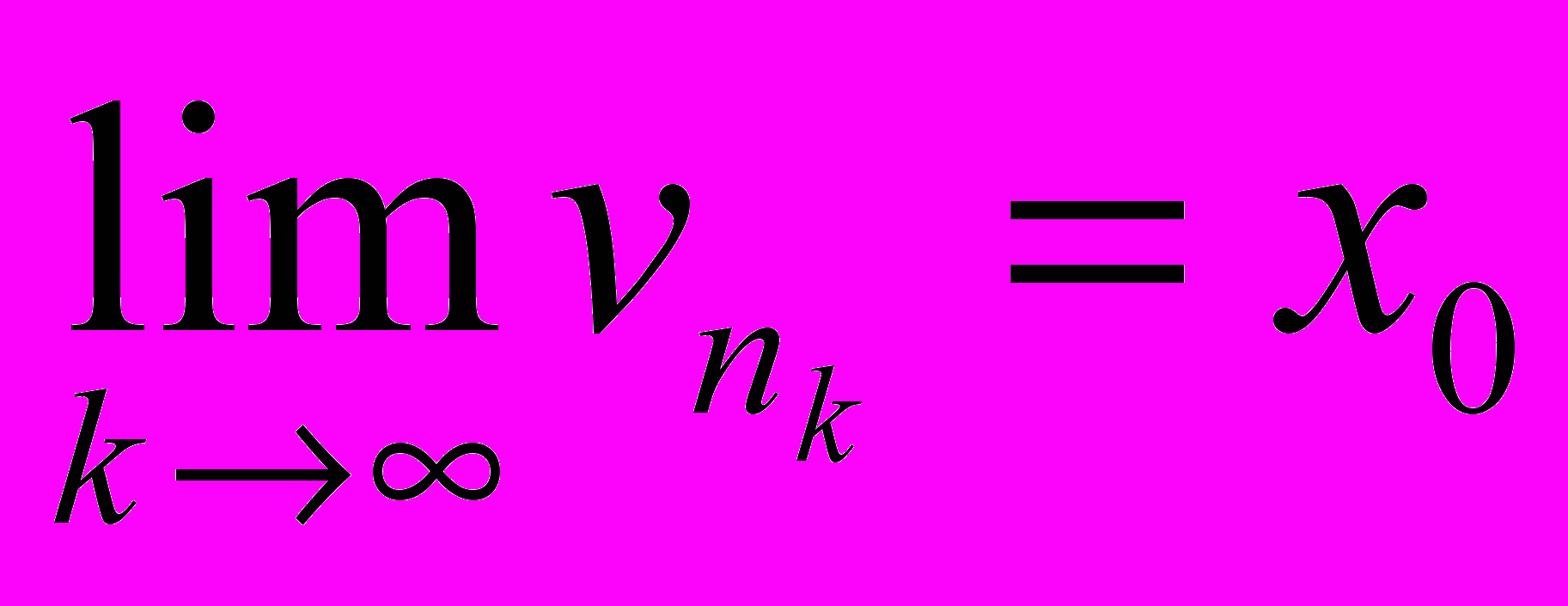. В силу непрерывности 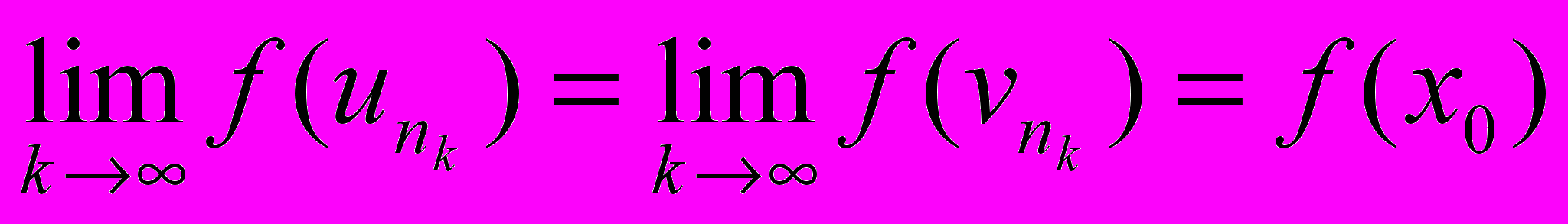. Таким образом

, что противоречит (1).