Календарный план учебных занятий по дисциплине математический анализ Индекс специальности
| Вид материала | Лекции |
- Анализа и теории функций календарный план учебных занятий по дисциплине «Высшая математика», 30.38kb.
- Календарный план учебных занятий по дисциплине "Высшая алгебра и аналитическая геометрия", 94.97kb.
- Календарный план курса учебных занятий по спецкурсу «Основы формальных методов описания, 48.19kb.
- Календарный план курса учебных занятий по спецкурсу «Карта процессов и информационная, 51.48kb.
- Календарный план курса учебных занятий по спецкурсу «Формальные языки моделирования, 61.45kb.
- Календарный план учебных занятий по обязательной дисциплине «Математическая логика»,, 39.04kb.
- Календарный план учебных занятий по дисциплине «Человек и его потребности» специальность, 95.86kb.
- Календарный план учебных занятий по дисциплине Компьютерный дизайн оптических наноструктур,, 39.38kb.
- Методические рекомендации по использованию учебных пособий «Алгебра и математический, 181.08kb.
- Календарный план учебных занятий по дисциплине «Математический синтез оптических покрытий»., 39.56kb.
Кафедра математического анализа и теории функций
Календарный план
учебных занятий по дисциплине математический анализ
Индекс специальности НП курс I семестр 1
Ведущий дисциплину - д.ф.-м.н. Галахов Е.И.
| Недели | Лекции | Число часов | Практические занятия | Число часов |
| 1 неделя | Элементы теории множеств. Мощность множества. Теорема Кантора. | 4 | Построение графиков функций. | 4 |
| 2 неделя | Действительные числа. Функция (отображение). | 4 | Построение графиков функций. | 4 |
| 3 неделя | Предел последовательности. Монотонные последовательности. Число е. | 4 | Построение графиков функций. Предел последовательности. | 2 2 |
| 4 неделя | Предел функции. Критерий Коши. | 4 | Предел функции. | 4 |
| 5 неделя | Непрерывность функции. Точки разрыва функции. Непрерывность сложной и обратной функций. Равномерная непрерывность. | 4 | Предел функции. | 4 |
| 6 неделя | Производная функции. | 4 | Непрерывность и равномерная непрерывность функции. Точки разрыва. Контрольная работа №1. | 2 2 |
| 7 неделя | Дифференциал. Производные высших порядков. Теоремы Ферма, Ролля, Коши, Лагранжа. | 4 | Производная и дифференциал функции. | 4 |
| 8 неделя | Формула Тейлора. | 4 | Производная обратной и сложной функции. Формула Тейлора. | 2 2 |
| 9 неделя | Экстремумы функции. Точки перегиба, асимптоты. Правила Лопиталя. | 4 | Исследование функций. | 4 |
| 10 неделя | Коллоквиум. Неопределенный интеграл. | 2 2 | Правила Лопиталя. | 4 |
| 11 неделя | Интегрирование по частям. Интегрирование рациональных функций. | 4 | Контрольная работа №2 Неопределенный интеграл. | 2 2 |
| 12 неделя | Интегрирование дифференциальных биномов. | 4 | Замена переменных в неопределенном интеграле, интегрирование по частям. | 4 |
| 13 неделя | Интегралы вида 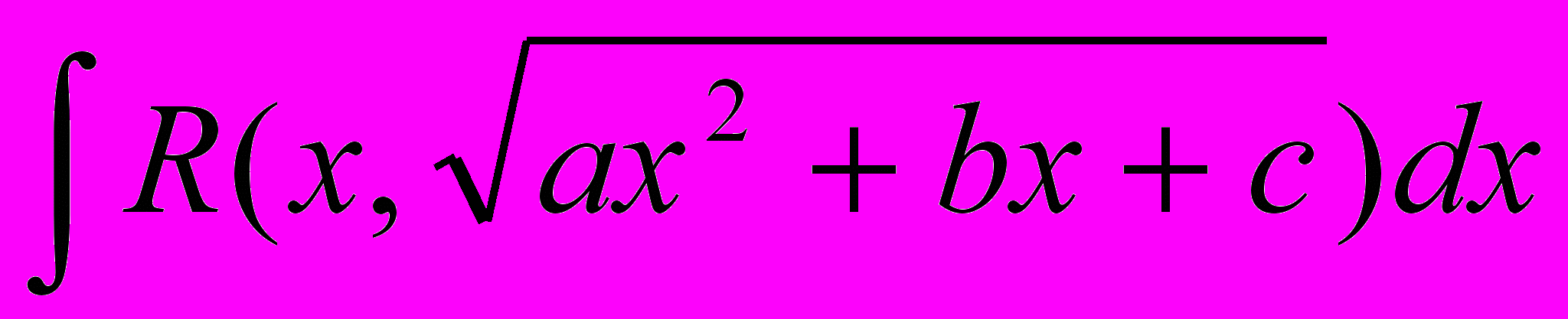 и т.д. и т.д.Подстановки Эйлера. | 4 | Интегрирование рациональных и иррациональных функций. | 4 |
| 14 неделя | Определенный интеграл. Критерий Лебега. | 4 | Интегралы вида 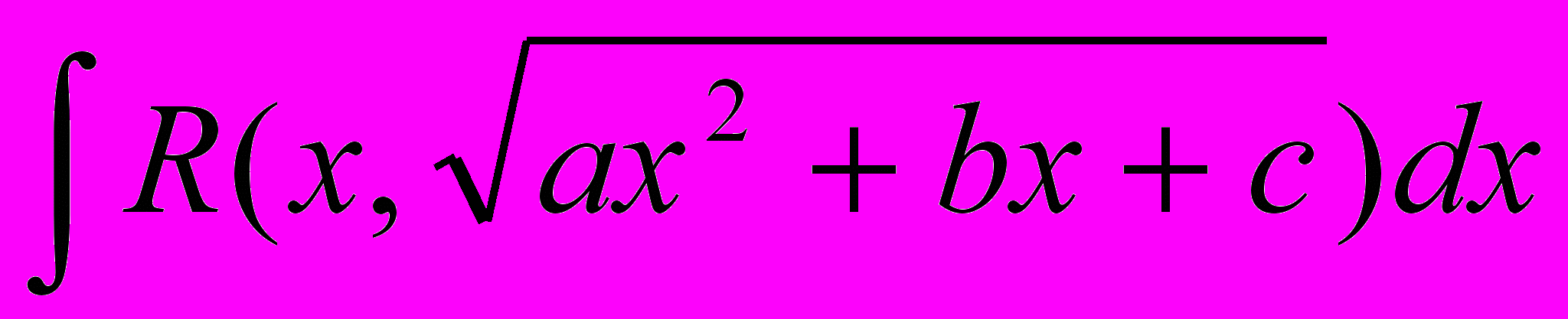 и т.д. и т.д. | 4 |
| 15 неделя | Суммы и интегралы Дарбу. Критерий Дарбу. | 4 | Подстановки Эйлера. | 4 |
| 16 неделя | Оценки интеграла Римана, монотонность интеграла и теорема о среднем. | 4 | Подстановки Эйлера. | 4 |
| 17 неделя | Интеграл и производная. Формула Ньютона-Лейбница. Замена переменной в интеграле Римана. | 4 | Интегрирование дифференциальных биномов | 4 |
| 18 неделя | Приложения интеграла и вычисление длины кривой, площади криволинейной трапеции и объема тел вращения. | 4 | Интегрирование выражений с тригонометрическими функциями | 4 |
| 19 неделя | Обзорные лекции. | 4 | Интегрирование выражений с тригонометрическими функциями | 4 |
| 20 неделя | Обзорные лекции. | 4 | Контрольная работа №3 | 2 |
Кафедра математического анализа и теории функций
Календарный план
учебных занятий по дисциплине математический анализ
Индекс специальности НП курс I семестр 2
Ведущий дисциплину - д.ф.-м.н. Галахов Е.И.
| Недели | Лекции | Число часов | Практические занятия | Число часов |
| 1 неделя | Приложения определенного интеграла к вычислению длины кривой, площади и объема. Кривые в евклидовом пространстве, кривизна кривой. | 4 | Определенный интеграл. Формула Ньютона-Лейбница. Замена переменных в определенном интеграле, интегрирование по частям. | 4 |
| 2 неделя | Несобственные интегралы (НИ). Критерий Коши, признаки Дирихле и Абеля сходимости НИ. | 4 | Несобственные интегралы. | 4 |
| 3 неделя | Метрические пространства. Открытые и замкнутые множества в 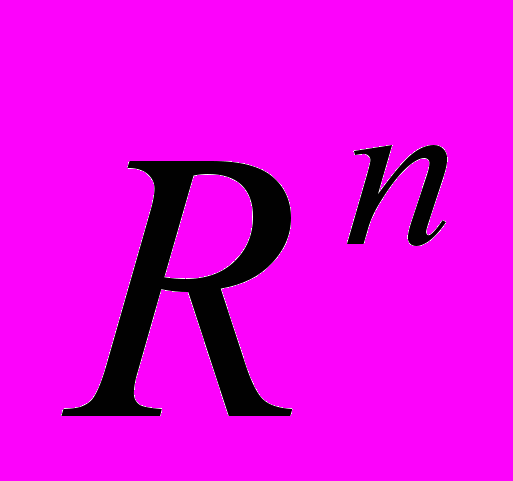 и их свойства. Компакты в и их свойства. Компакты в 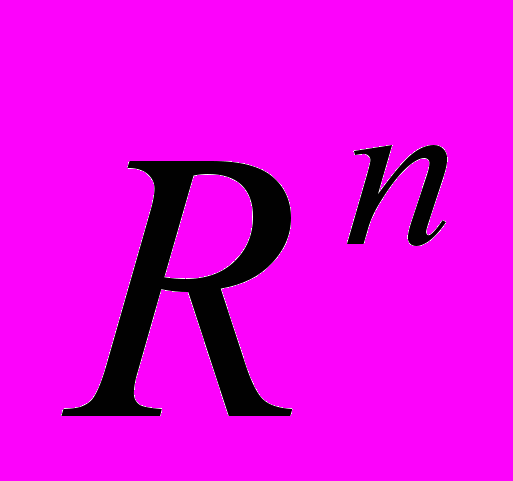 и их свойства. и их свойства. | 4 | Вычисление площадей. | 4 |
| 4 неделя | Последовательности в 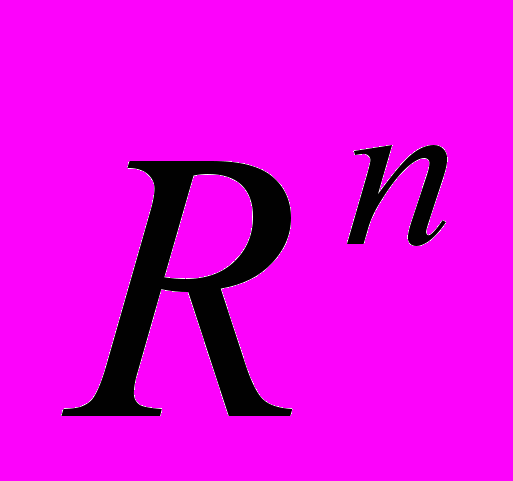 и их сходимость. и их сходимость. | 4 | Вычисление длины дуги, объема тела вращения, площади поверхности вращения. | 4 |
| 5 неделя | Непрерывные функции в 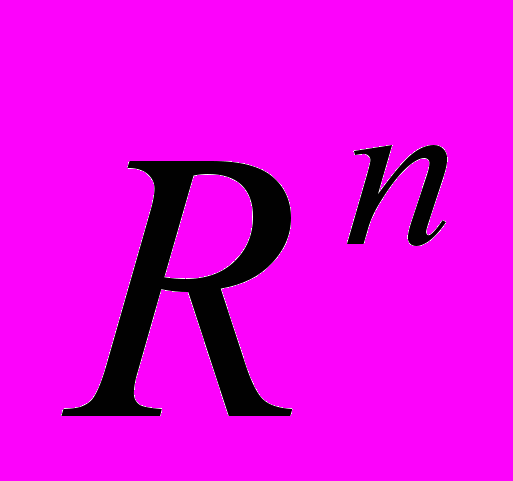 . Свойства функции, заданной на компакте. Дифференцируемые функции в . Свойства функции, заданной на компакте. Дифференцируемые функции в 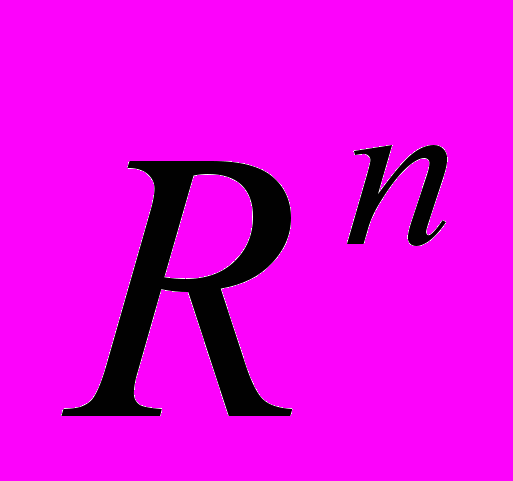 . . | 4 | Контрольная работа №1. Предел функции n переменных | 2 2 |
| 6 неделя | Дифференцирование сложной функции. Градиент, геометрический смысл дифференциала. | 4 | Непрерывность. Частные производные. Дифференциал функции. | 4 |
| 7 неделя | Частные производные и дифференциалы высших порядков. Формула Тейлора функции n переменных. | 4 | Производные и дифференциалы высших порядков. | 4 |
| 8 неделя | Точки локального экстремумам функции n переменных. | 4 | Дифференцирование неявных функций. Формула Тейлора. | 4 |
| 9 неделя | Основные теоремы о неявных функциях. Система неявных функций. Якобиан, теорема об обратном отображении. | 4 | Экстремумы функций n переменных. | 4 |
| 10 неделя | Условный экстремум функции n переменных. | 4 | Неявные функции. Условный экстремум. | 4 |
| 11 неделя | Числовые ряды. Критерий Коши. Основные свойства сходящихся рядов. Признаки сравнения, Даламбера и Коши сходимости рядов с неотрицательными членами. | 4 | Контрольная работа №2 Признаки сходимости знакопостоянных рядов. | 2 2 |
| 12 неделя | Интегральный признак Коши сходимости ряда. Признаки Раабе и Гаусса. | 4 | Признаки сходимости знакопостоянных рядов. | 4 |
| 13 неделя | Абсолютная и условная сходимость ряда. Признак Лейбница сходимости знакочередующегося ряда. Сочетательное и переместительное свойства сходящихся рядов. Теорема Римана. | 4 | Знакочередующиеся ряды | 4 |
| 14 неделя | Коллоквиум. Умножение рядов. Преобразование Абеля | 2 2 | Знакопеременные ряды | 4 |
| 15 неделя | . Признаки Абеля и Дирихле. Двойные и повторные ряды. Бесконечные произведения и их сходимость. | 4 | Знакопеременные ряды. | 4 |
| 16 неделя | Поточечная и равномерная сходимость функционального ряда. Критерий Коши, признак Вейерштрасса. | 4 | Функциональные ряды. | 4 |
| 17 неделя | Признаки Абеля и Дирихле равномерной сходимости функциональных рядов. Свойства равномерно сходящихся рядов. Степенной ряд и его свойства. | 4 | Функциональные ряды. | 4 |
| 18 неделя | Ряд Тейлора. Разложение функции в ряд Тейлора. | 4 | Степенные ряды. | 4 |
| 19 неделя | Равномерная сходимость функций по параметру. Собственные интегралы, зависящие от параметра. Дифференцирование и интегрирование собственных интегралов, зависящих от параметра. | 4 | Ряд Тейлора. | 4 |
| 20 неделя | Несобственные интегралы, зависящие от параметра. | 4 | Контрольная работа №3 | 2 |
Кафедра математического анализа и теории функций
Календарный план
учебных занятий по дисциплине математический анализ
Индекс специальности НП курс II семестр 1
Ведущий дисциплину - д.ф.-м.н. Галахов Е.И.
| Недели | Лекции | Число часов | Практические занятия | Число часов |
| 1 неделя | Интеграл Римана на n-мерном промежутке. Критерии Лебега и Дарбу интегрируемости функции. | 2 2 | Эйлеровы интегралы | 4 |
| 2 неделя | Допустимые множества и интегралы на них. | 2 | Двойные интегралы. Определение, изменение порядка интегрирования. | 4 |
| 3 неделя | Общие свойства интеграла Римана на множестве Rn. Сведение кратного интеграла к повторному. Теорема Фубини. | 2 2 | Двойные интегралы. Замена переменных. | 4 |
| 4 неделя | Двойной интеграл: приведение к повторному, замена переменных, приложения. | 2 | Вычисление площадей плоских фигур. | 4 |
| 5 неделя | Тройной интеграл и его вычисление. Замена переменных в тройном интеграле. Несобственные интегралы двух и трех переменных. | 2 2 | Вычисление объемов тел. | 4 |
| 6 неделя | Криволинейный интеграл 1-го рода. | 2 | Тройной интеграл. Изменение порядка интегрирования. | 4 |
| 7 неделя | Криволинейный интеграл 2-го рода. Условия независимости криволинейного интеграла от пути интегрирования. Формула Грина. | 2 2 | Замена переменных. Сферические, цилиндрические координаты. | 4 |
| 8 неделя | Поверхности и их ориентация, площадь поверхности. | 2 | Вычисление объемов тел. | 4 |
| 9 неделя | Поверхностный интеграл 1-го рода. Поверхностный интеграл 2-го рода. | 2 2 | Контрольная работа №1 Криволинейные интегралы I и II рода | 2 2 |
| 10 неделя | Формула Острогорадского-Гаусса. | 2 | Криволинейные интегралы I и II рода | 4 |
| 11 неделя | Коллоквиум. Формула Стокса. | 2 2 | Формула Грина. | 4 |
| 12 неделя | Скалярные и векторные поля. Градиент, дивергенция, циркуляция, ротор. | 2 | Поверхностные интегралы I рода. | 4 |
| 12 неделя | Специальные поля. Обратная задача векторного анализа. Ортогональная система функций. Ряды Фурье. | 2 2 | Поверхностный интеграл II рода. | 4 |
| 13 неделя | Свойства ряда Фурье. Неравенство Бесселя. Сходимость в среднем. | 2 | Формула Стокса. Формула Остроградского-Гаусса. | 4 |
| 14 неделя | Тригонометрический ряд Фурье и его свойства. Теорема Дирихле. Принцип локализации Римана. | 2 2 | Контрольная работа №2 Элементы теории поля: скалярные и векторные поля; градиент, дивергенция, циркуляция, ротор. | 2 2 |
| 15 неделя | Метод средних арифметических суммирования ряда Фурье. Теорема Вейерштрасса. | 2 | Элементы теории поля: скалярные и векторные поля; градиент, дивергенция, циркуляция, ротор. | 4 |
| 16 неделя | Интеграл Фурье. | 4 | Приложения криволинейных и поверхностных интегралов в задачах теории поля. | 4 |
| 17 неделя | Преобразование Фурье. | 2 | Ряды Фурье. Разложение функций в ряд Фурье. | 4 |
| 18 неделя | Преобразование Фурье. Обзорная лекция. | 2 2 | Ряды Фурье. Разложение функций в ряд Фурье. | 4 |
| 19 неделя | Обзорная лекция. | 2 | Ряды Фурье. Разложение функций в ряд Фурье. | 4 |
| 20 неделя | Обзорные лекции. | 4 | Контрольная работа №3 | 2 |
