Тема 3 Непрерывные функции. Точки разрыва функции. Теоретические вопросы
| Вид материала | Контрольные вопросы |
- В. И. Афанасьева 01 марта 2011 г. Программа, 116.92kb.
- Календарный план учебных занятий по дисциплине математический анализ Индекс специальности, 165.93kb.
- Определители и системы линейных уравнений. Матричная алгебра. Векторная алгебра. Аналитическая, 8.15kb.
- Элективный курс «Функции и их графики» (9 класс), 62.92kb.
- Вопросы к экзамену по дисциплине "физическая химия", 62.78kb.
- Лекция 21. Экстремум функции нескольких переменных, 60.44kb.
- Урок по теме: "Показательные функции, уравнения, неравенства", 69.08kb.
- Урок алгебры в 10 классе Тема: «Логарифмы, логарифмическая функция, её свойства и график», 66.6kb.
- Урока. Раздел. Тема урока, 316.06kb.
- Обмануть Мистера Фреймана), 10633 (На редкость простая задача, 509.81kb.
Тема 3
Непрерывные функции. Точки разрыва функции.
Теоретические вопросы
Определение непрерывной функции в точке.
- Односторонние пределы. Точки разрыва функции и их классификация.
- Операции над непрерывными функциями: непрерывность суммы конечного числа функций; непрерывность произведения конечного числа функций; непрерывность частного двух функций.
- Непрерывность основных элементарных функций: непрерывность линейной функции; непрерывность тригонометрических функций;
непрерывность показательной функции; непрерывность
логарифмической функции; непрерывность обратных
тригонометрических функций.
5. Теорема о сохранении знака непрерывной функции.
6. Свойства функций, непрерывных на отрезке.
Контрольные вопросы
1. Какие из следующих утверждений верны:
1) сумма двух функций, имеющих в точке х = а разрыв
первого рода, имеет в точке х = а разрыв первого рода;
2) произведение функции, имеющей в точке х = а разрыв
второго рода, и функции, непрерывной в точке х = а,
имеет в точке х = а разрыв второго рода;
3) сумма функции, имеющей в точке х = а разрыв второго
рода, и функции, непрерывной в точке х = а, может
иметь в точке х = а разрыв первого рода;
4) сумма функции, имеющей в точке х = а разрыв второго рода,
и функции, непрерывной в точке х = а , имеет в точке х = а
разрыв второго рода;
5) произведение двух функций, имеющих в точке х = а разрыв
второго рода, может иметь в точке х = а устранимый
разрыв;
6) сумма функции, имеющей в точке х = а разрыв первого
рода, и функции, имеющей в точке х = а разрыв второго
рода, может иметь в точке х = а разрыв первого рода;
7) сумма двух функций, имеющих в точке х = а разрыв
второго рода, может иметь в точке х = а разрыв
первого рода;
8) произведение функции, имеющей в точке х = а разрыв
первого рода, и функции, непрерывной в точке х = а,
имеет в точке х = а разрыв первого рода;
- сумма функции, имеющей в точке х = а разрыв первого
рода, и функции, имеющей в точке х = а разрыв второго
рода, может иметь в точке х = а разрыв второго рода;
10) произведение функции, имеющей в точке х = а разрыв
первого рода, и функции, имеющей в точке х = а разрыв
второго рода, имеет в точке х = а разрыв второго рода;
11) сумма функции, имеющей в точке х = а устранимый
разрыв, и функции, непрерывной в точке х = а, может
быть функцией, непрерывной в точке х = а;
12) сумма функции, имеющей в точке х = а разрыв первого
рода, и функции, непрерывной в точке х = а , имеет в
точке х = а разрыв первого рода;
13) произведение двух функций, имеющих в точке х = а
разрыв первого рода, может иметь в точке х = а
разрыв второго рода;
- сумма двух функций, имеющих в точке х = а разрыв второго рода, имеет в точке х = а разрыв второго рода;
- сумма функции, имеющей в точке х = а разрыв первого рода, и функции, непрерывной в точке х = а , может быть функцией, непрерывной в точке х = а;
- произведение двух функций, имеющих в точке х = а разрыв второго рода, имеет в точке х = а разрыв второго рода;
- сумма двух функций, имеющих в точке х = а разрыв первого рода, может быть непрерывной в точке х = а ;
- сумма двух функций, имеющих в точке х = а разрыв первого рода, может иметь в точке х = а разрыв второго рода.
2. Какие из следующих утверждений верны:
- множество значений функции, непрерывной на интервале, является интервалом;
- множество значений функции, непрерывной на интервале, может быть отрезком;
- если функция принимает на отрезке все промежуточные значения, то она непрерывна на этом отрезке;
- множество значений функции, непрерывной на отрезке, может быть интервалом;
- множество значений функции, непрерывной на всей числовой прямой, может быть полуинтервалом;
- множество значений функции, определённой на отрезке является отрезком;
- если функция имеет на отрезке наибольшее и наименьшее значения, то она непрерывна на этом отрезке;
- множество значений функции, непрерывной на всей числовой прямой, может быть отрезком;
- множество значений функции, определённой на отрезке может быть интервалом;
10)если функция непрерывна на интервале, то она ограничена на
этом интервале;
11)любая функция, определённая на отрезке, ограничена на этом
отрезке;
12)любая функция, определённая на отрезке, имеет наибольшее
значение.
3. Привести пример двух разрывных в точке xо функций f(x)
и g(x), таких, что их сумма будет непрерывной в точке xо.
4. Привести пример двух разрывных в точке xо функций f(x)
и g(x), таких, что их произведение будет функцией,
непрерывной в точке xо.
5. Функции p(x) и k(x) разрывны в точке хо, f(x) = p(x) k(x).
Можно ли утверждать, что функция f(x) разрывна в точке хо?
6. Функция p(x) непрерывна в точке хо , а функция k(x)
разрывна в точке хо, f(x) = p(x) k(x). Можно ли утверждать,
что функция f(x) разрывна в точке хо?
7. Функции p(x) и k(x) разрывны в точке хо, f(x) = p(x) + k(x).
Можно ли утверждать, что функция f(x) разрывна в точке хо?
8. Функция p(x) непрерывна в точке хо , а функция k(x) разрывна в
точке хо, f(x) = p(x) + k(x). Можно ли утверждать, что функция
f(x) разрывна в точке хо?
9. Привести пример функции, непрерывной и неограниченной
на данном интервале.
9. Привести пример функции, заданной на отрезке и
неограниченной на этом отрезке?
10.Верно ли, что если функция f(x) непрерывна при x > 0 и
ограничена, то существует правостронний предел этой функции в точке 0?
11.Является ли непрерывность функции в точке достаточным
условием её ограниченности в некоторой окрестности этой
точки?
12.Является ли непрерывность функции в точке необходимым
условием её ограниченности в некоторой окрестности этой
точки?
13.Всегда ли функция, непрерывная на отрезке, достигает на
этом отрезке наибольшего и наименьшего значений?
14. Может ли функция, непрерывная на интервале, достигать на
нём наибольшего и наименьшего значений?
15. Привести пример функции, имеющей устранимый разрыв в точке
а) х = 0; б) х = 2; в) х = 2.
Задачи для практических занятий
1. Найти точки разрыва функции:
а)
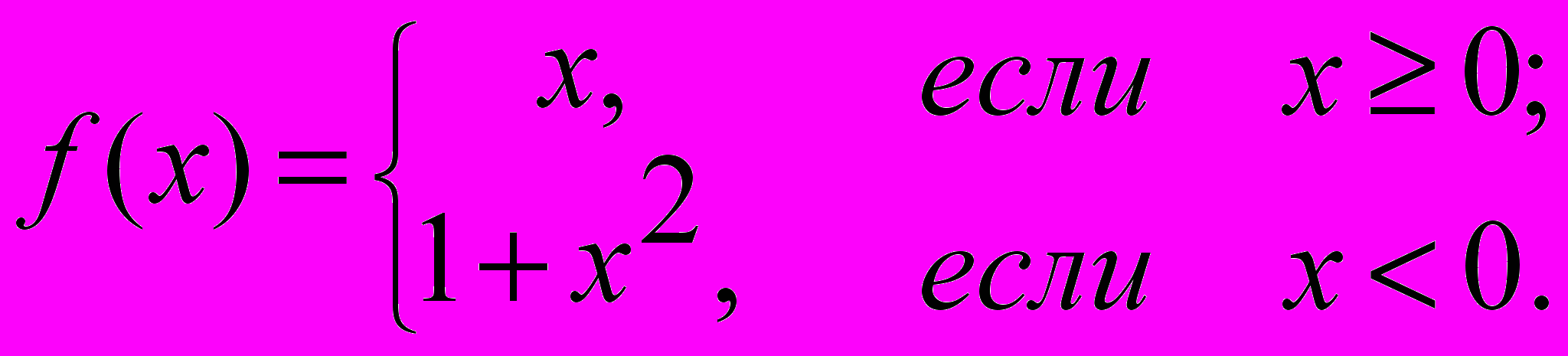 б)
б) 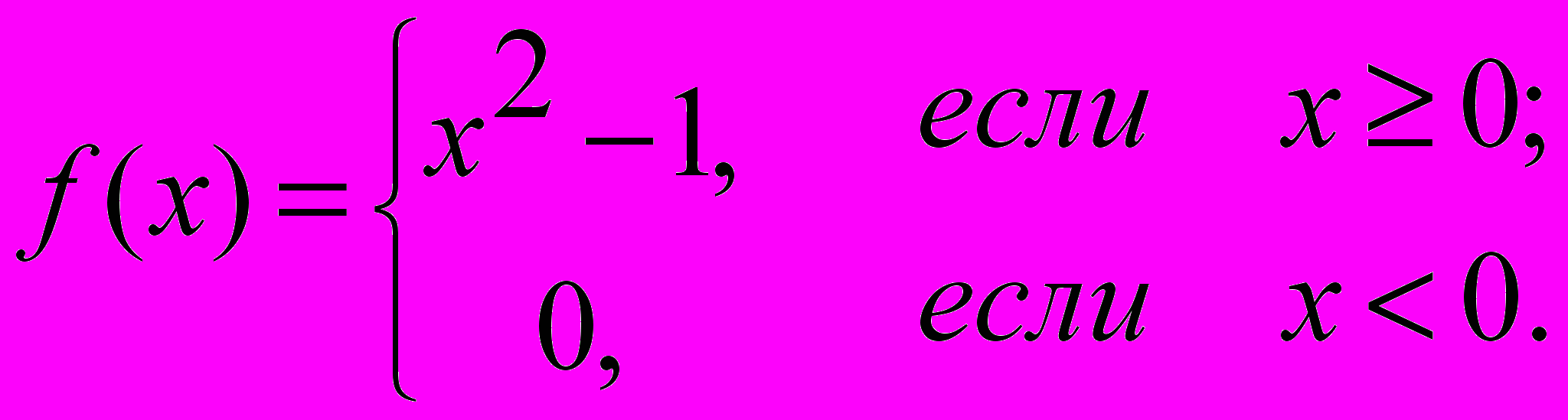
в)
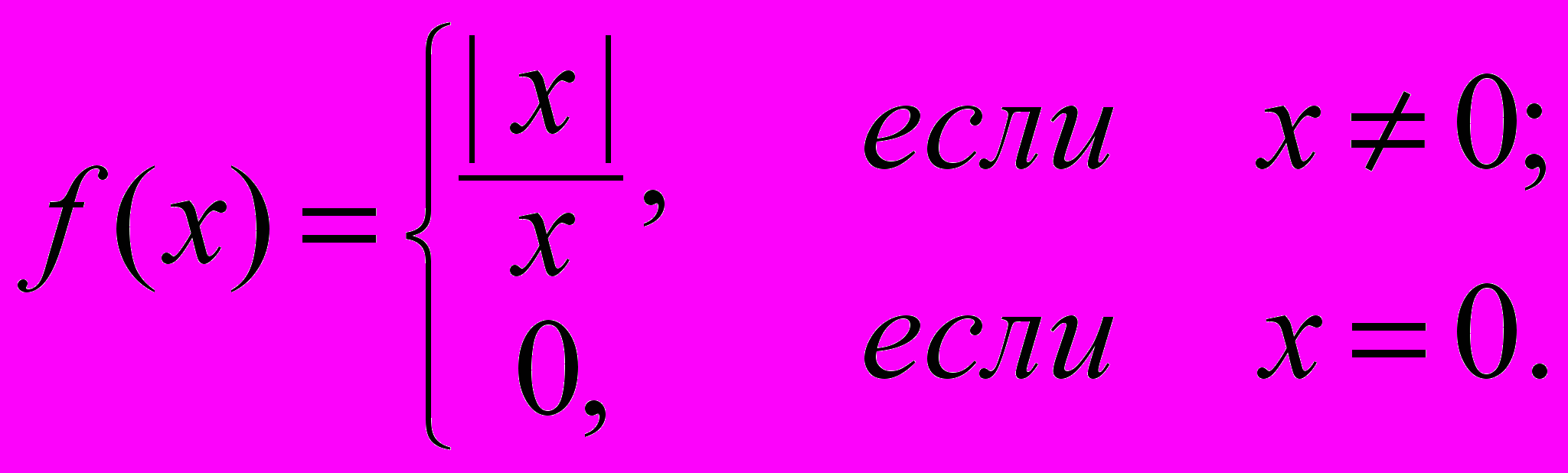
Определить скачок функции в каждой точке разрыва
и построить график.
2. Исследовать функцию
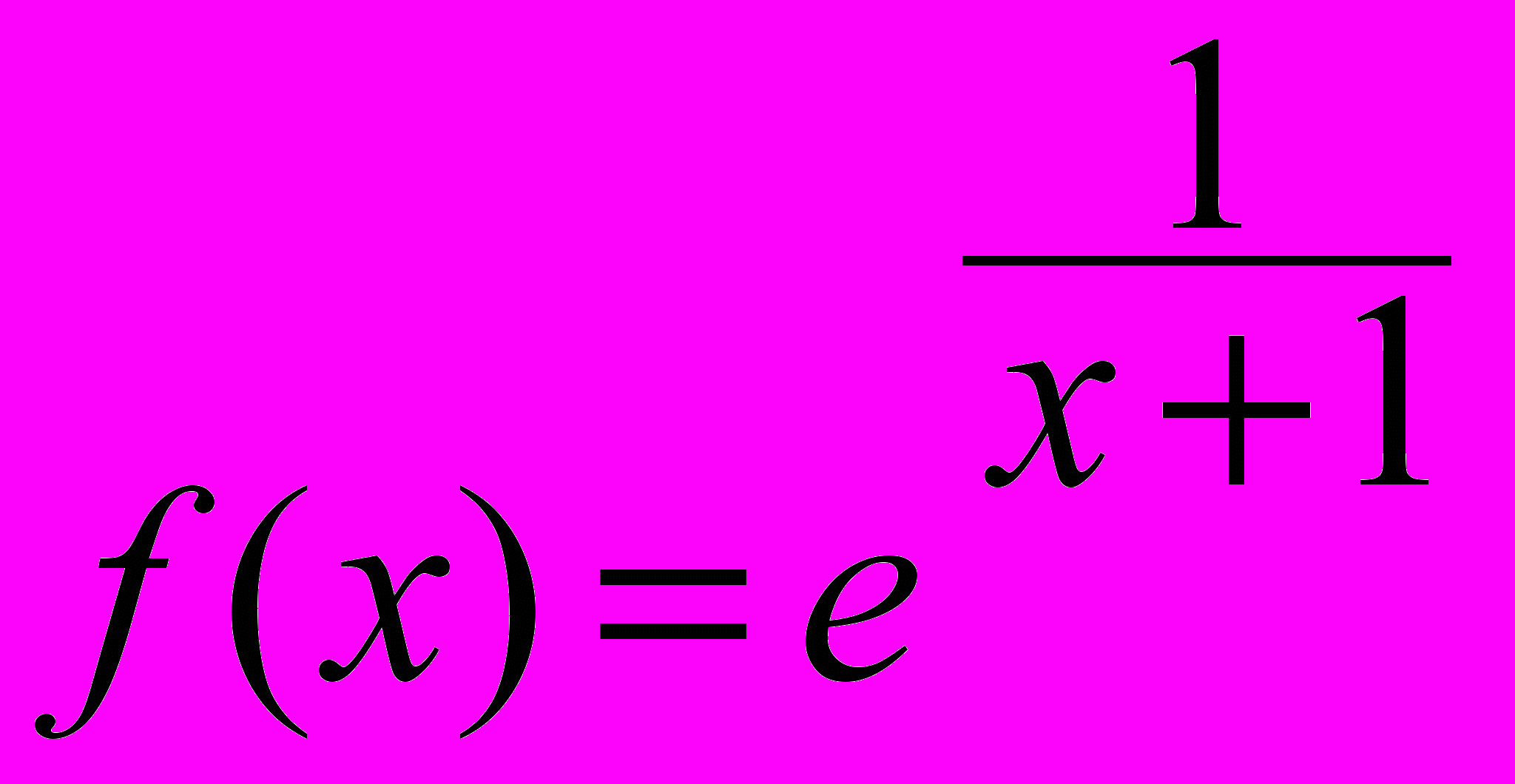 на непрерывность
на непрерывность в точке xо = 1.
3. Исследовать функцию
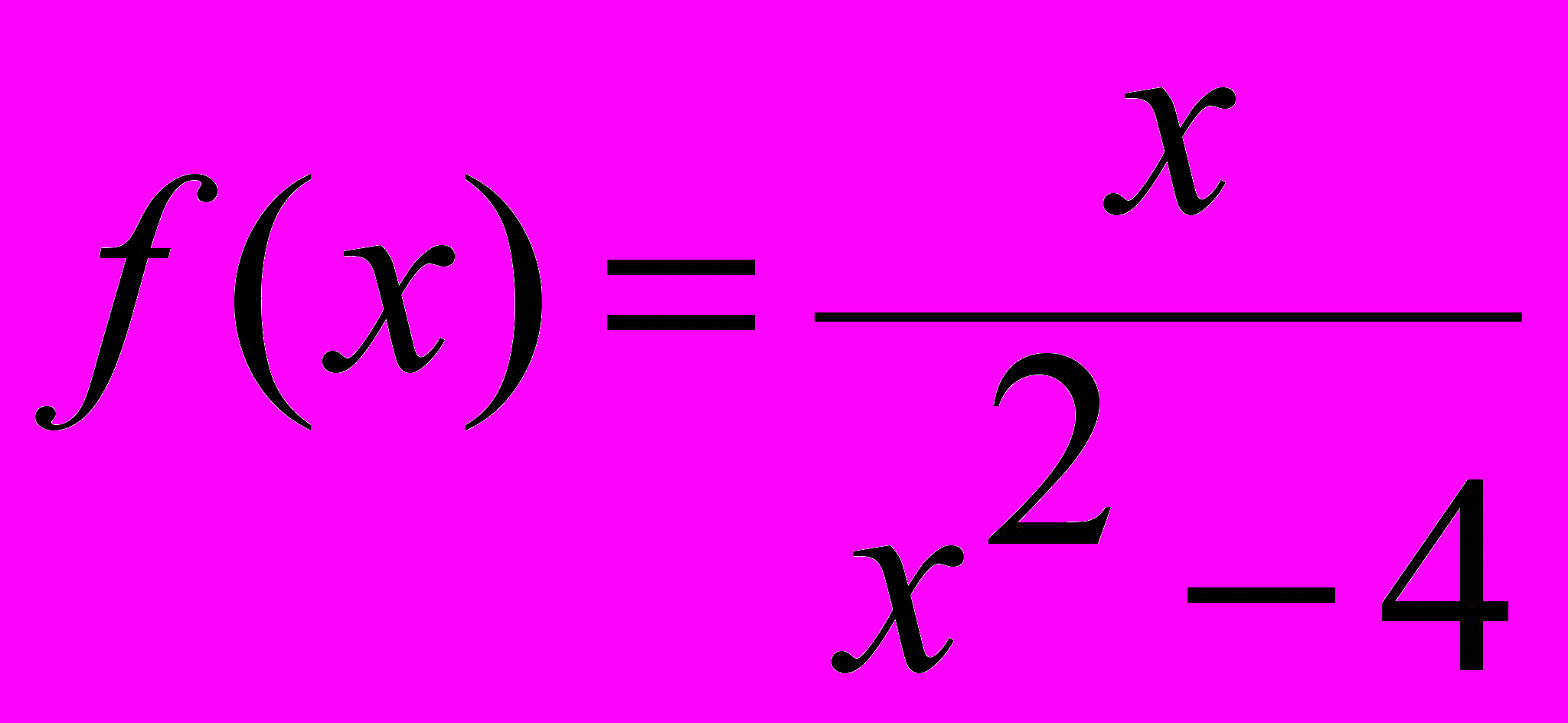 на непрерывность.
на непрерывность.4. В каких точках имеют разрывы функции
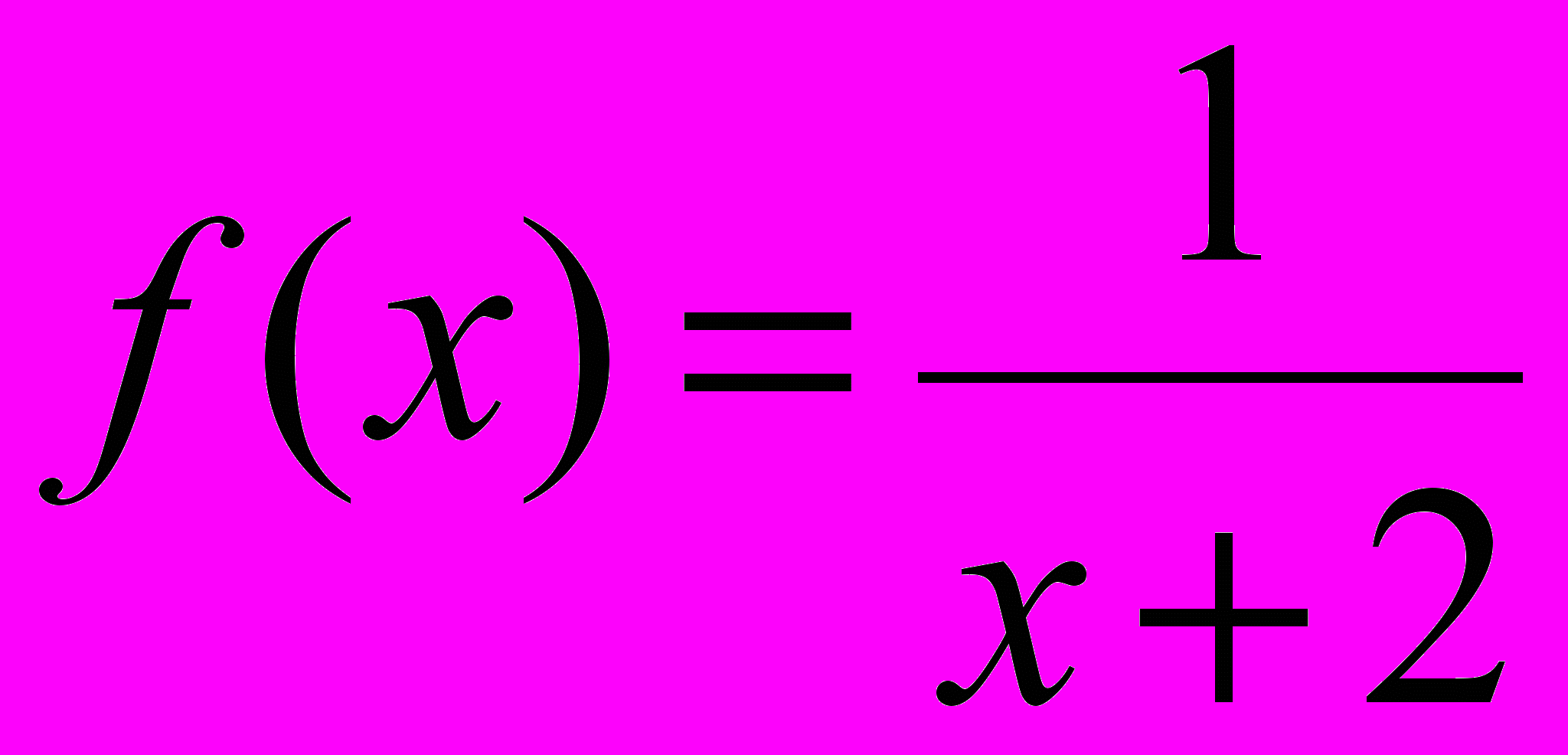 и
и 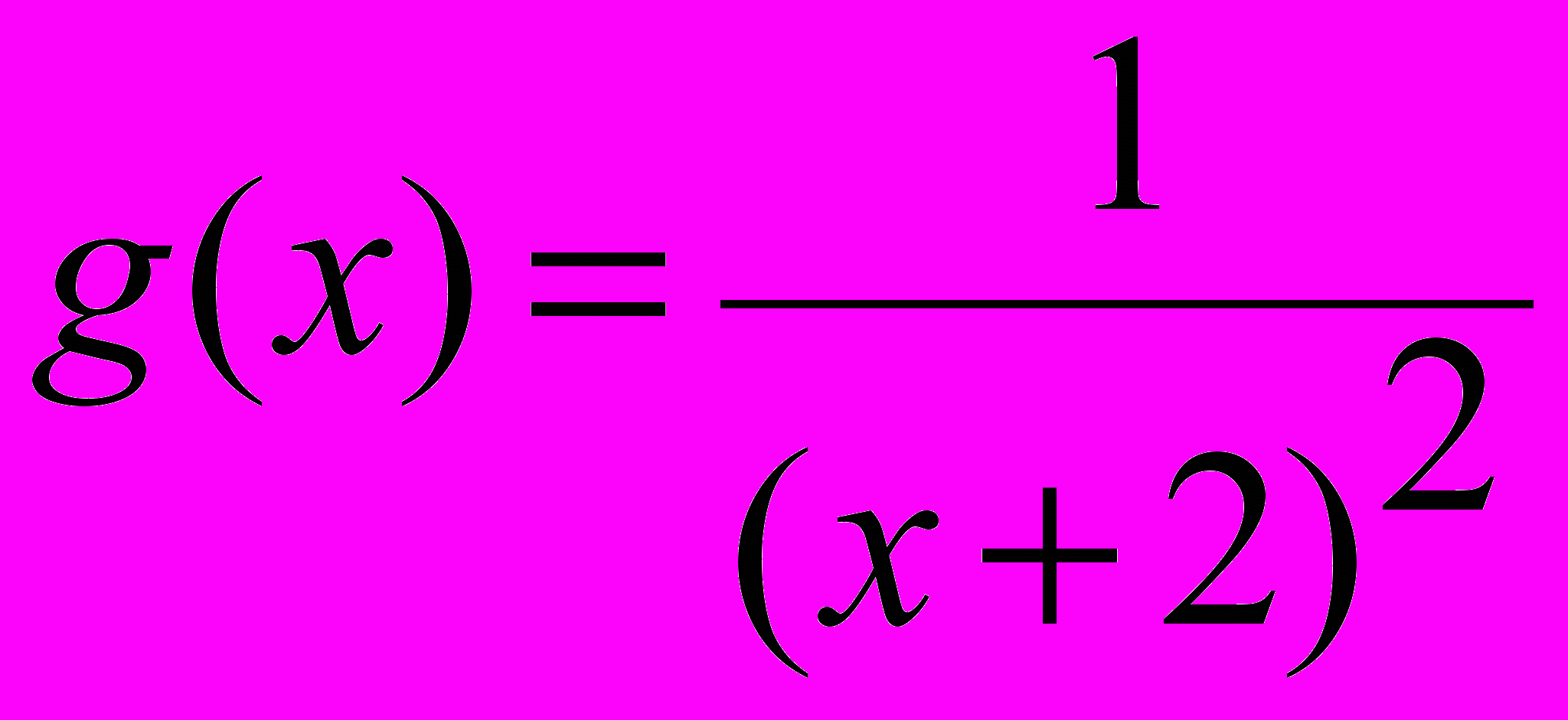 ? Выяснить разницу в поведении функций вблизи
? Выяснить разницу в поведении функций вблизи точек разрыва.
5. Функция
 не определена в точке x = 1.
не определена в точке x = 1. Каким должно быть
 , чтобы функция,
, чтобы функция, доопределённая таким образом стала непрерывной?
6. Функции
 и
и 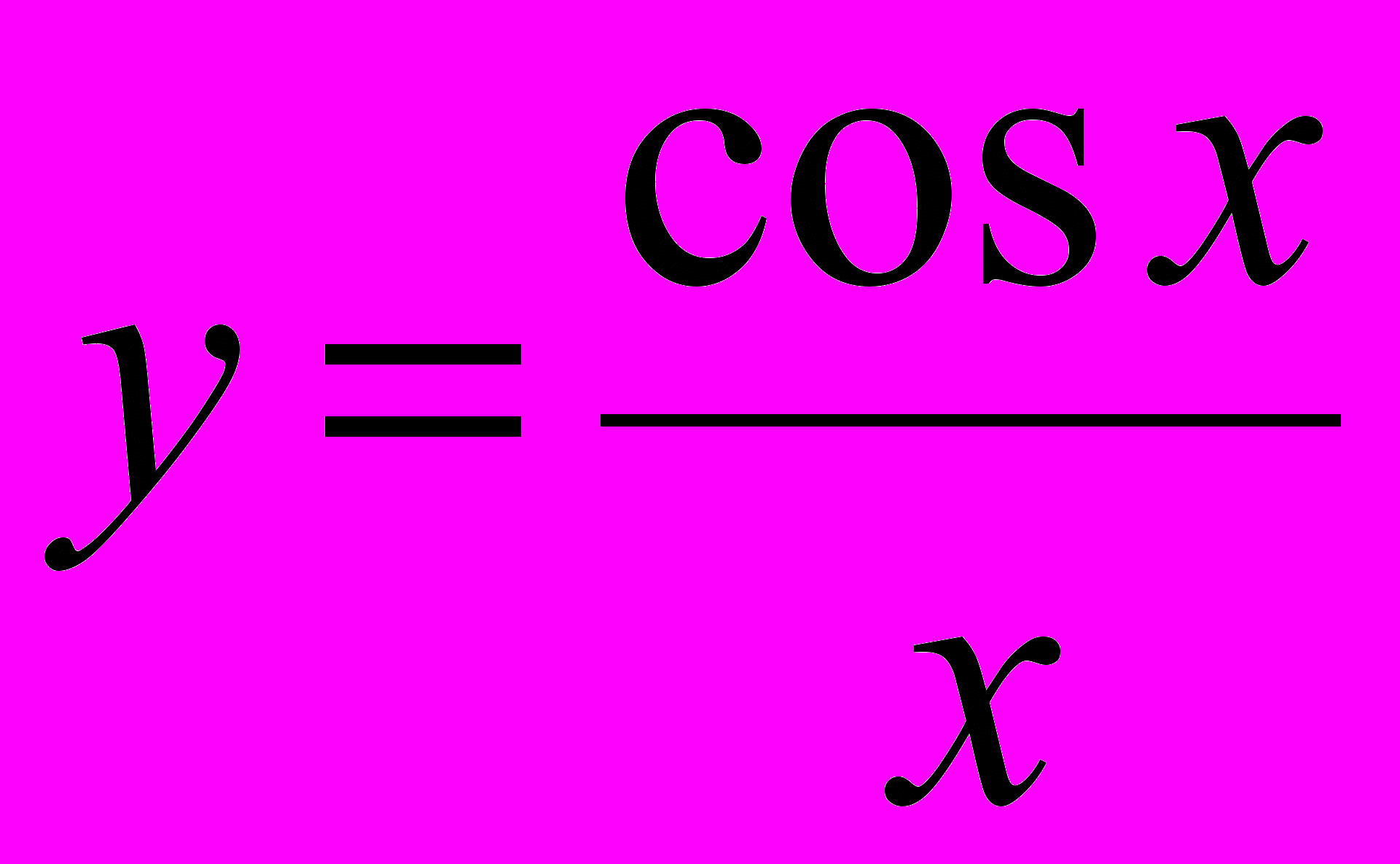 не определены в
не определены в точке x = 0. Указать характер графиков этих функций
в окрестности точки x = 0.
7. Сколько точек разрыва ( и какого рода) имеет
функция
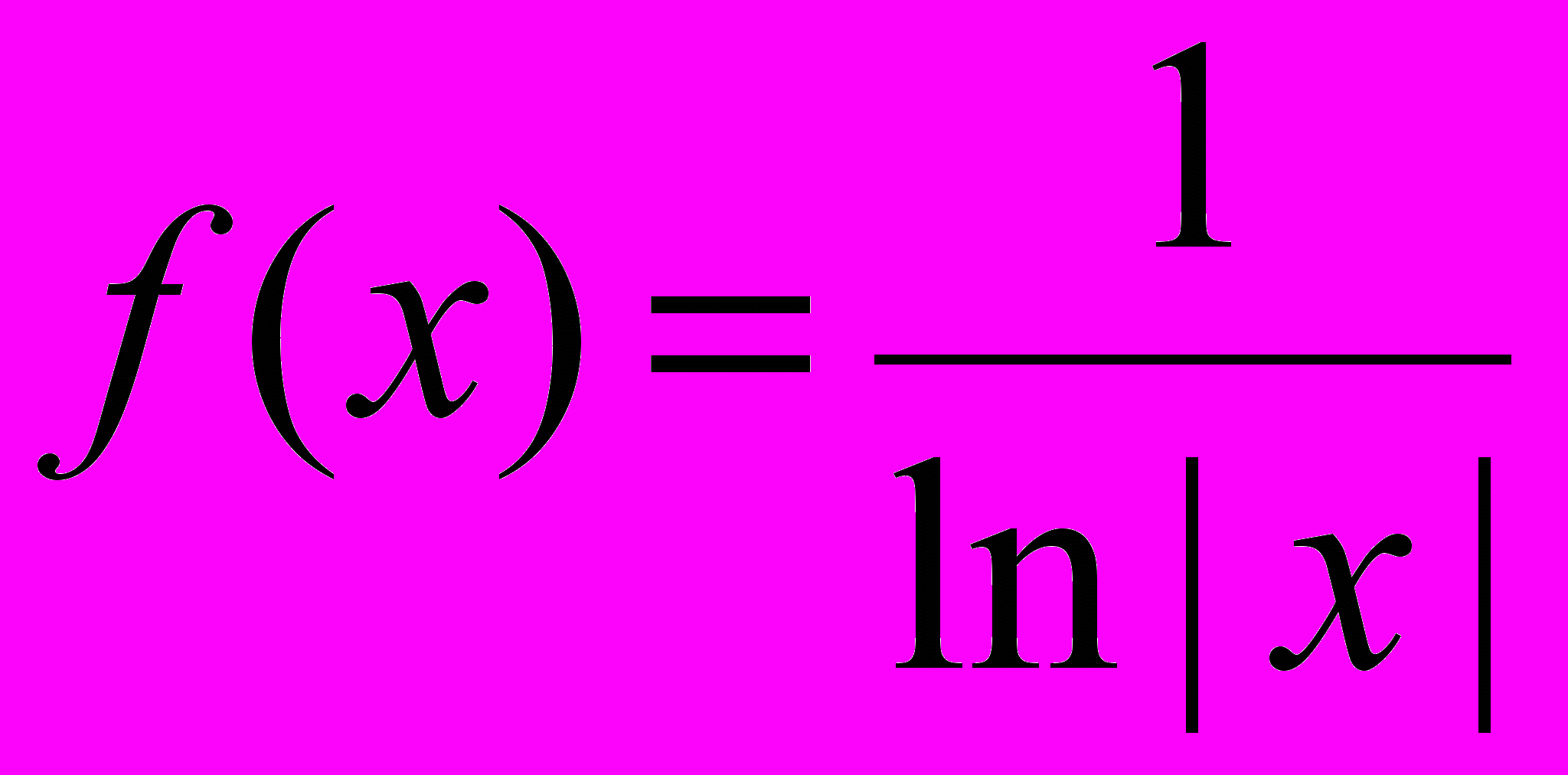 ?
?8. При каких значениях параметров а и b функция
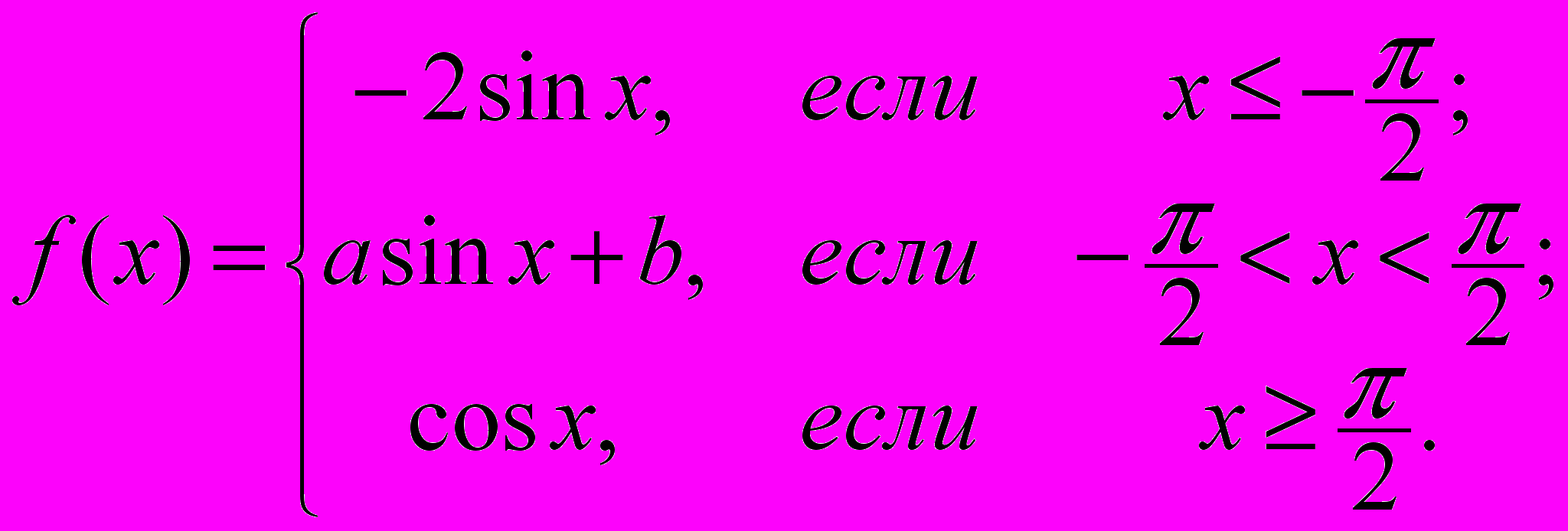
является непрерывной.
Задачи для самостоятельной работы
1. Найти точки разрыва функции. Определить скачок функции в
каждой точке разрыва и построить график:
а)
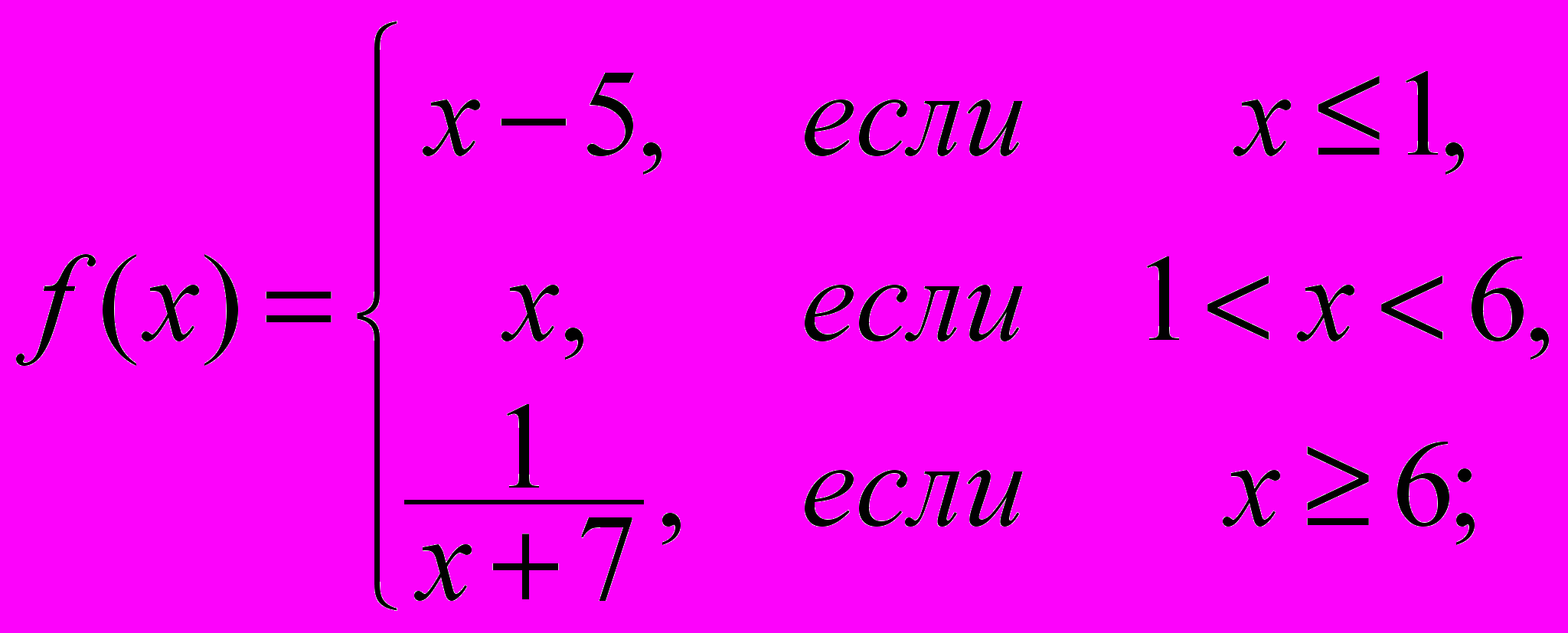 б)
б) 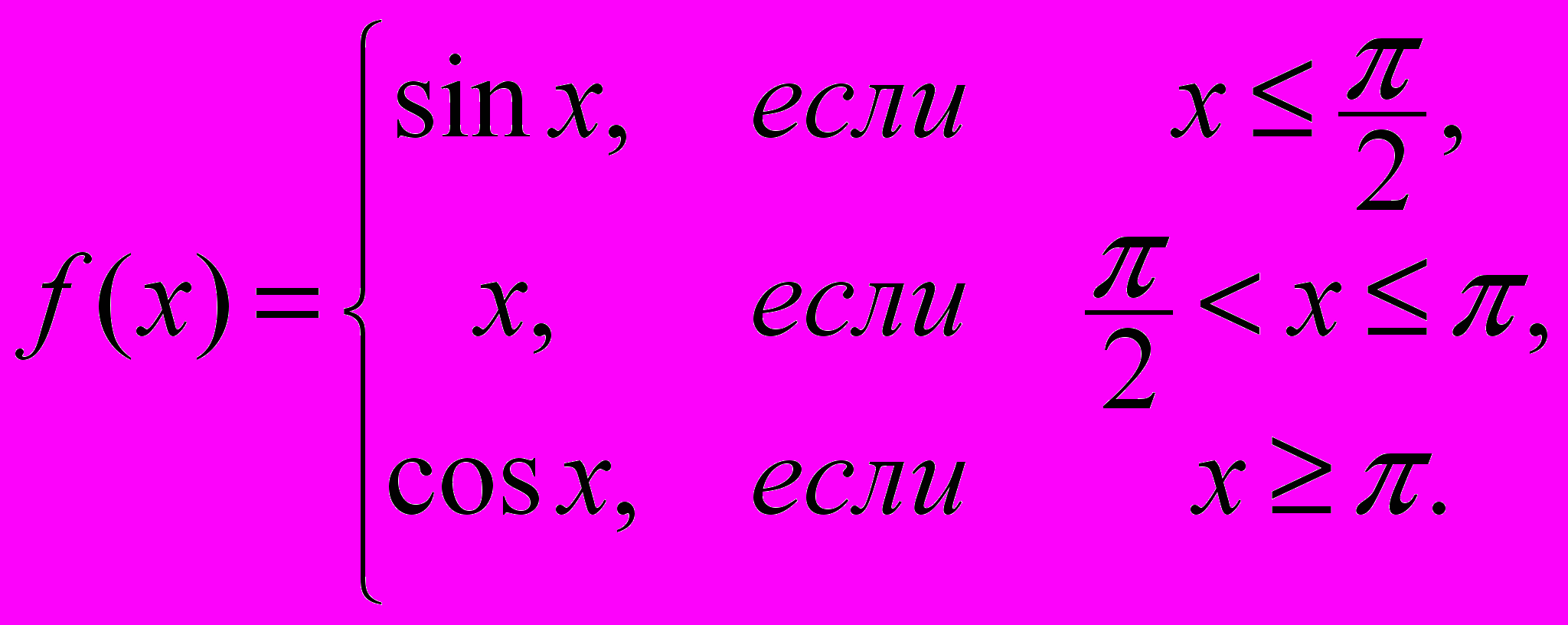
2. Установить характер разрыва функции f (x) в точке xо:
а)
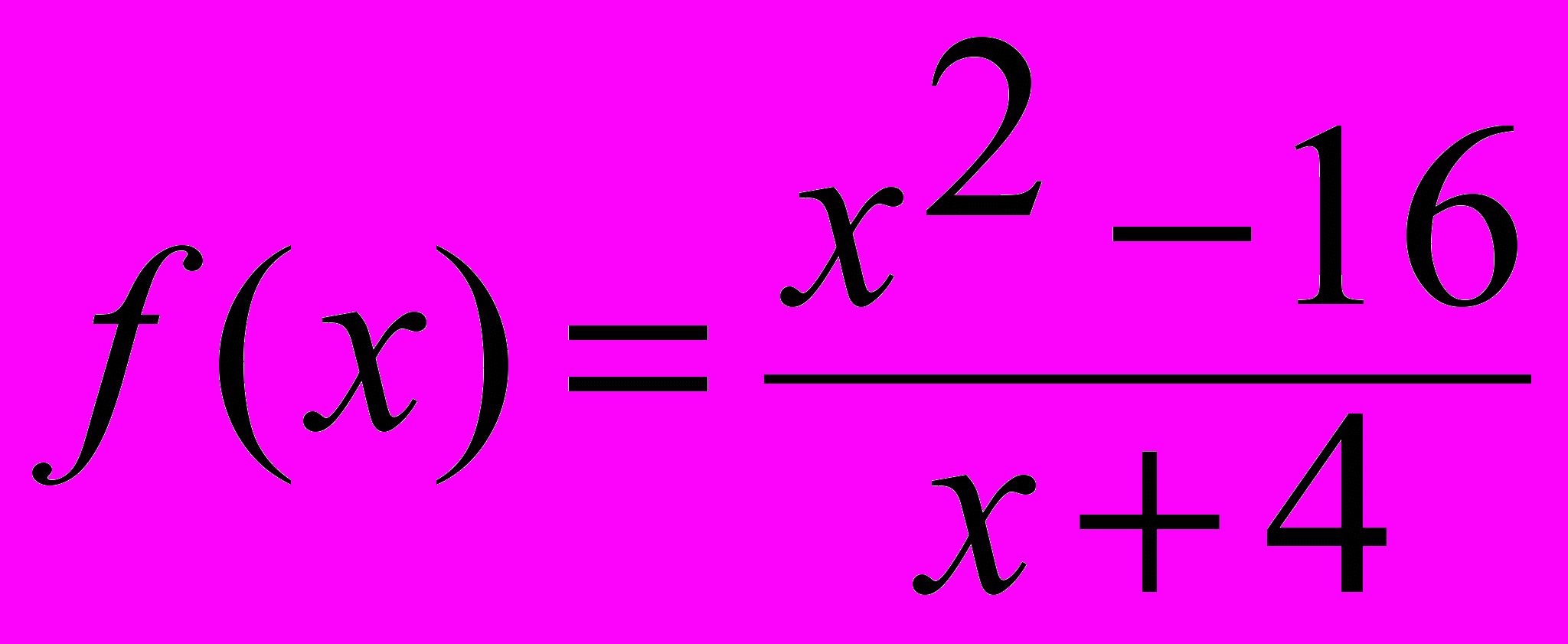 , xо = 4; б)
, xо = 4; б) 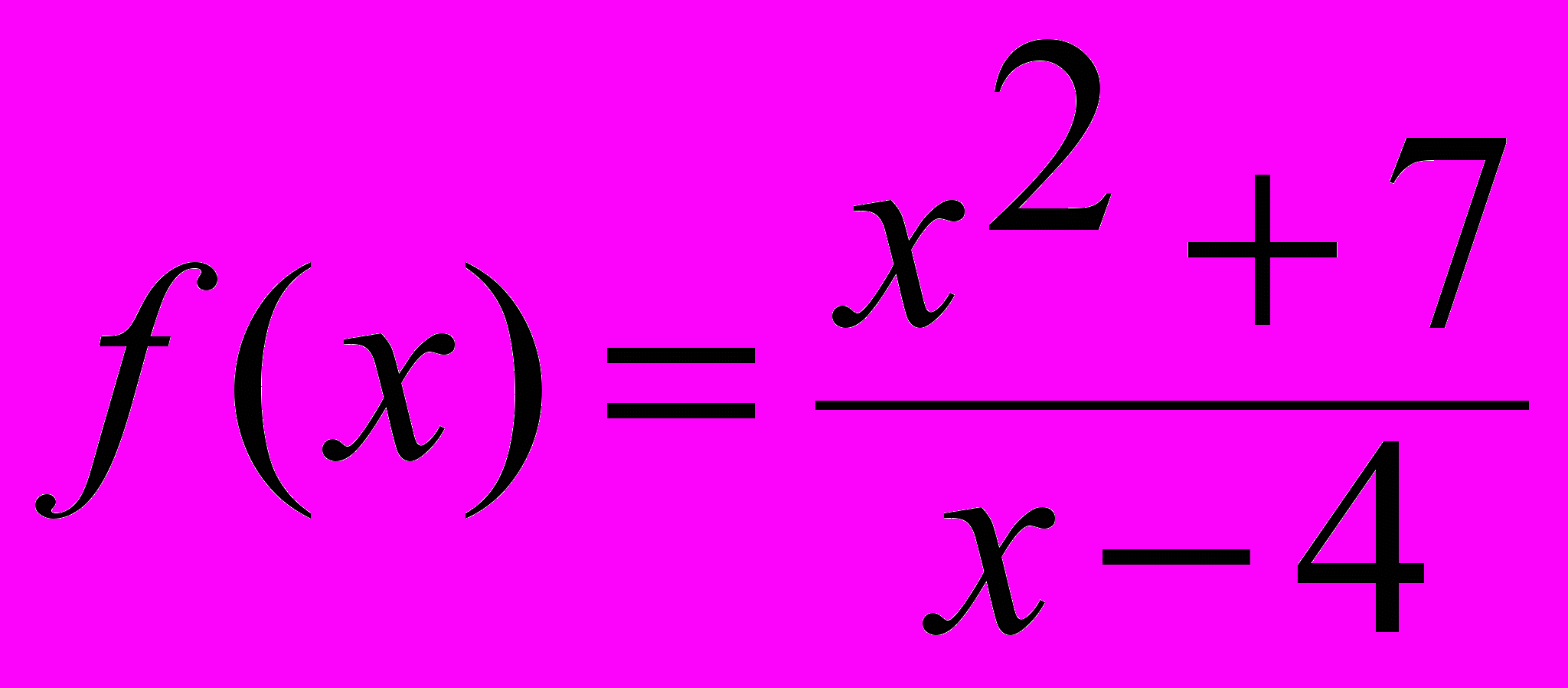 , xо = 4;
, xо = 4; в)
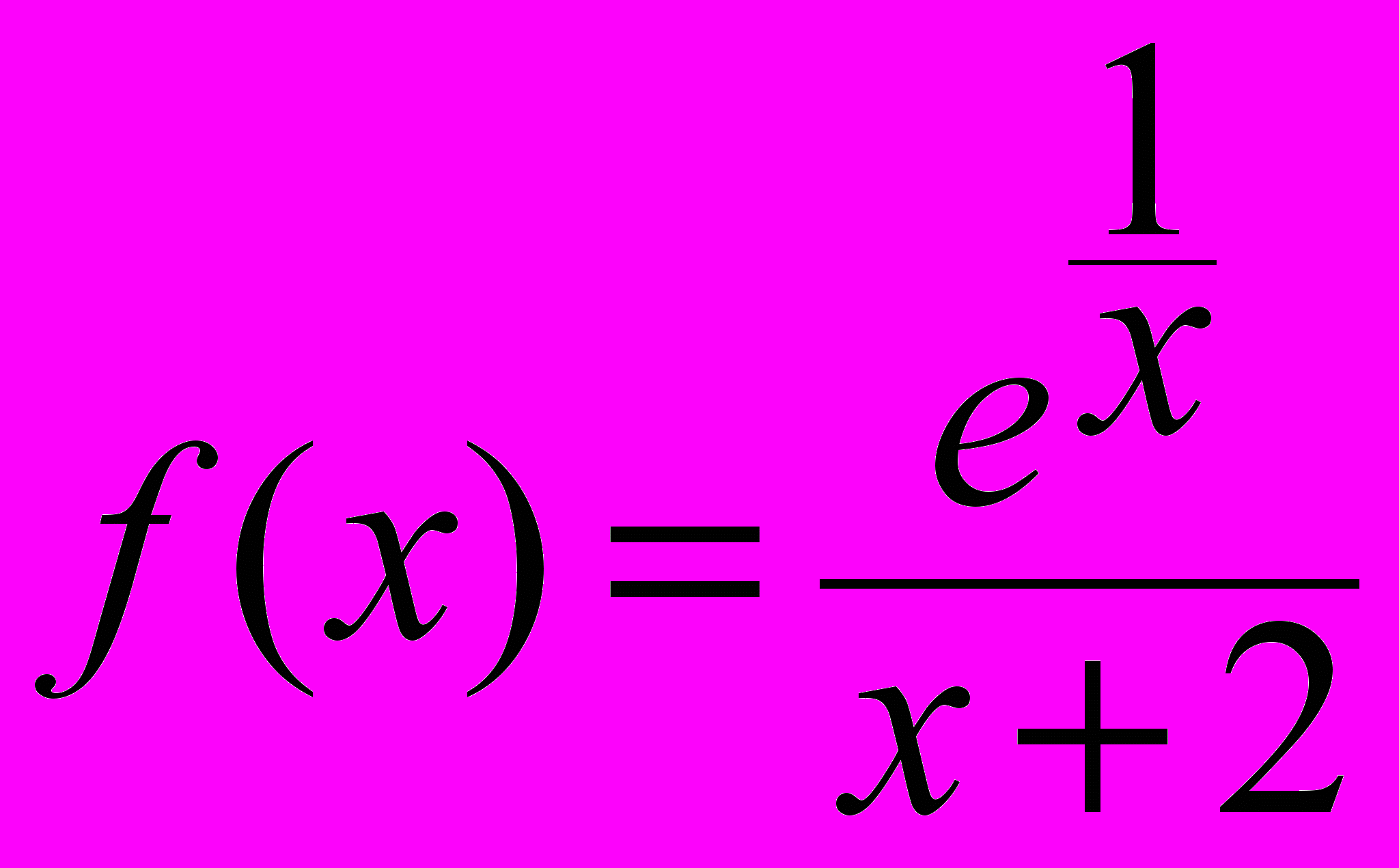 , xо = 0; г)
, xо = 0; г) 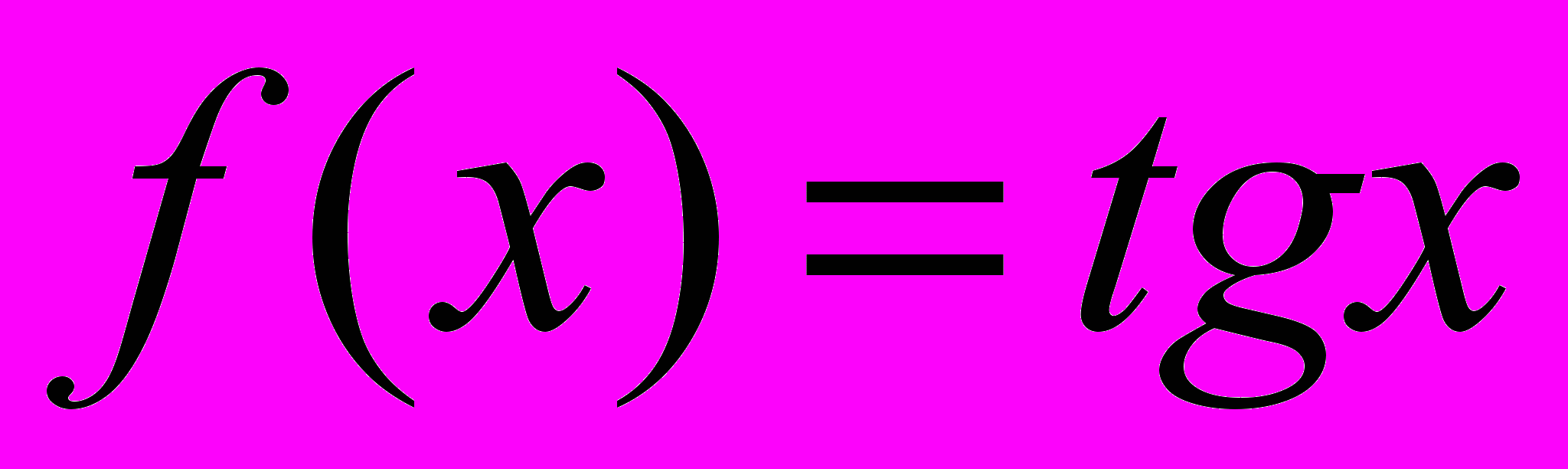 , xо =
, xо = 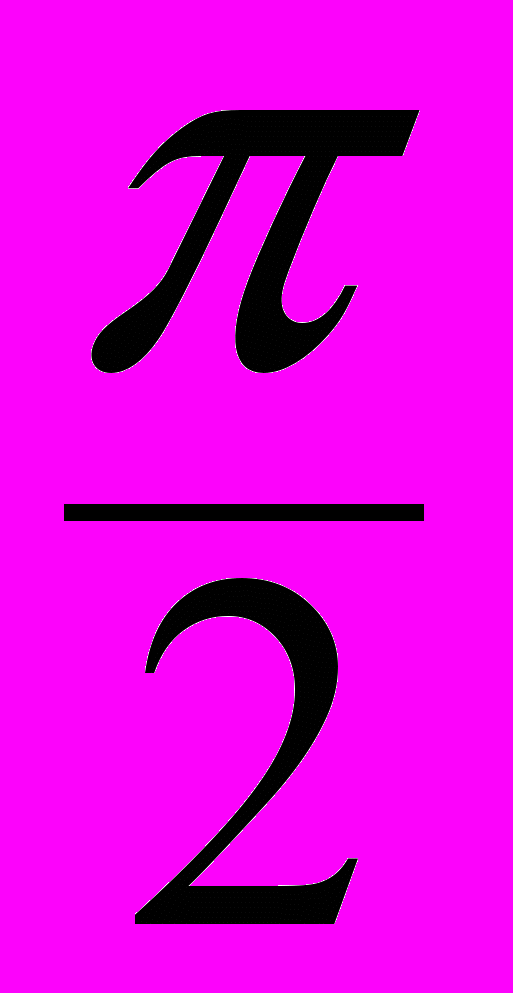 ;
;д)
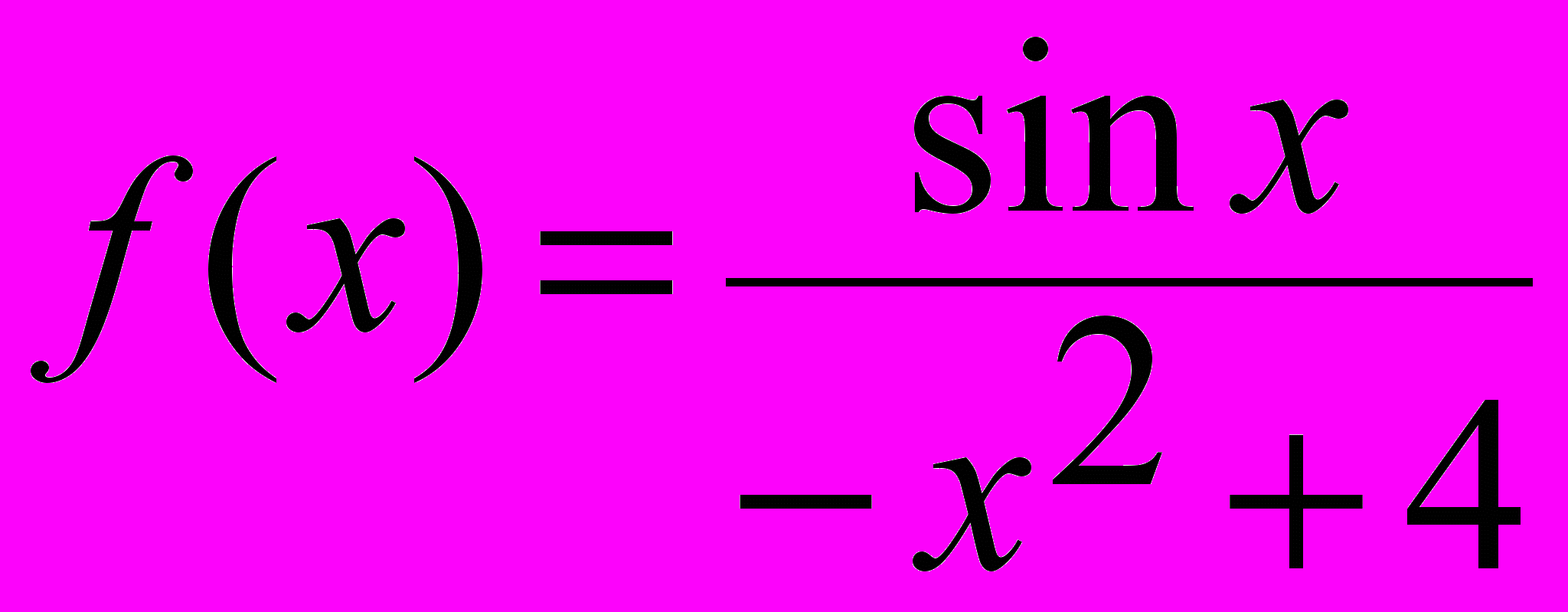 , xо =
, xо = 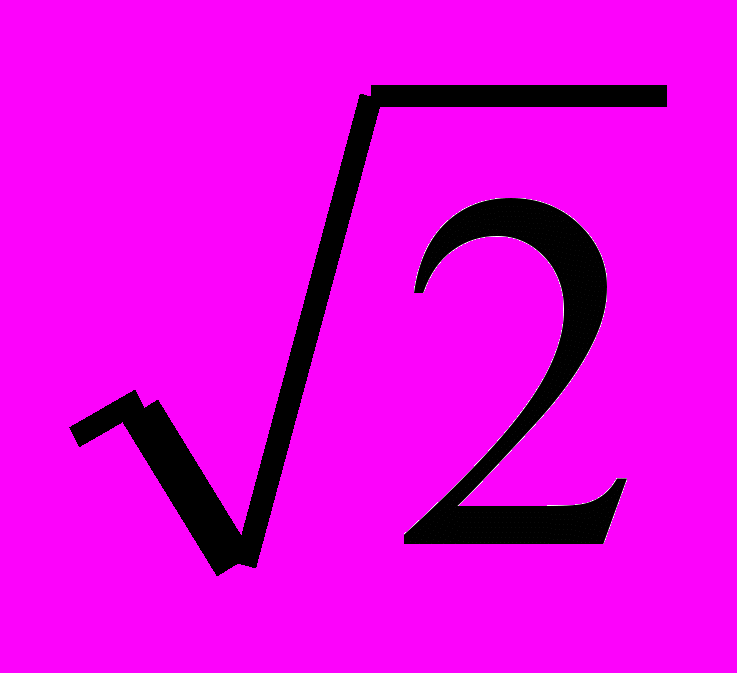 ; е)
; е) 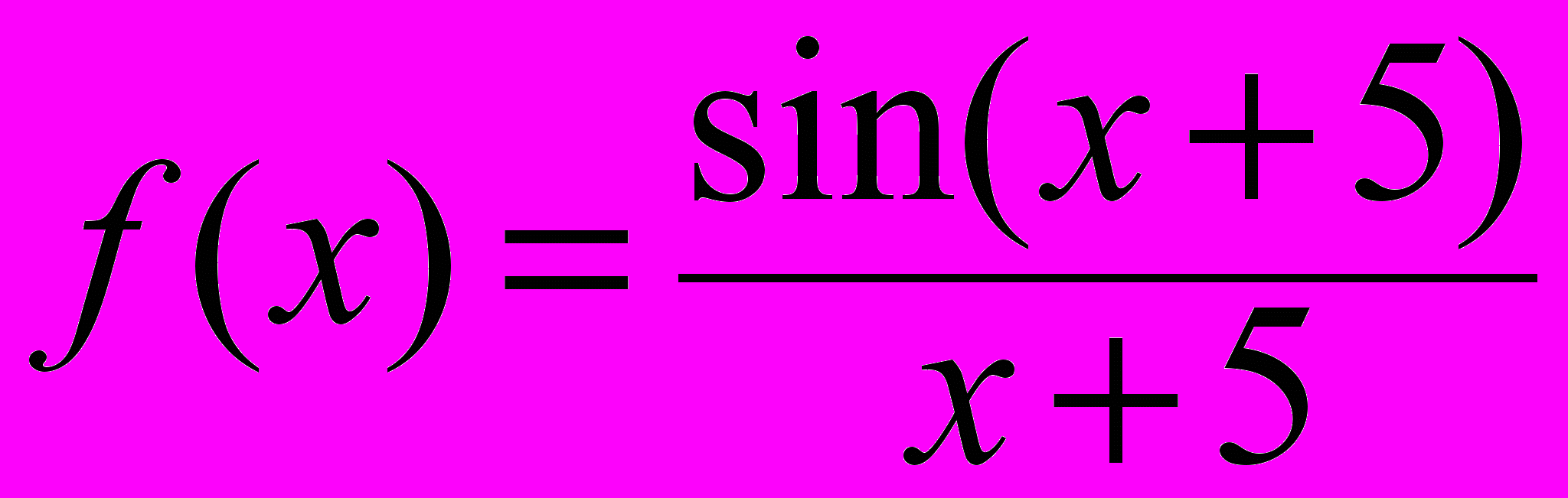 , xо = -5;
, xо = -5;ж)
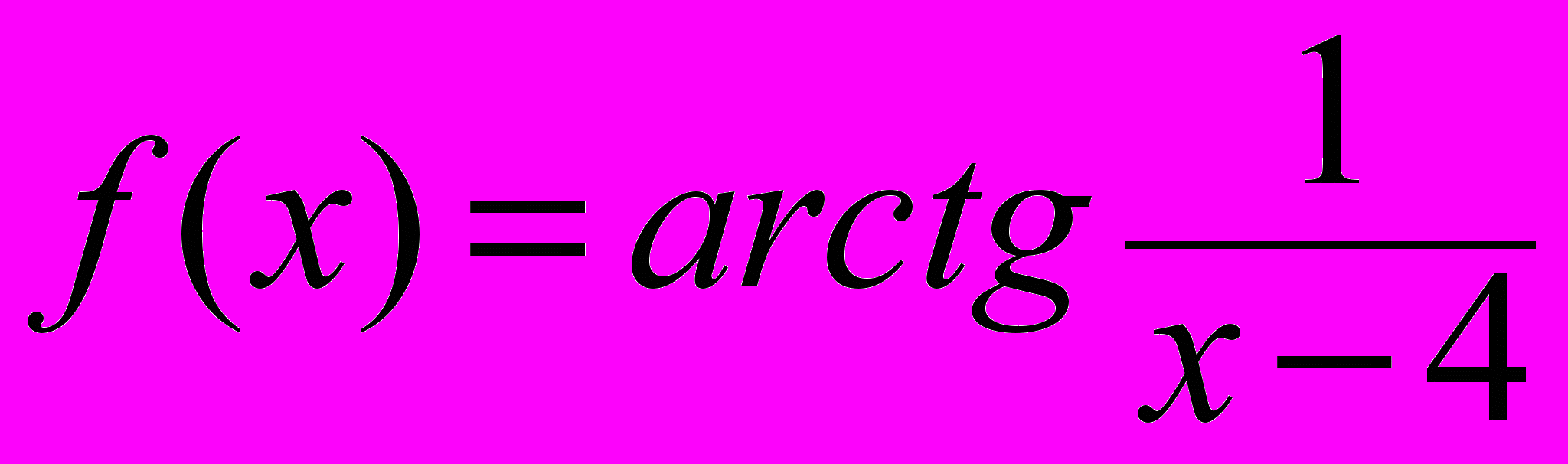 , xо = 4;
, xо = 4; 3. Исследовать функции на непрерывность:
а)
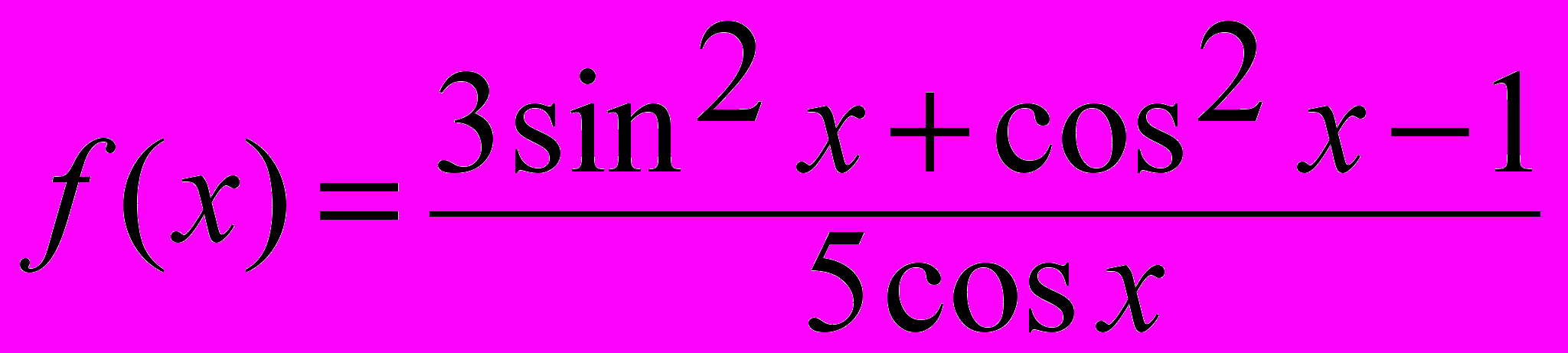 ; б)
; б) 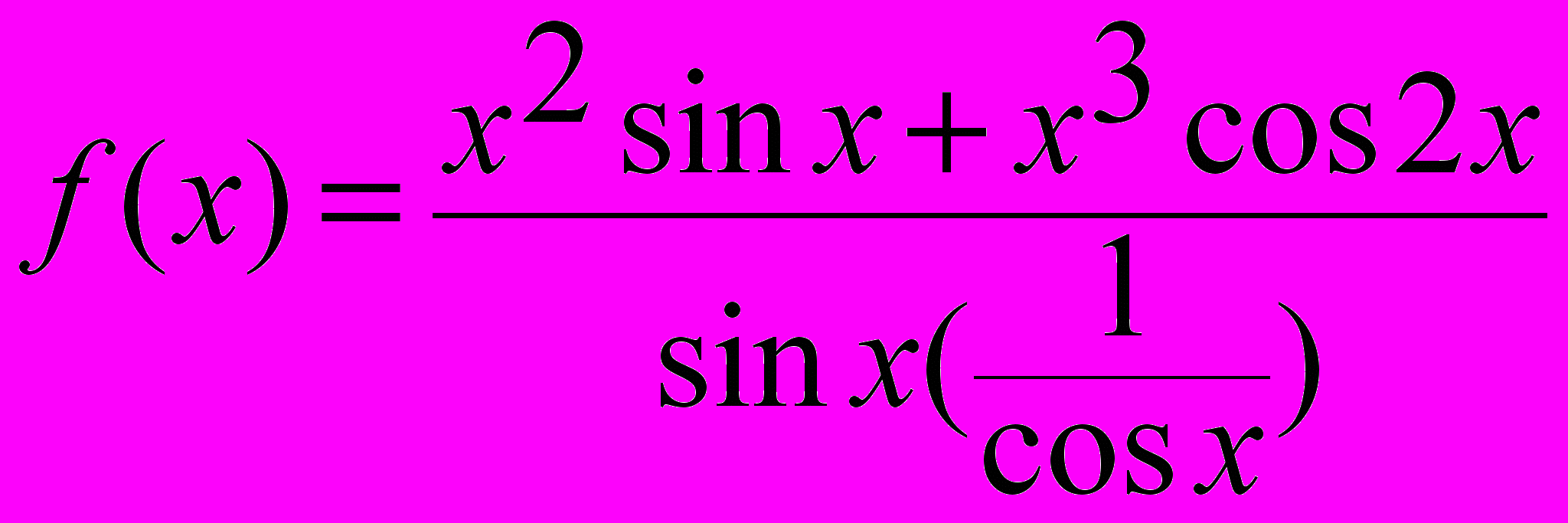 .
.4. а) Дана функция
 . Найти точки разрыва сложной
. Найти точки разрыва сложной функции
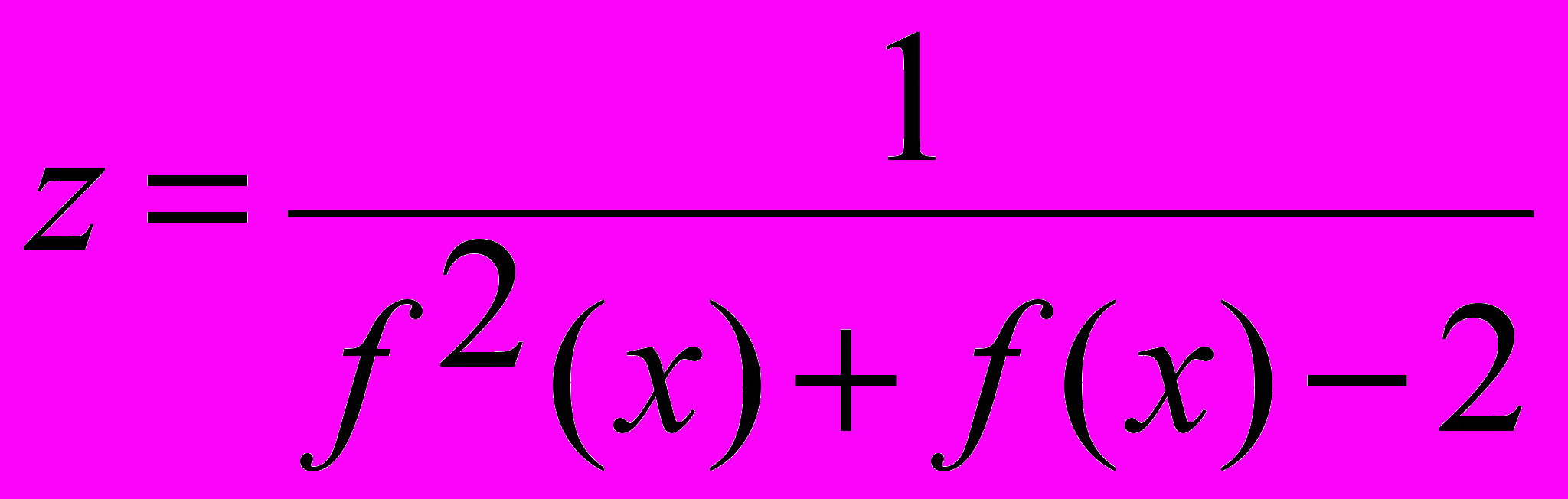 .
.б) Дана функция
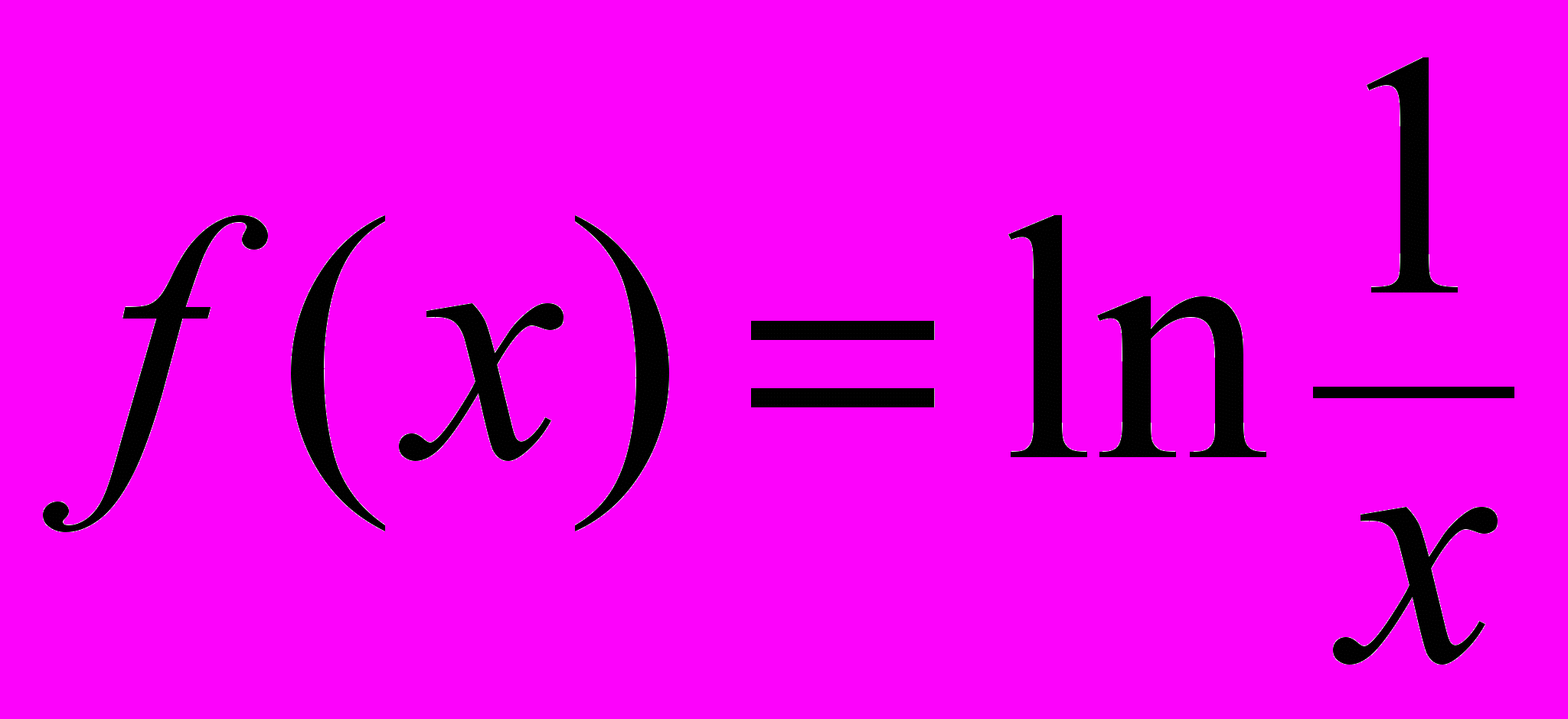 . Найти точки разрыва функции
. Найти точки разрыва функции 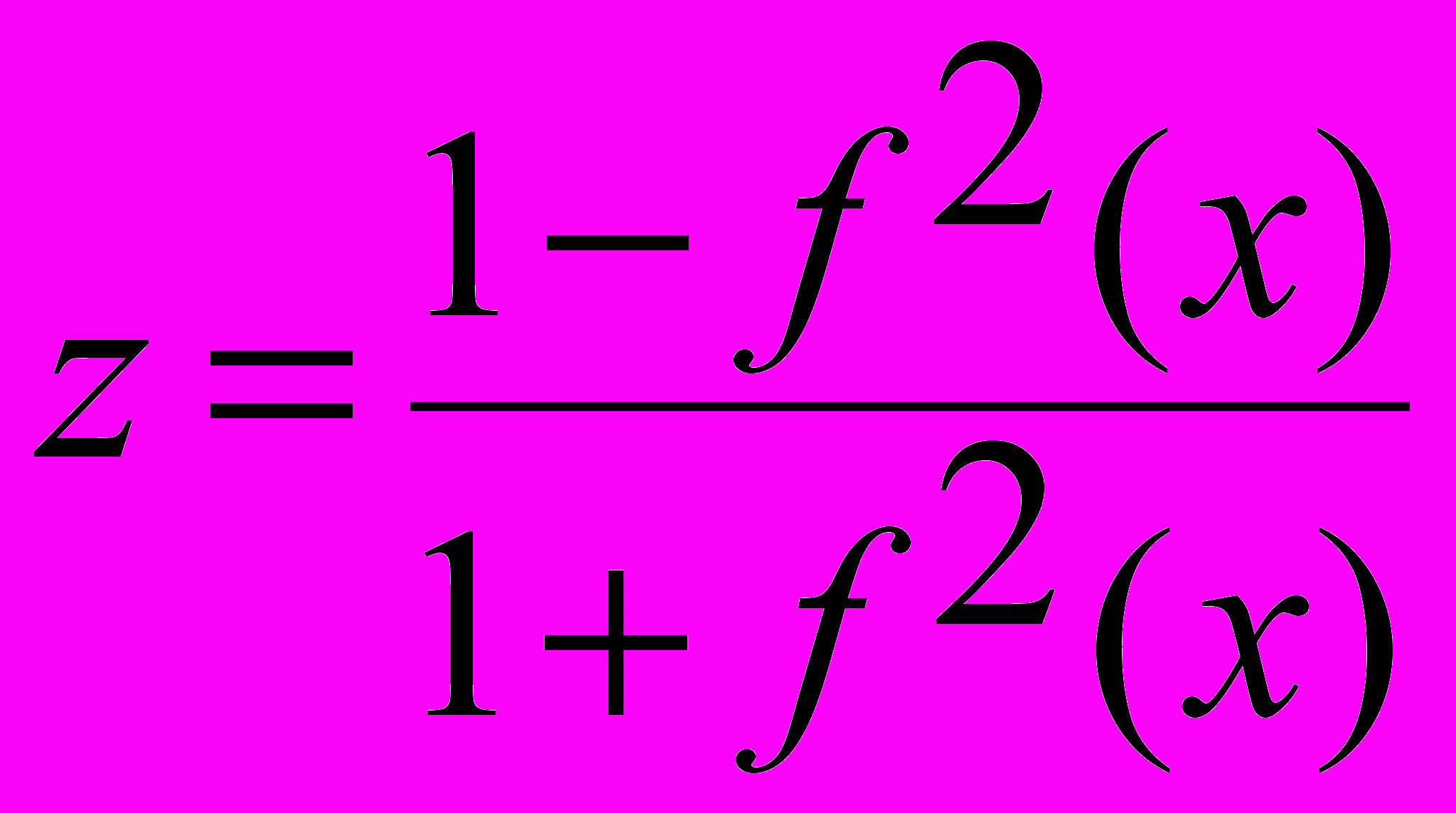 .
.в) Дана функция
 . Найти точки разрыва сложной
. Найти точки разрыва сложной функции z = f(f(x)).
г) Дана функция
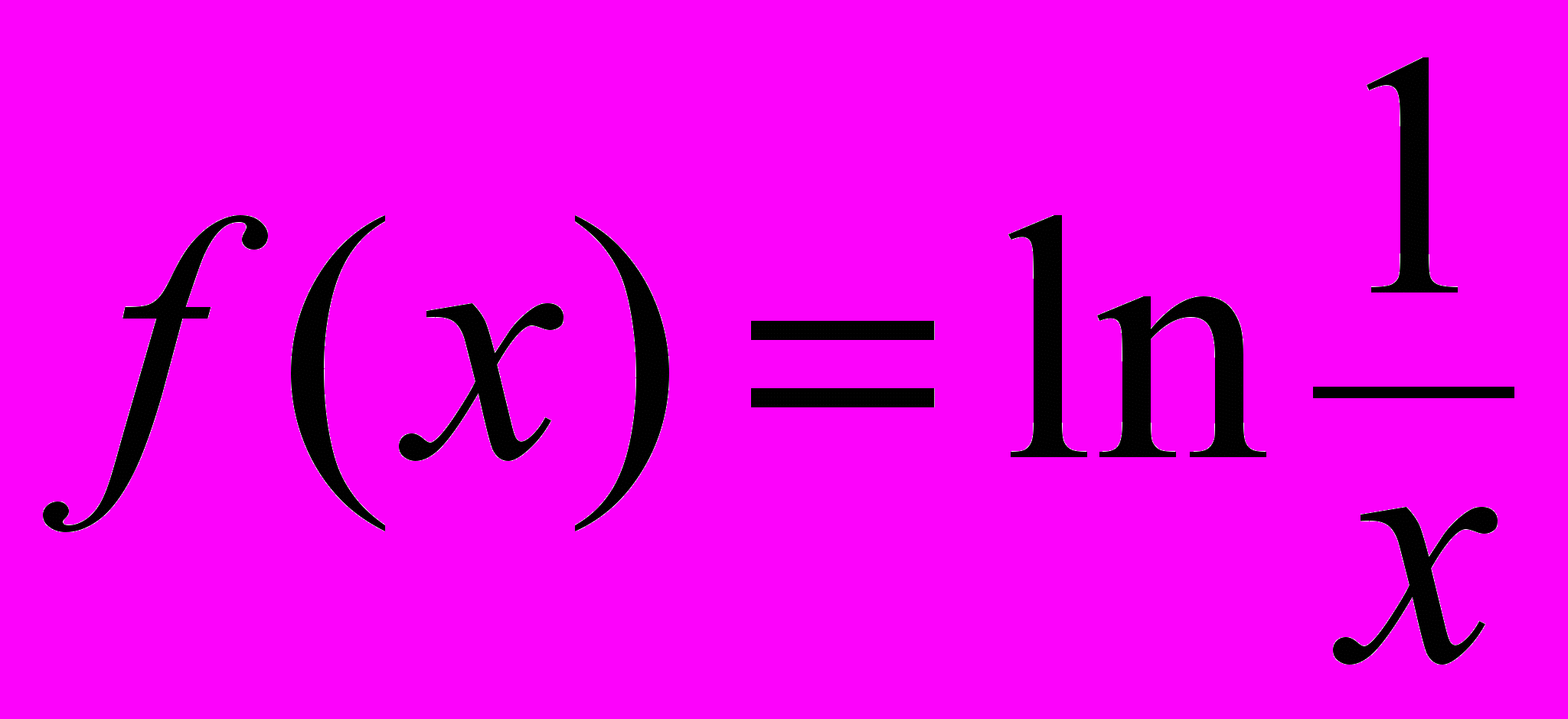 . Найти точки разрыва сложной
. Найти точки разрыва сложной функции z = f(f(x)).
- Доопределить следующие функции в точке разрыва так, чтобы они стали непрерывными:
а)
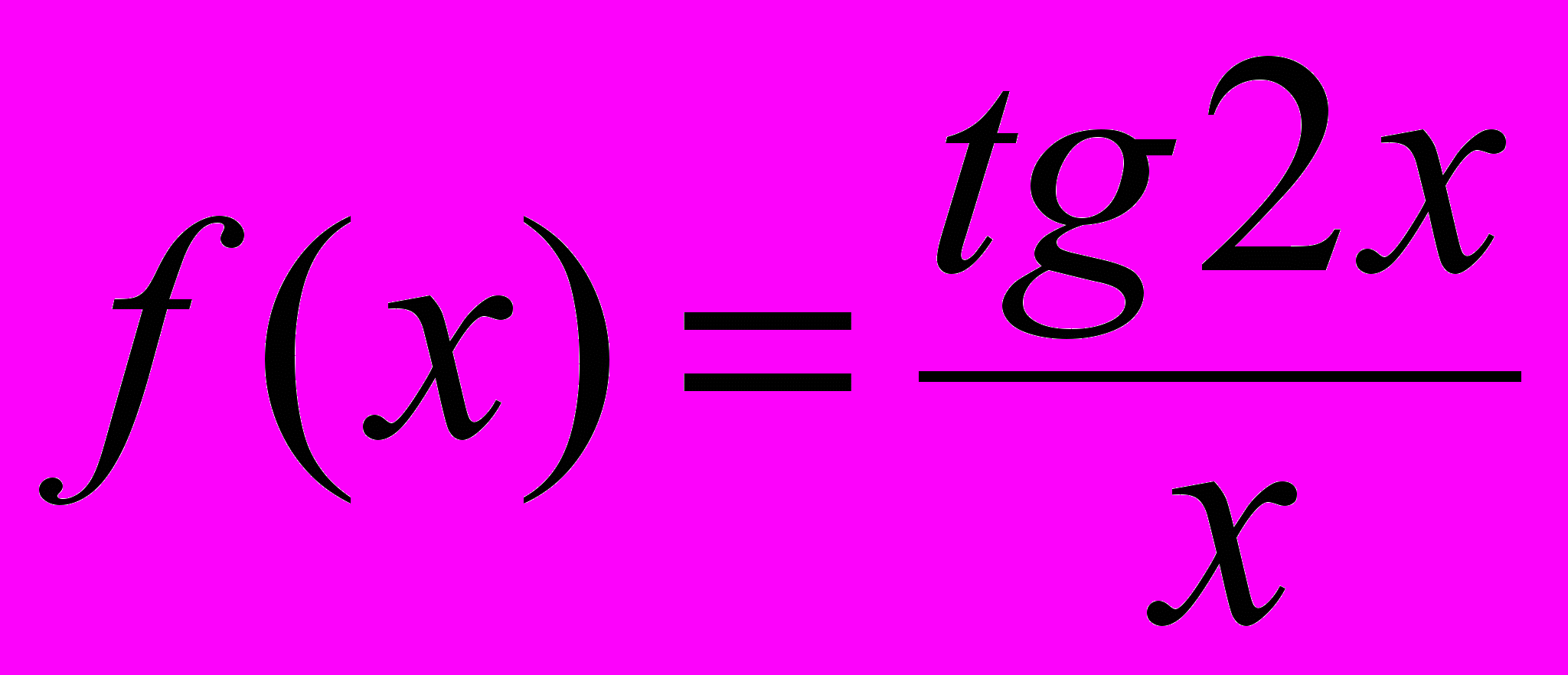 ; б)
; б) 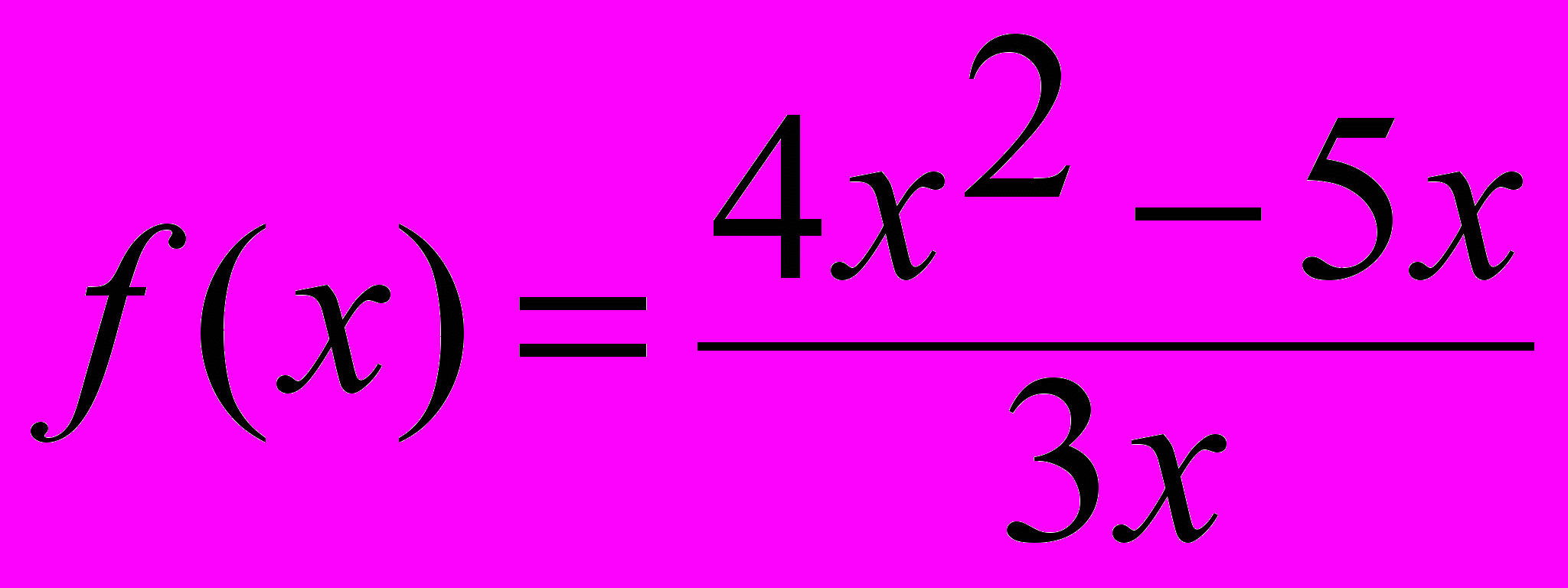 ; в)
; в)  ;
; г)
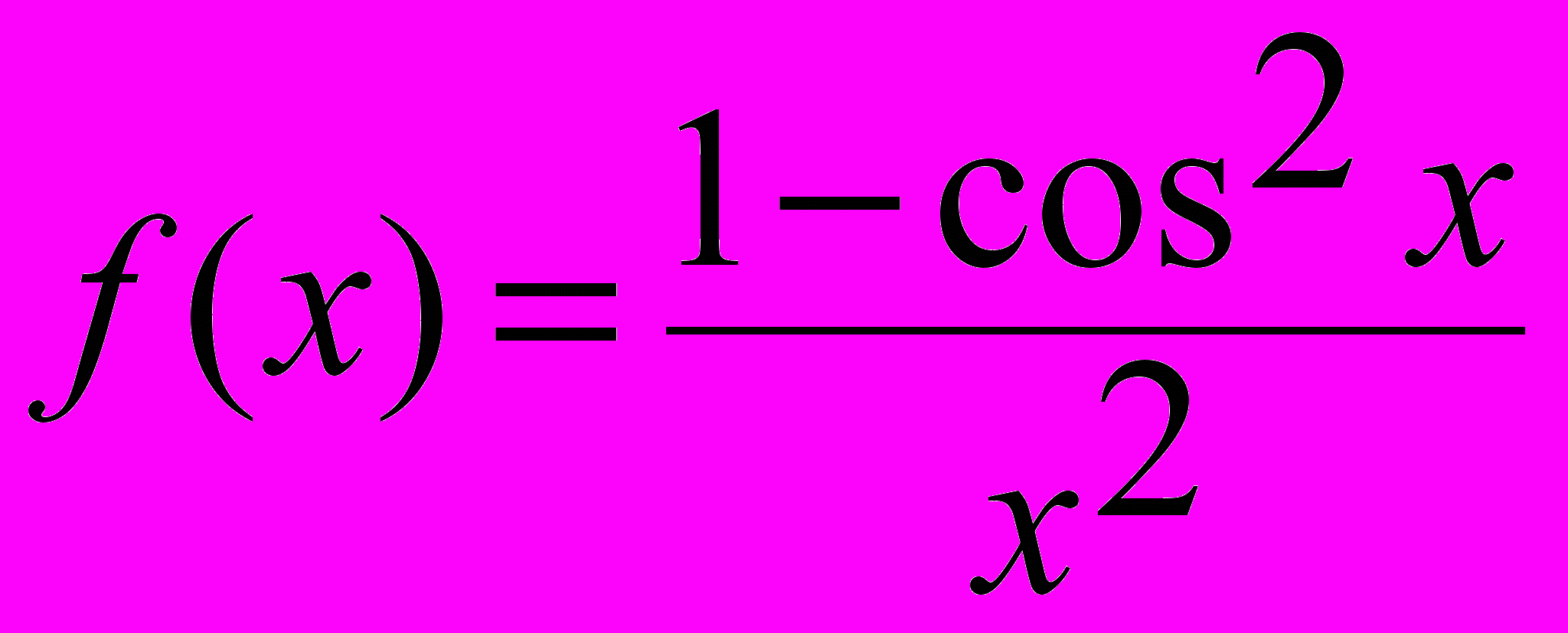 ; д)
; д)  ; e)
; e) 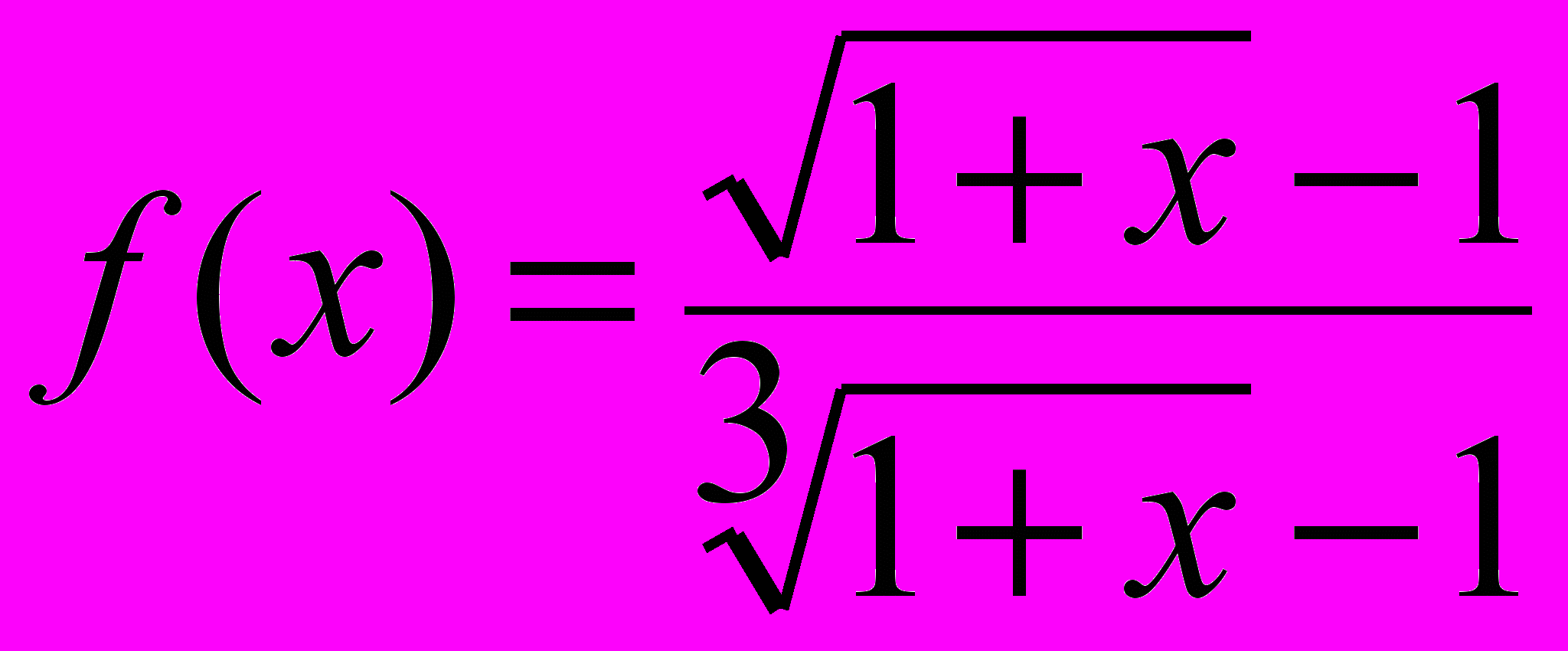 ;
;ж)
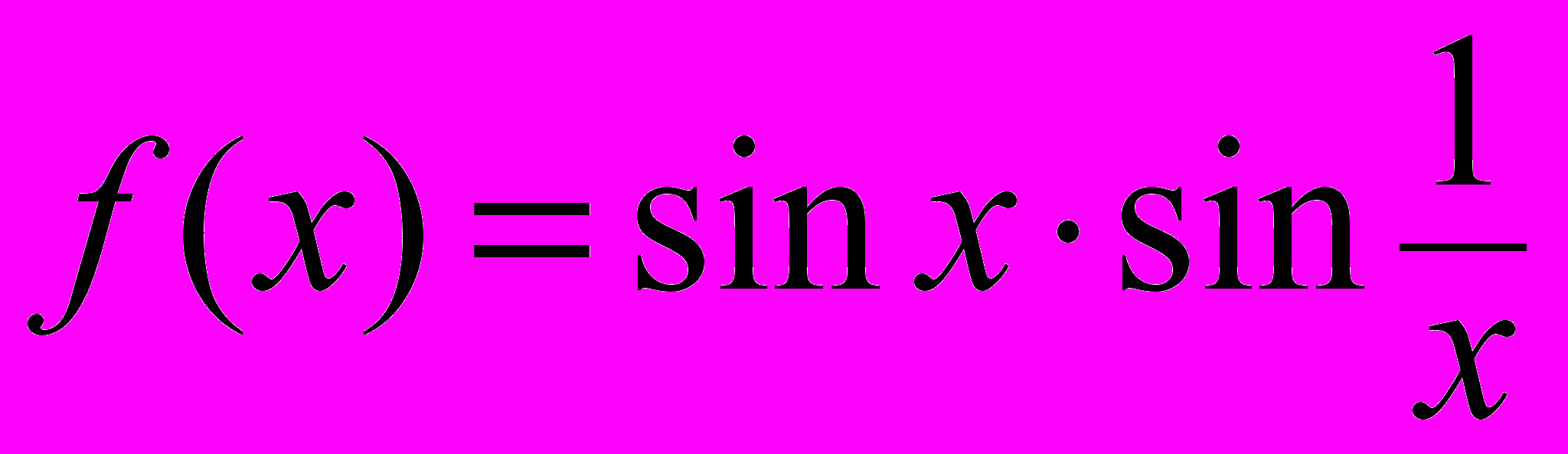 ; з)
; з) 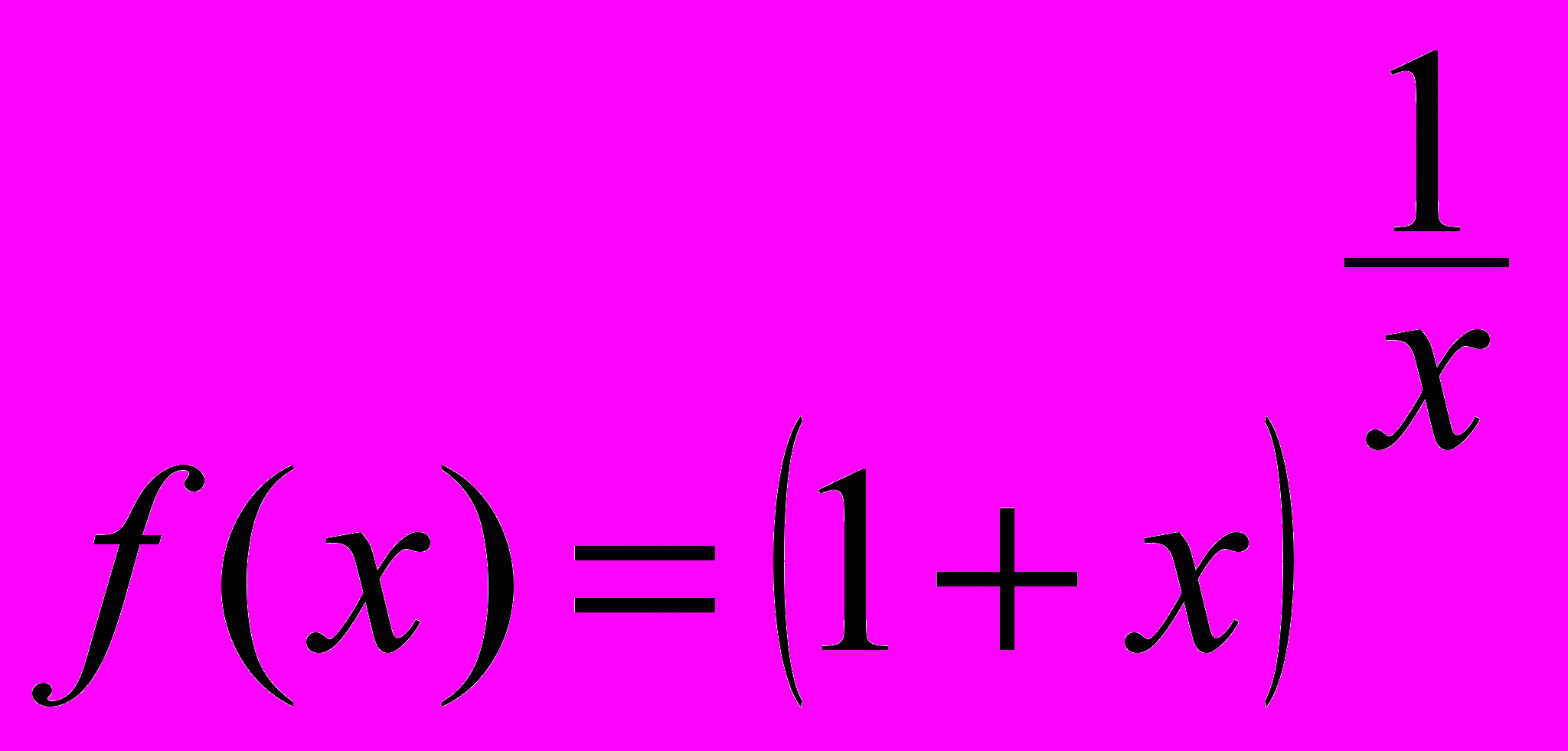 .
.Проверочная работа № 3 – 0
(с решением)
1. Пользуясь определением, доказать непрерывность функции
f(x) = 4x2 -5x + 2 в каждой точке xоÎ R.
2. Найти точки разрыва функции
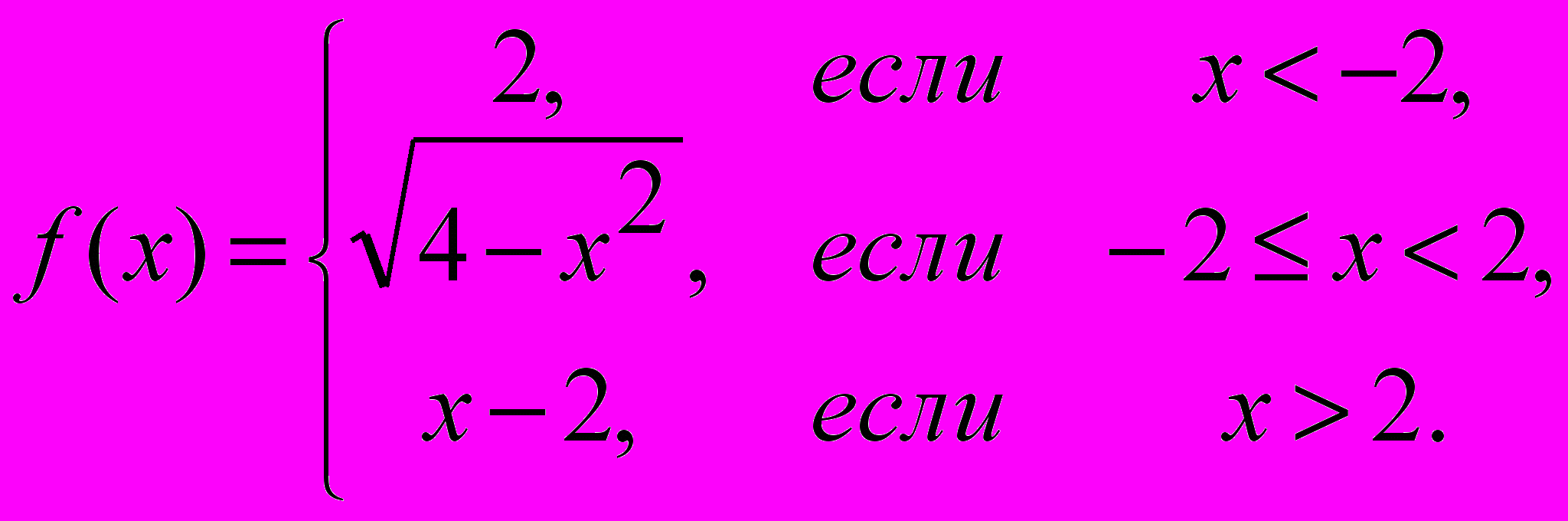
Определить скачок функции в каждой точке разрыва и
построить график.
3. Исследовать функцию f(x) =
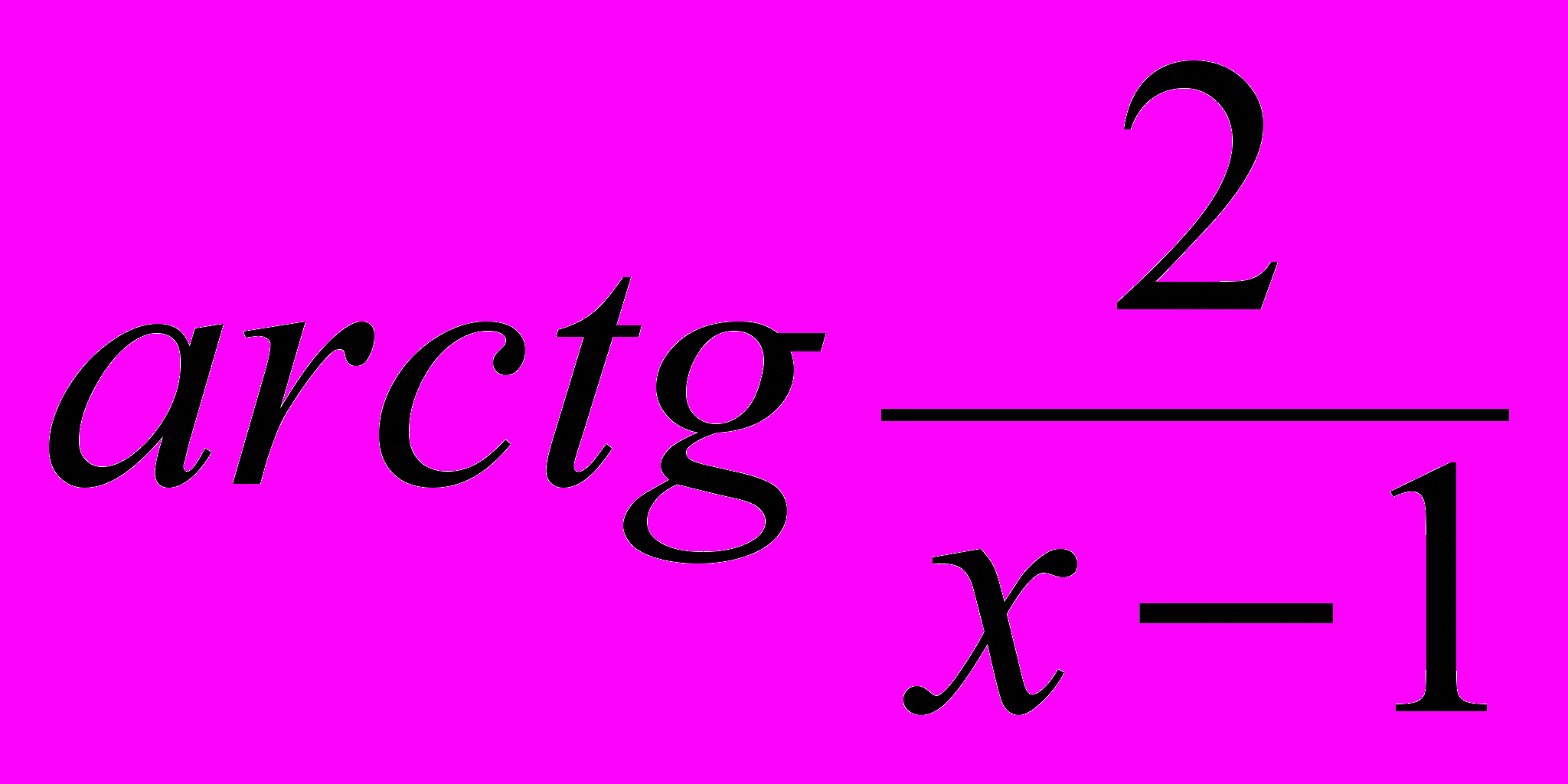 на непрерывность
на непрерывность в точке xо = 1.
4. Найти точки разрыва функции
 и
и определить их характер.
Решение проверочной работы № 3 – 0
1. Пусть Dх - приращение аргумента в точке xоÎ R.
Найдем соответствующее приращение функции:

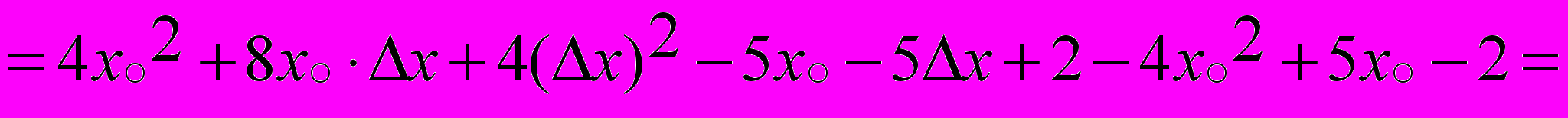
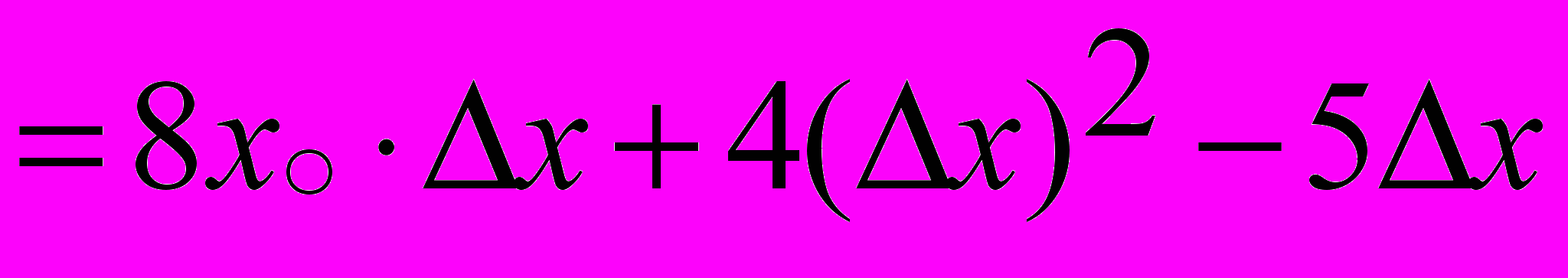
Применяя теоремы о пределе суммы и пределе произведения функций, получим:
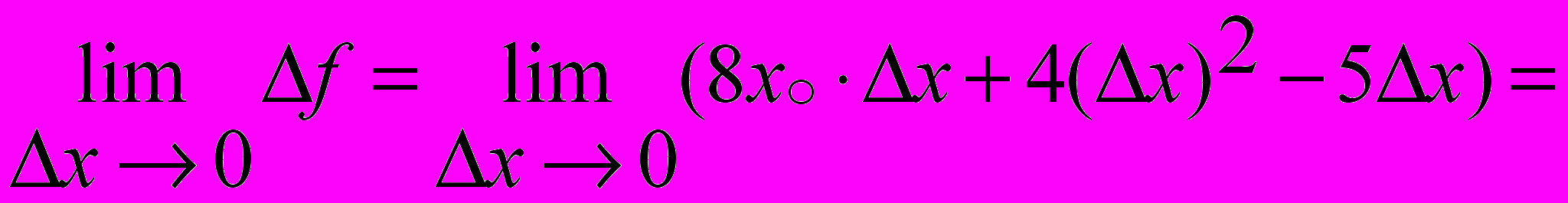
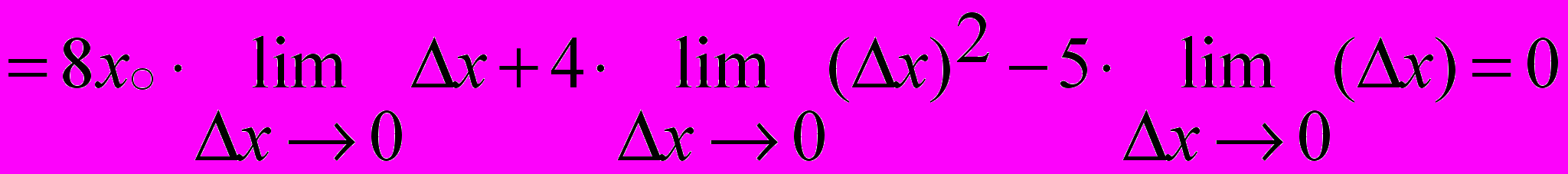 .
.Значит, по определению функция непрерывна в каждой точке
xоÎ R.
2. Рассмотрим односторонние пределы функции в точках, в которых меняется аналитическое задание функции числитель и знаменатель обращаются в ноль):
x = -2 и x = 2.
При x ® -2-0 предел рассматривается слева от точки x = -2,
имеем:

При x ® -2+0 предел рассматривается справа от точки x = -2, имеем:
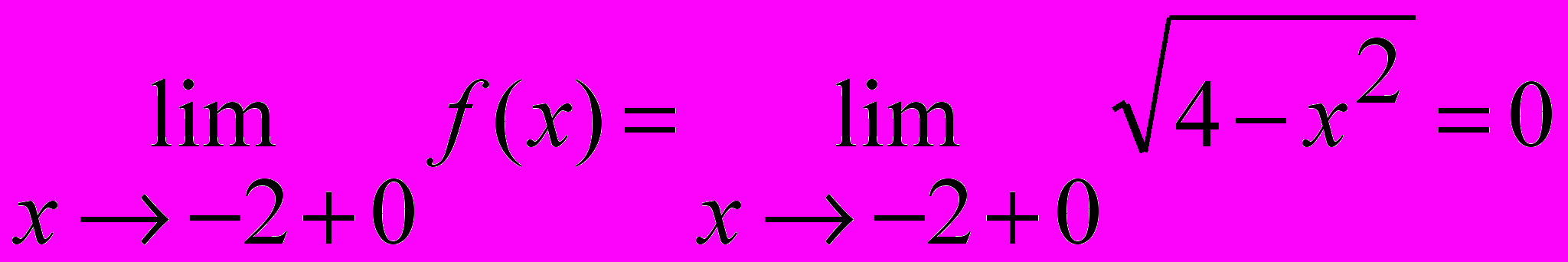 .
.Так как односторонние пределы конечны, но не равны
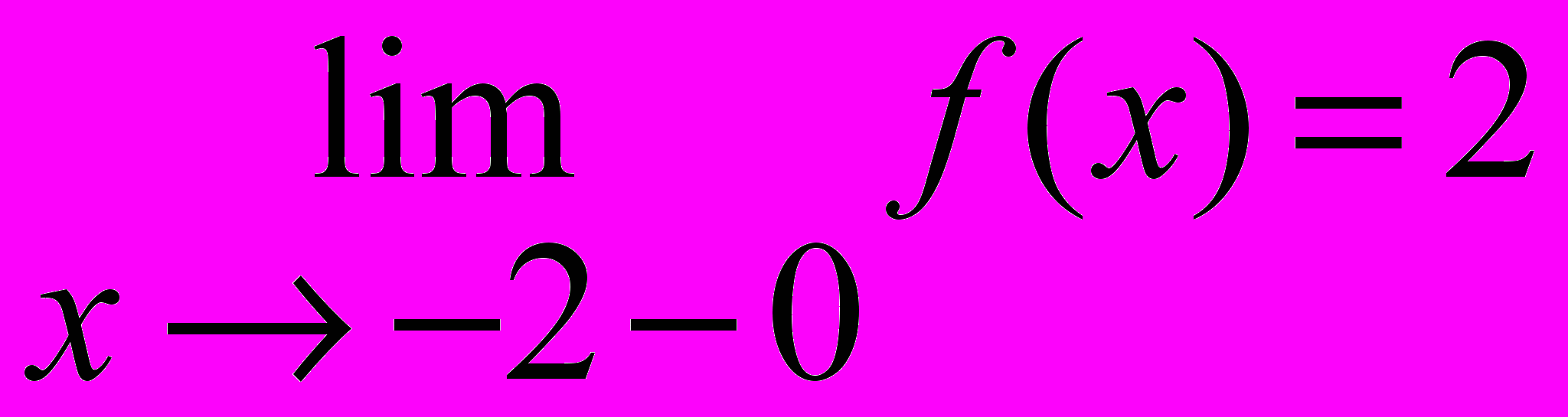 ,
, ,
, то x = -2 является точкой разрыва I рода.
Скачок функции в этой точке разрыва равен 2.
Рассмотрим односторонние пределы при x ®2 -0 и x ®2 +0:
 ,
,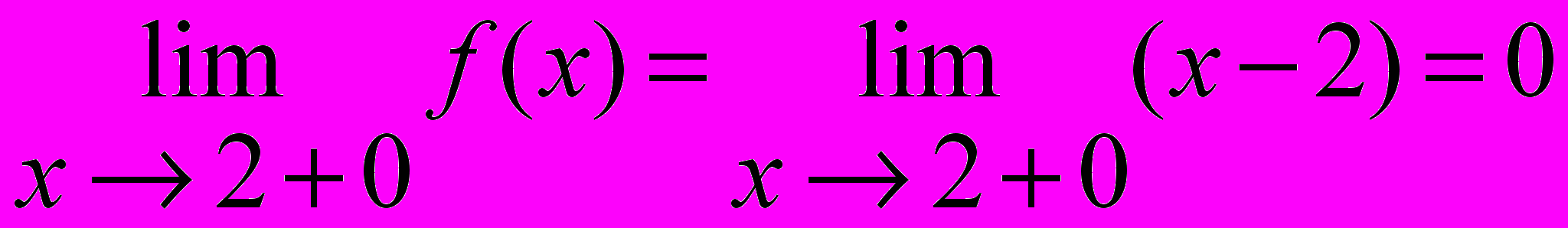 .
.Односторонние пределы конечны и равны, значит
существует предел функции в точке x = 2, но функция в этой точке не определена. x = 2 - точка устранимого разрыва.
3. Функция f (x) =
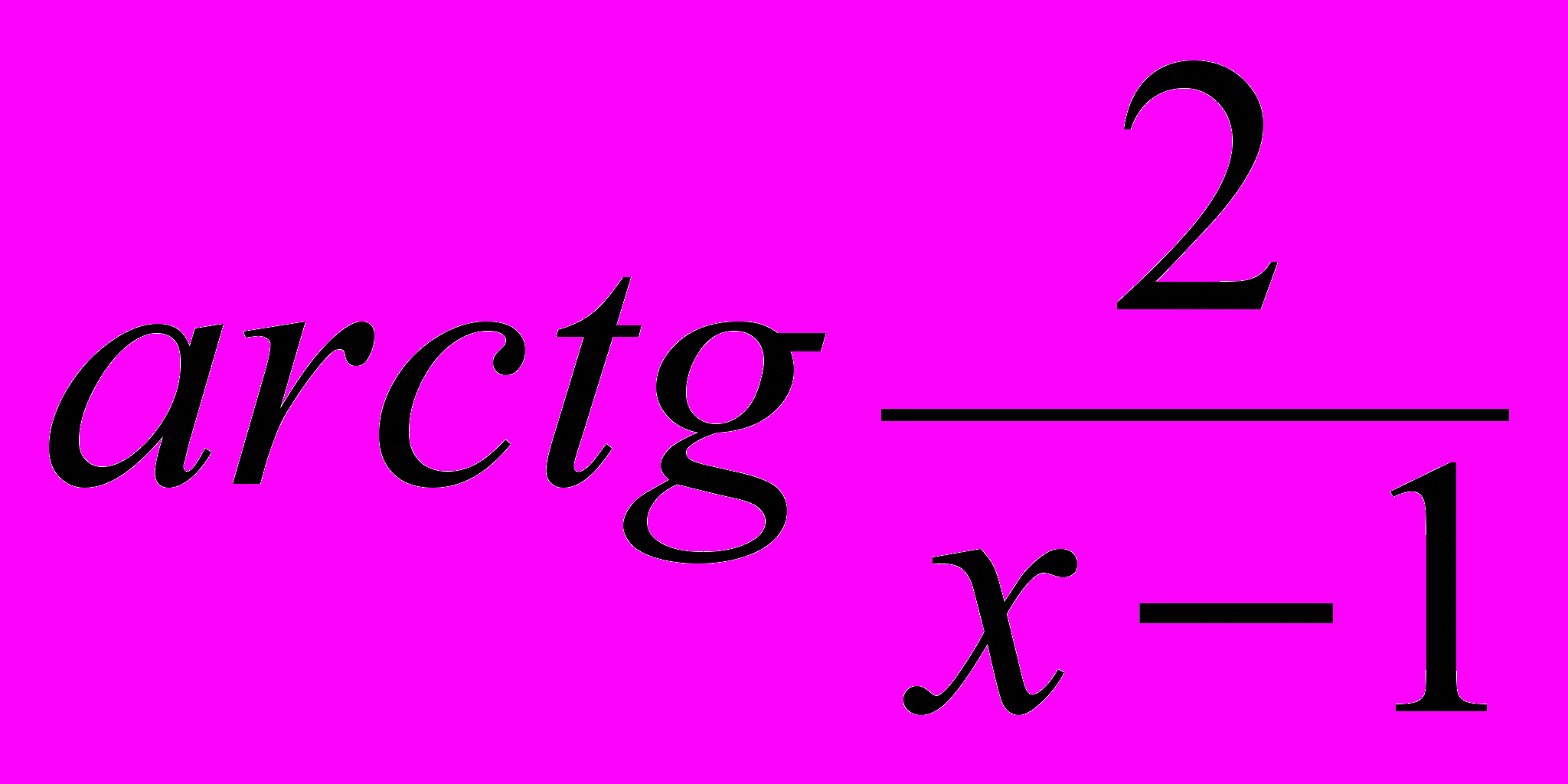 не определена в точке xо = 1,
не определена в точке xо = 1, нарушено условие существования f (1), значит, функция не
является непрерывной в этой точке.
Найдём односторонние пределы функции в этой точке:
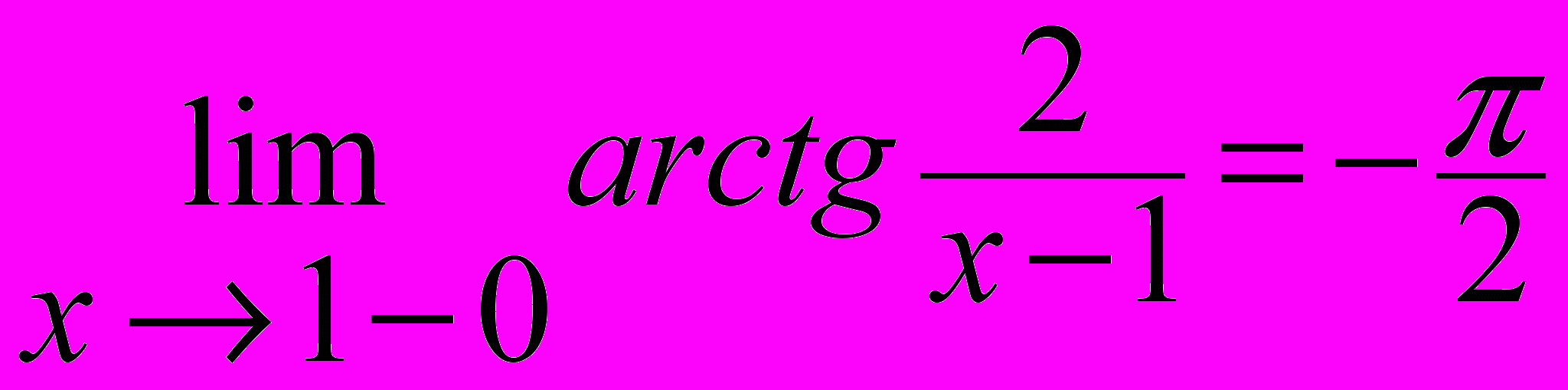 ,
, 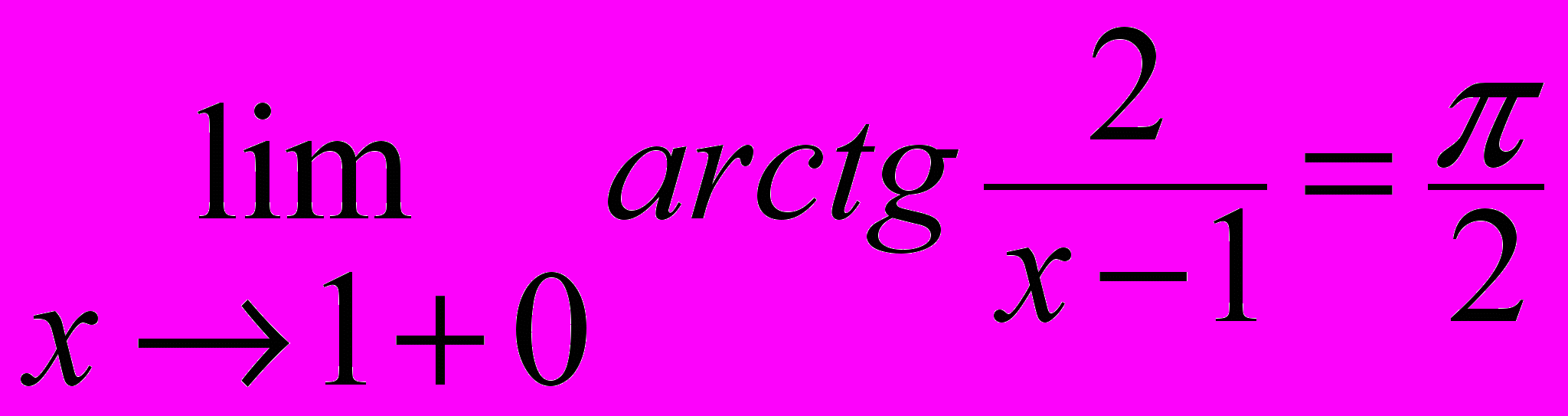 .
.Они конечны, но не равны. Значит, нарушено и второе
условие существования предела функции в этой точке.
Итак, точка xо = 1 - точка разрыва первого рода.
4. Представим данную функцию в виде:
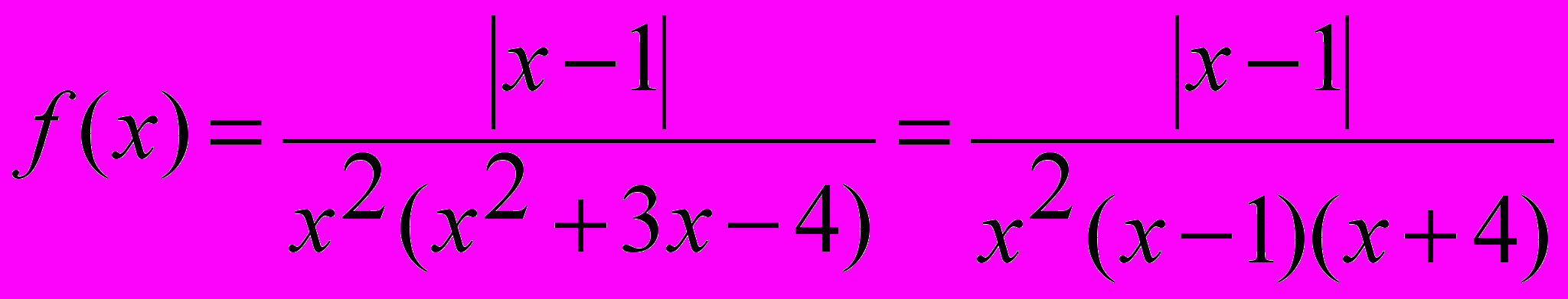 .
.Рассмотрим односторонние пределы функции в особых точках ( в которых числитель и знаменатель обращаются в ноль):
x = 1, x = 0, x = -4.
При x ® 1-0 предел рассматривается слева от точки x = 1, значит x < 1 и |x -1| = - (x -1). Имеем:
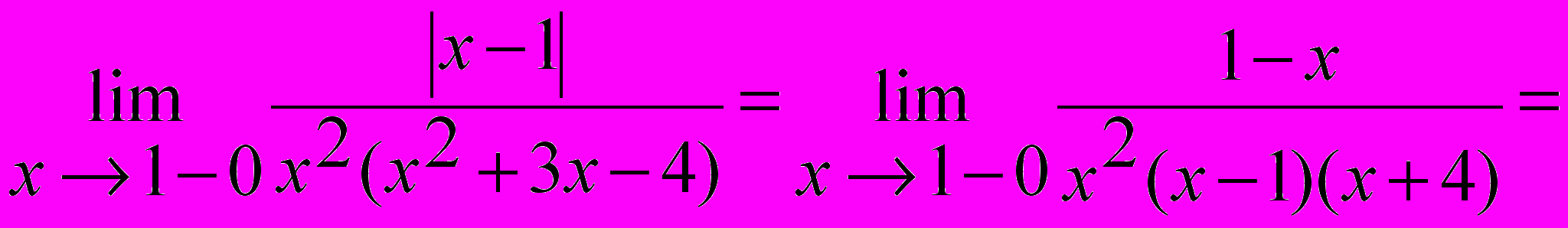
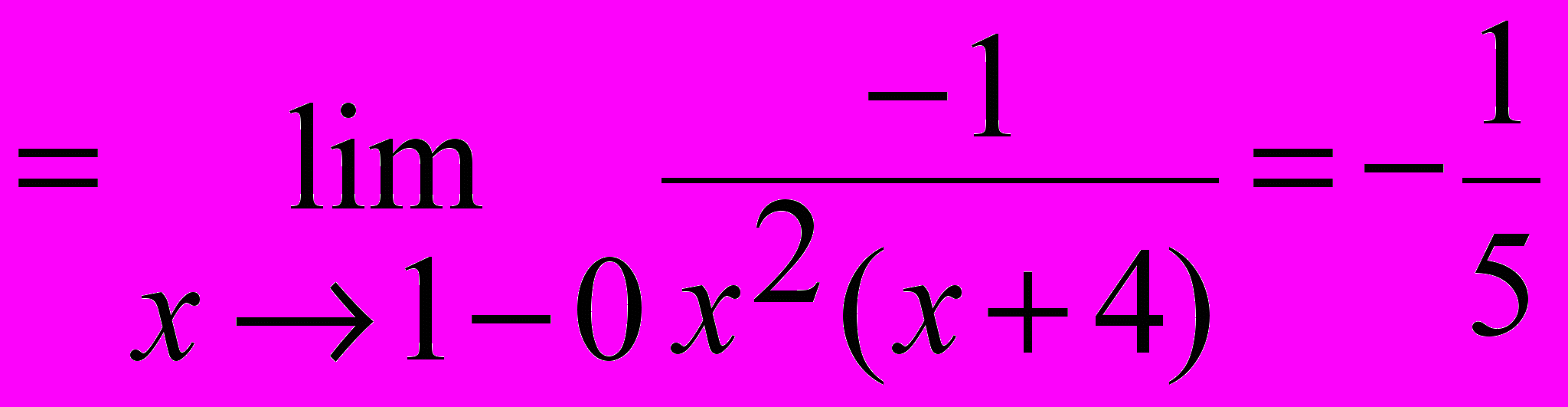 .
.При x ® 1+0 предел рассматривается справа от точки x = 1, значит x > 1 и |x -1| = (x -1). Имеем:
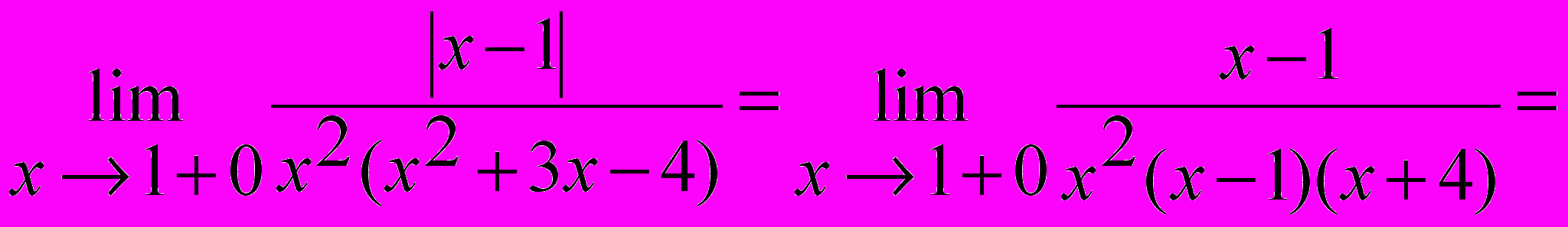
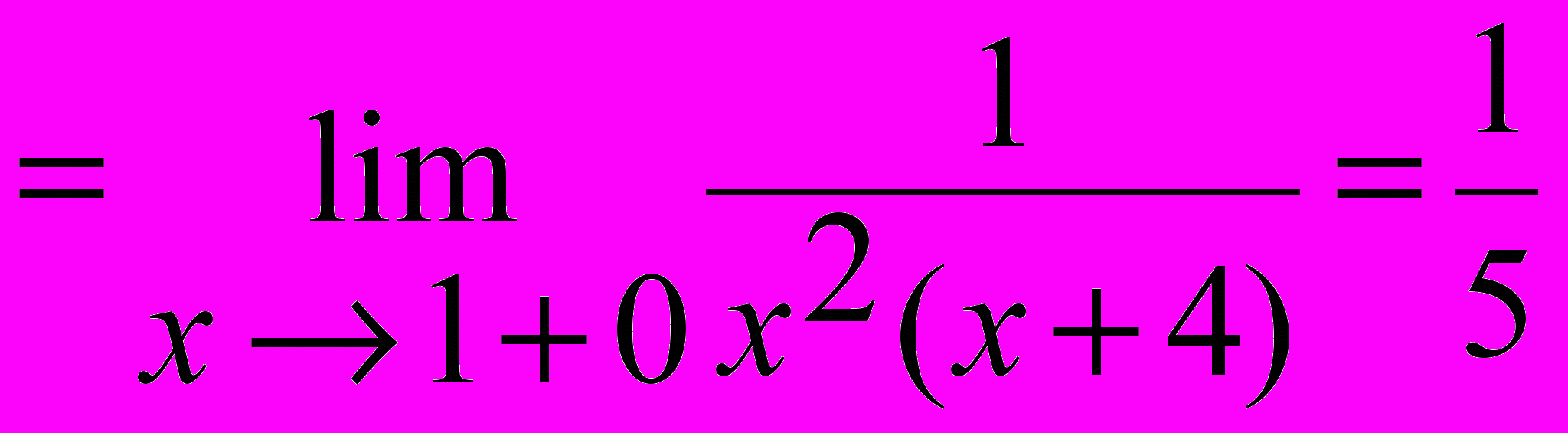 .
.Так как односторонние пределы конечны, но не равны
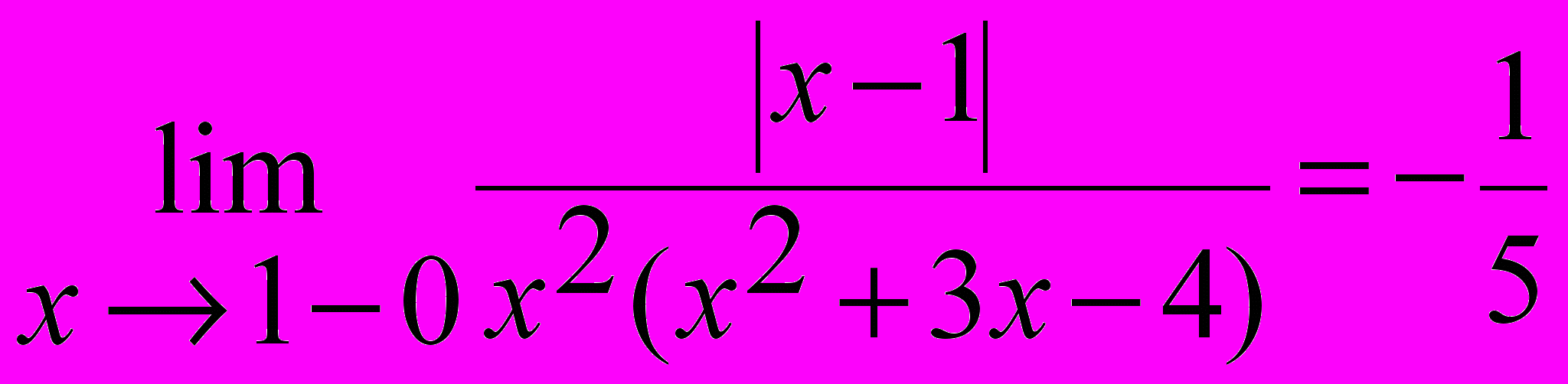 ,
, ,
, то x = 1 является точкой разрыва I рода.
Рассмотрим односторонние пределы при x ® -0 и x ® +0:
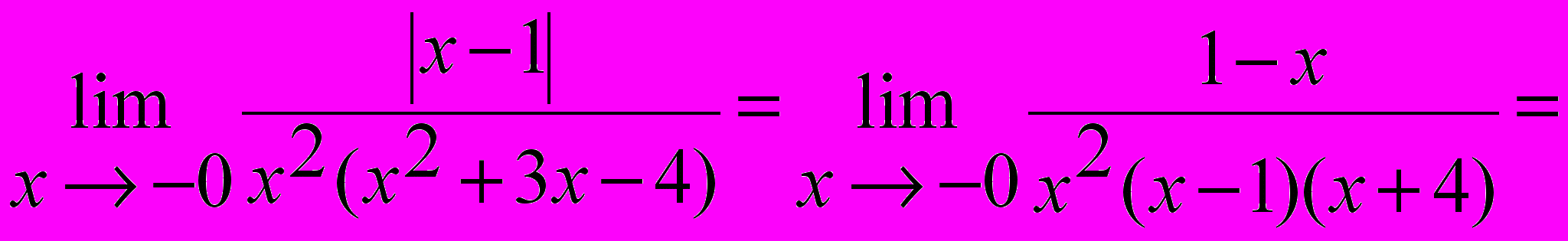
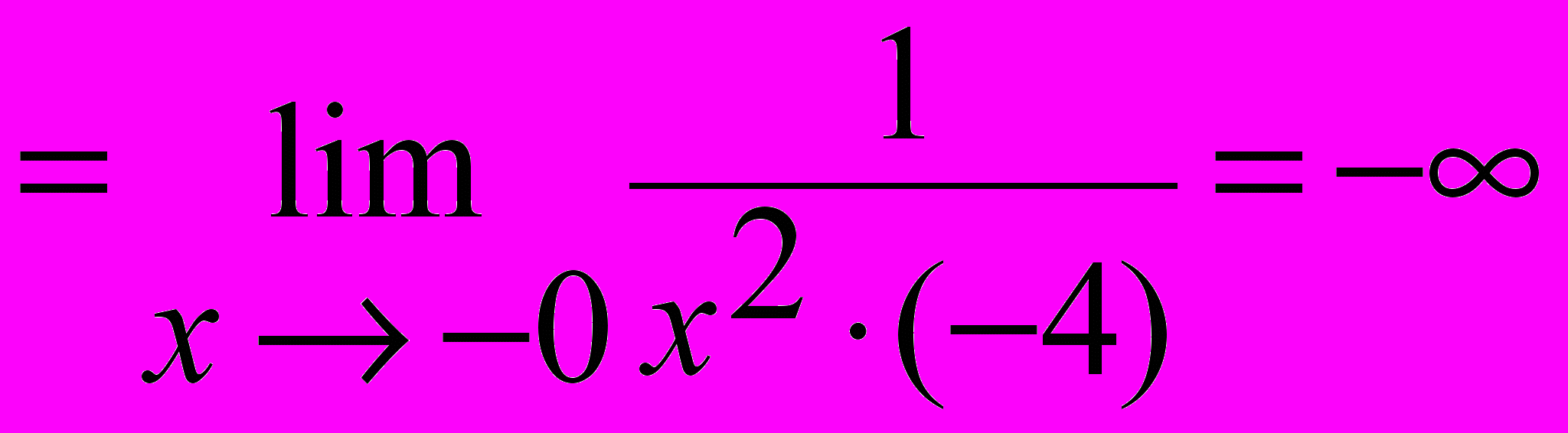 .
.Предел при x ® +0 можно и не рассматривать, поскольку x = 0 уже является точкой разрыва II рода.
Наконец, при x ® -4-0 предел рассматривается слева от точки x = -4 и (x + 4) < 0. Имеем:
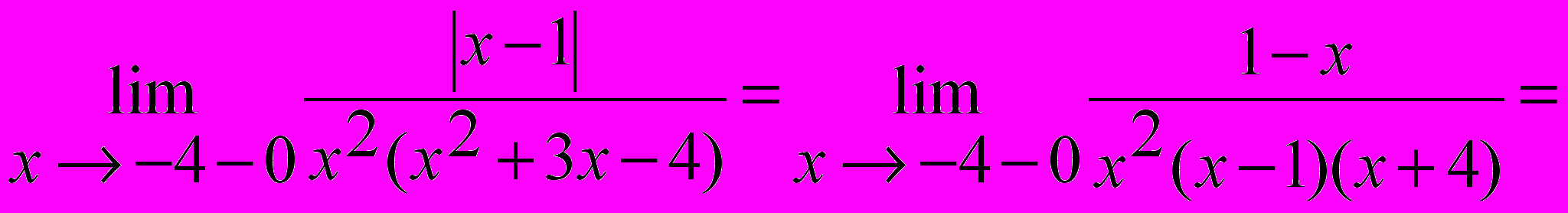
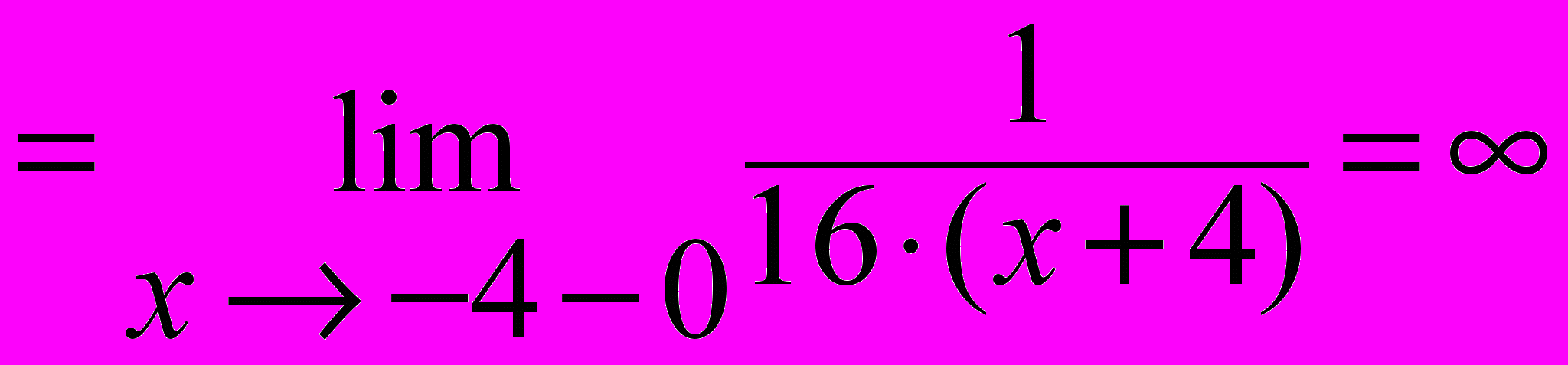 ,
,значит x = -4 является точкой разрыва II рода и второй односторонний предел можно не рассматривать.
Ответ. x = 1 - точка разрыва I рода, x = 0 и x = -4 - точки разрыва II рода.
