Спеціальність "Математика, статистика"
| Вид материала | Документы |
- Программа дисциплины математическая статистика, 31.07kb.
- Вопросы к зачету по курсу «Финансово-банковская статистика», 27.1kb.
- Аннотация примерной программы дисциплины : «Технологии и методы программирования» Цели, 44.55kb.
- Програма нормативного курсу "Математична статистика" 3 курс, "Математика", "Статистика", 29.02kb.
- Прикладная Статистика, 1137.98kb.
- Обери майбутнє у згек здіа! Спеціальність, 32.91kb.
- Міністерство освіти І науки України, 1538.9kb.
- Утверждаю, 335.72kb.
- Программа курса Тема I. Предмет, метод и задачи статистики Тема, 1602.61kb.
- Литература по предмету: Тарловская Статистика, 120.71kb.
П Р О Г Р А М А
нормативного курсу "Функціональний аналіз та інтегральні рівняння"
лекційних годин 105, практичних годин 35
спеціальність "Математика, статистика".
6 семестр
ПРОСТІР БАНАХА
Лінійні нормовані та банахові простори - означення, узгодженість структур лінійного, метричного та нормованого просторів. Приклад неповного нормованого простору. Сепарабельність нормованих просторів. Несепарабельність простору
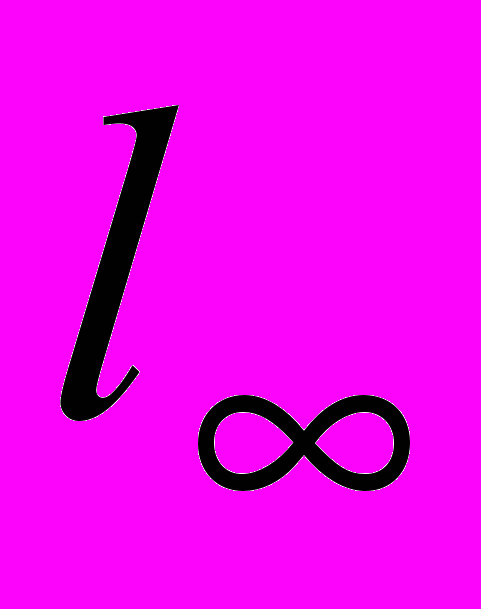. Еквівалентні норми. Еквівалентність норм, заданих на одному скінченновимірному просторі. Підпростори в нормованих просторах. Приклади.ПРОСТІР ГІЛЬБЕРТА
Скалярний добуток - означення в дійсному та комплексному випадках, властивості: антилінійність за ІІ аргументом, рівність паралелограма, нерівність Коші-Шварца. Норма, породжена скалярним добутком; запис скалярного добутку через норму в дійсному та комплексному випадках. Неперервність скалярного добутку. Означення гільбертового простору із скалярним добутком. Простір
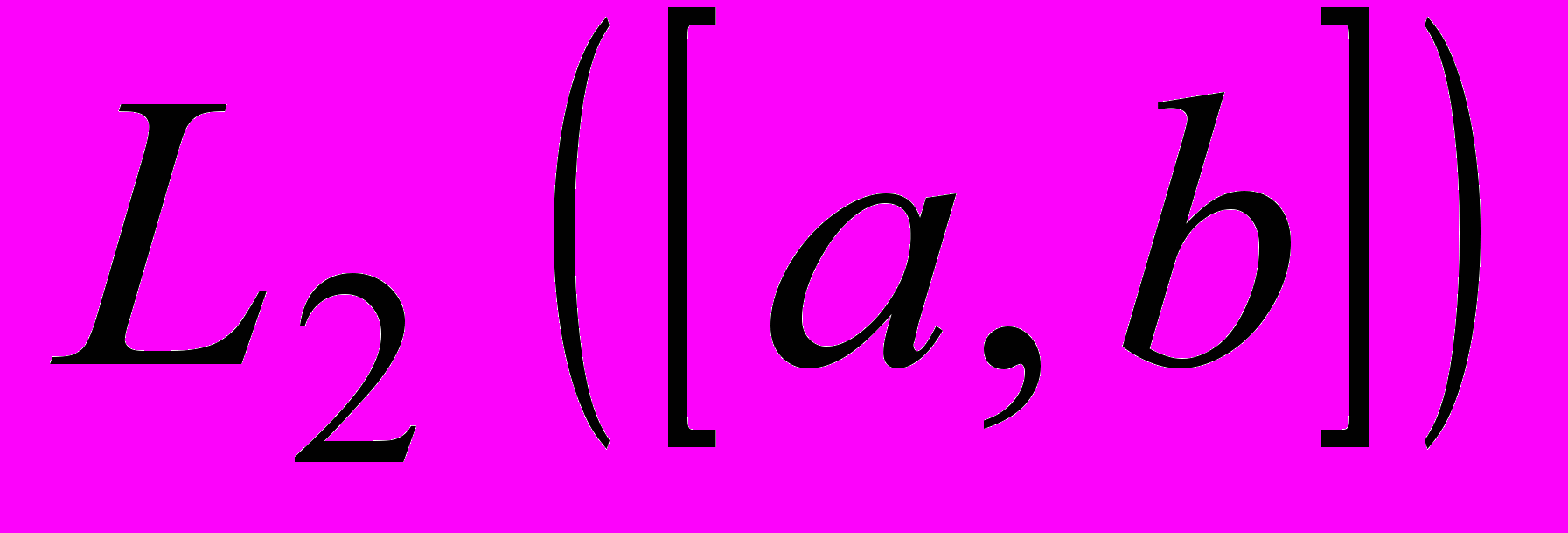як поповнення простору 
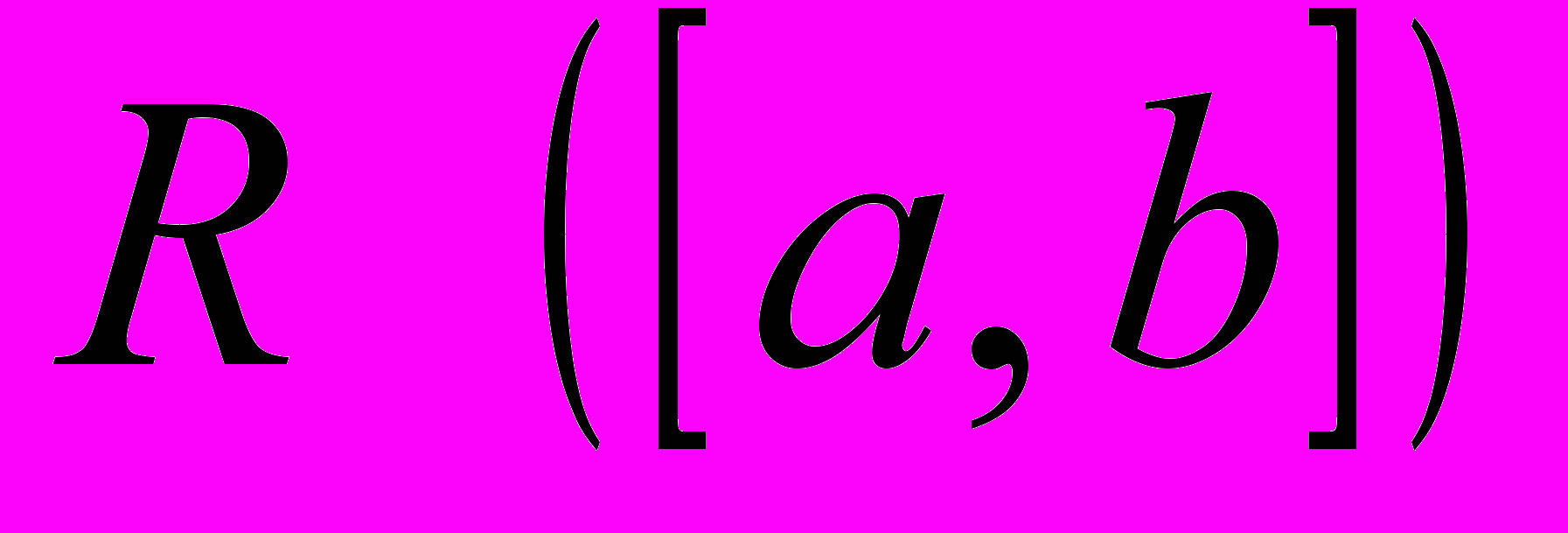. Ортогональність векторів гільбертового простору, ортогональне доповнення до множини. Теорема про існування найближчого елемента в підпросторі. Теорема про ортогональну проекцію. Проектування на площину та одновимірний підпростір. Ортогональна сума просторів. Приклади Ортонормовані системи векторів, приклади. Ряд Фур"є, нерівність Бесселя. Ортонормовані базиси: означення,єдиність розкладу, збіжність ряду Фур"є.
Рівність Парсеваля. Приклади базисів. Процедура ортогоналізації Грамма-Шмідта, існування ортонормованого базиса в сепарабельному гільбертовому просторі. Многочлени Лежандра. Ізометрія сепарабельних гільбертових просторів.
ЛІНІЙНІ ФУНКЦІОНАЛИ
Лінійні, обмежені та неперервні функціонали. Рівносильність обмеженості та неперервності лінійного функціоналу. Норма функціонала, приклади її обчислення.
Спряжений простір та його повнота. Теорема Рісса. Лінійні функціонали в
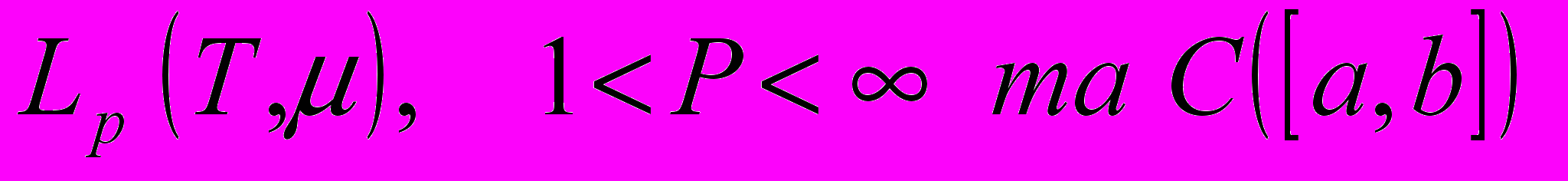. Продовження функціоналу з підпростору гільбертового простору.Півнорма в лінійному просторі. Опуклі та врівноважені множини, приклади. Функціонал Мінковського. Теорема Хана-Банаха про продовження функціонала, підпорядкованого півнормі, в дійсному сепарабельному випадку. Гіперпідпростір, гіперплощина, опорна гіперплощина до одиничної кулі. Теорема про опорну гіперплощину до відкритої опуклої множини. Класична теорема Хана-Банаха та її наслідки. Рефлексивні простори, приклади. Нерефлексивність простору 
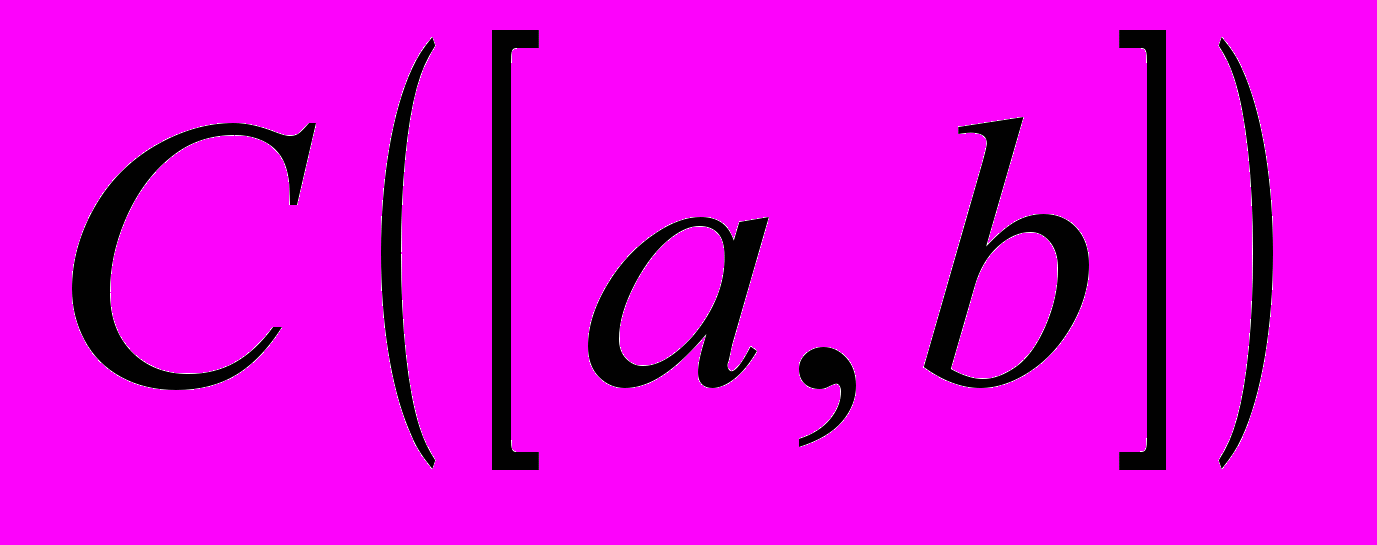.ЛІНІЙНІ ОПЕРАТОРИ
Лінійність. Обмеженість, неперервність операторів у нормованому
просторі. Норма оператора, простір лінійних операторів, його повнота. Приклади. Кільце обмежених лінійних операторів. Матричне представлення оператора в гільбертовому просторі. Пряма сума операторів та її матричне зображення у відповідному базисі. Функціонал як лінійний оператор.
ПРИНЦИП РІВНОМІРНОЇ ОБМЕЖЕНОСТІ. СЛАБКА ЗБІЖНІСТЬ.
Теорема Банаха-Штейгауза. Наслідки. Слабка збіжність
Функціоналів, критерій. Застосування. Слабка повнота спряженого простору та слабка компактність кулі. Слабка збіжність елементів простору, критерій. Приклади. Повнота рефлексивного простору відносно слабкої збіжності.
Операторні збіжності: рівномірна, сильна, слабка. Приклади, порівняння різних типів збіжності. Неперервність добутку відносно рівномірної збіжності. Критерій сильної операторної збіжності, повнота простору лінійних операторів.
ВЛАСТИВОСТІ ЛІНІЙНИХ ОПЕРАТОРІВ
Ядро та образ оператора. Алгебраїчний обернений до оператора, критерій його існування. Приклади. Неперервний обернений оператор, аналіз означення. Критерій неперервної оборотності, приклад. Теорема Банаха про обернений оператор. Оборотність збуреного одиничного оператора. Ряд Неймана.
Спряжений оператор в просторі Гільберта, приклади. Властивості спряжених операторів. Самоспряжені оператори: матричне зображення, критерій самоспряженості в термінах квадратичної форми. Ортопроектор.
Оператор Гільберта-Шмідта, норма Гільберта-Шмідта та її властивості. Ядро Гільберта-Шмідта та інтегральний оператор Гільберта-Шмідта в
. Спряжений інтегральний оператор, умова самоспряженості.Означення компактного оператора. Скінченновимірний оператор та його компактність. Приклади. Властивості компактних операторів. Наближення компактного оператора скінченновимірними операторами в гільбертовому просторі. Компактність оператора Гільберта-Шмідта.
7 семестр
ЕЛЕМЕНТИ СПЕКТРАЛЬНОЇ ТЕОРІЇ
Спектр лінійного неперервного оператора. Приклади. Означення регулярної точки, резольвентної множини, резольвенти, спектра.
Приклади. Власні значення, власні вектори, точковий спектр.Структура спектра: обмеженість, замкненість, ілюстрація на прикладах. Аналітичні операторно-значні функції, аналітичність резольвенти. Теорема про непорожність спектру. Спектральний радіус, приклади. Коректна розв'язність рівняння з оператором, спектральний радіус якого менше одиниці. Спектр самоспряженого оператора: ортогональність його власних підпросторів.
Спектральна теорія компактних операторів у гільбертовому просторі. Розв'язність системи лінійних рівнянь з дійсними коефіціентами, теорема Кронекера -Капеллі, альтернатива Фредгольма в просторі
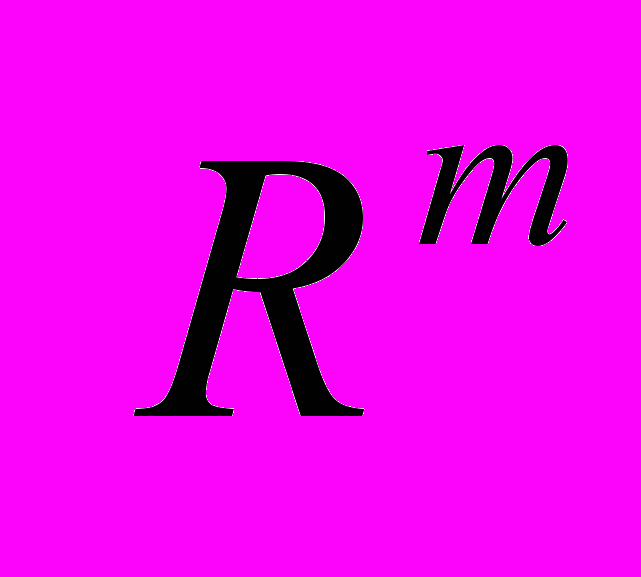.Рівняння з компактним оператором у гільбертовому просторі, приклади.
Аналітична теорема Фредгольма. Три теореми Фредгольма для рівнянь з компактними операторами. Теорема Рісса-Шаудера про спектр компактного оператора. Спектр компактного самоспряженого опратора. Інваріантний підпростір оператора, інваріантність власного підпростору. Інваріантність ортогонального доповнення до інваріантного підпростору самоспряженого оператора. Теорема про власний базис компактного оператора. Ряд Шмідта для компактного самоспряженого оператора, його рівномірна збіжність.
ІНТЕГРАЛЬНІ РІВНЯННЯ
Запис рівняння Фредгольма в просторі
з ядром Гільберта- Шмідта і рівнянь Фредгольма та Вольтерра в просторі 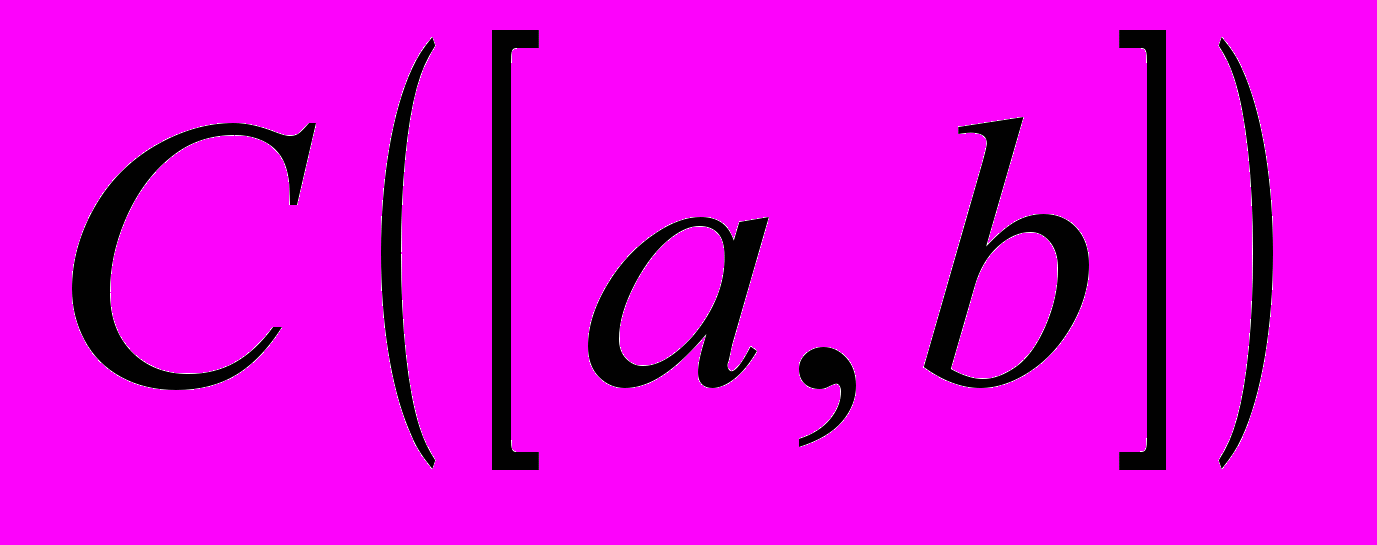з неперервним ядром, приклади. Рівняння Фредгольма ІІ роду з виродженим ядром. Приклад. Ряд Неймана для операторних рівнянь. Рівняння Фредгольма: запис розв'язку через визначник Фредгольма. Повторні ядра, резольвента інтегрального рівняння, збіжність резольвентного ряду для рівнянь в та 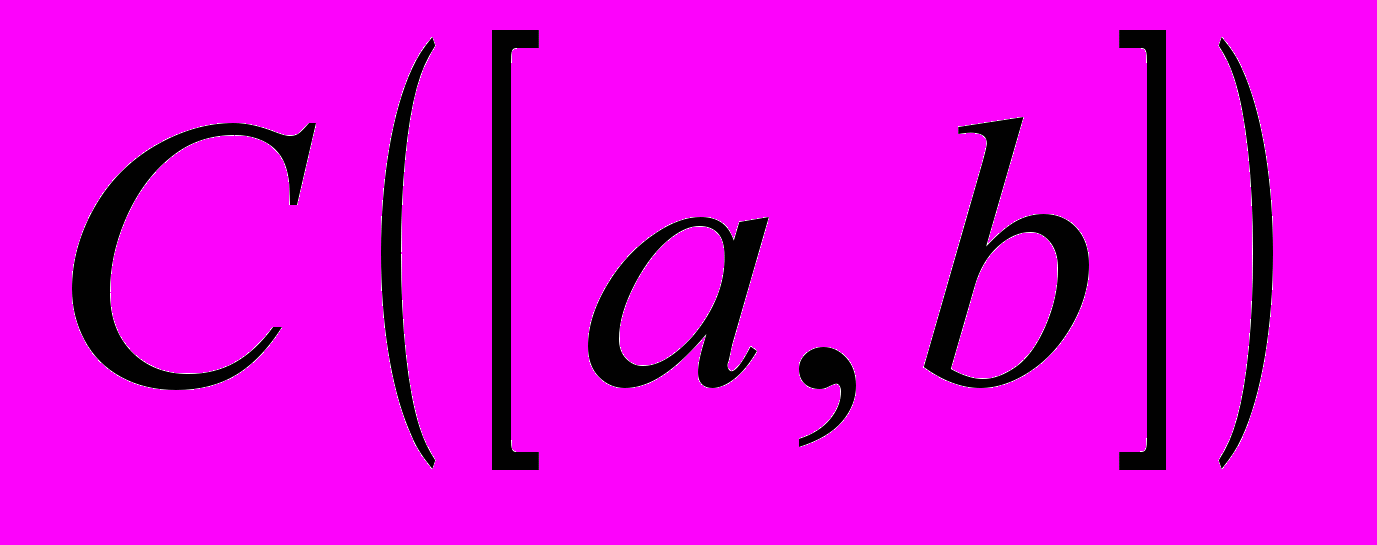. Формула розв'язку через резольвенту інтегрального рівняння. приклад. Рівняння Вольтерра в 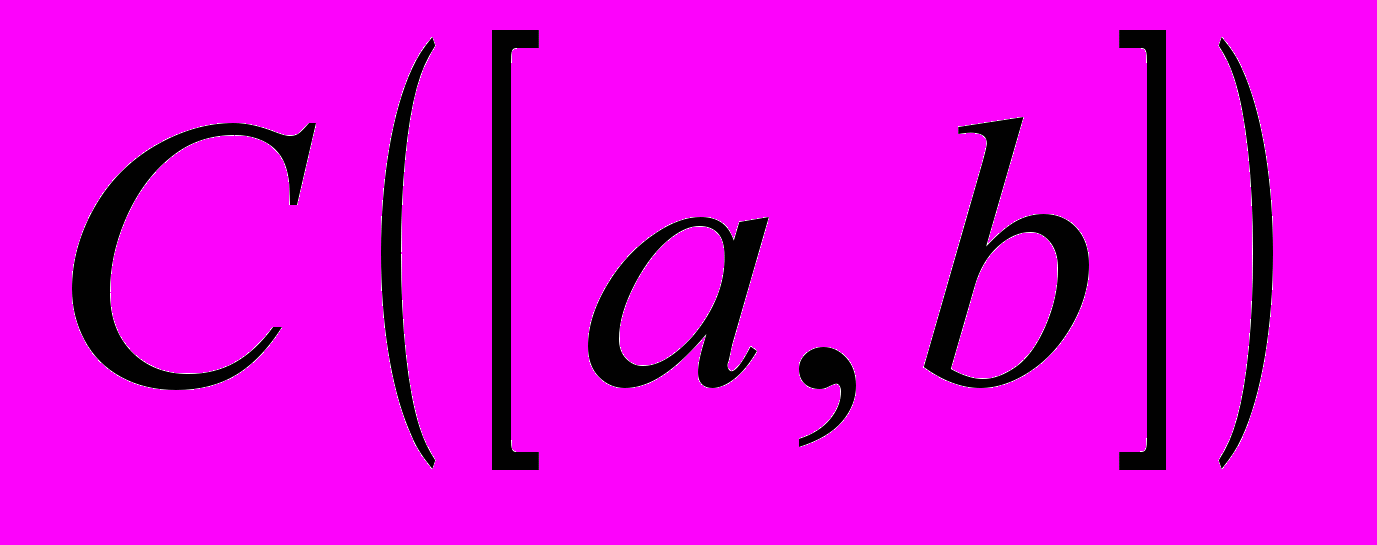: повторні ядра, резольвента інтегрального рівняння, рівномірна збіжність резольвентного ряду, формула розв'язку, приклад.Альтернатива Фредгольма для інтегральних рівнянь з ядром Гільберта-Шмідта. Випадок виродженого рівняння, ІV теорема Фредгольма. Приклад. Альтернатива Фредгольма для рівнянь з неперервним ядром. Інтегральні рівняння з ермітово-симетричним ядром: альтернатива Фредгольма, формула розв'язку, приклад.
Інтегральні рівняння з неперервним та симетричним ядром. Теорема Гільберта-Шмідта. Додатно визначені ядра, теорема Мерсера. Приклад.
ЕЛЕМЕНТИ НЕЛІНІЙНОГО АНАЛІЗУ
Похідна Фреше. Приклади. Похідна складної функції.Похідна Гато, приклади. Аналог теореми Лагранжа в термінах похідної Гато. Екстремум нелінійного функціоналу, необхідна умова екстремуму. Приклад.
УЗАГАЛЬНЕНІ ФУНКЦІЇ
Задача розширення сукупності звичайних функцій. Простір основних функцій
. Носій функції. Приклади основних функцій. Оператор осереднення, властивості. Збіжність у , збіжність осереднень від основної функції. Неперервність лінійних операцій, операцій диференціювання та множення на функцію з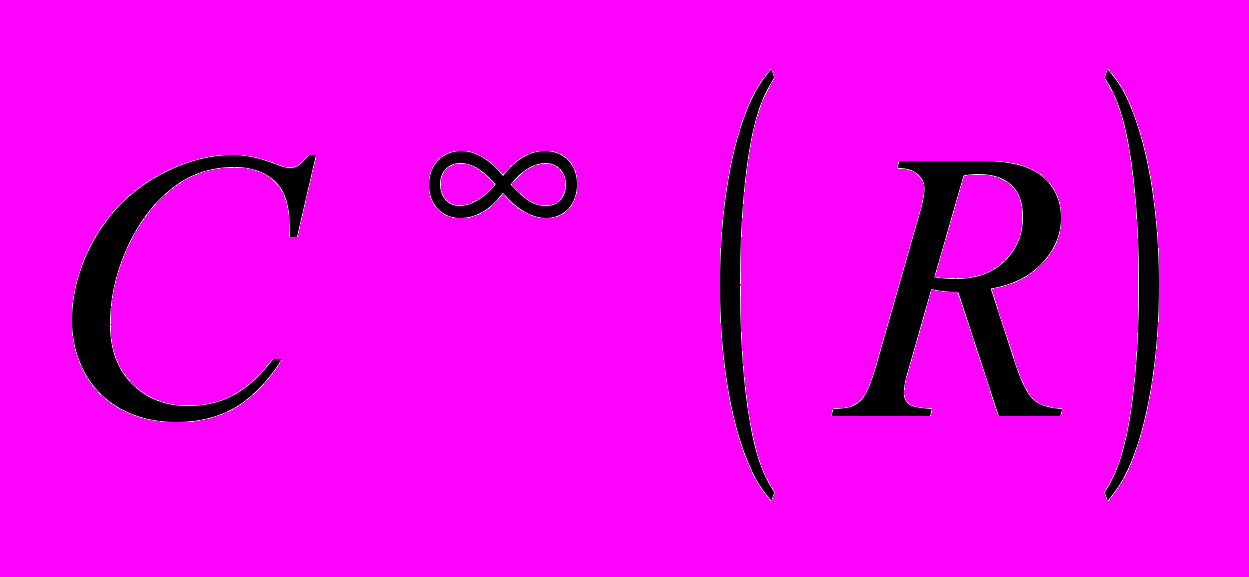 
.Простір узагальнених функцій Шварца
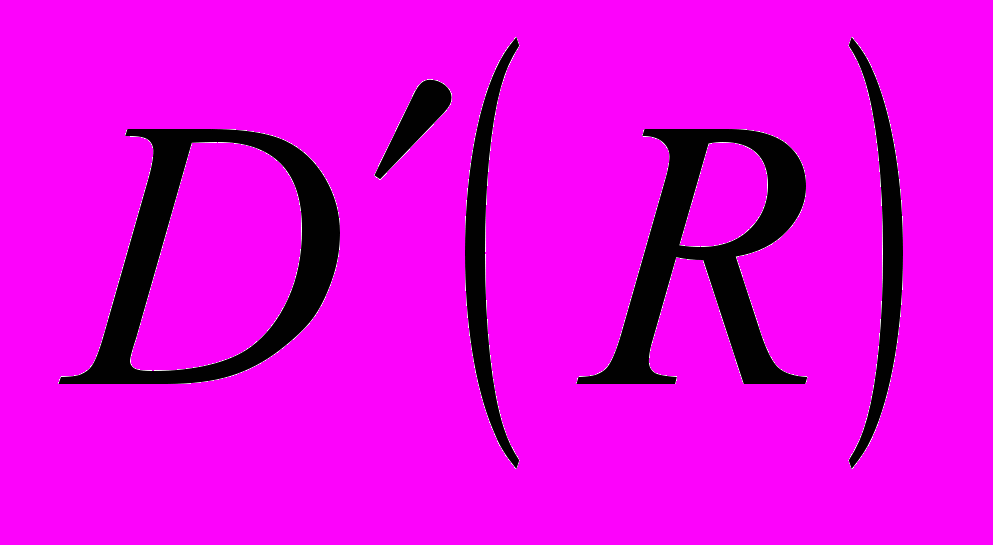. Регулярні узагальнені функції, лема Дюбуа-Реймона. Дельта-функція Дірака. Узагальнені функції, породжені мірами, достатня умова регулярності. Сингулярність 
- функції.Збіжність в
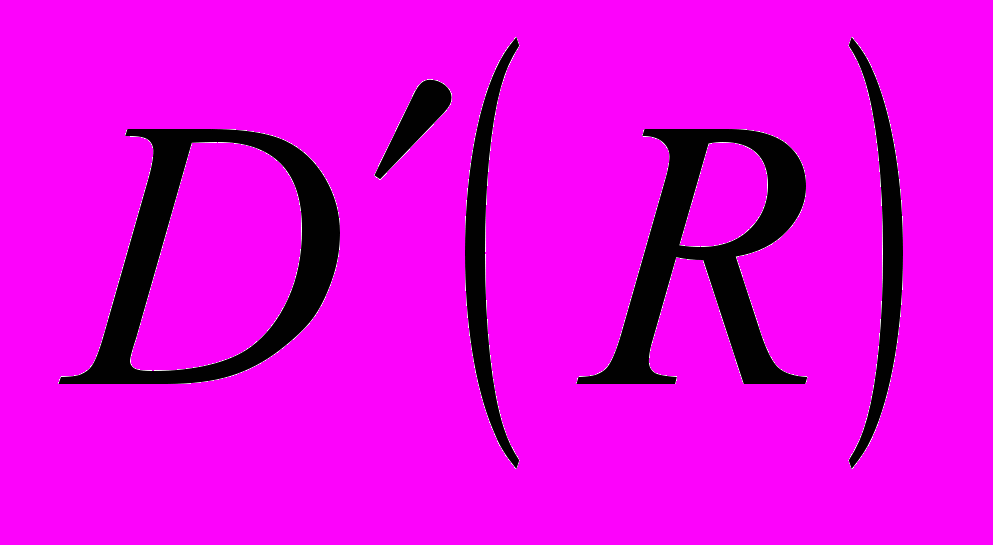. Приклади. Збіжність регулярних узагальнених функцій. Множення узагальненої функції на гладку та заміна змінної під знаком узагальненої функції - означення, приклади, властивості. Диференціювання узагальнених функцій. Старші похідні. Неперервність оператора диференціювання. Диференціювання суми ряду. Збіжність тригонометричних рядів з коефіцієнтами степеневого росту.Фундаментальні розв'язки диференціальних рівнянь. Первісна узагальненої функції. Згортка в
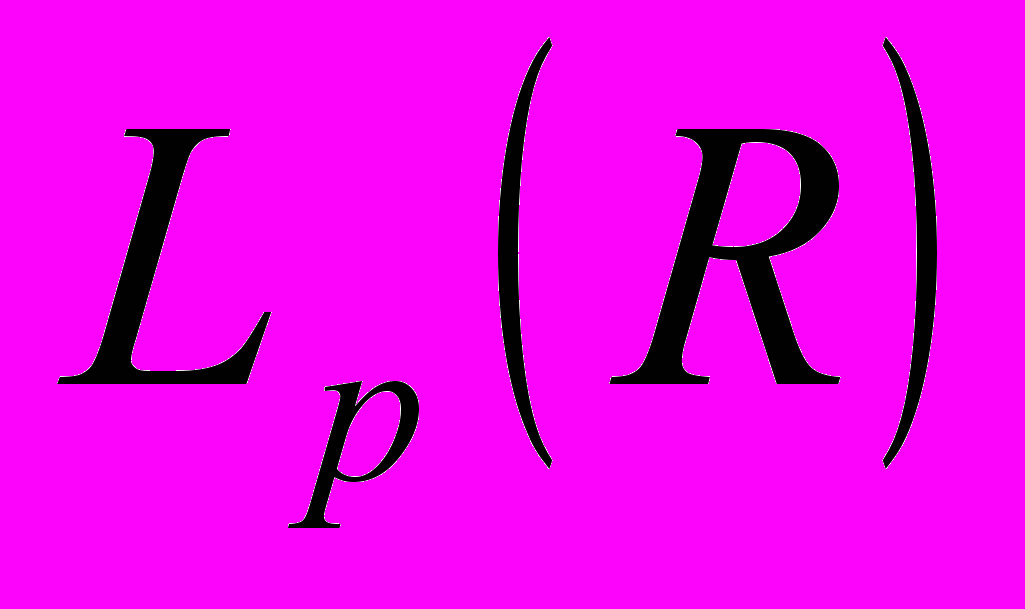, згортка локально інтегровної функції та основної. Згортка узагальненої та основної функції, приклад. Класичні та узагальнені розв'язки лінійних диференціальних рівнянь, приклади. Диференціальний оператор, означення його фундаментального розв'язку, приклад. Знаходження фундаментального розв'язку звичайного диференціального рівняння зі сталим коефіцієнтом, прикдад. Розв'язок неоднорідного диференціального рівняння як згортка.Перетворення Фур'є узагальнених функцій. Простір основних функцій
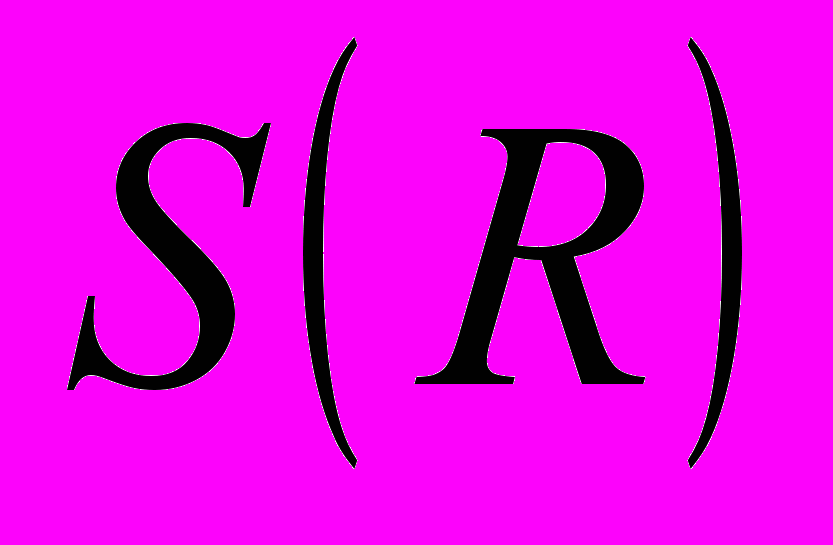, збіжність, приклади. Вкладення 
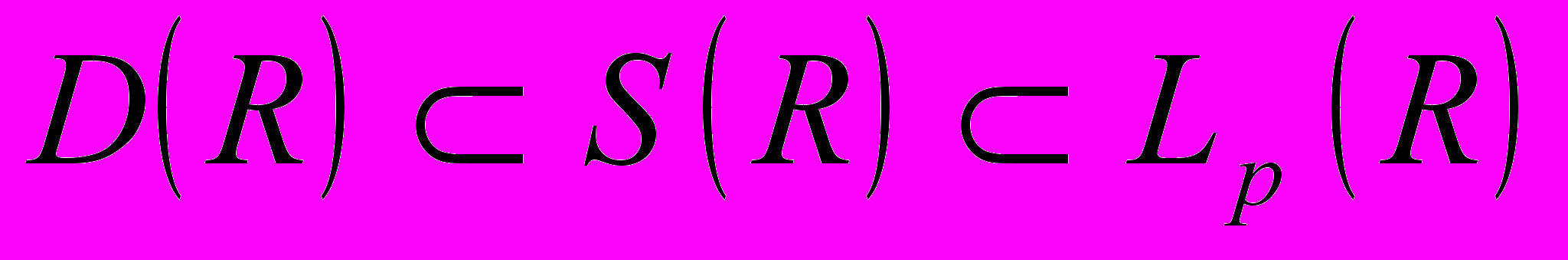. Перетворення Фур'є. Образ згортки при перетворенні Фур'є. Побудова фундаментального розв'язку із сталими коефіцієнтами.ЛІТЕРАТУРА
- Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. - М. : Наука, 1981.
- Люстерник Л.А., Соболев В.И. Краткий курс функционального анализа. - М.:В. ш., 1982.
- Петровский И.Г. Лекции по теории интегральных уравнений.-М.: Изд-во Моск. Ун- та, 1984.
- Шилов Г.Е. Математический анализ. Второй специальный курс. –
- Завдання для практичних і лабораторних занять з курсу”Функціональний аналіз та інтегральні рівняння” для студентів спеціальності “математика”. – Чернівці: ЧДУ. 1992.
- “Збірник задач з функціонального аналізу”, 1, 2 ч., /Упорядники: О.Ю. Константінов, Ю С. Мішура, ас. Нестеренко О.Н., доц.Чайковський А.В. – К: Видавничо-поліграфічний центр “Київський університет”, 2004.-124 с.
ДОДАТКОВА ЛІТЕРАТУРА
- Владимиров В.С. Уравнения математической физики. – М.: Наука,1971.
- 2. Березанский Ю.М., Ус Г.Ф., Шертель З.Г. Функциональный анализ “
- К.: В. ш., 1990.
3. Антоневич А.Б., Радино Я.В. Функциональный анализ и интегральные уравнения. – Минск: Изд-во “Университет”, 1984.
4. Васильева А.Б., Тихонов Н.А. Интегральные уравнения. – М.: Изд-во Моск. Ун-та, 1989.
5. Кирилов А.А., Гвишиани А.Д. Теоремы и задачии функционального анализа. – М.: Наука, 1979.